锥齿轮传动计算范文
锥齿轮理论计算

四驱变速箱锥齿轮计算基本参数:整车满载重量6.5吨,前轮直径0.86米;后轮直径0.745米。
马达排量:56ml/r1.四驱啮合状态下,因为是四轮驱动,整车质量6.5T。
前后桥计算均摊6.5吨/2=3.25吨。
后桥所需驱动力计算如下:T=3250*9.8*(0.745/2)*1*0.94=11152.28 N.m(机械传动效率0.94,摩擦系数选择1最大值)T1(马达分配动力)=11152.28/119.57=93.26 N.mP1=93.26*2π/56=10.45 KW以后桥分配11 KW计算,见以下公式功率(千瓦)P = 11小齿轮转速(转/分)n1 = 309大端端面模数(mm)m = 5.5工作齿宽(mm) b = 26使用系数KA=1.50轴承系数KHβbe=1.10润滑油粘度(mm2/s)ν40= 67设计寿命: 1000 小时类型: 动载直齿锥齿轮和零度锥齿轮类型为非鼓形直齿锥齿轮齿面点蚀: 允许少量点蚀第Ⅱ组公差等级: 8轴交角(°)Σ= 90齿形角(°)α= 20齿宽中点螺旋角(°)βm= 0最小接触强度安全系数SHmin= 1最小弯曲强度安全系数SFmin= 1.25小齿轮大齿轮齿数Z = 18 26高变位系数x1 =0.0000 x2=0.0000切向变位系数xt1 =0.0000 xt2=0.0000齿轮材料: 渗碳淬火的渗碳钢渗碳淬火的渗碳钢齿面粗糙度(μm)Ra = 1.6 1.6接触强度极限(MPa)ζHlim= 1500 1500弯曲强度极限(MPa)ζFlim= 400 400----------------------几何及精度参数-------------------------------小齿轮大齿轮当量圆柱齿轮分度圆直径(mm)dv =102.410 213.670 当量圆柱齿轮顶圆直径(mm)dva =111.765 223.025 当量圆柱齿轮基圆直径(mm)db =96.234 200.784 齿宽中点分度圆直径(mm)dm =84.201 121.623 参考点分度锥距(mm) Rm =73.963大轮齿距极限偏差(μm)fpt =25当量中心距(mm)av =158.040当量端面齿形角(°)αvt=20.000有效工作齿宽(mm)be =22.100当量端面重合度εvα=1.659当量纵向重合度εvβ=0.000当量总重合度εvγ=1.659齿宽中点分度圆上的名义切向力(N) Fmt=8074.343齿数比u=1.444当量圆柱齿轮齿数比uv=2.086当量啮合线长度(mm) gva=22.910无量纲的基准速度N=0.017共振转速(r/min) nE1 =18330.33两齿轮诱导质量(kg/mm) mredx=0.017中点圆周速度(m/s) vmt=1.362跑合量(μm) yα=1.875cv1=0.320cv2=0.340cv3=0.230cv4=0.900cv5=0.470cv6=0.470cv7=0.765名义转矩(Nm) T1=339.932齿宽中点法向模数(mm) mnm=4.678当量圆柱齿轮的齿数zvn=45.677βvb=0.000------------------------接触强度系数-------------------------------动载系数Kv =1.012轮齿中点接触线长度(mm) lbm =25.445齿向载荷分布系数KHβ=1.898齿间载荷分配系数KHα=1.000节点区域系数ZH =2.495弹性系数ZE =189.812螺旋角系数Zβ=1.000锥齿轮系数ZK =0.800润滑剂系数ZL =0.945速度系数ZV =0.958粗糙度系数ZR =0.915尺寸系数ZX =1.000中点区域系数ZM =1.054工作硬化系数ZW =1.000载荷分配系数ZLS =1.000小齿轮大齿轮寿命系数ZNT =1.255 1.282------------------------弯曲强度系数-------------------------------齿向载荷分布系数KFβ=1.898齿间载荷分配系数KFα=1.000重合度系数Yε=0.702螺旋角系数Yβ=1.000锥齿轮系数YK =1.000试验齿轮的应力修正系数YST =2.000载荷分配系数YLS =1.000小齿轮大齿轮尺寸系数YX =1.000 1.000齿形系数YFa =2.824 2.402应力修正系数YSa =1.624 1.782相对齿根圆角敏感系数YδrelT=0.995 1.000相对齿根表面状况系数YRrelT=1.004 1.004弯曲疲劳寿命系数YNT =0.964 0.971--------------------接触疲劳强度计算结果------------------------------接触强度极限(MPa)ζHlim=1500.000 1500.000计算齿轮接触极限应力(MPa)ζHP=1561.008 1594.072计算接触应力(MPa)ζH=1450.173 1450.173接触安全系数Sh =1.076 1.099小轮接触强度足够!大轮接触强度足够!--------------------弯曲疲劳强度计算结果------------------------------弯曲强度极限(MPa)ζFlim=400.000 400.000计算齿轮弯曲极限应力(MPa)ζFP=770.735 780.390计算弯曲应力(MPa)ζF=615.356 574.515弯曲安全系数Sf =1.253 1.358小轮弯曲强度足够!大轮弯曲强度足够!。
直齿锥齿轮传动计算例题图文稿

直齿锥齿轮传动计算例题集团文件发布号:(9816-UATWW-MWUB-WUNN-INNUL-DQQTY-例题10-3 试设计一减速器中的直齿锥齿轮传动。
已知输入功率P=10kw ,小齿轮转速n1=960r/min ,齿数比u=3.2,由电动机驱动,工作寿命15年(设每年工作300天),两班制,带式输送机工作平稳,转向不变。
[解] 1.选定齿轮类型、精度等级、材料及齿数(1)选用标准直齿锥齿轮齿轮传动,压力角取为20°。
(2)齿轮精度和材料与例题10-1同。
(3)选小齿轮齿数z1=24,大齿轮齿数z2=uz1=3.2×24=76.8,取z2=77。
2.按齿面接触疲劳强度设计(1)由式(10-29)试算小齿轮分度圆直径,即d 1d ≥√4d dd d 1d (1−0.5d )2d(d d d d [d d ])231) 确定公式中的各参数值。
① 试选d dd =1.3。
② 计算小齿轮传递的转矩。
d 1=9.55×106×10960d dd =9.948×104d ?dd③ 选取齿宽系数d =0.3。
④ 由图10-20查得区域系数d d =2.5。
⑤ 由表10-5查得材料的弹性影响系数d d =189.8MPa 1/2。
⑥ 计算接触疲劳许用应力[d d ]。
由图10-25d 查得小齿轮和大齿轮的接触疲劳极限分别为d ddddd =600ddd ,d dddd2=550ddd 。
由式(10-15)计算应力循环次数:d 1=60d 1dd d =60×960×1×(2×8×300×15)=4.147×109,N 2=d 1d =4.147×1093.2=1.296×109由图10-23查取接触疲劳寿命系数d HN1=0.90,d dd2=0.95。
取失效概率为1%,安全系数S=1,由式(10-14)得[d d ]1=d dd1d dddd1d =0.90×6001ddd =540ddd[d d ]2=d dd2d dddd2d =0.95×5501ddd =523ddd取[d d ]1和[d d ]2中的较小者作为该齿轮副的接触疲劳许用应力,即[d d ]=[d d ]2=523MPa2)试算小齿轮分度圆直径d 1d ≥√4d dd d 1d (1−0.5d )2d(d d d d [d d ])23=√4×1.3×9.948×1040.3×(1−0.5×0.3)2×(7724)×(2.5×189.8523)23dd =84.970mm(2)调整小齿轮分度圆直径1)计算实际载荷系数前的数据准备。
锥齿轮设 切向变位系数

锥齿轮设切向变位系数全文共四篇示例,供读者参考第一篇示例:锥齿轮是一种常用的传动装置,它通过齿轮的啮合来传递动力和扭矩。
在设计锥齿轮时,切向变位系数是一个重要的参数,它影响着齿轮的运行性能和寿命。
本文将介绍锥齿轮设切向变位系数的相关知识,并分析其在锥齿轮设计中的作用。
一、切向变位系数的定义切向变位系数是指在锥齿轮啮合时,齿轮齿廓的实际长度与理想长度之比。
在理想情况下,齿轮齿廓的长度应该与齿轮齿数和模数成正比,但由于加工和安装的误差,齿轮齿廓的实际长度会有所偏差,这就是切向变位系数的产生。
切向变位系数通常用εt表示,公式如下:εt = Lt / (π * m * z)Lt为实际长度,m为模数,z为齿数。
1.加工精度:锥齿轮的切向变位系数与齿轮的精度密切相关,加工精度越高,切向变位系数越小,齿轮的稳定性和传动效率也会相应提高。
2.安装误差:锥齿轮的安装误差会导致齿轮齿廓的形状和参数发生变化,从而影响切向变位系数的大小。
在安装锥齿轮时,应该注意避免误差的积累。
3.强度要求:锥齿轮的切向变位系数还与其强度要求有关,一般来说,切向变位系数越小,齿轮的承载能力和寿命就越高。
在锥齿轮的设计过程中,优化切向变位系数是提高齿轮性能的关键之一。
以下是一些优化设计的方法:1.合理选择齿轮材料和加工工艺,以保证齿轮齿廓的精度和稳定性。
2.采用精密的检测设备和技术,及时检测并修正齿轮的切向变位系数。
3.避免过大或过小的切向变位系数,以确保锥齿轮在运行过程中的稳定性和高效性。
通过优化切向变位系数的设计,可以提高锥齿轮的工作效率和寿命,降低故障率,为工程应用提供更好的保障和支持。
第二篇示例:锥齿轮是一种重要的传动元件,常用于各种机械设备中。
在设计和制造锥齿轮时,切向变位系数是一个重要的参数,它直接影响着锥齿轮的传动性能和工作稳定性。
本文将从锥齿轮的基本原理开始,逐步介绍切向变位系数的概念、计算方法及其在设计中的重要作用。
一、锥齿轮的基本原理锥齿轮是一种两轴交叉的齿轮,主要用于传递转矩和速度的机械元件。
锥齿轮设计计算

锥齿轮设计计算说明书一:初步设计1,已知条件该齿轮组是用于螺纹安装的,使用转速相当低(手拧一字扳手的速度),主要起变向作用。
初定小齿轮Z1=8(材料40Cr ,精度GB8级)、大齿轮Z2=16(材料45#,精度GB8级),齿数比u=i=Z2÷Z1=16÷8=2。
2,初定力矩设定一字槽扳手手柄处直径为¢20mm 、拧扳手所需要的力为50N 。
根据公式M=FL (图1-1)可得:M=10×10-3×50 N ·m=0.5 N ·m3,载荷系数K=K A ·K V ·K α·K β通过查表得:使用系数:K A =1 、动载系数:K V =1齿间载荷分配系数:K α=1 、齿向载荷分配系数:K β=1则K=1×1×1×1.2=1.24,估算齿轮许用接触应力:''lim 'HH HP s σσ=查图得'lim H σ=900N/mm 2 , 初定安全系数'H S =1.1'HPσ=900÷1.1 N/mm 2 =818.18 N/mm 25,估算 3'1'11951HPe u KT d σ≥ =14.925mm二:几何计算1, 分锥角:211arctan Z Z =δ=26.565°, 12arctan 2Z Z =δ=63.435°2, 大端模数:1'1Z d m e e ==1.8656(查表取m e =1.75)3, 大端分度圆直径:d e1=Z 1m e =8×1.75=14mm , d e2=Z 2m e =16×1.75=28mm4, 外锥距:11sin 2/δe e d R ==14÷2sin26.565°=12.516mm5, 齿宽系数:¢R =0.3 (一般取0.25-0.35)6, 齿宽:b=¢R Re=0.3×12.516=3.7548mm ,圆整后取整数4实际齿宽系数¢R =b/Re=4÷12.516=0.327, 中点模数:m m = m e (1-0.5¢R )=1.75(1-0.5×0.32)=1.47mm8, 中点分度圆直径:d m1=d e1(1-0.5¢R )=14(1-0.5×0.32)=11.76mmd m2=d e2(1-0.5¢R )=28(1-0.5×0.32)=23.52mm9, 顶隙:C=C *m e =0.2×1.75=0.35mm (C *查GB12369-1990齿制C *=0.2)10,切向变位系数:x t1=0 , x t2=0图1-111,高变位系数:x 1=0 ,x 2=012,大端齿顶高:h a1=(1+x 1)m e =1.75mm , h a2=(1+x 1) m e =1.75mm13,大端齿根高:h f1=(1+C *- x 1)m e =2.1mm ,h f2=(1+C *- x 2)m e =2.1mm14,全齿高:h=(2+ C *)m e =3.85mm15,齿根高:==e f f R h 11arctan θ9.5°,21f f θθ==9.5°16,齿顶角:θa1=θf2=9.5°, θa2=θf1=9.5°(采用等顶隙收缩齿) 17,顶锥角:δa1=δ1+θa1=36.065°, δa2=δ2+θa2=72.935°18,根锥角:δf1=δ1-θf1=17.065°, δf2=δ2-θf2=53.935°19,大端齿顶圆直径:d ae1=d e1+2h a1cos δ1=17.1304mm , d ae2=d e2+2h a2cos δ2=29.5645mm 20,冠顶距:1121sin 2δa e k h d A -==13.21775mm ,2212sin 2δa e k h d A -==5.4348mm 21,大端分度圆弧齿厚:s 1= m e (π/2+2x 1tan α+x t1)=2.7475mm , s 2=πm e - s 1=2.7475mm22,大端分度圆弦齿厚:=-=)61(212111e d s s s 2.73mm , =-=)61(222222e d s s s 2.743mm 23,大端分度圆弦齿高:=+=1121114cos e a d s h h δ 1.87mm ,=+=2222224cos e a d s h h δ 1.78mm 24,当量齿数:==111cos δz z v 8.9445(小于直齿圆柱齿轮的根切齿数17,但其工作载荷平稳、转速极小、安装空间小,故不做调整。
圆弧齿锥齿轮传动设计几何计算过程
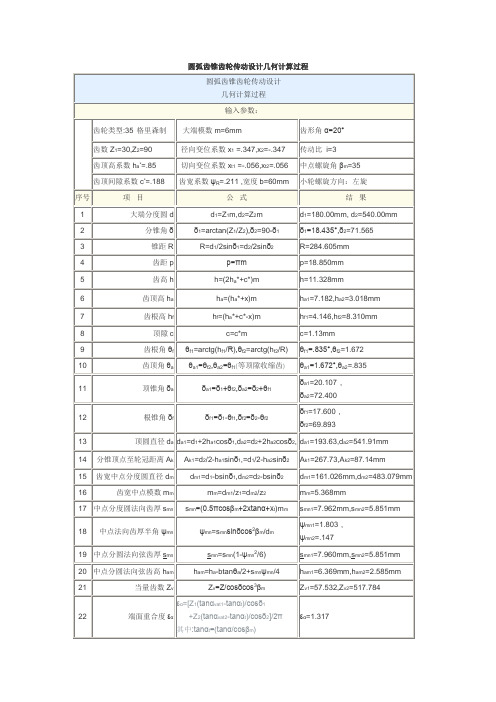
δa2=72.400°
12
根锥角δf
δf1=δ1-θf1,δf2=δ2-θf2
δf1=17.600°,
δf2=69.893°
13
顶圆直径da
da1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,
da1=193.63,da2=541.91mm
14
分锥顶点至轮冠距离Ak
圆弧齿锥齿轮传动设计几何计算过程
圆弧齿锥齿轮传动设计
几何计算过程
输入参数:
齿轮类型:35°格里森制
大端模数m=6mm
齿形角α=20°
齿数Z1=30,Z2=90
径向变位系数x1=.347,x2=-.347
传动比i=3
齿顶高系数ha*=.85
切向变位系数xt1=-.056,xt2=.056
中点螺旋角βm=35°
+Z2(tanαvat2-tanαt)/cosδ2]/2π
其中:tanαt=(tanα/cosβm)
cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]
εα=1.317
23
齿线重合度εβ
εβ=btanβmπ/mm
εβ=2.491
24
总重合度
ε=(εα2+εβ2)1/2
ε=2.818
8
顶隙c
c=c*m
c=1.13mm
9
齿根角θf
θf1=arctg(hf1/R),θf2=arctg(hf2/R)
θf1=.835°,θf2=1.672°
10
齿顶角θa
θa1=θf2,θa2=θf1(等顶隙收缩齿)
θa1=1.672°,θa2=.835°
弧齿锥齿轮计算范文

弧齿锥齿轮计算范文1.基本概念:-弧齿锥齿轮:是一种带有锥面的圆锥形齿轮,在用于传动时,锥齿轮的啮合点在轴心线上。
-基本参数:包括齿数、模数、齿顶高系数、齿根高系数等。
-啮合角:两个齿轮齿廓线的交线与轴线间的夹角。
2.弧齿锥齿轮计算的基本公式:-模数m:弧齿锥齿轮齿数与模数的比值。
-齿距p:两个邻齿间的同心圆周弧长。
-齿厚s:齿顶与齿底之间的距离。
-齿顶高h_a:从齿顶到基圆的距离。
-齿根高h_f:从齿底到基圆的距离。
-齿顶宽b:两齿轮在法向上的接触宽度。
-(注:以上参数表示的是单齿齿轮的大小)3.弧齿锥齿轮计算的步骤:a.齿轮参数的确定:确定需求参数,如传递功率、转速比、传动效率、齿轮种类等。
b.模数的选择:应满足传递功率与转速的要求,并考虑加工性与强度。
c.齿数及啮合角的计算:使用基本公式计算齿数和啮合角。
d.齿顶高和齿根高的计算:使用基本公式计算齿顶高和齿根高,考虑强度。
e.齿轮啮合宽度的计算:使用齿顶高和齿根高计算齿轮啮合宽度,与承载能力有关。
f.齿轮等效齿数的计算:计算齿轮的等效齿数,以确定传动比。
g.法向变位系数及挤压系数的计算:根据实际情况计算法向变位系数及挤压系数,控制齿轮传动质量。
h.齿轮加工校核:计算齿轮加工校核参数。
i.绘制齿轮图样:根据以上计算结果,绘制齿轮尺寸图样。
弧齿锥齿轮计算涉及到多个参数和公式的运用,需要根据实际情况进行具体的计算和校核。
以上给出的步骤和基本公式只是一个简单的概述,实际计算中还需要考虑更多的因素,如弯曲应力、接触应力、表面质量等。
因此,在实际应用中,建议根据实际情况进行具体的计算和校核,确保齿轮传动的正常运行。
圆锥齿轮计算过程及计算说明
(1)传动装置的总功率:
η总=η带×η2轴承×η齿轮×η联轴器×η滚筒
=0.96×0.982×0.97×0.99×0.96
=0.85
(2)电机所需的工作功率:
P工作=FV/1000η总
=1000×2/1000×0.8412
=2.4KW
3、确定电动机转速:
计算滚筒工作转速:
n筒=60×1000V/πD
=π×100×960/60×1000
=5.03m/s
在5~25m/s范围内,带速合适。
(3)确定带长和中心矩
根据课本P84式(5-14)得
0. 7(dd1+dd2)≤a0≤2(dd1+dd2)
0. 7(100+200)≤a0≤2×(100+200)
所以有:210mm≤a0≤600mm
由课本P84式(5-15)得:
符合这一范围的同步转速有750、1000、和1500r/min。
根据容量和转速,由有关手册查出有三种适用的电动机型号:因此有三种传支比方案:如指导书P15页第一表。综合考虑电动机和传动装置尺寸、重量、价格和带传动、减速器的传动比,可见第2方案比较适合,则选n=1000r/min。
4、确定电动机型号
根据以上选用的电动机类型,所需的额定功率及同步转速,选定电动机型号为Y132S-6。
四、运动参数及动力参数计算
1、计算各轴转速(r/min)
nI=n电机=960r/min
nII=nI/i带=960/2.095=458.2(r/min)
nIII=nII/i齿轮=458.2/6=76.4(r/min)
2、计算各轴的功率(KW)
PI=P工作=2.4KW
锥齿轮计算模版.pdf
锥齿轮传动设计1.设计参数1150150********=====d d z z u 式中:u ——锥齿轮齿数比;1z ——锥齿轮齿数;2z ——锥齿轮齿数;1d ——锥齿轮分度圆直径(mm ); 2d ——锥齿轮分度圆直径(mm )。
1.10621115021)2()2(2212221=+=+=+=u d d d R mm 25.125)33.05.01(150)5.01(11=⨯−⨯=−=R m d d φ mm同理 2m d =125.25 mm式中:1m d 、2m d ——锥齿轮平均分度圆直径(mm );R φ——锥齿轮传动齿宽比,最常用值为R φ=1/3,取R φ=0.33。
530150111===z d m 同理 2m =5式中:1m 、2m ——锥齿轮大端模数。
175.4)33.05.01(5)5.01(11=⨯−⨯=−=R m m m φ同理 2m m =4.175式中:m m 1、m m 2——锥齿轮平均模数。
2.锥齿轮受力分析因为锥齿轮1与锥齿轮2的传动比为1,且各项数据相同,则现以锥齿轮1为分析对象得:125015083.932211=⨯==m t d T F N 88.88345cos 45tan 1250cos tan 111=︒⨯︒⨯==δαt r F F N 88.88345cos 45tan 1250sin tan 111=︒⨯︒⨯==δαt a F F N 22.133020cos 1250cos 11=︒==αt n F F N 式中;1t F ——锥齿轮圆周力;1r F ——锥齿轮径向力;1a F ——锥齿轮轴向力;1n F ——锥齿轮法向载荷;α——锥齿轮啮合角;δ——锥齿轮分度角。
3.齿根弯曲疲劳强度计算(1) 确定公式内的各计算数值1) 由《机械设计》图10-20c 查得锥齿轮的弯曲疲劳强度极限=1FE σ580MPa2) 由《机械设计》图10-18取弯曲疲劳寿命系数=1FN K 13) 计算弯曲疲劳许用应力取弯曲疲劳安全系数S =1.4,由《机械设计》式(10-12)得=⨯==4.15801][111S K FE FN F σσ414.29 MPa 4) 计算载荷系数K23.235.111.15.1=⨯⨯⨯==βαF F v A K K K K K5) 查取齿形系数由《机械设计》表10-5查得8.21=Fa Y6) 查取应力校正系数由《机械设计》表10-5查得55.11=Sa Y7) 计算大、小齿轮的[]F Sa Fa Y Y σ并加以比较[]01048.029.41455.18.2111=⨯=F Sa Fa Y Y σ 由《机械设计》式(10-24)得弯曲强度的设计公式为 []27.029.4141130)33.05.01(33.055.18.283.9323.241)5.01(43222111221231=⨯+⨯⨯⨯−⨯⨯⨯⨯⨯=⨯+−≥F Sa Fa R R Y Y u z KT m σφφ 由m=5>0.27,则弯曲疲劳强度符合要求。
螺旋锥齿轮传动强度的计算
忽 略 有‘
一 .
,
.、
『 ‘[ ] / ( 一 ‘_ )
] ]
将公式( ) 8代如公式 ( )考虑公式( ) 4 , : 7, 3 和( )得
K 一 M2 () 9
; (/+ ̄ cs "2x) o r _ r
在公式() 9 中引入与大齿轮圆周速度有关 的动载荷系数 K 计算锥齿轮传动的基本尺寸由三个阶段组成 ,第一 阶段预 对 K 不研究 , 在近似计算时采用 K = ., 1 相对 m 展 开公式 ( ) 2 9 先计算应用于精加工齿时的刀具和传动参数。 应用的附加原始数 得到保证强度和弯曲疲劳强度的最小模数 m 。即: 据有 : 峰值载荷 ( 例如齿轮轴上峰值力矩 )杨 氏模量 、 、 泊松系
【 摘 要】 为了使 高强度齿轮 的齿面在传动过程 中具有更高的可靠性 , 论述 了孤齿锥齿轮传动预 强度的计算方法, 这种方法是基于两个椭圆双曲体接触 问题赫兹解提 出的, 并且在设计中充分考虑了齿 轮接触面"量曲率大小和齿面廓形局部接触及纵向局部接触等多个系数。通过计算表明, 3 - 无论是在较
=丁X 2
F
() 6
式 中:,一接触椭 圆半轴 ( n6 点接触 ,由于齿变形转变为椭 圆面 积 )。b的大小与接触面当量曲率 。 占 ,, 和 有关。
计算 约束处应力弯矩后 , 它等于外 力弯矩 , 使 考虑公式 ( ) 5
和() : 6有
M3 b t d = r x x 62 ・ s= 2 , 2 () 7
第 3期 21 0 2年 3月
文章 编 号 :0 13 9 (0 2 0 — 0 7 0 10 — 9 7 2 1 )3 0 5 — 3
机 械 设 计 与 制 造
锥齿轮传动设计计算
锥齿轮传动设计计算
一、传动参数的确定
在进行锥齿轮传动设计计算之前,需要确定一些传动参数,包括传动比、输入轴转速和输出轴转速等。
传动比是锥齿轮传动中一个重要的参数,一般由减速比或增速比来确定。
输入轴转速是指输入轴每单位时间旋转的
圈数,输出轴转速则是指输出轴每单位时间旋转的圈数。
二、几何尺寸的计算
锥齿轮传动的几何尺寸包括啮合点齿高、啮合点模数、齿轮齿数等,
这些参数对于锥齿轮传动的工作性能和传动效率有重要影响。
在进行几何
尺寸计算时,需要考虑齿轮的传动比、模数和齿数等因素,并确保齿轮的
啮合平稳和传动效率高。
三、强度计算
锥齿轮传动的传动强度是传动设计中一个重要的指标,其计算包括齿
轮弯曲强度和齿轮接触强度两个方面。
齿轮弯曲强度计算是通过计算齿轮
受力情况,进而确定齿轮的弯曲强度是否满足要求。
齿轮接触强度则是通
过计算尖接触法计算齿轮的接触应力,进而确定齿轮的接触强度是否满足
要求。
四、疲劳寿命计算
锥齿轮传动在长时间使用过程中,需要考虑其疲劳寿命。
疲劳寿命是
指锥齿轮传动在特定工况下能够承受的循环载荷次数,这对于锥齿轮传动
的可靠性和使用寿命有重要影响。
疲劳寿命计算需要考虑齿轮的载荷、工
作表面、材料强度以及齿轮的表面处理等因素。
五、稳定性分析
综上所述,锥齿轮传动设计计算需要考虑多个方面的因素,包括传动
参数的确定、几何尺寸的计算、强度计算、疲劳寿命计算和稳定性分析等。
只有在全面考虑传动要求的前提下,才能设计出安全可靠、经济高效的锥
齿轮传动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锥齿轮传动计算范文
1.载荷计算:首先需要确定传动的最大扭矩和转速,以及工作条件下
的载荷分布情况。
根据载荷特点,可以选择适当的齿轮材料和齿轮精度等级。
2.锥齿轮几何参数计算:锥齿轮传动有多个几何参数需要计算,包括
齿数、模数、法向齿厚、分度圆直径等。
其中,模数是一个非常关键的参数,决定了齿轮的尺寸和啮合性能。
3.锥齿轮啮合计算:在进行锥齿轮的啮合计算时,需要考虑到齿轮的
啮合特性,包括接触比、滚动比、啮合角等。
这些参数可以通过锥齿轮几
何验证和计算得到,用来评估啮合性能和寿命。
4.齿轮轴计算:锥齿轮传动中,轴的设计也非常重要。
需要计算轴的
强度和刚度,以确保传动的稳定性和可靠性。
轴的计算涉及到负载分析、
材料力学性能、几何形状等因素。
5.侧隙和预紧力计算:锥齿轮传动中,侧隙和预紧力的设置对于传动
性能和运动精度有重要影响。
侧隙是齿轮之间的间隙,通常根据实际应用
要求进行估算。
预紧力是为了减小侧隙而施加在锥齿轮上的力,需要根据
实际情况进行合理设置。
1.根据传动要求和齿轮几何特征,计算锥齿轮的模数、齿数、分度圆
直径等参数。
2.根据载荷要求、齿轮几何特征等,计算轴的强度和刚度,以确保传
动的稳定性和可靠性。
3.确定侧隙和预紧力的设置,根据实际应用要求进行估算和合理设置。
4.进行齿轮啮合计算,评估啮合性能和寿命。
总之,锥齿轮传动计算是一项复杂的工作,需要综合考虑多个因素。
在实际应用中,还需要结合实际情况,进行适当的调整和修正。
通过合理的计算和设计,可以确保锥齿轮传动的稳定性、可靠性和高性能。
