控制工程基础论文(神经网络)有图完整版
现代控制工程第13章神经网络控制
13.3.2 BP学习算法
▪ 两个问题：
（1）是否存在一个BP神经网络能够逼近给定的样本或者函数。
（ 2）如何调整BP神经网络的连接权，使网络的输入与输出与 给定的样本相同。
1986年，鲁梅尔哈特（D. Rumelhart）等提出BP学习算法。
13.3.2 BP学习算法
1. 基本思想
目标函数：
x1
y1m
x2
y2m
x p1
y
m pm
13.3.2 BP学习算法
2. 学习算法
d y wikj1
k i
k 1 j
d y y u m ( i
m
i
)
si
fm
(
m)
i
——输出层连接权调整公式
d u d k i
fk (
k)
i
w k 1 k
l
li
l
——隐层连接权调整公式
13.3.2 BP学习算法
2. 学习算法
13.2 神经元与神经网络
13.2.1 生物神经元的结构
人脑由一千多亿（1011亿－ 1014 亿）个神经细胞（神经元）交织 在一起的网状结构组成，其中大 脑皮层约140亿个神经元，小脑皮 层约1000亿个神经元。
神经元约有1000种类型，每个神经元大约与103－ 104个其他 神经元相连接，形成极为错综复杂而又灵活多变的神经网络。 人的智能行为就是由如此高度复杂的组织产生的。浩瀚的宇 宙中，也许只有包含数千忆颗星球的银河系的复杂性能够与大 脑相比。
13.2.1 生物神经元的结构
神经网络（neural networks，NN）
▪ 生物神经网络( natural neural network, NNN): 由中枢神经系 统（脑和脊髓）及周围神经系统（感觉神经、运动神经等）所 构成的错综复杂的神经网络，其中最重要的是脑神经系统。 ▪人工神经网络(artificial neural networks, ANN): 模拟人脑神经 系统的结构和功能，运用大量简单处理单元经广泛连接而组成 的人工网络系统。
神经网络论文1
基于倒立摆的PID神经元网络的控制系统的研究摘要摆系统是一个典型的强耦合、非线性、高阶次的不稳定系统。
由于摆系统的数学模型是在忽略了次要因素的基础上得出来的，而实际上是一个非线性的系统，当系统受到外部的干扰时，这些次要因素的影响比较突出。
实验采用PID神经元，设计一个神经网络间接自适应控制系统，首先用一个神经网络对摆系统模型进行辨识，辨识完成后，辨识模型的权值与隐层积分元的数值传递给具有同样结构的PID神经元的神经网络控制器，对倒立摆进行自适应控制。
最后根据以上算法，采用6．0编写控制程序，实现对平面一级摆系统的实时控制。
关键词：倒立摆，PID神经元，性能指标，神经网络控制1.倒立摆的数学模型平面一级倒立摆主要由小车和摆杆组成，如图1所示。
在该系统中，假设石()x t为小车至参考点的距离，为摆杆偏离垂直方向的角度，M(1.096kg)为小车的质量，m(0.109kg)为摆杆的质量，l (0.25m)为摆杆转动轴心到杆质心的长度。
J(0.0034kgm2)为摆杆的转动惯量，B (0.02N/m/sec)为摆杆连接处O的阻尼系数，1B(0.1N/m/sec)为小车与导轨丝杆之问的摩擦系数，u为小车的控制输入信号。
2图1 倒立摆在X轴方向的受力情况首先分析小车、摆杆的x轴方向受力情况。
摆杆的转动方向212sin cos d d J B Vl Hl dt dtθθθθ+=- (1) 摆杆的垂直方向22(cos )d l m V mg dtθ=- (2) 摆杆的水平方向，22(cos )d x l m H dt θ+= (3)小车的水平方向222d x dx M B u H dt dt+=- (4) 式中：J —摆杆的转动惯量，2/3J ml =；H 、V —摆杆和小车铰链处的水平与垂直方向的反作用力；12B B 、—小车与导轨之间、摆杆与小车之间的摩擦系数。
消除式(1)、(2)、(3)与(4)中的V 与H ，当θ趋于0时，可以进行线性化处理，即令sin θθ≈，cos 1θ≈，0θ∙≈，整理后得到系统的状态空间方程为[4]2222221222221222010()0()()()()0001()()0()()()x x J ml B mlB m l g J ml x x M J ml mJM J ml mJM J ml mJ M J ml B mlB M m mg M m M J ml mJM J ml mJM J ml mJ θθθθ∙∙∙∙∙∙∙∙⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥-++⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++++++++⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-++⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦++++++⎣⎦20()mJ u ml M J ml mJ ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦将参数代人方程之中，可得0100000.08830.62930.04710.88320001000.235727.8285 2.0841 2.3566x x x x θθθθ∙∙∙∙∙∙∙∙⎡⎤⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦⎢⎥⎣⎦(6)简化为：X AX Bu ∙=+(7)同样可得到摆系统在轴方向的数学模型。
(完整版)机器人神经网络控制汇总,推荐文档
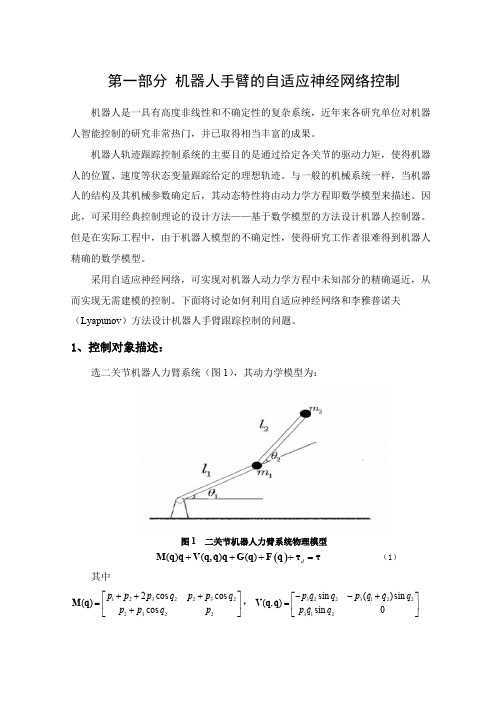
第一部分 机器人手臂的自适应神经网络控制
机器人是一具有高度非线性和不确定性的复杂系统，近年来各研究单位对机器人智能控制的研究非常热门，并已取得相当丰富的成果。
机器人轨迹跟踪控制系统的主要目的是通过给定各关节的驱动力矩，使得机器人的位置、速度等状态变量跟踪给定的理想轨迹。
与一般的机械系统一样，当机器人的结构及其机械参数确定后，其动态特性将由动力学方程即数学模型来描述。
因此，可采用经典控制理论的设计方法——基于数学模型的方法设计机器人控制器。
但是在实际工程中，由于机器人模型的不确定性，使得研究工作者很难得到机器人精确的数学模型。
采用自适应神经网络，可实现对机器人动力学方程中未知部分的精确逼近，从而实现无需建模的控制。
下面将讨论如何利用自适应神经网络和李雅普诺夫（Lyapunov ）方法设计机器人手臂跟踪控制的问题。
1、控制对象描述：
选二关节机器人力臂系统（图1）
，其动力学模型为：
图1 二关节机器人力臂系统物理模型
（1）
()()()()d ++++=M q q
V q,q q G q F q ττ 其中
，1232
232232
22cos cos ()cos p p p q p p q p p q p +++⎡⎤=⎢
⎥+⎣⎦M q 3223122312
sin ()sin (,)sin 0p q
q p q
q q p q q --+⎡⎤=⎢⎥⎣⎦
V q q
i与神经元j之间的连接强度(模拟生物神经元之间突触连接i的活跃值，即神经元状态；。
神经网络控制
从而使神经网络控制器逐渐在控制作用中占据主
导地位，最终取消反馈控制器的作用；
✓
一旦系统出现干扰，反馈控制器重新起作用。
✓
可确保控制系统的稳定性和鲁棒性，有效提高系
统的精度和自适应能力。
神经网络
控制器
期望输出
()
−1
()
+
-
()
传统控
网络实现；可进行离线辨识，也可进行在线辨识。
+
-
逆向建模
一般而言，建立逆模型对神经网络控制意义重大。
直接逆建模简化结构图：
可用于离线辨识，也可
用于在线辨识。
对 象
+
神经网络
逆模型
缺点：不是目标导向的，系统输入也不可能预先定义。
实际常采用正-逆建模结构。
正-逆建模
神经网络
逆模型
对 象
第3章 神经网络控制
第2部分 控制基础
3.5 神经网络控制基础
3.5.1 神经网络控制的优越性
神经网络可以处理那些难以用模型或规则描述的过
程或系统。
神经网络采用并行分布式信息处理，具有很强的容
错性。
神经网络是本质非线性系统，可实现任意非线性映
射。
神经网络具有很强的信息综合能力，能同时处理大
期望输出
()
稳定的参
考模型
参考模
型输入
()
+
()
()
+
-
神经网络
控制器
()
对象
()
神经网络PID控制
[
]
(10) 7. 采样得 (k + 1)、r(k + 1)。（仿真计算时由对象 y 。（仿真计算时由对象 y 数学模型计算 (k + 1))
12
NNC的权值进行修正。 8. 用 11)式及 10)式对 ( ( 的权值进行修正。 ∂Jc ∂Jc ∂y(k + 1) ∂u(k) ∆ki (k) = −λ = −λ ∂ki (k) ∂y(k + 1) ∂u(k) ∂ki (k) ˆ ∂y(k + 1) xi (k) = λ[r(k + 1) − y(k + 1)] ∂u(k) 0 < λ < 1 , i = 1,2,3 (11)
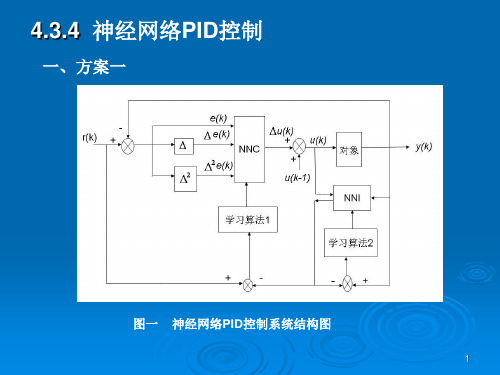
4.3.4 神经网络 神经网络PID控制 控制
一、方案一
图一
神经网络PID控制系统结构图 控制系统结构图 神经网络
1
x1(k) = e(k)
x2 (k) = ∆e(k) = e(k) − e(k −1)
x3 (k) = ∆2e(k) = e(k) − 2e(k − 1) + e(k − 2)
e(k) = r(k) − y(k)
13
9. 用下列各式对 的权值进行修正。 NNI的权值进行修正 的权值进行修正。
ˆ ∆ωi(3) (k) = η[ y(k + 1) − y(k + 1)]Oi(2) (k) +α∆ωi(3) (k −1)
( ˆ ∆ωij2) (k) = η[ y(k + 1) − y(k + 1)]ωi(3) (k) f ′ neti(2) (k) O(j1) (k) ( +α∆ωij2) (k −1)
神经网络控制
M—P模型的提出兴起了对神经网络的研究。
(2) 1949年心理学家D．O．Hebb提出神经元之间突触联系强度可变 的假设。他认为学习过程是在突触上发生的，突触的联系强度随其前 后神经元的活动而变化。根据这一假设提出的学习率为神经网络的学 习算法奠定了基础。
(3) 1958年，Rosenblatt提出感知机，第一次把神经网络的研究付 诸工程实践。这是一种学习和自组织的心理学模型，它基本上符合 神经生理学的知识，模型的学习环境是有噪声的，网络构造中存在 随机连接，这符合动物学习的自然环境。这种类型的机器显然有可 能应用于模式识别、联想记忆等方面。
3．兴盛阶段
再次兴起的原因：
（1）计算机不具备学习能力。在处理能明确定义的问题或运用能明 确定义的概念作为知识时，计算机比较容易对它们进行处理，但是对 一些知识背景不清楚、推理规则不明确、环境信息十分复杂的知识处 理或是算法难以提取的信息处理任务往往感到很困难。 （2）日本第五代机计划远未达到预想水平，也倾向使人觉得有必要 进一步弄清人们习以为常的认知功能是如何进行的．这些认知功能包 括视、听觉感知，学习记忆，运动控制等．从而使人们认识到不能拘 泥一格而必须开拓新的思路，探索新的人类智能实现途径。这时原来 已出现过的，与人脑的生理组织更为接近的神经网络模型就自然成为 理想的候选模型。
兴盛阶段的标志：
（1）近些年来．许多科学家提出了许多种具备不同信息处理能力的神 经网络模型，至今为止。约已开发出了三十多种。神经网络也 被应用到了许多信息处理领域，如模式别、自动控制、信号处理、辅助 决策、人工智能等等。 （2）神经计算机的研究也为神经网络的理论研究和应用研究促供了 强有力的支持，各大学、科研团体和公司开发了许多神经网络模拟软 件包、各种型号的电子神经计算机以及许多神经网络芯片。 （3）1987年6月在美国加州举行了第一届神经网络国际会议，并成立 了国际神经网络学会，以后每年召开两次国际联合神经网络大会 (IJCNN)。 1990年12月在北京召开了我国首届神经网络学术大会，在南 京召开的1991中国神经网络学术大会上成上了中国神经网络学会。当前 发行了两种专门介绍神经网络研究的刊物，《IEEE Transaction on Neural Network》和《Neural Network》
PID神经网络控制
r
Ｐ
v
（2）输出层神经元用线性模型，输入=输出： u(k ) x' (k ) , u(k) ：控制量
u
I
P
y
（3）控制器与被控对象一起作为广义网络考虑；
R
Ｄ
x'
（4）在线训练控制器，准则函数有所不同。
x q NNC
图 4 -7-1
PID
神经网络单变量控制结构
2
2. 控制器的学习算法
PID 神经网络控制器与对象一起作为广义网络，采用反向传播（BP）学习
qs1
(k)
1x,s1
(k
)
,
1 x s1 (k )
xs1 1
(k
)
1
r1
w 1 1
1,
xs1(k) 1
w 1 n
rn
2w P
u1
un
x'
R
xq
NNC
v1
y1
vn
yn
图 4-7-2 PID 神经网络多变量控制结构 7
qs2 (k 1) xs2 (k) , 1 qs2 (k) 1
uh (h 1,2,, n)
④ 输出端扰动
v(k ) v1 (k ), v2 (k ),, vn (k )
r1
w 1 1
2w
P
u1
w 1 n
rn un
x'
R
xq
NNC
v1
y1
vn
yn
5 图 4-7-2 PID 神经网络多变量控制结构
4-4神经网络控制PPT课件
4.4 几种典型的神经网络
网络输出 u x )的非线性映射，径向基 RBF网络的输入层到隐含层实现 x i( 网络隐含层节点的作用函数一般取下列几种形式
最常用的是高斯激活函数
采用高斯基函数，具备如下优点： (1)表示形式简单，即使对于多变量输入也不增加太多的复改性； (2)径向对称； (3)光滑性好，任意阶导数存在； (4)由于该基函数表示简单且解析性好，因而使于进行理论分析。
其中，f 函数为Sigmoid函数
4.4 几种典型的神经网络
(4)调整权值，按误差反向传播方向，从输出节点开始返回到隐层按下式 修正权值
(5)返回第(2)步重复，直至误差满足要求为止。 使用BP算法应注意的几个问题 (1)学习速率 η的选锋非常重要。 (2)在设置各训练样本的期望输出分量时，不能设置为1或0，以设置为 0.9或0.1较为适宜。 (3)若实际问题给予网络的输入量较大，需做归一化处理，网络的输出也 要进行相应的处理。 (4)各加权系数的初值以设置为随机数为宜。 (5)在学习过程中，应尽量避免落入某些局部最小值点上，引入惯性项有 可能使网络避免落入某一局部最小值。
4.4 几种典型的神经网络
4.4.2 径向基神经网络
1985年，Powell提出了多变量插值的径向基函数(Radial Basis Function，RBF)方法。 径向基函数网络比BP网络需要更多的神经元，但是它能够按时间片 来训练网络。径向基网络是一种局部逼近网络，已证明它能以任意精度 逼近任一连续函数。 构成RBF网络的基本思想：用RBF作为隐单元的“基”构成隐含层 空间，这样就可将输入矢量直接(即不通过权连接)映射到隐空间。当 RBF的中心点确定以后，这种映射关系也就确定了。而隐含层空间到输 出空间的映射是线性的，即网络的输出是隐单元输出的线性加权和。此 处的权即为网络可调参数。
神经网络控制大全
nj
三、多层神经网络结构
x1k
x2 k
y1k
y2 k
xni k
1 wij 2 wij
yn0k
(a)
x1k
x2 k
y1k
y2 k
xni k
1 wij L wij
yn0k
(b)
图4-14 多层前向传播网络结构示意图 (a)含一个隐含层前向传播网络结构示意图 (b)含L+1个隐含层前向传播网络结构示意图
达到极小的方法来实现的。
对于N个样本集，性能指标为：
E E p (t pi y pi )
p 1 p 1 i 1
N
N
n0
对于具有n0个输出的单元网络，每一个期望输出矢量Tp和实际的输出矢量 Yp之间的误差函数可以用平方差和来表示，即
1 n0 E p (t pi y pi ) 2 2 j 1
j 1
n
y ( Net ) ( 0 w j x j )
j 1
n
x1 x1
x2w11w12源自xnw1n wn1
y
xn
x1
wn 2 wnn
x2
xn
n n n
图4-12 只含二次项的神经元结构示意图
Net 0 w j x j w jk x j xk
若 r L 为输出单元层，则：
r pj
E p o r pj
r o r pj Net pj
(
k
E p
1 Net r pk
1 Net r o r pk pj
)r ( Net r pj )
r 1 r 1 ( pk wkj )r ( Net r pj ) k
神经网络控制完整版
神经网络控制HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】人工神经网络控制摘要: 神经网络控制，即基于神经网络控制或简称神经控制，是指在控制系统中采用神经网络这一工具对难以精确描述的复杂的非线性对象进行建模，或充当控制器，或优化计算，或进行推理，或故障诊断等，亦即同时兼有上述某些功能的适应组合，将这样的系统统称为神经网络的控制系统。
本文从人工神经网络，以及控制理论如何与神经网络相结合，详细的论述了神经网络控制的应用以及发展。
关键词: 神经网络控制；控制系统；人工神经网络人工神经网络的发展过程神经网络控制是20世纪80年代末期发展起来的自动控制领域的前沿学科之一。
它是智能控制的一个新的分支，为解决复杂的非线性、不确定、不确知系统的控制问题开辟了新途径。
是（人工）神经网络理论与控制理论相结合的产物，是发展中的学科。
它汇集了包括数学、生物学、神经生理学、脑科学、遗传学、人工智能、计算机科学、自动控制等学科的理论、技术、方法及研究成果。
在控制领域，将具有学习能力的控制系统称为学习控制系统，属于智能控制系统。
神经控制是有学习能力的，属于学习控制，是智能控制的一个分支。
神经控制发展至今，虽仅有十余年的历史，已有了多种控制结构。
如神经预测控制、神经逆系统控制等。
生物神经元模型神经元是大脑处理信息的基本单元，人脑大约含1012个神经元，分成约1000种类型，每个神经元大约与 102~104个其他神经元相连接，形成极为错综复杂而又灵活多变的神经网络。
每个神经元虽然都十分简单，但是如此大量的神经元之间、如此复杂的连接却可以演化出丰富多彩的行为方式，同时，如此大量的神经元与外部感受器之间的多种多样的连接方式也蕴含了变化莫测的反应方式。
图1生物神经元传递信息的过程为多输入、单输出，神经元各组成部分的功能来看，信息的处理与传递主要发生在突触附近，当神经元细胞体通过轴突传到突触前膜的脉冲幅度达到一定强度，即超过其阈值电位后，突触前膜将向突触间隙释放神经传递的化学物质，突触有两种类型，兴奋性突触和抑制性突触。
第三章神经网络控制及应用基础
类
〇
〇
反馈型网络
2019/9/16
31
3.1.3.3 人工神经网络的学习
神经网络能够通过对样本的学习训练， 不断改变网络的连接权值以及拓扑结构，以 使网络的输出不断地接近期望的输出。这一 过程称为神经网络的学习或训练，其本质是 可变权值的动态调整。
2019/9/16
32
3.1.3.2 人工神经网络模型
22
3.1.3.1 人工神经元模型
神 (1)阈值型转移函数
经 元
1 x≥0
f(x)=
的
0 x＜0
转
f (x)
移
函
1.0
数
0
(3-7)
x
2019/9/16
23
3.1.3.1 人工神经元模型
神 (2)非线性转移函数
经
元 的
f
(
x)
1
1 e
x
(3-8)
1 ex f (x) 1 ex
型
n
o j (t 1) f {[ wij xi (t)] T j}
(3-2)
i 1
2019/9/16
20
3.1.3.1 人工神经元模型
n
神
netj (t) wij xi (t)
经
i 1
元
的
net’j=WjTX
数
学 Wj=(w1 w2 … wn)T
模 型
X=(x1 x2 … xn)T
人工神经网络是一种旨在模仿人脑结构及其功能 的信息处理系统。
2019/9/16
1
3.1.1神经网络的基本特征与功能
结构特征： 并行式处理 分布式存储 容错性
第3章 神经网络控制- 网络结构2
������+1 ������������������ ������������
������ ������������������
− ������������
������+1
, ������ = 0,1, ⋯ , ������ − 1
������������������
������+1
=Γ
������+1 ������=1
依次输入，每输入一个样本 ������ ，沿着使 ������������ 降低的 负梯度方向更新一次权值，直到 ������ 个样本全部训 练完毕；
②
进入下一周期，重复第①步，即：对样本集中的
全部数据依次有序地进行第二遍训练，并相应更
新权值；
③
依此类推，直到全部样本数据的总误差性能指标������ 满足要求。
������=0
������
������−1
= ������������������
������−1
7
定义第������层第������个神经元的输出广义误差：
������ ������������������
≝−
������������������ ������������������������������������
������ ：学习步长； ������������������
������−1
������
：第������ − 1层第������ 个神经元的输出。
8
第二步，反向传播误差的计算
������
…
������o
(广义误差的计算)
������������������������
第五章_神经网络控制
适应与集成：神经网络能够适应在线运行，并能同时进 行定量和定性操作。神经网络的强适应和信息融合能力使 得网络过程可以同时输入大量不同的控制信号，解决输入 信息间的互补和冗余问题，并实现信息集成和融合处理。 这些特性特别适于复杂、大规模和多变量系统。
硬件实现：神经网络不仅能够通过软件而且可以借助硬 件实现并行处理。近来来，一些超大规模集成电路实现硬 件已经问世，而且可以从市场上购买到，这使得神经网络 成为具有快速和大规模处理能力的实现网络。
误差反传（学习算法）
j
i
k
x1
输 入 模 式
-
+
x1
x1
ij
M
输入层
q
隐含层 信息流
jk
L
输出层
BP算法的基本思想
其基本思想是最小二乘法。它采用梯度搜索技术，以 期使网络的实际输出值与期望值的误差均方值为最小。
BP算法的学习过程由正向传播和反向传播组成。
在正向传播过程中，输入信息从输入层经隐含层逐层 处理，并传向输出层，每层神经元（节点）的状态只影 响下一层神经元的状态。 如果在输出层不能得到期望的输出，则转入反向传播， 将误差信号沿原来的连接通路返回，通过修改各层神经 元的权值，使误差信号最小。
n
yi f ( I i )
x j 从其他神经元传来的输 入信号
ji 从神经元j到i的连接权值 i 阈值
f () 激发函数或作用函数
把 i 看成是恒等于1的输入 x0 的权值，这时可写为：
I i ji x j i
j 1
n
I i ji x j
4）按下式修正权值：
ij (k 1) ij (k ) [d (k ) y(k )]xi
控制工程基础论文【范本模板】
控制工程基础论文智能控制（intelligent controls）在无人干预的情况下能自主地驱动智能机器实现控制目标的自动控制技术。
对许多复杂的系统，难以建立有效的数学模型和用常规的控制理论去进行定量计算和分析，而必须采用定量方法与定性方法相结合的控制方式.定量方法与定性方法相结合的目的是，要由机器用类似于人的智慧和经验来引导求解过程。
因此，在研究和设计智能系统时，主要注意力不放在数学公式的表达、计算和处理方面，而是放在对任务和现实模型的描述、符号和环境的识别以及知识库和推理机的开发上，即智能控制的关键问题不是设计常规控制器,而是研制智能机器的模型.此外，智能控制的核心在高层控制，即组织控制.高层控制是对实际环境或过程进行组织、决策和规划,以实现问题求解.为了完成这些任务,需要采用符号信息处理、启发式程序设计、知识表示、自动推理和决策等有关技术。
这些问题求解过程与人脑的思维过程有一定的相似性，即具有一定程度的“智能”。
智能控制的主要技术方法及其特点:专家系统专家系统是利用专家知识对专门的或困难的问题进行描述。
用专家系统所构成的专家控制，无论是专家控制系统还是专家控制器,其相对工程费用较高,而且还涉及自动地获取知识困难、无自学能力、知识面太窄等问题. 尽管专家系统在解决复杂的高级推理中获得较为成功的应用,但是专家控制的实际应用相对还是比较少。
模糊逻辑模糊逻辑用模糊语言描述系统，既可以描述应用系统的定量模型也可以描述其定性模型。
模糊逻辑可适用于任意复杂的对象控制。
但在实际应用中模糊逻辑实现简单的应用控制比较容易. 简单控制是指单输入单输出系统(SISO) 或多输入单输出系统（MISO）的控制. 因为随着输入输出变量的增加，模糊逻辑的推理将变得非常复杂.遗传算法遗传算法作为一种非确定的拟自然随机优化工具，具有并行计算、快速寻找全局最优解等特点，它可以和其他技术混合使用,用于智能控制的参数、结构或环境的最优控制。
智能控制基础-神经网络
第6章 神经网络控制
7
智能控制 基是神经系统结构和功能基本单位，典型的神经 元结构图4-1所示。
第6章 神经网络控制
图4-1 神经元结构 8
智能控制 基础
4.1.1
神经网络原理
视网膜的信息处理机制
光感受器细胞将光波所携带的自 然图像信息转变成神经元电信息
囊泡
受体
K+ Na+ K+
4 神经网络具有自组织、自学习功能，是自适应组 织系统。
第6章 神经网络控制
26
智能控制 基础
4.1.2
神经网络的结构和特点
神经网络的研究主要包括： 神经网络基本理论研究 神经网络模型的研究 神经网络应用研究 神经网络及其融合应用技术
第6章 神经网络控制
27
智能控制 基础
4.1.3
神经网络学习
神经元之间高度互连实现并行处理而表现出的群体特性是非常 复杂，甚至是混沌的； 3利用神经网络通过学习过程可以从周围环境获取知识，中 间 神经元的连接强度（权值）用来表示存贮的知识。
第6章 神经网络控制
20
智能控制 基础
4.1.2
神经网络的结构和特点
神经网络的结构按照神经元连接方式可分成前馈网络 和反馈网络。
（2）Sigmoid函数
（2）
1
f ( X ) 1 eaX
a 0
图4-3 常用的几种激励函数
第6章 神经网络控制
16
智能控制 基础
4.1.1
神经网络原理
常用的激励函数如图4-3所示：
（3）双曲正切函数
（3）
f ( X ) 1 eaX 1 eaX
a 0
（4）高斯函数 X2
第八章：神经网络控制
并且给出神经网络逆建模的输入输出结构。
11/43 Beijing University of Technology
§8.1
adqiao@
基于神经网络的动态系统建模
2013-7-11
(1) 直接逆建模 直接逆建模也称广义逆学习，如图8.1.2所示。
从原理上说，这是一种最简单
的方法。待辨识系统的输出作 为神经网络的输入，神经网络 的输出与动态系统的输入进行
刻不可能知道 y(t 1) ，因此可用 t 1 时刻的期望输出 y d (t 1) 来代替 y(t 1)。 对于期望输出，其任意时刻的值总可以预先知道。此时有
u(t ) f 1[ yd (t 1), y(t ), , y(t n 1); u(t 1), , u(t m 1)]
第八章：神经网络控制
adqiao@ 2013-7-11
(3) 并行计算特点
神经网络中的信息是并行处理的，使其有潜力快速实现大量复 杂的控制算法(目前还有待于神经网络芯片技术的进步)； (4) 分布式信息存储 神经网络中的信息分布式地存贮于网络的连接权值中，可以提
高了控制系统的容错性；
6/43
Beijing University of Technology
§8.1
adqiao@
基于神经网络的动态系统建模
2013-7-11
神经网络逼近任意非线性映射的能力和良好的自学习、自适应 能力，使其成为当前非线性系统辨识的重要工具。与传统非线 性辨识方法不同的是：神经网络辨识不受非线性模型的限制。 它依据被控系统的输入输出数据对，通过学习得到一个描述系
adqiao@
基于神经网络的动态系统建模
2013-7-11
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
神经网络文献综述吴一凡（西南交通大学峨眉校区，四川 峨眉 614202）摘 要：本文着重介绍了神经网络的发展、优点及其应用、发展动向，文中着重论述了神经网络目前的几个研究热点，对神经网络有一个全面系统的概括。
关键词：神经网络 模糊控制 遗传算法 专家系统 小波分析Abstract ：Development,merits and application of neural network are introduced in this paper. Then,the trends are presented.And its several main research directs.This paper can give you a comprehensive and systematic exposition of the neural network.Keywords ：Neural network Fuzzy control Genetic algorithm Expert system Wavelet analysis0 绪论神经网络最早的研究是20世纪40年代心理学家Mcculloch 和数学家Pitts 合作提出的，他们提出的MP 模型拉开了神经网络研究的序幕，其结构如图1所示。
图1 人工神经元示意图图1中，n I I I ,,,21 表示其他n 个神经元的突触输出，n W W W ,,,21 为其他n个神经元的突触连接，其值可正可负，分别表示兴奋性突触和抑制性突触。
∑θ为阀值，神经元的输出()θf 称为变换函数，一般采用的形式有线性函数、阶跃函数、Sigmoid 函数及双曲正切函数等。
神经网络的发展大致经三个阶段：1947~1969年为初期。
在这期间科学家们提出了许多神经元模型和学习规则，如MP模型、HEBB学习规则和感知器等；1970~1986年为过渡期。
这个期间神经网络研究经过了一个低潮，继续发展。
在此期间，科学家们做了大量的工作，如Hopfield教授对网络引入能量函数的概念，给出了网络的稳定性判据，提出了用于联想记忆和优化计算的途径。
1984年，Hiton教授提出Boltzman机模型。
1986年Kumelhart等人提出误差反向传播神经网络，简称BP网络。
目前，BP网络已成为广泛使用的网络；1987年至今为发展期。
在此期间，神经网络受到国际重视，各个国家都展开研究，形成神经网络发展的另一个高潮。
神经网络具有以下优点：1）可以充分逼近任意复杂的非线性关系。
2）具有很强的鲁棒性和容错性，因为信息是分布贮于网络内的神经元中。
3）并行处理方法，使得计算快速。
4）可以处理不确定或不知道的系统，因神经网络具有自学习和自适应能力。
5）具有很强的信息综合能力，能同时处理定量和定性的信息，能很好地协调多种输入信息关系，适用于多信息融合和多媒体技术。
1 神经网络应用现状神经网络以其独特的结构和处理信息的方法，在许多实际应用领域中取得了显著的成效，主要应用如下：1）自动控制领域：神经网络方法已经覆盖了控制理论中的绝大多数问题，主要有系统建模与辨识、PID参数整定、极点配置、内模控制、优化设计、预测控制、最优控制、自适应控制、滤波与预测容错控制、模糊控制和学习控制等。
典型的例子是世纪，20世纪60年代初，美国“阿波罗”登月计划中，Kilmer和Mc-Clloch等人根据脊椎动物神经系统中网状结构的工作原理，提出了一个模型，以使登月车在远距离复杂环境下具有一定的自制能力；2）处理组合问题：最典型的例子是成功地解决了TSP问题，即旅行推销员问题（Travelling Salesman Problem），另外还有最大匹配问题、装箱问题和作业调度等；3）模式识别：已成功应用于手写字符、汽车牌照、指纹和声音识别，还可用于目标的自动识别和定位、机器人传感器的图像识别以及地震信号的鉴别等；4）图像处理：对图像进行边缘监测、图像分割、图像压缩和图像恢复5）传感器信号处理：传感器输出非线性特性的矫正、传感器故障检测、滤波与除噪、环境影响因素的补偿、多传感器信息融合；6）机器人控制：对机器人眼手系统位置进行协调控制，用于机械手的故障诊断及排除、智能自适应移动机器人的导航；7）卫生保健、医疗。
比如通过训练自主组合的多层感知器可以区分正常心跳和非正常心跳网络的波形分类和特征提取在计算机临床诊断中的应用。
8）经济。
能对商品价格、股票价格和企业的可信度等进行短期预测。
9）化工领域。
能对制药、生物化学和化学工程等进行分析。
如：进行蛋白质结构分析、谱分析和化学反应分析等。
10）地理领域。
在遥感图像分类中有广泛的应用，在GIS方面应用人工神经网络理论，提高系统对数据进行复杂的综合分析的功能。
11）另外，在数据挖掘、电力系统、交通、军事、矿业、农业和气象等方面亦有应用。
2 神经网络发展趋势神经计算的基础理论框架以及生理层面的研究仍需深入。
这方面的工作虽然很困难，但为了神经计算的进一步发展却是非做不可的。
增强神经网络的可理解性是神经网络界需要解决的一个重要问题。
这方面的工作在今后若干年中仍然会是神经计算和机器学习界的一个研究热点。
神经计算技术与其他技术尤其是进化计算技术的结合以及由此而来的混合方法和混合系统，正成为一大研究热点。
神经网络用于控制时还有许多问题值得研究：现行的学习算法收敛速度低，存在局部最优问题；分布式并行处理方式的网络内部机理并不清楚，选择网络层数、每层神经元个数，还得凭经验；泛化能力不足，制约了控制系统的鲁棒性；需要创造更适合于控制的专用神经网络；网络建立模算法和控制系统的收敛性与稳定性需进一步研究。
3 神经网络研究热点3.1 神经网络与模糊逻辑的结合模糊逻辑是一种处理不确定性、非线性问题的有力工具。
它比较适合于表达那些模糊或定性的知识，其推理方式比较类似于人的思维方式，这都是模糊逻辑的优点。
但它缺乏有效的自学习和自适应能力。
神经网络具有并行计算、分布式信息存储、容错能力强以及具备自适应学习能力等一系列优点。
但一般来说，神经网络不适于表达基于规则的知识，因此在对神经网络进行训练时，由于不能很好地利用已有的经验知识，常常只能将初始值取为零或随机数，从而增加了网络的训练时间或者陷入非要求的局部极值而将模糊逻辑与神经网络结合，则网络中的各个结点及所有参数均有明显的物理意义，因此这些参数的初值可以根据系统的模糊或定性的知识来加以确定，然后利用学习算法可以很快收敛到要求的输入输出关系，这是模糊神经网络比单纯的神经网络的优点所在。
同时，由于它具有神经网络的结构，因而参数的学习和调整比较容易，这是它比单纯的模糊逻辑系统的优点所在。
模糊神经网络控制已成为一种趋势，它能够提供更加有效的智能行为、学习能力、自适应特点、并行机制和高度灵活性，使其能够更成功地处理各种不确定的、复杂的、不精确的和近似的控制问题。
模糊神经控制包括两个方面：1）基于神经网络的模糊控制：它将模糊系统设计方法与神经网络的连接主义结构和学习方法结合起来，把模糊系统表达成连接主义方式的网络结构，模糊控制的模糊化、模糊推理和解模糊化三个基本过程全都用神经网络来实现；2）模糊神经网络：它在传统的神经网络中增加一些模糊部分，除了具有神经网络的功能外，还能处理模糊信息，完成模糊推理功能。
模糊神经控制的未来研究应集中于以下几个方面：1）研究模糊逻辑与神经网络的对应关系，将对模糊控制器的调整转化为等价的神经网络的学习过程，用等价的模糊逻辑来初始化神经网络；2）完善模糊神经控制的学习算法，以提高控制算法的速度与性能，可引入遗传算法、BP算法中的模拟退火算法等，以提高控制性能；3）模糊控制规则的在线优化，可提高控制器的实时性与动态性能；4）需深入研究系统的稳定性、能控性、能观性以及平衡吸引子、混沌现象等非线性动力学特性；5）关于神经网络与模糊逻辑相结合的研究已有很多，比如用于氩弧焊、机器人控制等。
3.2 神经网络与遗传算法的结合遗传算法是1962年由美国的Hollad提出的。
遗传算法是基于自然选择和基因遗传学原理的全局优化搜索算法，因其简单通用，鲁棒性强，适于并行处理，已成为人们用来解决高度复杂问题的一个新思路和新方法。
目前已被广泛用于许多实际问题。
遗传算法与神经网络的结合主要体现在以下几个方面：网络连接权重的进化训练；网络结构的进化计算；网络结构和连接权重的同时进化；训练算法的进化设计。
基于进化计算的神经网络设计和实现已在众多领域得到应用，如模式识别、机器人控制、财政预测等，并取得了较传统神经网络更好的性能和结果。
但从总体上看，这方面研究还处于初期阶段，理论方法有待于完善规范，应用研究有待于加强提高。
神经网络与进化算法相结合的其他方式也有待于进一步研究和挖掘。
3.3 神经网络与专家系统的结合人工神经网络是基于输入/输出的一种直觉性反射，适于发挥经验知识的作用，进行浅层次的经验推理；专家系统是基于知识、规则匹配的逻辑知识的作用，进行深层次的逻辑推理。
专家系统的特色是符号推理，神经网络擅长数值计算。
因此将两者科学地结合，可以取长补短。
基于神经网络与专家系统的混合系统的基本出发点立足于将复杂系统分解成各种功能子系统模块，各功能子系统模块分别由神经网络或专家系统实现。
其研究的主要问题包括：混合专家系统的结构框架和选择实现功能子系统方式的准则两方面。
由于该混合系统从根本上抛开了神经网络和专家系统的技术限制，是当前研究的热点。
3.4 神经网络与小波分析的结合神经网络与小波分析的结合小波变换是对Fourier分析方法的突破。
它不但在时域和频域同时具有良好的局部化性质，而且对低频信号在频域和对高频信号在时域里都有很好的分辨率，从而可以聚集到对象的任意细节。
目前可以将它与神经网络相结合实现间接辨识与建模。
在结合方法上，可以将小波函数作为基函数构造神经网络形成小波网络，或者以小波变换的多分辨率特性对过程状态信号进行处理，实现信噪分离，并提取出对加工误差影响最大的状态特性，作为神经网络的输入。
4 结论经过近半个世纪的发展，神经网络理论在模式识别、自动控制、信号处理、辅助决策、人工智能等众多研究领域取得了广泛的成功，但其理论分析方法和设计方法还有待于进一步发展。
相信随着神经网络的进一步发展，其将在工程应用中发挥越来越大的作用。
本文只简单介绍了神经网络的神经网络的发展、优点及其应用、发展动向，文中着重论述了神经网络目前的几个研究热点，对神经网络有一个全面系统的概括。
参考文献1.孙增圻，张再兴，邓志东.智能控制理论与技术[M].北京：清华大学出版社.19972.王学武，谭得健.神经网络的应用与发展趋势[J].计算机工程与应用，2003.33.周志华，何佳洲，陈世富.神经网络国际研究动向[J].模式识别与人工智能，2000.13。