投资学第9章--资本资产定价模型
投资学中的资本资产定价模型(CAPM)风险与预期收益的关系

投资学中的资本资产定价模型(CAPM)风险与预期收益的关系资本资产定价模型(Capital Asset Pricing Model, CAPM)是投资学中广泛应用的理论模型,它用于评估资产的预期收益与风险之间的关系。
该模型的核心思想是通过系统性风险,即贝塔系数,来解释预期收益率,从而提供了一种衡量投资风险的方法。
本文将探讨CAPM模型中风险与预期收益之间的关系。
一、CAPM模型基本原理CAPM模型是由美国学者威廉·夏普、约翰·莱特纳和杰克·特雷纳提出的。
该模型建立在一系列假设的基础上,包括投资者风险厌恶程度相同、无风险利率存在、市场资产组合是风险资产的惟一有效组合等。
根据这些假设,CAPM模型得出了风险与预期收益之间的线性关系,即预期收益率等于无风险利率加上风险溢价,而风险溢价等于资产的贝塔系数乘以市场风险溢价。
二、风险与预期收益的关系在CAPM模型中,风险通过资产的贝塔系数来度量。
贝塔系数是一个衡量资产价格与市场整体波动性之间关系的指标,它代表了资产相对于市场的敏感性。
贝塔系数大于1表示资产的价格波动幅度大于市场,小于1表示资产的价格波动幅度小于市场,等于1表示资产的价格波动与市场相同。
根据CAPM模型,贝塔系数越高,意味着资产的风险越高,预期收益也越高。
这是因为高风险资产需要提供更高的预期收益率来吸引投资者。
三、市场风险溢价CAPM模型中的市场风险溢价是指投资者愿意支付的超过无风险利率的溢价。
市场风险溢价表示了投资者对承担市场整体风险的回报要求。
根据CAPM模型,市场风险溢价等于市场整体风险与无风险利率之差,即市场风险溢价=市场预期收益率-无风险利率。
四、CAPM模型的应用与局限性CAPM模型在投资组合的风险评估、资产定价等方面具有广泛的应用。
通过使用CAPM模型,投资者能够评估特定资产的预期收益与风险,并与市场整体表现进行比较,以作出投资决策。
然而,CAPM模型也存在一定的局限性。
资本资产定价模型概述(ppt42张)

6、可以在无风险折现率R的水平下无限制地借 入或贷出资金; 7、所有投资者对证券收益率概率分布的看法一 致,因此市场上的效率边界只有一条; 8、所有投资者具有相同的投资期限,而且只有 一期; 9、所有的证券投资可以无限制的细分,在任何 一个投资组合里可以含有非整数股份;
10、税收和交易费用可以忽略不计; 11、市场信息通畅且无成本; 12、不考虑通货膨胀,且折现率不变; 13、投资者具有相同预期,即他们对预期收益率、 标准差和证券之间的协方差具有相同的预期值。 上述假设表明:第一,投资者是理性的,而且严格 按照马科威茨模型的规则进行多样化的投资,并将 从有效边界的某处选择投资组合;第二,资本市场 是完全有效的市场,没有任何磨擦阻碍投资。
又由(7.3)
dv 1 dE ( r E ( r )E ( r c) M j)
于是
d d d v c c d Er ( c) d vd Er ( c)
2 2 [ ( 1 v ) ( 1 2)c v o v ( r , r ) v ]/ j j m M c Er ( M) Er ( j)
假定2:针对一个时期,所有投资者的预期 都是一致的。
这个假设是说,所有投资者在一个共同的时期内 计划他们的投资,他们对证券收益率的概率分布 的考虑是一致的,这样,他们将有着一致的证券预 期收益率﹑证券预期收益率方差和证券间的协方 差。同时,在证券组合中,选择了同样的证券和同 样的证券数目。 这个假设与下面的关于信息在整个资本市场中畅 行无阻的假设是一致的。
故
2 c o v ( r , r ) d j M M c d Er ( c)v Er ( M) Er ( j) ) c( 1
资本资产定价模型

M
线变成了AM射线。
A
N
CML B
P
• M点是包括了所有证券的市场投资组合
•
AM是资本市场线:
RP
Rf
Rm R f
m
p
– 资本市场线描述的是市场投资组合与无风险资产所构
成的投资组合的收益率与风险之间的关系。
第五节、资本资产定价模型
• 威廉夏普对资本市场线进行了扩展,发现 个别证券或者证券组合的收益率和风险可
• 可行集:由n种证券所 RP
形成的所有可能的组合 的集合,如图ANBH所
N
示。
A
B H
P
• 有效集:满足两个条件的证券组合集合:
– 风险相同条件下,选择收益最高的组合
– 收益相同条件下,选择风险最低的组合
• 有效集的形状:NB曲线
第四节、无风险借贷与资本市场线
• 无风险资产:银行存贷款、国债、货币基金等。
2 A
xB2
2 B
2xA xB AB A B
–
多种证券组合:
证券i(Ri
,
, 2
i
xi
)
n
RP xi Ri i 1
nn
2 P
xi x j ih
i1 j1
风险的分散
•
多种证券组合的风险为:
2 P
n
n
xi x j ih
i1 j1
组合的风险
非系统性风险 系统性风险
证券的数量n
第三节、有效集与最优投资组合
CAPM模型的评价
• 资本资产定价模型在马科维茨的证券组合理论的基础上, 对金融资产和投资组合的风险衡量进行了更深入的研究, 并提出了单个金融资产预期收益率与其系统性风险的均衡 关系,从而导出了各种资产根据其系统性风险定价的资本 资产定价模型。应该说,夏普的研究是具有建设性的,他 把马科维茨的研究向前推进了一大步。
管理学投资学PPT第章资本资产定价模型

❖若某一个股票未包含在最优资产组合中,
会怎样?
2024/6/29
21
图 9.1 The Efficient Frontier and the
Capital Market Line
2024/6/29
22
9.1.2 消极策略的有效性
理由:
❖市场的有效性
❖投资于市场投资组合指数这样一个消极策略是有
26
▪ β系数。美国经济学家威廉·夏普提出的风险衡量
指标。
▪
用它反映资产组合波动性与市场波动性关系(
在一般情况下,将某个具有一定权威性的股指(
市场组合)作为测量股票β值的基准)。
▪ 如果β值为1.1,表明该股票波动性要比市场大盘
高10 %,说明该股票的风险大于整个市场的风险
,当然它的收益也应该大于市场收益,因此是进
则其收益 - 风险比率为:
wGE [ E (rGE ) rf ] E (rGE ) r f
wGE Cov(rGE , rM ) Cov(rGE , rM )
2024/6/29
25
9.1.4 单个证券的期望收益
市场组合M与CML相切,其收益风险比率为:
E (rM ) rf
2
M
(风险的市场价格)
率应该增加的数量。
▪ 在金融世界里,任何资产组合都不可能超越CML
。由于单个资产一般来说,并不是最优的资产组
合,因此,单个资产也位于该直线的下方。
2024/6/29
14
证券市场线
▪ 资本市场线描述了有效组合的预期收益率和标准
差之间的均衡关系―有效资产组合定价模型。
▪ 问题:
▪ (1) 单个风险资产的预期收益率和标准差之间
投资学第章资本资产定价模型剖析ppt课件

与指数模型的期望形式:
E(ri ) rf i i[E(rM ) rf ] 可知二者差别在于,CAPM认为所有的i都为0。 市场模型:rf E(ri ) i[rf E(rM )] ei
如果CAPM有效,则市场模型等同于指数模型。
E(Ri ) kE(Ci ) ( L1 L2 L3 )
其中,E(Ci )为期望流动性代价; k为所有资产的调整后的平均持有期
为平均市场流动性的市场风险溢价净值 为系统性市场风险敏感度, L1、 L 2、 L3为流动性 E(RM CM ),CM 表示市场平均流动性溢价。
37
流动性的三要素
25
9.3 CAPM符合实际吗?
CAPM的实用性取决于证券分析。 9.3.1 CAPM能否检验 ▪ 规范方法与实证方法 ▪ 实证检验的两类 错误(数据、统计方法) 9.3.2 实证检验质疑CAPM
26
9.3 CAPM符合实际吗?
9.3.3CAPM的经济性与有效性 ▪ CAPM在公平定价领域的广泛应用 ▪ CAPM被普遍接受的原因 9.3.4 投资行业与CAPM的有效性 投资公司更趋向于支持CAPM
39
27
9.4 计量经济学和期望收益-贝塔关系
▪ 计量经济方法可能是引起CAPM被错误拒 绝的原因
▪ 相关改进
➢ 用广义最小二乘法处理残差相关性 ➢ 时变方差模型ARCH
28
9.5 CAPM的拓展形式
两种思路: ▪ 假定的放宽 ▪ 投资者心理特征的应用
29
9.5.1 零模型
有效前沿的三大性质:
▪ 两种有效前沿上的资产组合组成的任意资产组合仍在有 效前沿上
23
9.2.2 指数模型和已实现收益
资本资产定价模型

资本资产定价模型
在金融领域,资本资产定价模型(Capital Asset Pricing Model,简称CAPM)是一种被广泛应用的理论模型,用于衡量资产的预期收益率。
资本资产定价模型基于市场有效性假设,即市场上的所有投资者都具有相同的信息和投资目标,在没有风险的市场中将做出相似的投资选择。
CAPM模型通过分析资产的系统性风险和风险溢价来确定资产的预期回报率。
资本资产定价模型的基本公式为:
\[ E(R_i) = R_f + \beta_i(E(R_m) - R_f) \]
其中,\( E(R_i) \) 表示资产的预期回报率,\( R_f \) 表示无风险利率,
\( \beta_i \) 表示资产的贝塔系数,\( E(R_m) \) 表示市场组合的预期回报率。
CAPM模型的核心概念是风险溢价,即投资者对承担风险所要求的回报。
贝塔系数代表了资产相对于市场组合的风险敞口,当贝塔系数大于1时,表示资产的风险大于市场平均水平;当贝塔系数小于1时,表示资产的风险低于市场平均水平。
资本资产定价模型的应用范围涵盖了各种金融资产,包括股票、债券、衍生品等。
投资者可以利用CAPM模型来评估资产的风险和回报之间的关系,从而制定有效的投资策略。
然而,CAPM模型也存在一些局限性,例如假设过于理想化、参数估计误差等问题,限制了其在实际投资中的应用。
总的来说,资本资产定价模型作为金融领域中重要的理论框架,为投资者提供了一种有效的资产定价方法。
通过对资产的风险和回报进行定量分析,CAPM模型帮助投资者更准确地评估资产的价值,优化投资组合,实现资产配置的最优化。
博迪《投资学》(第10版)章节题库-第九章至第十章【圣才出品】
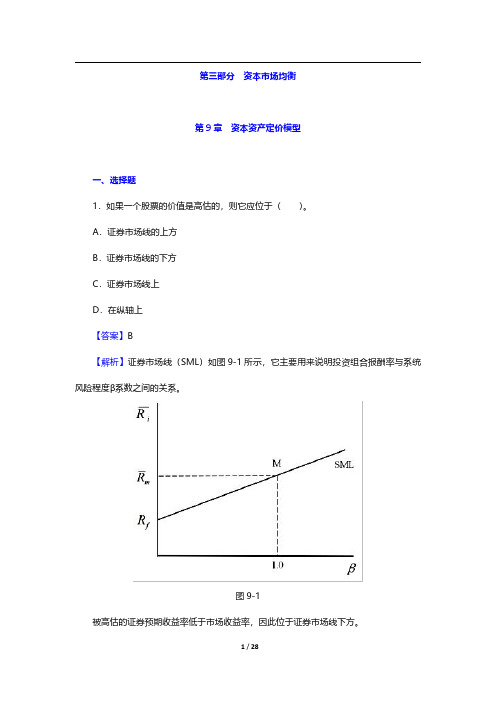
第三部分资本市场均衡第9章资本资产定价模型一、选择题1.如果一个股票的价值是高估的,则它应位于()。
A.证券市场线的上方B.证券市场线的下方C.证券市场线上D.在纵轴上【答案】B【解析】证券市场线(SML)如图9-1所示,它主要用来说明投资组合报酬率与系统风险程度β系数之间的关系。
图9-1被高估的证券预期收益率低于市场收益率,因此位于证券市场线下方。
2.无风险利率和市场预期收益率分别是3.5%和10.5%。
根据资本资产定价模型,一只β值是1.63的证券的预期收益是()。
A.10.12%B.14.91%C.16.56%D.18.79%【答案】B【解析】根据资本资产定价模型:E(r i)=r f+β[E(r M)-r f]=3.5%+1.63×(10.5%-3.5%)=14.91%。
3.资本资产定价模型给出了精确预测()的方法。
A.有效投资组合B.单一资产与风险资产组合期望收益率C.不同风险收益偏好下最优风险投资组合D.资产风险及其期望收益率之间的关系【答案】D【解析】根据资本资产定价模型,每一证券的期望收益率应等于无风险利率加上该证券由β系数测定的风险溢价。
4.假定一只股票定价合理,预期收益是15%,市场预期收益是10.5%,无风险利率是3.5%,这只股票的β值是()。
A.1.36B.1.52C.1.64D.1.75【答案】C【解析】既然α值假定为零,证券的收益就等于CAPM设定的收益。
因此,将已知的数值代入CAPM,即15%=[3.5%+(10.5%-3.5%)β],解得:β=1.64。
5.根据CAPM模型,市场期望收益率和无风险收益率分别是0.12和0.06,β值为1.2的证券A的期望收益率是()。
A.0.068B.0.12C.0.132D.0.142【答案】C【解析】根据资本资产定价模型,E(r i)=r f+[E(r M)-r f]βi=0.06+(0.12-0.06)×1.2=0.132。
Chap009 资本资产定价模型兹维 博迪 《投资学 》第九版课件PPT

9-18
图9.3 证券市场线和一只α值为正的股票
股票的实际期望 收益与正常期望收 益之间的差,称为 股票的阿尔法,。 被低估的股票期 望收益值将高于证 券市场线给出的正 常收益值。
INVESTMENTS | BODIE, KANE, MARCUS
INVESTMENTS | BODIE, KANE, MARCUS
9-24
9.4 计量经济学与期望收益—贝塔关系
9.3.2 实证检验不支持CAPM
• 实证拒绝了假设:α等于0。 • 统计偏差的引进。 • 米勒和斯科尔斯的论文证明了计量问题可 能会导致拒绝资本资产定价模型,即使该 模型是非常有效的。 • 但也可能是模型本身的问题。
E r r
M f
9-7
• 变换一下,我们可以得到:
ErGE rf GE ErM rf
– 风险溢价取决于两个因素:
• 一是市场组合风险报酬[E(r )-rf]; • 二是资产对市场组合的风险暴露程度β;
M
注意:预测的是收益
9-8
INVESTMENTS | BODIE, KANE, MARCUS
E (rM ) rf M E ( r ) r M f
INVESTMENTS | BODIE, KANE, MARCUS
9-15
9.1.5 证券市场线★
均衡市场中,所有证券 都必须在证券市场线上。 证券市场线:期望收益 -贝塔关系。斜率为市 场投资组合的风险溢价 :【E(rM)-rf 】。
• βi为个股对市场组合方差的贡献。
INVESTMENTS | BODIE, KANE, MARCUS
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在金融世界里,任何资产组合都不可能超越CML 。由于单个资产一般来说,并不是最优的资产组 合,因此,单个资产也位于该直线的下方。
资产这两种资产之间进行选择,实际上风险资产有许多
种,因此,他得出:各种风险资产在风险资产组合中的
比例与风险资产组合占全部投资的比例无关。这就是说
,投资者的投资决策包括两个决策,资产配置和风险资
产(股票)的选择。而后者应依据马克维茨的模型。即
无论风险偏好怎样,投资者的风险资产组合都应是一样
的。 2019/12/28
资比例,1 x1为无风险证券的投资比例,
则组合的期望收益rp为
rp x1r1 (1 x1)rf
(1)
2019/12/28
11
组合的标准差为
一种风险资产与无风险资产构 成的组合,其标准差是风险资 产的权重与标准差的乘积。
p x11
(2)
由(1)和(2)可得
rp
p 1
r1
2019/12/28
7
投资者是同质期望的。 这假设表明,投资者获得的信息相同于证券和市场的期望是一致的
,它保证了每个投资者的相同。
资本市场是有效的。这个假定消除了投资者获得最优投资组合的障碍 a. 不存在交易成本、佣金、证券交易费用。 b. 无税赋 c.资产可任意分割,使得投资者可获得任何比例的证券。 d.单个投资者的交易行为不影响证券价格。 • 投资者是理性的,是风险厌恶者。 • 投资只有一期。 这个假定排除了证券现价受到未来投资决定的影
单个资产的风险溢价与市场组合M的风险 溢价是成比例的,且比例为β
2019/12/28
9
资本市场线
有效边界的变化 命题:一种无风险资产与风险组合构成的
新组合的有效边界为一条直线。
2019/12/28
10
证明:假定风险组合(基金)已经构成,
其期望收益为r1,方差为
,无风险资产
1
的收益为rf ,方差为0。x1为风险组合的投
1955-56年,托宾发现马克维茨假定投资者在构筑资产组 合时是在风险资产的范围内选择,没有考虑无风险资产 和现金,实际上投资者会在持有风险资产的同时持有国 库券等低风险资产和现金的。由于利率是波动的,投资 者通常会同时持有流动性资产和风险资产。
托宾还指出,投资者并不是简单地在风险资产和无风险
(1
p 1
)rf
=rf
(r1 rf
1
)
p
可以发现这是一条以rf
为截距,以
r1
rf
1
为斜率的直线。
命题成立,证毕。
2019/12/28
12
收益rp M
rf
非有效
2019/12/28
不可行
风险σp
13
资本市场线
从无风险资产 r f 处作与风险资产组合有效边界相
切与M点的射线,该线称为资本市场线(CML)
投资学 第9章
资本资产定价模型 (CAPM)
资本资产定价模型(Capital Asset Pricing Model,CAPM)是由美国Stanford大学教授夏 普等人在马克维茨的证券投资组合理论基础上 提出的一种证券投资理论。
CAPM是现代金融学的奠基石,它解决了所有 的投资者按照组合理论投资下,资产的收益与 风险的问题。
3
夏普的CAPM模型
夏普(William Sharpe)是美国斯坦福大学教授。 诺贝尔经济学评奖委员会认为CAPM已构成金融 市场的现代价格理论的核心,它也被广泛用于经 验分析,使丰富的金融统计数据可以得到系统而 有效的利用。它是证券投资的实际研究和决策的 一个重要基础。
夏普1934年6月出生于坎布里奇,1951年,夏普 进入加大伯克莱分校学医,后主修经济学。1956 年进入兰德公司,同时读洛杉矶分校的博士学位 。在选择论文题目时,他向同在兰德公司的马克 维茨求教,在马克维茨的指导下,他开始研究简 化马克维茨模型的课题。
2019/12/28
5
9.1 模型综述
模型思路:
IF…… THEN……
2019/12/28
6
9.1 模型综述
IF:
完全竞争市场 投资周期相同,短视行为(myopic) 标的资产在金融市场上公开交易 市场无摩擦环境(无交易成本、无税收) 投资者符合Markovitz理性 投资者是同质预期(homogeneous expectations)
CML的方程为: rp
f
rM
M
rf
p
rP 和 P 表示有效资产组合的期望回报率
和标准差。
2019/12/28
14
CML是无风险资产与风险资产构成的组合的有效 边界。
CML的截距被视为时间的报酬,即无风险利率;
CML的斜率就是单位风险溢价,它告诉我们,当有效 证券组合回报率的标准差增加一个单位时,期望回报 率应该增加的数量。
响。
• 所有投资者都可以以同一无风险利率借入或借出任何数量的无风险 资产。
• 资本市场是均衡的。
2019/12/28
8
9.1 模型综述(续)
THEN: 所有投资者按市场组合M来配置资产 资本市场线(CML)与有效前沿相切于M点
市场组合的风险溢价与市场风险和个人投 资者的平均风险厌恶程度成比例
作用:对潜在投资项目估计收益率;对不在市 场交易的资产同样做出合理的估价。
CAPM 理论包括两个部分:资本市场线(CML )和证券市场线(SML)。
2019/12/28
2
托宾的收益风险理论
托宾(James Tobin)是著名的经济学家、他在1958年2月 The Review of Economic Studies发表文章,阐述了他对风 险--收益关系的理解。
2019/12/28
4
夏普的CAPM模型(续)
1961年夏普的博士论文,提出了单因素模型。这 极大地简少了计算数量。在1500只股票中选择资 产组合只需要计算4501个参数,而以前需要计算 100万个以上的数据。
1964年夏普提出CAPM模型。它不是用方差作资 产的风险度量,而是以证券收益率与全市场证券 组合的收益率的协方差作为资产风险的度量(β系 数)。这不仅简化了马模型中关于风险值的计算工 作,而且可以对过去难以估价的证券资产的风险 价格进行定价。他把资产风险进一步分为“系统 ”和“非系统”风险两部分。提出:投资的分散 化只能消除非系统风险,而不能消除系统风险。
