北科大机械原理大作业
机械原理大作业——牛头刨床

机械原理大作业——牛头刨床大作业,一,平面连杆机构的运动分析题号: 6班级 : 姓名 : 学号 : 同组者 :成绩 :完成时间 :目录题目、原始数据及要求 ..................................................................... .......................1 一平面连杆机构运动分析方程 ..................................................................... . (1)1.1速度计算公式 ..................................................................... .. (2)1.2加速度计算公式 ..................................................................... ..............2 二程序 ..................................................................... (3)2.1计算程序框图 ..................................................................... (3)2.2计算源程序 ..................................................................... .........................4 三 3.1 (一组数据 Lab =200mm)计算结果 (9)3.2运动线图 ..................................................................... . (10)3.3 体会 ..................................................................... .................................... 12 四 4.1(第二组数据 Lab =150mm)计算结果 . (12)4.2 运动线图 ..................................................................... .. (13)4.3 体会 ..................................................................... .................................... 15 五 5.1(第三组数据 Lab =220mm)计算结果 . (16)5.2 运动线图 ..................................................................... (17)5.3 体会 ..................................................................... ...................................... 21 六参考资料 ..................................................................... (21)题目、原始数据及要求:图所示为一牛头刨床(?级机构)。
北京科技大学机考201601机械原理
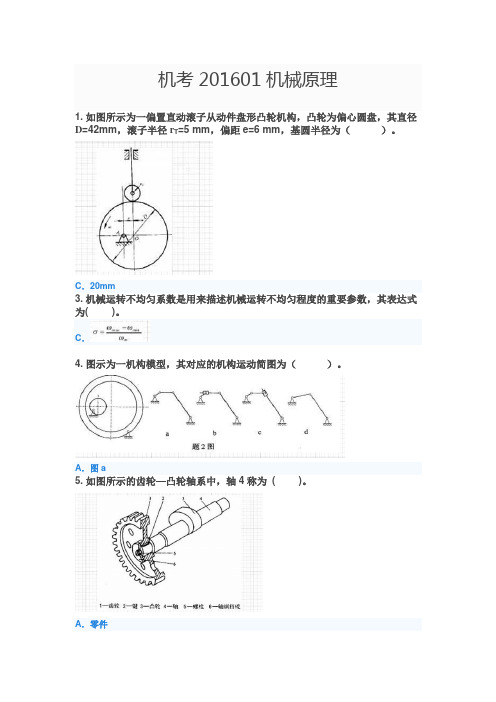
机考201601机械原理1. 如图所示为一偏置直动滚子从动件盘形凸轮机构,凸轮为偏心圆盘,其直径D=42mm,滚子半径r T=5 mm,偏距e=6 mm,基圆半径为()。
C.20mm3. 机械运转不均匀系数是用来描述机械运转不均匀程度的重要参数,其表达式为( )。
C.4. 图示为一机构模型,其对应的机构运动简图为()。
A.图a5. 如图所示的齿轮—凸轮轴系中,轴4称为( )。
A.零件6. 内燃机的主体机构是()C.连杆机构9. 一曲柄摇杆机构,若改为以曲柄为机架,则将演化为()C.双曲柄机构11.直齿圆锥齿轮的标准模数是()。
A.大端模数12.常用来传递两相交轴运动的齿轮机构是()。
C.圆锥齿轮机构13.一对齿轮啮合时,两齿轮的________始终相切C.节圆16.回转件静平衡条件是分布在回转件上的各个偏心质量的()。
A.离心惯性力合力为零18.槽轮机构所实现的运动变换是()。
C.变等速连续转动为间歇转动19.能满足超越要求的机构是()。
B.内啮合棘轮机构20.在设计直动滚子从动件盘形凸轮机构时,若发生运动失真现象,可以()。
C.增大基圆半径21.凸轮机构中的压力角是指()间的夹角A.凸轮上接触点的法线与从动件的运动方向22.在凸轮机构的从动件选用等速运动规律时,其从动件的运动( )A.将产生刚性冲击24.为保证四杆机构良好的传力性能,()不应小于最小许用值。
B.传动角25.连杆机构处在死点位置时,传动角γ是()C.等于0º26.铰链四杆机构中,若最短杆与最长杆长度之和小于其余两杆长度之和,则为了获得曲柄摇杆机构,其机架应取( )。
B.最短杆的相邻杆27.铰链四杆机构的死点位置发生在( )。
A.从动件与连杆共线位置29.在平面机构中,每增加一个低副将引入()。
C.2个约束其余为D。
机械原理大作业1
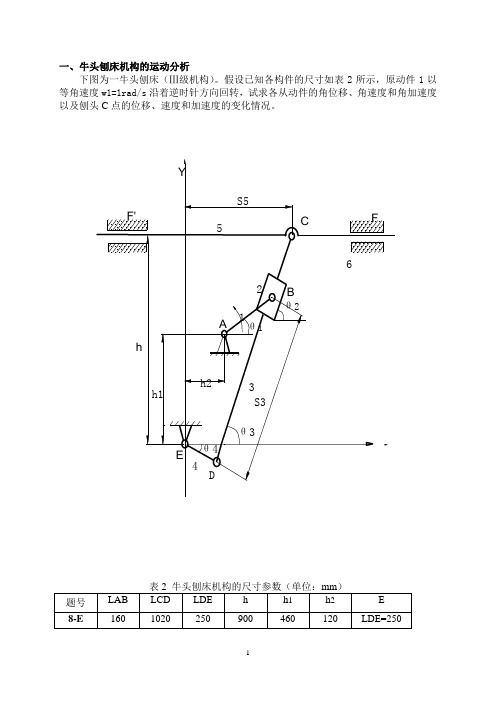
一、牛头刨床机构的运动分析下图为一牛头刨床(Ⅲ级机构)。
假设已知各构件的尺寸如表2所示,原动件1以等角速度w1=1rad/s沿着逆时针方向回转,试求各从动件的角位移、角速度和角加速度以及刨头C点的位移、速度和加速度的变化情况。
二、牛头刨床机构的运动分析方程 1)位置分析建立封闭矢量多边形建立一直角坐标系,并标出各杆矢量及其方位角,其中共有4个未知量3θ(θ2=3θ)、4θ、3S 、5S 。
利用两个封闭图形ABDEFA 和EDCGE ,建立两个封闭矢量方程,由此可得:3125DE AB DE CD l s h h l l l h s →→→→→→→→→⎧+=++⎪⎨⎪+=+⎩(1)把(1)写成投影方程得:433214331143543cos *cos *cos *sin *sin *sin *cos *cos 0*sin *sin DE AB DE AB DE CD DE CD l s h l l s h l l l s l l h θθθθθθθθθθ*+=+⎫⎪+=+⎪⎬+-=⎪⎪+=⎭(2) 由以上各式用型转化法可求得4335s s θθ、、、,滑块2的方位角23θθ=2111*cos *sin b AB b AB x h l y h l θθ=+⎧⎨=+⎩ 44*cos *sin d DE d DE x l y l θθ=⎧⎨=⎩3s =3)*sin *()/*cos *(/c d CD d CD b d c d CD d CD b d s x x l x l x x s y y l y l y y s αα=+=+-⎧⎪⎨=+=+-⎪⎩ 3tan c dc dy y x x θ-=- 5c s x =()ae AE =44()tan *cos d c DE y h y l θθ+-=高斯消去法求解 2)速度分析对(2)求一次导数得:44333331144333331144334433*sin *s '*cos *sin **sin **cos *'*sin *cos **cos **sin **sin *0*cos **cos *0DE AB DE AB DE CD c DE CD l s l l s s l l l v l l θωθθωθωθωθθωθωθωθωθωθω-+-=-⎫⎪++=⎪⎬---=⎪⎪+=⎭(3)矩阵式:3334313334313443cos *sin *sin 0'*sin sin *cos *cos 0*cos 0*sin *sin 100*cos *cos 00DE AB DE AB CD DE CD DE c s l s l s l l l l l l v θθθθθθθθθθωθθ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥ω⎢⎥⎢⎥⎢⎥=ω1⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (4)采用高斯消去法可求解(4)可解得角速度ω2,ω3; 3)加速度分析把(4)对时间求导数得:333433334334434cos *sin *sin 0''sin *cos *cos 00*sin *sin 10*cos *cos 0DE DE CD DE CD DE c s l s s l l l l l a θθθθθθθθαθθ--⎡⎤⎡⎤⎢⎥⎢⎥α⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦33333444433333343443334443344*sin '*sin **cos **cos 0'*cos '*cos **sin **sin 00**cos **cos 00**sin **sin 0DE DE CD DE CD DE c s s l s s s l l l l l v ωθθωθωθωθθωθωθωθωθωωθωθ----⎡⎤⎡⎤⎢⎥⎢⎥--ω⎢⎥⎢⎥=-⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦1111**cos **sin 00AB AB l l ωθωθ-⎡⎤⎢⎥-⎢⎥+ω1⎢⎥⎢⎥⎣⎦(5)采用高斯消去法可求解(5)可解得角加速度α2,α3,α5,α6三、程序流程图四、计算源程序#include<stdio.h>#include<stdlib.h>#include<math.h>/* 定义变量*/const double PI = 3.14159265358979;const int N = 4;const double EPSILON = 0.0001;const int T = 1000;/* 代入已知量*/double Lab=160,Lcd=1020,Lde=250,h=900,h1=460,h2=120,Omega1=1;/* 声明子函数*/void AngleDisplacement(double[12],double);/* 角位移函数*/void AngleVelocity(double[N][N],double[N],double[12],double);/* 角速度函数*/void AngleAcceleration(double[N][N],double[N][N],double[N],double [12]);/* 角加速度函数*/void GaussE(double [N][N],double [N],double [N]);/* 高斯消去法函数*/void ModulusMatrixA(double [12],double [N][N]);/* 矩阵A函数*/void ModulusMatrixB(double [12],double ,double [N]);/* 矩阵B函数*/void MatrixDA(double [12],double [N][N]);/* 矩阵DA函数*/void MatrixDB(double [12],double ,double [N]);/* 矩阵DB函数*//* 主函数*/void main(){int i,j;FILE *fp;double data[36][12];double value[12],a[N][N],da[N][N],b[N],db[N],Phi1;char flag;/* 打开文件*/if((fp = fopen("Data","w")) == NULL){printf("文件打开错误!\n");exit(0);}fprintf(fp,"Lab =%lf \n",Lab);fprintf(fp,"s3\tPhi3\tPhi4\ts5\t");fprintf(fp,"s3'\tOmega3\tOmega4\ts5'\t");fprintf(fp,"s3''\tEpsilon3\tEpsilon4\ts5''");printf("\n\n 牛头刨床机构运动分析程序\n\n\n");printf("\n");printf(" 是否开始计算(Y/N):");scanf("%c",&flag);if(flag =='Y'){/*计算并写入文件*/value[0] = 480;value[1] = 65 * PI / 180;value[2] = 10 * PI / 180;value[3] = 500;for(i = 0;i < 36; i++){Phi1 = i * PI / 18;AngleDisplacement(value,Phi1);ModulusMatrixB(value,Phi1,b);ModulusMatrixA(value,a);AngleVelocity(a,b,value,Phi1);MatrixDA(value,da);MatrixDB(value,Phi1,db);AngleAcceleration(a,da,db,value);for(j = 1;j < 3; j++)value[j] = value[j] * 180 / PI;for(j = 0;j < 12; j++)data[i][j] = value[j];fprintf(fp,"\n");for(j = 0;j < 12; j++)fprintf(fp,"%12.3f\t",data[i][j]);}fclose(fp);/* 输出数据*/printf("\n\n\n计算结果如下:\n");for(i = 0;i < 36; i++){Phi1=i * PI / 18;printf("\n输出Phi1=%d时的求解\n",i*10);printf(" S3 Phi3 Phi5 S5\n");for(j = 0;j < 4; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3' Omega3 Omega5S5'\n");for(j = 4;j < 8; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3'' Epsilon3 Epsilon5 S5''\n");for(j = 8;j < 12; j++)printf("%lf\t",data[i][j]);printf("\n");}printf("\n程序运行结束,计算结果已写入Date文件中,请打开查看。
机械原理大作业1(连杆机构)27题matlab程序

附录:程序清单yy=(0:0.1:360); %杆AB的角位移,每隔0.1度计数yy1=yy/180*pi;%转化为弧度xb=280*cos(yy1);%点B的x坐标yb=280*sin(yy1);%点B的y坐标w=10;%杆AB的角速度vxb=-w*yb;%点B的速度在x方向的分量vyb=w*xb;% 点B的速度在y方向的分量axb=-w*w*xb;% 点B的加速度在x方向的分量ayb=-w*w*yb;% 点B的加速度在y方向的分量xd=0;%点D的x坐标yd=160;% 点D的y坐标vxd=0;%点D的速度在x方向的分量vyd=0;% 点D的速度在y方向的分量axd=0;% 点D的加速度在x方向的分量ayd=0;%点D的加速度在y方向的分量jbcd=ones(1,3601);%给角BCD赋初值fdb=ones(1,3601);%?给角BD赋初值li=350;%杆BC的长度lj=320;%杆CD的长度lbd=ones(1,3601);%给BD赋初值fi=ones(1,3601);% 给杆BC的角位移赋初值fj=ones(1,3601);%给杆CD的角位移赋初值xc=ones(1,3601);% 给点Cx坐标赋初值yc=ones(1,3601);% 给点Cy坐标赋初值ci=ones(1,3601);%给中间变量赋初值cj=ones(1,3601);% 给中间变量赋初值wi=ones(1,3601);% 给杆BC的角速度赋初值wj=ones(1,3601);% 给杆CD的角速度赋初值ss=ones(1,3601);% 给ss赋初值ffg=ones(1,3601);%给构件5的角位移赋初值xg=-25;%点G的x坐标yg=80;% 点G的y坐标vxg=0;%点G的速度在x方向的分量vyg=0;% 点G的速度在y方向的分量axg=0;% 点G的加速度在x方向的分量ayg=0;% 点G的加速度在y方向的分量wgf=ones(1,3601);%给杆GF的角速度赋初值%求角BCD,角BDfor m=1:3601lbd(1,m)=sqrt((xd-xb(1,m))^2+(yd-yb(1,m))^2);if (lbd(1,m)<(li+lj)&&lbd(1,m)>abs(lj-li))jbcd(1,m)=acos((li*li+lbd(1,m)*lbd(1,m)-lj*lj)/(2*li*lbd(1,m)));elseif lbd(1,m)==(li+lj)jbcd(1,m)=0;elseif (lbd(1,m)==abs(lj-li)&&(li>lj))jbcd(1,m)=0;elseif (lbd(1,m)==abs(lj-li)&&(li<lj))jbcd(1,m)=pi;endif (xd>xb(1,m) && yd>=yb(1,m))fdb(1,m)=atan((yd-yb(1,m))/(xd-xb(1,m)));elseif (xd==xb(1,m) && yd>yb(1,m))fdb(1,m)=pi/2;elseif (xd<xb(1,m)&&yd>=yb(1,m))fdb(1,m)=atan((yd-yb(1,m))/(xd-xb(1,m)))+pi;elseif (xd==xb(1,m)&&yd<yb(1,m))fdb(1,m)=3*pi/2;elseif (xd>xb(1,m)&&yd<yb(1,m))fdb(1,m)=atan((yd-yb(1,m))/(xd-xb(1,m)))+2*pi;elseif (xd<xb(1,m)&&yd<yb(1,m))fdb(1,m)=atan((yd-yb(1,m))/(xd-xb(1,m)))+pi;endfi(1,m)=fdb(1,m)-jbcd(1,m);% 杆BC的角位移if fi(1,m)<0fi(1,m)=fi(1,m)+2*pi;endend%求点C的坐标xc=xb+li*cos(fi);yc=yb+li*sin(fi);for n=1:3601%求杆CD的角位移if (xc(1,n)>xd && yc(1,n)>=yd)fj(1,n)=atan((yc(1,n)-yd)/(xc(1,n)-xd));elseif (xc(1,n)==xd && yc(1,n)>yd)fj(1,n)=pi/2;elseif (xc(1,n)<xd && yc(1,n)>=yd)fj(1,n)=atan((yc(1,n)-yd)/(xc(1,n)-xd))+pi;elseif (xc(1,n)<xd && yc(1,n)<yd)fj(1,n)=atan((yc(1,n)-yd)/(xc(1,n)-xd))+pi;elseif (xc(1,n)==xd && yc(1,n)<yd)fj(1,n)=pi/2*3;elseif (xc(1,n)>xd && yc(1,n)<=yd)endendci=li*cos(fi);cj=lj*cos(fj);si=li*sin(fi);sj=lj*sin(fj);g1=ci.*sj-cj.*si;%求杆BC、CD的角速度wi=(cj*vxd-cj.*vxb+sj*vxd-sj.*vyb)./g1;wj=(ci*vxd-ci.*vxb+si*vxd-si.*vyb)./g1;g2=-axb+wi.^2.*ci-wj.^2.*cj;g3=-ayb+wi.^2.*si-wj.^2.*sj;%求杆BC、CD的角加速度ei=(g2.*cj+g3.*sj)./g1;ej=(g2.*ci+g3.*si)./g1;lbf=281.113856;ai=51.499/180*pi;fii=fi+ai*ones(1,3601);%求点F的坐标、速度、加速度xf=xb+lbf*cos(fii);yf=yb+lbf*sin(fii);vxf=vxb-lbf*wi.*sin(fii);vyf=vyb+lbf*wi.*cos(fii);axf=axb-lbf*wi.^2.*cos(fii)-lbf*ei.*sin(fii);ayf=ayb-lbf*wi.^2.*sin(fii)-lbf*ei.*cos(fii);%求杆GF的角位移for i=1:3601ss(1,i)=sqrt((xg-xf(1,i))^2+(yg-yf(1,i))^2);if xf(1,i)>xg && yf(1,i)>=ygffg(1,i)=atan((yf(1,i)-yg)/(xf(1,i)-xg));elseif xf(1,i)==xg && yf(1,i)>ygffg(1,i)=pi/2;elseif xf(1,i)<xg && yf(1,i)>=ygffg(1,i)=atan((yf(1,i)-yg)/(xf(1,i)-xg))+pi;elseif xf(1,i)<xg && yf(1,i)<ygffg(1,i)=atan((yf(1,i)-yg)/(xf(1,i)-xg))+pi;elseif xf(1,i)==xg && yf(1,i)<ygffg(1,i)=3*pi/2;elseif xf(1,i)>xg && yf(1,i)<ygendend%求杆GF的角速度for i=1:3601if ss(1,i)==0wgf(1,i)=0;else wgf(1,i)=(vyf(1,i)*cos(ffg(1,i))-vxf(1,i)*sin(ffg(1,i)))/ss(1,i); endend%求杆GF的角加速度vss=vxf.*cos(ffg)+vyf.*sin(ffg);egf=(ayf.*cos(ffg)-axf.*sin(ffg)-2*vss.*wgf)./ss;%画图%plot(xf,yf,'r')%plot(yy,xf,'k-',yy,yf,'r--')%plot(yy,vxf,'k-',yy,vyf,'r--')%plot(yy,axf,'k-',yy,ayf,'r--')%plot(yy,ffg,'k-')%plot(yy,wgf,'k-')plot(yy,egf,'k-')grid on%画网格线。
北科大机械原理全书习题解答集
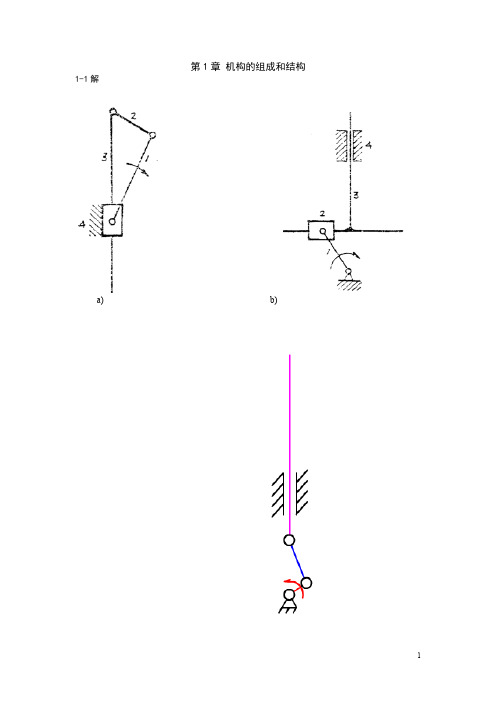
第1章机构的组成和结构1-1解a) b)c) 缺 d)1-2解 a)该机构中的F 处为符合铰链。
计算机构自由度: b)将机构中的虚约束部分去掉不计,则c)将机构中的虚约束(H 处)、局部自由度(B 处)去掉,则 F = 3n - 2P 5- P 4 = 3×6- 2×8- 1=1 此机构应有1个原动件。
1-3解1)绘制机构运动简图。
选定一适当的比例尺和视图平面,并依次定出各转动副的位置和移动副导路的方位;画出各运动副的符号,并用线条连接,即得该初拟方案的运动简图如图所示。
1072532345=-⨯-⨯=--=p p n F 07545===p p n ,处为复合铰链) (C , , 0, 13, 945===p p n 10132932345=-⨯-⨯=--=p p n F2)计算其机构自由度。
由机构运动简图可知,该机构具有三个活动构件1、3、4三个转动副A 、B 、C 、一个移动副和一个高副,没有局部自由度和虚约束,故此机构的自由度为:3)分析能否实现设计意图F = 0 ,说明该方案不能实现设计意图,从图中C 的运动也可分析出:构件3上C 点的运动轨迹应为圆弧,而构件4上的C 点的运动轨迹应为直线,显然不可能实现设计意图。
4)实现设计意图 需在C 处增加一个自由度,其改进后的方案如图所示(还可有其他方案)。
1-4解a) 计算运动链的自由度:分析能否实现设计意图:不能实现从动件的往复移动,设计意图不能满足。
b) 计算运动链的自由度:分析能否实现设计意图:不能实现从动件的往复移动,设计意图不能满足。
1-5解a)(原题1-2)b) 自由度计算:n = 7, P 5 =10, P 4 = 0162432345=-⨯-⨯=--=p p n F 0142332345=-⨯-⨯=--=p p n F 0142332345=-⨯-⨯=--=p p n FF = 3×7-2×10-0= 1结构分析:依次拆下6-7,4-5,2-3 三个Ⅱ级杆组,故该机构为Ⅱ级机构。
机械原理大作业凸轮机构设计

机械原理大作业凸轮机构设计一、凸轮机构概述凸轮机构是一种常见的传动机构,它通过凸轮的旋转运动,带动相应零件做直线或曲线运动。
凸轮机构具有结构简单、运动平稳、传递力矩大等优点,在各种机械设备中得到广泛应用。
二、凸轮基本结构1. 凸轮凸轮是凸起的圆柱体,通常安装在主轴上。
其表面通常为圆弧形或其他曲线形状,以便实现所需的运动规律。
2. 跟随件跟随件是与凸轮配合的零件,它们通过接触面与凸轮相互作用,并沿着规定的路径做直线或曲线运动。
跟随件可以是滑块、滚子、摇臂等。
3. 连杆连杆连接跟随件和被驱动部件,将跟随件的运动转化为被驱动部件所需的运动。
连杆可以是直杆、摇杆等。
三、凸轮机构设计要点1. 几何参数设计设计时需要确定凸轮半径、角度和曲率半径等参数,这些参数的选择将直接影响凸轮机构的运动规律和性能。
2. 运动规律设计根据被驱动部件的运动要求,选择合适的凸轮曲线形状,以实现所需的运动规律。
3. 稳定性设计在设计凸轮机构时,需要考虑其稳定性。
例如,在高速旋转时,可能会发生跟随件脱离凸轮或者产生振动等问题,因此需要采取相应措施提高稳定性。
4. 材料和制造工艺设计在材料和制造工艺方面,需要考虑凸轮机构所承受的载荷和工作环境等因素,选择合适的材料和制造工艺。
四、几种常见凸轮机构及其应用1. 摇臂式凸轮机构摇臂式凸轮机构由摇臂、连杆和被驱动部件组成。
它通常用于实现直线运动或旋转运动,并且具有结构简单、运动平稳等优点。
摇臂式凸轮机构广泛应用于各种机械设备中,如发动机气门控制系统、纺织设备等。
2. 滑块式凸轮机构滑块式凸轮机构由凸轮、滑块、连杆和被驱动部件组成。
它通常用于实现直线运动,并且具有结构简单、运动平稳等优点。
滑块式凸轮机构广泛应用于各种机械设备中,如冲压设备、印刷设备等。
3. 滚子式凸轮机构滚子式凸轮机构由凸轮、滚子、连杆和被驱动部件组成。
它通常用于实现圆弧形运动,并且具有运动平稳、传递力矩大等优点。
滚子式凸轮机构广泛应用于各种机械设备中,如汽车发动机气门控制系统等。
机械原理大作业范文

机械原理大作业范文摘要:机械传动是机械学中的基础内容之一,广泛应用于各个行业和领域。
本文将对机械传动的原理、类型以及应用进行系统的介绍和探讨。
首先介绍了机械传动的定义和作用,然后详细介绍了各种常见的机械传动类型,包括齿轮传动、皮带传动、链传动等,并分别对其工作原理进行了分析。
最后列举了一些机械传动的应用案例,证明了机械传动在现实生活中的重要性和广泛性。
一、引言机械传动是将动力从一个地方传递到另一个地方的机械装置。
它作为机械工程学的基础内容,广泛应用于工业、农业、建筑等各个领域。
机械传动具有传递力量的功能,并能实现运动的改变、平衡、变速等目的。
本文将对机械传动的类型、原理以及应用进行详细介绍。
二、机械传动的类型机械传动可以分为多种类型,常见的有齿轮传动、皮带传动、链传动等。
齿轮传动是利用齿轮间的啮合来传递扭矩和运动的一种传动方式,具有传动效率高、传动比稳定等优点。
皮带传动则是通过绕在两个轮子上的带子来传递力量,常用于需要减速的场合。
链传动与皮带传动类似,但是链传动的传动效率更高,扭矩传递更稳定。
三、机械传动的工作原理1.齿轮传动:齿轮传动采用齿轮之间的啮合来实现传动的目的。
主要通过齿轮的大小、齿数来调整传递的速度和扭矩。
其中,齿轮的齿数比称为传动比,可以实现速度的改变。
齿轮传动通常包括齿轮轴、轴承、齿轮齿廓等组成部分。
2.皮带传动:皮带传动通过绕在轮子上的带子来传递力量。
常见的皮带传动有平行轴带传动和交叉轴带传动。
通过调整轮子的直径和材料来改变传递效果。
皮带传动具有传递动力平稳、减震效果好的特点。
3.链传动:链传动与皮带传动类似,也是通过绕在轮子上的链条来传递力量。
链传动具有噪音低、传动效率高等优点,广泛应用于自行车、摩托车等交通工具中。
四、机械传动的应用1.工业应用:机械传动在工业制造中有广泛的应用。
例如,齿轮传动被广泛应用于机床、起重机械、输送设备等,实现力量的传递和工作的协调。
皮带传动常用于风机、泵等需要平稳传递动力的设备中。
机械原理课程大作业

机械原理课程大作业基于MATLAB平面连杆机构运动学和动力学分析指导老师:王玉丹目录作业一:平面连杆机构运动学分析第2页作业二:平面连杆机构动力学分析第15页作业一L(AE)=70mm,L(AB)=40mm,L(EF)=60mm,L(DE)=35mm,L(CD)=75m m,L(BC)=50mm,原动件以等角速度W1=10rad/s回转。
试以图解法求在θ1=50°时C点的速度和加速度.对机构进行运动分析,写出C点的位置、速度及加速度方程。
解题过程:令AB=r1, BC=r2, CD=r3, DE=r4,AE=r6,EF=r8, AF=r7,角EAF=θ1。
分析:对机构进行位置分析由封闭形ABCDEA可得:r1+r2=r6+r3+r4 (1)由封闭图形AEFA可得:r7=r6+r8 (2)将(1)(2)两式整理可得:r2-r3-r4=-r1+r6-r8+r7=r6【一】(1)位置方程:【二】速度方程:【三】加速度方程:【四】根据位置方程式编制如下函数:【五】进行数据输入,运行程序进行运算。
根据上面分析的θ1 的极限位置取θ1 的范围为40°-55°并均分成15个元素:输出的P、矩阵的第二列到第四列分别是θ2 、θ3 、4θ4 的值,第一列是AF杆的长度r1’。
【六】第二步根据速度方程式编写如下函数:根据第一步得到的数据进行数据输入,运行程序计算各速度值。
程序如下:程序运行得到q矩阵,第一行到第三行分别是a2、a3、a4 的值,第四行是杆AF上滑块运动的速度,即F点的速度。
【七】第三步编写加速度计算函数:【八】根据第一步和第二步输入数据,运行程序得到各加速度的值:【1】计算C点在θ1 =55°,w1 =10rad/s时的速度,加速度:总结数据绘出各构件的位置、速度和加速度的表格如下:【2】输出图像1)角位置程序及输出的图像:2)F点速度程序及输出的图像:3)角加速度程序及输出的图像:4)F点的加速度程序及输出图像:作业二在图示的正弦机构中,已知:L(AB)=100mm,h1=120mm,h2=80mm, W1=10rad/s(常数),滑块2和构件3的重量分别为,G2 =40 N 和G3 =100 N,质心S2 和S3 的位置如图所示,加于构件3上的生产阻力Fr=400 N,构件1的重力和惯性力略去不计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械原理大作业
项目名称:直折伞机构分析
组员:
1、实物图
2、雨伞的使用功能及使用场合
提供阴凉环境或遮蔽雨、雪的工具。
也可作为装饰物,拐杖或兵器。
3、分析机构的运动,判断原动件的数目、画出机构运动简图,并计算其自由度
机构运动简图1为主动件,向上运动压缩弹簧可实现打开,向下
运动时通过拉伸弹带动2向下运动可实现收伞。
原动件数目:5
计算自由度:F=3(n-1)-2p4-p5,
该机构中6视为机架,共5个构件,7个低副,0个高副,即n=5,p4=7,p5=0。
F=3x5-2x7-0=1自由度为1。
4、大致测绘出构件尺寸,并进行高副低代。
数据测绘如下(mm):
AB=50,BC=80,AC=70,AD=225,DE=230
该机构不存在高副。
5、确定机构所含杆组的数目和级别(拆杆组),并判断机构的级别。
该机构可拆分为1个三级杆组,所以该机构等级为三级。
6、用图解法求出最小传动角值
最小传动角为图中
7、分析该机构有无急回特性和死点位置
无
8、机构运动分析
位移分析如图
速度分析如图
加速度分析如图
9、分析该机构的优缺点,如何改进其不足
优点:防风效果好,结实耐用,结构简单,制造方便,经济成本低。
缺点: 打开及收回时比较费力,携带不方便,闲置时占空间较大。
将伞柄处设计为自动按钮控制收缩,每次使用完毕按照伞布面的褶印进行整理装入指定的收纳袋里根据空间合理选择放置方式。
