六年级数学最小公倍数
六年级数学因数和倍数试题答案及解析

六年级数学因数和倍数试题答案及解析1.根据下列概念间的逻辑关系将下表补充完整。
因数、偶数、倍数、公因数、质数、最大公因数、公倍数、1、最小公倍数、分解质因数、2、5、3倍数特征、奇数、合数、互质数。
【答案】【解析】本题根据相关概念之间的逻辑关系进行分析填空即可:题目有两个关系表:表一:第一个概念是因数,两个整数相乘,其中这两个数都叫做积的因数因数.由此可知,因数中包括大于0的自然数,即1,合数与质数,而几个有共同因数的合数共有公因数;因数中包含最大公因数,几个数共有的因数,叫做这几个数的公因数.其中最大的公因数叫做这几个数的最大公因数.通过对最大公因数进行分解质因数,可以得到互质数。
表二:倍数为一个整数能够被另一整数整除,这个整数就是另一整数的倍数.倍数中包含公倍数,即几个数公有的倍数叫公倍数.公倍数中包含最小公倍数.能被2整数的数个位数一定为偶数;各个数位上的数相加的和能被3整数,则这个数也能被3整数,能被3整除的数可为奇数,也可为偶数;个位数为0或5的数能被5整数,能被5整除的数可为偶数,也可能是奇数。
据此填表即可.解:根据相关概念之间的逻辑关系可得:2.古希腊认为:如果一个数恰好等于它的所有因数(本身除外)相加之和,那么这个数就是“完全数”。
例如:6有四个因数1、2、3、6,除本身6以外,还有1、2、3三个因数。
6 = 1+2+3,恰好是所有因数之和,所以6就是“完全数”。
下面的数中是“完全数”的是()。
A.12B.28C.36D.48【答案】B【解析】这道题能正确理解完全数的定义是关键。
根据题中叙述的完全数的定义,分别找出这四个数的因数后发现28的因数有1、2、4、7、14、28,除 28外 ,1+2+4+7+14=28,所以28是完全数。
3.(2011•武汉)某个四位数有如下特点:它加上1之后是15的倍数,它减去3之后是38的倍数.把它的各数位上的数字左右倒过来写,所得的新数与原数之和能被10整除,这个四位数是多少?【答案】所求的四位数是1409或1979【解析】原数加1后是15的倍数,所以这个四位数必是5的倍数,所以个位数字是4或9,又因为原数减去3后是38的倍数,是一个偶数,可得原数应该是奇数,所以原数的个位数字只能是9,再从条件(3)可知:原数的个位数字与千位数字之和是10,所以千位数字是10﹣9=1,设原数为38m+3(m为自然数),则有1009≤38m+3≤1996,据此可得26≤m≤53,据此再进行分析即可解答.解答:解:原数加1后是15的倍数,所以这个四位数必是5的倍数,所以个位数字是4或9,又因为原数减去3后是38的倍数,是一个偶数,可得原数应该是奇数,所以原数的个位数字只能是9,再从条件(3)可知:原数的个位数字与千位数字之和是10,所以千位数字是10﹣9=1,设原数为38m+3(m为自然数),则有1009≤38m+3≤1996,可得26≤m≤53,因为原数38m+3的个位数字是9,所以8m的个位数字是6.从而m的个位数字是2或7,在26到53之间,个位数字是2或7的数有27、32、37、42、47、52,又因为原数加上1后是15的倍数,则38m+3+1=38m+4是3的倍数,则19m+2必定是3的倍数,19m+2=3×6m+m+2,所以m+2是3的倍数,即m被3除余1,在27、32、37、42、47、52中,只有37和52被3除余1,所以m=37或52,所以38×37+3=1409,38×52+3=1979,经检验正好满足题意,答:所求的四位数是1409或1979.点评:根据题干,明确四位数的个位数字和千位数字分别是9和1,再根据被15整除的数的特征和偶数特征进行分析即可解答.4.(2014•长沙县)下面哪些数能被11整除()A. 323532 B. 38380 C. 978768【答案】A【解析】能被11整除的数,奇数位(从左往右数)上的数字和与偶数位上的数字和之差(大数减小数)能被11整除,则该数就能被11整除.由此方法判定即可.解答:解:A.(3+3+3)﹣(2+5+2)=0,能被11整除,故A正确;B.(8+8)﹣(3+3+0)=10,不能被11整除,故B错误;C.(9+8+6)﹣(7+7+8)=2,不能被11整除,故C错误.故选:A.点评:掌握被一个数整除数的特征,牢记判定方法是解决问题的根本.5.(2011•武汉)某个四位数有如下特点:它加上1之后是15的倍数,它减去3之后是38的倍数.把它的各数位上的数字左右倒过来写,所得的新数与原数之和能被10整除,这个四位数是多少?【答案】所求的四位数是1409或1979.【解析】原数加1后是15的倍数,所以这个四位数必是5的倍数,所以个位数字是4或9,又因为原数减去3后是38的倍数,是一个偶数,可得原数应该是奇数,所以原数的个位数字只能是9,再从条件(3)可知:原数的个位数字与千位数字之和是10,所以千位数字是10﹣9=1,设原数为38m+3(m为自然数),则有1009≤38m+3≤1996,据此可得26≤m≤53,据此再进行分析即可解答.解答:解:原数加1后是15的倍数,所以这个四位数必是5的倍数,所以个位数字是4或9,又因为原数减去3后是38的倍数,是一个偶数,可得原数应该是奇数,所以原数的个位数字只能是9,再从条件(3)可知:原数的个位数字与千位数字之和是10,所以千位数字是10﹣9=1,设原数为38m+3(m为自然数),则有1009≤38m+3≤1996,可得26≤m≤53,因为原数38m+3的个位数字是9,所以8m的个位数字是6.从而m的个位数字是2或7,在26到53之间,个位数字是2或7的数有27、32、37、42、47、52,又因为原数加上1后是15的倍数,则38m+3+1=38m+4是3的倍数,则19m+2必定是3的倍数,19m+2=3×6m+m+2,所以m+2是3的倍数,即m被3除余1,在27、32、37、42、47、52中,只有37和52被3除余1,所以m=37或52,所以38×37+3=1409,38×52+3=1979,经检验正好满足题意,答:所求的四位数是1409或1979.点评:根据题干,明确四位数的个位数字和千位数字分别是9和1,再根据被15整除的数的特征和偶数特征进行分析即可解答.6.(2013•浦口区)甲、乙两个数,甲数除以乙数商2余17,乙数的10倍除以甲数商3余45.求甲、乙二数.【答案】甲数是 65,乙数是 24【解析】被除数、除数、商和余数的关系:被除数=除数×商+余数.如果设乙数为 x,则根据甲数除以乙数商 2 余 17,得甲数=2x+17.又根据乙数的 10 倍除以甲数商3余45得10x=3(2x+17)+45,列出方程并解方程,即可得解.解答:解:设乙数为x,则甲数为2x+1710x=3(2x+17)+4510x=6x+51+454x=96x=242x+17=2×24+17=65.答:甲数是 65,乙数是 24.点评:灵活应用余数的性质“被除数=除数×商+余数”来解决实际问题.7.我国著名的数学家陈景润要证明“哥德巴赫猜想”:“任何一个大于4的偶数,一定是两个奇素数的和.”俗称“1+1=2”.试将大于4且小于30的偶数分别写成2个奇素数的和.【答案】22=5+17,24=7+17,26=3+23,28=5+23.【解析】只有1和它本身两个约数的数是质数,除了1和它本身还有别的约数的数是合数,是2的倍数的数是偶数,不是2的倍数的数是奇数,由此即可得答案.解答:解:大于4且小于30的偶数分别写成2个奇素数的和有:22=5+17,24=7+17,26=3+23,28=5+23.点评:解答本题要明确自然数,质数,合数的概念,熟记30以内的质数表.要注意写出的两个数都要是质数.8.一个合数至少有()个约数.A. 1 B. 2 C. 3【答案】C【解析】根据合数的概念即可解答.解答:解:一个数,如果除了1和它本身还有别的因数,这样的数叫做合数;由此一个合数至少有3个约数.答:一个合数至少有3个约数.故选:C.点评:此题考查的目的是理解和掌握合数的概念和内涵,据此解决有关的问题.9.把726分解质因数.【答案】726=3×2×11×11【解析】分解726,可以先用质数3去除,得242,再用质数2去除,再用质数11去除即可解答.解:726=3×2×11×11,故答案为:726=3×2×11×11.点评:考查了分解质因数的方法,一般要先用质数3、2、5去除.10.a口bc是一个四位数,已知a+b+c=15,且以a口bc是3的倍数,方框中可填的数有( )个。
如何求最小公倍数

如何求最小公倍数和最大公因数1、列举法例如:求6和8的最小公倍数。
6的倍数有:6,12,18,24,30,36,42,48,……8的倍数有:8,16,24,32,40,48,……6和8的公倍数:24,48,……其中24是6和8的最小公倍数。
这种方法是先分别写出各自的倍数,再找出它们的公倍数,然后在公倍数里找出它们的最小公倍数。
2、分解质因数法。
我们也可以利用分解质因数的方法,比较简便地求出两个数的最小公倍数。
例如:求60和42的最小公倍数。
60=2×2×3×5 42=2×3×760和42的最小公倍数=2×3×2×5×7=420 。
这种方法是把60和42分别质因数后,观察相同的质因数只取一个(如2,3),把各自独有的质因数全部乘进去,所得的积就是这两个数的最小公倍数。
相同的质因数的乘积就是最大公因数。
3、短除法。
用短除法求。
例如:18和24的最小公倍数。
4、判断法。
(1)如果a.b是互质数,那么a.b的最小公倍数是a×b。
如:求4和5的最小公倍数。
4和5是互质数,那么4和5的最小公倍数是4×5=20 。
(2)如果两个数中,较大的数是较小数的倍数,那么较大的数是这两个数的最小公倍数。
较小的数就是这两个数的最大公因数。
如:求16和8的最小公倍数。
16是8的倍数,那么16就是16和8的最小公倍数。
8就是16和8的最大公因数。
过关练习一、找出每组数的最小公倍数。
2和4 6和10 5和8 10和48和10 6和12 12和10 15和5二、找出每组数的最大公因数。
10和6 20和30 12和24 14和2133和11 13和7 15和21 35和25三、填空。
1、如果a ÷b =4,(a 和b 均为非0自然数),那么a 与b 的最大公因数是( ),最小公倍数是( )。
2、一个数它既是12的倍数,也是12的因数,这个数是( ),它与8的公因数有( ),最小公倍数是( )。
六年级公倍数和最小公倍数

公倍数和最小公倍数一.知识点总结1.几个整数的公有的倍数叫做它们的公倍数,其中最小的一个叫做它们的最小公倍数。
2.求两个整数的最小公倍数,只要取它们所有公有的素因数,再取它们各自剩余的素因数,将这些连乘,所得的积就是这两个数的最小公倍数。
3.如果两个整数中某一个数是另一个数的倍数,那么这个数就是它们的最小公倍数。
如果两个数互素,那么它们的乘积就是它们的最小公倍数。
二.例题解析例题1:求12和30的最小公倍数.例题2:求36和84的最小公倍数.例题3:求30和45的最大公因数和最小公倍数.例题4:3和15的最小公倍数是:;18和36的最小公倍数是:;6和7的最小公倍数是:;8和15的最小公倍数是: .通过求这四组数的最小公倍数,你发现什么规律了吗?规律:两个整数中,如果:1)某个数是另一个数的,那么它们的最小公倍数就是;2)这两个数,那么它们的最小公倍数就是 .三.课堂练习一、填空题3.3和5的最大公因数是 ,最小公倍数是 .二、选择题4.36和48的最小公倍数是 ( )A .12B .48C .96D .1445.甲数=2×2×3×5,乙数=2×3×3×5,甲数和乙数的最小公倍数是 ( )A .2×3×5B .2×2×3×5C .2×3×3×5D .2×2×3×3×56.a 、b 都是正整数,如果a =3b ,那么a 、b 的最小公倍数是 ( )A .3abB .aC .bD .ab三、简答题7.求下列分数中两个分母的最小公倍数:365和607 3911和787 173和6858.求下列各组数的最大公因数和最小公倍数.16和20 23和92 21和35提高题:1.一对互素数的最小公倍数是20,那么这两个数分别是和 .2.两个数的最大公因数是4,最小公倍数是24,其中一个数是12,则另一个数是 .3.甲、乙两户人家住在同一个小区,甲每6天去超市购物一次,乙每9天去同一家超市购物一次,元旦这一天两户人家都去这家超市购物,至少再经过多少天他们又会在同一天都去超市购物?四.课后练习一、填空题3.8和9的最小公倍数是,相邻两数的最小公倍数是 .4. 4和7的最小公倍数是,如果两数互素,它们的最小公倍数就是 .5.3和6的最小公倍数是 .6.72和12的最小公倍数是 .二、选择题7.下列说法中正确的是的是…………………………………()(A)5和6 的最小公倍数是1(B)21和9的最小公倍数是21×9(C)7和11没有最小公倍数(D)甲数=2×2×3,乙数=2×3×3,甲数和乙数的最小公倍数是2×2×3×3三、求下列各题中两数的公倍数8、8和12 9、42和14 10、16和24提高训练四、简答题11.已知甲数=2×3×5×A,乙数=2×3×7×A,甲乙两数的最大公因数是30,求甲乙两数的最小公倍数.课后练习2一、填空题2.50以内的正整数中,3和5的公倍数有 .3.3和5的最大公因数是,最小公倍数是 .4.5和15的最大公因数是,最小公倍数是 .5.10和25的最大公因数是,最小公倍数是 .二、简答题6、求下列每组数最大公因数和最小公倍数.(1)15和65 (2)24和307、6年级1班大约有50人左右,排座位时老师发现刚好可以排成6排或8排,求6年级1班的学生人数.五、简答题8、某数被2除余1,被3除余2,被4除余3,被5除余4,满足以上条件的数有多少个?求最小的一个.。
六年级公因数与公倍数

学员姓名:学科教师:年级:辅导科目:授课日期××年××月××日时间A / B / C / D / E / F段主题公因数与公倍数教学内容1.理解公因数,最大公因数和素因数的意义,并会求两个数的公因数,最大公因数,知道互素和素数的区别;2.理解公倍数、最小公倍数的意义,掌握求公倍数、最小公倍数的基本方法;3.会合理使用列举法、分解素因数法、短除法求两个数的最大公因数、最小公倍数.(此环节设计时间在40-50分钟)案例1:公因数、最大公因数操作:请分别写出6的因数,8的因数;6 的因数:1 、2 、3 、6 ;8 的因数:1 、2 、4 、8 ;问题:6与8相同的因数是什么?你能否给出几个数的公因数的定义?定义:几个数共有的因数,叫做这几个数的公因数,其中最大的一个数叫做这几个数的最大公因数例1:求8和9的所有公因数,并求它们的最大公因数。
解:8的因数有1,2,4,8;9的因数有1,3,9;8和9只有公因数1,因此8和9的最大公因数是1;结论:如果两个整数只有公因数1,那么称这两个数互素.练习1.下列每组数中的两个数不是互素的是()A、5和6;B、21和9;C、7和11;D、25和26.2.下列每组数中的两个数是互素数的是( )A 、35和36;B 、27和36;C 、7和21;D 、78和26.参考答案:1.B ; 2.A ;例2:求18和30的最大公因数.解法1:18的因数有1,2,3,6,9,1830的因数有1,2,3,5,6,10,15,3018和30的公因数有1,2,3,6最大的公因数是6解法2:把18和30分别分解素因数18=2×3×330=2×3×518和30全部共有的素因数是2和3,因此2和3的乘积6就是18和30的最大公因数;结论:求几个整数的最大公因数,只要把它们所有的公共素因数连乘,所得的积就是它们的最大公因数 解法3:为了简便,也可以用短除法计算21830(2)39153 35 用公有的素因数除(用公有的素因数除)(除到两个商互素为止)18和30的最大公因数是2×3=6求下列各组数中的最大公因数;(1)45和75 (2)36和90 (3)48和72参考答案:(1)15; (2)18; (3)24案例2:公倍数、最小公倍数操作:请分别写出3的倍数,4的倍数;3的倍数: 3,6,9,12,15,18,21,24,27…;4 的倍数: 4,8,12,16,20,24,28,36,40…;问题:3与4相同的倍数是什么?你能否给出几个数的公倍数的定义?练习例:求18和30的最小公倍数.解法1:18的倍数有18,36,54,72,90,…;30的倍数有 30,60,90,120,160,….所以18和30的最小公倍数是90.解法2:把18和30分解素因数18=2×3×330=2×3×5探究:18和30的公倍数里,应当既包含18 的所有素因数,又包括30的所有素因数,但相同的素因数可以只取一个,只要取出18,30的所有公有的素因数(1个2和1个3),再取各自剩余的素因数(3和5),将这些数连乘,所得得积2×3×3×5(90)就是30和18的最小公倍数所以18和30的最小公倍数是90(2×3×3×5)结论:求两个整数的最小公倍数,只要取它们所有公有的素因数,再取它们各自剩余的素因数,将这些数连乘,所得得积就是这两个数的最小公倍数解法3:用短除法 21830(2)39153 35 用公有的素因数除(用公有的素因数除)(除到两个商互素为止)18和30的最小公倍数是2×3×3×5=90求下列各组数中的最小公倍数;(1)36和84; (2)42和14; (3)16和24;参考答案:(1)252;(2)42;(3)48练习3 532 18的素因数30的素因数 18与30公有的素因数定义:几个整数的公有的倍数叫做他们的公倍数,其中最小的一个叫做它们的最小公倍数.(此环节设计时间在20-30分钟)例题1:(1)因为10与11 是互素数,所以10与11的公因数是;(2)17和18的最大公因数是___________;(3)两个相邻正整数的最大公因数是;参考答案:(1)1;(2)1;(3)1试一试:(1)3和11的最大公因数是;(2)8和15的最大公因数是(2)18和36的最大公因数是;(3)6和48的最大公因数是;通过求这四组数中的最大公因数,你发现了什么规律?规律:两个整数中,如果两个数互素,那么它们的最大公因数就是1 ;如果某个数是另一个数的因数,那么这个数就是这两个数的最大公因数。
小学六年级数学公式大全

小学数学公式大全1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径?=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积=长×宽×高V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷3小学数学图形计算公式1 、正方形C周长S面积a边长周长=边长×4 C=4a 面积=边长×边长S=a×a2 、正方体V:体积a:棱长表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3 、长方形C周长S面积a边长周长=(长+宽)×2 C=2(a+b) 面积=长×宽S=ab4 、长方体V:体积s:面积a:长b: 宽h:高(1)表面积(长×宽+长×高+宽×高)×2 S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5 三角形s面积a底h高面积=底×高÷2 s=ah÷2 三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形s面积a底h高面积=底×高s=ah7 梯形s面积a上底b下底h高面积=(上底+下底)×高÷2 s=(a+b)× h÷28 圆形S面积C周长∏ d=直径r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9 圆柱体v:体积h:高s;底面积r:底面半径c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10 圆锥体v:体积h:高s;底面积r:底面半径体积=底面积×高÷31、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数总数÷总份数=平均数和差问题(和+差)÷2=大数(和-差)÷2=小数和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1 非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2 封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)时间单位换算1世纪=100年1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时1时=60分1分=60秒1时=3600秒积=底面积×高V=Sh第一部分:概念1、加法交换律:两数相加交换加数的位置,和不变。
小学六年级数学公式大全

小学数学公式大全1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4 C=4a3、长方形的面积=长×宽 S=ab4、正方形的面积=边长×边长 S=a.a= a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r 半径=直径÷2 r= d÷29、圆的周长=圆周率×直径=圆周率×半径×2 c=πd =2πr10、圆的面积=圆周率×半径×半径?=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积 =长×宽×高 V =abh13、正方体的表面积=棱长×棱长×6 S =6a14、正方体的体积=棱长×棱长×棱长 V=a.a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2) +2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高 V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πr h÷3=π(d÷2) h÷3=π(C÷2÷π) h÷319、长方体(正方体、圆柱体)的体1、每份数×份数=总数总数÷每份数=份数总数÷份数=每份数2、 1倍数×倍数=几倍数几倍数÷1倍数=倍数几倍数÷倍数=1倍数3、速度×时间=路程路程÷速度=时间路程÷时间=速度4、单价×数量=总价总价÷单价=数量总价÷数量=单价5、工作效率×工作时间=工作总量工作总量÷工作效率=工作时间工作总量÷工作时间=工作效率6、加数+加数=和和-一个加数=另一个加数7、被减数-减数=差被减数-差=减数差+减数=被减数8、因数×因数=积积÷一个因数=另一个因数9、被除数÷除数=商被除数÷商=除数商×除数=被除数小学数学图形计算公式1 、正方形 C周长 S面积 a边长周长=边长×4 C=4a 面积=边长×边长S=a×a2 、正方体 V:体积 a:棱长表面积=棱长×棱长×6 S表=a×a×6 体积=棱长×棱长×棱长V=a×a×a3 、长方形C周长 S面积 a边长周长=(长+宽)×2C=2(a+b)面积=长×宽S=ab4 、长方体V:体积 s:面积 a:长 b: 宽 h:高(1)表面积(长×宽+长×高+宽×高)×2S=2(ab+ah+bh)(2)体积=长×宽×高V=abh5 三角形s面积 a底 h高面积=底×高÷2s=ah÷2三角形高=面积×2÷底三角形底=面积×2÷高6 平行四边形s面积 a底 h高面积=底×高s=ah7 梯形s面积 a上底 b下底 h高面积=(上底+下底)×高÷2 s=(a+b)× h÷28 圆形S面积 C周长∏ d=直径 r=半径(1)周长=直径×∏=2×∏×半径C=∏d=2∏r(2)面积=半径×半径×∏9 圆柱体v:体积 h:高 s;底面积 r:底面半径 c:底面周长(1)侧面积=底面周长×高(2)表面积=侧面积+底面积×2(3)体积=底面积×高(4)体积=侧面积÷2×半径10 圆锥体v:体积 h:高 s;底面积 r:底面半径体积=底面积×高÷3总数÷总份数=平均数和差问题(和+差)÷2=大数(和-差)÷2=小数和倍问题和÷(倍数-1)=小数小数×倍数=大数(或者和-小数=大数)差倍问题差÷(倍数-1)=小数小数×倍数=大数(或小数+差=大数)植树问题1 非封闭线路上的植树问题主要可分为以下三种情形:⑴如果在非封闭线路的两端都要植树,那么:株数=段数+1=全长÷株距-1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树,另一端不要植树,那么:株数=段数=全长÷株距全长=株距×株数株距=全长÷株数⑶如果在非封闭线路的两端都不要植树,那么:株数=段数-1=全长÷株距-1全长=株距×(株数+1)株距=全长÷(株数+1)2 封闭线路上的植树问题的数量关系如下株数=段数=全长÷株距全长=株距×株数株距=全长÷株数盈亏问题(盈+亏)÷两次分配量之差=参加分配的份数(大盈-小盈)÷两次分配量之差=参加分配的份数(大亏-小亏)÷两次分配量之差=参加分配的份数相遇问题相遇路程=速度和×相遇时间相遇时间=相遇路程÷速度和速度和=相遇路程÷相遇时间追及问题追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间流水问题顺流速度=静水速度+水流速度逆流速度=静水速度-水流速度静水速度=(顺流速度+逆流速度)÷2水流速度=(顺流速度-逆流速度)÷2浓度问题溶质的重量+溶剂的重量=溶液的重量溶质的重量÷溶液的重量×100%=浓度溶液的重量×浓度=溶质的重量溶质的重量÷浓度=溶液的重量利润与折扣问题利润=售出价-成本利润率=利润÷成本×100%=(售出价÷成本-1)×100%涨跌金额=本金×涨跌百分比折扣=实际售价÷原售价×100%(折扣<1)利息=本金×利率×时间税后利息=本金×利率×时间×(1-20%)时间单位换算1世纪=100年 1年=12月大月(31天)有:1\3\5\7\8\10\12月小月(30天)的有:4\6\9\11月平年2月28天, 闰年2月29天平年全年365天, 闰年全年366天1日=24小时 1时=60分1分=60秒 1时=3600秒积=底面积×高 V=Sh第一部分:概念1、加法交换律:两数相加交换加数的位置,和不变。
小学六年级寻找最大公约数和最小公倍数

小学六年级寻找最大公约数和最小公倍数在小学数学的学习中,最大公约数和最小公倍数是比较重要的概念。
学好这两个概念对于解决数学题目和日常生活中的实际问题都有帮助。
本文将介绍如何寻找最大公约数和最小公倍数,并通过一些实例来加深理解。
一、最大公约数最大公约数,又称为最大公因数,简称为gcd(Greatest Common Divisor)。
最大公约数是指两个或多个整数共有的约数中最大的一个。
寻找最大公约数有几种常见的方法,包括质因数分解法、短除法和辗转相除法。
1.1 质因数分解法质因数分解法是一种通过将一个数分解成质数的乘积的形式来找到最大公约数的方法。
具体步骤如下:(1)将两个或多个数都进行质因数分解,写成乘积形式;(2)找出所有数中共有的质因数;(3)将这些质因数相乘,即得到最大公约数。
举例说明,假设我们要找出48和60的最大公约数:48 = 2 * 2 * 2 * 2 * 360 = 2 * 2 * 3 * 5共有的质因数为2和3,因此最大公约数为2 * 2 * 3 = 12。
1.2 短除法短除法是一种通过反复进行除法运算,找到最大公约数的方法。
具体步骤如下:(1)将两个或多个数中较大的数除以较小的数,得到商和余数;(2)将上一步的除数除以余数,再得到商和余数;(3)重复上述步骤,直到余数为0为止。
举例说明,假设我们要找出48和60的最大公约数:60 ÷ 48 = 1 余 1248 ÷ 12 = 4 余 0余数为0时,最后一次的除数12即为最大公约数。
1.3 辗转相除法辗转相除法也称为欧几里德算法,是一种通过反复用较大数除以较小数,再将所得的余数作为除数,被除数作为除数,继续进行除法运算,直到余数为0为止,从而找到最大公约数的方法。
举例说明,假设我们要找出48和60的最大公约数:60 ÷ 48 = 1 余 1248 ÷ 12 = 4 余 0余数为0时,最后一次的除数12即为最大公约数。
小升初22次课程02-公因数和公倍数(教师版)
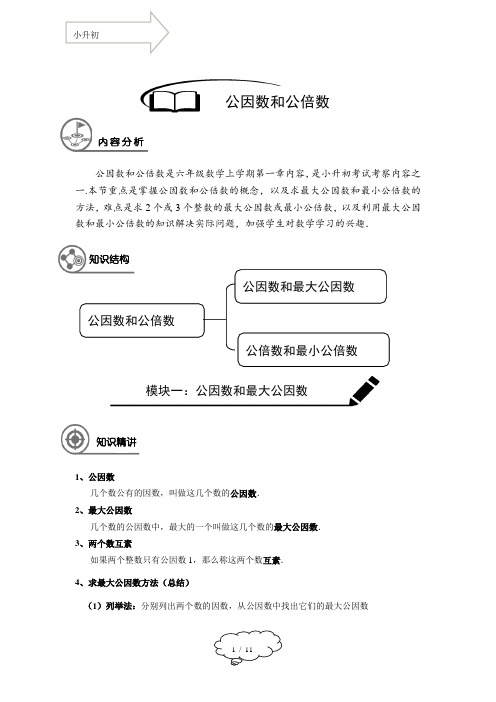
公因数和公倍数内容分析公因数和公倍数是六年级数学上学期第一章内容,是小升初考试考察内容之一.本节重点是掌握公因数和公倍数的概念,以及求最大公因数和最小公倍数的方法,难点是求2个或3个整数的最大公因数或最小公倍数,以及利用最大公因数和最小公倍数的知识解决实际问题,加强学生对数学学习的兴趣.知识结构公因数和最大公因数公因数和公倍数公倍数和最小公倍数模块一:公因数和最大公因数知识精讲1、公因数几个数公有的因数,叫做这几个数的公因数.2、最大公因数几个数的公因数中,最大的一个叫做这几个数的最大公因数.3、两个数互素如果两个整数只有公因数1,那么称这两个数互素.4、求最大公因数方法(总结)(1)列举法:分别列出两个数的因数,从公因数中找出它们的最大公因数(2)分解素因数法:把两个数分解素因数,最大公因数就是它们共有素因数的乘积 (3)短除法:用两个数的公因数去除,除到商是互素为止,所有除数的乘积就是这两个数的最大公因数(一般用它们的公有素因数去除,为了计算更加灵活简便除数不一定非得是素数,可用较大的公因数去除)例: 2 18 24 3 9 12 3 4 所以,18和24的最大公因数为632=⨯(4)特征法:如果两个数是互素,它们的最大公因数是1;如果两个数之间存在倍数关系,则它们的最大公因数是其中较小的一个数注:如果两个数既不互素,也不存在倍数关系,一般可用短除法或者分解素因数法【例1】求出下列各组数的公因数.(1)14和42; (2)121和44; (3)28和56; (4)17和9.【难度】★【答案】(1)14; (2)11; (3)28; (4)1. 【解析】(1)两个数是倍数关系,最大公因数是较小数;(2)两个数既不是倍数关系,也不是互素关系,用短除法; (3)两个数是倍数关系,最大公因数是较小数; (4)两个数互素,最大公因数是1;【例2】指出下列哪组中的两个数互素.(1)3和5; (2)6和9; (3)14和15; (4)18和1.【难度】★【答案】(1)(3)(4).【解析】如果两个整数只有公因数1,那么称这两个数互素.【总结】互素两数的几种常见类型:(1)两个数都是素数;(2)一个素数,一个合数;(3)1和其它的任意正整数.例题解析【例3】用短除法求56和36的最大公因数. 【难度】★ 【答案】4.【解析】 2 56 36 2 28 18 14 9∴56与36的最大公因数是2×2=4.【例4】用分解素因数的方法求24和90的最大公因数. 【难度】★【答案】6; 360.【解析】因为24=2×2×2×3,90=2×3×3×5;所以18与24的最大公因数是2×3=6;最小公倍数是2×2×2×3×3×5=360. 【总结】本题考察了用分解素因数法求两个数的最大公因数.【例5】已知m n p 、、都为自然数,且2n p ÷=,12m n ÷=,那么m n p 、、的最大公因数是多少? 【难度】★★ 【答案】p【解析】m 是n 的倍数,n 是p 的倍数,因此m 是p 的倍数;所以最大公因数是p . 【总结】若三个数都是倍数关系,则它们的最大公因数是最小的那个数.【例6】求出下列各组数的最大公因数.(1)48和60 (2)112和182 (3)410和 123 (4)96、128和160 【难度】★★ 【解析】略【答案】(1)12;(2)14;(3)41;(4)32【例7】一张长方形的纸片,长为36cm ,宽为21cm ,要把这张纸片裁成同样大小的正方形小纸片而且没有任何剩余,则裁成的正方形纸片的边长最大可以是多少厘米?至少有多少个小正方形? 【难度】★★★【解析】没有任何纸片剩余,所以小正方形的边长一定要整除36和21,同时还要求小正方形的边长尽可能地长,因此正方形的边长就是36和21的最大公因数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
