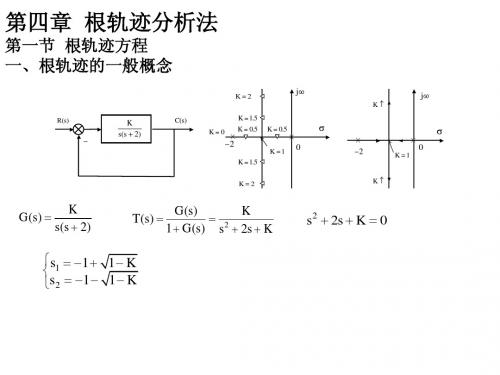
第四章根轨迹分析法
合集下载
自动控制原理-第4章 根轨迹

又 ∵ 根轨迹方程
n
n
(spi) sn( pi)sn 1L
n
m
Kim 1
i 1 m
snm( pi zj)snm 1L
(szj) sm( zj)sm 1L
i 1
j 1
j 1
j 1
n
m
∴ sn-m-1项系数对应相等
(nm)(a) pi zj
n
m
i1
j1
(2k 1) ,
nm
pi zi
闭环零、极点与开环零、极点的关系
闭环传递函数 (s) G(s)
1G(s)H(s)
开环传递函数 Gk(s)G(s)H(s)
f
l
(s zi)
(s z j)
G (s) KG
i 1 q
H
(s)
K
H
j 1 h
(s pi)
(s p j)
i 1
j 1
f
l
(szi)(szj)
Gk(s)G(s)H(s)K
如何应用根轨迹方程在[s]平面上找到闭环极点。
解: G ( s ) K 0 .5 K K * s(2 s 1) s(s 0.5) s(s 0.5)
K * 0.5 K 开 环 极 点 p1 0, p2 0.5 无开环零点 根据相角方程
s2
p2 4 5 o -0.5 s1
135o
p1 0
m
(s z j)
K j1 n
1
(s pi)
i1
m
n
(szj) (spi)(2k1)
j1
i1
k0,1,2,L
(1)相角条件是决定闭环根轨迹的充要条件; 在测量相角时,规定以逆
自动控制原理(胡寿松版)课件第四章

第一节 根轨迹的基本概念
二、根轨迹与系统性能
根轨迹图可以分析系统的各种性能: ω j ∞ ↑ 稳定性: 根轨迹均在s的左半平 Kr 面,则系统对所有k>0的值是稳定的。 s K =0 1 1 s1 2 r 0 σ -1 稳态性能:如图有一个开环极点 -2 -1 s=0,说明属于I型系统,阶跃作用 Kr ∞ 下的稳态误差为0。 动态性能:过阻尼 临界阻尼 欠阻 尼。 K越大,阻尼比 越小,超调量σ%越大。
第四章 根轨迹分析法
第一节 根轨迹的基本概念
当系统的某个参数变化时,特征方程的根随 之在S平面上移动,系统的性能也跟着变化。研究 S 平面上根的位置随参数变化的规律及其与系统 性能的关系是根轨迹分析法的主要内容。
第一节 根轨迹的基本概念
一、根轨迹
设系统的结构如图 K r变化时,闭环特征 Kr 根在 s平面上的轨迹 : 极点;右半平面为 C(s) 2+2s+K s1 s2 Kr 不稳定极点;虚轴 R(s) =s∞ ω r j ↑ -2 0 0 上为临界极点。 闭环特征方程式 Kr 1 -1 -1 1 2 (2) 0<Kr<1时,系统 s 0 s2 +2s+K Kr=0 1r= s1 -1-j -1+j 2 0 σ -1 有呈过阻尼状态。 -2 特征方程的根 -1 -1+j∞ -1-j∞ Kr (3) 当 时,系统 ∞Kr=1 s1.2 =-1± 1-Kr ∞ 呈临界阻尼状态 。 得相应的闭环特征根值: (4) 1<Kr<∞时,系统呈欠阻尼状态。
↑
↑
第一节 根轨迹的基本概念
三、闭环零、极点与开环零、极点的关系
系统传递函数为
G( s) ( s) 1 G(s) H (s)
自动控制原理第四章-根轨迹分析法

jω
×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4:根轨迹的分会点(分离点和会合点)d。 (1)定义:分会点是指根轨迹离开实轴进入复平面的点(分 离点)或由复平面进入实轴的点(汇合点),位于相邻两极点 或两零点之间。
(2)位置:大部分的分会点在实轴上,若出现在复平面内时,则 成对出现。
(3)特点:分会点对应于闭环特征方程有重根的点;根轨迹离开
(4)与虚轴的交点:
方法1:闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得:-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2:闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下:
规则1:根轨迹的起点和终点。 根轨迹起始于开环极点,终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 (, n
m)条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段,如某段右边 开环零、极点(包括该段的端点)数之和为奇数,则该段就 是根轨迹,否则不是。如下图所示。
又因为开环传函的零极点表达式为:
m
GK (s)
G(s)H(s)
K
n
(s
×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4:根轨迹的分会点(分离点和会合点)d。 (1)定义:分会点是指根轨迹离开实轴进入复平面的点(分 离点)或由复平面进入实轴的点(汇合点),位于相邻两极点 或两零点之间。
(2)位置:大部分的分会点在实轴上,若出现在复平面内时,则 成对出现。
(3)特点:分会点对应于闭环特征方程有重根的点;根轨迹离开
(4)与虚轴的交点:
方法1:闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得:-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2:闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下:
规则1:根轨迹的起点和终点。 根轨迹起始于开环极点,终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 (, n
m)条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段,如某段右边 开环零、极点(包括该段的端点)数之和为奇数,则该段就 是根轨迹,否则不是。如下图所示。
又因为开环传函的零极点表达式为:
m
GK (s)
G(s)H(s)
K
n
(s
第四章控制系统的根轨迹分析法
○
− p4
− p3
∠s + z 2
∠s + p2
− p2
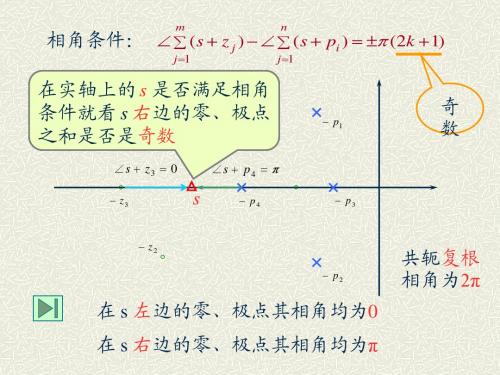
共轭复根 相; ∠s + p2 = 2π 在 s 左边的零、极点其相角均为0
∠s + z1 + ∠s + z2 = 2π 在 s 右边的零、极点其相角均为π
n m 0 出射角公式: 出射角公式: θ pc =180 + ∑θzj − ∑θ pi j =1 i=1
ζ = 0.707
s’ s’
-2 0
K −1
Re
-1
根轨迹法的分析基本思路: 根轨迹法的分析基本思路 目的: 目的
①解决高阶系统求解特征根比较困难 的实现; 寻找到一种方便、 的实现 ②寻找到一种方便、有效的描述 系统的根轨迹的方法。 系统的根轨迹的方法。
方法: 方法
① 根据开环零极点的分布绘制出系统 的根轨迹图; 的根轨迹图;②利用根轨迹法来分析和设 计系统. 计系统
S1
0 -1 -1+j -1+j∞
∞ ↑ K
S2
-2 -1 -1-j -1-j∞ jω
1 S1 0 σ -1
闭环特征方程式 S2+2S+K= 0
S2 -2
特征方程的根 S1.2 = -1± 1-K ±
K变化时,闭环特征根 变化时,
在S平面上的轨迹图形
-1 K ∞ ↑
系统特征方程为 求得两个极点: 求得两个极点:
jω
z1 p3 -2 p2 -1 z2 1 p
1 0
-1
3、实轴上的根轨迹 、
实轴上某区间存在根轨迹, 实轴上某区间存在根轨迹,则 该区间右边的开环零、 该区间右边的开环零、极点数之和 必为奇数。 必为奇数。
− p4
− p3
∠s + z 2
∠s + p2
− p2
共轭复根 相; ∠s + p2 = 2π 在 s 左边的零、极点其相角均为0
∠s + z1 + ∠s + z2 = 2π 在 s 右边的零、极点其相角均为π
n m 0 出射角公式: 出射角公式: θ pc =180 + ∑θzj − ∑θ pi j =1 i=1
ζ = 0.707
s’ s’
-2 0
K −1
Re
-1
根轨迹法的分析基本思路: 根轨迹法的分析基本思路 目的: 目的
①解决高阶系统求解特征根比较困难 的实现; 寻找到一种方便、 的实现 ②寻找到一种方便、有效的描述 系统的根轨迹的方法。 系统的根轨迹的方法。
方法: 方法
① 根据开环零极点的分布绘制出系统 的根轨迹图; 的根轨迹图;②利用根轨迹法来分析和设 计系统. 计系统
S1
0 -1 -1+j -1+j∞
∞ ↑ K
S2
-2 -1 -1-j -1-j∞ jω
1 S1 0 σ -1
闭环特征方程式 S2+2S+K= 0
S2 -2
特征方程的根 S1.2 = -1± 1-K ±
K变化时,闭环特征根 变化时,
在S平面上的轨迹图形
-1 K ∞ ↑
系统特征方程为 求得两个极点: 求得两个极点:
jω
z1 p3 -2 p2 -1 z2 1 p
1 0
-1
3、实轴上的根轨迹 、
实轴上某区间存在根轨迹, 实轴上某区间存在根轨迹,则 该区间右边的开环零、 该区间右边的开环零、极点数之和 必为奇数。 必为奇数。
第4章 根轨迹法
i =1
m n
sk
s+
jω
s+p
s
j=1 n
=
1 ; K gk
−z j
z
j
i
αj
βi
σ
0
∑ α jk − ∑ βik = ±180 (1 + 2k) (k = 1, 2,⋯)
j=1 i =1
−p i
幅值条件为:
∏ s + zj ∏ s + pi
i =1 j=1 n
m
1 = Kg
幅角条件:
∑ α j − ∑ βi = ±180 (1 + 2k)
j=1 i =1
m
n
(k = 1, 2,⋯)
三、应用幅值条件确定 K g 值
jω
△
某控制系统的开环传递函数为
1 K g (s + ) K(8s + 1) 8 G(s)H(s) = 2 = s (2s + 1) s 2 (s + 1 ) 2
-0.5 L3
sk L 1,2 l 60° σ
1 8 1 p1 = − 2 z1 = −
可见,闭环零点由前向通道的零点和反馈通道的极点组成, 闭环零极点放大系数等于前向通道零极点放大系数 K Gg 。
一、根轨迹的连续性 第二节 绘制根轨迹的一般规则 二、根轨迹的分支数 三、根轨迹的对称性 四、根轨迹的起点和终点
m m
j=1 lim n s→∞ i =1
∏ s + zj ∏ s + pi
六、根轨迹的分离点和会合点
D(s) K g (s) = − N(s)
dK g (s) ds
=0
D' (s)N(s) − N ' (s)D(s) = 0
m n
sk
s+
jω
s+p
s
j=1 n
=
1 ; K gk
−z j
z
j
i
αj
βi
σ
0
∑ α jk − ∑ βik = ±180 (1 + 2k) (k = 1, 2,⋯)
j=1 i =1
−p i
幅值条件为:
∏ s + zj ∏ s + pi
i =1 j=1 n
m
1 = Kg
幅角条件:
∑ α j − ∑ βi = ±180 (1 + 2k)
j=1 i =1
m
n
(k = 1, 2,⋯)
三、应用幅值条件确定 K g 值
jω
△
某控制系统的开环传递函数为
1 K g (s + ) K(8s + 1) 8 G(s)H(s) = 2 = s (2s + 1) s 2 (s + 1 ) 2
-0.5 L3
sk L 1,2 l 60° σ
1 8 1 p1 = − 2 z1 = −
可见,闭环零点由前向通道的零点和反馈通道的极点组成, 闭环零极点放大系数等于前向通道零极点放大系数 K Gg 。
一、根轨迹的连续性 第二节 绘制根轨迹的一般规则 二、根轨迹的分支数 三、根轨迹的对称性 四、根轨迹的起点和终点
m m
j=1 lim n s→∞ i =1
∏ s + zj ∏ s + pi
六、根轨迹的分离点和会合点
D(s) K g (s) = − N(s)
dK g (s) ds
=0
D' (s)N(s) − N ' (s)D(s) = 0
第四章 控制系统根轨迹分析法
i j 1 j
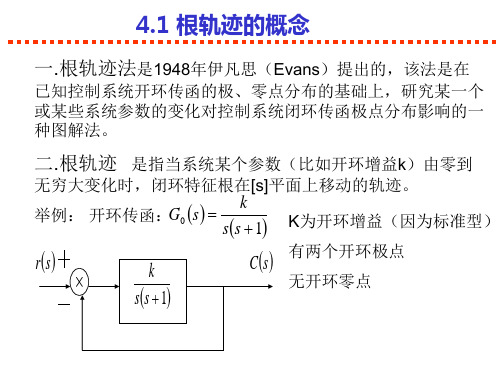
4.1 根轨迹的概念
模条件与角条件的作用: 1、角条件与k无关,即s平面上所有满足角条件的 点都属于根轨迹。(所以绘制根轨迹只要依据角条 件就足够了)。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论:实轴上线段右侧的零、极点数目之和为奇 数时,此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例: 开环传函: ss 1
K为开环增益(因为标准型) 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函: s sk
2 D s s sk 0 则闭环特征方程为:
1 1 闭环特征根(即闭环传函的极点): s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四:根轨迹的渐近线: (1)条数: (n-m)条 (2)与实轴所成角度 当
m n 2k 1
n m
s 时,认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
4.1 根轨迹的概念
模条件与角条件的作用: 1、角条件与k无关,即s平面上所有满足角条件的 点都属于根轨迹。(所以绘制根轨迹只要依据角条 件就足够了)。 2、模条件主要用来确定根轨迹上各点对应的根轨 I 迹增益k值。
m
k
j 1 m
n
s p
j
s Zi
args Z i
1
所以结论:实轴上线段右侧的零、极点数目之和为奇 数时,此区段为根轨迹。
jω
例
k G0 ( s ) Ts 1
1 T
×
×
×
×
σ
1 p T
j
1 1 T F 1 T 2k 1 1
k' G0 ( s ) s( s 0.5 )
j
p1 0 p2 0.5
k G0 s 举例: 开环传函: ss 1
K为开环增益(因为标准型) 有两个开环极点 无开环零点
rs
k ss 1
C s
k G s 2 闭环传函: s sk
2 D s s sk 0 则闭环特征方程为:
1 1 闭环特征根(即闭环传函的极点): s1 1 4k
0 0 .5 F 0.25 2 2k 1 3 , 2 2 2
-0.5 0
4.2 根轨迹的绘制规则
规则四:根轨迹的渐近线: (1)条数: (n-m)条 (2)与实轴所成角度 当
m n 2k 1
n m
s 时,认为所有开环零极点引向s的角相同
Z1 Z m p1 p n
G 0 s k
m
为m个开环零点
根轨迹分析法

在极点0和极点-1之间的根轨迹上一定有分离点存在, 令d[G(s)H(s)]/ds=0,整理后求得s1= -0.42(在根轨迹上, 是分离点),s2 = -1.58 (不在根轨迹上,舍),所对应K* 由幅值条件确定:
K1* s1 s1 1 s1 2 0.42 0.581.58 0.38 用劳斯判据法与虚轴交点:
s 3 3s 2 2s K * 0
s3 s2 s
1
1 3 6 K* 0 3 K*
2 K*
3s 2 6 0
K* 6 s j 2
自动控制原理
12
s0
(8)根轨迹的出射角和入射角
(8)根轨迹的入射角和出射角 出射角:根轨迹离开开环复数极点处的切线方向与正实 轴之间的夹角 入射角:根轨迹进入开环复数零点处的切线方向与正实 轴之间的夹角 结论:开环复数极、零点的出射角与入射角由下面公式 计算 出射角: p 180 ( s zi ) ( s p j )
j 1
n
j
K
*
sz
i 1
m
i
0
当K* →0时, s→pj (j=1,2,…,n)为系统的开环极点; 当K*→∞时,s→zi (i=1,2,…,m)为系统的开环零点。 结论:根轨迹起始于开环极点,终止于开环零点。如果开环 零点数目m小于开环极点数目n,则有n-m条根轨迹终止于无 穷远处。
令K从0到∞变化,则闭环特征根在复 平面上描绘出若干曲线(根轨迹)。
自动控制原理
4
4.2
根轨迹的概念(续)
(2)从根轨迹图分析闭环系统各种性能 分析稳定性:在0<K<∞范围内,系统是稳定的。 分析动态性能:当0<K<0.5时,系统是过阻尼的; 当K=0.5时,系统为临界阻尼状态; 当K>0.5时,系统是欠阻尼的。 若已知K=1,则闭环极点为-1±j,参数ζ=0.707, ω=0.414,系统的瞬态响应指标超调量σ%= 4.3%,调节 时间ts=3秒。 当K继续增大时,其超调量σ%将增大,而调节时 间基本不变。 分析稳态性能:系统是Ⅰ型的,阶跃函数作用下的稳态误 差为零。
第4章 根轨迹

m
(s p
j 1
n
1
j
)
因s为复变量,根轨迹方程又可分解为幅值方程和相 角方程。 幅值方程为
K r (s zi )
i 1 m
(s p
j 1
n
1 或
(s z )
i
m
j
)
(s p
j 1
i 1 n
j
)
1 Kr
相角方程为
(s z ) (s p ) (2k 1)
设p3的出射角为θ3,如图所示。
假设s1为根轨迹上的一点,则s1应 满足相角方程
(s
i 1
1
1
z i ) ( s1 p j ) (2k 1)
j 1
4
由此可推得出射角的一般表达式
l ( pl zi ) ( pl p j ) i j
例4-6 已知系统的开环传递函数为
K r (s 1.5)(s 2 4s 5) G( s) H ( s) s(s 2.5)(s 2 s 1.5)
试绘制系统的根轨迹图。
18
7. 根轨迹与虚轴的交点
根轨迹与虚轴的交点是系统稳定与不稳定的分界点,常 常需要求得这一交点和相应的Kr值。 设与虚轴相交的闭环极点为s=jω,代入闭环特征方程得:
根为两个复数根,系统呈欠阻尼 状态,即输出呈衰减振荡形式。 特征根的实部σ为衰减系数,虚 部ω为振荡频率。
4
4.1.2 根轨迹方程
设系统的结构如图所示。 系统的闭环传递函数为
C ( s) G(s) R( s ) 1 G ( s ) H ( s )
开环传递函数的一般表达式为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
Re
4-2 根轨迹绘制的基本法则
一. 绘制根轨迹的基本法则
法则一. 根轨迹的起点和终点
K G ( s) H (s)
*
(s z )
j 1 j i
m
(s p )
i 1
n
* ( s p ) K (s zi ) 0 j j 1 i 1
n
m
s p j ,根轨迹起于开环极点。 当 K * 0 时,
j 1 j i 1 i
m
n
相角条件
K
*
| s z
j 1 i
m
j
| 1
K*
(s p ) (s z )
j 1 j i 1 m i
n
| s p |
i 1
n
模值条件
凡是满足相角条件的点一定是根轨迹上的点(相 角条件是确定根轨迹的充要条件),而其对应的 值由幅值条件求出。
另一方面
K *| s z j |
j 1 m
| s z
1
j 1 n i 1
m
j
|
| s p |
i 1 i
n
| s p |
i
.
1 * K
* K 时,右边 0 当
s zj
或者
s
s zi , 有m条根轨迹终止在开环传递函数的零点。 s ,有(n m)条根轨迹终止在无穷远处。
φ2
z2
θ1
0
sk
θ4
法则四.实轴上根轨迹 考虑幅角条件: ( s z j ) ( s pi ) (2k 1)
j 1 i 1 m n
只有当 sk 点右侧实轴上的开环极点和开环零点的个 数之和为奇数时,才满足相角条件。 结论:实轴上的右边开环零极点个数之和为 奇数时,则此线段为实轴上的根轨迹。
用根轨迹图来分析自动控制系统十分方便。 对于高阶系统,求解特征方程的根非常困难。 如果要研究系统参数的变化对闭环系统特征方程 根的影响,就需要大量反复的计算。 1948年伊万斯(W·R·EVANS)解决了这个问题,提 出了根轨迹法。 根轨迹方法不需要求解闭环系统的特征方程,只 需依据开环传函便可会绘制系统的根轨迹图。
前向通路根 轨迹增益
G ( s ) K1
( s 1)
s (T j s 1)
j 1 i 1 q i
f
* KG
(s z ) (s p
j 1 i 1 h i j
f
)
H ( s) K * H
反馈通路根 轨迹增益
(s z ) (s p
j 1 i 1 h i j
二. 根轨迹方程
通常,系统的开环零、极点已知,因此建 立开环零、极点与闭环极点之间的关系, 有助于闭环系统根轨迹的绘制。
R(s)
-
G(s) H(s)
G (s) (s) 1 G (s) H (s)
C(s)
前向通路传递函数G(s)和反馈通路传递函数H(s) 可分别表示成因式相乘的形式:
j
K
( K 0)
-2
( K 0.5) ( K 0)
-1 0
K
系统的根轨迹
根轨迹变化与系统性能的关系 根轨迹
K
0 1 2 … ∞
s1
0 -1 -1+j … -1+j∞
s2
稳定性
动态性能
系统稳定 过阻尼系统 -2 临界阻尼系统 -1 欠阻尼系统 -1-j … 无阻尼系统 -1-j∞
pj )
sk
nm
n m n m 1 p j zi sk j 1 i 1
(s
j 1 m i 1
n
k
pj ) zi )
.
(s
n
sk n m (n m) a sk n m 1
j
A
a
B -4 -3
180 °
60°
a 0 -2 -1
300°
60°
C
图 根轨迹的渐近线
法则四. 实轴上根轨迹 令 sk 为实轴上的试探点 左侧开环零极点构成 的向量夹角均为零度; 右侧开环零极点构成 的向量夹角均为 ; 一对共轭零点或极点 的向量夹角之和为2 。
p3 j
θ3
i 1 i
n
开环极点
K
*
(s z )
j 1 j i
m
(s p )
i 1
n
1 e j (2 k 1)
K
*
sz
j 1
m
j
e
j ( s z j )
i 1
n
e
j (2 k 1)
s pi e j ( s pi )
(s z ) (s p ) (2k 1)
G(s) H(s) s 2 (s 1)(s 4) K r (s 2)
试画出该系统根轨迹的渐近线。 解:对于该系统有n=4,m=1,n-m=3;三条渐 近线与实轴交点位置为
1 4 2 σa 1 3
它们与实轴正方向的交角分别是
(2k 1) a : , 3 3
第四章 线性系统的根轨迹分析
4-1 根轨迹法的基本概念 4-2 根轨迹绘制的基本法则 4-3 广义根轨迹 4-4 系统性能的分析 (自学)
4-1 根轨迹法的基本概念
一. 根轨迹概念及应用
• • 系统的参数发生变化,其特征方程式的 根的值改变。 当系统参数连续变化时(如从0→∞), 其特征方程的根在根平面上留下的轨迹, 叫根轨迹。 根轨迹与系统性能密切相关。
n n 1 n n m 1 p j sk p j sk n m 1 j j 1 1 n m 1 p j sk 1 zi sk m m i 1 sk m zi sk m 1 1 zi sk 1 j 1 i 1 i 1
a ) a ) ( sk a ) n m sk n m (n m) a sk n m 1
(s
k
k
n n 1 n n 1 sk p j sk ( sk p j ) p j sk n sk j 1 j 1 j 1 m m m 1 m m 1 m m 1 m m m ( sk zi ) sk zi sk sk zi sk sk z i s k i 1 i 1 i 1 i 1
k
( n m) k p j z i
j 1 i 1
m
a
p z
j 1 j i 1
n
m
i
nm
法则三. 根轨迹的渐近性
(2k 1) a n m n m p j zi i 1 a j 1 nm
例: 已知系统的开环传递函数为
n n
当
sk
m n
1 x 0时, 1 x 1-x
sk
m nm
.
sk m zi sk m 1 i 1
1 zi sk 1 i 1
sk
nm
m 1 m n m 1 nm 1 zi sk sk zi sk i 1 i 1
例:已知单位负反馈系统的开环传递函数为:
K ( s 1) G (s) s (T1s 1)(T2 s 1)
试画出根轨迹。 解:将开环传函进行变换后得到:
K g ( s z1 ) K ( s 1) G (s) s (T1s 1)(T2 s 1) s ( s p1 )( s p2 )
(s
j 1 m i 1
n
m n m nm2 nm n m 1 n m 1 sk zi sk p j sk zi sk i 1 j i 1 1 (sk zi ) k
法则三. 根轨迹的渐近性
当开环极点数n大于开环零点数m时,系统有 n-m条根轨迹终止于S平面的无穷远处,这n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近 线,因此,浙近线也有n-m条,且它们交于实 轴上的一点。
确定渐近线:
1)渐近线与实轴间夹角a 由两个因素决定 2)渐近线与实轴交点 a
l
)
开环系统根轨 迹增益
G ( s) H ( s) K *
( s z ) ( s z ) ( s p ) ( s p
j 1 j j 1 i 1 h i i 1 h i j
f
l
)
开环零点
G ( s) H ( s)
K * (s z j )
j 1
m
(s p )
设 K 的变化范围是〔0, ∞﹚,K 当K 0时, s1 0, s 2 2 ; 当 0 K 0.5 时, s1 与 s 2 为不等的两个负实 根: s1 1 1 2 K , s2 1 1 2 K 当 K 0.5 时, s1 s 2 1,为等实根; 当K 0.5 时, s1,2 1 j 2 K 1为共轭复根; 当 K 时, s1、 s 2 的实部都等于-1,是 常数,虚部趋向无穷远处
夹角 a 计算: 设试探点 sk 在无穷远处的根轨迹上,所以,渐近 线与实轴交角 a 与到各零极点的幅角均相等。
Re
4-2 根轨迹绘制的基本法则
一. 绘制根轨迹的基本法则
法则一. 根轨迹的起点和终点
K G ( s) H (s)
*
(s z )
j 1 j i
m
(s p )
i 1
n
* ( s p ) K (s zi ) 0 j j 1 i 1
n
m
s p j ,根轨迹起于开环极点。 当 K * 0 时,
j 1 j i 1 i
m
n
相角条件
K
*
| s z
j 1 i
m
j
| 1
K*
(s p ) (s z )
j 1 j i 1 m i
n
| s p |
i 1
n
模值条件
凡是满足相角条件的点一定是根轨迹上的点(相 角条件是确定根轨迹的充要条件),而其对应的 值由幅值条件求出。
另一方面
K *| s z j |
j 1 m
| s z
1
j 1 n i 1
m
j
|
| s p |
i 1 i
n
| s p |
i
.
1 * K
* K 时,右边 0 当
s zj
或者
s
s zi , 有m条根轨迹终止在开环传递函数的零点。 s ,有(n m)条根轨迹终止在无穷远处。
φ2
z2
θ1
0
sk
θ4
法则四.实轴上根轨迹 考虑幅角条件: ( s z j ) ( s pi ) (2k 1)
j 1 i 1 m n
只有当 sk 点右侧实轴上的开环极点和开环零点的个 数之和为奇数时,才满足相角条件。 结论:实轴上的右边开环零极点个数之和为 奇数时,则此线段为实轴上的根轨迹。
用根轨迹图来分析自动控制系统十分方便。 对于高阶系统,求解特征方程的根非常困难。 如果要研究系统参数的变化对闭环系统特征方程 根的影响,就需要大量反复的计算。 1948年伊万斯(W·R·EVANS)解决了这个问题,提 出了根轨迹法。 根轨迹方法不需要求解闭环系统的特征方程,只 需依据开环传函便可会绘制系统的根轨迹图。
前向通路根 轨迹增益
G ( s ) K1
( s 1)
s (T j s 1)
j 1 i 1 q i
f
* KG
(s z ) (s p
j 1 i 1 h i j
f
)
H ( s) K * H
反馈通路根 轨迹增益
(s z ) (s p
j 1 i 1 h i j
二. 根轨迹方程
通常,系统的开环零、极点已知,因此建 立开环零、极点与闭环极点之间的关系, 有助于闭环系统根轨迹的绘制。
R(s)
-
G(s) H(s)
G (s) (s) 1 G (s) H (s)
C(s)
前向通路传递函数G(s)和反馈通路传递函数H(s) 可分别表示成因式相乘的形式:
j
K
( K 0)
-2
( K 0.5) ( K 0)
-1 0
K
系统的根轨迹
根轨迹变化与系统性能的关系 根轨迹
K
0 1 2 … ∞
s1
0 -1 -1+j … -1+j∞
s2
稳定性
动态性能
系统稳定 过阻尼系统 -2 临界阻尼系统 -1 欠阻尼系统 -1-j … 无阻尼系统 -1-j∞
pj )
sk
nm
n m n m 1 p j zi sk j 1 i 1
(s
j 1 m i 1
n
k
pj ) zi )
.
(s
n
sk n m (n m) a sk n m 1
j
A
a
B -4 -3
180 °
60°
a 0 -2 -1
300°
60°
C
图 根轨迹的渐近线
法则四. 实轴上根轨迹 令 sk 为实轴上的试探点 左侧开环零极点构成 的向量夹角均为零度; 右侧开环零极点构成 的向量夹角均为 ; 一对共轭零点或极点 的向量夹角之和为2 。
p3 j
θ3
i 1 i
n
开环极点
K
*
(s z )
j 1 j i
m
(s p )
i 1
n
1 e j (2 k 1)
K
*
sz
j 1
m
j
e
j ( s z j )
i 1
n
e
j (2 k 1)
s pi e j ( s pi )
(s z ) (s p ) (2k 1)
G(s) H(s) s 2 (s 1)(s 4) K r (s 2)
试画出该系统根轨迹的渐近线。 解:对于该系统有n=4,m=1,n-m=3;三条渐 近线与实轴交点位置为
1 4 2 σa 1 3
它们与实轴正方向的交角分别是
(2k 1) a : , 3 3
第四章 线性系统的根轨迹分析
4-1 根轨迹法的基本概念 4-2 根轨迹绘制的基本法则 4-3 广义根轨迹 4-4 系统性能的分析 (自学)
4-1 根轨迹法的基本概念
一. 根轨迹概念及应用
• • 系统的参数发生变化,其特征方程式的 根的值改变。 当系统参数连续变化时(如从0→∞), 其特征方程的根在根平面上留下的轨迹, 叫根轨迹。 根轨迹与系统性能密切相关。
n n 1 n n m 1 p j sk p j sk n m 1 j j 1 1 n m 1 p j sk 1 zi sk m m i 1 sk m zi sk m 1 1 zi sk 1 j 1 i 1 i 1
a ) a ) ( sk a ) n m sk n m (n m) a sk n m 1
(s
k
k
n n 1 n n 1 sk p j sk ( sk p j ) p j sk n sk j 1 j 1 j 1 m m m 1 m m 1 m m 1 m m m ( sk zi ) sk zi sk sk zi sk sk z i s k i 1 i 1 i 1 i 1
k
( n m) k p j z i
j 1 i 1
m
a
p z
j 1 j i 1
n
m
i
nm
法则三. 根轨迹的渐近性
(2k 1) a n m n m p j zi i 1 a j 1 nm
例: 已知系统的开环传递函数为
n n
当
sk
m n
1 x 0时, 1 x 1-x
sk
m nm
.
sk m zi sk m 1 i 1
1 zi sk 1 i 1
sk
nm
m 1 m n m 1 nm 1 zi sk sk zi sk i 1 i 1
例:已知单位负反馈系统的开环传递函数为:
K ( s 1) G (s) s (T1s 1)(T2 s 1)
试画出根轨迹。 解:将开环传函进行变换后得到:
K g ( s z1 ) K ( s 1) G (s) s (T1s 1)(T2 s 1) s ( s p1 )( s p2 )
(s
j 1 m i 1
n
m n m nm2 nm n m 1 n m 1 sk zi sk p j sk zi sk i 1 j i 1 1 (sk zi ) k
法则三. 根轨迹的渐近性
当开环极点数n大于开环零点数m时,系统有 n-m条根轨迹终止于S平面的无穷远处,这n-m 条根轨迹变化趋向的直线叫做根轨迹的渐近 线,因此,浙近线也有n-m条,且它们交于实 轴上的一点。
确定渐近线:
1)渐近线与实轴间夹角a 由两个因素决定 2)渐近线与实轴交点 a
l
)
开环系统根轨 迹增益
G ( s) H ( s) K *
( s z ) ( s z ) ( s p ) ( s p
j 1 j j 1 i 1 h i i 1 h i j
f
l
)
开环零点
G ( s) H ( s)
K * (s z j )
j 1
m
(s p )
设 K 的变化范围是〔0, ∞﹚,K 当K 0时, s1 0, s 2 2 ; 当 0 K 0.5 时, s1 与 s 2 为不等的两个负实 根: s1 1 1 2 K , s2 1 1 2 K 当 K 0.5 时, s1 s 2 1,为等实根; 当K 0.5 时, s1,2 1 j 2 K 1为共轭复根; 当 K 时, s1、 s 2 的实部都等于-1,是 常数,虚部趋向无穷远处
夹角 a 计算: 设试探点 sk 在无穷远处的根轨迹上,所以,渐近 线与实轴交角 a 与到各零极点的幅角均相等。
