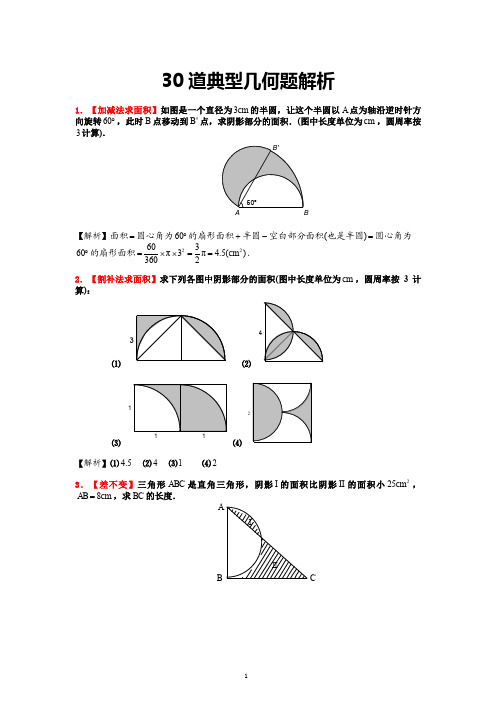
几何计算题
中考专题--几何计算题(1)

中考专题--几何计算题(1)1.已知,如图△ABC内接于⊙O,AB=3,AC=4,AD=1,AD⊥BC于D,则⊙O半径是 .2.如图所示,直角梯形ABCD中,AB⊥BC,AD∥BC,BC>AD,AD=2,AB=4,点E在AB上,将△CBE沿CE翻折,使B 点与D点重合,则tan∠BCE= .3.已知直角梯形ABCO的底边在x轴上,BC∥OA,AB⊥AO,过点C、D的双曲线kyx交OB于点D,且OD:DB=1:2,S△OBC=3,则k= .4.如图,等边△ABC中,DE分别在ABBC边上,AD=BE,AE与CD交于点F,AG⊥CD于点G,则A GA F= .5.如图, △ABC中,AB=AC=13,BC=10,将△ABC沿DE折叠,使点C落在AB边的C'处,且DE∥AB,则BC'=.6.如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC交AC于点D,且AB=4,BD=5,则点D到BC的距离为 .7.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°,且DM交AC于F,ME交BC于G,若AB=则FG= .8.如图,直角△ABC中,∠C=90°,AB=5,点P为BC边上一动点,PD∥AB,PD交AC于点D,连结AP,则BC长= .9.如图,在矩形ABCD中,AD=5,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,AF=CG=2,BE=DH=1,点P是直线EF、GH间任意一点,连结PE、PF、PG、PH,则S△PEF +S△PGH= .10.直角△ABC纸片的两直角边长为6和8,将△ABC如图那样折叠,使A与B重合,折痕为DE,则S△CBE= .11.如图所示,△ABC被分成4个面积相等的三角形CD=6,CE=3,BC=12.在△ABC中,AD相交BC于D,CE相交AB于E,AD和CE交点为F,AF=DF,CD=2BD, △ABC的面积是30平方厘米,S△AEF +S△CDF=。
40道四年级简便几何练习题

40道四年级简便几何练习题1. 题目:长方形的边长分别为3厘米和5厘米,它的面积是多少?答案:面积=长×宽=3厘米×5厘米=15平方厘米2. 题目:正方形的周长是12厘米,它的边长是多少?答案:周长=4×边长=12厘米,所以边长=12厘米÷4=3厘米3. 题目:一个三角形的底边长是4厘米,高是3厘米,它的面积是多少?答案:面积=底边长×高÷2=4厘米×3厘米÷2=6平方厘米4. 题目:判断以下形状是否是正方形?答案:是正方形5. 题目:判断以下形状是否是长方形?答案:不是长方形6. 题目:判断以下形状是否是三角形?答案:是三角形7. 题目:画一个边长为5厘米的正方形,并计算它的面积。
答案:正方形图如下:面积=边长×边长=5厘米×5厘米=25平方厘米8. 题目:画一个边长为6厘米的长方形,并计算它的周长。
答案:长方形图如下:周长=2×(长+宽)=2×(6厘米+4厘米)=20厘米9. 题目:画一个底边长为7厘米,高为5厘米的三角形,并计算它的面积。
答案:三角形图如下:面积=底边长×高÷2=7厘米×5厘米÷2=17.5平方厘米10. 题目:画一个正方形,并计算它的周长和面积。
其中边长自定义。
答案:请根据边长自行画图,并计算周长和面积。
...继续列出剩余的练题,每道题目都包含图示和解答。
参考答案:请在此处提供参考答案。
空间几何体的综合计算测试题

空间几何体的综合计算测试题1. 综合计算题求以下空间几何体的表面积和体积:1.1 直方体已知直方体的长、宽、高分别为10 cm、6 cm、8 cm,求其表面积和体积。
解答:该直方体的表面积可通过公式2*(长×宽 + 长×高 + 宽×高)计算,代入数值计算得:表面积 = 2*(10 × 6 + 10 × 8 + 6 × 8) = 2*(60 + 80 + 48) = 376 cm²。
该直方体的体积可通过公式长×宽×高计算,代入数值计算得:体积 = 10 × 6 × 8 = 480 cm³。
1.2 正方体已知正方体的边长为5 cm,求其表面积和体积。
解答:该正方体的表面积可通过公式6×边长²计算,代入数值计算得:表面积 = 6×5² = 6×25 = 150 cm²。
该正方体的体积可通过公式边长³计算,代入数值计算得:体积 = 5³ = 125 cm³。
1.3 圆柱体已知圆柱体的底面半径为4 cm,高为10 cm,求其表面积和体积(π取3.14)。
解答:该圆柱体的表面积可分为两部分计算:侧面积和底面积。
侧面积可通过公式2×π×半径×高计算,代入数值计算得:侧面积 = 2×3.14×4×10 = 251.2 cm²。
底面积为圆的面积,可通过公式π×半径²计算,代入数值计算得:底面积 = 3.14×4² = 50.24 cm²。
因此,该圆柱体的表面积为251.2 + 50.24 = 301.44 cm²。
该圆柱体的体积可通过公式π×半径²×高计算,代入数值计算得:体积 = 3.14×4²×10 = 502.4 cm³。
30道小升初数学几何问题(附答案)
连接
AC,AF,HC,还可得 S
EFB
6S
ABC
,S
DHG
6S
,
ACD
有 S EFB S DHG 6 S ABC S ACD 6SABCD =30 平方厘米.
有四边形 EFGH 的面积为 EAH, FCG, EFB, DHG,ABCD 的面积和,即为 30+30+5=65(平方厘米.)
5 0 5 0 2 5 0(0块).
8. 【化整为零】正方形 ABCD 与等腰直角三角形 BEF 放在一起(如图),M、N 点为正方
形的边的中点,阴影部分的面积是 14cm2,三角形 BEF 的面积是多少平方厘米?
【解析】因为 M、N 是中点,故我们可以将该图形进行分割,所得图形如下
F
A
MD
N
F
A
MD
7
(法 2)三视图法.从前后面观察到的面积为 52 32 22 38 平方厘米,从左右 两个面观察到的面积为 52 32 34 平方厘米,从上下能观察到的面积为 52 25 平方厘米.
表面积为 38 34 25 2 194 (平方厘米).
20.【表面积计算】用棱长是 1 厘米的立方块拼成如右图所示的立体图形,问该图形的表 面积是多少平方厘米?
如图,这样阴影部分就划分成了 4 个半圆减去三角形,我们可以求得,
S阴影 4 S半圆 S三角形
4
1
2
a 2 2
1a 2
a
2
1 a2 2
15.【表面积计算】中是一个边长为 4 厘米的正方体,分别在前后、左右、上下各面的中 心位置挖去一个边长 1 厘米的正方体,做成一种玩具.它的表面积是多少平方厘米?
13.【曲线开型面积】如右图,有 8 个半径为 1 厘米的小圆,用它们的圆周的一部分连成
【奥数系列训练】(含答案)12——几何体的计算

【奥数系列训练】(含答案)12——几何体的计算请填入正确答案:【题目1】用棱长为1cm的18个正方体做长方体,要使他的表面积最小,问最小表面积应该多大?【题目2】有两个边长为8cm正方体盒子。
A盒子放入直径8cm,高8cm的圆柱体铁块一个,B盒子放入直径4cm、高8cm的圆柱体铁块4个。
现在A盒注满水,把A盒中水倒入B盒,使B盒注满水。
A盒剩下水是多少立方公分?【题目3】一个正方体木块,棱长是5,如果在他上面截去一个棱长为5×3×2的长方体,那么,他的表面积减少百分之几?【题目4】现有一张长40公分,宽20公分的长方形铁皮。
请你用它做一只深是5公分的正方体无盖铁片盒(焊接处及铁片厚度不计,容积越大越好)。
你做的铁皮盒的容积是多少立方公分?【题目5】把12件同样的长17、宽7、高3的长方体物品拼装成一件大的长方体包装物。
如何包装使长方体的表面积最小,最小表面积是多少?【题目6】从一个长9公分、宽7公分、高5公分的长方体中截下一个最大的立方体,剩下部分的棱长总和最大是多少公分?【题目7】在底面是正方形,棱长都是整公尺数,棱长总和为96公尺的长方体中,居中打一个底面为正方形,面积为4平方公尺的上下直穿的长方体的洞。
前、后、左、右也分别居中打一个长14公尺,宽2公尺的长方体洞。
这个几何体的表面积是多少平方公尺?【题目8】一个长方体盒子,从里面量长40公分,宽12公分,高7公分。
在这个盒子里放一个长5公分,宽4公分,高3公分的方形木块。
问最多可以放多少块?【题目9】一个棱长为6公分的正方体,沿着△ADE所在的平面将正方体切掉一个角,问切掉的三棱锥EABD的体积是多少?【题目10】用一张长30公分,宽20公分的长方形铁皮,做一个深5公分的长方体无盖铁皮盒(焊接处与铁皮厚度不计)。
这个铁皮盒的容积最大是多少立方公分?【参考答案】1.【解答】要使着18个棱长为1cm的小正方体做成的长方体的表面积最小,就应该使做成的长方体接近于正六面体(正方体)。
生活中的初中数学几何题

生活中的初中数学几何题
以下是一些生活中与初中数学几何相关的题目:
1. 请测量你家的客厅长、宽和高,计算其体积。
2. 你正在画一幅画,画布的形状是一个长方形,长为80厘米,宽为50厘米。
你想在画布的四周各留出相同的边框,边框的宽度为5厘米。
请计算边框内的有效画面的面积。
3. 你的房间是一个长方体,长为4米,宽为3米,高为2.5米。
你打算贴墙纸,一卷墙纸的长度为10米,宽度为0.5米。
请计算你需要多少卷墙纸才能完整地贴满四面墙。
4. 你有一个圆形的花坛,直径为2米。
你计划在花坛周围修建一条小径,宽度为0.5米。
请计算小径的长度。
5. 你正在建造一个游泳池,你决定使用一个半径为3米的圆形围墙作为游泳池的边界。
请计算你需要多少米的围墙材料来围绕整个游泳池。
这些问题结合了生活场景和几何概念,可以帮助学生将数学与实际生活相结合,提高对几何知识的理解和应用能力。
小学生几何练习题

小学生几何练习题
1. 题目一:三角形面积计算
小明有一块三角形的菜地,底边长为10米,高为6米。
请问这块菜地的面积是多少平方米?
2. 题目二:平行四边形周长计算
一个平行四边形的两组对边分别是8厘米和6厘米,求这个平行四边形的周长。
3. 题目三:圆形周长计算
一个圆形花坛的直径是14米,求这个花坛的周长。
4. 题目四:正方形面积计算
小华的房间是一个正方形,边长为5米,求房间的面积。
5. 题目五:长方形面积与周长计算
一个长方形的长是12厘米,宽是8厘米,求这个长方形的面积和周长。
6. 题目六:梯形面积计算
一个梯形的上底是6厘米,下底是10厘米,高是4厘米,求这个梯形的面积。
7. 题目七:正五边形内角计算
一个正五边形的每个内角是多少度?
8. 题目八:长方体体积计算
一个长方体的长是9厘米,宽是7厘米,高是5厘米,求这个长方
体的体积。
9. 题目九:圆柱体体积计算
一个圆柱体的底面直径是8厘米,高是10厘米,求这个圆柱体的体积。
10. 题目十:圆锥体体积计算
一个圆锥体的底面半径是3厘米,高是9厘米,求这个圆锥体的体积。
高中几何体试题及答案

高中几何体试题及答案试题一:正方体的体积和表面积计算某正方体的边长为a,求该正方体的体积和表面积。
解答:正方体的体积 V = a³正方体的表面积 S = 6a²试题二:圆柱的体积和表面积计算已知圆柱的底面半径为r,高为h,求圆柱的体积和表面积。
解答:圆柱的体积V = πr²h圆柱的表面积S = 2πrh + 2πr²试题三:圆锥的体积和表面积计算已知圆锥的底面半径为r,高为h,求圆锥的体积和表面积。
解答:圆锥的体积V = (1/3)πr²h圆锥的表面积 S = πr(r + l),其中l是圆锥的斜高,可通过勾股定理计算:l = √(r² + h²)试题四:球的体积和表面积计算已知球的半径为R,求球的体积和表面积。
解答:球的体积V = (4/3)πR³球的表面积S = 4πR²试题五:棱锥的体积计算已知一个正四棱锥的底面边长为a,高为h,求棱锥的体积。
解答:正四棱锥的体积 V = (1/3)ah²试题六:棱柱的体积和表面积计算已知一个正六棱柱的底面边长为a,高为h,求棱柱的体积和表面积。
解答:正六棱柱的体积 V = 6a²h正六棱柱的表面积S = 6a(a + √3h)试题七:椭圆的面积计算已知椭圆的长轴为2a,短轴为2b,求椭圆的面积。
解答:椭圆的面积A = πab试题八:双曲线的面积计算已知双曲线的实轴为2a,虚轴为2b,求双曲线的面积。
解答:双曲线的面积A = πa(b + a)结束语:以上试题涵盖了高中几何体的常见体积和面积计算问题,希望同学们能够熟练掌握这些基本公式,并能够灵活运用到实际问题中去。
通过不断的练习和思考,相信你们能够在几何学领域取得优异的成绩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分类训练:几何计算题
几何计算题。
1.计算下面各图中阴影部分的面积。
(单位:厘米)
2.看图计算。
下左图中阴影部分的面积是37平方厘米,求长方形的周长。
(单位:厘米)
3.上右图中,已知平行四边形中空白部分的面积是77平方厘米,求图中阴影部分面积。
(单位:厘米)
4.下左图中长方形的面积是40平方米,求阴影部分的面积。
5.上右图中平行四边形中空白部分的面积是10平方分米,求阴影部分的面积。
6.用篱笆靠墙围一块花圃(如下左图)。
如果用这个篱笆改围成一个靠墙的正方形,正方形的面积是多少?
7.上左图是一个长方体纸盒的表面展开图,这个纸盒的用料面积至少是多少平方厘米?(单位:厘米)
8.计算下左图形的周长和面积。
(单位:厘米)
9.求上右图形的面积。
(单位:厘米)
10.下左图中,直角三角形AOB的面积是12平方厘米,那么圆的面积是多少平方厘米?
11.上右图中,半圆中三角形ABO的面积(S1)是11平方厘米,O为圆心,半径长5厘米,求阴影部分的面积。
12.下左图是一块土地的形状,可以分割成一个平行四边形和一个三角形。
这块土地的面积是多少公顷。
13.求上右图中圆锥的体积。
(单位:厘米)
14.如右图:ACEG是梯形、BDFG是正方形,GE=30厘米,GB=24厘米,C=39厘米。
求梯形ACEG的面积。
