几何计算题选讲
高二数学几何选讲试题答案及解析

高二数学几何选讲试题答案及解析1.如图,在梯形中,,若,,,则梯形与梯形的面积比是()A.B.C.D.【答案】D【解析】延长,相交于,由相似三角形知识,则有,设,,(),则梯形的面积,梯形的面积,所以梯形与梯形的面积比是,故选择D.【考点】平面几何中的相似三角形.2.如图⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于点N,过点N的切线交CA的延长线于P.(1)求证:;(2)若⊙O的半径为,OA=OM,求MN的长.【答案】(1)证明见解析;(2)2.【解析】解题思路:(1)利用等腰三角形与切割线定理进行证明;(2)利用三角形的相似性进行求解. 规律总结:直线与圆的位置关系,是平面几何问题的常见题型,常考知识由:圆内接四边形、切割线定理、相似三角形、全等三角形等.试题解析:(1)连结ON,则ON⊥PN,且△OBN为等腰三角形,则∠OBN=∠ONB,∵∠PMN=∠OMB=900-∠OBN,∠PNM=900-∠ONB∴∠PMN=∠PNM, ∴PM=PN由条件,根据切割线定理,有所以(2)OM=2,在Rt△BOM中,延长BO交⊙O于点D,连接DN由条件易知△BOM∽△BND,于是即,得BN=6所以MN=BN-BM=6-4=2.【考点】1.切割线定理;2.相似三角形.3.如图所示,△ABC内接于⊙O,AB=AC,直线XY切⊙O于点C,BD∥XY,AC、BD相交于E.(1)求证:△ABE≌△ACD;(2)若AB=6 cm,BC=4 cm,求AE的长.【答案】(1)见解析;(2).【解析】(1)欲证三角形全等,需牢牢掌握这种证明方法和所需要的条件.本小题,(已知),下寻找另外的边和角,考虑到这里有圆,所以运用同弧所对应的圆周角相等可得(弧所对),接着证明(其他角和边不好证,同时这里有弦切角可以利用).(2)欲求,因,则可转化为求,考虑到,需将联系起来就得考虑三角形相似.注意到,.试题解析:(1)证明因为XY是⊙O的切线,所以.因为,所以,∴. 2分因为,所以. 4分因为,又因为,所以. 5分(2)解因为,,所以, 7分所以,即 8分因为,,所以.所以. 10分【考点】(1)三角形全等的证明;(2)三角形相似的证明与应用;(3)圆性质的应用.4.如图,是⊙的直径延长线上一点,与⊙相切于点,的角平分线交于点,则的大小为_________.【答案】【解析】如图所示,连接OC,则又因为∠APC的角平分线为PQ,,在中,又【考点】圆的切线的性质及判定定理5.如图所示,在△ABC中,AH⊥BC于H,E是AB的中点,EF⊥BC于F,若HC=BH,则FC∶BF等于A.B.C.D.【答案】D【解析】由AH⊥BC,EF⊥BC知EF∥AH,又∵AE=EB,∴BF=FH,∴HC=BH=BF,∴FC=BF.6.如图所示,⊙O的两条弦AD和CB相交于点E,AC和BD的延长线相交于点P,下面结论:①PA·PC=PD·PB;②PC·CA=PB·BD;③CE·CD=BE·BA;④PA·CD=PD·AB.其中正确的有A.1个 B.2个 C.3个 D.4个【答案】A【解析】根据割线定理知①式正确,②③④不正确.7.如图所示,PA切圆于A,PA=8,直线PCB交圆于C、B,连接AB、AC,且PC=4,AD⊥BC于D,∠ABC=α,∠ACB=β,则的值等于A. B. C.2 D.4【答案】B【解析】要求,注意到sin α=,sin β=,即=,又△PAC∽△PBA,得===.8.如图,AB是圆O的直径,直线CE和圆O相切于点C,AD⊥CE于D,若AD=1,∠ABC=30°,则圆O的面积是________.【答案】4π【解析】∵在⊙O中,∠ACD=∠ABC=30°,且在Rt△ACD中,AD=1,∴AC=2,AB=4,又∵AB是⊙O的直径,∴⊙O的半径为2,∴圆O的面积为4π.9.若三角形的三条边之比为3∶5∶7,与它相似的三角形的最长边为21 cm,则其余两边的长度之和为A.24 cm B.21 cm C.19 cm D.9 cm【答案】A【解析】设其余两边的长度分别为x cm,y cm,则==,解得x=15 cm,y=9 cm.故x+y=24 cm.10.如图所示,设l1∥l2∥l3,AB∶BC=3∶2,DF=20,则DE=________.【答案】8【解析】EF∶DE=AB∶BC=3∶2,∴=,又DF=20,∴DE=8.11.若两个相似三角形的对应高的比为2∶3,且周长的和为50 cm,则这两个相似三角形的周长分别为________.【答案】20 cm,30 cm【解析】设较大的三角形的周长为x cm,则较小的三角形的周长为(50-x)cm.由题意得=,解得x=30,50-x=50-30=20.12.如图所示,D为△ABC中BC边上的一点,∠CAD=∠B,若AD=6,AB=8,BD=7,求DC的长.【答案】9【解析】解∵∠CAD=∠B,∠C=∠C,∴△CAD∽△CBA.∴==.∴AC=,AC=.∴=.设CD=x,则=,解得x=9.故DC=9.13.如图所示,PA、PB是⊙O的两条切线,A、B为切点,连接OP交AB于C,连接OA、OB,则图中等腰三角形、直角三角形的个数分别为A.1,2 B.2,2 C.2,6 D.1,6【答案】C【解析】∵PA、PB为⊙O切线,∴OA⊥AP,OB⊥PB,PA=PB,OP平分∠APB,∴OP⊥AB.∴直角三角形有6个,等腰三角形有2个.即直角三角形有:△OAP,△OBP,△OCA,△OCB,△ACP,△CBP;等腰三角形有:△OAB,△ABP.14.如图所示,AB为⊙O的直径,CB切⊙O于B,CD切⊙O于D,交BA的延长线于E,若EA=1,ED=2,则BC的长为________.【答案】3【解析】∵CE为⊙O切线,D为切点,∴ED2=EA·EB.又∵EA=1,ED=2,∴EB=4,又∵CB、CD均为⊙O切线,∴CD=CB.在Rt△EBC中,设BC=x,则EC=x+2.由勾股定理:EB2+BC2=EC2得42+x2=(x+2)2,得x=3,∴BC=3.15.如图,⊙O内切于△ABC,切点分别为D、E、F.已知∠B=50°,∠C=60°,连接OE、OF、DE、DF,那么∠EDF等于A.40° B.55°C.65° D.70°【答案】B【解析】∵∠B=50°,∠C=60°,∴∠A=70°,∴∠EOF=110°,∴∠EDF=55°.16.如图所示,AD切⊙O于点F,FB,FC为⊙O的两弦,请列出图中所有的弦切角________________________.【答案】∠AFB、∠AFC、∠DFC、∠DFB【解析】弦切角的三要素:(1)顶点在圆上,(2)一边与圆相交,(3)一边与圆相切.三要素缺一不可.17.如图所示,已知BC是⊙O的弦,P是BC延长线上一点,PA与⊙O相切于点A,∠ABC=25°,∠ACB=80°,求∠P的度数.【答案】55°【解析】解因为PA与⊙O相切于点A,所以∠PAC=∠ABP=25°.又因为∠ACB=80°,所以∠ACP=100°.又因为∠PAC+∠PCA+∠P=180°,所以∠P=180°-100°-25°=55°.18.如图,点A、B、C是圆O上的点,且AB=4,∠ACB=30°,则圆O的面积等于A.4π B.8πC.12π D.16π【答案】D【解析】连接OA、OB,∵∠ACB=30°,∴∠AOB=60°,又∵OA=OB,∴△AOB为等边三角形,又AB=4,∴OA=OB=4,∴S=π·42=16π.⊙O19.如图所示,AB是⊙O的直径,弦AC=3 cm,BC=4 cm,CD⊥AB,垂足为D,求AD、BD 和CD的长.【答案】cm cm cm【解析】解∴AB是⊙O的直径,∵AC⊥BC.∵CD⊥AB,∴AC2=AD·AB,BC2=BD·AB.∵AC=3 cm,BC=4 cm,∴AB=5 cm.∴AD=cm,BD=cm.∵CD2=AD·BD=×=cm2.∴CD==cm,AD=cm,BD=cm.20.如图所示,四边形ABCD是矩形,∠BEF=90°,①②③④这四个三角形能相似的是__________.【答案】①③【解析】因为四边形ABCD为矩形,所以∠A=∠D=90°.因为∠BEF=90°,所以∠1+∠2=90°.因为∠1+∠ABE=90°,所以∠ABE=∠2.又因为∠A=∠D=90°,所以△ABE∽△DEF.21.如图,已知Rt△ABC的周长为48 cm,一锐角平分线分对边为3∶5两部分.(1)求直角三角形的三边长;(2)求两直角边在斜边上的射影的长.【答案】(1) 20 cm,12 cm,16 cm (2)cm, cm【解析】解(1)如图,设CD=3x,BD=5x,则BC=8x,过D作DE⊥AB,由Rt△ADC≌Rt△ADE可知,DE=3x,BE=4x,∴AE+AC+12x=48,又AE=AC,∴AC=24-6x,AB=24-2x,∴(24-6x)2+(8x)2=(24-2x)2,解得:x1=0(舍去),x2=2,∴AB=20,AC=12,BC=16,∴三边长分别为:20 cm,12 cm,16 cm.(2)作CF⊥AB于F点,∴AC2=AF·AB,∴AF=== (cm);同理:BF=== (cm).∴两直角边在斜边上的射影长分别为cm, cm.22.如图,设AA1与BB1相交于点O,AB∥A1B1且AB=A1B1.若△AOB的外接圆的直径为1,则△A1OB1的外接圆的直径为__________.【答案】2【解析】∵AB∥A1B1且AB=A1B1,∴△AOB∽△A1OB1,∴两三角形外接圆的直径之比等于相似比.∴△A1OB1的外接圆直径为2.23.如图所示,AD是△ABC的中线,E是CA边的三等分点,BE交AD于点F,则AF∶FD为A.2∶1B.3∶1C.4∶1D.5∶1【答案】C【解析】要求AF∶FD的比,需要添加平行线寻找与之相等的比.注意到D是BC的中点,可过D作DG∥AC交BE于G,则DG=EC,又AE=2EC,故AF∶FD=AE∶DG=2EC∶EC=4∶1.24.如图所示,在△ABC中,MN∥DE∥BC,若AE∶EC=7∶3,则DB∶AB的值为________.【答案】3∶10【解析】由AE∶EC=7∶3,有EC∶AC=3∶10.根据MN∥DE∥BC,可得DB∶AB=EC∶AC,即得DB∶AB=3∶10.25.如图所示,在△ABC中,AE∶EB=1∶3,BD∶DC=2∶1,AD与CE相交于F,求+的值.【答案】【解析】解过点D作DG∥AB交EC于G,则===,而=,即=,所以AE=DG,从而有AF=DF,EF=FG=CG,故+=+=+1=.26.如图所示,已知a∥b∥c,直线m、n分别与a、b、c交于点A、B、C和A′、B′、C′,如果AB=BC=1,A′B′=,则B′C′=________.【答案】【解析】由平行线等分线段定理可直接得到B′C′=.27.已知梯形的中位线长10 cm,一条对角线将中位线分成的两部分之差是3 cm,则该梯形中的较大的底是________ cm.【答案】13【解析】设梯形较大,较小的底分别为a,b,则有可得:a=13.28.如图,在▱ABCD中,设E和F分别是边BC和AD的中点,BF和DE分别交AC于P、Q 两点.求证:AP=PQ=QC.【答案】见解析【解析】证明∵四边形ABCD是平行四边形,E、F分别是BC、AD边上的中点,∴DF綉BE,∴四边形BEDF是平行四边形.∵在△ADQ中,F是AD的中点,FP∥DQ.∴P是AQ的中点,∴AP=PQ.∵在△CPB中,E是BC的中点,EQ∥BP,∴Q是CP的中点,∴CQ=PQ,∴AP=PQ=QC.29.如图,直线交圆于两点,是直径,平分,交圆于点,过作丄于.(1)求证:是圆的切线;(2)若,求的面积【答案】(1)连结OD,则OA=OD,所以∠OAD=∠ODA.,然后利用∠EDA+∠ODA=90°,即DE⊥OD来得到证明。
几何选讲习题

图31、如图,M 是平行四边形ABCD 的边AB 的 中点,直线l 过点M 分别交,AD AC 于点,E F . 若3AD AE =,则:AF FC = .2、如图3,在⊙O 中,直径AB 与弦CD 垂直,垂足为E ,EF ⊥BC ,垂足为F ,若AB=6,CF ·CB=5,则AE= 。
3、如右图所示,⊙O 上一点C 在直径AB 上的射影为D ,CD =4,BD =8,则⊙O 的半径等于4、如图,PA 切⊙O 于点A ,割线PBC 经过圆心O ,1OB PB ==,OA 绕点O 逆时针旋转60 到OD ,则PD 的长为 .5、如图,四边形ABCD 是圆O 的内接四边形,延长AB 和DC 相交于点P .若1,3PB PD ==,则BCAD的值为 .6、如图4,已知圆O 的半径为2,从圆O 外一点A 引切线AB 和割线AD ,C 为AD 与圆O 的交点,圆心O 到AD 的距离AB =AC 的长为__ __.7、如图3,△ABC 的外角平分线AD 交外接圆于D,4BD =,则CD = .8、如图3,已知AB 是⊙O 的一条弦,点P 为AB 上一点,PC OP ⊥,PC 交⊙O 于C ,若4AP =,2PB =, 则PC 的长是第1题图FABCDEMlP图3DA9、如图3,圆O 的割线PAB 交圆O 于A 、B 两点,割线PCD 经过圆心。
已知6=PA ,317=AB ,12=PO 。
则圆O 的半径____=R .10、如图,圆O 内的两条弦AB 、CD 相交于P ,4==PB PA ,PC PD 4=.若O 到AB 的距离为4,则O到CD 的距离为 .11、如图,⊙O 的直径6AB cm =,P 是AB 延长线上的一点,过P 点作⊙O 的切线,切点为C ,连接AC ,若30CPA ∠= ,PC =_____________12、如右图,O 是半圆的圆心,直径AB =PB 是圆的 一条切线,割线PA 与半圆交于点C ,AC=4,则PB=____.13、如图,正ABC ∆的边长为2,点,M N 分别是边,AB AC 的中点,直线MN 与ABC ∆的外接圆的交点为P 、Q ,则线段PM = .14、如图3,AB 的延长线上任取一点C ,过C 作圆的切线CD ,切点为D ,ACD ∠的平分线交AD 于E ,则CED ∠= .15、如图PM 为圆O 的切线,T 为切点, 3ATM π∠=,圆O 的面积为2π,则PA =.第13题图APMNBC。
高考数学综合能力题30讲第14讲 立体几何中的有关计算

数学高考综合能力题选讲14立体几何中的有关计算100080 北京中国人民大学附中 梁丽平题型预测立体几何中的计算主要是求角和距离.其中二面角的平面角和点到平面的距离(体积)常常作为考查的重点.范例选讲例1 长方体1111D C B A ABCD -中,1==BC AB ,21=AA ,E 是侧棱1BB 中点.(1)求直线1AA 与平面E D A 11所成角的大小;(2)求二面角B AC E --1的大小; (3)求三棱锥E D C A 11-的体积.讲解:(1)要求线面所成角,首先需要找到这个角,为此,我们应该先作出面E D A 11的一条垂线.不难发现,AE 正为所求.由长方体1111D C B A ABCD -知:1111A ABB A D 面⊥,又11A A B B AE 面⊂,所以,AE A D ⊥11.在矩形11A ABB 中,E 为1BB 中点且21=AA ,1=AB ,所以,21==E A AE ,所以,AE A 1∆为等腰直角三角形,AE EA ⊥1.所以,⊥AE 面E D A 11.所以,AE A 1∠就是直线1AA 与平面E D A 11所成的角,为︒45.(2)要作出二面角的平面角,一般的思路是最好能找到其中一个面的一条垂线,则可利用三垂线定理(或逆定理)将其作出.CA C 1注意到11B C CB AB 面⊥,所以,面⊥1A B C 11B C C B 面,所以,只需在11BCC B 面内过点E 作1BC EF ⊥于F ,则⊥EF 面1ABC .过F 作1AC FG ⊥于G ,连EG ,则EGF ∠就是二面角B AC E --1的平面角.在1EBC ∆中,55211111=⋅==∆BC B C EB BC S EF EBC ,所以,5532211=-=EF E C F C .在1ABC ∆中,1030sin 1111=⋅=∠⋅=AC AB F C G FC F C FG . 在EFG Rt ∆中,36tan ==∠FG EF EGF . 所以,二面角B AC E --1的平面角的大小为36arctan.(3)要求三棱锥E D C A 11-的体积,注意到(2)中已经求出了点E 到平面11D AC 的距离EF .所以,61613111111111=⋅⋅=⋅==∆--EF CD AD EF S V V D AC D AC E E D C A .另一方面,也可以利用等积转化.因为11//C D AB ,所以,//AB E D C 11面.所以,点A 到平E D C 11面的距离就等于点B 到平E D C 11面的距离.所以,6161311111111111111=⋅⋅=⋅===∆---C D B C EB C D S V V V EBC EBC D E D C B E D C A .点评:求角的一般方法是:先作出所求角,然后再解三角形.利用三垂线定理作出二面角的平面角是很常用的方法.AC A C 1例2 如图:三棱台111C B A ABC -中,侧棱1CC ⊥底面ABC ,︒=∠120ACB ,a BC a AC 2,==,a C B =11,直线1AB 与1CC 所成的角等于60°.(1)求二面角B AC B --1的大小; (2)求点B 到平面AC B 1的距离.讲解 无论从已知(直线1AB 与1CC 所成的角等于60°)的角度还是从所求(二面角B AC B --1)的角度,过1B 作1CC 的平行线都是当然之举.在平面CB C B 11中,过1B 作C C D B 11//交CB 于点D ,连接AD ,则1ADB ∠就是直线1AB 与1CC 所成的角.所以,︒=∠601ADB .又因为1CC ⊥底面ABC ,所以,D B 1⊥底面ABC .在平面ABC 内过点D 作AC DE ⊥于E ,连E B 1,则AC E B ⊥1,所以,ED B 1∠就是二面角B AC B --1的平面角. 在ACD ∆中,a CD AC CD AC AD 3120cos 222=︒⋅-+=.在Rt D AB 1∆中,a AD D B =︒⋅=60cot 1.在Rt CED ∆中,a CE DE 2360sin =︒⋅=.在Rt D EB 1∆中,33223tan 1==∠a a ED B . AC ABC所以,二面角B AC B --1的平面角的大小为:332arctan.(2)由D 为BC 中点,故点B 到平面AC B 1的距离等于点D 到平面AC B 1的距离的2倍,作E B DH 1⊥于H .由(1)知ED B AC 1面⊥,所以,DH AC ⊥,所以,AC B DH 1面⊥,所以,DH 就是点D 到平面AC B 1的距离.在Rt D EB 1∆中,a DB DE DB DE EB DB DE DH 721212111=+⋅=⋅=.所以,点B 到平面AC B 1的距离等于a 7212. 另外,我们也可以用体积法求出这个距离.设点B 到平面AC B 1的距离为h .则由=-ACB B V 11ACB B V -及31163sin 2131311a D B ACB BC AC D B S V ABC ACB B =⋅⎪⎭⎫⎝⎛∠⋅⋅⋅=⋅=∆-, 221214721211a D B ED AC E B AC S ACB =+⋅=⋅=∆可得: =⋅==∆-4763332311a a S V h ACB ACB B a 7212.所以,点B 到平面AC B 1的距离等于a 7212.点评 等积变形是求体积和求距离时常用的方法.高考真题1.(1998年全国高考)已知斜三棱柱ABC -A'B'C'的侧面A'ACC'与底面ABC 垂直,∠ABC =︒90,BC =2,AC =32且AA'⊥A'C,AA'=A'C.①求侧棱AA'与底面ABC 所成角的大小;②求侧面A'ABB'与底面ABC 所成二面角的大AB小;③求顶点C 到侧面A'ABB'的距离. 2.(1999年全国高考)如图,已知四棱柱ABCD -A'B'C'D',点E 在棱D'D 上,截面EAC ∥D'B,且面EAC 与底面ABCD 所成的角为45°,AB =a(1)求截面EAC 的面积;(2)求异面直线A'B'与AC 之间的距离; (3)求三棱锥B'-EAC 的体积.3.(2001年全国高考)如图:在底面是直角梯形的四棱锥S-ABCD 中,∠ABC=90°,SA ⊥面ABCD ,SA=AB=BC=1,AD=21.(1) 求四棱锥S-ABCD 的体积; (2) 求面SCD 与面SBA 所成的二面角的平面角的正切值.[答案与提示:1.︒45;︒60;3. 2.222a ;a 2;342a . 3.2241;. ] SB C A DAC。
高中数学几何证明选讲详解

【命题立意】本题考查几何证明选做题的解法,属送分题
【思路点拨】条件
【规范解答】因为以AC为直径的圆与AB交于点D,所以
A. B. C. D.
【解析】设半径为 ,则 ,由 得 ,从而 ,故 ,选A.
7.在 中, 分别为 上的点,且 , 的面积是 ,梯形 的面积为 ,则 的值为( )
A. B. C. D.
【解析】 ,利用面积比等于相似比的平方可得答案B.
8.半径分别为1和2的两圆外切,作半径为3的圆与这两圆均相切,一共可作( )个.
5. (2010·天津高考理科·T14)如图,四边形ABCD是圆O的内接四边形,延长AB和DC相交于点P,若 ,则 的值为
【命题立意】考查三角形的相似性质的应用。
【思路点拨】利用相似三角形的性质进行转化。
【规范解答】由题意可知 ∽ 相似,
所以 ,由 及已知条件
可得 ,又 , 。
【答案】
6.(2010·广东高考文科·T14)如图3,在直角梯形ABCD中,DC∥AB,CB⊥AB,AB=AD=a,CD= ,点E,F分别为线段AB,CD的中点,则EF=.
【答案】
7.(2010·广东高考理科·T14)如图3,AB,CD是半径为a的圆O的两条弦,它们相交于AB的中点P,PD= ,∠OAP=30°,则CP=______.
【命题立意】本题考察垂径定理及相交弦定理.
【思路点拨】由垂径定理得 ,算出 ,再由相交弦定理求出
【规范解答】因为 为 的中点,由垂径定理得 ,在 中, ,由相交弦定理得: ,即 ,
几何证明选讲训练

几何证明选讲专题1.如图所示,在四边形ABCD 中,//,//EF BC FG AD ,则EF FGBC AD+=1 由平行线分线段成比例可知,EF AF FG FC BC AC AD AC ==,所以1EF FG AF FCBC AD AC++==2.在平行四边形ABCD 中,点E 在边AB 上,且:1:2,AE EB DE =与AC 交于点F ,若AEF ∆的面积为6cm 2,则ABC ∆的面积为 cm 272 不妨设,AEF ABC ∆∆,AE AB 边上的高分别为12,h h ,因为四边形ABCD 为平行四边 形,:1:2,AE EB =,所以12:1:3,:1:3,:1:4AE AB EF FD h h ===,所以:1:12AEF ABC S S ∆∆=,从而ABC ∆的面积为72 cm 23.如图,圆O 上一点C 在直径AB 上的射影为D ,4,8CD BD ==,则圆O 的半径等于5 由直角三角形射影定理2CD BD DA =⋅可知2DA =,10AB =,即半径为5 4.如图,从圆O 外一点P 作圆O 的割线,,PAB PCD AB 是圆O 的直径,若4,5,3PA PC CD ===,则CBD ∠=30 由割线定理知PA PB PC PD ⋅=⋅,即4(4)5(53)AB ⨯+=⨯+,得6AB =即圆O 的半径为3,因为弦3CD =,所以60COD ∠=,从而1302CBD COD ∠=∠= 5.已知PA 是圆O 的切线,切点为A ,2,PA AC =是圆O 的直径,PC 与圆O 交于点B ,1PB =,则圆O 的半径R =由切割线定理知2PA PB PC =⋅,即221PC =⨯,4PC =,所以AC =6.如图,PC 切圆O 于点C ,割线PAB 经过圆心O ,弦C D A B ⊥于E ,4,8PC PB ==,则CD =245由切割线定理知2PC PA PB =⋅得2,826PA AB ==-=,圆O 半径为3,连接CO ,则在直角三角形PCO 中,有3512,235CO CP OP CE CE ⨯⋅=⋅==+,从而245CD = 7.如图,,AB CD 是圆O 的两条弦,交点为E 且AB 是线段CD 的中垂线,已知6,AB CD ==AD 的长度为由条件可知AB 为圆O 的直径,所以3r =,连接OD ,则2OE ==,所以5,AE AD ===8.如图,在梯形ABCD 中,////AD BC EF ,E 是AB 的中点,EF 交BD 于G ,交AC 于H ,若5,7AD BC ==,则GH =1 由条件可知EF 为梯形ABCD 的中线,且1(57)62EF =+=;由相似三角形的相似比可知,57EG BG GF DG BD BD ==,从而6157EG EG -+=,解得52EG =,同理可解得52HF =,所以1GH =9.如图,圆的内接ABC ∆的C ∠的平分线CD 延长后交圆于点E ,连接BE ,已知3BD =,7,5CE BC ==,则线段BE =215因为CD 为C ∠的平分线,所以BCE ECA ∠=∠,又圆周角EBA ECA ∠=∠,所以BCE EBA ∠=∠,又E E ∠=∠,所以EBC EBD ∆∆ ,从而BE BD EC BC =,即375BE =,所以215BE =10.如图,四边形ABCD 内接于圆O ,BC 是直径,MN 切圆O 于A ,25MAB ∠=, 则D ∠=115 连接AC ,由条件可知25C MAB ∠=∠= ,又BC 为直径,所以90BAC ∠= ,、从而180902565B ∠=--= ,又180B D ∠+∠= ,所以115D ∠=11.如图,在ABC ∆中,D 是AC 的中点,E 是BD 的中点,AE 交BC 于F ,则BFBC=12过E 作//EG DC 交BC 于G ,因为E 是BD 的中点,D 是AC 的中点,所以1124EG DC AC ==,BG GC =,又1143FG FC GC ==,所以2132BF BG FG GC FC =-==12.如图,圆'O 和圆O 相交于A 和B ,PQ 切圆O 于P ,交圆'O 于,Q M ,交AB 的延长线于N ,3,15,MN NQ ==则PN =由割线定理、切割线定理,有2NM NQ NB NA NP ⋅=⋅=,所以2315PN =⨯,即PN =13.如图,,EB EC 是圆O 的两条切线,,B C 是切点,,A D 是圆上两点,如果46E ∠=32DCF ∠= ,则A ∠的度数是因为,EB EC 是圆O 的两条切线,所以EB EC =,又46E ∠=,所以1(18046)672EBC ECB ∠=∠=-= ,又32DCF ∠= ,所以180673281BCD ∠=--= ,从而1808199A ∠=-=14.已知圆O 的半径为3,从圆O 外一点A 引切线AD 和割线ABC ,圆心O 到AC 的距离为3AB =,则切线AD 的长为依题意,2BC ==,所以5AC =,由215AD AB AC =⋅=,得AD =15.如图,已知P 是O 外一点,PD 为O 的切线,D 为切点,割线PEF 经过圆心O ,若12,PF PD ==则EFD ∠的度数为30由切割线定理得2PD PE PF =⋅2163412PD PE PF ⨯⇒===8EF ⇒=,4OD =, ∵OD PD ⊥,12OD PO =∴30P ∠= ,60,30POD PDE EFD ∠=∠=∠=。
几何证明选讲解三角形排列组合(教师版)
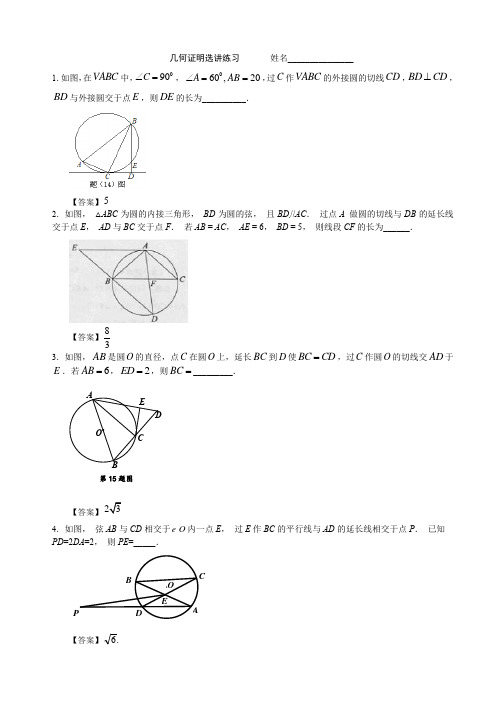
几何证明选讲练习 姓名_______________1.如图,在中,,,过作的外接圆的切线,,与外接圆交于点,则的长为__________.【答案】2.如图, △ABC 为圆的内接三角形, BD 为圆的弦, 且BD //AC . 过点A 做圆的切线与DB 的延长线交于点E , AD 与BC 交于点F . 若AB = AC , AE = 6, BD = 5, 则线段CF 的长为______.【答案】833.如图,AB 是圆O 的直径,点C 在圆O 上,延长BC 到D 使BC CD =,过C 作圆O 的切线交AD 于E .若6AB =,2ED =,则BC =_________.【答案】4.如图, 弦AB 与CD 相交于O 内一点E , 过E 作BC 的平行线与AD 的延长线相交于点P . 已知PD =2DA =2, 则PE =_____.【答案】.6 ABC 090C ∠=060,20A AB ∠==C ABC CD BD CD ⊥BD EDE5.A ED CB O 第15题图5.如图2,O 中,弦,AB CD 相交于点,2P PA PB ==,1PD =,则圆心O 到弦CD 的距离为____________.【答案】23 6.如图,圆O 上一点C 在直线AB 上的射影为D ,点D 在半径OC 上的射影为E .若3AB AD =,则CEEO的值为___________.【答案】8 7.如图,AB 为圆O 的直径,P A 为圆O 的切线,PB 与圆O 相交于D .若PA=3,916PD DB =::,则PD=_________;AB=___________.【答案】95;4 解三角形练习1.如图,△ABC 中,AB=AC=2,BC=点D在BC 边上,∠ADC=45°,则AD 的长度等于______.【命题意图】本题考查运用正余弦定理解三角形,是中档题.【解析】(法1)过A 作AE ⊥BC,垂足为E ,∵AB=AC=2,BC=∴E 是BC 的中点,且EC=O D EBACRt AEC ∆中,AE=又∵∠ADE=45°,∴DE=1,∴AD=(法2) ∵AB=AC=2,BC=由余弦定理知,cos C =2222AC BC AB AC BC +-⨯∴C=30°, 在△ADC 中,∠ADE=45°,由正弦定理得,sin sin AD AC C ADC=∠, ∴AD=sin sin AD C ADC ∠=12⨯2.如图,在△ABC 中,D 是边AC 上的点,且AB AD =,2AB =,2BC BD =,则sin C 的值为( )A.3 B.6 C3 D6【答案】D【解析】设BD a =,则由题意可得:2,BC a =2AB AD a ==,在ABD ∆中,由余弦定理得: 222cos 2AB AD BD A AB AD +-==⋅2232a a ⨯-=13,所以sin A=,在△ABC 中,由正弦定理得,sin sin AB BC C A =,所以2sin C =,解得sin CD . 3.,EF 是等腰直角ABC ∆斜边AB 上的三等分点,则tan ECF ∠=( )A .1627B .23 CD .34【答案】D4.在△ABC 中, 4ABC π∠=,AB 3BC =,则sin BAC ∠ =( ) (A )(B )(C )(D )【答案】C5.ABC ∆中,90C ∠=,M 是BC 的中点,若31sin =∠BAM ,则=∠BAC sin ________.【答案】36.在△ABC 中,已知AB=4,AC=7,BC 边的中线27=AD ,求边BC 的长.7.如图,在四边形ABCD 中,AC 平分∠DAB ,∠ABC=60°,AC=7,AD=6,S △ADC =2315,求AB 的长.排列组合练习题1.有6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到份纪念品的同学人数为( ) 或 或 或 或【解析】选①设仅有甲与乙,丙没交换纪念品,则收到份纪念品的同学人数为人②设仅有甲与乙,丙与丁没交换纪念品,则收到份纪念品的同学人数为人.2.将字母排成三行两列,要求每行的字母互不相同,每列的字母也互不相同,则不同的排列方法共有A .12种B .18种C .24种D .36种答案A【命题意图】本试题考查了排列组合的用用.4()A 13()B 14()C 23()D 24D 261315132C -=-=4244,,,,,a a b b c c【解析】利用分步计数原理,先填写最左上角的数,有3种,再填写右上角的数为2种,在填写第二行第一列的数有2种,一共有.3.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这些卡片不能是同一种颜色,且红色卡片至多1张,不同取法的种数为(A )232 (B)252 (C)472 (D)484解析:,答案应选C . 另解:. 4. 两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )A .10种B .15种C .20种D .30种【解析】甲赢和乙赢的可能情况是一样的,所以假设甲赢的情况如下:若两人进行3场比赛,则情况只有是甲全赢1种情况;若两人进行4场比赛,第4场比赛必为甲赢前3场任选一场乙赢为种情况;若两人进行5场比赛,第5场比赛必为甲赢前4场任选一场乙赢为种情况;综上,甲赢有10种情况,同理,乙赢有10种情况,则所有可能出现的情况共20种,故选C .5.若从1,2,2,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有A .60种B .63种C .65种D .66种【解析】1,2,2,…,9这9个整数中有5个奇数,4个偶数.要想同时取4个不同的数其和为偶数,则取法有:4个都是偶数:1种;2个偶数,2个奇数:种; 4个都是奇数:种.∴不同的取法共有66种.【答案】D6.某艺校在一天的6节课中随机安排语文、数学、外语三门文化课和其他三门艺术课个1节,则在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为 (用数字作答).【解析】概率为 语文、数学、英语三门文化课间隔一节艺术课,排列有种排法,语文、数学、英语三门文化课相邻有种排法,语文、数学、英语三门文化课两门相邻有种排法. 32212⨯⨯=472885607216614151641122434316=-=--⨯⨯=--C C C C 472122642202111241261011123212143431204=-+=⨯⨯+-⨯⨯=+-C C C C C 313=C 624=C 225460C C =455C =3____53344A A 3312122223A C C A C3故所有的排法种数有在课表上的相邻两节文化课之间最多间隔1节艺术课的概率为5。
几何证明选讲定理大全

6.ΔABC内接于⊙O,AD是⊙O旳直径, CE⊥AD,E为垂足,CE旳延长线交AB
于点F,求证:AC2=AF·AB.
7.已 知BC是 圆O的直 径,AD BC,垂足 为D, BF交AD于E, 且AE BE. (1)求证 :弧AB 弧AF; (2)如 果sinFBC 3,AB 4 5, 求AD的 长.
直线CE和⊙O切于点C,AD⊥CE,垂
足为D,
求证:AC平分∠BAD
E
O
A
C
D
2.如图,⊙O和⊙O′都经过A、B 两点,AC是⊙O ′旳切线,交 ⊙O于C,AD是⊙O旳切线,交 ⊙O ′于D,
求证:AB2=BC·BD.
A
O CB
O' D
3.在△ABC中,∠A旳平分线AD交BC 于D,⊙O过点A,且和BC切于D, 和AB、AC分别交于E、F, 求证:EF//BC.
若∠PAD=∠DCB,则ABCD四点共圆;
D
若∠ADB=∠ACB,则ABCD四点共圆;
C O
PA
B
练习
情况唯一吗?
1.⊙O1和⊙O2都经过A、B两点,经过A点旳直线CD与
⊙O1交于点C,与⊙O2交于点D,经过B点旳直线EF与
⊙O1交于点E,与⊙O2交于点F,求证:CE∥DF.
D
E
A
A
D
C
C O1
O2
F
D
E
B
C
A
D
E
16
16 8
CF DE , BF 8
.
3
33
B
第12讲立体几何问题选讲

第12讲立体几何问题选讲【赛点突破】常用思想:转化与化归新的工具:空间向量【范例解密】例1一个平面与正方体相交所得的截面可能是正五边形吗?解:不能为正五边形,因为截面必然和正方体的五个面相交,必有两个面是相对的平行面,故截得的五边形必有两条边互相平行,而正五边形中没有两条边平行,故结论成立。
注:本答案是刘未末同学首创。
例2与三条异面直线,,a b c都相交的直线有多少条?解:有无数条。
在直线a上选一点A,在直线b上选一点B,当B在直线b上运动时,所有的直线轨迹是过点A和直线b的平面,如果这个平面和直线c有交点C,则过A,B,C的直线和三条异面直线都相交。
如果变换A的位置,将有无数个过直线b的平面,而这些平面中至多只有一个平面和直线c平行(否则直线c和直线b平行),故满足条件的直线有无数条。
注:本题运用了动态变化的观点。
例3如果一个四面体的三组对棱分别相等,则称这个四面体为等腰四面体。
若一个等腰四面体的三组对棱长分别为,,a b c。
(1)证明四面体的每个面都是锐角三角形;(2)求四面体的体积。
分析与解:(1)如图,取BD的中点E,则AE CE==AE CE AC+>,故c>,即222a b c+>,同理222b c a+>,222a c b+>,故每个面都是锐角三角形;(2)如图,将四面体放入长方体内,即可求得体积。
注:第一问比较难于说明,第二问得构造值得学习。
例4用平面截一个四棱锥,使平面与棱锥的四条侧棱分别相交,则一定能使截面为平行四边形吗?分析与解:如图,设两组相对侧面的两条交线分别为,l m,直线,l m确定的平面为α,则平行于α的平面与四棱锥截得的四边形为平行四边形。
注:本题的交线比较隐蔽,需注意。
例5如图,四面体PABC 中,,PA BC PB AC ⊥⊥,证明:PC AB ⊥。
证明:作PH ⊥面ABC 于H 。
由于PA BC ⊥,由三垂线定理逆定理知AH BC ⊥,同理 BH AC ⊥,故H 为ABC ∆垂心,CH AB ⊥,由三垂线定理得PC AB ⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
几何计算题选讲 Corporation standardization office #QS8QHH-HHGX8Q8-GNHHJ8江苏地区中考数学复习几何计算题选讲几何计算题历年来是中考的热点问题。
几何计算是以推理为基础的几何量的计算,主要有线段 与弧的长度计算、角和弧的度数计算、三角函数值的计算、线段比值的计算以及面积、体积的计算,从图形上分类有:三角形、四边形、多边形以及圆的有关计算。
解几何计算题的常用方法有:几何法、代数法、三角法等。
一、三种常用解题方法举例例1. 如图,在矩形ABCD 中,以边AB 为直径的半圆O 恰与对边CD 相切于T ,与对角线AC 交于P ,PE ⊥AB 于E ,AB=10,求PE 的长.解法一:(几何法)连结OT ,则OT ⊥CD ,且OT=21AB =5BC=OT=5,AC=25100+=55 ∵BC 是⊙O 切线,∴BC 2 =CP ·CA. ∴PC=5,∴AP=CA-CP=54. ∵PE ∥BC ∴AC AP BC PE =,PE=5554×5=4. 说明:几何法即根据几何推理,由几何关系式进行求解的方法,推理时特别要注意图形中的隐含条件. 解法二:(代数法)∵PE ∥BC ,∴AB AE CB PE =. ∴21==AB CB AE PE .设:PE=x ,则AE=2 x ,EB=10–2 x . 连结PB. ∵AB 是直径,∴∠APB=900.在Rt △APB 中,PE ⊥AB ,∴△PBE ∽△APE . ∴21==AE PE EP EB .∴EP=2EB ,即x=2(10–2x ). 解得x =4. ∴PE=4.说明:代数法即为设未知数列方程求解,关键在于找出可供列方程的相等关系,例如:相似三角形中的线段比例式;勾股定理中的等式;相交弦定理、切割线定理中的线段等积式,以及其他的相等关系. 解法三:(三角法)连结PB ,则BP ⊥AC.设∠PAB=α 在Rt △APB 中,AP=10COS α,在Rt △APE 中,PE=APsin α, ∴PE=10sin αCOS α. 在Rt △ABC 中, BC=5,AC=55.∴sin α=55555=, COS α=5525510=.∴PE=10×55255⨯=4.说明:在几何计算中,必须注意以下几点:(1) 注意“数形结合”,多角度,全方位观察图形,挖掘隐含条件,寻找数量关系和相等关系.(2) 注意推理和计算相结合,先推理后计算,或边推理边计算,力求解题过程规范化.(3) 注意几何法、代数法、三角法的灵活运用和综合运用. 二.其他题型举例例2.如图,ABCD 是边长为2 a 的正方形,AB 为半圆O 的直径,CE 切⊙O 于E ,与BA 的延长线交于F ,求EF 的长.分析:本题考察切线的性质、切割线定理、相似三角形性质、以及正方形有关性质.本题可用代数法求解. 解:连结OE ,∵CE 切⊙O 于E , ∴OE ⊥CF ∴△EFO ∽△BFC ,∴FB FE BC OE,又∵OE=21AB=21BC ,∴EF=21FB设EF=x ,则FB=2x ,FA=2x –2a∵FE 切⊙O 于E ∴FE 2=FA ·FB ,∴x 2=(2x –2a )·2x解得x =34a , ∴EF=34a.例3.已知:如图,⊙O 1 与⊙O 2相交于点A 、B ,且点O 1在⊙O 2上,连心线O 1O 2交⊙O 1于点C 、D ,交⊙O 2于点E ,过点C 作CF ⊥CE ,交EA 的延长线于点F ,若DE=2,AE=52(1) 求证:EF 是⊙O 1的切线; (2) 求线段CF 的长; (3) 求tan ∠DAE 的值.分析:(1)连结O 1A ,O 1E 是⊙O 2的直径,O 1A ⊥EF ,从而知EF 是⊙O 1的切线.(2)由已知条件DE=2,AE=52,且EA 、EDC 分别是⊙O 1的切线和割线,运用切割线定理EA 2=ED ·EC ,可求得EC=10.由CF ⊥CE ,可得CF 是⊙O 1的切线,从而FC=FA.在Rt △EFC 中,设CF= x ,则FE= x +52.又CE=10,由勾股定理可得:(x +52)2= x 2+102,解得 x =54.即CF=54.(3)要求tan ∠DAE 的值,通常有两种方法:①构造含∠DAE 的直角三角形;②把求tan ∠DAE 的值转化为求某一直角三角形一锐角的正切(等角转化).在求正切值时,又有两种方法可供选择:①分别求出两线段(对边和邻边)的值;②整体求出两线段(对边和邻边)的比值. 解:(1)连结O 1A ,∵O 1E 是⊙O 2的直径,∴O 1A ⊥EF∴EF 是⊙O 1的切线..(2)∵DE=2,AE=52,且EA 、EDC 分别是⊙O 1的切线和割线∴EA 2=ED ·EC ,∴EC=10由CF ⊥CE ,可得CF 是⊙O 1的切线,从而FC=FA.在Rt △EFC 中,设CF= x ,则FE= x +52.又CE=10,由勾股定理可得:(x +52)2= x 2+102,解得 x =54.即CF=54.(3)解法一:(构造含∠DAE 的直角三角形)作DG ⊥AE 于G ,求AG 和DG 的值.分析已知条件,在Rt △A O 1E 中,三边长都已知或可求(O 1A=4,O 1E=6),又DE=2,且DG ∥A O 1(因为DG ⊥AE ),运用平行分线段成比例可求得DG=,354,34=AG 从而tan ∠DAE=55. 解法二:(等角转化)连结AC ,由EA 是⊙O 1的切线知∠DAE=∠ACD.只需求tan ∠ACD.易得∠CAD=900,所以只需求ACAD的值即可.观察和分析图形,可得△ADE ∽△CAE ,551052===CE AE AC AD .从而tan ∠ACD=55=AC AD ,即tan ∠DAE=55. 说明:(1)从已知条件出发快速地找到基本图形,得到基本结论,在解综合题时更显出它的基础性和重要性.如本题(2)求CF 的长时,要能很快地运用切割线定理,先求出CE 的长.(2)方程思想是几何计算中一种常用的、重要的方法,要熟练地掌握.例4.如图,已知矩形ABCD ,以A 为圆心,AD 为半径的圆交AC 、AB 于M 、E ,CE 的延长线交⊙A 于F ,CM=2,AB=4.(1) 求⊙A 的半径;(2) 求CF 的长和△AFC 的面积. 解:(1)∵四边形ABCD 是矩形,∴CD=AB=4,在Rt △ACD 中,AC 2=CD 2+AD 2,∴(2+AD )2=42+AD 2,解得AD=3.(2) A 作AG ⊥EF 于G.∵BG=3,BE=AB ―AE=1,∴CE=10132222=+=+BE BC由CE ·CF=CD 2,得CF=105810422==CE CD .又∵∠B=∠AGE=900,∠BEC=∠GEA ,∴△BCE ∽△GAE.∴AE CE AG BC =,即,3103=AG S △AFC =21CF ·AG=536. 例5.如图,△ABC 内接于⊙O ,BC=4,S △ABC =36,∠B 为锐角,且关于x 的方程x 2–4xcosB+1=0有两个相等的实数根.D 是劣弧AC 上的任一点(点D 不与点A 、C 重合),DE 平分∠ADC ,交⊙O 于点E ,交AC 于点F. (1) 求∠B 的度数;(2) 求CE 的长.分析:本题是一道综合了代数知识的几何计算题,考察了圆的有关性质,解题时应注意线段的转化.解:(1)∵关于x 的方程x 2–4xcosB+1=0有两个相等的实数根,∴Δ=(-4cosB )2-4=0.∴cosB=21,或cosB=-21(舍去).又∵∠B 为锐角,∴∠B=600.(2) 点A 作AH ⊥BC ,垂足为H. S △ABC =21BC ·AH=21BC ·AB ·sin600=36,解得AB=6 在Rt △ABH 中,BH=AB ·cos600=6×21=3,AH=AB ·sin600=6×3323=,∴CH=BC-BH=4-3=1. 在Rt △ACH 中,AC 2+CH 2=27+1=28.∴AC=72±(负值舍去).∴AC=72.连结AE ,在圆内接四边形ABCD 中,∠B+∠ADC=1800,∴∠ADC=1200.又∵DE 平分∠ADC ,∴∠EDC=600=∠EAC. 又∵∠AEC=∠B=600,∴∠AEC=∠EAC ,∴CE=AC=72.例6. 已知:如图,⊙O 的半径为r ,CE 切⊙O 于点C ,且与弦AB 的延长线交于点E ,CD ⊥AB 于D.如果CE=2BE ,且AC 、BC 的长是关于x 的方程x 2–3(r –2)x+ r 2–4=0的两个实数根.求(1)AC 、BC 的长;(2)CD 的长.分析:(1)图中显然存在切割线定理的基本图形,从而可得△ECB ∽△EAC ,AC=2BC.又∵AC 、BC 是方程的两根,由根与系数关系可列出关于AC 、BC 的方程组求解.(2)∵CD 是Rt △CDB 的一边,所以考虑构造直角三角形与之对应.若过C 作直径CF ,连结AF ,则Rt △CDB ∽Rt △CAF ,据此可列式计算.解:(1)∵CE 切⊙O 于C ,∴∠ECB=∠A.又∵∠E 是公共角,∴△ECB ∽△EAC ,21==CE BE AC BC ,∴AC=2BC.由AC 、BC 的长是关于x 的方程x 2–3(r –2)x+ r 2–4=0的两个实数根,∴AC+BC=3(r-2);AC ·BC=r 2-4,解得r=6,∴BC=4,AC=8.(2) CO 并延长交⊙O 于F ,连结AF ,则∠CAF=900,∠CFA=∠CBD. ∵∠CDB=900=∠CAF ,∴△CAF ∽△CDB ,BCCFCD AC =.∴CD=381248=⨯=⋅CF BC AC . 说明:(1)这是一道代数、几何的综合题,关键是寻找相似三角形,建立线段之间的比例关系,再根据根与系数关系列等式计算;(2)构造与相似的直角三角形的方法有许多种,同学们不妨试一试.例7.如图,△ABC 内接于⊙O ,AB 是⊙O 的直径,PA 是过A 点的直线,∠PAC=∠B.(1)求证:PA 是⊙O 的切线;(2)如果弦CD 交AB 于E ,CD 的延长线交PA 于F ,AC=CE ∶EB=6∶5,AE ∶EB=2∶3,求AB 的长和∠FCB 的正切值. 解:(1)∵AB 是⊙O 的直径,∴∠ACB=900. ∴∠CAB+∠B=900,又∠PAC=∠B ,∴∠CAB+∠PAC=900.即PA ⊥AB ,∴PA 是⊙O 的切线.(2) 设CE=6a ,AE=2x,则ED=5a ,EB=3 x.由相交弦定理,得2x ·3x=5a ·6a ∴x=5a. 连结AD.由△BCE ∽△DAE ,得553==ED EB AD BC .连结BD.由△BED ∽△CEA ,得25==AE BE AC BD . ∴BD=54.由勾股定理得BC=228-AB ,AD=2)54(-AB . ∴553)54(82222=--AB AB .两边平方,整理得1002=AB ,∴10=AB (负值舍去).∴AD=52.∵∠FCB=∠BAD ,∴tan ∠FCB= tan ∠BAD=25254==AD BD . 解几何计算题要求我们必须掌握扎实的几何基础知识,较强的逻辑推理能力,分析问题时应注意分析法与综合法的同时运用,还特别要注意图形中的隐含条件,在平时的学习中要善于总结归纳,只有这样才能掌握好几何计算题的解法.。
