2016-2017 最新 高一 衔接教材
初高中数学衔接教材

2017初高中数学衔接教材目录第一章数与式1.1 数与式的运算1.1.1 绝对值1.1.2 乘法公式1.1.3 二次根式1.1.4 分式1.2 分解因式第二章二次方程与二次不等式2.1 一元二次方程2.1.1 根的判别式2.1.2 根与系数的关系2.2 二次函数2.2.1 二次函数y=ax2+bx+c的图像和性质2.2.2 二次函数的三种表达方式2.2.3 二次函数的应用2.3 方程与不等式2.3.1 二元二次方程组的解法第三章相似形、三角形、圆3.1 相似形3.1.1 平行线分线段成比例定理3.1.2 相似三角形形的性质与判定3.2 三角形3.2.1 三角形的五心3.2.2 解三角形:钝角三角函数、正弦定理和余弦定理及其应用3.3 圆3.3.1 直线与圆、圆与圆的位置关系:圆幂定理3.3.2 点的轨迹3.3.3 四点共圆的性质与判定3.3.4 直线和圆的方程(选学)1.1 数与式的运算1.1.1.绝对值绝对值的代数意义:正数的绝对值是它的本身,负数的绝对值是它的相反数,零的绝对值仍是零.即,0,||0,0,,0.a a a a a a >⎧⎪==⎨⎪-<⎩绝对值的几何意义:一个数的绝对值,是数轴上表示它的点到原点的距离. 两个数的差的绝对值的几何意义:b a -表示在数轴上,数a 和数b 之间的距离. 例1 解不等式:13x x -+->4.解法一:由01=-x ,得1=x ;由30x -=,得3x =; ①若1<x ,不等式可变为(1)(3)4x x ---->, 即24x -+>4,解得x <0, 又x <1, ∴x <0;②若12x ≤<,不等式可变为(1)(3)4x x --->, 即1>4,∴不存在满足条件的x ;③若3x ≥,不等式可变为(1)(3)4x x -+->, 即24x ->4, 解得x >4. 又x ≥3, ∴x >4.综上所述,原不等式的解为 x <0,或x >4.解法二:如图1.1-1,1-x 表示x 轴上坐标为x 的点P 到坐标为1的点A 之间的距离|P A |,即|P A |=|x -1|;|x -3|表示x 轴上点P 到坐标为2的点B 之间的距离|PB |,即|PB |=|x -3|.所以,不等式13x x -+->4的几何意义即为 |P A |+|PB |>4. 由|AB |=2,可知点P 在点C (坐标为0)的左侧、或点P 在点D (坐标为4)的右侧.x <0,或x >4.练 习 1.填空:(1)若5=x ,则x =_________;若4-=x ,则x =_________.(2)如果5=+b a ,且1-=a ,则b =________;若21=-c ,则c =________. 2.选择题:下列叙述正确的是 ( )(A )若a b =,则a b = (B )若a b >,则a b > (C )若a b <,则a b < (D )若a b =,则a b =±A B C P |x -1||x -3|图1.1-13.化简:|x -5|-|2x -13|(x >5).1.1.2. 乘法公式我们在初中已经学习过了下列一些乘法公式:(1)平方差公式 22()()a b a b a b +-=-;(2)完全平方公式 222()2a b a a b b ±=±+. 我们还可以通过证明得到下列一些乘法公式:(1)立方和公式 2233()()a b a a b b a b+-+=+; (2)立方差公式 2233()()a b a a b b a b-++=-; (3)三数和平方公式 2222()2()a b c a b c a b b c ac ++=+++++; (4)两数和立方公式 33223()33a b a a b a b b+=+++; (5)两数差立方公式 3322()33a b a a b a b b -=-+-. 对上面列出的五个公式,有兴趣的同学可以自己去证明. 例1 计算:22(1)(1)(1)(1)x x x x x x +--+++.解法一:原式=2222(1)(1)x x x ⎡⎤-+-⎣⎦=242(1)(1)x x x -++=61x -.解法二:原式=22(1)(1)(1)(1)x x x x x x +-+-++ =33(1)(1)x x +- =61x -.例2 已知4a b c ++=,4ab bc ac ++=,求222a b c ++的值. 解: 2222()2()8a b c a b c ab bc ac ++=++-++=.练 习 1.填空:(1)221111()9423a b b a -=+( ); (2)(4m + 22)164(m m =++ );(3 ) 2222(2)4(a b c a b c +-=+++ ). 2.选择题:(1)若212x mx k ++是一个完全平方式,则k 等于 ( ) (A )2m (B )214m (C )213m (D )2116m(2)不论a ,b 为何实数,22248a b a b +--+的值 ( )(A )总是正数 (B )总是负数(C )可以是零 (D )可以是正数也可以是负数1.1.3.二次根式一般地,形如0)a ≥的代数式叫做二次根式.根号下含有字母、且不能够开得尽方的式子称为无理式. 例如 32a b ,等是无理式,而21x ++,22x y +1.分母(子)有理化把分母(子)中的根号化去,叫做分母(子)有理化.为了进行分母(子)有理化,需要引入有理化因式的概念.两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,我们就说这两个代数式互为有理化因式,例如等等. 一般地,b 与b 互为有理化因式.分母有理化的方法是分母和分子都乘以分母的有理化因式,化去分母中的根号的过程;而分子有理化则是分母和分子都乘以分母的有理化因式,化去分子中的根号的过程在二次根式的化简与运算过程中,二次根式的乘法可参照多项式乘法进行,运算中要运0,0)a b =≥≥;而对于二次根式的除法,通常先写成分式的形式,然后通过分母有理化进行运算;二次根式的加减法与多项式的加减法类似,应在化简的基础上去括号与合并同类二次根式.2.二次根式a ==,0,,0.a a a a ≥⎧⎨-<⎩例1 将下列式子化为最简二次根式:(1 (20)a ≥; (30)x <.解: (1=(20)a ==≥;(3220)x x x ==-<.例2 (3.解法一: (3)解法二: (3). 例3 试比较下列各组数的大小:(1 (2解: (1)∵1===,1110=,又>∴(2)∵1===又 4>22,∴6+4>6+22,∴例4 化简:20042005⋅.解:20042005⋅=20042004⋅⋅=2004⎡⎤⋅⋅⎣⎦=20041⋅-例 5 化简:(1; (21)x <<.解:(1)原式===2=2=.(2)原式=1x x =-,∵01x <<,∴11x x >>,所以,原式=1x x-.例 6 已知x y ==22353x xy y -+的值 .解: ∵2210x y +==+=,1xy ==, ∴22223533()1131011289x xy y x y xy -+=+-=⨯-=.练 习 1.填空:(1=__ ___;(2(x =-x 的取值范围是_ _ ___;(3)=__ ___;(4)若x ==______ __. 2.选择题:=成立的条件是 ( ) (A )2x ≠ (B )0x > (C )2x > (D )02x <<3.若b =,求a b +的值.4.比较大小:2-4(填“>”,或“<”).1.1.4.分式1.分式的意义形如A B 的式子,若B 中含有字母,且0B ≠,则称A B 为分式.当M ≠0时,分式AB具有下列性质: A A M B B M ⨯=⨯; A A M B B M÷=÷. 上述性质被称为分式的基本性质.2.繁分式 像ab c d+,2m n pm n p +++这样,分子或分母中又含有分式的分式叫做繁分式.例1 若54(2)2x A Bx x x x +=+++,求常数,A B 的值. 解: ∵(2)()2542(2)(2)(2)A B A x Bx A B x A x x x x x x x x x ++++++===++++,∴5,24,A B A +=⎧⎨=⎩ 解得 2,3A B ==.例2 (1)试证:111(1)1n n n n =-++(其中n 是正整数);(2)计算:1111223910+++⨯⨯⨯; (3)证明:对任意大于1的正整数n , 有11112334(1)2n n +++<⨯⨯+. (1)证明:∵11(1)11(1)(1)n n n n n n n n +--==+++,∴111(1)1n n n n =-++(其中n 是正整数)成立.(2)解:由(1)可知1111223910+++⨯⨯⨯ 11111(1)()()223910=-+-++-1110=- =910. (3)证明:∵1112334(1)n n +++⨯⨯+=111111()()()23341n n -+-++-+=1121n -+,又n ≥2,且n 是正整数,∴1n +1 一定为正数,∴1112334(1)n n +++⨯⨯+<12 . 例3 设ce a=,且e >1,2c 2-5ac +2a 2=0,求e 的值.解:在2c 2-5ac +2a 2=0两边同除以a 2,得 2e 2-5e +2=0, ∴(2e -1)(e -2)=0,∴e =12 <1,舍去;或e =2. ∴e =2.练 习1.填空题:对任意的正整数n ,1(2)n n =+ (112n n -+);2.选择题:若223x y x y -=+,则xy= ( ) (A )1 (B )54 (C )45(D )653.正数,x y 满足222x y xy -=,求x yx y-+的值.4.计算1111 (12233499100)++++⨯⨯⨯⨯.习题1.1A 组1.解不等式:(1) 13x ->; (2) 327x x ++-< ; (3) 116x x -++>.2.已知1x y +=,求333x y xy ++的值. 3.填空:(1)1819(2(2=________;(22=,则a 的取值范围是________;(3=________.B 组1.填空:(1)12a =,13b =,则2223352a aba ab b-=+-____ ____; (2)若2220x xy y +-=,则22223x xy y x y ++=+__ __;2.已知:11,23x y ==的值.C 组1.选择题:(1=( )(A )a b < (B )a b > (C )0a b << (D )0b a <<(2)计算 ( )(A (B (C ) (D )2.解方程22112()3()10x x x x +-+-=.3.计算:1111132435911++++⨯⨯⨯⨯. 4.试证:对任意的正整数n ,有111123234(1)(2)n n n +++⨯⨯⨯⨯++<14.1.2因式分解因式分解的主要方法有:十字相乘法、提取公因式法、公式法、分组分解法,另外还应了解求根法及待定系数法.1.十字相乘法例1 分解因式:(1)x 2-3x +2; (2)x 2+4x -12; (3)22()x a b xy aby -++; (4)1xy x y -+-. 解:(1)如图1.1-1,将二次项x 2分解成图中的两个x 的积,再将常数项2分解成-1与-2的乘积,而图中的对角线上的两个数乘积的和为-3x ,就是x 2-3x +2中的一次项,所以,有x 2-3x +2=(x -1)(x -2).说明:今后在分解与本例类似的二次三项式时,可以直接将图1.1-1中的两个x 用1来表示(如图1.1-2所示).(2)由图1.1-3,得x 2+4x -12=(x -2)(x +6). (3)由图1.1-4,得22()x a b xy aby -++=()()x ay x by -- (4)1xy x y -+-=xy +(x -y )-1=(x -1) (y+1) (如图1.1-5所示).课堂练习一、填空题:1、把下列各式分解因式:(1)=-+652x x __________________________________________________。
高数2017新高一数学衔接教材

暑期衔接班新高一数学目录第一讲:代数式及恒等变形第二讲:方程与方程组第三讲:不等式与不等式组第四讲:函数及其表示第五讲:二次函数的图像与性质第六讲:二次函数在给定区间上的最值第七讲:二次方程根的分布问题第八讲:常见函数图像与性质第九讲:函数图像变换第十讲:方法篇第十一讲:思想篇第十二讲:集合附件:两套衔接教材测试卷第一讲 代数式及恒等变形 1、乘法公式:(1)平方差公式 ;(2)完全平方公式 。
(3)立方和公式 ;(4)立方差公式 ;(5)三数和平方公式 ;(6)两数和立方公式 ;(7)两数差立方公式 。
2、二次根式:的代数式叫做二次根式,化简后被开方数相同的二次根式叫做同类二次根式。
3、指数运算法则及推广①规定:1)N *)个 2);3)) ②性质:1)、);2)、 );3) )。
4、次根式:若存在实数,使得,则称为的次方根。
在实数范围内,正数的奇次方根是一个正数,负数的奇次方根是一个负数,零的奇次方根是零,负数没有偶次方根。
5、分数指数幂:6、因式分解(1)提取公因式法; (2)运用公式法; (3)分组分解法;22()()a b a b a b +-=-222()2a b a ab b ±=±+2233()()a b a ab b a b +-+=+2233()()a b a ab b a b -++=-2222()2()a b c a b c ab bc ac ++=+++++33223()33a b a a b ab b +=+++33223()33a b a a b ab b -=-+-0)a ≥∈⋅⋅⋅=n a a a a n( n )0(10≠=a a 11(pp p ap a a -⎛⎫==∈ ⎪⎝⎭R (0,rsr sa a a a r +⋅=>∈s R r a aa sr sr ,0()(>=⋅∈s R ∈>>⋅=⋅r b a b a b a rrr ,0,0()(R n x a x n =n a x =a n nma =(4)十字相乘法; (5)求根公式法; (6)换元法、待定系数法典型例题讲解1、乘法公式的应用例1:已知,计算的值。
新高一语文衔接教材资料

7.[大扫除时],同学们干得<热火朝天>
8.他[静静地]坐<在桌子旁>
9.科学[终于以伟大的不可抑制的力量]战胜了神权
10.(桥)的设计[完全]合乎(科学)原理
四、句子成分的分析在高中语文学习中的点击。
(一)文言文中实词的意义的解释尤其是识别词类活用这一常见语法现象,依据现代汉语语法规律来分析文言句中的语法现象。
6.补语:用在动词、形容词这些作谓语词的后面,补充说明动作、行为的结果、程度、趋向、时间、处所、数量等,通常有数量短语、介宾结构,动词、形容词或其组成的短语充当。
划分举例:
1.他打了王强<三拳>
2.中国人民志气高
3.提高整个中华民族的科学文化水平是(亿万人民群众)的(切身)事业
4.什么书他都看
5.去北大荒的[就]是他
三、单句(句子)
句子是由词或短语构成的,具有一定的语调,并表达一个完整意思的语言运用单位,根据用途和语气,句子可分为陈述句、疑问句、祈使句、感叹句;根据结构可分为单句和复句;单句有主谓句和非主谓句。
(一)简单单句的类型(根据谓语的性质分)(画横线的表示谓语)
1.名词性主谓语句:今天星期六(名),四月五日清明
数词:表确数:1、2;表概数:几、一些;表序数:第一
量词:表物量:尺、寸、斤、元;表动量:次、趟
代词:人称代词:我、你、他;疑问代词:谁、什么;指示代词:这、那
虚
词
副词:表程度:很、极、大;表时间:已、刚、才;表范围:都、全、总;表情形:正好、果然;表肯定:准保、确实;表否定:不、没有;表语气:岂、难道;表重复:再、又、还
2.动词性主谓语:火车开动了,(那个)小孩哭了(动)
初高中英语衔接教材(2017)

实用文档初高中英语衔接教材目录前言第一章高中新教材简介及学习方法第二章词汇知识及实践演练第三章句子成分和基本句型第四章简单句的种类第五章动词的时态语态第六章复合句:宾语从句,状语从句,定语从句第一章初、高中英语的区别及学习方法一、认识初、高中英语的区别即将开始的高中学习生活,特别是英语的学习是与初中阶段有着很大不同的:1. 课本编排上的区别:初中的每一个单元是分为4课的,每篇中有的是对话,有的是阅读文,也配有一些练习,而高中的每个单元并不分课,而是基本上按模块(module)划分。
教材把话题、结构、功能和任务型活动有机地结合在一起,既符合中国学生英语学习的规律和特点,又体现了新的教育教学理念。
教材系统性强,各单元采用板块的设计形式,有利于教师灵活整合教材内容。
大体分为“Warming up”(热身),即是针对本单元的话题提出的一些问题,以练习口语的形式做引子,便于进入本单元的主题,下个部分就是“Reading”了,高中的阅读文分为阅读前和阅读后的讨论、思考问题并加入了有关的语言知识的学习及练习,在阅读教学的安排上。
读后活动的练习层次清楚,体现对课文理解考察的三个维度:弄清事实(Factual) —分析信息(Analytical) —判断和推理(Inferential)。
可以说是极大地丰富了教学内容。
除此之外还会有稍短的阅读与听力及写作等方面的练习,写作训练既重视结果,更重视过程,提供铺垫性活动以加强对过程性写作的监督。
通过听、读活动从语言和写作技巧方面进行相关输入,为学生的最终成长奠定基础。
2. 在词汇上的区别:我们初中的教材已是新版本了,每个单元的单词可能大家觉得已经不少了,但高中教材中的词汇更是成倍地增加了,增加了大约2000词。
这也是新编教材的一个特点,加入了许多当前常用的,新出现的流行的词汇,也是与我们学的新编初中课本相承接的,所以,为了能尽快适应高中词汇的学习,我们应该及早着手把初中阶段的词汇再熟悉一遍。
初高中英语衔接教材(2017)

初高中英语衔接教材目录前言第一章高中新教材简介及学习方法第二章词汇知识及实践演练第三章句子成分和基本句型第四章简单句的种类第五章动词的时态语态第六章复合句:宾语从句,状语从句,定语从句第一章初、高中英语的区别及学习方法一、认识初、高中英语的区别即将开始的高中学习生活,特别是英语的学习是与初中阶段有着很大不同的:1. 课本编排上的区别:初中的每一个单元是分为4课的,每篇中有的是对话,有的是阅读文,也配有一些练习,而高中的每个单元并不分课,而是基本上按模块(module)划分。
教材把话题、结构、功能和任务型活动有机地结合在一起,既符合中国学生英语学习的规律和特点,又体现了新的教育教学理念。
教材系统性强,各单元采用板块的设计形式,有利于教师灵活整合教材内容。
大体分为“Warming up”(热身),即是针对本单元的话题提出的一些问题,以练习口语的形式做引子,便于进入本单元的主题,下个部分就是“Reading”了,高中的阅读文分为阅读前和阅读后的讨论、思考问题并加入了有关的语言知识的学习及练习,在阅读教学的安排上。
读后活动的练习层次清楚,体现对课文理解考察的三个维度:弄清事实(Factual) —分析信息(Analytical) —判断和推理(Inferential)。
可以说是极大地丰富了教学内容。
除此之外还会有稍短的阅读与听力及写作等方面的练习,写作训练既重视结果,更重视过程,提供铺垫性活动以加强对过程性写作的监督。
通过听、读活动从语言和写作技巧方面进行相关输入,为学生的最终成长奠定基础。
2. 在词汇上的区别:我们初中的教材已是新版本了,每个单元的单词可能大家觉得已经不少了,但高中教材中的词汇更是成倍地增加了,增加了大约2000词。
这也是新编教材的一个特点,加入了许多当前常用的,新出现的流行的词汇,也是与我们学的新编初中课本相承接的,所以,为了能尽快适应高中词汇的学习,我们应该及早着手把初中阶段的词汇再熟悉一遍。
初高中数学衔接教材(完整版)

初高中数学衔接教材(完整版)篇一:初高中衔接教材数学《初高中数学衔接教材》序言童永奇高一新生,你们好,祝贺大家考入临潼区马额中学!进入我校,同学们必须努力学好《初高中数学衔接教材》,理由如下:一方面,由于我校是普通农村高中学校,生源质量相对较差;另一方面,由于高中数学是初中数学的延伸与拓展,初中我们学到的知识、方法在高中会经常使用。
既然学习《初高中数学衔接教材》如此重要,那么我们应该如何学习呢?提几点建议:一、“信心”是源泉。
人缺乏信心,就丧失了驱动力,终将一事无成。
二、“恒心”是保障。
人缺乏恒心,将“三天打鱼,两天晒网”。
三、“巧心”是支柱。
人无巧心,就缺乏灵气和创造力。
最后,衷心祝愿同学们在《初高中数学衔接教材》的学习中获得成功,请将那么成功的经验及时告诉我们,以便让更多的朋友分享你们成功的喜悦!临潼区马额中学高一数学校本教材童永奇结合我校学生的实际情况——基础知识较差,能力较差,没有掌握较好的学习方法,特设计适合我校高一学生使用的校本教材。
主要包括以下两个内容:一是《怎样学好数学》,二是《初高中数学衔接》。
怎样学好数学?A.要学好数学,就应该了解数学本身具有的三大特点。
(一)抽象性:数学的抽象性是无条件的,它的概念一经产生和定义之后,就稳定下来并且被看作是已知的,它们与现实的比较不是数学本身,而是它的应用问题。
(二)严谨性:由于数学的严谨性,人们往往认为数学是一种“冷而严肃的美”。
罗素说:“数学,如果正确地看它,不但拥有真理,而且也是具有至高的美,正像雕刻的美,是一种冷而严肃的美,这种美不是投合我们天性的微弱的方面,这种美没有绘画或音乐的那些华丽的装饰,它可以纯净到崇高的地步,能够达到严格的只有最伟大的艺术才能显示的那种完美的境地。
”(三)应用的广泛性:在任何一个领域,只要能从数学的角度提出问题,数学就能给出与所提问题的精确度相符合的答案,数学的这种威力恰恰是来源于它的抽象性。
b.要学好数学,就应该重视数学思想方法的学习。
初升高数学衔接教材 第01章 第03节 集合的基本运算(解析版)

第一章第三节集合的基本运算一、电子版教材二、教材解读知识点 集合的运算1.由所有属于集合A 或属于集合B 的元素组成的集合叫A 与B 的并集,记作A ∪B ;符号表示为A ∪B ={x |x ∈A 或x ∈B } 2.并集的性质A ∪B =B ∪A ,A ∪A =A ,A ∪∅=A ,A ⊆A ∪B .3.对于两个给定的集合A 、B ,由所有属于集合A 且属于集合B 的元素组成的集合叫A 与B 的交集,记作A ∩B 。
符号为A ∩B ={x |x ∈A 且x ∈B }。
4. 交集的性质A ∩B =B ∩A ,A ∩A =A ,A ∩∅=∅,A ∩B ⊆A .5、对于一个集合A ,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,记作∁U A 。
符号语言:∁U A ={x |x ∈U ,且x ∉A }。
【例题1】(2020·全国高一)已知集合{}1,2,3,4A =,{}1,4,5B =,C A B =,则C 的子集共有( )A .2个B .3个C .8个D .4个【答案】D 【解析】{1,4}C AB ==,C 的子集有{}1,{}4,{}1,4,∅,共4个.【例题2】(2020·山东省邹城市第一中学高三其他)已知集合{|2}A x x k k ==∈Z ,,{|22}B x x =-≤≤,则AB =( )A .[11]-,B .[22]-,C .{02},D .{202}-,, 【答案】D 【解析】{|2}A x x k k ==∈Z ,,{|22}B x x =-≤≤,∴{202}A B =-,,,故选:D.【例题3】(2020·安徽省舒城中学高二月考(文))已知集合{}}242{60M x x N x x x =-<<=--<,,则M N ⋂= A .}{43x x -<<B .}{42x x -<<-C .}{22x x -<<D .}{23x x <<【答案】C【解析】由题意得,{}{}42,23M x x N x x =-<<=-<<,则{}22M N x x ⋂=-<<.故选C .【例题4】(2020·肥城市教学研究中心高三其他)已知全集U =R ,集合{}1,0,1,2A =-,{}1B x x =≥,则()U A C B ⋂=( )A .{}1,0,1-B .{}1,0-C .{}1x x <D .{}11x x -≤<【答案】B 【解析】由题可知{}1U C B x x =<,则{}()1,0U C A B ⋂=-.【例题5】(2020·重庆高三月考(文))已知全集为R ,集合{}02M x x =<≤,{}1,0,1,2,3N =-,则()R C M N =( )A .{}0,1B .{}1,0,1-C .{}1,0,3-D .{}1,1,2,3-【答案】C 【解析】(](),02,R C M =-∞+∞,则(){}1,0,3R C M N =-.故选:C.【例题6】(2020·全国高一)设全集为R ,{}|37A x x =≤<,{}|210B x x =<<. (1)求A B ;(2)求()R C A B ⋃.【解析】(1)由题意{|37}A B x x =≤<;(2)由题意{|210}A B x x ⋃=<<, ∴(){|2RC A B x x ⋃=≤或10}x ≥.【例题7】(2020·全国高一)已知集合{|121}A x a x a =-<<+,{}B 03x x =<≤,U =R . (1)若12a =,求A B ⋃;()U A C B ⋂. (2)若A B φ⋂=,求实数a 的取值范围.【解析】(1)若12a =时1|22A x x ⎧⎫=-<<⎨⎬⎩⎭,{}|03B x x =<≤,∴1|32AB x x ⎧⎫=-<≤⎨⎬⎩⎭,由{|0U C B x x =≤或3}x >,所以()1|02UA CB x x ⎧⎫⋂=-<≤⎨⎬⎩⎭(2)由AB =∅知当A =∅时121a a -≥+∴2a ≤-当A ≠∅时21113a a a +>-⎧⎨-≥⎩或211210a a a +>-⎧⎨+≤⎩∴4a ≥或122a -<≤-综上:a 的取值范围是1|24a a a ⎧⎫≤-⎨⎬⎩⎭≥或. 三、素养聚焦1.已知集合{}{}2|1,|0A x x B x x ==<≤,则()R AB C =( )A .{|0}x x <B .{|01}x x ≤≤C .{|10}x x -≤<D .【答案】D【解析】{|11},{|0}A x x B x x =-≤≤=<,所以 (){|1}R AB xC x =≤-.故选:D2.已知集合{1,2,3}A =,{|(1)(2)0,}B x x x x Z =+-<∈,则A B ⋃= A .{1} B .{12}, C .{0123},,, D .{10123}-,,,, 【答案】C【解析】集合{}{|12,}0,1B x x x Z =-<<∈=,而{}1,2,3A =,所以{}0,1,2,3A B ⋃=,故选C. 3.已知集合{}0,1,2,3,4,5A =,{}1,3,5,7,9B =则A B =( )A .{}1,2,3,5B .{}0,1,3,5C .{}1,3,5D .{}0,1,2,3,4,5,7,9【答案】C【解析】因为集合{}0,1,2,3,4,5A =,{}1,3,5,7,9B =,故{}1,3,5A B =.故选:C4.若集合{}|03A x x =<<,{}|11B x x =-<<,则A B =( )A .{}13x x -<< B .{}10x x -<< C .{}01x x << D .{}13x x <<【答案】A【解析】由于集合{}|03A x x =<<,{}|11B x x =-<<,所以A B ={}13x x -<<5.已知集合A ={x |﹣1<x <5},B ={1,3,5},则A ∩B =( ) A .{1,3} B .{1,3,5}C .{1,2,3,4}D .{0,1,2,3,4,5} 【答案】A【解析】∵A ={x |﹣1<x <5},B ={1,3,5},∴A ∩B ={1,3}. 故选:A.6.若集合{|2}M x x =<,{|01}N x x =≤≤,则M N =( )A .[0,1]B .[0,2]C .[1,2)D .(,2]-∞【答案】A【解析】因为{|2}M x x =<,{|01}N x x =≤≤, 所以MN ={|01}x x ≤≤.7.已知集合{1,1,2,3,4,5}A =-,{|(1)(5)0}B x x x =∈--<N ,则AB =( ).A .{3}B .{2,3}C .{2,3,5}D .{1,1,5}-【答案】D【解析】{|(1)(5)0}{2,3,4}B x x x =∈--<=N ,所以{1,1,5}AB =-.8.满足条件{}{}1,31,3,5A ⋃=的所有集合A 的个数是 ( ) A .1 B .2C .3D .4【答案】D【解析】因为{}{}1,31,3,5A ⋃=,所以,集合A 可能为{}{}{}{}5,1,5,5,3,1,3,5, 即所有集合A 的个数是4,故选D.9.已知集合P ,S 满足P S P ⋂=,则下列关系式恒成立的是( )A .P ⫋SB .P S ⊆C .P S =D .S ⫋P【答案】B 【解析】集合P ,S 满足P S P ⋂=,∴P 中的元素都在集合S 中, ∴P S ⊆.10.已知集合I ,M ,N 的关系如图,则I ,M ,N 的关系为( ).A .I I C M C N ⊇B .I MC N ⊆C .I I C M C N ⊆D .I M C N ⊇【答案】C【解析】由韦恩图可知,N M I I I C M C N ∴⊆,11.设{}2(,)||1|(2)0A x y x y =++-=,{1,2}B =-,则必有( ). A .A B ⊇ B .A ⊆BC .A B =D .AB =∅【答案】D【解析】{}2(,)||1|(2)0{(1,2)}A x y x y =++-==-,{1,2}B =-,A B ∴⋂=∅12.设全集{,,,,}U a b c d e =,集合{,,}M a c d =,{,,}N b d e =,那么()()U U C M C N 是( ). A .∅ B .{}dC .{,}a cD .{,}b e【答案】A【解析】因为全集{,,,,}U a b c d e =,集合{,,}M a c d =,{,,}N b d e =, 所以{,}U C M b e =,{,}U C N a c =,所以()()UU C M C N ∅=,13.已知集合{}2|1,M y y x x R ==-∈,集合{|N x y ==,MN =( ).A .{}( B .[- C .D .∅【答案】B【解析】[1,)M =-+∞,[N =,故[M N ⋂=-14.已知全集{}1,0,1,2,3U =-,集合{}0,1,2A =,{}1,0,1B =-,则()UA B ⋂=( )A .{}1-B .{}0,1C .{}1,2,3-D .{}1,0,1,3-【答案】A【解析】={1,3}U C A -,则(){1}U C A B =-15.已知集合{1A x x =<-或}2x >,集合{}03B x x =≤<,则()RA B =( )A .{}02x x ≤≤ B .{}02x x <≤C .{}02x x ≤<D .{}02x x <<【答案】A【解析】依题意R C A {}12x x =-≤≤,所以()RA B ={}02x x ≤≤.16.已知函数()f x =A ,则R C A = ( )A .{|0x x ≤或}1x ≥B .{|<0x x 或}>1xC .{}|01x x ≤≤D .{}|0<<1x x【答案】D【解析】已知函数2y x x =-的定义域为A ,所以20x x -≥,得01x x ≤≥,或,即{}01A x x x ,或=≤≥,故C A =R {}1|0x x <<.17.设集合(){}(){}2,2,,A x y x y B x y y x =+===,则AB =( )A .(){}1,1 B .(){}2,4-C .()(){}1,1,2,4-D .∅【答案】C【解析】首先注意到集合A 与集合B 均为点集,联立22x y y x +=⎧⎨=⎩, 解得11x y =⎧⎨=⎩,或24x y =-⎧⎨=⎩,从而集合{(1,1),(2,4)}AB =-,18.下列表示图形中的阴影部分的是( )A .()()A CBC B .()()A B A C C .()()AB B CD .()AB C【答案】A【解析】由已知中阴影部分所表示的集合元素满足 “是A 的元素且是B 的元素,或是C 的元素”, 故阴影部分所表示的集合是()()()CA B A C B C =19.集合A ,B ,C 满足A B A C ⋃=⋃,则成立的等式是( ). A .B C =B .()()R R A BC C C A ⋂=⋂C .A B A C ⋂=⋂D .R R A C B A C C ⋂=⋂【答案】B【解析】因为A B A C ⋃=⋃,所以B A ⊆且C A ⊆,而集合,B C 不一定相等, 所以选项A,C,D 错误; 又由A B A C ⋃=⋃可知()()RR A B A C =∅=,故B 做正确.20.如图所示的韦恩图中,A 、B 是非空集合,定义*A B 表示阴影部分的集合,若x ,y ∈R ,2{|4}{|3,0}x A x y x x B y y x ==-==>,则A *B 为( )A .{|04}x x <≤B .{|01x x ≤≤或4}x >C .{|01x x ≤≤或2}x ≥D .{|01x x ≤≤或2}x >【答案】B【解析】依据定义,*A B 就是指将A B ⋃除去A B ⋂后剩余的元素所构成的集合; 对于集合A ,求的是函数24y x x =-的定义域, 解得:{|04}A x x =≤≤;对于集合B ,求的是函数3(0)xy x =>的值域,解得{}1B y y =;依据定义,借助数轴得:*{|01A B x x =≤≤或4}x >.21.设全集为U 定义集合A 与B 的运算:{*|A B x x A B =∈⋃且}x A B ∉⋂,则(*)*A B A =( ) A .A B .BC .U A C BD .U B C A【答案】B 【解析】{*|A B x x A B =∈⋃且}x A B ∉⋂ ()()U UB C A A C B =(*)*[(*)][(*)]()()U U U A B A A C A B A B C A A B B C A B ∴===22.设集合{}2A x x a=>,{}32B x x a =<-,若AB =∅,则a 的取值范围为( )A .()1,2B .()(),12,-∞⋃+∞C .[]1,2D .(][),12,-∞+∞【答案】D【解析】因为A B φ⋂=,所以232a a ≥-,解得1a ≤或2a ≥.23.设集合{}{}{|08},1,2,4,5,3,5,7U x N x S T =∈<≤==,则()U S C T ⋂=( ) A .{}1,2,4 B .{}1,2,3,4,5,7C .{}1,2D .{}1,2,4,5,6,8【答案】A【解析】∵{}1,2,3,4,5,6,7,8U =,∴{}1,2,4,6,8U C T =,∴{}()1,2,4U S C T ⋂= 24.已知集合A 4{|log (1)1}x x =+≤,{|21,}B x x k k Z ==-∈,则AB =( )A .{}113-,, B .{1,3} C .{1,3}- D .{1,1}-【答案】B【解析】由()411log x +≤可得:014x <+≤解得13x -<≤,即](13A =-, {}|21,B x x k k Z ==-∈, 则{}13A B ,⋂=25.设集合{|10}A x x =+>,{|210}B x x =+>,则()R AB C =( )A .1,2⎛⎤-∞- ⎥⎝⎦B .[)1,-+∞C .11,2⎛⎫- ⎪⎝⎭ D .11,2⎛⎤-- ⎥⎝⎦【答案】D【解析】由题意,集合(){|10}{|1}1,A x x x x =-=+>=>-+∞, 集合1{|210}{|}21(,)2B x x x x =+=->>-+=∞, 所以1,2B ∞-⎛⎤=- ⎥⎝⎦R ,所以()11,2A B ⎛⎤=--⎥⎝⎦R . 故选:D.26.已知非空集合A ,B 满足以下两个条件(){1,i A B ⋃=2,3,4,5,6},A B φ⋂=; ()ii 若x A ∈,则1x B +∈.则有序集合对(),A B 的个数为( ) A .12 B .13C .14D .15【答案】A【解析】由题意分类讨论可得: 若{}1A =,则{2,B =3,4,5,6}; 若{}2A =,则{1,B =3,4,5,6}; 若{}3A =,则{1,B =2,4,5,6}; 若{}4A =,则{1,B =2,3,5,6}; 若{}5A =,则{2,B =3,4,1,6}; 若{}1,3A =,则{2,B =4,5,6}; 若{}1,4A =,则{2,B =3,5,6}; 若{}1,5A =,则{2,B =3,4,6}; 若{}2,4A =,则{1,B =3,5,6}; 若{}2,5A =,则{1,B =3,4,6}; 若{}3,5A =,则{1,B =2,4,6}; 若{1,A =3,5},则{2,B =4,6}. 综上可得:有序集合对(),A B 的个数为12.27.已知集合21,01,2A =--{,,},{}|(1)(2)0B x x x =-+<,则AB =( )A .{}1,0-B .{}0,1C .{}1,0,1-D .{}0,1,2【答案】A【解析】由已知得{}|21B x x =-<<,因为21,01,2A =--{,,},所以{}1,0A B ⋂=-,故选A .28.某单位周一、周二、周三开车上班的职工人数分别是14,10,8.若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是( ) A .5 B .6C .7D .8【答案】B【解析】如图所示,(a +b +c +x )表示周一开车上班的人数,(b +d +e +x )表示周二开车上班人数,(c +e +f +x )表示周三开车上班人数,x 表示三天都开车上班的人数,则有:1410820a b c x b d e x c e f x a b c d e f x +++=⎧⎪+++=⎪⎨+++=⎪⎪++++++=⎩, 即22233220a b c d e f x a b c d e f x ++++++=⎧⎨++++++=⎩,即212b c e x +++=,当b =c =e =0时,x 的最大值为6, 即三天都开车上班的职工人数至多是6.29.设集合{}1,2,3,4,5,6M =,12,,,k S S S 都是M 的含两个元素的子集,且满足:对任意的{},i i i S a b =,{},j j j S a b =((),1,2,3,,i j i j k ≠∈、),都有max ,max ,j j i i i i j j a b a b b a b a ⎧⎫⎧⎫⎪⎪≠⎨⎬⎨⎬⎪⎪⎩⎭⎩⎭({}max ,x y 表示两个数x ,y 中的较大者),则k 的最大值是( )A .10B .11C .12D .13【答案】B【解析】根据题意,对于M ,含2个元素的子集有15个, 但{1,2}、{2,4}、{3,6}只能取一个; {1,3}、{2,6}只能取一个; {2,3}、{4,6}只能取一个,故满足条件的两个元素的集合有11个;30.当一个非空数集G 满足“如果,a b G ∈,则,,a b a b ab G +-∈,且0b ≠时,aG b∈”时,我们称G 就是一个数域,以下四个关于数域的命题:①0是任何数域的元素;②若数域G 有非零元素,则2017G ∈;③集合{}|2,P x x k k Z ==∈是一个数域;④有理数集是一个数域,其中真命题有() A .1个 B .2个C .3个D .4个【答案】C【解析】①:当0a =时,有0aG b=∈,所以0是任何数域的元素,正确; ②:取G 为实数域,令2016a G =∈,1b G =∈,则2017a b G +=∈,正确; ③:若{}|2,P x x k k Z ==∈为数域,取2a =,4b =,则12a Pb =∈不成立,错误; ④:取有理数1x ,2x ,令1a x =,2b x =,则()12a b x x +=+∈有理数集, ()12a b x x -=-∈有理数集,()12a b x x ⋅=⋅∈有理数集,且12x a b x =∈有理数集(20x ≠),所以有理数集是数域.正确的有:①②④.31.全集(){},Z,Z U x y x y =∈∈,非空集合S U ⊆,且S 中的点在平面直角坐标系xOy 内形成的图形关于x 轴、y 轴和直线y x =均对称.下列命题: ①若()1,3S ∈,则()1,3S --∈; ②若()0,4S ∈,则S 中至少有8个元素; ③若()0,0S ∉,则S 中元素的个数一定为偶数;④若(){},4,Z,Z x y x y x y S +=∈∈⊆,则(){},4,Z,Z x y x y x y S +=∈∈⊆.其中正确命题的个数是( ) A .1 B .2C .3D .4【答案】C 【解析】S 中的点在平面直角坐标系xOy 内形成的图形关于x 轴、y 轴和直线y x =均对称.所以当(),x y S ∈,则有(),x y S -∈,(),x y S -∈,(),y x S ∈, 进而有:(),x y S --∈,(),y x S -∈,(),y x S -∈,(),y x S --∈ ①若()1,3S ∈,则()1,3S --∈,正确;②若()0,4S ∈,则()0,4S -∈,()4,0S ∈,()4,0S -∈,能确定4个元素,不正确;③根据题意可知,(),x y S ∈,若00x y =≠,能确定4个元素,当00x y ≠=,也能确定四个,当00x y ≠≠,也能确定8个所以()0,0S ∉,则S 中元素的个数一定为偶数正确;④若(){},4,Z,Z x y x y x y S +=∈∈⊆,由S 中的点在平面直角坐标系xOy 内形成的图形关于x 轴、y 轴和直线y x =均对称可知,(){},4,Z,Z x y x y x y S -=∈∈⊆,(){},4,Z,Z x y x y x y S -+=∈∈⊆,(){},4,Z,Z x y x y x y S --=∈∈⊆,即(){},4,Z,Z x y x y x y S +=∈∈⊆,故正确,综上:①③④正确. 故选C.32.已知集合{}{}2|4,|1A x y x B x a x a ==-=≤≤+,若A B A ⋃=,则实数的取值范围为( )A .(][),32,-∞-⋃+∞ B . C .D .【答案】C 【解析】试题分析:集合{}{}2|4|22A x y x x x ==-=-≤≤,若A B A ⋃=,则B A ⊆,所以有2{12a a ≥-+≤,所以21a -≤≤,故选C.33.(多选题)给定数集M ,若对于任意a ,b M ∈,有M b a ∈+,且a b M -∈,则称集合M 为闭集合,则下列说法中不正确的是( ) A .集合{}4,2,0,2,4M =--为闭集合 B .正整数集是闭集合C .集合{}3,M n n k k Z ==∈为闭集合 D .若集合1A ,2A 为闭集合,则12A A ⋃为闭集合【答案】ABD【解析】A. 当集合{}4,2,0,2,4M =--时,2,4M ∈,而24M +∉,所以集合M 不为闭集合. B.设,a b 是任意的两个正整数,当a b <时,0a b -<不是正整数, 所以正整数集不为闭集合. C .当{}3,M n n k k Z ==∈时,设12123,3,,a k b k k k Z ==∈ 则123abk k M (?为∈),()123a b k k M -=-∈,所以集合M 是闭集合.D .设{}13,A n n k k Z ==∈,{}22,A n n k k Z ==∈由C 可知,集合1A ,2A 为闭集合,122,3A A ∈⋃,而1223A A +∉⋃,此时12A A ⋃不为闭集合. 所以说法中不正确的是ABD34.(多选题)集合A ,B 是实数集R 的子集,定义{|}A B x x A x B -=∈∉且,*()()A B A B B A =-⋃-叫做集合的对称差,若集合{}2|(1)1,03A y y x x ==-+≤≤,{}2|1,13B y y x x ==+≤≤,则以下说法正确的是( ) A .[1,5]A =-B .[2,10]B =C .[1,2)A B -=D .(5,10]B A -=E.*(1,2](5,10]A B =⋃ 【答案】BCD【解析】{}{}2|(1)1,0315A y y x x y y ==-+≤≤=≤≤,{}{}2|1,13210B y y x x y y ==+≤≤=≤≤,故{}{|}12A B x x A x B x x -=∈∉=≤<且,{}{|}510B A x x B x A x x -=∈∉=<≤且.[)*()()1,2(5,10]A B A B B A =--=.35.(多选题)已知集合{}|4A x Z x =∈<,B N ⊆,则( ) A .集合B N N ⋃= B .集合AB 可能是{}1,2,3C .集合AB 可能是{}1,1-D .0可能属于B【答案】ABD【解析】∵B N ⊆,∴B N N ⋃=,故A 正确.∵集合{}4A x Z x =∈<,∴集合A 中一定包含元素1,2,3, ∵B N ⊆,∴集合AB 可能是{}1,2,3,故B 正确;∵1-不是自然数,∴集合AB 不可能是{}1,1-,故C 错误;∵0是最小的自然数,∴0可能属于集合B ,故D 正确.。
新高一2016暑期衔接课【物理】第11讲
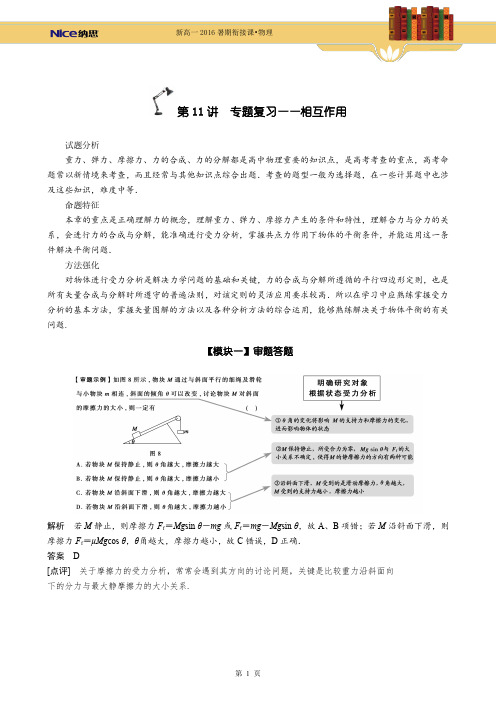
第11讲专题复习——相互作用试题分析重力、弹力、摩擦力、力的合成、力的分解都是高中物理重要的知识点,是高考考查的重点,高考命题常以新情境来考查,而且经常与其他知识点综合出题.考查的题型一般为选择题,在一些计算题中也涉及这些知识,难度中等.命题特征本章的重点是正确理解力的概念,理解重力、弹力、摩擦力产生的条件和特性,理解合力与分力的关系,会进行力的合成与分解,能准确进行受力分析,掌握共点力作用下物体的平衡条件,并能运用这一条件解决平衡问题.方法强化对物体进行受力分析是解决力学问题的基础和关键,力的合成与分解所遵循的平行四边形定则,也是所有矢量合成与分解时所遵守的普遍法则,对该定则的灵活应用要求较高.所以在学习中应熟练掌握受力分析的基本方法,掌握矢量图解的方法以及各种分析方法的综合运用,能够熟练解决关于物体平衡的有关问题.【模块一】审题答题解析若M静止,则摩擦力F f=Mg sinθ-mg或F f=mg-Mg sinθ,故A、B项错;若M沿斜面下滑,则摩擦力F f=μMg cosθ,θ角越大,摩擦力越小,故C错误,D正确.答案D[点评]关于摩擦力的受力分析,常常会遇到其方向的讨论问题,关键是比较重力沿斜面向下的分力与最大静摩擦力的大小关系.【模块二】求解平衡问题的两种特殊方法求解平衡问题的常用方法有合成分解法、正交分解法、图解法和整体与隔离法,前面对这几种方法的应用涉及较多,这里不再赘述,下面介绍四种其他方法.一、三力汇交原理物体受三个共面非平行外力作用而平衡时,这三个力必为共点力.如图所示,重为G 的均匀链条挂在等高的两钩上,链条悬挂处与水平方向成θ角,试求:(1)链条两端的张力大小;(2)链条最低处的张力大小.[解析](1)整个链条受三个力作用而处于静止,这三个力必为共点力,由对称性可知,链条两端受力必大小相等,受力分析如图甲.由平衡条件得:2F sin θ=GF =G 2sin θ.(2)在求链条最低处张力时,可将链条一分为二,取一半链条为研究对象.受力分析如图乙所示,由平衡条件得水平方向所受力为F ′=F cos θ=G 2sin θcos θ=G2cot θ.[答案](1)G 2sin θ(2)G cot θ2二、临界假设法运用假设法解题的基本步骤是:(1)明确研究对象;(2)画受力图;(3)假设可发生的临界现象;(4)列出满足所发生的临界现象的平衡方程求解.倾角为θ=37°的斜面与水平面保持静止,斜面上有一重为G 的物体A ,物体A 与斜面间的动摩擦因数μ=0.5.现给A 施以一水平力F ,如图所示.设最大静摩擦力与滑动摩擦力相等(sin 37°=0.6,cos 37°=0.8),如果物体A 能在斜面上静止,水平推力F 与G 的比值可能是()A .3B .2C .1D .0.5[解析]设物体刚好不下滑时F =F 1则F 1·cos θ+μF N =G ·sin θF N =F 1·sin θ+G ·cos θ得:F 1G =sin 37°-0.5×cos 37°cos 37°+0.5×sin 37°=0.21.1=211设物体刚好不上滑时F =F 2,则F 2·cos θ=μF N +G ·sin θF N =F 2·sin θ+G ·cos θ得:F 2G =sin 37°+0.5×cos 37°cos 37°-0.5×sin 37°=10.5=2即211≤FG≤2,故选B 、C 、D.[答案]BCD 【突破训练】1.在均匀棒的两端各系一轻绳,棒的上端的轻绳的另一端固定在天花板上,再将系下端的绳用力F 拉到水平方向,上端的绳与水平面成α角,棒与水平面成β角而静止.则下面各式正确的是()A .tan α=2tan βB .sin α=2sin βC .cos α=2cos βD .sin α=2cos β2.如图所示,物体A 的质量为2kg ,两轻绳AB 和AC (L AB =2L AC )的一端连接在竖直墙上,另一端系在物体A 上.现在物体A 上施加一个与水平方向成60°角的拉力F ,要使两绳都能伸直,试求拉力F 大小的取值范围.(g 取10m/s 2)3.为了避免某些大型机床在外力作用下发生位置移动,在机械设计中常用到“自锁”的力学原理.如图,只要使连杆AB 与滑块m 所在平面间的夹角α大于某个值,那么,无论连杆AB 对滑块施加多大的作用力,都不可能使之滑动,且连杆AB 对滑块施加的作用力越大,滑块就越稳定,工程力学上称之为“自锁”现象.为使滑块能“自锁”,α应满足的条件?设滑块与所在平面间的动摩擦因数为μ.【模块三】热点强化突破热点1物体的受力分析受力分析是解决静力学问题、动力学问题、力电综合等问题的基础和关键,对其单独考查的试题在近几年高考中也时有出现,主要涉及弹力、摩擦力的有无和方向的判断.1.如图所示,位于倾角为θ的斜面上的物块B由跨过定滑轮的轻绳与物块A相连.从滑轮到A与B的两段绳都与斜面平行.已知A与B之间及B与斜面之间均不光滑,若用一沿斜面向下的力F拉B并使它做匀速直线运动,则B受力的个数为()A.4个B.5个C.6个D.7个2.如图所示,倾斜天花板平面与竖直方向夹角为θ,推力垂直天花板平面作用在木块上,使其处于静止状态,则()A.木块一定受到三个力的作用B.天花板对木块的弹力F N>FC.木块受到的静摩擦力等于mg cosθD.木块受到的静摩擦力等于mg/cosθ3.如图所示,一物体在粗糙水平地面上受斜向上的恒定拉力F作用而运动,则下列说法正确的是()A.物体可能只受两个力作用B.物体可能受三个力的作用C.物体可能受四个力作用D.物体一定受四个力作用4.如图所示,A、B两个物体叠放在一起,放于斜面C上,物体B的上表面水平,现三者在水平外力F的作用下一起向左做匀速直线运动,下列说法正确的是()A.物体A可能受到3个力的作用B.物体B可能受到3个力的作用C.物体C对物体B的作用力竖直向上D.物体C和物体B之间可能没有摩擦力热点2物体的平衡物体的平衡条件是本章的重点内容,广泛应用于力、热、电等各部分内容的试题之中,更应特别关注以生产、生活中的实际问题为背景考查平衡条件的灵活应用.5.如图所示,铁板AB 与水平地面之间的夹角为θ,一块磁铁吸附在铁板下方.在缓慢抬起铁板的B 端使θ角增大(始终小于90°)的过程中,磁铁始终相对于铁板静止.下列说法正确的是()A .磁铁所受合外力逐渐减小B .磁铁始终受到三个力的作用C .磁铁受到的摩擦力逐渐减小D .铁板对磁铁的弹力逐渐增大6.如图所示,水平固定且倾角为30°的光滑斜面上有两个质量均为m 的小球A 、B ,它们用劲度系数为k 的轻质弹簧连接,现对B 施加一水平向左的推力F 使A 、B 均静止在斜面上,此时弹簧的长度为l ,则弹簧原长和推力F 的大小分别为()A .l +mg 2k ,233mg B .l -mg 2k ,233mgC .l +mg2k ,23mgD .l -mg2k ,23mg7.如图,墙上有两个钉子a 和b ,它们的连线与水平方向的夹角为45°,两者的高度差为l .一条不可伸长的轻质细绳一端固定于a 点,另一端跨过光滑钉子b 悬挂一质量为m 1的重物.在绳子距a 端l /2得c 点有一固定绳圈.若绳圈上悬挂质量为m 2的钩码,平衡后绳的ac 段正好水平,则重物和钩码的质量比m 1/m 2为()A.5B .2C.52D.2图2图38.如图所示,A 、B 两物体叠放在水平地面上,已知A 、B 的质量分别为m A =10kg ,m B =20kg ,A 、B 之间,B 与地面之间的动摩擦因数均为μ=0.5.一轻绳一端系住物体A ,另一端系于墙上,绳与竖直方向的夹角为37°,今欲用外力将物体B 匀速向右拉出,求所加水平力F 的大小.(取g =10m/s 2,sin 37°=0.6,cos 37°=0.8)【模块四】分组训练一、作用力与反作用力、弹力、摩擦力1.如图1所示,甲、乙两人在冰面上“拔河”.两人中间位置处有一分界线,约定先使对方过分界线者为赢.若绳子质量不计,冰面可看成光滑,则下列说法正确的是()A .甲对绳的拉力与绳对甲的拉力是一对平衡力B .甲对绳的拉力与乙对绳子的拉力是作用力与反作用力C .若甲的质量比乙大,则甲能赢得“拔河”比赛的胜利D .若乙收绳的速度比甲快,则乙能赢得“拔河”比赛的胜利2.如图2所示,将两相同的木块a 、b 置于粗糙的水平地面上,中间用一轻弹簧连接,两侧用细绳固定于墙壁.开始时a 、b 均静止.弹簧处于伸长状态,两细绳均有拉力,a 所受摩擦力F f a ≠0,b 所受摩擦力F f b =0,现将右侧细绳剪断,则剪断瞬间()A .F f a 大小不变B .F f a 方向改变C .F f b 仍然为零D .F f b 方向向右3.一根轻质弹簧一端固定,用大小为F 1的力压弹簧的另一端,平衡时长度为l 1;改用大小为F 2的力拉弹簧,平衡时长度为l 2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为()A.F 2-F 1l 2-l 1 B.F 2+F 1l 2+l 1C.F 2+F 1l 2-l 1D.F 2-F 1l 2+l 14.如图3,粗糙的水平地面上有一斜劈,斜劈上一物块正在沿斜面以速度v 0匀速下滑,斜劈保持静止,则地面对斜劈的摩擦力()A .等于零B .不为零,方向向右C .不为零,方向向左D .不为零,v 0较大时方向向左,v 0较小时方向向右图1图4图5图6图7二、力的合成与分解5.墙上有两个钉子a 和b ,它们的连线与水平方向的夹角为45°,两者的高度差为l .一条不可伸长的轻质细绳一端固定于a 点,另一端跨过光滑钉子b 悬挂一质量为m 1的重物.在绳上距a 端l /2的c 点有一固定绳圈.若绳圈上悬挂质量为m 2的钩码,平衡后绳的ac 段正好水平,则重物和钩码的质量比m 1m 2为()A.5B .2 C.52 D.26.如图5所示,一物块置于水平地面上,当用与水平方向成60°角的力F 1拉物块时,物块做匀速直线运动;当改用与水平方向成30°角的力F 2推物块时,物块仍做匀速直线运动.若F 1和F 2的大小相等,则物块与地面之间的动摩擦因数为()A.3-1B .2-3 C.32-12D .1-32三、受力分析共点力平衡7.一质量为m 的物体恰好静止在倾角为θ的斜面上.现对物块施加一个竖直向下的恒力F ,如图6所示.则物块()A .仍处于静止状态B .沿斜面加速下滑C .受到的摩擦力不变D .受到的合外力增大8.如图7所示,质量分别为m 1、m 2的两个物体通过轻弹簧连接,在力F 的作用下一起沿水平方向做匀速直线运动(m 1在地面上,m 2在空中),力F 与水平方向成θ角.则m 1所受支持力F N 和摩擦力F f 正确的是()A .F N =m 1g +m 2g -F sin θB .F N =m 1g +m 2g -F cos θC .F f =F cos θD .F f =F sin θ图9图10图11图12【模块五】课后限时规范训练(限时:45分钟)1.如图9所示,一木板B 放在水平地面上,木块A 放在木板B 的上面,木块A 的右端通过轻质弹簧固定在竖直墙壁上.用力F 向左拉木板B ,使它们以速度v 运动,这时弹簧的拉力为F .下列说法中正确的是()A .木板B 受到的滑动摩擦力的大小等于F B .地面受到的滑动摩擦力的大小等于FC .若木板以2v 的速度运动,木块A 受到的滑动摩擦力的大小等于2FD .若用力2F 拉木板B ,木块A 受到的滑动摩擦力的大小等于F2.木块A 、B 分别重50N 和60N ,它们与水平地面之间的动摩擦因数均为0.25,夹在A 、B 之间的轻弹簧被压缩了2cm ,弹簧的劲度系数为400N/m ,系统置于水平地面上静止不动.如图10所示,现用F =1N的水平拉力作用在木块B 上,则下列说法正确的是()A .木块A 所受摩擦力大小是12.5NB .木块A 所受摩擦力大小是11.5NC .木块B 所受摩擦力大小是9ND .木块B 所受摩擦力大小是7N3.如图11所示,一辆运送沙子的自卸卡车装满沙子,沙粒之间的动摩擦因数为μ1,沙子与车厢底部材料的动摩擦因数为μ2,车厢的倾角用θ表示(已知μ2>μ1),下列说法正确的是()A .要顺利地卸干净全部沙子,应满足tan θ>μ2B .要顺利地卸干净全部沙子,应满足sin θ>μ2C .只卸去部分沙子,车上还留有一部分沙子,应满足μ2>tan θ>μ1D .只卸去部分沙子,车上还留有一部分沙子,应满足μ2>μ1>tan θ4.如图12所示,物体B 与竖直墙面接触,在竖直向上的力F 的作用下A 、B 均保持静止,则物体B 的受力个数为()A .2个B .3个C .4个D .5个5.L 形木板P (上表面光滑)放在固定斜面上,轻质弹簧一端固定在木板上,另一端与置于木板上表面的滑块Q 相连,如图13所示.若P 、Q 一起沿斜面匀速下滑,不计空气阻力.则木板P 的受力个数为()图13A .3B .4C .5D .6图14图156.如图14所示物体A 、B 、C 在外力F 的作用下在水平面上向右做匀加速直线运动,则有关A 、B 、C 三个物体的受力情况,下列说法中正确的是()A .物体A 一定受5个力作用B .物体B 可能受4个力作用,也可能受5个力作用C .物体C 一定受3个力作用D .物体A 可能受4个力作用,也可能受5个力作用7.在建筑装修中,工人用质量为5.0kg 的磨石A 对地面和斜壁进行打磨,已知A 与地面、A 与斜壁之间的动摩擦因数μ均相同.(g 取10m/s 2)(1)当A 受到水平方向的推力F 1=25N 打磨地面时,A 恰好在水平地面上做匀速直线运动,求A 与地面间的动摩擦因数μ.(2)若用A 对倾角θ=37°的斜壁进行打磨(如图15所示),当对A 施加竖直向上的推力F 2=60N 时,则磨石A 从静止开始沿斜壁向上运动2m(斜壁长>2m)所需时间为多少?(sin 37°=0.6,cos 37°=0.8)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)连词→连接词、短语、句子或段落,表示它们之间的各种关系的词。只起连接作用,不能起修饰和 补充作用。表示联合关系的连词:和、跟、与、同、及、而、或、或者。表示偏正关系的连词:如果、只要、 因为、虽然、即使、不但。
(3)介词→起介引作用的词,一般用在名词、代词或名词性词组的前边,合起来组成介词结构,以表示 处所、时间、状态、方式、原因、目的、比较对象等。
说扩大想打发行驶能够进来
形容词 数词 量词
表示性质或状态 表示数目 表示计算单位
高愉快可敬 十九一半0.5 个尺年杯回
代词
代替别的词语以表示人、事物或数量、性质、状态、程度 等
我你们他人谁这那某
2.虚词:意义较虚,包括副词、连词、介词、助词、叹词和拟声词。 (1)副词→用来修饰或限制动词、形容词的词。 判断标志→①一般只能用在动词、形容词前作状语。②一般不能修饰和限制名词。
1.搭配不当。 (1)主谓搭配不当。 如:江西贵溪市一头原本默默耕田的母牛,最近因勇斗野猪救主人而被广为流传。(母牛被流传。这明 显不对,被广为流传的应是母牛的故事)
(2)动宾搭配不当。 如:广东湛江市进行首届教育艺术节。(把“进行”改为“举办”) (3)定语与中心语搭配不当。 如:这里大有藏龙卧虎的人才啊!(定语“藏龙卧虎”与中心语“人才”搭配不当)
一、语言文字运用 初中阶段的考查定位为“语言积累与运用”。“语言积累”板块中包括汉字、词语、诗文三部分;“语 言运用”板块中包括规范性运用语言(准确、简明、连贯、得体)、形象性运用语言(拟广告语等)、创造 性运用语言(句式仿写等)三部分。
高中阶段的考查定位为“语言文字运用”。包括字音,字形,标点符号,词语(包括熟语),病句,扩 展语句、压缩语段,选用、仿用、变换句式,正确运用常见的修辞手法,语言表达简明、连贯、得体、准确、 鲜明、生动,图文转换等十个方面的内容。
初升高衔接,你准备好了吗? 初中是高中学习的基础,高中是初中所学的延伸,把初中与高中衔接起来,助你领先新起点,赢在高中
起跑线上!
揭开高中语文学习神秘的面纱 初中语文课程标准从“识字与写字”“阅读” “写作”“口语交际”“综合性学习”五个方面提 出要求;高中语文课程标准则从“积累·整合” “感受·鉴赏”“思考·领悟”“应用·拓展” “发现·创新”五个方面提出发展要求。 可见,初中阶段偏重积累,高中阶段偏重运用。
启示: 高中阶段看似要求的内容没有变化,但是能力层级不同
五、写作
对比项
初中阶段
高中阶段
考试难度
45分钟能完成不少于600字的习作 45分钟能完成不少于800字的习作
命题形式
命题作文
新材料作文
文体要求
多要求写记叙文
以议论文为主,兼顾其他文体
对比项 习作内容
初中阶段 多为再现生活
高中阶段 多为评价社会现象,需要有一定的思辨能力
2.偏正短语:由名词中心语或定语或由动词、形容词中心语和状语组成。如“我的老师”“一个同 学”“一孔之见”“特别快”等。
3.主谓短语:由主语和谓语组成。如“阳光灿烂”“心情舒畅”等。 4.动宾短语:由动词和宾语组成。如“歌唱祖国”“顾全大局”“做作业”等。
5.动补短语:由动词(形容词)和补语组成。如“看清楚”“做得完”“住一宿”等。 此外,还有复指短语(如:首都北京)、连动短语(如:画蛇添足)、兼语短语(如:引狼入室)等。
启示: 高中阶段需要我们关注人生、社会和生活,并学会积极思考
掌握高中必用的语法知识 一、现代汉语语法知识 (一)词语
现代汉语的词可以分为两类: 1.实词:意义较实在,包括名词、动词、形容词、数词、量词和代词。
分类 名词
表示人或事物名称
阐释
举例 李白秋季上左
动词
表示动作、行为,或存在、变化,或心理活动,或使令, 或可能、意愿,或判断
(4)状语与中心语搭配不当。 如:人们众口一词地认为……(状语“众口一词”与中心语“认为”搭配不当)
(三)句子成分 句子的主干成分及代表符号:主语、谓语、 宾语。 枝叶成分及代表符号:(定语)、[状语]、<补 语>。 1.主语:是谓语陈述的对象,指明说的是“什 么人”或“什么事物”。
2.谓语:是陈述主语、说明主语的,说明主语“是什么”或“怎么样”。 3.宾语:在动词后面,表示动作、行为所涉及的人或事物,回、短语、句子后,起辅助作用的词,不能单用。
(5)叹词→表示感叹、应答的词。如哈哈、哎哟、哼。 (6)拟声词→模拟事物的声音的词。
(二)短语 短语又叫词组,是由词和词组合而成的语言单位。这种组合关系是给词组分类的依据。短语的类型主要 有以下几种: 1.并列短语:有两个或两个以上的名词、动词、形容词组成。如“调查研究”“你们和他们”等。
高中阶段的考查点比初中多,且考查难度明显加大。
二、文言文阅读 初中阶段学习的文言文篇幅短、词汇少、难度小;高中阶段学习的文言文篇幅长、词汇多、难度大。
高中阶段考查文言文,由初中的小故事类渐变成正史的人物传记,由偏重故事偏向说理抒情,且由课内 文言文变成课外文言文。并进一步强调重点掌握120个常用文言实词,18个文言虚词,判断句、被动句、宾语 前置、成分省略和词类活用等句式用法,理解并翻译文中的句子,会分析综合文章内容,具备一定的鉴赏评 价能力。
4.定语:在句子中起着修饰、限制主语或宾语中心语的作用。 5.状语:修饰、限制谓语中心语,一般在谓语中心语前面,有的在句子最前面,交代时间、地点、范围、 情况等。
6.补语:对谓语中心语起补充说明作用,一般放在谓语中心语之后。
No Image
(四)病句类型。 病句主要有以下六种类型:搭配不当、成分残缺或赘余、语序不当、结构混乱、表意不明、不合逻 辑。
三、古代诗歌阅读
初中阶段
诵读了解内容,积累运用,提高欣赏品味
高中阶段
分析鉴赏,分析形象,鉴赏语言、表达技巧,评价古代诗歌的内容情感
四、现代文阅读 初中阶段要求
高中阶段要求
1.理解:理解主要内容 2.鉴赏评价:对课文的内容有自己的心得, 能提出自己的看法和疑问
1.理解:理解文章表达的情感、思想和观点 2.鉴赏评价:善于发现问题,提出问题。能从不同的角度 阐发、评价和质疑
