Ch2-抽样分布的应用介绍
Ch2-抽样分布的应用介绍
样本均值分布
_
P(X) .3
.2 .1 0
8
18 18 19 20 21 20 19 20 21 22 22 20 21 22 23 24 21 22 23 24
18 19 20 21 22 23
24
_
X
(不再是均匀的)
抽样分布举例(续)
抽样分布的概括指标：
μX
X N
i
18 19 21 24 21 16
μX 21
_
P(X) .3 .2 .1 X
10
σ X 1.58
0
18 19 20 21 22 23
24
_
X
A
B
C
D
抽样分布的均值
抽样分布
均值的抽样 分布
总体比例的 抽样分布
11
均值的标准差
来自同一总体容量相同的不同样本将会有不同的样本均 值 均值的标准差是衡量不同样本间均值差异的指标：
更小的样本容量
μ
16
x
若总体不是正态的
我们可以应用中心极限定理：
即使总体不是正态的，
…只要样本容量足够大，来自总体的样本均值就会近 似于正态。 抽样分布的性质：
μx μ
和
σ σx n
17
中心极限定理
当样本容 量足够大 时…
n↑
无论总体形状 如何，抽样分 布都服从正态 分布
x
18
40
调查误差的种类
范围误差或抽样偏差
如果某些组不包含在总体中，且没有被选择的机会，那么 就存在这种误差
非回应误差或偏差
没有回应的人可能与回应的人不同
抽样误差
几个抽样分布的性质及其应用
几个抽样分布的性质及其应用重庆师范大学涉外商贸学院数学与应用数学（师范）2008级阮国勇指导老师陈勇摘要在概率论中，我们是在随机变量的分布是假设已知的前提下去研究的；而数理统计中，随机变量的分布是未知或不完全知道。
我们通过对随机变量进行重复独立观察得到许多观察值，并对观察值的数据进行分析，从而对所研究的随机变量的分布做出推断。
本文介绍三种重要的抽样分布及其性质，并给出了抽样分布在参数估计、假设检验、分布拟合检验的简单应用。
χ分布；t分布；F分布关键词抽样分布；2Abstract In the theory of probability, we are in the distribution of random variable is assumed known base on the research, however，in the mathematical statistics, random variable distribution is unknown or incompletely known. we base on the random variables are independent observations are repeated many observed value, and the observation data analysis, to study the distribution of random variable to make inference. This paper introduces three kinds of important sampling distribution and its properties, and gives the sampling distribution in parameter estimation, hypothesis testing, fitting of distribution of the simple application.Key words sampling distribution, 2χdistribution, t distribution, F distribution第 1 页共 13 页目录1 引言 (4)2 几个有关概念2.1 总体、个体 (4)2.2 简单随机抽样 (4)2.3 统计量 (5)2.3.1 统计量的定义 (5)2.3.2 常用统计量 (5)2.4 自由度 (5)2.5 抽样分布 (6)3 常用抽样分布及其性质χ分布 (6)3.1 2χ分布的定义 (6)3.1.1 2χ分布的性质 (6)3.1.2 23.2 t分布 (7)3.2.1 t分布的定义 (7)3.2.2 t分布的性质 (7)3.3 F分布 (7)3.3.1 F分布的定义 (7)3.3.2 F分布的性质 (7)4 几个常用抽样分布的应用χ分布的应用 (8)4.1 2χ分布在参数估计中的应用 (8)4.1.1 2χ分布在假设检验中的应用 (8)4.1.2 2χ分布在分布拟合检验中的应用 (8)4.1.3 24.2 t分布的应用 (9)4.2.1 t分布在参数估计中的应用 (9)4.2.2 t分布在假设检验中的应用 (9)4.3 F分布的应用 (10)4.3.1 F分布在参数估计中的应用 (10)4.3.2 F分布在假设检验中的应用 (11)5 总结 (11)6 致谢 (12)7 参考文献 (13)1 引言数理统计中的统计估计与推断需要我们进行抽样估计，样本是统计估计和推断的依据，然而，在处理具体的理论与应用问题时，却很少直接利用样本，而利用他们经过适当处理导出来的量，这个量即统计量，统计量的分布称为抽样分布，三大分布都是在正态分布产生的，他们是正态总体统计估计和校验的基础。
抽样分布的概念及重要性
抽样分布的概念及重要性抽样分布是统计学中一个重要的概念，它描述了从总体中抽取样本的过程中，统计量的分布情况。
在统计学中，我们通常无法对整个总体进行研究，而是通过抽取样本来推断总体的特征。
抽样分布的概念帮助我们理解样本统计量的变异性，并为统计推断提供了理论基础。
本文将介绍抽样分布的概念及其重要性。
一、抽样分布的概念抽样分布是指在相同条件下，重复从总体中抽取样本，并计算样本统计量的分布情况。
在抽样过程中，每次抽取的样本可能不同，因此样本统计量也会有所不同。
抽样分布描述了这些样本统计量的分布情况。
常见的抽样分布包括正态分布、t分布和F分布。
其中，正态分布是最常见的抽样分布，它在大样本情况下逼近于正态分布。
t分布适用于小样本情况，它相对于正态分布具有更宽的尾部。
F分布用于比较两个样本方差是否相等。
二、抽样分布的重要性1. 参数估计抽样分布为参数估计提供了理论基础。
在统计学中，我们通常通过样本统计量来估计总体参数。
抽样分布告诉我们，样本统计量的分布情况，从而帮助我们确定参数估计的可靠性和精确度。
例如，通过样本均值来估计总体均值，我们可以利用抽样分布计算置信区间，从而确定估计值的范围。
2. 假设检验抽样分布在假设检验中起着重要的作用。
假设检验是统计学中常用的推断方法，用于判断总体参数是否满足某种假设。
抽样分布提供了计算检验统计量的分布情况，从而帮助我们确定拒绝域和计算p值。
通过与抽样分布进行比较，我们可以判断样本统计量是否显著，从而对总体参数进行推断。
3. 抽样方法选择抽样分布对于选择合适的抽样方法具有指导意义。
不同的抽样方法会对样本统计量的分布产生影响。
通过了解抽样分布的特点，我们可以选择合适的抽样方法，从而提高样本的代表性和可靠性。
例如，在总体分布未知的情况下，我们可以选择使用无偏估计的抽样方法，以减小抽样误差。
4. 统计模型建立抽样分布为统计模型的建立提供了基础。
在建立统计模型时，我们通常需要假设样本统计量服从某种分布。
抽样分布知识点总结
抽样分布知识点总结抽样分布是统计学中一个重要的概念，它描述了在进行抽样时得到的样本统计量的分布情况。
抽样分布是统计推断的基础，它可以帮助我们理解抽样误差以及估计参数的可信度。
在本文中，我们将对抽样分布的基本概念、性质和相关理论进行总结和讨论。
一、基本概念1.1 抽样与总体在统计学中，总体是指我们想要研究的所有个体的集合，而抽样则是从总体中选取一部分个体作为样本，以获得对总体特征的估计。
抽样可以是随机抽样、分层抽样、系统抽样等方法，目的是代表性地反映总体的特征。
1.2 样本统计量在抽样中，对样本数据进行统计分析得到的统计量称为样本统计量，常见的样本统计量有均值、方差、标准差、比例等。
样本统计量能够提供有关总体参数的估计和推断。
1.3 抽样分布抽样分布是描述样本统计量的分布情况的统计学概念。
当我们从总体中抽取多个样本，并计算每个样本的统计量时，得到的这些统计量的分布就是抽样分布。
抽样分布可以反映出样本统计量的可变性、偏移和分布形态等特征。
二、性质2.1 中心极限定理中心极限定理是抽样分布理论中的重要定理，它描述了在一定条件下，样本均值的抽样分布近似服从正态分布。
中心极限定理对于理解抽样分布的性质和应用具有重要意义，也为许多统计推断方法提供了理论基础。
2.2 大数定律大数定律是另一个重要的抽样分布性质，它描述了当样本容量足够大时，样本均值会收敛于总体均值，即样本均值的抽样分布会集中在总体均值附近。
大数定律为我们理解样本统计量的稳定性和准确性提供了重要参考。
2.3 置信区间置信区间是根据抽样分布推断总体参数的一种方法，通过对抽样分布的分布情况进行分析，我们可以建立对总体参数的置信区间，从而对总体特征进行推断。
置信区间对于统计推断的可信度和精度有着重要的作用。
三、理论基础3.1 样本容量样本容量是影响抽样分布的一个重要因素，在实际抽样中，样本容量的大小对于样本统计量的分布情况有着重要的影响。
通常情况下，样本容量越大，抽样分布的稳定性和准确性越高。
数理统计CH2抽样分布22ppt课件
2020/12/21
王玉顺：数理统计02_抽样分布
5
2.3 统计量分位数
(3)统计量观察值表为xα便于应用
➢解决两类问题：
✓已知x求事件X>x的概率 ✓已知概率反求观察值x
➢xα蕴含统计量 观察值xα、随机 事件X>xα、事件 概率α三方面的信 息
2020/12/21
王玉顺：数理统计02_抽样分布
2
~
2 n 1
X
n
X T ~ t n 1
n 1 S2
Sn
2
n 1
2020/12/21
王玉顺：数理统计02_抽样分布
37
2.4 抽样分布定理
(4)正态总体近似标准化样本均值及分布
示例
X N 1 0,1 6 , n 9
X N 1 0,1 6 9
n 1S 2
2
2 8
X t8
Sn
2020/12/21
(1)F统计量分位数Fα(n1,n2)
➢设F~F(n1,n2)，F统计量分位数记作Fα(n1,n2) ➢则分位数Fα(n1,n2)、事件F>Fα(n1,n2)、尾概 率α、事件F≤Fα(n1,n2) 、分布函数F{Fα(n1,n2)} 等五者之间满足下面的关系：
PFF n1,n2 1FF n1,n2
数理统计CH2抽样分布22ppt课件
2 抽样分布
本章内容
2.1 总体与样本 2.2 抽样分布 2.3 统计量分位数 2.4 抽样分布定理 2.5 中心极限定理
2020/12/21
王玉顺：数理统计02_抽样分布
2
2.3 统计量分位数
(2)统计量观察值是事件概率的函数
➢统计量观察值x表为xα，意 义之一是建立了xα与α的一一 对应函数关系，实现了统计 量观察值x按概率α的分割。
抽样分布
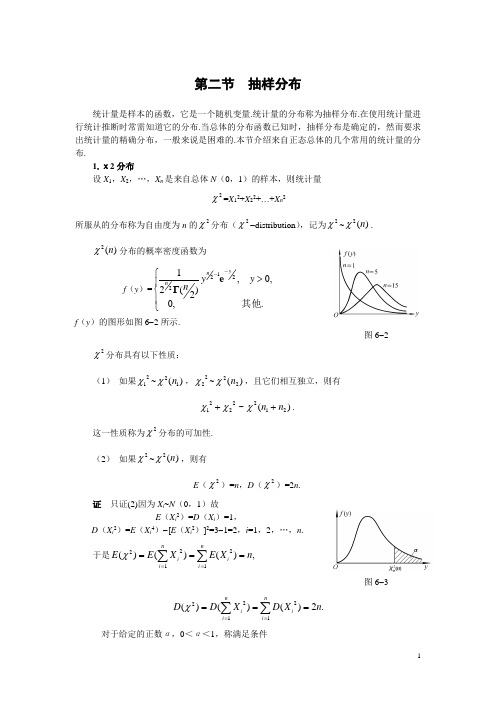
第二节 抽样分布统计量是样本的函数，它是一个随机变量.统计量的分布称为抽样分布.在使用统计量进行统计推断时常需知道它的分布.当总体的分布函数已知时，抽样分布是确定的，然而要求出统计量的精确分布，一般来说是困难的.本节介绍来自正态总体的几个常用的统计量的分布.1.χ2分布设X 1，X 2，…，X n 是来自总体N （0，1）的样本，则统计量2χ=X 12+X 22+…+X n 2所服从的分布称为自由度为n 的2χ分布（2χ-distribution ），记为2χ~)(2n χ.)(2n χ分布的概率密度函数为f （y ）=⎪⎩⎪⎨⎧>--.,0,0,)2(212122其他y y n y n n e Γf （y ）的图形如图6-2所示.图6-22χ分布具有以下性质：（1） 如果21χ~)(12n χ，22χ~)(22n χ，且它们相互独立，则有)(~2122221n n ++χχχ.这一性质称为2χ分布的可加性. （2） 如果2χ~)(2n χ，则有E （2χ）=n ，D （2χ）=2n .证 只证(2)因为X i ~N （0，1）故E （X i 2）=D （X i ）=1，D （X i 2）=E （X i 4）-[E （X i 2）]2=3-1=2，i =1，2，…，n . 于是,)()()(12122n X E XE E ni i ni i===∑∑==χ图6-3.2)()()(12122n X D X D D ni i n i i ===∑∑==χ对于给定的正数α，0＜α＜1，称满足条件{}⎰∞==>)(222)()(n y y f n P αχααχχd的点)(2n αχ为)(2n χ分布的上α分位点（Percentile of α），如图6-3所示，对于不同的α，n ，上α分位点的值已制成表格，可以查用（见附表），例如对于α=0.05,n =16,查附表得)16(205.0χ=26.296.但该表只详列到n =45为止.当n >45时,近似地有)(2n αχ≈2)12(21-+n z α，其中z α是标准正态分布的上α分位点.例如)50(205.0χ≈122=67.221.2.t 分布设X ~N （0，1），Y ~2()n χ，并且X ，Y 独立，则称随机变量t =nYX服从自由度为n 的t 分布（t -distribution ），记为t ~t （n ）.t （n ）分布的概率密度函数为h （t ）=[]2/)1(21)2/(2/)1(+-⎪⎪⎭⎫⎝⎛++n n t n n n ΓΓπ， -∞＜t ＜∞.（证略）.图6-4中画出了当n =1，10时h （t ）的图形.h （t ）的图形关于t =0对称，当n 充分大时其图形类似于标准正态变量概率密度的图形.但对于较小的n ，t 分布与N（0，1）分布相差很大（见附表）.图6-4 图6-5对于给定的α，0＜α＜1，称满足条件P （t ＞t α（n ））=⎰∞)()(n t t t h αd =α的点t α（n ）为t （n ）分布的上α分位点（见图6-5）.由t 分布的上α分位点的定义及h （t ）图形的对称性知t 1-α（n ）=-t α（n ）.t 分布的上α分位点可从附表查得.在n ＞45时，就用正态分布近似：t α（n ）≈z α.3.F 分布设U ~)(12n χ，V ~)(22n χ，且U ，V 独立，则称随机变量F =21//n V n U 服从自由度为（n 1，n 2）的F 分布（F -distribution ），记F ~F （n 1，n 2）. F （n 1，n 2）分布的概率密度为[][]⎪⎩⎪⎨⎧>++=-.,0,0,)/(1)2/()2/()/(2/)()(21211)2/(2/21212111其他y n y n n n y n n n n y n n ΓΓΓψ (证略).)(y ψ的图形如图6-6所示.图6-6 图6-7F 分布经常被用来对两个样本方差进行比较.它是方差分析的一个基本分布，也被用于回归分析中的显著性检验.对于给定的α，0＜α＜1，称满足条件P {F ＞F α（n 1，n 2）}=⎰∞),(21)(n n F y y αψd =α的点F α（n 1，n 2）为F （n 1，n 2）分布的上α分位点（图6-7）.F 分布的上α分位点有表格可查（见附表）.F 分布的上α分位点有如下的性质：F 1-α（n 1，n 2）=),(112n n F α.这个性质常用来求F 分布表中没有包括的数值.例如由附表查得F 0.05(9,12)=2.80，则可利用上述性质求得F 0.95(12,9)=1/F 0.05(9,12)=12.80=0.357. 4.正态总体的样本均值与样本方差的分布设正态总体的均值为μ，方差为σ2，X 1，X 2，…，X n 是来自正态总体X 的一个简单样本，则总有E （X ）=μ，D （X ）=σ2/n ，X ~N （μ，σ2/n ）.对于正态总体N (μ,σ2）的样本方差S 2， 我们有以下的性质.定理6.1 设X 1，X 2，…，X n 是总体N （μ，σ2）的样本，X ，S 2分别是样本均值和样本方差，则有（1）)1(~)1(222--n S n χσ；（2）与S 2独立.（证略）.定理6.2 设X 1，X 2，…，X n 是总体N （μ，σ2）的样本，X ，S 2分别是样本均值和样本方差，则有)1(~/--n t nS X μ.证 因为)1,0(~/N nX σμ-，)1(~)1(222--n S n χσ且两者独立，由t 分布的定义知)1(~)1()1(//22----n t n S n nX σσμ. 化简上式左边，即得)1(~/--n t nS X μ.定理6.3 设X 1，X 2，…，1n X 与Y 1，Y 2，…，2n X 分别是来自具有相同方差的两正态总体N （μ1，σ2），N （μ2，σ2）的样本，且这两个样本相互独立.设∑==1111n i i X n X ，∑==2121n i i Y n Y 分别是这两个样本的均值.S 12=∑=--1121)(11n i i X X n ，S 22=∑=--2122)(11n i i Y Y n 分别是这两个样本的样本方差，则有：)2(~/1/1)()(212121-++---n n t n n S Y X W μμ，其中 S W 2=)2()1()1(21222211-+-+-n n S n S n . （证略）.本节所介绍的三个分布以及三个定理,在下面各章中都起着重要的作用.应注意，它们都是在总体为正态总体这一基本假定下得到的.例6.2 设总体X 服从正态分布N （62，100），为使样本均值大于60的概率不小于0.95，问样本容量n 至少应取多大？解 设需要样本容量为n ，则)1,0(~/N n X nX ⋅-=-σμσμ，P （X ＞60）=⎭⎬⎫⎩⎨⎧⋅->⋅-n n X P 1062601062.查标准正态分布表，得Φ（1.64）≈0.95.所以0.2n ≥1.64,n ≥67.24.故样本容量至少应取68.。
最新第四节--抽样分布(1)教学讲义PPT课件
一、正态分布与渐进正态分布
▪ （一）如果总体呈正态分布，且总体方差已知，
那么，样本平均数的抽样分布为正态分布。
▪ 此时，样本平均数的平均数等于总体平均数，样
本平均数在抽样分布上的标准差，等于总体标准
差除以N的平方根。
EX
X
n
志存高远，பைடு நூலகம்强拼搏
（二） t分布的特征
▪ 1. t分布的平均值为0。 ▪ 2. t分布是以过平均值0的垂线为轴的对称分布,分布左侧t
志存高远，顽强拼搏
三、χ2 （卡方）分布
▪ （一） χ2 （卡方）分布的含义
▪ 从一个服从正态分布的总体中,每次随机抽取随机变量 X1,X2,X3…XN，并分别将其平方,即可得到X12,X22，X32…, XN2，这样可抽取无限多个数量为n的随机变量X,并可求得 无限多个n个随机变量X的平方的和,也可计算其标准分数Z =X-μ/δ,及其平方Z2=(X-μ/δ)2。这无限多个n个随机变量平 方和或标准分数的平方和的分布,即为χ2分布。
志存高远，顽强拼搏
▪ 统计学上的自由度是指当以样本的统计量来估计总体的参数 时， 样本中独立或能自由变化的自变量的个数，称为该统 计量的自由度。 统计学上的自由度包括两方面的内容：
▪ 首先，在估计总体的平均数时，由于样本中的 n 个数都是相 互独立的，从其中抽出任何一个数都不影响其他数据，所以 其自由度为n。
统计学_抽样分布
统计学_抽样分布统计学——抽样分布在统计学的广袤领域中，抽样分布无疑是一个至关重要的概念。
它就像是一把神奇的钥匙，能够帮助我们从局部的样本数据中窥探到总体的特征和规律。
那么，究竟什么是抽样分布呢？想象一下，我们面前有一个巨大的“总体”，这个总体可以是某个城市所有居民的收入情况，也可以是某批产品的质量数据等等。
但由于总体太过庞大，我们无法对其进行全面的测量和分析。
这时候，抽样就派上用场了。
我们从这个总体中抽取一部分个体，这部分个体就构成了一个样本。
而抽样分布，简单来说，就是指从同一个总体中抽取相同大小的多个样本，这些样本统计量（比如均值、方差等）所形成的概率分布。
为了更直观地理解抽样分布，我们以一个简单的例子来说明。
假设我们要研究某个班级学生的考试成绩。
这个班级学生的成绩总体就是我们要研究的对象。
我们先随机抽取 10 名学生的成绩作为一个样本，计算这 10 名学生成绩的平均值。
然后，我们重复这个抽样过程，多次抽取 10 名学生的成绩，每次都计算平均值。
这些平均值就会形成一个分布，这就是抽样分布。
抽样分布有着不同的类型，其中最常见的就是样本均值的抽样分布和样本方差的抽样分布。
先来说说样本均值的抽样分布。
根据中心极限定理，如果总体的分布不论是什么形状，只要样本容量足够大（通常认为大于 30），那么样本均值的抽样分布就近似服从正态分布。
这意味着，我们可以利用正态分布的性质来进行很多统计推断。
比如说，我们可以计算出样本均值落在某个区间内的概率，从而对总体均值进行估计和推断。
再谈谈样本方差的抽样分布。
样本方差的抽样分布与自由度有关。
自由度这个概念可能有些抽象，但可以简单理解为在计算样本方差时能够自由取值的变量个数。
对于样本容量为 n 的样本，其自由度为 n 1。
了解抽样分布对我们有什么实际用处呢？它的作用可大了！首先，抽样分布能够帮助我们进行参数估计。
比如说，我们想要知道总体均值是多少，但又无法直接测量总体中的每一个个体。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
22
举例(续)
解(续)：
7.8 - 8 X -μ 8.2 - 8 P(7.8 X 8.2) P 3 σ 3 36 n 36 P(-0.4 Z 0.4) 0.3108
总体分布 ? ??? ?? 抽样分布 标准正态分布 .1554 +.1554
不包含的总体里
非回应误差
抽样误差 测量误差
42
随访非回应者
样本间的随机差异
坏的或主要问题
本章总结
介绍了抽样分布 描述了均值的抽样分布 正态总体 应用中心极限定理 描绘了总体比例的抽样分布 应用抽样分布计算了概率 描述了不同的样本类型和抽样技术 检验了调查价值和调查误差的类型
4
抽样分布举例
假设一个总体…
总体大小 N=4 随机变量 X 表示
A B C D
每个人的年龄
X 取值：18, 20, 22, 24 (岁)
5
抽样分布举例(续)
总体分布的概括指标：
X μ N
i
P(x)
.3 .2 .1 0
18 19 20 21 22 23 24
18 20 22 24 21 4
40
调查误差的种类
范围误差或抽样偏差
如果某些组不包含在总体中，且没有被选择的机会，那么 就存在这种误差
非回应误差或偏差
没有回应的人可能与回应的人不同
抽样误差
样本间的差异总会存在
测量误差
问题设计的弱点，回应者误差以及采访者对回应者的影响
41
调查误差(续)
范围误差
43
置信区间估计
44
学习目标
本章中，你将学到：
建立并描述均值和比例的置信区间估计 如何决定样本容量大小，且样本容量对于构建 均值和比例的置信区间是必要的
45
置信区间
本章内容 总体均值 μ 的置信区间
当已知总体标准差 σ 时 当不知道总体标准差 σ 时
总体比例 π 的置信区间 确定所需样本容量
46
点估计和区间估计
一个点估计是一个数字， 一个置信区间给出了可变性的额外信息
置信下限
置信上限
点估计 置信区间的宽度
47
点估计
我们可以对一个总体参数进行 估计…
样本统计量(一个点估 计)
均值
总体比例
μ
π
X
p
48
置信区间
总体参数的点估计带有多少不确定性呢？ 区间估计比点估计提供了更多关于总体特征的 信息
16个样本 均值
1st 2nd Observation Obs 18 20 22 24
18 18 19 20 21 20 19 20 21 22 22 20 21 22 23 24 21 22 23 24
16种可能的样本 (放回抽样)
7
抽样分布举例(续)
所有样本均值的抽样分布
16个样本均值
1st 2nd Observation Obs 18 20 22 24
更小的样本容量
μ
16
x
若总体不是正态的
我们可以应用中心极限定理：
即使总体不是正态的，
…只要样本容量足够大，来自总体的样本均值就会近 似于正态。 抽样分布的性质：
ቤተ መጻሕፍቲ ባይዱ
μx μ
和
σ σx n
17
中心极限定理
当样本容 量足够大 时…
n↑
无论总体形状 如何，抽样分 布都服从正态 分布
x
18
28
举例(续)
如果 π = 0.4，n = 200，那么 P(0.40 ≤ p ≤ 0.45)为多少?
σp
求 σp ：
(1 )
n
0.4(1 0.4) 0.03464 200
转化为标准 P(0.40 p 0.45) P 0.40 0.40 Z 0.45 0.40 正态： 0.03464 0.03464
P(0 Z 1.44)
29
举例(续)
如果 π = 0.4，n = 200，那么 P(0.40 ≤ p ≤ 0.45)为多少?
应用累积标准正态分布表： P(0 ≤ Z ≤ 1.44) = P(Z ≤1.44) – P(Z < 0)
= 0.9251-0.5000 = 0.4251
抽样分布 标准正态分布
将总体分为4层
样本
37
整群样本
总体被分为一些“群”，每一个都代表总体
从群中选择一个简单随机样本
可以选取所选群中所有的元素，或通过另一种概率抽样技术选择 出一个群并从中抽取元素
将总体分为 16个群。
为样本随机选取出群
38
优劣对比
简单随机样本和系统样本
易于应用 可能不能很好地表示出总体的基本特征
未知)
样本
51
通用公式
求置信区间的通用公式为：
点估计 ± (临界值)(标准差)
52
置信水平
置信水平
区间中包含未知总体参数的可信度
百分比(小于100%)
53
置信水平(1-) (续)
假设，置信水平 = 95% 也可写为(1 - ) = 0.95 相对频率的解释：
最终，所建立置信区间将有95%的可能包含未知 的真实参数
(其中，π = 总体比例)
26
总体比例的Z分位数
用如下公式将p标准化为Z分位数：
p Z σp
p (1 ) n
27
举例
如果支持A提议的投票人的真实比例为 π = 0.4， 容量为200的样本，其比例在0.40和0.45之间的 概率为多大？
也就是： 如果 π = 0.4，n = 200, 那么 P(0.40 ≤ p ≤ 0.45)为多少?
0.4251
标准化
0.40
0.45
p
30
0
1.44
Z
抽样的原因
比普查花的时间更少
比管理普查的代价更小 比管理目标总体的普查更容易，更现实
31
所选样本的类型
非概率样本
其中所含元素与其出现的概率无关
概率样本
样本所选各元素以已知概率为基础
32
所选样本的类型(续)
样本
非概率样本
σ
(X μ)
i
2
N
2.236
A
B
C
D
x
均匀分布
6
抽样分布举例(续)
现在，考虑所有可能的大小n=2的样本
第1 个 观测值 18 20 22 24 第2个观测值 18 18,18 20,18 22,18 24,18 20 18,20 20,20 22,20 24,20 22 18,22 20,22 22,22 24,22 24 18,24 20,24 22,24 24,24
特定的区间会或不会包含真实参数
一个特定的区间与概率无关
54
置信区间
置信 区间
总体均值
总体比例
σ已知
σ未知
55
μ的置信区间(σ已知)
假设 已知总体标准差 σ 总体服从正态分布 如果总体不是正态的，那么要使用大样本 置信区间估计：
σ XZ n
其中， X 为点估计 Z 为正态分布的临界值，在每个尾部 /2 处的概率 σ/ n 为标准差
这样的区间估计被称为置信区间
49
置信区间估计
区间给出了数值间的距离：
考虑不同样本间样本统计量的差异
以1个样本的观测值为基础 给出了对未知总体参数接近程度的信息
用置信水平来表示
不可能达到100%可信
50
估计步骤
随机样本
总体
(均值μ 均值 X = 50
μ在40到60之 间的置信水平 为95%
56
求临界值Z
考虑置信度为95%的置信区间： 1 0.95
Z 1.96
σX
2 ( X μ ) i X
N (18 - 21)2 (19 - 21)2 (24 - 21)2 1.58 16
9
总体及抽样分布的对比
μ 21
P(X) .3 .2 .1 0
18 19 20 21 22 23 24
总体 N=4
样本均值分布 n=2
σ 2.236
μX 21
_
P(X) .3 .2 .1 X
10
σ X 1.58
0
18 19 20 21 22 23
24
_
X
A
B
C
D
抽样分布的均值
抽样分布
均值的抽样 分布
总体比例的 抽样分布
11
均值的标准差
来自同一总体容量相同的不同样本将会有不同的样本均 值 均值的标准差是衡量不同样本间均值差异的指标：
Z
( X μX ) σX
( X μ) σ n
其中：
μ = 总体均值
X = 样本均值
σ = 总体标准差
n = 样本容量
14
抽样分布的性质
μx μ
(也就是，
正态总体分布
μ
x
无偏倚 )
x
抽样分布也是正态的 (且均值相同)
μx
15
x
抽样分布的性质(续)
随n的增加，
更大的样本容量
σ x 递减
样本均值分布
_
P(X) .3
.2 .1 0
8
18 18 19 20 21 20 19 20 21 22 22 20 21 22 23 24 21 22 23 24