从吃药中想到的数学问题
一次函数应用——分段问题
某医药研究所开发了一种新药，在试验药效时发现，如果成人按规定剂量服用，那么服药2后血液中的含药量最高，达每升6，接着逐步衰减，10后血液中的含药量为每升3，每升血液中的含药量随时间的变化情况如图所示．当成人按规定剂量服药后：(1)分别求出≤2和≥2时，与之间的函数关系式；(2)如果每升血液中的含药量为4或4以上时，治疗疾病是有效的，那么这个有效时间是多长?【思路点拨】（1）根据题意由待定系数法求函数的解析式.（2）令≥4，分别求出的取值范围，便可得出这个药的有效时间． 【答案与解析】解：(1)由图知，≤2时是正比例函数，≥2时是一次函数．设≤2时，，把(2，6)代入，解得＝3， ∴ 当0≤≤2时，．设≥2时，，把(2，6)，(10，3)代入中，得，解得，即．当＝0时，有，． ∴ 当2≤≤18时，．(2)由于≥4时在治疗疾病是有效的，∴ ，解得． 即服药后得到为治病的有效时间， 这段时间为．【总结升华】分段函数中，自变量在不同的取值范围内函数的解析式也不相同，因此注意根据自变量或函数的取值确定某段函数来解决问题．h mg h mg y mg x h x x y x mg mg y x x x x y kx =y kx =k x 3y x =x y k x b '=+y k x b '=+26103k b k b '+=⎧⎨'+=⎩38274k b ⎧'=-⎪⎪⎨⎪=⎪⎩32784y x =-+y 327084x =-+18x =x 32784y x =-+y 34327484x x ≥⎧⎪⎨-+≥⎪⎩42233x ≤≤43h 223h 224186()333h -==24．（2013•荆州）如图，某个体户购进一批时令水果，20天销售完毕．他将本次销售情况进行了跟踪记录，根据所记录的数据可绘制的函数图象，其中日销售量y（千克）与销售时间x（天）之间的函数关系如图甲所示，销售单价p（元/千克）与销售时间x（天）之间的函数关系如图乙所示．（1）直接写出y与x之间的函数关系式；（2）分别求出第10天和第15天的销售金额；（3）若日销售量不低于24千克的时间段为“最佳销售期”，则此次销售过程中“最佳销售期”共有多少天？在此期间销售单价最高为多少元？考点：一次函数的应用分析：（1）分两种情况进行讨论：①0≤x≤15；②15＜x≤20，针对每一种情况，都可以先设出函数的解析式，再将已知点的坐标代入，利用待定系数法求解；（2）日销售金额=日销售单价×日销售量．由于第10天和第15天在第10天和第20天之间，当10≤x≤20时，设销售单价p（元/千克）与销售时间x（天）之间的函数关系式为p=mx+n，由点（10，10），（20，8）在p=mx+n的图象上，利用待定系数法求得p与x的函数解析式，继而求得10天与第15天的销售金额；（3）日销售量不低于24千克，即y≥24．先解不等式2x≥24，得x≥12，再解不等式﹣6x+120≥24，得x≤16，则求出“最佳销售期”共有5天；然后根据p=﹣x+12（10≤x≤20），利用一次函数的性质，即可求出在此期间销售时单价的最高值．解答：解：（1）分两种情况：①当0≤x≤15时，设日销售量y与销售时间x的函数解析式为y=k1x，∵直线y=k1x过点（15，30），∴15k1=30，解得k1=2，∴y=2x（0≤x≤15）；②当15＜x≤20时，设日销售量y与销售时间x的函数解析式为y=k2x+b，∵点（15，30），（20，0）在y=k2x+b的图象上，∴，解得：，∴y=﹣6x+120（15＜x≤20）；综上，可知y与x之间的函数关系式为：y=；（2）∵第10天和第15天在第10天和第20天之间，∴当10≤x≤20时，设销售单价p（元/千克）与销售时间x（天）之间的函数解析式为p=mx+n，∵点（10，10），（20，8）在z=mx+n的图象上，∴，解得：，∴p=﹣x+12（10≤x≤20），当x=10时，p=10，y=2×10=20，销售金额为：10×20=200（元），当x=15时，p=﹣×15+12=9，y=30，销售金额为：9×30=270（元）．故第10天和第15天的销售金额分别为200元，270元；（3）若日销售量不低于24千克，则y≥24．当0≤x≤15时，y=2x，解不等式2x≥24，得x≥12；当15＜x≤20时，y=﹣6x+120，解不等式﹣6x+120≥24，得x≤16，∴12≤x≤16，∴“最佳销售期”共有：16﹣12+1=5（天）；∵p=﹣x+12（10≤x≤20），﹣＜0，∴p随x的增大而减小，∴当12≤x≤16时，x取12时，p有最大值，此时p=﹣×12+12=9.6（元/千克）．故此次销售过程中“最佳销售期”共有5天，在此期间销售单价最高为9.6元．点评：此题考查了一次函数的应用，有一定难度．解题的关键是理解题意，利用待定系数法求得函数解析式，注意数形结合思想与函数思想的应用．23.（本小题满分8分）某楼盘一楼是车库（暂不出售），二楼至二十三楼均为商品房（对外销售）.商品房售价方案如下：第八层售价为3000元/米2，从第八层起每上升一层，每平方米的售价增加40元；反之，楼层每下降一层，每平方米的售价减少20元.已知商品房每套面积均为120平方米.开发商为购买者制定了两种购房方案：方案一：购买者先交纳首付金额（商品房总价的30%），再办理分期付款（即贷款）.方案二：购买者若一次付清所有房款，则享受8%的优惠，并免收五年物业管理费（已知每月物业管理费为a元）⑴请写出每平方米售价y（元/米2）与楼层x（2≤x≤23，x是正整数）之间的函数解析式.⑵小张已筹到120000元，若用方案一购房，他可以购买哪些楼层的商品房呢？⑶有人建议老王使用方案二购买第十六层，但他认为此方案还不如不免收物业管理费而直接享受9%的优惠划算.你认为老王的说法一定正确吗？请用具体数据阐明你的看法.23.（8分）解：（1）1o当2≤x≤8时，每平方米的售价应为：3000－（8－x）×20=20x＋2840 (元／平方米)2O当9≤x≤23时，每平方米的售价应为：3000+（x－8）·40=40x＋2680(元／平方米) ∴{8)x (22840,20x 23)x (92680,40x ≤≤+≤≤+=y , x 为正整数 ………………………２分（2）由（1）知：1o 当2≤x ≤8时，小张首付款为 （20x ＋2840）·120·30%=36（20x ＋2840）≤36（20·8＋2840）=108000元＜120000元∴2～8层可任选 …………………………１分 2o当9≤x ≤23时，小张首付款为（40x ＋2680）·120·30%=36（40x ＋2680）元36（40x ＋2680）≤120000，解得：x ≤3116349= ∵x 为正整数，∴9≤x ≤16 …………………………１分综上得：小张用方案一可以购买二至十六层的任何一层。
数学建模药物疗效问题
药物疗效问题摘要随着临床给药方案的日益多样化，等剂量、等间隔的给药方案已远远不能满足临床需要，因此寻找出合理的剂量及时间间隔的给药方案具有重要的意义。
因此在我们充分理解题意的基础上，提出了合理的假设。
并通过对问题的深入分析与把捏，我们将本题最终归结为非血管给药问题，并建立了单房室模型。
在处理问题（一）时，本文首先将人体服药后的血药浓度和时间的关系利用最小二乘法拟合得到二次多项式，建立了模型一；接着利用药动学中房室模型中的血管外给药单室模型，利用残数法通过matlab 建立了模型二。
对两个模型分别进行相关系数检验，得出其相关系数矩阵，从而比较出模型二较模型一能更好地描述人体服药后的血药浓度与时间的关系。
得到的药理方程为：)(0011.586785.03056.0t t e e y ---=在处理问题（二）时，本文以易懂的静脉注射给药模型为基础再导向复杂的多剂量血管外给药模型，并提出了“稳定血药浓度”这一概念。
利用matlab 软件得出当病人服用剂量为200mg 的药物时，服药时间间隔为4个或5个小时，可使其体内的血药浓度维持在4-8之间；当服药剂量为300mg 时，服药时间间隔为7个小时，可使病人体内的血药浓度维持在4-8之间。
在处理问题（三）时，本文根据问题（二）中提出的多剂量血管外给药模型，考虑到若病人两次服同类药物，第二次服药的浓度只有80%的效应，对多剂量血管外给药模型进行修正，从而得到考虑二次服药药效的多剂量血管外给药模型。
利用matlab 软件得出当病人服用剂量为200mg 的药物时，服药时间间隔为3个或4个小时，可使其体内的血药浓度在一天内维持在4-8之间；当服药剂量为300mg 时，服药时间间隔为5个小时，可使病人体内的血药浓度在一天内维持在4-8之间。
然后，我们通过分析，考虑若服用200mg 剂量的药，服药时间间隔过短，对于病人来说是一种精神负担，经济负担略重，再加上日常生活中往往要缩短病愈的时间，最终我们提出服用间隔为5个小时的300mg 的大剂量药物的结论。
数学建模
医生给病人开处方的时候必须注明两点：服药的剂量和服药的时间间隔，超剂量的药品会对身体产生不良后果，甚至死亡，而剂量不足，则不能达到治病的目的。
已知患者服药后，随时间推移，药品在体内逐渐被吸收，发生生化反应，也就是体内药品的浓度逐渐降低，药品浓度降低的速度与体内当时药品的浓度成正比。
当服药量为a，服药间隔为T时，试分析体内药品浓度随时间的变化规律。
本题研究服药时间间隔对药物疗效的影响。
一、问题摘要我们知道，患者服药后，随时间推移，药品在体内逐渐被吸收，发生化学反应，也就是体内药品的浓度逐渐降低，药品浓度的变化量与服药量成正比。
医生给病人开处方时，必须注明两点：服药的剂量和服药的时间间隔。
超剂量的药品回对身体产生严重不良后果，甚至死亡，而剂量不足，则达不到治病的目的。
试研究药品在体内浓度的变化规律。
二、问题分析及补充2.1药物浓度变化指数模型患者服药后,随时间推移,药品在体内逐渐被吸收,体内药品浓度降低的速率与体内当时药品的浓度成正比.当服药量为A，初始药物浓度为a，服药间隔为T,体内药的浓度随时间的变化规律分析：浓度方程：dx=−kx,t≠nTdt满足条件：x(0)=a,x(nT)=a+x(nT)解得：x(t)=x(nT)e−k(t−nT),t∈[nT,(n+1)T]在0≤t≤T内，方程的解为x(t)=ae−kx，0≤t<T在T≤t<2T内，方程的解为x(t)=(a+ae−kT)e−k(t−T),T≤t<2T⋯⋯在T≤t<(n+1)T内,方程的解为x(t)=(a+ae−kT+ae−2kT+⋯+ae−nkT)e−k(t−nT),nT≤t<(n+1)T 由于a+ae−kT+ae−2kT+⋯+ae−nkT=a 1−e−(n+1)T1−e−kT→a1−e−kT由此看出，在等间隔服药的情况下，药物的浓度在人体中呈上升趋势，且最后会稳定在一定的水平。
浓度变化曲线如图示：（其中原方程解中：K=0.1，A=0.1;T=8）注：解题及编程参考自《数学建模》，高等教育出版社。
中药与数学
中药与数学
中药与数学之间看似毫无关系，但实际上，它们之间存在一些联系和应用。
首先，中药中的许多草药的配方和使用方法涉及到一些计量和计算的工作。
中药师需要根据病情、体质等因素准确计算出草药的使用量和剂量，以确保草药的疗效和安全性。
这涉及到一些基本的数学运算，如加减乘除。
例如，根据病人的体重和病情，中药师需要计算出每次使用的草药的克数或毫升数。
此外，中药的研究也需要一定的数学知识和技能。
通过不同草药的化学成分分析、药效的测定和药物相互作用的研究，可以得出一些定量的数据。
数学在这些数据的处理和分析中起到了重要的作用，如统计学的应用、数据拟合和回归分析等。
数学还应用于中药的质量控制和生产过程中。
在中药的提取、制剂和储存过程中，需要严格控制草药的含量和药效，保证其质量和稳定性。
数学方法可以帮助制定合理的质量控制标准和生产工艺，并进行质量评价和监控。
此外，近年来，数学模型和计算机模拟在中药的药效评价、药物相互作用研究和草药配方设计等方面得到了广泛应用。
通过建立数学模型和模拟实验，可以更好地理解中药的作用机制、预测草药的药效和药物相互作用，从而指导中药的研发和临床应用。
总之，中药与数学之间虽然看似没有直接联系，但实际上数学
在中药的配方计算、质量控制、研究分析和模拟模型等方面都发挥着重要作用。
这也说明了数学的广泛应用和重要性。
程序员思维题
NO.1有20瓶药丸，其中19瓶装有1克/粒的药丸，余下一瓶装有1.1克/粒的药丸。
给你一台称重精准的天平，怎么找出比较重的那瓶药丸？天平只能用一次。
NO.2有个8×8棋盘，其中对角的角落上，两个方格被切掉了。
给定31块多米诺骨牌，一块骨牌恰好可以覆盖两个方格。
用这31块骨牌能否盖住整个棋盘？请证明你的答案（提供范例，或证明为什么不可能）。
NO.3有两个水壶，容量分别为5夸脱（美制：1夸脱=0.946升，英制：1夸脱=1.136升）和3夸脱，若水的供应不限量（但没有量杯），怎么用这两个水壶得到刚好4夸脱的水？注意，这两个水壶呈不规则形状，无法精准地装满“半壶”水。
NO.4有个岛上住着一群人，有一天来了个游客，定了一条奇怪的规矩：所有蓝眼睛的人都必须尽快离开这个岛。
每晚8点会有一个航班离岛。
每个人都看得见别人眼睛的颜色，但不知道自己的（别人也不可以告知）。
此外，他们不知道岛上到底有多少人是蓝眼睛的，只知道至少有一个人的眼睛是蓝色的。
所有蓝眼睛的人要花几天才能离开这个岛？NO.5有栋建筑物高100层。
若从第N层或更高的楼层扔下来，鸡蛋就会破掉。
若从第N层以下的楼层扔下来则不会破掉。
给你2个鸡蛋，请找出N，并要求最差情况下扔鸡蛋的次数为最少。
NO.6走廊上有100个关上的储物柜。
有个人先是将100个柜子全都打开。
接着，每数两个柜子关上一个。
然后，在第三轮时，再每隔两个就切换第三个柜子的开关状态（也就是将关上的柜子打开，将打开的关上）。
照此规律反复操作100次，在第i轮，这个人会每数i个就切换第i个柜子的状态。
当第100轮经过走廊时，只切换第100个柜子的开关状态，此时有几个柜子是开着的？本帖隐藏的内容NO.1有20瓶药丸，其中19瓶装有1克/粒的药丸，余下一瓶装有1.1克/粒的药丸。
给你一台称重精准的天平，怎么找出比较重的那瓶药丸？天平只能用一次。
解法有时候，严格的限制条件有可能反倒是解题的线索。
日常生活中一次函数的应用
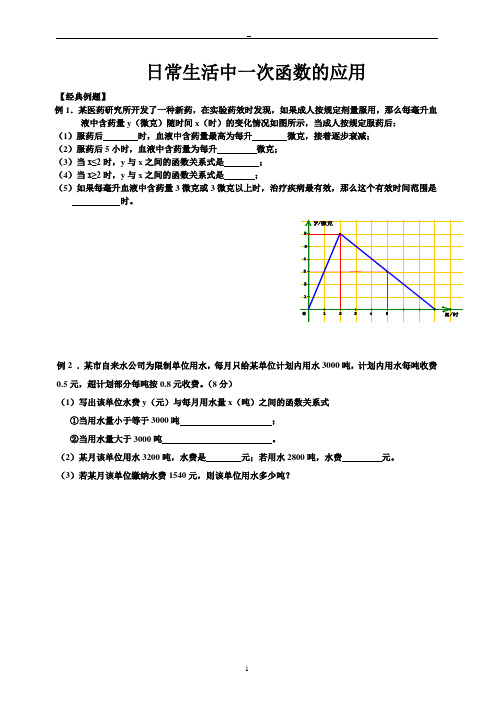
日常生活中一次函数的应用【经典例题】例1．某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，当成人按规定服药后：（1）服药后时，血液中含药量最高为每升微克，接着逐步衰减；（2）服药后5小时，血液中含药量为每升微克；（3）当x≤2时，y与x之间的函数关系式是；（4）当x≥2时，y与x之间的函数关系式是；（5）如果每毫升血液中含药量3微克或3微克以上时，治疗疾病最有效，那么这个有效时间范围是时。
例2 ．某市自来水公司为限制单位用水，每月只给某单位计划内用水3000吨，计划内用水每吨收费0.5元，超计划部分每吨按0.8元收费。
（8分）（1）写出该单位水费y（元）与每月用水量x（吨）之间的函数关系式①当用水量小于等于3000吨；②当用水量大于3000吨。
（2）某月该单位用水3200吨，水费是元；若用水2800吨，水费元。
（3）若某月该单位缴纳水费1540元，则该单位用水多少吨？例3 甲、乙两家体育用品商店出售同样的乒乓球拍和乒乓球，乒乓球拍每付定价20元，乒乓球每盒定价5元，现两家商店搞促销活动，甲店：每买一付球拍赠一盒乒乓球；乙店：按定价的9折优惠，某班级需购球拍4付，乒乓球若干盒（不少于4盒）（1）设购买乒乓球盒数为ｘ（盒），在甲店购买的付款数为ｙ甲（元）；在乙店购买的付款数为ｙ乙（元），分别写出ｙ甲、ｙ乙与ｘ的函数关系式。
（2）就乒乓球的盒数讨论去哪家商店购买合算。
例4．为了保护学生的视力，课桌椅的高度是按一定的关系配套设计的。
研究表明：假设课桌的高度为ｙcm，椅子的高度（不含靠背）为ｘcm，则ｙ应是ｘ的一次函数，右边的表中给出两套符合条件的桌椅的高度：（1）请确定ｙ与ｘ的函数关系式；（2）现有一把高42.0cm的椅子和一张高78.2cm的课桌，它们是否配套？请通过计算说明理由。
例5 ．全国每年都有大量土地被沙漠吞没，改造沙漠、保护土地资源已经成为一项十分紧迫的任务。
药物代谢问题 数学模型作业
药物代谢问题一 摘要药物经口服而进入体内，因代谢而逐步消除药物。
此建模根据t=0时含有X 剂量的药物后血内药物量y （纳克）与时间t 的关系d exp( ) d a a y K F X K t K y t =--，以及问题中的数据可推算出口服一定药物后的最高血药浓度Cmax 。
随代谢的进行，体内的血药浓度会逐渐降低，当血药浓度降低到一定值时，为保证药效需要再次服药，模型中给出第二次服药与第一次服药的时间间隔以及第二次服药的药剂量，为病人的再次服药提供了好的参考。
模型中还给出了24小时之内的血药浓度曲线，可以直观地看出血药浓度的变化情况。
二问题重述设()y t 表示t 时刻体内药量，药物经口服吸收而进入血内，因代谢而逐步消除药物(排泄). 已知在t = 0时口服含X(克)剂量的药物后血内药物剂量 y (纳克) (1纳克=910-克)与时间t (小时)的关系为d exp( ) d a a y K F X K t K y t =--，其中a K 为未知的吸收速度常数，F 为未知的吸收比例常数，K 为未知的消除速度常数. 问题：1. 问一体重60千克的人第一次服药X=X 1=0.1克剂量后的最高血药浓度Cmax(纳克/毫升);2. 为保证药效, 在血药浓度降低到437.15纳克/毫升时应再次口服药物, 其剂量应使最高浓度等于Cmax(纳克/毫升). 求第二次口服的时间与第一次口服的时间的间隔T 2(小时)和剂量X 2(克).3. 画出符合2的二次服药情况下在24小时之内的血药浓度曲线(将所要求的三个量Cmax, T 2，X 2的数值的最后结果皆舍入到4位数字, 且要保证4位数字都是有效数字). 三参考数据与参数说明现有一体重60千克的人在t =T 1= 0时, 第一次口服某药(含剂量X=0.1(克))，经3次检测得到数据如下: t =3(小时)时血药浓度为763.9(纳克/毫升)(血药浓度()()y t C t V = (纳克/毫升), V表示未知血液容积(毫升). t = 18(小时)时血药浓度为76.39纳克/毫升，t = 20(小时)时血药浓度为53.4(纳克/毫升).()y t ：表示t 时刻体内药量a K ：未知的吸收速度常数F ：未知的吸收比例常数K ：未知的消除速度常数.C(t): 表示t 时刻体内血药浓度 单位（纳克/毫升）V ：表示身体内的血液的容积X :表示服药的剂量 单位（克）四问题分析本题要解决人体服药后，血液中药物的含量是多少及下一次服药的时间间隔与服药剂量的问题。
药物中毒数学建模问题
实验一药物中毒问题146510019 李童1.问题描述问题1：利用1.5节药物中毒施救模型确定对于孩子（血液总量为2000ml）及成人（血液总量为4000ml）服用氨茶碱能引起严重中毒和致命的最小剂量。
问题2：对于1.5节的模型，如果采用的是体外血液透析的办法，求解药物中毒施救模型的血液中药量的变化并作图。
2.问题分析人体服用一定量的药物之后，血液浓度与人体的血液总量有关。
成人有4000ml左右的血液，并可认为孩子有2000ml的血液，血液系统中的血药浓度与药量之间可以相互转换。
血液系统对药物的吸收率和排除率可以由半衰期确定，氨茶碱的半衰期约5h，排除的半衰期约6h如果血药浓度达到危险水平，临床上施救的一种方法是采用口服活性炭来吸附药物，可使药物的排除率增加到原来的两倍，另一种方法是进行体外血液透析，药物排除率可增加到原来的6倍当孩子血液中药量达到200mg和400mg时，分别会出现严重中毒和致命。
当成人血液中药量达到400mg和800mg时，分别会出现严重中毒和致命。
3.模型假设和建立1.胃肠道中药物向血液系统的转移率与药量x（t）成正比，比例系数记为λ，药物在t=0时进入胃肠道。
2.血液系统中药物的排除率与药量y（t）成正比，比例系数记为μ，t=0时血液中无药物。
3.氨茶碱被吸收的半衰期为5h,排除的半衰期为6h。
4.孩子的血液总量为2000ml，成人的血液总量为4000ml。
根据假设对胃肠道中药量x（t）和血液系统中药量y（t）建立如下模型。
由假设1，令x（0）=a mg，随着药物从胃肠道向血液系统的转移，x（t）的下降速度与x（t）成正比（比例系数λ＞0），所以有dx=−λx，x(0)=a（1）dt由假设2，y（0）=0，药物从胃肠道向血液系统的转移相当于血液系统对药物的吸收，y(t)由于吸收作用而增长的速度是λx，由于排除而减少的速度与y(t)本身成正比（比例系数μ>0），所以y(t)满足微分方程dy=λx−μy，y(0)=0（2）dt4.模型求解微分方程（1）是可分离变量方程，容易得到x（t）=m e−λt（3）表明胃肠道中的药量x（t）随时间单调减少并趋于0.为了确定λ，利用药物吸收的半衰期为5h，可得λ=0.1386（1/h）。
数学日记,,,,,喝药
数学日记,,,,,喝药
作文标题：数学日记-----喝药
关键词：数学日记小学三年级
本文适合：小学三年级
作文来源： https://Zw.
这几天天气太冷，我不小心就感冒了，一直在喝药。
今天中午喝药时，妈妈对我说：“你算一算你喝的这一小包药有几颗？你每次喝4颗，要喝2次，还多1颗才能喝完。
”
我想：每次喝4颗，喝两次就是42=8（颗），加上还剩的1颗，那就8+1=9（颗）。
我就告诉妈妈：“妈妈，我一共要喝9颗药。
”妈妈笑着说：“答对了。
”我高兴的连喝药也不怕苦了。
哈哈，数学真是无处不在，喝个药妈妈都能找出数学知识来！。
数学思维在新药研发中的应用有哪些
数学思维在新药研发中的应用有哪些在当今的医学领域，新药研发是一项极其复杂且充满挑战的工作。
它不仅需要深厚的生物学和化学知识，还需要运用各种先进的技术和方法。
而数学思维，作为一种强大的工具，正逐渐在新药研发中发挥着重要的作用。
数学思维中的建模方法，为新药研发提供了一个有效的分析框架。
通过建立数学模型，研究人员可以模拟药物在体内的吸收、分布、代谢和排泄过程（ADME）。
例如，利用微分方程来描述药物浓度随时间和空间的变化，从而预测药物在不同器官和组织中的分布情况。
这有助于优化药物的给药方案，确保药物在治疗部位达到有效的浓度，同时减少副作用的发生。
概率与统计在新药研发的临床试验阶段有着关键的应用。
临床试验需要收集大量的数据，包括患者的症状改善情况、药物的不良反应等。
统计分析可以帮助研究人员从这些海量的数据中提取有价值的信息。
比如，通过假设检验来判断新药是否比现有药物更有效，或者通过生存分析来评估药物对患者生存时间的影响。
此外，概率理论还可以用于估计临床试验成功的可能性，为研发决策提供依据。
优化理论在药物设计中也发挥着重要作用。
药物分子的结构与活性之间存在着复杂的关系。
研究人员可以运用数学优化方法，在众多可能的药物分子结构中寻找最优的设计方案。
例如，通过建立目标函数来衡量药物的活性、选择性和毒性等特性，然后利用优化算法寻找能够使这些目标函数达到最优值的分子结构。
这大大提高了药物研发的效率，减少了实验的盲目性。
数学中的图论和网络分析可以帮助研究人员理解药物与生物靶点之间的相互作用关系。
生物体内的蛋白质、基因等可以看作是一个复杂的网络，药物作用于这个网络中的特定节点（靶点）来发挥治疗作用。
通过分析网络的结构和特性，研究人员可以发现潜在的新靶点，以及预测药物的多靶点作用机制。
这为开发更有效的多靶点药物提供了思路。
数学中的模拟退火、遗传算法等智能算法也在新药研发中得到了应用。
例如，在药物筛选过程中，可以利用这些算法从大量的化合物库中快速筛选出具有潜在活性的化合物。
数学在药物研发中的应用
数学在药物研发中的应用数学与药物研发似乎是两个完全不同的领域，但实际上，数学在药物研发中发挥着重要的作用。
药物研发是一个复杂而精细的过程，而数学提供了工具和方法来解决其中的一些难题，促进了药物研发的进展。
本文将介绍数学在药物研发中的几个主要应用领域。
1. 药物动力学模型药物动力学是研究药物在体内吸收、分布、代谢和排泄过程的学科。
数学模型可以帮助科研人员更好地理解药物在体内的行为，并预测药物的疗效、毒性和剂量等参数。
例如，血药浓度-时间曲线是评估药物在体内有效浓度的重要指标，而数学模型可以从这些曲线中提取药物的代谢速率常数、半衰期等参数。
这些参数可以指导药物的合理用药，优化治疗效果。
2. 药物代谢途径预测药物代谢途径可以影响药物的疗效和安全性。
通过数学模型和计算机仿真，科研人员可以预测药物在体内经过的代谢途径，进而预测药物的代谢产物和毒性。
这些预测结果可以帮助药物研发人员设计更安全、更有效的药物分子。
3. 药物相互作用模拟药物相互作用是指两种或多种药物在体内共同使用时的相互作用效应。
一些药物可能会相互影响代谢、吸收或副作用等方面，因此在药物研发中需要对药物相互作用进行评估。
数学模型可以模拟和预测不同药物之间的相互作用效应，并为临床用药提供指导。
4. 药物释放与控释药物控释指的是通过合适的技术和材料将药物按照一定速率释放到体内，从而实现长效治疗的方式。
数学模型可以帮助科研人员优化药物控释系统的设计和工艺参数，预测药物的释放速率等。
这对于合理控制药物浓度、减少给药频次以及提高患者依从性具有重要意义。
5. 药物优化与剂量个体化通过数学模型和计算方法，科研人员可以对药物分子进行优化设计，提高药物的活性和选择性。
此外，数学模型还可以针对不同个体的特征进行剂量个体化预测，帮助医生制定个性化的用药方案。
综上所述，数学在药物研发中的应用广泛而重要。
数学模型提供了解决药物研发难题的一种有效手段，为药物的合理使用和优化设计提供了科学依据。
数学小医生通过医疗案例帮助孩子们理解数学在医学中的应用
数学小医生通过医疗案例帮助孩子们理解数学在医学中的应用数学一直是被广泛应用于各个领域的学科，医学也不例外。
而作为一门抽象的学科，数学对于一些学生来说可能显得枯燥难懂。
为了解决这一问题，数学小医生应运而生。
他通过医疗案例，帮助孩子们在课堂上理解并应用数学知识，使得数学的学习更加生动有趣。
本文将通过具体案例，介绍数学在医学中的实际应用，以及数学小医生如何帮助孩子们理解和掌握这些数学知识。
第一部分：药物剂量计算在医学中，药物的剂量计算是一项非常重要的工作。
准确计算药物的剂量可以确保患者的安全和治疗效果。
数学在药物剂量计算中起到了关键作用。
数学小医生通过一个实际案例来介绍这个过程。
例如，一名儿童患者需要按体重计算给予一种特定药物的剂量。
假设该药物的标准剂量为每千克体重给予0.1毫克。
如果患者的体重是30千克，那么他需要接受多少毫克的药物呢？数学小医生首先会帮助孩子们理解问题的背景和要求，然后引导他们用数学解决这个问题。
在这个案例中，孩子们需要计算30千克体重对应的药物剂量，可以通过以下公式进行计算：药物剂量 = 体重（千克） ×单位剂量根据这个公式，孩子们可以得出该患者需要接受3毫克的药物。
通过这个案例，孩子们不仅学到了如何进行药物剂量计算，更重要的是他们理解了数学在医学中的实际应用，增加了对数学的实际认识。
第二部分：病人人数统计和概率在医院里，医务人员需要根据过去的病人数据来预测未来的病人人数，以便安排合理的医疗资源。
此时，数学的统计和概率理论被用于分析和预测病人人数。
数学小医生通过一个实际案例来帮助孩子们理解病人人数统计和概率的应用。
假设某医院过去一年每天的病人人数服从正态分布，并且平均每天有100名病人，标准差为10。
那么在接下来一周内，预计有多少天的病人人数超过120人呢？数学小医生会引导孩子们用统计和概率知识解决这个问题。
他们需要计算超过120人的概率，并根据概率计算出预计的天数。
通过这个案例，孩子们不仅掌握了统计和概率的基础知识，还加深了对数学在医学中应用的理解。
从吃药中想到的数学问题
从吃药中想到的数学问题寒假时天很冷，刘畅得了病，便去医院开了药。
他发现，当打开瓶盖吃药时，里面必定会散出一点药味。
并且，他便将这现象告诉了我。
于是，我们便一起讨论。
显然，这是药品挥发的结果。
有挥发，就必然有损失。
可是，每次打开瓶盖只吃一片药，其余的药片也要跟着一块损失。
为了减少损失，我们找到了一个空瓶，如果从原瓶里倒出一些药放到新瓶里，再从新瓶里吃药，这样要比只从一个瓶里吃药要少一些损失。
一．提出问题上面我们已经说过，用两个瓶吃药比较好。
那么具体如何取药，即分几次取，每次取几片呢？这便是我们提出的问题。
对于这个问题，必须做出一个合理的假设，既每打开一次瓶盖，瓶里每一个药片都减少相同的质量。
有了这个假设，我们就可以继续了。
二．提出命题现在我们把刚才提出的实际问题变成严格的数学问题：已知：1. 原瓶中有n片药，一次吃一片，要求全部吃完。
2．有一个新瓶，也可以装药片，它和原瓶是一样大的（即足够大）。
3．每打开一次瓶盖，里面的每一片药都减少1个单位的质量。
问：如何吃药可使损失最少。
四．分析问题１．首先，我们要确定一个规则，即把吃药的过程看成都从新瓶里吃药。
实际上，这条存在与否，是与实际的损失无关的，因为我们从原瓶里取药装入新瓶的时候是要吃一片药的。
但是我们可以把它看成是：把药片装入新瓶后先不要盖瓶盖，而先拿出一片药吃，再盖上瓶盖。
我们定这个规则的目的是为了下面说明的方便。
当然，我们只是用这种规则想问题，在实际操作时是不会这样麻烦的去吃药的。
２．其次，我们要证明一个预备命题。
命题1：要想得到最优解，每次应该把新瓶的药吃完，再从原瓶里拿药吃。
证明：假设命题不成立。
则可设上一次从原瓶里取了p+m片药，吃了p片后，新瓶里还剩m片。
这时，又要从原瓶里取药。
那么如果上次取药时只取p片药，吃完了再取。
同样是吃p片药。
第二种方法就比第一种节省（p-1）*m 个单位的质量。
又因为p>=1，m>0，所以（p-1）*m>=0，即采用第二种方法一定不会比第一种方法差。
中学趣味数学药品混乱
中学趣味数学药品混乱一家药店收到运来的某种药品十瓶。
每瓶装药丸1000粒。
药剂师怀特先生刚把药瓶送上架子，一封电报接踵而来。
怀特先生把电报念给药店经理布莱克小姐听。
怀特先生：特急！所有药瓶须检查后方能出售。
由于失误，其中有一瓶药丸每粒超重10毫克。
请即退回重量有误的那瓶药。
怀特先生专门气恼。
怀特先生：倒霉极了，我只好从每瓶中取出一粒来秤一下。
真是胡闹。
怀特先生刚要动手，布莱克小姐挡住了他。
布莱克小姐：等一下，没必要秤十次，只需秤一次就够了。
这如何可能呢？布莱克小姐的妙主意是从第一瓶中取出1粒，从第二瓶中取出2粒，第三瓶中取出3粒，以此类推，直至从第十瓶中取出10粒。
把这55粒药丸放在秤上，记下总重量。
假如重5510毫克，也确实是超过规格10毫克，她当即明白其中只有一粒是超重的，同时是从第一瓶中取出的。
假如总重量超过规格20毫克，则其中有2粒超重，同时是从第二瓶中取出的，以此类推进行判定。
因此布莱克小姐只要秤一次，不是吗？六个月后，药店又收到此种药品十瓶。
一封加急电报又接踵而至，指动身生了一个更糟糕的错误。
这一次，对超重药丸的瓶数无可奉告。
怀特先动气恼极了。
怀特先生：布莱克小姐，如何办？我们上次的方法不中用了。
布莱克小姐没有赶忙回答，她在思索那个问题。
布莱克小姐：不错。
但假如把那个方法改变一下，我们仍旧只需秤一次就能把重量有误的药品识别出来。
这回布莱克小姐又有什么好主意？在第一个秤药丸问题中，我们明白只有一瓶药丸超重。
从每瓶中取出不同数目的药丸（最简单的方式确实是采纳计数序列），我们就可使一组数字和一组药瓶成为一一对应的关系。
为了解决第二个问题，我们必须用一个数字序列把每瓶药单独标上某个数字，且此序列中的每一个子集必须有一个单独的和。
有没有如此的序列？有的，最简单的确实是下列二重序列：1，2，4，8，16，。
这些数字是2的连续次幂，这一序列为二进制记数法奠定了基础。
在那个问题中，解法是把药瓶排成一行，从第一瓶中取出1粒，从第二瓶中取出2粒，从第三瓶中取出4粒，以此类推。
吃药前得解一道数学题 药丸服用说明书让人发蒙
吃药前得解一道数学题药丸服用说明书让人发蒙作者：佚名中国宁波网讯“吃五子衍宗丸前，得先做一道算术题。
这款药，１００粒重１０克，一次６克，一日２次，每瓶６０克。
一次吃多少粒？昨天，网友“虎皮春卷”在微博上发出的这样一条信息，引来不少网友的围观。
网友“虎皮春卷”说，最近，他的一个男同事在吃这个药丸，每次看到同事吃药，都要先倒出一大把药，一粒粒数后，才服用。
昨天，他从同事桌上拿起了这瓶补肾中药，翻看了一下瓶身介绍，懵了足足一分钟。
这个药的用法用量，要解一道数学题才能明白。
“１００粒重１０克，一次６克，一日２次，每瓶６０克。
”网友“虎皮春卷”说，一次吃多少粒？他想了好一会儿才列出了这道数学题１００÷１０×６，一次用药量为６０粒。
一般说来，“教师”概念之形成经历了十分漫长的历史。
杨士勋（唐初学者，四门博士）《春秋谷梁传疏》曰：“师者教人以不及，故谓师为师资也”。
这儿的“师资”，其实就是先秦而后历代对教师的别称之一。
《韩非子》也有云：“今有不才之子……师长教之弗为变”其“师长”当然也指教师。
这儿的“师资”和“师长”可称为“教师”概念的雏形，但仍说不上是名副其实的“教师”，因为“教师”必须要有明确的传授知识的对象和本身明确的职责。
“标注每次６０粒，不就行了嘛，年纪大一点的人，万一算不过来，不就麻烦了？”网友“虎皮春卷”说，他试了一下，６０粒有满满一瓶盖，吞下去的过程，也不轻松。
他甚至担心这药的用量有问题。
据他了解，有同样功效的六味地黄丸，用量一次多是６粒或８粒。
一次６０粒的用量，有点吓人。
其实,任何一门学科都离不开死记硬背,关键是记忆有技巧,“死记”之后会“活用”。
不记住那些基础知识,怎么会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基础知识抓起,每天挤一点时间让学生“死记”名篇佳句、名言警句,以及丰富的词语、新颖的材料等。
吃药二分之一是多少
吃药二分之一是多少问题一：吃药每日3次,每次二分之一,怎么解分那一颗药？一颗药一分为二不就是二分之一了，一天3次，拿三颗药来分不就刚好是两天的量了。
问题二：小孩吃药吃二分之一的正确说法1、根据小儿体重计算多数药物已算出每公斤体重，换天或每次的用量，因此根据小儿体重决定用药剂量的方法，目前应用相当广泛。
对于已测知体重的小儿，可按实际测得的体重(千克)计算用药量：按公斤折算剂量公式：小儿剂量=每公斤每天(或每次)用药量*体重(千克)小儿剂量=成人剂量*儿童体重/50(即成人平均体重)对没有测知体重的小儿可按下列公式推算：婴儿6月前体重(千克)=月龄*0.6+37个月～12个月体重(千克)=月龄*0.5十3一周岁以上体重(千克)=年龄x2+72、简易快速计算法此法适用于药品说明书未规定小儿剂量，或忘记按公斤体重计算的剂量。
公式如下：1岁以内剂量：成人剂量×0.01×(月龄+3)1岁以上剂量：成人剂量×0.05×(月龄+2)例：成人服痢特灵每次100毫克(即1片)，8岁儿童1次该服多少?按上式计算：100(毫克)×0.05×(8+2)=50(毫克)。
即8岁儿童服痢特灵剂量每次为50毫克(即半片)。
3、根据体表面积计算近年来，国外推荐药物按小儿体表面积计算，既适于儿童，也适用于成人，科学性较强。
其计算方法如下：①体重在30公斤以下者，其体表现积计算公式为：体重(公斤)×0.035+0.1=体表现积(平方米)。
②体重在30公斤以上者，在前公式基础上每增加体重5公斤，体表面积增加0.1平方米。
比如30公斤体重者，体表面积为1.15平方米，35公斤体重者为1.25平方米，40公斤体重者为1.35平方米。
4、根据成人剂量折算这种计算方法只要知道成人剂量就可以按年龄比例推算出小儿剂量，所以简便易行，但每个小儿的个体生长发育不同，虽是同一年龄，但体重各有差异，这种方法比较粗糙：小儿年龄相当于成人用量的比例出生～1月1/18～1/141月～6月1/14～1/76月～1岁1/7～1/51岁～2岁1/5～1/42岁～4岁1/4～1/34岁～6岁1/3～2/56岁～9岁2/5～1/29岁～14岁1/2～2/314岁～18岁2/3～3/4问题三：医嘱:服药一右二分之一是啥意思就是一粒半的意思。
一个医生给了你三颗药丸,让你每隔半小时吃一颗,那么这三颗药丸能维持你多久？
一个医生给了你三颗药丸，让你每隔半小时吃一颗，那么
这三颗药丸能维持你多久？
这个问题需要用到一些基本的数学知识和逻辑思维。
首先，我们需要知道每颗药丸的作用时间，也就是药效持续时间。
假设每颗药丸的作用时间为4个小时。
接着，我们需要计算出三颗药丸的总作用时间。
因为每隔半小时吃一颗，所以三颗药丸的间隔时间为1个小时，也就是说，三颗药丸的总作用时间为4个小时× 3 = 12个小时。
最后，我们需要将总作用时间除以每隔半小时吃一颗药丸的时间间隔，也就是12 ÷ 0.5 = 24。
因此，三颗药丸可以维持你24个半小时，也就是12个小时。
综上所述，三颗药丸可以维持你12个小时，或者说24个半小时。
这个问题的关键在于将不同的时间单位进行换算，需要用到一些基本的数学知识和逻辑思维。
用函数观点认识实际问题
用函数观点认识实际问题
——初中函数教学的误区
前几天和学生探讨了用函数方法解决实际问题，有这样两个问题：
问题1、在抗击“非典”中，某医药研究所开发了一种预防“非典”的药品，经实验这种药品的效果得知：当成年人按规定剂量服用该药后1小时时，血液中含药量最高，达到每毫升5微克，接着逐步衰减，至8小时时血液中含药量为每毫升1.5毫克,每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示，在成年人按规定剂量服药后：
（1）分别求出x≤1和x＞1时，y与x的函数关系式；
（2）如果每毫升血液中含药量为2微克或2微克以上，
对预防“非典”是有效的，那么这个有效时间为多少小时？
问题2、一根弹簧的弹性限度是20
弹簧的长度y（cm）是所挂物体的重量x（kg）的一次函数，当
所挂物体的重量为1kg时，弹簧长度是10cm；当所挂物体的重量
为3kg时，弹簧长度为12cm．（1）写出y与x之间的函数关系
式；（2）求不挂物体时，弹簧的长度；（3）画出该函数的图象.
教学后有所感悟：一是教学中没有深刻认识函数解决实际问
题的重要性，认为函数的概念，图像，性质重要，而忽视了解决
实际问题的教学；二是在教学过程中，对于实际问题中函数的取值这一难点突破不够。
我认为在教学函数的过程中，要加强函数解决实际问题的训练，一次函数，反比例函数，二次函数等。
从图像，从实际问题相结合，多举例子，让学生理解函数在实际问题中的取值和在坐标系中的体现。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
从吃药中想到的数学问题寒假时天很冷，刘畅得了病，便去医院开了药。
他发现，当打开瓶盖吃药时，里面必定会散出一点药味。
并且，他便将这现象告诉了我。
于是，我们便一起讨论。
显然，这是药品挥发的结果。
有挥发，就必然有损失。
可是，每次打开瓶盖只吃一片药，其余的药片也要跟着一块损失。
为了减少损失，我们找到了一个空瓶，如果从原瓶里倒出一些药放到新瓶里，再从新瓶里吃药，这样要比只从一个瓶里吃药要少一些损失。
一．提出问题上面我们已经说过，用两个瓶吃药比较好。
那么具体如何取药，即分几次取，每次取几片呢？这便是我们提出的问题。
对于这个问题，必须做出一个合理的假设，既每打开一次瓶盖，瓶里每一个药片都减少相同的质量。
有了这个假设，我们就可以继续了。
二．提出命题现在我们把刚才提出的实际问题变成严格的数学问题：已知：1. 原瓶中有n片药，一次吃一片，要求全部吃完。
2．有一个新瓶，也可以装药片，它和原瓶是一样大的（即足够大）。
3．每打开一次瓶盖，里面的每一片药都减少1个单位的质量。
问：如何吃药可使损失最少。
四．分析问题１．首先，我们要确定一个规则，即把吃药的过程看成都从新瓶里吃药。
实际上，这条存在与否，是与实际的损失无关的，因为我们从原瓶里取药装入新瓶的时候是要吃一片药的。
但是我们可以把它看成是：把药片装入新瓶后先不要盖瓶盖，而先拿出一片药吃，再盖上瓶盖。
我们定这个规则的目的是为了下面说明的方便。
当然，我们只是用这种规则想问题，在实际操作时是不会这样麻烦的去吃药的。
２．其次，我们要证明一个预备命题。
命题1：要想得到最优解，每次应该把新瓶的药吃完，再从原瓶里拿药吃。
证明：假设命题不成立。
则可设上一次从原瓶里取了p+m片药，吃了p片后，新瓶里还剩m片。
这时，又要从原瓶里取药。
那么如果上次取药时只取p片药，吃完了再取。
同样是吃p片药。
第二种方法就比第一种节省（p-1）*m 个单位的质量。
又因为p>=1，m>0，所以（p-1）*m>=0，即采用第二种方法一定不会比第一种方法差。
所以不应该采用第一种方法。
即原假设不成立，原命题成立。
证毕。
３．有了这个命题，我们就可以得到一个计算公式了。
设：n片药分i次吃完，第一次取p1片，第二次取p2片，依次类推，第i次取pi片。
则我们用（p1，p2，…，pi）来表示整个的取法。
符号［p1，p2，…，pi］表示浪费的总的损失。
对于任意一取法（p1,p2,…..,pi），再吃前p1片药时，浪费的总量是，(p1+1)*p1/2（吃药时的浪费）+(p2+p3+…+pi)（开盖时的浪费），对于其他的，式子形式同前。
最后的总和是：［p1,p2,…,pi］=∑(pj+1)pj/2+∑(j-1)pj４．根据上面的计算公式，我们继而证明了下面两个命题。
命题2：整个的吃药过程中会从原瓶里取若干次药，但对于相邻的两次，不妨设为第k次和第k+1次，Ak，A(k+1)分别代表第k次和第k+1次所取的药片的数量。
则若要得到最优解，则应有Ak>A(k+1)。
证明：假设命题不成立，即有Ak<A(k+1)。
则如果把Ak，A(k+1)调换，即第k次取A2个，第k+1次取Ak个。
则实际上是将（A(k+1)-Ak）个药片由第k+1次吃转移到第k次吃。
设总共取I次。
第一种吃法的总耗费：[A1,A2,…A(k-1),Ak,A(k+1),A(k+2),…Ai]=∑(pj+1)pj/2+∑(j-1)pj =∑(pj+1)pj/2+∑(j-1)pj +(k-1)*Ak+k*A(k+1)+∑(j-1)pj第二种吃法的总耗费：[A1,A2,…A(k-1),A(k+1),Ak,A(k+2),…Ai]= ∑(pj+1)pj/2+∑(j-1)pj +(k-1)*A(k+1)+k*Ak+∑(j-1)pj可以看出，这两种方法只有在红字方面有所不同。
现在暂称红色的式子的和为特殊和。
经化简，特殊和１＝k*Ak+k*A(k+1)-Ak;特殊和２＝k*Ak+k*A(k+1)-A(k+1)因为Ak<A(k+1),所以特殊和１>特殊和２。
即[第一种]>[第二种]。
即第二种取法比第一种好。
所以不应采用第一种取法。
即原假设不成立。
所以原命题成立。
证毕。
命题3：整个的吃药过程中会原瓶里取若干次药，但对于相邻的两次，不妨设为第k次和第k+1次。
Ak，A(k+1)分别代表第k次和第k+1次所取的药片的数量。
则若要得到最优解，则应有Ak－A(k+1)<2。
证明：假设命题不成立。
即Ak-A(k+1)>=2。
如果我们第k次取Ak-1个，第k+1次取A(k+1)+1个。
第一种吃法的总耗费：[A1,A2,…A(k-1),Ak,A(k+1),A(k+2),…Ai]=∑(pj+1)pj/2+∑(j-1)pj =∑(pj+1)pj/2+∑(j-1)pj +(k-1)*Ak+k*A(k+1)+∑(j-1)pj第二种吃法的总耗费：[A1,A2,…A(k-1),Ak-1,A(k+1)+1,A(k+2),…Ai]=∑(pj+1)pj/2+∑(j-1)pj +(k-1)*(Ak-1)+k*(A(k+1)+1)+∑(j-1)pj可以看出，这两种方法只有在红子方面有所不同。
现在也暂称红色的式子的和为特殊和。
经计算，特殊和１－特殊和２＝Ak-A(k+1)-2因为Ak-A(k+1)>=2,所以特殊和１>特殊和２，即第二次一定不会比第一次差。
即原假设不成立，原命题成立。
证毕。
５．根据第2，3个命题，我们设计了一条规则，称其为规则１。
即对于任意一种取法，我们应先把它按取药的数量从大到小排序。
这时找到了一个新取法，那么这个取法不比原来的取法差。
（根据命题2）。
然后把这列新数，从高到低依次做这样的处理：如果此数比大2或2以上，则把这个数减一，把下个数加一。
如此循环往复，直到没有数再可以变更为止。
又得到了一个新取法。
这个取法又一定不比第二种取法差（根据命题３）。
我们认为，经过这种法则变换后的数列，一定是比较好的吃药法则。
我们试了几个数：当n=6即吃6片药时，对于取法（1，1，4），我们根据上法则，做如下变换：（1，1，4）——（4，1，1）——（3，2，1）。
对于取法（1，5），则这样变换：（1，5）——（5，1）——（4，2）——（3，3）——（3，2，1）。
（对最后一步，可以看成是由（3，3，0）——（3，2，1））我们发现，对于大多数的取法，经过上规则的变换，总能变成（3，2，1）的形式。
当n=7即吃7片药是，对于取法（1，1，5），可做如下变换：（1，1，5）——（5，1，1）——（4，2，1）——（3，3，1）——（3，2，2）——（3，2，1，1）对于其他的大部分取法，我们同样可以把他变成（3，2，1，1）的形式。
通过上面的结论，我们找到了一个规律。
即，若k(k+1)/2<=n<(k+1)(k+2)/2,则另b=n-(k+1)k/2 应该这样取，（k，k-1，…，b+1，b，b，b-1，…，1），我们称其为规律１。
但我们也发现，有些取法是不能变成如上形式的。
譬如，当n=7时，若对于取法（1，1，1，1，1，2），最后只能变成（2，1，1，1，1，1）。
而这种取法是比（3，2，1，1）差的。
６．通过研究，我们发现刚才的规则略有不妥之处。
于是我们又制定了一个规则，称其为规则2。
即对于一种取法，先将其用规则1处理。
然后从高到低检查，如果有两对相同的数字，如（…5，5，4，3，2，2，…）,则须对其进行如下改动：将两对相同数字中的之一，较大的加一，较小的减一。
对于上例，变为（…6，5，4，3，2，1…）。
这样改的原因，和命题２，３类似，都是不与整体有关，只与特殊和有关，这里不再赘述。
证明：有了规则１和规则２的共同作用，我们找到的规律就对上面的所有例子都成立了。
那么我们设计一个函数，F(n)，表示吃n片药，最理想时，损失药片时的总质量。
根据我们找到的规律，并根据计算公式得出了F(n)的解析式。
F(n)=b*n-(b-1)b(b+1)/6其中，(b-1)*b/2<=n<(b+1)*b但这只是找规律得出的结论，下面我们希望对其进行科学的论证。
五．解决问题我们将用数学归纳法对其进行论证。
当n=1时，F(n)=1,式子显然成立，这时规律一也成立。
则若n∈[1,k]时式子成立（规律一也成立）。
当n=k+1时，设第一次取p1片药。
则吃完后还剩（n-p1）片。
则(n-p1)∈[1,k],根据归纳假设。
这剩下的n-p0片的最省情况是F(n-p1)。
所以整个的损失为 n-p0(第一次开盖时别的药片的损失)＋p0(p0+1)/2(吃前p0片药的损失)＋F(n-p0)。
将其化简，即F(n-p1)+n+p1(p1-1)/2 =b(n-p1)－(b+1)(b-1)b/6+n+p1(p1-1)/2其中，b是这样的自然数，（b-1）*b/2 <= n-p1 <(b+1)*b，根据规律一，第二次取药应取b-1片，即p2=(b-1),而根据命题３，p1－２应小于p2。
又根据命题３，p1>=p2。
那么，最后的只有一种取法。
即满足规律一的取法。
即对于n=k+1,式子也是成立的。
则对于一切n，n∈Ｎ，F(n)的解析式都是正确的。
证毕六．总结我们的这个研究结果不仅适用于吃药问题，还可以解决同一个模型的问题。
比如，一台电脑里储存了一些信息，现要用软盘将其一点点的拷贝走。
要把一条信息转移到软盘上要搜索整个硬盘上的信息，这就要耗费一些时间。
已知手上有两个硬盘，则如何拷贝最省时间。
此问题就可以用我们的研究结果解决。