解决逻辑电路自启动问题的方式
(整理)《数字逻辑电路》试题2.

一、选择题(每小题1.5分)第一章:1. 带符号位二进制数10011010的反码是( )。
A. 11100101B. 10011010C. 10011011D. 111001102. 十进制数5对应的余3码是( )。
A. 0101B. 1000C. 1010D. 11003. 二进制代码1011对应的格雷码是( )。
A. 1011B. 1010C. 1110D. 0001第二章:1. 下列公式中哪一个是错误的? ( )A. A A 0=+B. A A A =+C. B A )B A ('+'='+D. )C A )(B A (BC A ++=+2. 下列各式中哪个是三变量A 、B 、C 的最小项? ( )A. B A ''B. C B A +'+'C.ABCD. C B '+'3. 下列函数中不等于A 的是( )。
A. A +1B. A +AC. A +ABD. A (A +B )4. 在逻辑代数的加法运算中,1+1=( )。
A. 2B. 1C. 10D. 05. A ⊕1=( )。
A. AB. 1C. A 'D. 06. 含有A 、B 、C 、D 四个逻辑变量的函数Y=A+B+D 中所含最小项的个数是()。
A. 3 B. 8 C. 14 D. 167. 下列函数中等于AB 的是( )。
A. (A +1)BB. (A +B )BC. A +ABD. A (AB )8. 为了将600份文件顺序编码,如果采用二进制代码,最少需要用( )位。
A. 3B. 10C. 1024D. 6009. 为了将600个运动员顺序编码,如果采用八进制代码,最少需要用( )位。
A. 3B. 4C. 10D. 75第三章:1. 采用漏极开路输出门电路(OD 门)主要解决了( )。
A. CMOS 门不能相“与”的问题B. CMOS 门的输出端不能“线与”的问题C. CMOS 门的输出端不能相“或”的问题2. 下列哪个特点不属于CMOS 传输门?( )A. CMOS 传输门属于双向器件。
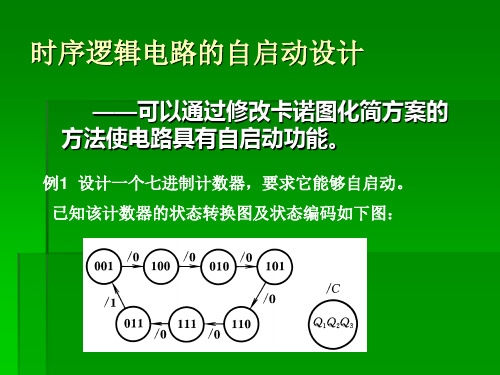
时序逻辑电路的自启动设计
图化简得到最简单的形式:
Q1n+1 = Q3 Q2n+1 = Q1
Q3n+1 = Q2
Q3Q2Q1的无效状 态000、011、101 、110、111分别 带入,得到如下图 中的实线链连接的
状态转换图。
显然设计的电路不能自启动
为保持移位寄存器内部结构不变,只允许修改第一位触发器的 输入。所以修改Q1,
Q1n+1 = Q2 Q3 Q2n+1 = Q1 + Q2 Q3 Q3n+1 = Q2,
修改后的电路状态转换图如下:
例2 设计一个能自启动的3位环形计数器。要求它的有效循环状态为 100010 001 100
解:根据题目要求的状态循环,电路的状态转换图和次态卡诺图如图:
如只考虑使状态方程图化简方案的 方法使电路具有自启动功能。
例1 设计一个七进制计数器,要求它能够自启动。 已知该计数器的状态转换图及状态编码如下图:
根据状态转换图,可以得到:
按照卡诺图化简的最简 要求可得到方程:
Q1n+1 = Q2 Q3 Q2n+1 = Q1 Q3n+1 = Q2
得到修改后的次态卡诺图如下:
修改后的状态方程如:
Q1n+1 = Q1 Q2 Q2n+1 = Q1 Q3n+1 = Q2
若选用D触发器构造此计数器,驱动方程为: D1 = Q1n+1 = Q1 Q2 = Q1 + Q2 D2 = Q2n+1 = Q1 D3 = Q3n+1 = Q2
逻辑图如下:
实际上,包括在圈里的任意项取为1,而在圈外的任意项取 为0。即无效状态的次态已被指定。
若这个指定的次态属于有效循环中的状态,电路可以自启 动;反之则不可以自启动。
数字电子技术基础-第六章_时序逻辑电路(完整版)

T0 1
行修改,在0000 时减“1”后跳变 T1 Q0 Q0(Q3Q2Q1)
为1001,然后按
二进制减法计数
就行了。T2 Q1Q0 Q1Q0 (Q1Q2Q3 )
T3 Q2Q1Q0
50
能自启动
47
•时序图 5
分 频
10 分 频c
0
t
48
器件实例:74 160
CLK RD LD EP ET 工作状态 X 0 X X X 置 0(异步) 1 0 X X 预置数(同步) X 1 1 0 1 保持(包括C) X 1 1 X 0 保持(C=0) 1 1 1 1 计数
49
②减法计数器
基本原理:对二进 制减法计数器进
——74LS193
异步置数 异步清零
44
(采用T’触发器,即T=1)
CLKi
CLKU
i 1
Qj
j0
CLKD
i 1
Qj
j0
CLK0 CLKU CLKD
CLK 2 CLKU Q1Q0 CLK DQ1Q0
45
2. 同步十进制计数器 ①加法计数器
基本原理:在四位二进制 计数器基础上修改,当计 到1001时,则下一个CLK 电路状态回到0000。
EP ET 工作状态
X 0 X X X 置 0(异步)
1 0 X X 预置数(同步)
X 1 1 0 1 保持(包括C)
X 1 1 X 0 保持(C=0)
1 1 1 1 计数
39
同步二进制减法计数器 原理:根据二进制减法运算 规则可知:在多位二进制数 末位减1,若第i位以下皆为 0时,则第i位应翻转。
Y Q2Q3
数字电路与逻辑设计第5章时序逻辑电路

(b) 74194构成扭环形计数器
Q and A Q :电路是否具备自启动特性?请检验。
77
➢ 检验扭环形计数器的自启动特性
模值M=2n=2×4=8 状态利用率稍高;环 形计数器和扭环形计 数器都具有移存型的 状态变化规律,但它 们都不具有自启动性
10
分析工具 常见电路
状态转移真值表 状态方程 状态转移图 时序图
数码寄存器 移位寄存器 同步计数器 异步计数器
11
5.2.1 时序逻辑电路的分析步骤
12
例1:分析图示时序逻辑电路
解 ➢ 1. 写激励方程:
13
➢ 2. 写状态方程和输出方程:
根据JK触发器特性方程:Qn1 J Qn K Qn
LD
置入控制输入
CP
时钟输入
CR
异步清0输入
CTT ,CTP 计数控制输入
输出端子
Q0~Q3 数据输出
CO
进位输出
CO
Q3n
Q
n 2
Q1n
Q0n
26
➢ 功能表:
27
2.十进制同步计数器(异步清除)74160
➢ 逻辑符号: ➢ 功能表:
CO Q3n Q0n
28
3.4位二进制同步计数器(同步清除)74163
51
1.二-五-十进制异步计数器7490
52
CT7490: 2-5-10进制异步计数器
4个触发器(CP1独立触发FF0实现二分频,
CP2独立触发FF1、FF2、FF3构成的五分频计数器)
异步清0输入 R01、 R02
异步置9输入 S91、S92
可实现 8421BCD 和 5421BCD计数
3篇5章习题解答
nn
=Q Q
+
AQ n
n
=Q
+
AQ n
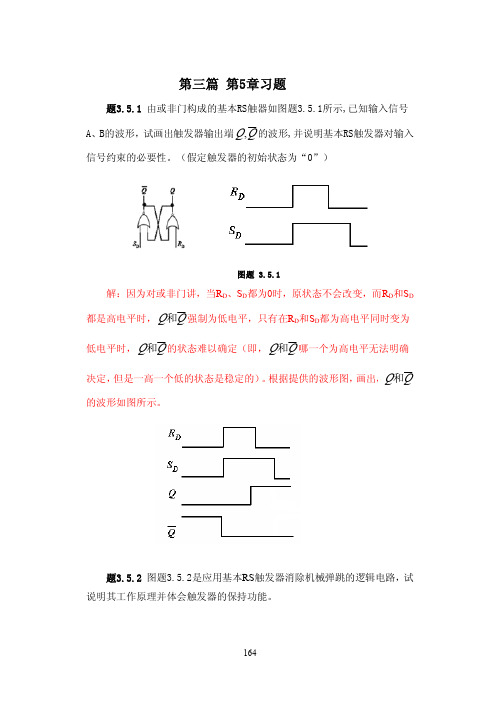
题3.5.6 根据图题3.5.6所示电路及A、B、C波形,画出触发器Q端的波 形。(设触发触器初态为“0”)。
图题 3.5.6
n
解:如果 D = Q ,则是一个计数触发器(翻转触发器),加了异或门后,只有当异或
n
门输出高电平时,才满足 D = Q ,所以画出的波形图如图所示。
=
J 0 Q0n
+
K 0 Q0n
= Q2n Q0n
+ Q1n Q0n
依次设定初态,计算出次态如下:
初态设定从 Q2nQ1nQ0n = 000 开始,→001→010→011→100→001
164
图题 3.5.2
解:由基本RS触发器构成消除机械弹跳时的原理可以用波形加以说明。 当机械开关S从上端打到下端时,触点已离开了上端,但下端有一个接触和 非接触的过程,决定于触点的弹性好坏。波形说明开关离开上端,在下端弹 跳几下的情况。
由于 S D变高电平RD变低电平后 , RD再次变高电平时 触发器的输
题3.5.5 试写出图题3.5.5各触发器的次态逻辑函数表达式。
166
(a)
(b)
(c)
(d)
解:(a)电路: Qn+1
=
n
AQ
图题 3.5.5
(b)电路: Qn+1
=
n
Q
+
AQn
=
n
A+Q
(c)电路: Qn+1 = AQnQn + AQ nQ n = AQ n
(d)电路: Qn+1
启动电路的工作原理

启动电路的工作原理
启动电路是指在启动电动机时控制电机正常运行所需的电气设备。
它通过控制电源电压、实现各种保护和监控功能,保证电动机能够顺利启动。
工作原理如下:
1. 主电源:启动电路通过交流电源或直流电源提供电力,电压大小与电动机的额定电压相匹配。
2. 减速器:当电机中的转子停止转动时,启动电路通过减速器将电源电压降低并平稳地施加到电动机电源回路上,减少起动电流的冲击。
3. 起动方式:启动电路有多种启动方式,包括直接启动、自启动、星三角启动、自耦启动等。
选择启动方式取决于电动机的功率、负载类型及用户需求。
4. 控制元件:启动电路包括各种控制元件,例如启动按钮、控制继电器、热继电器、热继电器等,用于控制电动机的启动、停止、保护和监控等功能。
5. 保护功能:启动电路还包括各种保护功能,例如过载保护、短路保护、电源失压保护等。
这些保护功能可以保证电动机在异常情况下安全运行,避免损坏和安全事故。
6. 控制电路:启动电路通过逻辑电路、控制电路和信号接口等
实现对电动机的控制。
它能根据外部条件或用户设置的参数,自动调整电机的运行模式和运行状态。
总的来说,启动电路的工作原理是通过控制电源电压、选择合适的启动方式和监测电机运行状态,实现电动机的安全、稳定启动和正常工作。
解决逻辑电路自启动问题的方法

解决逻辑电路自启动问题的方法在时序逻辑电路中,当逻辑电路可能出现的总状态数不等于有效状态时,就会有无效状态。
如果无效状态能回到有效状态时,称电路能够自启动.反之,则不能自启动.能自启动的电路不会对电路工作状态造成影响,但不能自启动的电路会对电路的可靠性及稳定性形成较大的隐患。
当电路加电时就可能偶然落入无效状态,这时电路将不能正常工作. 在电路正常工作时,如果受外部意外的干扰,也可能落入无效状态,此时电路的正常工作将被终止、并出错.所以自启动问题是数字电路系统设计中必须解决的问题.(1)自启动问题的典型解决方法自启动问题是设计过程中必须考虑的问题.自启动问题在相关书籍和文章中,都有较经典的解决方法. 为叙述方便, 以时序电路设计中的典型设计,计数器电路的设计为例来说明.在计数器中,如果无效状态形成循环(无效循环),则电路不能自启动(无效状态不能回到有效状态) .解决方法通常是修改无效循环中的状态转换关系,断开无效循环并把无效状态引导至有效状态,使电路的状态图形成能自启动的状态图,从而解决不能自启动的问题。
现用3位扭环形计数器(图1)为例来说明:无效状态010和101形成一个无效循环,所以电路不能自启动。
解决的方法是断开无效循环,把无效状态101引导至有效状态110上, 完成自启动, 最后设计结果如图2所示.此方法直接、彻底的解决了自启动问题.但这个方法有一个很大的局限性:当无效循环较多时,把无效状态一个一个的引导至有效状态的步骤可能很繁杂, 要有一定的经验和技巧,虽然最后都能解决自启动问题,但最终的设计结果可能会很复杂.对于设计过程困难、设计结果复杂的设计,是否还有另外的设计方法呢?这就是本文讨论的要点。
(2)加电预置电路和检测复位电路解决自启动问题首先想到的是加电预置,在打开电源的瞬间,使电路处在一个有效状态下,从而避免进入无效状态,来解决自启动问题.图3电路在打开电源的瞬间,电路处在111状态(可任选一个有效状态来预置. 由于加电瞬间电容电压为零, 异步置位端使触发器瞬间置“1”.加电后、电容电压很快升高为“1"触发器异步置位端的置位作用消失,电路开始正常工作)。
第6章 时序逻辑电路-习题答案
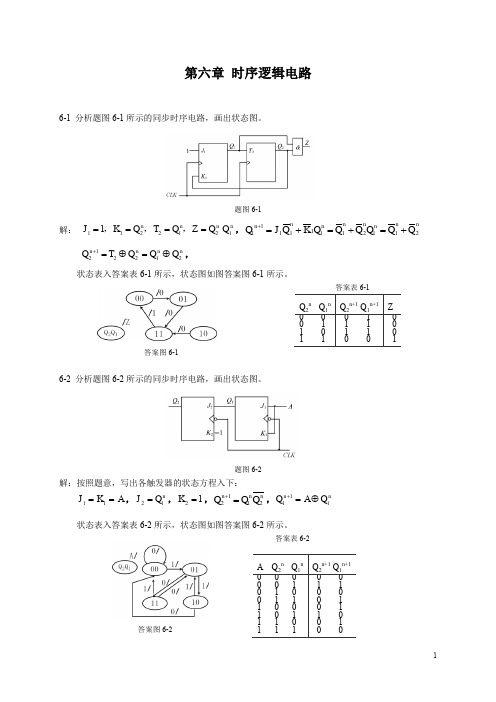
第六章 时序逻辑电路6-1 分析题图6-1所示的同步时序电路,画出状态图。
题图6-1解: 11221211n n n n J K Q T Q Z Q Q ====,,,,11111111212n n n n nn n nQ J Q K Q Q Q Q Q Q +=+=+=+122212n n n n Q T Q Q Q +=⊕=⊕,状态表入答案表6-1所示,状态图如图答案图6-1所示。
答案表6-1答案图6-16-2 分析题图6-2所示的同步时序电路,画出状态图。
题图6-2 解:按照题意,写出各触发器的状态方程入下:11J K A ==,21n J Q =,21K =,1212n n nQ Q Q +=,111n n Q A Q +=⊕状态表入答案表6-2所示,状态图如图答案图6-2所示。
答案表6-2答案图6-2Q 2n Q 1n Q 2n+1 Q 1n+1 Z0 0 0 1 1 0 1 1 0 1 1 1 1 1 0 0 0 0 0 1A Q 2n Q 1n Q 2n+1 Q 1n+1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 0 1 1 0 0 0 1 0 1 1 0 0 1 0 0CLK D 1D 2D 3Q 3Q 2Q 1Q 2Q 3Q 1Q 1Q 2Q 3&6-3分析题图6-3所示的同步时序电路,画出状态图。
题图6-3解:按照题意,写出各触发器的状态方程入下:1112213232131n n n nn J K T J K Q Q T J Q Q K Q ========1,,, 133********n n n n n n n nQ J Q K Q Q Q Q Q Q +=+=+ 1222132n n n n nQ T Q Q Q Q +=⊕=⊕ 1111111n n n n Q T Q Q Q +=⊕=⊕=答案表6-3答案图6-36-4 在题图6-4所示的电路中,已知寄存器的初始状态Q 1Q 2Q 3=111。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解决逻辑电路自启动问题的方法在时序逻辑电路中,当逻辑电路可能出现的总状态数不等于有效状态时,就会有无效状态。
如果无效状态能回到有效状态时,称电路能够自启动。
反之,则不能自启动。
能自启动的电路不会对电路工作状态造成影响,但不能自启动的电路会对电路的可靠性及稳定性形成较大的隐患。
当电路加电时就可能偶然落入无效状态 ,这时电路将不能正常工作. 在电路正常工作时,如果受外部意外的干扰,也可能落入无效状态,此时电路的正常工作将被终止、并出错.所以自启动问题是数字电路系统设计中必须解决的问题.
(1)自启动问题的典型解决方法
自启动问题是设计过程中必须考虑的问题.自启动问题在相关书籍和文章中,都有较经典的解决方法. 为叙述方便, 以时序电路设计中的典型设计,计数器电路的设计为例来说明.在计数器中, 如果无效状态形成循环(无效循环) ,则电路不能自启动(无效状态不能回到有效状态) .解决方法通常是修改无效循环中的状态转换关系,断开无效循环并把无效状态引导至有效状态,使电路的状态图形成能自启动的状态图,从而解决不能自启动的问题.现用3位扭环形计数器(图1)为例来说明:无效状态010和101形成一个无效循环,所以电路不能自启动.解决的方法是断开无效循环,把无效状态101引导至有效状态110上, 完成自启动, 最后设计结果如图2所示.
此方法直接、彻底的解决了自启动问题.但这个方法有一个很大的局限性:当无效循环较多时,把无效状态一个一个的引导至有效状态的步骤可能很繁杂, 要有一定的经验和技巧, 虽然最后都能解决自启动问题,但最终的设计结果可能会很复杂.对于设计过程困难、设计结果复杂的设计,是否还有另外的设计方法呢? 这就是本文讨论的要点.
(2)加电预置电路和检测复位电路解决自启动问题首先想到的是加电预置,在打开电源的瞬间,使电路处在一个有效状态下,从而避免进入无效状态,来解决自启动问题.图3电路在打开电源的瞬间,电路处在111状态(可任选一个有效状态来预置. 由于
加电瞬间电容电压为零, 异步置位端使触发器瞬间置“1”.加电后、电容电压很快升高为“1”触发器异步置位端的置位作用消失, 电路开始正常工作) .电阻R 的阻值应能保证触发器的异步置位端为“1”.电容 C 的容量由置位时间的长短决定( T =RC),只要置位时间大于触发器的翻转时间就可以使电路正常工作.
加电预置的方法虽然简单, 但它无法避免电路受外部意外干扰,落入无效状态的可能.也就是电路的可靠性还有一定的问题. 如何解决这个问题? 在工业逻辑控制电路中, 为使逻辑电路的可靠性得到充分的保证,采用了一个称之为”看门狗电路”的技术,基本原理是”看门狗电路”定时采集逻辑电路的工作信息,当电路工作不正常时,立即发出一个中断申请, 使逻辑电路初始化重起, 恢复电路的正常工作.按照上面的思路, 只要在不能自启动电路上加装检测复位电路, 就能解决电路的自启动问题. 例如: 在图1上加装检测复位电路后,图4所示电路就能很好的解决逻辑电路的自启动问题.图4电路在打开电源的瞬间, 电容C使电路处在一个有效状态111(与加电预置电路相似,可任选一个有效状态来预置.由于加电瞬间电容电压为零,异步
置位端使触发器瞬间置”1”, 而采集电路采集到的111状态, 又使电容电压瞬间升高为”1”, 异步置位端的置位作用消失,电路开始正常工作) ,解决了自启动的预置问题.检测逻辑电路工作是否正常的信息,由采集电路: 三输入端与门和二极管D完成; 电路正常工作时, 采集电路能循环采集到有效状态111 , 并能定时对电容C充电, 使触发器的异步置位端始终为”1”,不影响电路的正常工作;当电路工作不正常时,电容C通过电阻R放电, 使触发器的异步置位端电压下降为”1”, 电路重新预置, 恢复电路正常工作.
电阻R的阻值应能保证触发器的异步置位端为“0”;电容C决定电路的放电时间,它必须保证在一个有效循环的整个周期内, 电容两端的电压始终保持为“1”,所以RC必须大于一个有效周期T.一般只要等于2T , 电路就能可靠工作. 如果太大,当电路工作不正常时, 会使电路的恢复响应时间增大.
3 总结
加电预置电路、检测复位电路与常规典型解决方法相比较,各有所长、各有所短.加电预置电路解决自启动问题:电路结构简单,设计容
易,但电路工作的稳定性稍差,但只要解决电路布线干扰问题,也能满
足一般电路的要求.检测复位电路解决自启动问题: 电路结构可能会复杂一点,但设计容易,并可以保证电路工作的高可靠性.常规典型解
决方法:电路结构有时会很复杂,设计过程繁杂、并有一定的难度.电路工作同样也具有高可靠性.检测复位电路的方法是一种非常规的解决方案,由于它借鉴了提高工业逻辑控制稳定性的方法,设计出来的电路稳定可靠,并能方便的完成设计工作.这在典型解决方法较困难时,
就更能发挥出它的优势.检测复位电路的方法要应用到其它方面的知识, 知识相对比较综合. 在借鉴时, 也不是完全照搬原来的方法,而只是借鉴了它的思路,把原来的逻辑处理方法进行了电路化处理. 它使解决自启动问题的设计方法更加多样化.
参考文献:
[ 1] 清华大学电子学教研组编,余孟尝主编. 数字电子技术基础简明教程(第二版) [M ]. 北京:高等教育出版社, 2000 . 329 .
[ 2] 华中工学院电子学教研室编,康华光. 电子技术基础数字部分(第三版) [M ]. 北京:高等教育出版社, 1988 .
[ 3] 清华大学电子学教研组编,闫石. 数字电子技术基础(第三版) [M ]. 北京:高等教育出版社, 1989 .
[ 4] 童诗白, 徐振英.现代电子学及应用[M ]. 北京:高等教育出版社, 1994 .
[ 5] 李大友. 数字电路逻辑设计[M ].北京: 清华大学出版社, 1997 . [ 6] 陈跃斌. 时序电路自启动的一种设计方法[ J] .云南民族学院学
报(自然科学版), 1997 , 6( 2): 31- 34 .。
