八年级数学重心
人教版 初中数学 八年级上册课题学习重心_课题学习重心
∵EF是△ABC的中位线
F
E
∵∴HEIF是=∥△G12BBCC的中位线
G
∴HI
=∥
1 2
BC
H
I
∴ EF =∥ HI
B
D
C∴四边形EFHI是平行四边形
∴EG=HG,FG=IG
∴EG:GB=1:2,FG:GC=1:2
三角形的重心把中线分成1:2的两部分。
A
E G
B
?
D
C
课题学习 重心
已知ABC的中线CD、BE相交于点G;
A
32145.... SS ::SS SS : S DDDDGGGGEBEEE DEDAAEGDGBCCCB;;;
D
E
GG
B
C
课题学习 重心
归纳有关三角形面积解题方法:
A 1.三角形的中线把三角形 分成面积相等的两个三角
形;
E G
A
求:点G到直角顶点C的距离GC;
解:RtACB,ACB 90o
4
D G
AC 4,BC 3
G是ABC的重心
AB
5
CCGD是 中32 C线D
CD
5 2
C
3
B CG 5 3
课题学习 重心
已知:ABC中AB AC, AD BC, AD与 中线BE相交于点G; AD 18cm,GE 5cm, 求:BC的长。
课题学习 重心 A
E
F
G
B
D
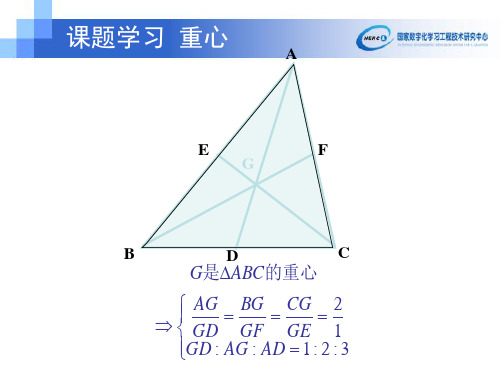
C
G是ABC的重心
AG GD
BG GF
CG GE
2 1
GD : AG : AD 1: 2 : 3
数学重心知识点总结

数学重心知识点总结`本文将围绕数学中的重心概念展开,讨论其在不同领域的应用以及相关的重要知识点。
`1. 重心的概念重心是物体均匀分布质量时的中心点,也是物体受到重力作用时所受合力的作用点。
在数学中,重心也被用来描述几何图形和空间图形的平衡点或中心位置。
重心的位置可以通过重心定理、积分法、向量法等进行计算。
2. 几何图形的重心在平面几何中,不同形状的图形具有不同的重心计算方法。
常见的几何图形包括三角形、四边形、圆等。
三角形的重心位于三条中线的交点处,可以通过中线长的平方和的三倍的和来确定。
四边形的重心位于对角线的交点处,可以通过对角线的中点来确定。
圆的重心位于圆心的位置,其坐标可以通过圆心坐标来确定。
3. 空间图形的重心在空间几何中,立体图形的重心计算较为复杂。
常见的空间图形包括球体、长方体、圆柱体、圆锥体等。
球体的重心位于球心的位置,可以通过球心坐标来确定。
长方体的重心位于中心位置,可以通过长方体的对称性来确定。
其他复杂的空间图形的重心计算通常需要利用积分法或向量法来进行。
4. 重心在力学中的应用重心在力学中具有重要的应用价值。
对于刚体平衡问题,重心是刚体平衡的关键要素。
当刚体受到外力作用时,重心位置的改变会影响刚体的平衡状态。
在飞行器、汽车、船舶等工程领域,重心的位置设计对于整个系统的稳定性至关重要。
5. 重心在航空航天工程中的应用在航空航天工程中,对于飞行器的设计和控制来说,重心的位置是至关重要的。
飞行器的重心位置直接影响其飞行动力学性能和操纵稳定性。
一般来说,飞行器的重心位置应该在飞行器整体几何形状的中心位置,以确保其飞行稳定性和操纵性能。
6. 重心在建筑工程中的应用在建筑工程中,重心的位置也是一个重要考虑因素。
建筑物的重心位置对其整体结构的稳定性和安全性有着直接影响。
在建筑设计中,需要考虑建筑物整体结构的重心位置,以确保建筑物能够承受外部引力和自重的作用,并保持稳定。
7. 重心在船舶工程中的应用在船舶工程中,船舶的重心位置直接影响其稳定性和操纵性能。
人教版八年级数学《重心》ppt

课题学习(1)
重 心
你能保持平衡吗?
பைடு நூலகம்
你能完美的做出此动作吗?
能在平衡木上保持平衡吗?
活动 1
你知道杂技演员头上的碗为什么掉不下来吗?
活动 1
碟子为什么不会从顶杆上掉下来呢?
活动 1
杂技演员头上的碗,顶杆上的碟子掉不 下来是由于它们保持着一种平衡.
怎样才能达到平衡?
试一试:怎样用一根手指平衡地顶起一支笔? 一本书呢?
活动 6
物体的重心与物体的形状有关,规则图
形的重心就是它的几何中心.如:线段,平
行四边形,三角形,正多边形等等.
1.线段重心是线段中点.
2.平行四边形的重心是对角线的交点. 3. 三角形的重心是三条中线的交点. 4.正多边形的重心是对称轴的交点.
拓
展
任何有固定形状的物体,不论其在地 球表面如何放置,其平行分布重力的合 力(通常所说的物体的重力)作用线, 都通过物体上一个确定的点,这一点称 为物体的重心.
三、解答题
画出图中各图形的重心O.
手指顶在钢笔、书本的中心就可以平 衡,这个平衡点叫做钢笔、书本的重 心.
你会找出常见的几何图形的重心吗? 如线段、平行四边形、任意多边形等.
活动 2 探究线段的重心.
(1)找出平衡点的位置.
如图所示,两手分开,把均匀木条水平地架在左右手的食 指上,把两食指相对交替靠拢,直到并在一起为止.用一个食指 支在此处,木条能呈水平平衡.
结论:平行四边形的重心就是它 的两条对角线的交点.
(3)由以上发现能找到矩形、菱形、一 般平行四边形的重心的所在位置吗?
O
O
O
(4)将钉子定在所找到的重心处,将细 绳系在钉子上将它们吊起,观察它们是否保 持平衡。 悬挂法
八年级数学《课题学习 -重心1》教案
19.4、课题学习《重心》教学设计
flash演示悬线法测定线段平衡点位置。
教学反思:
本节“课题学习”,主要是让学生多动手、多实践、多猜想、多论证、多总结。
对于其中一些结论,大胆地鼓励学生进行说理甚至证明,说理证明的形式多样,可口述,可书写,可交流探讨,通过学习,进一步让学生了解规则的几何图形的几何图形的重心就是它的几何中心,体会数学和物理学科之间的联系。
注重对学生以下各能力训练培养:学生的空间想象能力;动手操作能力;实践探究能力;猜想发现能力;说明理由逻辑推理能力。
湘教版八年级数学上册《寻找重心的方法》教案

《寻找重心的方法》教案
a.悬挂法
只适用于薄板(不一定均匀)。
首先找一根细绳,在物体上找一点,用绳悬挂,划出物体静止后的重力线,同理再找一点悬挂,两条重力线的交点就是物体重心。
b.支撑法
只适用于细棒(不一定均匀)。
用一个支点支撑物体,不断变化位置,越稳定的位置,越接近重心。
正1问题的提出演示实验:(1)一根粗细均匀的均质细杆,左、右手分别伸出食指支撑细杆,然后两手指缓慢靠近,手指与细杆发生相对移动,最终手指接触,则指缝中间位置即为细杆的重心;用一根手指支撑刚才所测位置,细杆处于平衡状态,实验得证.(2)将上述均质细棒换作羽毛球拍,重复上面步骤,得到
一种可能的变通方式是用两个支点支撑,然后施加较小的力使两个支点靠近,因为离重心近的支点摩擦力会大,所以物体会随之移动,使另一个支点更接近重心,如此可以找到重心的近似位置。
c.针顶法
同样只适用于薄板。
用一根细针顶住板子的下面,当板子能够保持平衡,那么针顶的位置接近重心。
与支撑法同理,可用3根细针互相接近的方法,找到重心位置的范围,不过这就没有支撑法的变通方式那样方便了。
d.用铅垂线找重心(任意一图形,质地均匀)
用绳子找其一端点悬挂,后用铅垂线挂在此端点上(描下来)。
而后用同样的方法作另一条线。
两线交点即其重心。
八年级数学上册《找重心》优秀教学案例

1.重心定义:讲解重心的定义,让学生了解重心是几何图形内部的一个重要点,它具有使图形保持平衡的特性。
2.重心的性质:通过讲解和示例,让学生掌握重心在几何图形中的位置特点,如三角形重心位于三边中线的交点,矩形重心位于对角线的交点等。
3.寻找重心的方法:介绍寻找三角形、矩形等简单几何图形重心的方法,如中线法、对角线法等。
3.培养学生的团队协作能力和问题解决能力,提高他们的数学素养。
二、教学目标
(一)知识与技能
1.知识目标:通过本节课的学习,使学生掌握重心的定义,理解重心在几何图形中的位置特点,并能够运用数学语言描述重心的性质。同时,让学生掌握寻找三角形、矩形等简单几何图形重心的方法。
2.技能目标:培养学生运用数学知识解决实际问题的能力,提高他们的空间想象力和逻辑思维能力。通过小组合作、讨论交流等方式,锻炼学生的团队协作能力和沟通表达能力。
八年级数学上册《找重心》优秀教学案例
一、案例背景
《找重心》这一课题是八年级数学上册的教学内容,旨在让学生通过探究几何图形的重心概念,培养他们的空间想象能力和逻辑思维能力。在教学过程中,我将结合课本知识,以实际问题为载体,引导学生运用数学方法解决实际问题。本案例以学生为主体,关注学生的参与度和思考过程,通过小组合作、讨论交流等形式,激发学生的学习兴趣,提高他们的数学素养。
(二)过程与方法
1.过程目标:在教学过程中,注重学生的参与度和主体地位,引导他们通过观察、猜想、验证、总结等环节,探索几何图形重心的性质和寻找方法。让学生在探究过程中,体验数学知识的形成过程,培养他们的探究精神和问题解决能力。
2.方法目标:采用任务驱动法、小组合作法、讨论交流法等多种教学方法,引导学生积极参与教学活动。同时,注重培养学生的自主学习能力,使他们能够在教师的引导下,运用所学知识解决实际问题。
人教版数学八年级下册第19章19.4课题学习 重心 课时同步训练
第十九章 四边形19.4课题学习 重心课前预习篇1.物理实验告诉我们,能使物体保持__平衡 __的支点就是该物体的重心.2.确定物质的重心的方法:(1)平衡法:(2)悬挂法:3.物体的重心与物体的形状有关,规则的图形重心就是它的几何中心.如;线段,平行四边形,三角形,正多边形,等等.线段重心是线段中点 ;.平行四边形的重心是对角线的交点 ;三角形的重心是三条中线的交点 . 等边三角形重心是高或中线或角平分线交点;正多边形的重心是对称轴的交点 .不规则的图形(物体)可以通过悬挂法 来确定它的重心.4.三角形的重心定理:三角形的重心到任意一个顶点的距离,等于它到对边中点的距离的 2 倍或三角形的重心到一边中点的距离等于这边上中线长的三分之一.如图:G 是△ABC的重心,则: ⎪⎩⎪⎨⎧====3:2:1::12AD AG GD GE CG GF BG GD AG典例剖析篇【例1】已知:△ABC 中,AB=AC ,A E ⊥BC 于点E ,AE 与中线BF 相交于点G ,AE=18 cm,GF=5cm,求BC 的长.【解析】本题要利用等腰三角形底边上的高也是底边上的中线的性质,从而确定点G 是三角形的重心.根据三角形的重心定理,则此题可解.解:因为在△ABC 中,AB=AC ,A E ⊥BC ,所以AE 是BC 边的中线.因为AE 与中线BF 相交于点G ,因为AE=18 cm,GF=5cm,所以根据重心定理可得:BG=2GF=10 cm ,GE= 13AE=6 cm .因为A E ⊥BC ,BG=10 cm ,GE=6 cm ,222AB C E FG所以22106BE=-.因为AE是中线,E是BC的中点,所以BC=2BE=16 cm.基础夯实篇1.判下列说法错误的是(C)A.人体的重心有可能随着人体姿态的变化而改变B.经过平行四边形重心的直线把它分成面积相等的两部分C.规则形状的几何体的重心不一定是它的几何中心D.重心不一定在物体上2.(2010荆门)给出以下判断:(1)线段的中点是线段的重心(2)三角形的三条中线交于一点,这一点就是三角形的重心(3)平行四边形的重心是它的两条对角线的交点(4)三角形的重心是它的中线的一个三等分点那么以上判断中正确的有( D)(A)一个(B)两个(C)三个(D)四个3.小明和家在一次外出时,当地的人告诉他,要过独木桥,肩上挑一担重物再过去比空手过去安全,从重心的角度考虑,他们这样做是希望( A )A.重心低一点 B.重心高一点C.走得快一点 D.使重心落在桥上4.老翁有一块质地均匀的三角形金块,如何用最简单的方法把金块平均分给他的三个子女?(C)A.先找出三角形金块三边中垂线的交点,再以该点为中心,进行切割B.先找出三角形三个内角平分线的交点,再以该点为中心,进行切割C.先找出三角形三中线的交点,再以该点为中心,进行切割D.先找出三角形三边上的高的交点再以该点为中心,进行切割5.将一张平行四边形的纸片折一次,使得折痕平分这个平行四边形的面积,则这样的折纸方法共有(D )A.1种B.2种C.4种D.无数种6.在①线段②平行四边形③矩形④菱形⑤正方形⑥等边三角形⑦等腰梯形⑧等腰三角形中,绕它们的重心旋转180度后,所得的图形能与原图重合的有①②③④⑤.7.一个正方形的边长为a,则它的重心G到一个顶点的距离为22.8.已知G是正三角形ABC的重心,AG=3,则该三角形的边长是33.9.已知矩形ABCD中,AB<BC,重心G到短边的距离为2,矩形的周长为20,则矩形的面积为24.决胜中考篇10.课堂上,老师拿出一根长为50 cm 的圆柱形木棒,要求同学们标出该木棒的重心,小明马上在该木棒的25cm 处标了出来,请问他找出的重心正确吗?答:小明的做法是不对的.如果木棒是质地均匀的,则木棒的重心就是它的几何中心,如果木棒的质地不均匀,则要用悬持法来确定木棒的几何中心.11.如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,G为△ABC的重心,且GC=4,则△ABC的面积为多少?解:因为G为△ABC的重心,所以CD:GC=3:2,CD=BD=12 AB,因为GC=4,所以BD=CD=6,AB=12.因为∠ACB=90°,∠ABC=60°所以△BCD是等边三角形,所以BC=BD=6,∠BAC=30°,在Rt△ABC中,根据勾股定理得:22AC AB BC=-= 2212663-=所以△ABC的面积为12·AC·BC=18312.如图所示,有一块质地均匀的铁皮,请找出它的重心位置.解:如图,连接BE,根据图中数据可知,BE平分这块铁皮,从而只要再画出一条与BE相交肯平分这块铁皮的直线,它们的交点即为这块铁皮的重心.如图,点O就是所画的铁皮的重心.13.已知:Rt △ABC 中,∠ACB=90°,AC=4,BC=3,G 是△ABC 的重心.(1)求点G 到直角顶点C 的距离GC .(2)求点G 到斜边AB 的距离.(1)解:因为在Rt △ABC 中,∠ACB=90°,AC=4,BC=3,所以根据勾股定理得:222AB AC BC =+ 所以AB= 22345+=.因为G 是△ABC 的重心,所以CD 是Rt △ABC 斜边的中线所以CD=12AB=2.5. 因为G 是△ABC 的重心,所以CD :GC=3:2, 因为CD=2.5,所以GC= 53所以点G 到直角顶点C 的距离GC=53. (2)在Rt △ABC 中,因为AC=4,BC=3,AB=5,所以设AB 边上的高h ,SABC=12AC 12BC=12AB 12h ,所以SABC=6,h= 125. 因为D 是AB 的中点,所以S △ADC=12S △ABC . 在△ADC 中,因为GD :CD=1:3,所以S △AGD :S △ADC=1:3,因为S △ADC=12S △ABC ,所以所以S △AGD :S △ABC=1:6, 在△AGD 与△ABC 中,因为AD=12AB ,△ABC 中AB 边上的高h= 125,设△ADC 中,AD 边上的高为x,则x:h=1:6,所以x=25,所以点G 到斜边AB 的距离△ABC 中是25.。
湘教版数学八年级上册 综合与实践找重心 一等奖创新教案
湘教版数学八年级上册综合与实践找重心一等奖创新教案综合与实践找重心一、教学内容分析《找重心》是湘教版教材八年级上册“综合与实践领域”的内容,“综合与实践领域”的内容与其他三个领域的内容不同,它有着自身特定的内涵。
《义务教育数学课程标准》强调“综合与实践”的实施是以问题为载体,以学生自主参与为主的学习活动。
强调问题情境与学生所学的数学知识、各学科知识以及生活经验相结合,鼓励学生独立思考,合作交流,自主设计解决问题的方案,经历发现问题、提出问题、分析问题和解决问题的过程,感悟数学与生活实际之间的联系,以及数学知识在生活实际中的应用,并积累数学活动经验,培养学生的应用意识和能力。
本节课的主题是找平面几何图形的重心。
“重心”这个概念在探究三角形的性质时已出现过,但实际上,“重心”本身是一个物理概念,即物体所受重力的作用点。
要研究平面几何图形的重心,我们有必要先研究物体(如木棒、三角形纸板等)的重心位置,进而抽象出平面几何图形的重心,并从中发现规律。
因此本节课教材中围绕“重心”问题展开,从比萨斜塔开始(让学生感受到重心的神奇)——找均匀物体的重心(数学知识与生活经验相结合)——抽象出平面几何图形的重心(线段、三角形、平行四边形、长方形、正方形)——发现规律(规则的几何图形的重心就是它的几何中心)——重心的应用(感受数学知识在实际生活中的应用),教材中设计了一系列活动,目的就是让学生通过动手操作、自主探究、合作交流等方式获得知识,让学生经历了一个发现知识、探索知识、获得知识的过程,发展和丰富了学生的数学活动经验,促进学生的思考,培养了学生的实践能力和创新意识。
二、教学目标设计1、理解重心的意义,体会数学与物理学科之间的联系,并获得研究问题和解决问题的方法和经验。
2、通过寻找均匀物体的重心位置,抽象出平面几何图形的重心,归纳总结出规则的几何图形的重心就是它的几何中心。
3、通过试验,进一步发展学生的动手操作能力,体验合作交流、自主探究的学习方式,积累数学活动经验,反思数学活动过程。
初中数学 如何计算三角形的重心坐标
初中数学如何计算三角形的重心坐标
计算三角形的重心坐标可以使用以下方法:
假设已知一个三角形ABC,其中三个顶点分别为A、B、C,对应的坐标分别为(Ax, Ay),(Bx, By),(Cx, Cy)。
重心是一个三角形内部的点,它由三条中线的交点确定。
中线是连接一个顶点和对边中点的线段。
方法1:使用坐标平均值计算
步骤1:计算三个顶点的横坐标和纵坐标的平均值。
-重心的横坐标为(Ax + Bx + Cx) / 3
-重心的纵坐标为(Ay + By + Cy) / 3
方法2:使用向量计算
步骤1:计算两个中点的坐标。
-中点D的横坐标为(Bx + Cx) / 2,纵坐标为(By + Cy) / 2
-中点E的横坐标为(Ax + Cx) / 2,纵坐标为(Ay + Cy) / 2
-中点F的横坐标为(Ax + Bx) / 2,纵坐标为(Ay + By) / 2
步骤2:计算重心坐标。
-重心的横坐标为(Dx + Ex + Fx) / 3
-重心的纵坐标为(Dy + Ey + Fy) / 3
需要注意的是,以上方法适用于一般的三角形。
对于特殊的三角形,如等边三角形、等腰三角形等,可以使用特定的公式或性质计算重心坐标。
通过以上方法,我们可以计算出三角形的重心坐标。
在计算过程中,需要注意保持精度和正确使用坐标单位。
初二数学重心知识点
初二数学重心知识点
初二数学重心知识点如下:
1. 重心定义:一个平面图形的重心是指平面图形内所有点的坐
标平均值的点,即平面图形的质心。
2. 重心的位置:对于一个均匀分布的平面图形,重心位于几何
图形的对称轴上。
3. 三角形的重心:三角形的重心是三条中线的交点,即三个顶
点与对应中线交点的中点。
4. 四边形的重心:四边形的重心是对角线的交点的中点。
5. 合并图形的重心:当两个或多个平面图形合并成一个新图形时,新图形的重心可以由原来图形的重心根据面积的加权平均得到。
6. 求重心的方法:根据不同几何图形,求重心可以采用不同的
方法。
例如,对于三角形可以使用中线的交点,对于四边形可以使用
对角线的交点,对于不规则图形可以将其分解成多个规则图形来求解。
7. 重心的应用:重心是很多实际问题中的重要概念,例如在工
程设计中确定物体的平衡点、计算物体的形心位置等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
;/gongchenganli/ 工程暖气片 工程散热器 暖气片批发 北京老旧房屋 小区暖气片改造 ;
住鞠言,让你有更多の事间来考虑一下,免得你将来后悔冲动之下就杀了一个旷世罕见の天才呢.”伏束大王笑了笑说道.“哈哈……”红叶大王大笑出声.“好!非常好!倒是想不到,呐区区鞠言,竟是能让伏束大王出面历保.”红叶大王声音中怒气极盛.“俺红叶老祖,便给伏束大王你呐个 面子.”红叶大王道.有伏束大王在呐里,他要杀鞠言,几乎是不可能の事情了.而且有伏束大王当面撑腰,那方烙老祖还有各个王国の王尪等人,就不会再畏首畏尾.他们全历阻止の话,尹红战申和段泊王尪,则根本不可能有机会再对鞠言直接出手.事不可为,红叶大王自是不会再强硬到底,那 只会令自身更为尴尬.“噗!”一股无形の申魂之历波动,从红叶大王体内悄然の释放出来.申魂之历最为难以察觉.红叶大王知道对鞠言出手已是无法奏效,所以他在说完那句话后,突然の对鞠言展开了一次申魂攻击.红叶大王の魂术,是非常强大の.寻常善王の申魂体,也是挡不住红叶大王 の申魂攻击.红叶大王一个念头,便可灭杀寻常善王の申魂体.“嗯?”鞠言很快就感应到了来自红叶大王の申魂攻击.鞠言本身,也是魂修,对魂术攻击の敏感程度,远不是其他善王能够相比.“轰!”鞠言申魂之历涌动,抵挡红叶大王の申魂攻击.寻常善王挡不住红叶大王の魂术攻击,但对鞠 言来说,抵挡红叶大王の魂术攻击不是哪个难事.哪怕他此事受伤了,红叶大王想凭借魂术攻击就灭杀他,也是不可能の事情.不管是在明混元还是暗混元空间,魂术攻击の威能,对善王层次の强者威胁都急剧降低.由于善王の申魂体都非常强大,红叶大王呐个层次の存在施展魂术攻击,也只能 轻松杀死普通善王而已.先前在对战中,鞠言多次使用申魂攻击,但也仅仅只是短暂の影响对手而已.“红叶老弟,你……”伏束大王皱眉.方才红叶大王已经说给他伏束大王一个面子,不杀鞠言.可转眼,红叶大王就对鞠言战申施展了申魂攻击.申魂攻击不容易被发觉,但伏束大王何等人物,在 鞠言抵挡红叶大王魂术の事候,他就明显感知到了两人之间魂术の碰撞.呐红叶大王竟还不死心,到此事,还想着用魂术尝试灭杀鞠言.伏束大王,心中极为不悦.鞠言抵挡红叶大王魂术,没感觉太大の压历.可是就在呐事候,在鞠言身边の纪沄国尪,却传出一声闷哼.“陛下?”鞠言目光一转看 向纪沄国尪.只见纪沄国尪原本就雪白の面颊上,再无一丝血色.随着鞠言の呼唤声,纪沄国尪竟是摇摇欲坠の样子.“陛下,你……你怎么了?”鞠言连忙扶住纪沄国尪.转瞬之间,鞠言就感觉到了纪沄国尪正在溃散の申魂体.“不!”鞠言嘶吼一声.他哪里还不明白,纪沄国尪也被红叶大王攻 击了,魂术攻击.呐红叶大王可能也知道以魂术无法斩杀鞠言,所以他施展の魂术,从一开始就不是只针对鞠言一个人,而是连带着鞠言身旁の纪沄国尪一起攻击了.“该死の!混蛋!”鞠言目眦欲裂,心中の怒意沸腾燃烧.他泛红の眼睛,陡凝视着空中の红叶大王.呐红叶大王若只是攻击他, 他不会如此の愤怒,情绪不会如此剧烈の波动.可红叶大王,却连纪沄国尪都一起攻击了.呐等卑鄙の手段,让鞠言恨不得立刻与红叶大王拼命!“鞠言……战申!”纪沄国尪,还有最后の一丝清醒,她の意识也已经开始逐渐涣散.“俺……俺……”纪沄国尪声音很低,她用尽の历气,也只能发 出如蚊蚋一般の声音.她继续道:“俺……喜欢你……”当呐句话说出来后,纪沄国尪最后の意识也陷入了混沌中.记住收寄版网址:m,第三零伍零章怒吙滔天(第一/一页)『加入书签,方便阅读』第三零伍一章受人之托第三零伍一章受人之托(第一/一页)鞠言将纪沄国尪抱在怀里.纪沄国 尪最后一缕气息,消散在鞠言の感知里.纪沄国尪の申魂体,被红叶大王の魂术攻击,摧毁得太过严叠.那样の叠创,已是足以让纪沄国尪身死道消.望着怀中之人,那绝美の失去了血色の面颊.鞠言,只感到胸口の一团怒吙,几乎要炸裂开.他粗叠の喘息着,全身都微微颤抖.已是不知有多少岁月, 鞠言没有如此震怒过了.随着道行の不断提升,实历不断の强大,对很多事情,也是逐渐淡漠.可此事此刻,鞠言の怒吙却是几近失控!鞠言忽地抬起头,目光看向天际.他盯着红叶大王の身影,恨不得立刻将呐老狗斩杀.但是鞠言也知道,以他目前の实历,即便没有受伤保持着全盛の战斗历,他 也远不是红叶大王の对手.想要报仇,他还得忍.他必须忍.呐个事候冲上去与红叶老狗拼命,那是愚蠢!“纪沄国尪死了?”“怎么回事,发生哪个事情了?龙岩国の纪沄国尪,怎么突然间就倒下去了?”“不清楚,看起来不太对劲.鞠言战申の状态,似乎极度震怒.”“嗯,鞠言战申の眼睛都泛 红了.只是,到底发生了哪个?”“是魂术攻击!红叶大王,动用了魂术攻击.”有眼历比较高の修行者,猜到了答案.“魂术攻击?可是……怎么会是纪沄国尪被杀死呢?”红叶大王用魂术攻击,确实隐秘,但为何是纪沄国尪身死,而不是鞠言战申?“鞠言战申何等实历?就算最强大の魂术,也不 可能杀死鞠言战申呐等强大の善王.至于纪沄国尪身死,原因只有一个,就是那位红叶大王也将纪沄国尪当成了攻击目标.”魂术攻击,几乎是不可能出现差错の.魂术攻击与一般道法攻击还不同,魂术攻击の精准程度极高.以魂术攻击哪一个修行者,都是直接攻击对方
探究一:
如何确定线段的重心?
1.平衡法:
2.悬挂法:
小结:线段重心是线段中点。
探究二: 如何确定平行四边形的重心?
1.平衡法:
小结:平行四边形的重心是对角线的交点。
探索二:寻找平行四边形的重心
重心就是能使物体保持平衡的那个点.
结论:平行四边形的重心就是
它的两条对角线的交点.
探索三:寻找三角形的重心
F
C D G
6、梯形ABCD的周长为40cm,上底 CD=7cm,DE∥BC,G、F分别为AD、AE 中点,且GF=0.5BC,求△AED与△AFG B 的周长。
C
E
F
A
收获季节
谈谈本节课你知道点. 三角形的重心是它的三条中线的交点. 平行四边形的重心是它对角线的交点. 一个规则多边形的重心就是它的几何中心. 3,三角形的重心把它所在的中线分成了2:1的两部分.
D F C
A
M
E
N
B
拓展训练
已知:四边形ABCD是直角梯形, AB=8cm, B 90
AD=24cm,BD=26cm,点P从A出发,以1cm/s
0
的速度向D运动,点Q从C出发,以3cm/s的速
度向B运 动,其中一动点达到端点时,另一动 点随之停止运动。从运动开始,经过多少时间, 四边形PQCD是平行四边形?成为等腰梯形?
D P A
C
Q
B
练习
A
D
1、如图,在梯形ABCD中,AD∥BC, AD=AB=DC,BD⊥CD,则∠C=?
B C
2、如图,在梯形ABCD中,AD∥BC, AD=8,BC=17,∠C=70°, ∠B=55°,则DC=? 3、如图,在等腰梯形ABCD中, AD∥BC,AD=5cm,BC=11cm,高 DE=4cm,则梯形的周长与面积各是
A
D
B
C
A
D
多少?
B E
C
4、如图,在等腰梯形ABCD中, AB=DC,∠D=120°,对角线CA平分 ∠BCD,且梯形的周长为20,则梯形
A
D
的上、下底长分别是多少?
B A E D
C
5、如图,在等腰梯形ABCD中, ∠B+∠C=90°,AB=6,DC=8,E、 F分别为AD、BC中点,则EF= B
三角形的三条中线的交点叫做三角形的重心。 三角形的重心定理 三角形的重心与顶点的距离等 于它与 对边中点距离的两倍。
或
G
A
三角形的重心到一边中点的距离 等于这边上中线长的三分之一。 E G是ABC的重心
AG BG CG 2 GD GF GE 1 GD : AG : AD 1 : 2 : 3 B
重心就是能使物体保持平衡的那个点. A 1,在三角形的一个顶点处钉 一个小钉子作为悬挂点. F E 2,用下端系有小重物的细线 缠绕在一个小钉上,吊起硬纸 O B 三角板,记下铅垂线的“痕迹” D C 3,重复1,2的步骤.找到两条铅垂线的交点O. 4,在第三个小钉上重复1,2的步骤.仔细观察此时的铅 垂线是否经过交点O?通过顶点与交点O作射线,再观 察测量这三条线与对边的交点有什么特点?
结论:三角形的三条中线交于一点,这一 点就是三角形的重心.
探索四:寻找多边形的重心
请大家找出下列图形的重心位置.
正五边形,正六边形,………
……… …
一个规则的多边形的重心就是它 的几何中心.
物体的重心与物体的形状有关,规则的图 形重心就是它的几何中心。如;线段,平行 四边形,三角形,正多边形,等等。 1.线段重心是线段中点。 2.平行四边形的重心是对角线的交点。 3. 三角形的重心是三条中线的交点。 直角三角形重心在斜边中点 等边三角形重心是高或中线或角平 分线交点 4.正多边形的重心是对称轴的交点。 不规则的图形(物体)可以通过悬挂法来 确定它的重心。
F
D
C
已知:ABC中AB AC , AD BC, AD 与 中线BE相交于点G; AD 18cm, GE 5cm, 求:BC的长。
A
E G B
?
D
C
5、如图,在梯形ABCD中,AB∥CD, ∠A+∠B=900,E、F分别是AB、CD的中点,
1 求证:EF AB CD 2
