基于CFD_CSD耦合的机翼跨音速颤振计算_张苏华
大展弦比柔性机翼气动弹性分析中的气动力方法研究进展

大展弦比柔性机翼气动弹性分析中的气动力方法研究进展杨超;杨澜;谢长川【摘要】近20年来长航时飞行的需求强烈,大柔性飞行器的几何非线性气动弹性问题逐渐凸显,使得气动弹性力学面临新的挑战.本文针对大展弦比大变形的柔性飞行器,调研和分析了目前几何非线性气动弹性工程研究领域中主要使用的气动建模方法,着重介绍基于片条理论、面元法和计算流体力学(Computational Fluid Dynamics,CFD)技术等气动建模方法在静、动气动弹性分析中的主要特点、研究现状与应用状况,并对大展弦比大变形机翼的气动弹性分析中气动力方法的发展提出若干建议,供气动弹性基础研究和工程应用研究人员参考.【期刊名称】《空气动力学学报》【年(卷),期】2018(036)006【总页数】10页(P1009-1018)【关键词】气动弹性;大展弦比机翼;几何非线性;气动建模【作者】杨超;杨澜;谢长川【作者单位】北京航空航天大学航空科学与工程学院,北京 100191;航空器先进设计技术工信部重点实验室,北京 100191;北京航空航天大学航空科学与工程学院,北京 100191;航空器先进设计技术工信部重点实验室,北京 100191;北京航空航天大学航空科学与工程学院,北京 100191;航空器先进设计技术工信部重点实验室,北京100191【正文语种】中文【中图分类】V211.470 引言自20世纪90年代末起,由于长航时无人机、大型运输机和大型客机等长航时飞行器的高性能要求,高升阻比和轻质结构的设计充分体现在大展弦比机翼设计中,随之而来的一类新的非线性气动弹性问题开始受到关注,即大柔性飞行器的大变形几何非线性气动弹性问题。
采用轻质材料的大展弦比机翼是该问题的主要研究对象,其力学本质在于结构求解中的小变形假设不再适用,结构受力变形后的平衡态相对未变形的结构呈现明显的几何差异,结构的承载和变形状态引起的几何非线性因素使得结构静、动特性发生改变,并且改变静、动气动弹性耦合关系,从而使气动弹性的研究及应用面临新的挑战。
基于CFD/CSD耦合算法的机翼颤振分析

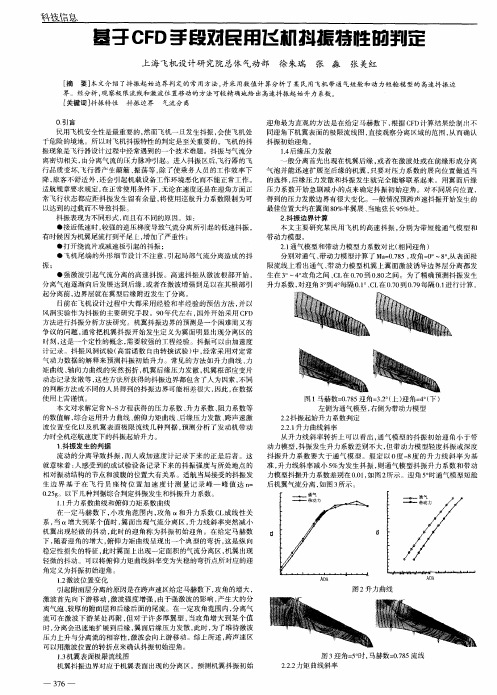
算 方法 的一 个 标 准模 型 , 有 着 较 为完 备 的风洞 试 它 验数 据[ 。 5 AGAR 4 5 6 翼展 弦 比是 1 6 , 根 ] D 4 . 机 .5梢 比为 0 6 , 长 0 7 2m, 弦 长 0 5 87m, .6 展 . 6 根 . 5 四分
维普资讯
20 2月 08年
西 北 工 业 大 学 学 报
J u n l fNo t we t r l t c n c l o r a r h s e n Po y e h ia Un v r iy o i e st
Fe b.
一——■——■ 一 一
( a 一阶模态 ( t ) -g ̄ ) () 二阶模态 ( 阶扭 转 ) b 一 ( 三阶模 态 ( c ) 二阶弯 曲 ) ( 四阶模态 ( d ) 二阶扭转 )
图 1 A GAR 4 . 翼前 四 阶模 态 变 形 图 D 4 56机 收 稿 日期 ;0 7O —7 2 0 一11 基金项 目; 国家 自然 科 学 基 金 ( 00 0 2 资 助 9450)
之 一 弦 线 后 掠 角 为 4 。 机 翼 采 用 NAC 5 0 5该 A6 A0 4 翼型 。采用 4节点 等参 壳单 元建 立该机 翼 的有 限元
飞行器 结 构 的变形 及 流 场 的 变化 , 且 它 还可 以计 并 算较为 复杂的外 形 。本文 首先 利用 有 限元 方法对机 翼结 构 进行 模 态分 析 ; 后 采 用 Eue 然 lr方程 计 算 非
20 08
第2卷第1 6 期
V o1 26N o. . 1
基 于 C D/ S 耦 合算 法 的机 翼 颤 振 分 析 F CD
基于CFD手段对民用飞机抖振特性的判定
迎 角最为直观 的方 法是在给定 马赫数 下 , 根据 C D计算结果 绘制 }不 F “ 同迎 角下机翼 表面的极限流线图 , 直接观察分离区域 的范 同, 从而确认 抖振 初 始迎 角 。 1 后缘压 力发散 . 4 般分离首先 出现在机翼后 缘 , 或者在 激波处或在前缘 形成分离 气 泡并能迅速 扩展 至后缘 的机翼 , 只要对压 力系数的展 向位 置做适 当 的选择 , 后缘压 力发散和抖振 发生就完全 能够联系起来 。用翼面后缘 压力系数开始 急剧减小 的点来 确定抖振初 始迎角。对不 同展向位置 , 得到的压力发散边界有很大变化 。一般情况预跨声速抖振开始发生 的 最佳位置大约在翼 面 8%半翼展 、 0 当地弦长 9 %处 。 5 2抖振边界计算 . 本文主要研究 某民用飞机 的高速抖振 , 分别为带短 舱通气模型 和 带 动 力模 型 。 21 .通气模 型和带动 力模型力 系数对 比( 同迎角 ) 相 分别对 通气 、 带动力模型计算 了Ma 07 5, = ,8 攻角= 。 。 O 一8, 从表 面极 限流线上看 出通气 、 带动力模 型机翼上翼 面激波诱导边 界层分离都 发 生在 3 ~4 攻角之间 、 L在 07 到 08 之 间。为了精 确预测抖振 发生 。 。 C .0 .O 升力系数 , 对迎 角 3到4 每隔 01 、 L O7 到 07 每隔 01 。 。 .。C 在 .0 .9 .进行计算 。
流动的分离 导致抖振 , 而人 或加速度计记 录下来 的正是后 者 。这 就意味着 : 感受到 的或试 验设 备记录下来 的抖振强度与所 处地点 的 人 相对振动结构的节点和波腹的位置大有关系 。适航 当局接受 的抖振发 生 边 界基 于 在 飞 行 员 座 椅位 置 加 速 度 计 测 量记 录峰 一 峰 值 达 n = 0 5 。以下几种判据综合判定抖振发生和抖 振升力系数 。 .g 2 I 升力系数 曲线 和俯仰 力矩系数 曲线 . 1 在一定 马赫 数下 , 小攻 角范 围内 , 攻角 o和升 力系数 C L L成线性关 系 , 增大到某个值时 , 面出现气 流分 离区 , 当 翼 升力线斜 率突然减小 机翼 出现轻 微的抖动 , 时的迎角称为抖 振初始迎角 。在 给定马赫数 此 下, 随着 迎角的增大 , 仰力矩 曲线呈 现出一个典型 的弯 折 , 俯 这是纵 向 稳定性损失的特征 , 此时翼面 上出现一定面积 的气流分离 区, 机翼 出现
基于CFD

第8卷㊀第6期2023年11月气体物理PHYSICSOFGASESVol.8㊀No.6Nov.2023㊀㊀DOI:10.19527/j.cnki.2096 ̄1642.1088基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析李泳德ꎬ㊀郭㊀力ꎬ㊀季㊀辰(中国航天空气动力技术研究院ꎬ北京100074)CharacterizationofTransonicAerodynamicDampingofRocketsBasedonCFD/CSDCouplingLIYong ̄deꎬ㊀GUOLiꎬ㊀JIChen(ChinaAcademyofAerospaceAerodynamicsꎬBeijing100074ꎬChina)摘㊀要:随着新型大推力火箭的发展ꎬ弯曲模态频率的不断降低ꎬ以及流动分离和跨声速飞行时产生的激波震荡等因素ꎬ其在跨声速飞行过程中更容易出现非定常振动发散ꎮ文章以某带助推的运载火箭模型为研究对象ꎬ通过数值计算获取火箭强迫振动时的气动阻尼ꎬ并对影响火箭气动阻尼的因素进行了分析ꎮ包括结构节点位置㊁振动振幅大小㊁脉动压力等ꎮ研究表明:助推主要起到增大气动阻尼的作用ꎻ前节点主要影响收缩段的气动阻尼ꎻ振动振幅大小和脉动压力对气动阻尼的影响可忽略不计ꎮ关键词:气动阻尼ꎻ数值计算ꎻ跨声速ꎻ气动弹性ꎻ运载火箭㊀㊀㊀收稿日期:2023 ̄09 ̄25ꎻ修回日期:2023 ̄10 ̄23第一作者简介:李泳德(1995 ̄)㊀男ꎬ工学硕士ꎬ助理工程师ꎬ主要研究方向为气动弹性分析ꎮE ̄mail:562064169@qq.com通信作者简介:季辰(1982 ̄)㊀男ꎬ工学博士ꎬ研究员ꎬ主要研究方向为气动弹性力学ꎮE ̄mail:jichen167@hotmail.com中图分类号:V475.1㊀㊀文献标志码:AAbstract:Withthedevelopmentofnewhigh ̄thrustrocketsꎬthedecreasingfrequencyofthebendingmodesoftherocketꎬaswellasthefactorssuchasflowseparationandshockoscillationsgeneratedduringtransonicflightmakeitmorepronetonon ̄constantvibration.Inthispaperꎬalaunchvehiclemodelwithboostwastakenastheresearchobjectꎬandtheaerody ̄namicdampingoftherocketduringforcedvibrationwasobtainedthroughnumericalcalculation.Thefactorsaffectingtheaerodynamicdampingoftherocketwereanalyzedꎬincludingthepositionofstructuralnodesꎬthemagnitudeofvibrationam ̄plitudeꎬpulsatingpressureandsoon.Thestudyshowsthattheboostmainlyplaystheroleofincreasingaerodynamicdamp ̄ingandthefrontnodemainlyaffectstheaerodynamicdampingofthecontractionsection.Thevibrationamplitudesizeandthepulsatingpressurehaveanegligibleeffectontheaerodynamicdamping.Keywords:aerodynamicdampingꎻnumericalcalculationꎻtransonicꎻaeroelasticityꎻlaunchvehicle引㊀言通常情况下人们认为气动力对火箭的振动起到阻尼作用ꎬ即气动阻尼为正值ꎮ然而随着大推力火箭发展ꎬ火箭的长细比逐渐加大ꎬ导致弯曲刚度越来越小ꎬ同时为了满足有效载荷的外形要求ꎬ火箭头部整流罩尺寸不断加大ꎬ后续箱体的直径却保持不变ꎬ形成了典型的锤头体外形ꎮ国内外大量的火箭研制经验表明[1 ̄9]ꎬ对于此类锤头体外形火箭的气动设计ꎬ必须要进行动态气动载荷与动态气弹稳定性分析ꎬ否则设计的疏忽可能会导致火箭结构出现毁灭性的破坏进而导致发射失败ꎮ目前常用的衡量气弹稳定性的方法是通过风洞试验来获取气动阻尼系数ꎮ早在1963年ꎬ美国国家航空航天局Ames研究中心(NASAAmesRe ̄searchCenter)采用半刚性模型开展试验研究[10]ꎬ获取火箭头部的气动阻尼来评估其稳定性ꎬ但这只能用来模拟火箭弯曲振型前节点之前部分的结构动力学特性ꎮ直到兰利研究中心(NASALangleyResearchCenter)开发了全弹性模型气动阻尼试验气体物理2023年㊀第8卷技术ꎬ其可以模拟整体的结构动力学特性以及气动外形ꎬ并应用于多款运载火箭研制[11 ̄15]ꎮ国内ꎬ中国航天空气动力技术研究院对气动阻尼问题开展过较多的研究[16 ̄20]ꎬ从模型设计方法㊁模型制作工艺㊁试验机构设计和数据处理等诸多方面ꎬ逐步改进实现了从半刚性模型到全弹性模型的过渡ꎬ并在多个型号上得到验证ꎮ然而通过风洞试验研究气动弹性问题ꎬ技术难度大ꎬ试验成本高ꎬ同时几乎不可能开展全尺寸试验ꎮ因此通过数值计算的方法开展相关研究是另一种重要的手段ꎮ刘子强等[21]实现了通过数值计算确定气动阻尼系数的技术和方法ꎬ并与试验结果进行对比ꎬ证实了该方法的可靠性ꎮ冉景洪等[22]通过模态数据结合准定常理论的方法分析了减阻杆加后体这一弹性结构的气动阻尼ꎬ结果表明减阻杆造成的分离流会对后体的气动阻尼系数产生影响ꎮ朱剑等[23]针对新一代捆绑式运载火箭发展了非结构网格下的气动阻尼计算方法ꎬ并分析了攻角㊁Mach数等参数对气动阻尼的影响ꎮ本文在之前的计算方法[23]的基础上采用IDDES模型ꎬ考虑脉动压力的影响ꎬ通过强迫振动的方式ꎬ针对捆绑式运载火箭的某一特定模态进行数值计算仿真ꎬ研究前节点位置ꎬ振动振幅ꎬ脉动压力等参数对气动阻尼的影响规律ꎮ1㊀计算方法图1为本文所用的捆绑式运载火箭的计算模型ꎬ是典型的锤头体结构ꎮ在跨声速阶段ꎬ其头部会产生激波造成激波边界层干扰ꎬ而在锤头体外形的过渡段会出现气流分离ꎮ为探究各部分气动阻尼的变化ꎬ将整个箭体分为头部㊁过渡段㊁弹身3个部分ꎮ图1㊀表面网格及区域划分Fig.1㊀Surfacegridandregiondivision1.1㊀流场仿真模型本文分别用Reynolds平均法(Reynolds ̄averagedNavier ̄StokesꎬRANS)和改进的延迟分离涡模拟(improveddelayeddetached ̄eddysimulationꎬID ̄DES)[24 ̄25]进行计算ꎬ在RANS方程中ꎬ将变量分为平均值和波动值两部分ꎬ对于速度分量有ui=ui+uᶄi其中ꎬi=1ꎬ2ꎬ3ꎬui和uᶄi分别代表平均量和波动量ꎬ对于压强和其他标量也采用类似的形式ꎬ将这种形式代入连续性方程和动量方程中ꎬ并写成张量形式∂ρ∂t+∂∂xi(ρui)=0(1)∂∂t(ρui)+∂∂xj(ρuiuj)=∂p∂xi+∂∂xjμ∂ui∂xj+∂uj∂xi-23δij∂uk∂xkæèçöø÷éëêêùûúú+∂∂xj(-ρuᶄiuᶄj)(2)其中ꎬiꎬjꎬk可分别取1ꎬ2ꎬ3ꎻρ是密度ꎻt是时间ꎻ当i=j时δij取0ꎬ否则取1ꎮ式(1)㊁(2)是RANS方程ꎬ由方程可知RANS方法将湍流脉动对平均流动的作用模化为Reynolds应力项即-ρuᶄiuᶄjꎬ之后采用湍流模型进行封闭ꎬ本文采用的湍流模型为SSTk ̄ω模型ꎬ其输运方程为∂∂t(ρk)+∂∂xi(ρkui)=∂∂xjΓk∂k∂xjæèçöø÷+Gk-Yk∂∂t(ρω)+∂∂xi(ρωui)=∂∂xjΓω∂ω∂xjæèçöø÷+Gω-Yω其中ꎬk和ω分别代表湍流动能和湍流耗散率ꎬΓk和Γω分别代表k和ω的有效扩散系数ꎬGk和Gω分别代表k和ω的生成率ꎬYk和Yω分别代表k和ω的耗散率ꎮ因此RANS方法只能计算大尺度的平均流动ꎬ本文采用IDDES方法计算脉动压力对气动阻尼的影响ꎮIDDES方法是由分离涡模拟(detached ̄eddysimulationꎬDES)方法改进而来ꎬ其本质思想与DES方法相同ꎬ是想以网格尺度和模型中的特征尺度隐式划分RANS和大涡模拟(large ̄eddysimulationꎬLES)区域ꎬ使其既能处理RANS方法无法得到的脉动场ꎬ也能降低LES方法在模拟高Reynolds数流动时所需的计算资源ꎮ区别在于当边界层较厚或者分离区域较窄时ꎬDES方法会出现如模型应力损耗(modeledstressdepletionꎬMSD)ꎬ网格诱导分离(grid ̄inducedseparationꎬGIS)以及对数层不匹配(logarithmic ̄layermismatchꎬLLM)问题[24]ꎬ而IDDES模型通过改良计算区域划分ꎬ结合延迟分离涡模拟(delayeddetached ̄eddysimulationꎬDDES)和03第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析壁面模型大涡模拟(wall ̄modeledlarge ̄eddysimula ̄tionꎬWMLES)ꎬ定义新的长度尺度解决了这些问题ꎬ具体公式详见文献[25]ꎮ流场网格如图2㊁图3所示ꎬ边界层采用棱柱层结构ꎬ并调整第1层网格高度使得y+小于1ꎬ远场部分采用六面体结构网格ꎬ与边界层的过渡层采用非结构网格ꎮ整体网格单元数量为4.2ˑ106ꎮ图2㊀y方向截面网格示意图Fig.2㊀Schematicdiagramofcross ̄sectionalgridinthey ̄direction图3㊀x方向截面网格示意图Fig.3㊀Schematicdiagramofcross ̄sectionalgridinthex ̄direction物面边界条件为无滑移壁面条件ꎬ远场采用压力远场边界条件ꎬ湍流模型采用SSTk ̄ω模型ꎬ采用密度基求解ꎬ气体黏性采用Sutherland定律ꎬ空间离散采用2阶迎风格式ꎬ对流通量采用Roe格式ꎮ1.2 结构分析模型结构与流场耦合分析过程中ꎬ结构部分可以采用模态方法描述ꎮ结构模态可以通过有限元方法与结构模态试验方法获得ꎮ本文采用有限元分析结果获得的模态ꎬ图4所示为结构的前3阶模态ꎬ本文只分析计算结果中气动阻尼最小的第2阶模态ꎮ(a)f=1.200Hz(b)f=2.460Hz(c)f=2.957Hz图4㊀结构的前3阶模态Fig.4㊀Firstthreemodesofthestructure由于火箭结构外形简单ꎬ一般不考虑其扭转影响ꎬ因此可以将其简化为简单的梁模型ꎬ这样就可以给出其模态振动方程q㊆i+2biωiq˙i+ω2iqi=fi(3)式中ꎬqi为第i阶模态的广义位移ꎬbi为第i阶模态的结构阻尼系数ꎬωi为第i阶模态的固有频率ꎬ13气体物理2023年㊀第8卷fi为第i阶模态下质量归一化的广义气动力ꎮ若将fi按照Taylor展开并略去高阶项ꎬ可以将其转化为气动阻尼项与气动刚度项的形式ꎬ则式(3)可写为q㊆i+2(bi+Bi)ωiq˙i+(Ki+1)ω2iqi=0(4)式中ꎬBi为气动阻尼系数ꎬKi为气动刚度系数ꎬ研究表明[26]ꎬ气动刚度相对于结构刚度为小量可以忽略不计ꎬ而在计算中结构阻尼往往设置为0ꎬ因此气动阻尼可以直接反映其气弹稳定性ꎮ1.3㊀气动阻尼分析原理气动阻尼的分析可以采用强迫振动或者自由振动的方式进行ꎬ这两种方法获得的时域数据不同ꎬ提取气动阻尼的方式也不同ꎮ强迫振动方法初始演化过程较短ꎬ因此计算量较小ꎬ同时能够分析某一种振动形式的气动阻尼ꎬ明确该振动形式是收敛还是发散ꎮ分析过程中能够获得不同部位与部件的气动阻尼ꎮ但是对于多模态相互作用引起的发散(例如颤振)较难预测ꎮ自由振动方法需要一定的自由演化时间才能够对时域数据进行分析ꎬ不过自由振动方法能够获得最能够吸收能量的模态及其振动频率ꎮ对于本研究所关注的问题ꎬ气动载荷对结构振动的过程中气动阻尼的影响较大ꎬ而对气动刚度与气动质量影响较小ꎬ即结构的固有振动频率受到来流的影响较小ꎬ其稳定性问题主要由气动阻尼的正㊁负引起ꎬ所以采用强迫振动方法分析ꎮ强迫振动下结构做简谐模态振动qi(t)=Asin(ωit)式中ꎬA表示振动的振幅ꎬ将其代入计算气动力的公式中[21]并做正交积分可得Bi=ʏl0Bx(x)dx=-1MiAω2iTʏl0ʏt0+Tt0G(xꎬt)cos(ωit)dtdx(5)式中ꎬMi为第i阶模态的模态质量ꎬT为整数倍周期ꎬG为广义气动力ꎮ根据式(5)便可以得到局部或分区域的气动阻尼ꎮ1.4㊀耦合计算流程首先进行模态分析ꎬ以确定结构的模态频率与振型ꎬ用以设计强迫振动的频率和振幅ꎮ非定常流场计算前先进行定常流场计算ꎬ来加快非定常计算的演化速度并增强收敛性ꎬ结构节点位移通过径向基函数(RBF)插值方法[27]映射到气动网格节点上ꎬ来进行网格的变形ꎬ这里径向基函数选用WendlandC2ꎬ如下所示φ(x)=(1-x)4(4x+1)最后将计算出来的广义力提取出来ꎬ截取演化完毕的整数倍周期ꎬ进行气动阻尼计算ꎮ耦合计算流程图如图5所示ꎮ图5㊀耦合计算流程图Fig.5㊀Flowchartofcoupledcalculation2㊀结果分析与讨论2.1㊀流场分析结果计算的来流Mach数范围为0.7~1.2ꎮ其中中截面的压力分布如图6所示ꎮ可以看出在头部出现了膨胀波以及跨声速激波ꎬ在过渡段存在流动分离ꎬ随着Mach数的增大ꎬ头部低压区域逐渐扩张ꎬ并且能明显看到ꎬ在流动再附的位置产生了再附激波ꎮ(a)Ma=0.7023第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析(b)Ma=0.75(c)Ma=0.80(d)Ma=0.85(e)Ma=0.88(f)Ma=0.90(g)Ma=0.92(h)Ma=0.96(i)Ma=0.9833气体物理2023年㊀第8卷(j)Ma=1.00(k)Ma=1.05(l)Ma=1.10图6㊀不同Mach数下的中截面压力分布Fig.6㊀PressuredistributioninthemiddlesectionatdifferentMachnumbers2.2 气动阻尼分布通过上述流场分析ꎬ可以看出火箭不同部位流动结构并不相同ꎬ在头部与箭身上ꎬ流动主要为附着流动ꎬ而在过渡段会出现较为复杂的波系结构以及流动分离ꎮ针对不同的流动结构随流向站位x的变化ꎬ设该位置上广义力与广义位移的相位差为φ(x)ꎬ并且简谐振动没有引入其他模态的广义力ꎬ则广义力的表达式为G(xꎬt)=Fgen sin[ωt+φ(x)]+F0(6)其中ꎬFgen为广义力的振动幅度ꎬF0为广义力的常数偏移量ꎮ将式(6)代入到式(5)中得到B(x)=-FgenMAω2Tʏt0+Tt0sin[ωt+φ(x)]cos(ωt)dt其中ꎬ广义力的常数偏移量F0的积分为0ꎬ因此省略ꎮ通过将等式中的正弦函数部分进行和差化积得到B(x)=-FgenMAω2Tʏt0+Tt0sin(ωt)cos[φ(x)]cos(ωt)dt+[ʏt0+Tt0sin[φ(x)]cos(ωt)cos(ωt)dt](7)式(7)中第1部分在整个周期中的积分为0ꎬ只有第2部分保留ꎬ因此得到B(x)=-Fgensin[φ(x)]MAω2Tʏt0+Tt0cos2(ωt)dt(8)式(8)中积分部分恒为正值ꎬ决定整个气动阻尼的部分只有相位角φ(x)的正弦值sin[φ(x)]ꎬ为了能够更加直观地获得相位角与气动阻尼B之间的关系ꎬ须将符号转化为对应的正弦函数转角ꎬ根据正弦关系ꎬ此转角为πꎬ因此得到B(x)=-Fgen(x)sin[φ(x)+π]MAω2Tʏt0+Tt0cos2(ωt)dt(9)图7为气动阻尼变化曲线ꎬ可以看出随着Mach数的增大ꎬ整体气动阻尼先增大后减少ꎬ在Mach数为0.98时达到最大值ꎬ过渡段与箭体的气动阻尼变化趋势与整体基本相同ꎬ而头部区域则不同ꎬ是随着Mach数的增大一直增大ꎬ只是增长速率变缓ꎮ图7㊀有助推时气动阻尼变化曲线Fig.7㊀Aerodynamicdampingchangecurvewithboost根据式(9)ꎬ得到相位角与气动阻尼B之间的关系为:当φ(x)ɪ(-πꎬ0)时ꎬ相位角滞后ꎬ气动阻尼B为负值ꎻ当φ(x)ɪ(0ꎬπ)ꎬ相位角提前ꎬ43第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析气动阻尼B为正值ꎻ为当φ(x)=0时ꎬ无相位角差别ꎬ气动阻尼B为0ꎮ在过渡段上ꎬ复杂的波系结构以及流动分离ꎬ使得气动力与结构位移之间会出现较为明显的迟滞现象ꎬ从而导致相位角φ(x)ɪ(-πꎬ0)ꎬ由此在过渡段上产生了负的气动阻尼ꎮ计算过程中的广义力与广义位移随时间变化曲线如图8所示ꎬ可以看出所有工况计算结果都表现良好ꎬ需要注意的是在非定常计算初期ꎬ演化的不完全导致广义力存在一些突变异常的结果ꎬ计算气动阻尼时须剔除ꎬ选择后面演化完全的周期ꎮ本文计算了9个周期ꎬ剔除了第1个周期出现的错误结果ꎬ采用后8个周期进行气动阻尼分析ꎮ强迫运动振幅为芯级直径的0.5%ꎮ(a)Ma=0.70㊀㊀㊀(b)Ma=0.75(c)Ma=0.80㊀㊀㊀(d)Ma=0.85(e)Ma=0.88㊀㊀㊀(f)Ma=0.9053气体物理2023年㊀第8卷(g)Ma=0.92㊀㊀㊀(h)Ma=0.96(i)Ma=0.98㊀㊀㊀(j)Ma=1.00(k)Ma=1.05㊀㊀㊀(l)Ma=1.10图8㊀不同工况下的广义力与广义位移随时间变化曲线Fig.8㊀Timedependentcurvesofgeneralizedforceandgeneralizeddisplacementunderdifferentoperatingconditions2.3㊀气动阻尼影响因素2.3.1㊀有无助推对气动阻尼的影响捆绑式运载火箭相比于传统的运载火箭ꎬ最大的区别就是在尾部四周捆绑了助推器ꎬ使得其流场特性变得复杂ꎬ因此须分析其对气动阻尼的影响ꎮ图7㊁图9分别为有无助推时气动阻尼变化曲线ꎬ可以看出随着Mach数的增大整体气动阻尼先增大后减少ꎬ在Mach数为0.98时达到最大值ꎬ过63第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析渡段与箭体的气动阻尼变化趋势与整体基本相同ꎬ而头部区域则不同ꎬ是随着Mach数的增大一直增大ꎬ只是增长速率变缓ꎮ对比两个图可知ꎬ助推主要起增大气动阻尼的作用ꎮ还可以看出有无助推情况下头部的气动阻尼变化很小ꎬ意味着在箭体尾部施加控制很难影响到头部的气动阻尼ꎬ特别是在超声速流场中ꎮ图9㊀无助推时气动阻尼变化曲线Fig.9㊀Aerodynamicdampingchangecurvewithoutboost2.3.2㊀前节点位置影响为了考察前节点位置变化对气动阻尼的影响ꎬ在保持振动频率不变㊁头部最大振型位置与振幅不变的条件下移动前节点ꎬ变化后的振型如图10所示ꎮ(a)Frontnodeafterthetransitionregion(b)Frontnodeinthetransitionregion(c)Frontnodebeforethetransitionregion图10㊀前节点变化后的振型Fig.10㊀Vibrationmodeafterthechangeofformernode根据对计算结果的分析分别获得了不同前节点位置的整体气动阻尼对比与过渡段气动阻尼对比ꎬ如图11㊁图12所示ꎬ可以看出前节点位置的改变并没有影响整体气动阻尼随Mach数增大而增大的趋势ꎬ且前节点在过渡段上与过渡段前的整体气动阻尼相差不大ꎬ而前节点在过渡段后的整体气动阻尼要高于另两种情况ꎬ因此过渡段与头部放在同一侧有助于提高气动阻尼ꎮ过渡段的气动阻尼会随着前节点的变化发生剧烈改变ꎬ前节点在过渡段前后随Mach数增大的变化规律相反ꎬ节点前后的振动相位变化导致不同节点位置过渡段的振动相位不同ꎬ进而导致气动阻尼发生变化ꎮ图11㊀不同节点位置的整体气动阻尼Fig.11㊀Overallaerodynamicdampingatdifferentnodepositions图12㊀不同节点位置的过渡段气动阻尼Fig.12㊀Aerodynamicdampingofthetransitionregionatdifferentnodepositions2.3.3㊀强迫振动振幅大小对气动阻尼的影响为了考察强迫振动振幅大小对气动阻尼的影响ꎬ在保证流场结构不发生改变的前提下ꎬ振动振幅分别为原来的一半和两倍ꎬ根据工程经验ꎬ如果振幅超过芯级直径的5%ꎬ则须考虑流场结构改变所造成的影响ꎮ图13㊁图14分别为不同振幅下的整体与头部气动阻尼ꎮ73气体物理2023年㊀第8卷图13㊀不同振幅下整体气动阻尼Fig.13㊀Overallaerodynamicdampingatdifferentamplitudes图14㊀不同振幅下头部气动阻尼Fig.14㊀Aerodynamicdampingoftheheadregionatdifferentamplitudes可以发现改变振幅无论是对整体气动阻尼还是头部气动阻尼来说变化都很小ꎬ这意味着气动阻尼的大小主要取决于气动力与结构振动的相位差ꎬ不依赖于振动幅度的大小ꎮ2.3.4㊀脉动压力对气动阻尼的影响为了模拟出脉动压力的影响ꎬ采用IDDES方法对火箭气动阻尼进行计算ꎬ计算来流Mach数为0.92ꎬ计算过程中的广义力与广义位移如图15所示ꎬ相较于图8可以看出广义力随时间变化曲线并不光滑ꎬ脉动压力的存在导致广义力由多个频率叠加而成ꎮ由于第2阶模态的频率为2.46Hzꎬ而由分离流㊁激波振荡等引起的脉动压力频率往往远大于此频率ꎬ因此这里选择3.5Hz为分界ꎬ将高于3.5Hz的部分视为由抖振脉动压力引起的广义力ꎬ低于3.5Hz的部分视为强迫振动引起的广义力ꎬ通过低通滤波把高于3.5Hz的广义力滤掉ꎬ可以获得由强迫振动引起的广义力与广义位移变化曲线ꎬ如图16所示ꎬ通过此广义力计算的气动阻尼为2.08ɢꎮ同样地ꎬ进行高通滤波将低于3.5Hz的广义力滤掉ꎬ可以获得由抖振脉动压力引起的气动阻尼为(2.94ˑ10-3)ɢꎬ由此得到脉动压力引起的气动阻尼变化为0.14%ꎬ可以忽略不计ꎮ同时使用RANS方法计算的气动阻尼为2.07ɢꎬ与IDDES的计算结果相比误差约为(2.94ˑ10-3+2.08-2.07)/2.07ʈ0.48%ꎬ这说明针对气动阻尼的模拟ꎬ抖振引起的脉动压力对气动阻尼的计算结果影响很小ꎬ起主要作用的还是广义力的变化ꎬ该变化由强迫振动引起的结构边界变化所导致ꎮ图15㊀基于IDDES的广义力与广义位移变化曲线Fig.15㊀VariationcuresofgeneralizedforceandgeneralizeddisplacementbasedonIDDES图16㊀滤波后的广义力与广义位移变化曲线Fig.16㊀Variationcuresofgeneralizedforceandgeneralizeddisplacementvariationcurveafterfiltering3㊀结论本文通过数值计算方法研究了火箭的气动阻尼特性ꎮ根据流动特征分析与理论推导ꎬ发现火箭过渡段几何外形的收缩导致该区域出现复杂的分离与激波结构ꎬ从而造成了气动力相对于结构振动83第6期李泳德ꎬ等:基于CFD/CSD耦合的火箭跨声速气动阻尼特性分析相位的滞后ꎬ导致了该区域为气动负阻尼ꎬ即气动不稳定性的主要来源ꎮ在此机理的基础上ꎬ分析了前节点位置㊁振动振幅㊁脉动压力等因素对气动阻尼的影响规律ꎮ可以得出以下结论:1)助推增加了正阻尼区域的面积ꎬ从而相对于没有助推的构型起到了增加气动阻尼的作用ꎮ2)前节点位置的改变对过渡段气动阻尼影响很大ꎬ节点前后的振动方向相反ꎬ导致节点在过渡段前后的气动阻尼变化规律也截然相反ꎬ将过渡段与头部区域放在节点的同一侧有助于增加气动阻尼ꎮ3)在不改变流场结构的前提下ꎬ改变振动的振幅ꎬ气动力也会产生相应幅度的变化ꎬ因此结构振幅对气动阻尼的影响可忽略不计ꎮ4)高频部分的广义力对气动阻尼的贡献很小ꎬ即结构振动引起的广义力变化对气动阻尼起主要作用ꎬ而脉动压力对计算气动阻尼影响不大ꎬ可忽略不计ꎮ参考文献(References)[1]㊀CoeCF.Steadyandfluctuatingpressuresattransonicspeedsontwospace ̄vehiclepayloadshape[R].NASATMX ̄503ꎬ1961.[2]ColeSRJrꎬHenningTLꎬRaineyAG.NASAspaceve ̄hicledesigncriteria[R].NASASP ̄8001(REV)ꎬ1964. [3]EricssonLEꎬRedingJP.Analysisofflowseparationeffectsonthedynamicsofalargespacebooster[J].Jour ̄nalofSpacecraftandRocketsꎬ1965ꎬ2(4):481 ̄490. [4]RedingJPꎬEricssonLE.Effectofaeroelasticconsidera ̄tionsonseasat ̄Apayloadshrouddesign[J].JournalofSpacecraftandRocketsꎬ1981ꎬ18(3):241 ̄247. [5]程镇煌.宇航飞行器跨音速气动弹性问题探讨[J].上海航天ꎬ1997(6):16 ̄21.ChengZH.Discussionontransonicpneumaticelasticityofspacecraft[J].AerospaceShanghaiꎬ1997(6):16 ̄21(inChinese).[6]倪嘉敏.我国运载火箭气动设计回顾[C].近代空气动力学研讨会论文集ꎬ2005.NiJM.ReviewofaerodynamicdesignofChinaᶄslaunchvehicle[C].Proceedingsofthemodernaerodynamicssymposiumꎬ2005(inChinese).[7]臧涛成ꎬ胡焕性.大长细比弹箭弹性效应研究综述[J].弹道学报ꎬ1999ꎬ11(3):89 ̄93ꎬ96.ZangTCꎬHuHX.Areviewofgreatslendernessratioprojectileelasticeffectresearch[J].JournalofBallisticsꎬ1999ꎬ11(3):89 ̄93ꎬ96(inChinese). [8]吴志刚ꎬ杨超.细长体弹箭的气动弹性问题与研究方法[C].第九届(2005年)全国空气弹性学术交流会论文ꎬ2005.WuZGꎬYangC.Aeroelasticityproblemsandresearchmethodsofslenderbodymissiles[C].9thNationalSym ̄posiumonAeroelasticityꎬ2005(inChinese). [9]张贺ꎬ黄晓鹏.弹性细长旋转弹箭运动稳定性问题的研究进展[C].第九届(2005年)全国空气弹性学术交流会论文ꎬ2005.ZhangHꎬHuangXP.Researchprogressonthestabilityofelasticslenderrotatingprojectiles[C].9thNationalSymposiumonAeroelasticityꎬ2005(inChinese). [10]ColeHAJr.Dynamicresponseofhammerheadlaunchvehiclestotransonicbuffeting[R].NASATND ̄1982ꎬ1963.[11]BartelsREꎬWiesemanCDꎬMineckRE.ComputationalaeroelasticanalysisoftheAreslaunchvehicleduringas ̄cent[R].AIAA2010 ̄4374ꎬ2010.[12]AzevedoJLF.Aeroelasticanalysisoflaunchvehiclesintransonicflight[J].JournalofSpacecraftandRocketsꎬ1989ꎬ26(1):14 ̄23.[13]SinclairAꎬFlowersG.Low ̄orderaeroelasticmodeloflaunch ̄vehicledynamics[R].AIAA2010 ̄7725ꎬ2010. [14]DotsonKW.Transientcouplingoflaunchvehiclebendingresponseswithaerodynamicflowstatevariations[J].JournalofSpacecraftandRocketsꎬ2001ꎬ38(1):97 ̄104.[15]ColeSRꎬHenningTL.Buffetresponseofahammerheadlaunchvehiclewind ̄tunnelmodel[J].JournalofSpacecraftandRocketsꎬ1992ꎬ29(3):379 ̄385.[16]崔尔杰.流固耦合力学研究与应用进展[C].钱学森科学贡献暨学术思想研讨会论文集ꎬ2001.CuiEJ.Researchandapplicationprogressoffluid ̄struc ̄tureinteractionmechanics[C].ProceedingsofSeminarofQianXuesenScientificContributionsandAcademicThoughtsꎬ2001(inChinese).[17]冯明溪ꎬ王志安.火箭跨音速动导数和抖振实验[J].宇航学报ꎬ1987(1):55 ̄63.FengMXꎬWangZA.Experimentsoftransonicderiva ̄tivesandbuffetingofrocket[J].JournalofAstronauticsꎬ1987(1):55 ̄63(inChinese).[18]白葵ꎬ冯明溪.弹性模型实验技术[J].流体力学实验与测量ꎬ1999ꎬ13(1):38 ̄42.BaiKꎬFengMX.Aeroelasticmodelandthebuffetex ̄perimentaltechnique[J].ExperimentsandMeasurementsinFluidMechanicsꎬ1999ꎬ13(1):38 ̄42(inChinese). [19]JiCꎬRanJHꎬLiFꎬetal.Theaerodynamicdamping93气体物理2023年㊀第8卷testofelasticlaunchvehiclemodelintransonicflow[C].Proceedingsofthe64thInternationalAstronauticalCon ̄gressꎬ2013.[20]季辰ꎬ吴彦森ꎬ何岗ꎬ等.运载火箭气动阻尼风洞试验研究[C].第十二届全国空气弹性学术交流会论文集ꎬ2011.JiCꎬWuYSꎬHeGꎬetal.Experimentalstudyonaero ̄dynamicdampingwindtunneloflaunchvehicle[C].Pro ̄ceedingsofthe12thNationalAeroelasticityConferenceꎬ2011(inChinese).[21]刘子强ꎬ白葵ꎬ毛国良ꎬ等.锤头体弹性振动跨音速气动阻尼系数的确定[J].宇航学报ꎬ2002ꎬ23(6):1 ̄7.LiuZQꎬBaiKꎬMaoGLꎬetal.Thedeterminationofaerodynamicdampingonhammerheadlaunchvehiclesattransonicspeeds[J].JournalofAstronauticsꎬ2002ꎬ23(6):1 ̄7(inChinese).[22]冉景洪ꎬ刘子强ꎬ胡静ꎬ等.减阻杆气动阻尼研究[J].力学学报ꎬ2014ꎬ46(4):636 ̄641.RanJHꎬLiuZQꎬHuJꎬetal.Researchofaero ̄dampingforbluntwithspike[J].ChineseJournalofThe ̄oreticalandAppliedMechanicsꎬ2014ꎬ46(4):636 ̄641(inChinese).[23]朱剑ꎬ冉景洪ꎬ吴彦森ꎬ等.捆绑式运载火箭的气动阻尼数值计算方法[C].第十三届全国空气弹性学术交流会论文集.哈尔滨:中国力学学会ꎬ中国空气动力学会ꎬ2013.ZhuJꎬRanJHꎬWuYSꎬetal.Numericalcalculationmethodforaerodynamicdampingofbundlelaunchvehicles[C].Proceedingsofthe13thNationalAeroelasticityCon ̄ference.Harbin:ChineseSocietyofTheoreticalandAp ̄pliedMechanicsꎬChinaAeromechanicsSocietyꎬ2013(inChinese).[24]SpalartPR.Detached ̄eddysimulation[J].AnnualReviewofFluidMechanicsꎬ2009ꎬ41:181 ̄202. [25]GritskevichMSꎬGarbarukAVꎬSchützeJꎬetal.Devel ̄opmentofDDESandIDDESformulationsforthek ̄ωshearstresstransportmodel[J].FlowꎬTurbulenceandCombustionꎬ2012ꎬ88(3):431 ̄449.[26]季辰ꎬ吴彦森ꎬ侯英昱ꎬ等.捆绑式运载火箭跨声速气动阻尼特性试验研究[J].实验流体力学ꎬ2020ꎬ34(6):24 ̄31.JiCꎬWuYSꎬHouYYꎬetal.Experimentalstudyofaerodynamicdampingcharacteristicsofalaunchvehiclewithboostersintransonicflow[J].JournalofExperimentsinFluidMechanicsꎬ2020ꎬ34(6):24 ̄31(inChinese). [27]AllenCꎬRendallTCS.UnifiedapproachtoCFD ̄CSDinterpolationandmeshmotionusingradialbasisfunctions[R].AIAA2007 ̄3804ꎬ2007.04。
某全机跨声速颤振模型颤振特性仿真与试验验证

某全机跨声速颤振模型颤振特性仿真与试验验证钱卫;杨国伟;张桂江;郑冠男【摘要】针对某全机结构相似跨声速颤振模型,进行了有限元(FEM)模型结构模态分析和偶极子网格法(DLM)法颤振计算以及 CFD 方法的跨声速颤振特性仿真。
在 FL-26风洞中完成了跨声速颤振风洞试验。
通过试验结果与仿真结果的相关性分析,验证了一种全机复杂耦合的颤振形式。
通过对基于 N-S 方程的跨声速颤振仿真程序进行评估与验证,证实在飞机非定常 CFD 仿真上取得了进展并且具有足够的精度。
综合 CFD 仿真与跨声速颤振风洞试验,可以对全机复杂耦合的颤振特性进行工程颤振设计。
%Transonic flutter simulation and transonic flutter wind tunnel test are the main techniques in the design process for the high maneuver aircraft.In this paper,the finite element method (FEM)based mo-dal analysis,flutter calculation using doublet lattice method (DLM),and the transonic flutter simulation by CFD method are carried out for the structural similar flutter mode of a whole aircraft.The transonic flutter wind tunnel test is accomplished in FL-26 wind tunnel.By correlation analysis of the results by the numerical simulation with those of the wind tunnel test,a complex flutter mode of the whole aircraft is investigated and verified.The effectiveness and the accuracy of the Navier-Stokes equations based transonic CFD code with hybrid mesh are verified,and it shows the progress we have made on the unsteady aerodynamic CFD simula-tion of bining transonic flutter wind tunnel test with CFD simulation,the complex coupling flutter design for the whole aircraft could be accomplished.【期刊名称】《空气动力学学报》【年(卷),期】2014(000)003【总页数】5页(P364-368)【关键词】跨声速颤振;全机结构相似颤振模型;CFD 颤振仿真;跨声速颤振风洞试验;N-S 方程【作者】钱卫;杨国伟;张桂江;郑冠男【作者单位】沈阳飞机设计研究所,沈阳 110035;中国科学院力学研究所,北京100190;沈阳飞机设计研究所,沈阳 110035;中国科学院力学研究所,北京100190【正文语种】中文【中图分类】V215.30 引言对于高机动飞机,经典颤振边界在跨声速区往往存在一个凹坑,因此跨声速颤振特性是飞机设计限制的关键设计参数。
基于 CFD 和 CSD 耦合的涡激振和颤振气弹模拟

基于 CFD 和 CSD 耦合的涡激振和颤振气弹模拟李永乐;朱佳琪;唐浩俊【摘要】以 FLUENT 为研究工具,利用微分方程的数值解法和动网格技术,基于松耦合方法将 Newmark 算法通过UDF 嵌入 Fluent 软件中,实现了 CFD 和CSD 耦合的分析方法。
通过建立二维方柱绕流模型,计算了竖向单自由度振动方柱在不同风速下的斯托罗哈数和最大振幅的变化情况,模拟了涡激共振锁定现象,并与静态绕流的结果进行了对比。
建立了具有竖向振动和扭转振动二自由度的薄平板模型,并识别了该平板的颤振导数,进一步对其弯扭耦合颤振临界风速进行了逼近计算,本方法得到的颤振临界风速与 Scanlan 理论公式和 Selberg 理论公式吻合较好。
%Taking advantage of the software FLUENT and using the numerical solution of differential equation and the dynamic mesh model,a CFD/CSD coupling solution based on loose coupling was realized by embedding the Newmark method into FLUNT with the help of UDF function.A 2D-square cylinder model was established to investigate the change of Strouhal number and the maximum vertical vortex-excited amplitude of the square cylinder under different wind speed. The lock-in phenomenon of vortex-excited resonance was observed in the process of simulation and it was compared with the result of static square cylinder.A 2D flat plate model with vertical and torsional degrees of freedom was established to identify the flutter derivatives of the flat plate and to determine the flutter critical wind speed of flutter.The simulation result agrees well with the critical wind speeds of flutter calculated by using the Scanlan's formula and Selberg's formula.【期刊名称】《振动与冲击》【年(卷),期】2015(000)012【总页数】6页(P85-89,114)【关键词】CFD 和 CSD 耦合分析;动网格;涡激振;颤振;气弹效应【作者】李永乐;朱佳琪;唐浩俊【作者单位】西南交通大学桥梁工程系,成都610031;西南交通大学桥梁工程系,成都 610031; 嘉兴市交通工程质量安全监督站,浙江嘉兴 314001;西南交通大学桥梁工程系,成都 610031【正文语种】中文【中图分类】O351.2空气与弹性体的相互作用是一个复杂的流固耦合作用过程。
基于CFD的机翼颤振分析
freeplay position and friction in the freeplay on aeroelastic response is analyzed. They have a
Key words: aeroelasticity ,stall flutter ,UDF,Fluent ,dynamic stall,freeplay nonlinearity
ii
南京航空航天大学硕士学位论文
图清单
图 1.1 气动弹性力三角形 .................................................................................................. 1 图 2.1CFD 流程图 .............................................................................................................. 9 图 2.2 基于弹簧光滑节点开始状况 ................................................................................ 17 图 2.3 基于弹簧光滑节点结束状况 ................................................................................ 17 图 2.4 二维网格数据结构示意图 .................................................................................... 19 图 2.5 三维网格数据结构示意图 ................................................................................... 20 图 3.1 第一套网格 ............................................................................................................ 23 图 3.2 第二套网格 ............................................................................................................ 23 图 3.3 第一套网格升力系数曲线 .................................................................................... 24 图 3.4 第二套网格升力系数曲线 .................................................................................... 24 图 3.5 阻力系数曲线比较 ................................................................................................ 24 图 3.6 失速机翼周围的流场速度分布 ............................................................................ 24 图 3.7 α 0 = 5° 时升力系数迟滞曲线和力矩系数迟滞曲线 ............................................. 25 图 3.8 α 0 = 10° 时升力系数迟滞曲线和力矩系数迟滞曲线 ........................................... 26 图 3.9 α 0 = 12° 时升力系数迟滞曲线和力矩系数迟滞曲线 ........................................... 26 图 3.10 α 0 = 15° 时升力系数迟滞曲线和力矩系数迟滞曲线 ......................................... 26 图 3.11 深度失速时( α 0 = 12° )机翼周围流场的速度分布 ........................................ 28 图 3.12 α1 = 2° 时升力系数迟滞曲线和力矩系数迟滞曲线 ........................................... 29 图 3.13 α1 = 5° 时升力系数迟滞曲线和力矩系数迟滞曲线 ........................................... 29 图 3.14 α1 = 10° 时升力系数迟滞曲线和力矩系数迟滞曲线.......................................... 29 图 3.15 α1 = 15° 时升力系数迟滞曲线和力矩系数迟滞曲线.......................................... 30 图 3.16 k = 0.05 ,不同雷诺数下的非定常特性比较..................................................... 30 图 3.17 k = 0.1 ,不同雷诺数下的非定常特性比较 ....................................................... 31 图 3.18 k = 0.15 ,不同雷诺数下的非定常特性比较..................................................... 31 图 3.19 k = 0.2 ,不同雷诺数下的非定常特性比较....................................................... 31 图 3.20 k = 0.4 ,不同雷诺数下的非定常特性比较....................................................... 32 图 4.2 具有 2 个自由度的翼型示意图 ............................................................................ 36 图 4.3 复合材料夹层板结构机翼模型 ............................................................................ 38 图 4.4V=40m/s,二维翼型的颤振响应 ........................................................................ 39 图 4.5V=46.75m/s,二维翼型的颤振响应 ................................................................... 39
机翼跨音速风洞颤振试验模型的计算分析
机翼跨音速风洞颤振试验模型的计算分析陈千一;窦忠谦;周铮;章俊杰【摘要】以某民机机翼跨音速颤振模型为研究对象,采用N-S方程求解固定边界流场的气动力,简化的跨音速小扰动方程求解运动边界流场的气动力,结合结构动力学的模态分析结果进行颤振特性分析.模型风洞试验前完成所有计算工作,试验后通过比较表明,计算结果与试验结果吻合:①颤振频率一致;②颤振速度随马赫数的变化趋势一致;③跨音速凹坑的底部位置一致;④颤振速度的偏差最大不超过10%,且在马赫数0.60和0.70处,偏差<1%.由此可见该计算方法的计算精度高,可用于风洞试验结果的预判,提升风洞试验结果的可信度和风洞试验的效率,也可作为民机适航符合性验证的一种手段.%A transonic flutter model of a civil plane wing was investigated.The aerodynamic force in a flow field with fixed boundary was solved with N-S equations.The aerodynamic force in a flow field with moving boundary was solved with the simplified transonic small disturbance equations.The flutter characteristics were studied by combining the modal analysis results of structural dynamics and the aerodynamic force.The numerical simulations of flutter were finished before the model wind tunnel tests.Ater tests,the comparisons showed that the numerical results agree well with the test data;the calculated flutter frequencies are close to the those of test data;the flutter speed varies with Mach number,the flutter speed of the former and that of the latter have the same trend;the bottom positions of transonic pits measured and calculated agree well;the flutter speed difference between simulation and test is less than 10%,and less than 1% when Mach number is 0.60 or0.70;the numerical method has a high accuracy,it can be used to predict wind tunnel tests' results,and improve the reliability and the efficiency of wind tunnel tests;the method can also be a means of the compliance verification of civil aviation air worthness.【期刊名称】《振动与冲击》【年(卷),期】2017(036)007【总页数】5页(P99-103)【关键词】跨音速颤振;风洞试验;频域计算方法;计算流体动力学计算;适航验证【作者】陈千一;窦忠谦;周铮;章俊杰【作者单位】中国商飞上海飞机设计研究院,上海201210;中国商飞上海飞机设计研究院,上海201210;中国商飞上海飞机设计研究院,上海201210;中国商飞上海飞机设计研究院,上海201210【正文语种】中文【中图分类】V215.3大展弦比超临界机翼、一体化设计的翼梢小翼,以及翼吊发动机低平尾布局是现代民用飞机常用的布局形式之一。
基于CFD_CSD耦合算法的机翼颤振分析_曾宪昂
基于CFD /CSD 耦合算法的机翼颤振分析¹曾宪昂,徐 敏,安效民,陈士橹(西北工业大学航天学院,陕西西安 710072)摘 要:用计算流体力学/计算结构力学(CFD/CSD)耦合算法对标准气动弹性模型AGARD 445.6机翼作了颤振分析,主要研究机翼的跨音速颤振求解问题。
采用常体积转换法(CVT )进行流体与结构之间的数据交换并运用松耦合方法对气动弹性方程进行时域推进仿真。
计算机翼在M a =0.499~1.072的颤振边界,并将计算结果同偶极子格网法(DLM )的计算结果与试验结果比较,结果显示CFD/CSD 耦合计算结果较DLM 计算结果更接近于试验值,尤其是在非线性强的跨音速区域。
可见,CFD /CSD 耦合计算比DLM 具有很大的优越性。
关 键 词:计算流体力学/计算结构力学(CFD/CSD)耦合算法,AGARD 445.6机翼,颤振分析,常体积转换(CVT ),偶极子格网法(DLM )中图分类号:V 211.47 文献标识码:A 文章编号:1000-2758(2008)01-0079-04 颤振是飞行器飞行时常见的一种气动弹性现象,它对飞行器的破坏是灾难性的。
在过去,广泛运用于飞行器的颤振计算方法是偶极子格网法(DLM),它是基于线化位流理论的一种颤振计算方法。
在很多的商业软件中都应用DLM 进行气弹分析,如广泛应用于工业设计的M SC .NASTRAN 的气动弹性模块[1]等。
但是DLM 是一种基于线化理论的方法,无法解决非线性强的流场,而且它大多采用的是平面模型,无法计入机翼的厚度、迎角等。
近年来,CFD 计算技术发展十分迅速,计算机的性能也有很大提高,因此CFD/CSD 耦合计算方法[2,3]也迅速发展起来。
由于CFD 计算求解的是非线性方程组,因此这种方法可以计算飞行器在非线性强的流场中的运动,同时这种方法可更加直观、实时地显示飞行器结构的变形及流场的变化,并且它还可以计算较为复杂的外形。
基于风洞试验模型的跨声速颤振研究
基于风洞试验模型的跨声速颤振研究侯良学;张戈;刘南;王冬;钱卫;杨希明【摘要】飞行器跨声速工况下颤振边界快速下降,是结构设计和强度校核重点关注的状态之一.目前工程中采用基于偶极子格网法的线性分析手段无法准确预测跨声速颤振边界,风洞试验仍然是研究飞行器跨声速颤振特性的重要手段;以两套颤振试验标准模型为研究对象,在FL-3风洞中开展了风洞跨声速试验研究,采用PEAK-HOLD亚临界响应分析方法预测了模型的跨声速颤振边界,并利用ZAERO和CFD/CSD耦合两种数值计算方法预测了试验模型的颤振边界.结果表明:PEAK-HOLD亚临界响应分析方法预测颤振边界具有较好的趋势性,颤振边界合理可靠;ZAERO线性方法对跨声速颤振边界的预测精度较低,而基于CFD/CSD耦合的非线性方法得到的跨声速颤振边界与试验吻合较好,相互验证了风洞试验和数值计算的可靠性.【期刊名称】《振动与冲击》【年(卷),期】2019(038)013【总页数】7页(P236-241,260)【关键词】跨声速颤振;颤振标模;亚临界响应;风洞试验;数值计算【作者】侯良学;张戈;刘南;王冬;钱卫;杨希明【作者单位】中国航空工业空气动力研究院,沈阳 110034;高速高雷诺数气动力航空科技重点试验室,沈阳110034;中国航空工业空气动力研究院,沈阳 110034;高速高雷诺数气动力航空科技重点试验室,沈阳110034;中国航空工业空气动力研究院,沈阳 110034;高速高雷诺数气动力航空科技重点试验室,沈阳110034;中国航空工业空气动力研究院,沈阳 110034;高速高雷诺数气动力航空科技重点试验室,沈阳110034;大连理工大学航空航天学院,辽宁大连116024;中国航空工业空气动力研究院,沈阳 110034;高速高雷诺数气动力航空科技重点试验室,沈阳110034【正文语种】中文【中图分类】V215.3在跨声速区,由于压缩性和气动非线性的影响,飞行器的颤振速压边界一般降低较大,颤振边界随马赫数的变化曲线会呈现出所谓的跨声速“凹坑”现象,最小临界颤振速压值通常出现在跨声速范围。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Abstract CFDCSD coupling method is the mainstream approach in predicting transonic flutter characteristics of wing. In this paper,we take international standard model of transonic flutter Wing AGARD 445. 6 as the investigation object,and predict the unsteady transonic aerodynamic forces acting on the surface of wing by using multifield coupling solver ANSYS. MFX to solve Euler equations. For the structural vibration equations,direct numerical integral with HHT method is used to obtain structural responses. The transonic flutter characteristics of Wing AGARD 445. 6 are computed with the coupling of CFD and CSD. Numerical simulation results agree well with those of the NASA wind tunnel test. This indicates that the use of the ANSYS. MFX to solve the problems transonic flutter of wing is feasible. Keywords Transonic flutter MFX ( MultiField Solver) HHT method Wing AGARD 445. 6
第 29 卷第 12 期 2012 年 12 月
计算机应用与软件 Computer Applications and Software
Vol. 29 No. 12 Dec. 2012
CSD 耦合的机翼跨音速颤振计算 基于 CFD张苏华 赵永辉
( 南京航空航天大学机械结构力学及控制国家重点实验室 江苏 南京 210016 )
. . .
计算机应用与软件
t ( 3)
2012 年
dΩ = U ·ndS
g Ω Ω
( 14 )
载荷插值实现了在两场间传递广义载荷 ( 气动力、 结构位 移) 。结构场与流场在耦合面上的网格划分情况一般是不一样 的, 不能直接将流场的气动力或结构场的位移加载到耦合面另 图形保留插值 一侧场的网格节点上。MFX 具有两种插值方法, 和守恒插值。图形保留插值主要应用在耦合面两侧场网格局部 存在一致时直接插入对应节点的值, 其余情况使用守恒插值 。
- bs ωα 槡 μ
( 6)
Q 为守恒变量, F 为无粘通量, 其中, Ω 为当前控制体, Ω 为控 n 为边界外法线单位矢量 。守恒变量可写成: 制体边界, dΩ = QdΩ - Q( U ·n) dS Q t t
g Ω Ω Ω
( 18 )
( 7)
珔 b s 为翼根半弦长, 其中, ω α 为第二阶扭转频率, μ 为质量比。
[ a0 M + a1 C + ( 1 - α f ) K] u n +1 = ( 1 - α f ) f n +1 + int u n + a3 珔 un ) M + α f ( f n - f n ) + ( a0 u n + a2 珔 ( a1 u n + a4 ü n + a5 ü n ) C 1 - αm a0 = 2 αΔt ( 1 - αf ) δ a1 = αΔt 1 - αm a2 = αΔt ( 5) ( 4)
收稿日期: 2011 - 12 - 13 。国家自然科学基金项目( 10972100 ) 。 张 苏华, 硕士生, 主研领域: 气动弹性力学。赵永辉, 教授。
( 2)
40
ü n +1 - α m = ( 1 - α m ) ü n +1 + α m ü n u n +1 - α f = ( 1 - α f ) u n +1 + α f u n u n +1 - α f = ( 1 - α f ) u n +1 + α f u n f n +1 - α f = ( 1 - α f ) f n +1 + α f f n 将式( 3 ) 代入式( 2 ) , 结合 Newmark 方法, 整理有:
1
1. 1
CFDCSD 耦合颤振计算方法
颤振控制方程
颤振本质上属于结构振动, 其方程为: . Mü( t) + C u( t) + Ku( t) = f( t) ( 1)
M、 C、 K 分别为结构的质量矩阵 、 f 其中, 阻尼矩阵和刚度矩阵, ( t) 为结构受到的非定常气动力矩阵, u 为结构各自由度在物理 空间内的位移向量。 求解上述方程常用两种方法, 模态叠加法和直接数值积分 法。为了防止结构振动方程有限元迭代过程中高频区域数值耗 本文采用根据 Newmark 方法改进的 散会影响低频信号的精度, HHT 方法[8] , 将式( 1 ) 写成: . Mü n -1 - α m + C u n +1 - α f + Ku n +1 - α f = f n +1 - α f 其中:
V215. 3
文献标识码
DOI: 10. 3969 / j. issn. 1000386x. 2012. 12. 012
PREDICTING TRANSONIC FLUTTER OF WING USING CFDCSD COUPLING METHOD
Zhang Suhua Zhao Yonghui
( State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics,Nanjing 210016 , Jiangsu,China)
2
( 15 )
δ - 1 ) Δt 2α
HHT 无 δ ≥ 0. 5, α ≥ 0 . 5 δ, δ = 0. 5 - αm + αf , α m ≤ α f ≤ 0 . 5 时, HHT 退 化 为 Newmark 但 是 当 α m 与 α f 都 取 零 时, 条件稳 定, 方法。
结合等熵流特性, 则流场中任意控制体的压强为: ( 1 + 0. 5Cp γMa2 ) Cp 2 p = (1 + γMa ) p∞ = 2 0. 7Ma2 ( 1 + 0. 2Ma2 ) 得到物面边界每个网格中心的压强 p' : f' ( t) = p' ·s
[2 ]
由于时间离散隐式格式无条件稳定, 用双时间步隐式向后 差分离散时间导数项如下: 1 [ 3 ( Q Ω) n + 1 - 4 ( Q Ω) 2 Δt n +1 而式( 10 ) 中的 R( Q ) 为: R( Q n +1 ) = -
n
+ 2 ( Q Ω)
n -1
] = R( Q
n +1
) ( 10 )
·n ( t ) Δ S ∑[F - QU ( t) ]
g
( 11 )
对式( 10 ) 和式( 11 ) 选择隐式迭代求解。
1. 3
网格变形与载荷插值
耦合面用于衔接流场与结构场 。基于耦合面变形的流场空 间动网格迭代与耦合面的载荷插值计算独立于 Euler 方程和结 构振动方程的求解。对于网格变形, 满足: ·( Γ disp ξ) = 0 下式定义: Γ disp = ( 1 ) σ
槡
-3 . 5
q∞ ( 16 )
对近物面若干层网格控制体中心的 p 进行加权变换, 近似 ( 17 )
1. 2
式为:
流体控制方程
不考虑体积力和外部热源, 三维非定常 Euler 方程积分形 dΩ + F·ndS = 0 Q t
Ω Ω
可见, 结构表面受到的气动力大小与来流动压 q ∞ 直接相 关, 一般根据结构响应, 变化动压寻找临界颤振点 。对于给定马 赫数及密度的情况, 改变动压即在改变速度 。 本文通过不断修 改无因次速度进行迭代, 以找到简谐的物理响应 。 无因次速度 表达式为: V* = V
U g 为边界运动速度矢量, 其中, 将式( 7 ) 代入式( 6 ) 有: t
2
( 8)
MFX 求解器
MFX 多场耦合求解器是基于弱耦合理论[2] 开发的。 计算
QdΩ + ( F - QU ) ·ndS = 0
g Ω Ω
式( 8 ) 半离散形式为: ( Q Ω ) &#CSD 耦合计算是预计机翼跨音速颤振特性的主流方法 。以跨音速颤振国际标准模型 AGARD 445. 6 机翼为研 摘 要 采用 CFD利用 ANSYS. MFX 多场耦合求解器对 Euler 方程进行求解来获得作用在机翼表面上的非定常气动力; 对结构振动方程采用 究对象, HHT 方法直接数值积分以获得结构响应 。通过 CFD 和 CSD 的耦合, 计算了 AGARD 445. 6 机翼的跨音速颤振特性 。 数值模拟结果 表明利用 ANSYS. MFX 计算机翼跨音速颤振问题是可行的 。 与 NASA 风洞实验结果符合良好, 关键词 中图分类号 跨音速颤振 TP311 MFX 多场求解器 HHT 方法 A AGARD 445. 6 机翼
