Stata_之面板数据处理—长面板
STATA面板数据模型操作命令讲解
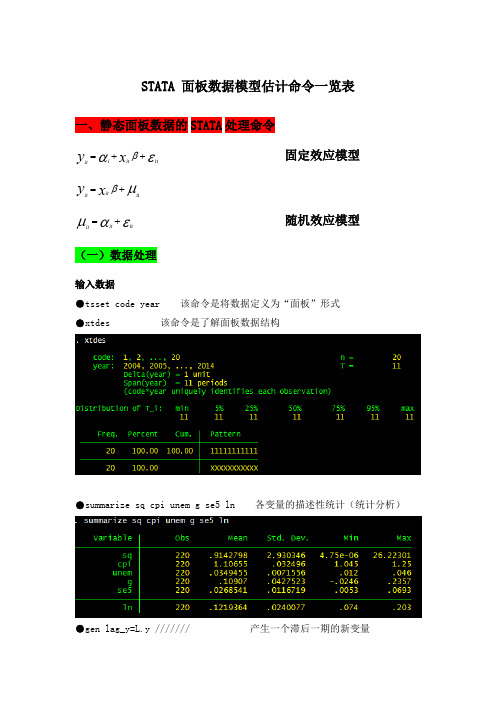
STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it (一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
chap13_stata面板数据分析

型的回归、固定效应和随机效应模型的拟合、Hausman检 验以及模型预测等内容。
实验操作指导
1 组间效应模型
对于“wage.dta”的数据,我们要分析受教育年数、年龄、工作年数、
现有岗位的任职时间、是否是黑人、是否居住在SMSA区、是否生活 在南方等因素对工资收入的影响。考虑到年龄、工作年数、现有岗位 任职时间等因素对工资收入的影响可能不是线性的,我们先生成这三 个变量的平方项,并在模型中包括这三个变量的水平项和平方项。输 入命令: gen age2=age*age gen exp2=ttl_exp*ttl_exp gen tenure2=tenure*tenure 我们生成变量age、ttl_exp和tenure的平方项,并分别将其命名为age2、 exp2和tenure2。 此外,我们需要由变量race生成一个虚拟变量,来表示是否是黑人。 输入命令: gen byte black = race==2 这里,我们生成新变量black,并令其类型为type。注意,race后为两 个等号。该命令的含义为,对race是2的(黑人)观测值,我们令 black的值为1;对race取其他值的观测值,我们令black的值为0。也就 是说新生成的变量black为虚拟变量,1表示黑人,0表示其他人种。
对于“wage.dta”的数据,我们下面进行固定效应回归。输入命令: xtreg ln_wage grade age age2 ttl_exp exp2 tenure tenure2 black
not_smsa south, fe 这里,选项fe表明是进行固定效应回归分析。
3 随机效应模型
对于“wage.dta”的数据,我们要知道其数据分布情况,
stata之面板数据处理-长面板

在Stata中,可以使用`import delimited`命令导入长面板数据。需 要指定数据文件的位置和格式,以及 时间变量和个体变量的名称。
导出数据
在Stata中,可以使用`export`命令将 长面板数据导出为其他格式,例如 CSV或Excel。需要指定数据文件的位 置、格式和名称。
长面板数据的描述性统计
长面板数据的创建
创建长面板数据
在Stata中,可以使用`xtset`命令 创建长面板数据。需要指定数据 的时间变量和个体变量,以及数
据的时间和个体范围。
时间变量的选择
时间变量通常是每个观测值所属的 时间点标识,例如年份或月份。
个体变量的选择
个体变量是每个观测值所属的个体 标识,例如公司或家庭。
长面板数据的导入与导
可视化功能相对较弱
相比一些其他统计分析软件,Stata的可视化功能相 对较弱。
无法处理实时数据
Stata主要用于处理离线数据,对于实时数据处理能 力有限。
Stata长面板数据处理的发展趋势
云计算与大数据处理
随着云计算技术的发展,未来Stata可能会加强在云计算环境下 的数来自处理能力,以应对大数据的挑战。
描述性统计
在Stata中,可以使用各种描述性统计命令来分析长面板数据,例如 `summarize`、`tabulate`和`codebook`等。这些命令可以帮助了解数据的分 布和特征。
数据清洗
在进行描述性统计之前,可能需要对数据进行清洗,例如处理缺失值、异常值 和重复值等。可以使用Stata中的各种数据清洗命令来进行处理。
根据研究目的和数据特征选择合适的面板数 据分析模型。
模型建立
使用Stata命令构建面板数据分析模型,并 指定相应的参数和选项。
最新STATA面板数据模型操作命令讲解资料

STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型(一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
面板数据stata处理步骤介绍

xA6_Panel_Data - Printed on 2011-11-25 10:43:02 149 reg y x dum1 dum2 dum3, nocons 150 est store m_pooldum3 151 152 *-M2:放入两个虚拟变量,三家公司有一个公共的截距项 153 reg y x dum2 dum3 154 est store m_pooldum2 155 156id t 158 xtreg y x, fe 159 est store m_fe 160 est table m_*, b(%6.3f) star(0.1 0.05 0.01) 161 162 163 *-6.1.4.3 stata的估计方法解析 164 165 * 目的:如果截面的个数非常多,那么采用虚拟变量的方式运算量过大 166 * 因此,要寻求合理的方式去除掉个体效应 167 * 因为,我们关注的是 x 的系数,而非每个截面的截距项 168 * 处理方法: 169 * 170 * y_it = u_i + x_it*b + e_it (1) 171 * ym_i = u_i + xm_i*b + em_i (2) 组内平均 172 * ym = um + xm*b + em (3) 样本平均 173 * (1) - (2), 可得: 174 * (y_it - ym_i) = (x_it - xm_i)*b + (e_it - em_i) (4)//within估计 175 * (4)+(3), 可得: 176 * (y_it-ym_i+ym) = um + (x_it-xm_i+xm)*b + (e_it-em_i+em) 177 * 可重新表示为: 178 * Y_it = a_0 + X_it*b + E_it 179 * 对该模型执行 OLS 估计,即可得到 b 的无偏估计量 180 181 egen y_meanw = mean(y), by(id) /*公司内部平均*/ 182 egen y_mean = mean(y) /*样本平均*/ 183 egen x_meanw = mean(x), by(id) 184 egen x_mean = mean(x) 185 gen dy = y - y_meanw + y_mean 186 gen dx = x - x_meanw + x_mean 187 reg dy dx 188 est store m_stata 189 190 est table m_*, b(%6.3f) star(0.1 0.05 0.01) 191 192 193 *-6.1.4.4 解读 xtreg,fe 的估计结果 194 195 use invest2.dta, clear 196 tsset id t 197 edit 198 xtreg market invest stock, fe 199 200 *-- R^2 201 * y_it = a_0 + x_it*b_o + e_it (1) pooled OLS 202 * y_it = u_i + x_it*b_w + e_it (2) within estimator 203 * ym_i = a_0 + xm_i*b_b + em_i (3) between estimator 204 * 205 * -> R-sq: within 模型(2)对应的R2,是一个真正意义上的R2 206 * -> R-sq: between corr{xm_i*b_w,ym_i}^2 207 * -> R-sq: overall corr{x_it*b_w,y_it}^2 208 209 *-- F(2,93) = 33.23 检验除常数项外其他解释变量的联合显著性 210 * 93 = 100-2-5 211 212 *-- corr(u_i, Xb) = 0.5256 213 214 *-- sigma_u, sigma_e, rho 215 * rho = sigma_u^2 / (sigma_u^2 + sigma_e^2) 216 dis e(sigma_u)^2 / (e(sigma_u)^2 + e(sigma_e)^2) 217 dis 1023.5914^2 / (1023.5914^2 + 370.9569^2) 218 219 *-- 个体效应是否显著?(假设检验) 220 * F(4, 93) = 97.68 H0: a1 = a2 = a3 = a4 = 0 221 * Prob > F = 0.0000 表明,固定效应高度显著 222 Page 3
用stata处理面板数据(中文版)_stata关于面板数据说明

Chp8 Panel Data一直想把看Panel模型时的感悟整理成笔记,但终因懒惰而未能成行。
今天终于下决心开了个头,可遗憾的是,这个开头却是从本章的结尾写起,因为这一部分最容易写。
不过,凡事有了好的开头基本上也算成功一半了,所以后面的整理工作还要有劳各位的督促。
文中的不足还望不吝指出。
8.1简介8.2一般模型8.2.1固定效应模型(Fixed Effect Model)8.2.2随机效应模型(Random Effect Model)8.3自相关性8.4动态Panel Data8.5门槛Panel Data8.6非稳定Panel Data及协整8.7Panel V AR8.8Stata8.0实现在介绍了Panel Data的基本理论后,下面我们介绍如何使用STATA8.0软件包来实现模型的估计。
前面我们已经提到,Panel Data具有如下数据存储格式:company year invest mvalue11951755.94833.011952891.24924.9119531304.46241.7119541486.75593.621951588.22289.521952645.52159.421953641.02031.321954459.32115.531951135.21819.431952157.32079.731953179.52371.631954189.62759.9其中,变量company和year分别为截面变量和时间变量。
显然,通过这两个变量我们可以非常清楚地确定panel data的数据存储格式。
因此,在使用STATA8.0估计模型之前,我们必须告诉它截面变量和时间变量分别是什么,所用的命令为tsset1,命令格式如下:tsset panelvar timevar这里需要指出的是,由于Panel Data本身兼具截面数据和时间序列二者的特性,所以对时间序列进行操作的运算同样可以应用到Panel Data身上。
STATA面板数据模型操作命令(完整资料).doc
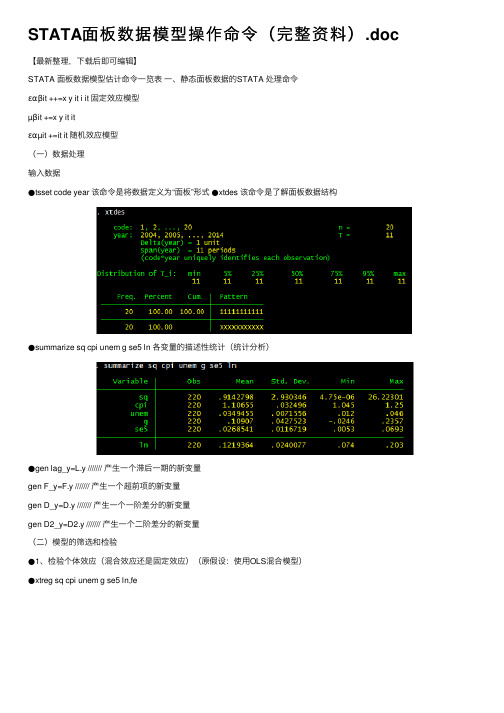
STATA⾯板数据模型操作命令(完整资料).doc 【最新整理,下载后即可编辑】STATA ⾯板数据模型估计命令⼀览表⼀、静态⾯板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型µβit +=x y it itεαµit +=it it 随机效应模型(⼀)数据处理输⼊数据●tsset code year 该命令是将数据定义为“⾯板”形式●xtdes 该命令是了解⾯板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产⽣⼀个滞后⼀期的新变量gen F_y=F.y /////// 产⽣⼀个超前项的新变量gen D_y=D.y /////// 产⽣⼀个⼀阶差分的新变量gen D2_y=D2.y /////// 产⽣⼀个⼆阶差分的新变量(⼆)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使⽤OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型⽽⾔,回归结果中最后⼀⾏汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例⼦中发现F 统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验⽅法:LM 统计量)(原假设:使⽤OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第⼀幅图将不会呈现)xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应⾮常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验⽅法:Hausman 检验)原假设:使⽤随机效应模型(个体效应与解释变量⽆关)通过上⾯分析,可以发现当模型加⼊了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
STATA面板数据模型操作命令讲解

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it (一)数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量(二)模型的筛选和检验●1、检验个体效应(混合效应还是固定效应)(原假设:使用OLS混合模型)●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言,回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。
在我们这个例子中发现F统计量的概率为0.0000,检验结果表明固定效应模型优于混合OLS模型。
●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量)(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现)xttest0可以看出,LM检验得到的P值为0.0000,表明随机效应非常显著。
可见,随机效应模型也优于混合OLS模型。
●3、检验固定效应模型or随机效应模型(检验方法:Hausman检验)原假设:使用随机效应模型(个体效应与解释变量无关)通过上面分析,可以发现当模型加入了个体效应的时候,将显著优于截距项为常数假设条件下的混合OLS模型。
但是无法明确区分FE or RE的优劣,这需要进行接下来的检验,如下:Step1:估计固定效应模型,存储估计结果Step2:估计随机效应模型,存储估计结果Step3:进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出,hausman检验的P值为0.0000,拒绝了原假设,认为随机效应模型的基本假设得不到满足。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(二)组内自相关检验
原假设:不存在一阶自相关 xtserial lnc lnp lnpmin lny state2-state10 t
相关性
(三)组间截面检验 原假设:不存在组间截面相关 Syntax:quietly xtreg lnc lnp lnpmin lny t,fe
当i j ,i j
Syntax: xtpcse lnc lnp lnpmin lny state2-state10 t,corr(psar1)
若仅考虑不同个体扰动项存在异方差,而忽略自相关,则: Syntax:xtpcse lnc lnp lnpmin lny state2-state10 t,hetonly
3、异方差与之相关检验
(一)组间异方差检验
2 H0: i2 ( i 1, ...,n)
1、wald 异方差检验 quietly xtgls lnc lnp lnpmin lny state2-state10 t,panels(cor) cor(ar1) xttest3
2、似然比检验
Syntax: tab state,gen(state) gen t=year-62 quietly xtgls lnc lnp lnpmin lny state2-state10 t,igls panels(het) estimates store hetero quietly xtgls lnc lnp lnpmin lny state2-state10 t,igls estimates store homo local df=e(N_g)-1 irtest hetero homo,df(`df' )
2、同时处理组内、组间同期相关
xtgls y x1 x2 x3,panels(option) corr(option)
panels(iid):假定不同个体的扰动项为独立同分布; panels(het):假定不同个体的扰动项相互独立但有不同方差; panels(cor):假定不同个体的扰动项同期相关且有不同方差; corr(ar1):对应 i 的组内自相关情形; corr(psar1):允许每个面板有自己的自回归系数 在执行以上命令“xtpcse”或“xtgls”时,如果没有个 体虚拟变量,则为随机变量;如果加上个体虚拟变量,则 为固定效应。
(1)Breusch-Pagan LM检验: xttest2 (只能用在 “xtreg,fe”,”xtgls”,”ivreg2”之后) (2)cross-sectional dependence ——xtcds (适用于n大T小的短面板数据) Pesaran检验:xtcsd,pes Friedman检验:xtcsd,fri Frees检验:xtcsd,fre
Stata 之面板数据处理
——长面板
——周建锋
, yit xit it
x
虚拟变量、以及不随时间变化的解释变量Zi
, it 包括了常数项、时间趋势项、个体
it i i,t -1 it
1、仅组内异方差
(1)当 i syntax: tab state,gen(state) gen t=year-62 xtpcse lnc lnp lnpmin lny
