自动控制理论实验报告-根轨迹仿真分析
自动控制原理第5章根轨迹分析法

04
CATALOGUE
根轨迹分析法的限制与挑战
参数变化对根轨迹的影响
参数变化可能导致根轨迹的形状和位置发生变化 ,从而影响系统的稳定性和性能。
对于具有多个参数的系统,根轨迹分析可能变得 复杂且难以预测。
需要对参数变化进行细致的监测和控制,以确保 系统的稳定性和性能。
复杂系统的根轨迹分析
对于复杂系统,根轨 迹分析可能变得复杂 且难以实现。
02
CATALOGUE
根轨迹的基本概念
极点与零点
极点
系统传递函数的极点是系统动态 特性的决定因素,决定了系统的 稳定性、响应速度和超调量等。
零点
系统传函数的零点对系统的动 态特性也有影响,主要影响系统 的幅值和相位特性。
根轨迹方程
根轨迹方程是描述系统极点随参数变 化的关系式,通过求解根轨迹方程可 以得到系统在不同参数下的极点分布 。
05
CATALOGUE
根轨迹分析法的改进与拓展
引入现代控制理论的方法
状态空间法
将根轨迹分析法与状态空间法相结合,利用状态空间法描述系统的动态行为,从而更全 面地分析系统的稳定性。
最优控制理论
将根轨迹分析法与最优控制理论相结合,通过优化系统的性能指标,提高系统的稳定性 和动态响应。
结合其他分析方法
根轨迹方程的求解方法包括解析法和 图解法,其中图解法是最常用的方法 。
根轨迹的绘制方法
手工绘制
通过选取不同的参数值,计算对应的极点,然后绘制极点分布图。这种方法比较繁琐,但可以直观地了解根轨迹 的形状和变化规律。
软件绘制
利用自动控制系统仿真软件,如MATLAB/Simulink等,可以方便地绘制根轨迹图,并分析系统的动态特性。
自动控制原理实验报告
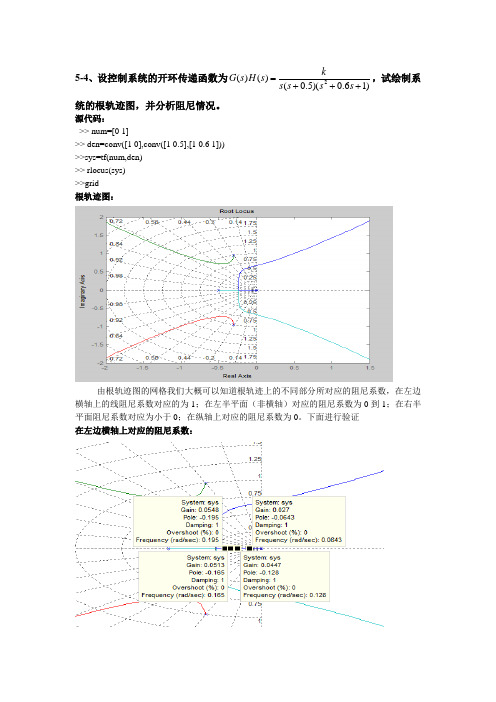
5-4、设控制系统的开环传递函数为)16.0)(5.0()()(2+++=s s s s k s H s G ,试绘制系统的根轨迹图,并分析阻尼情况。
源代码:>> num=[0 1]>> den=conv([1 0],conv([1 0.5],[1 0.6 1]))>>sys=tf(num,den)>> rlocus(sys)>>grid根轨迹图:由根轨迹图的网格我们大概可以知道根轨迹上的不同部分所对应的阻尼系数,在左边横轴上的线阻尼系数对应的为1;在左半平面(非横轴)对应的阻尼系数为0到1;在右半平面阻尼系数对应为小于0;在纵轴上对应的阻尼系数为0。
下面进行验证在左边横轴上对应的阻尼系数:在左半平面(非横轴)对应的阻尼系数:在右半平面对应的阻尼系数:经过验证可知,之前的阻尼系数分析正确5-6、已知单位反馈控制系统的开环传递函数为)3()1()(-+=s s s k s G ,试绘制系统的根轨迹图,并求出使系统稳定的k 值范围。
源代码:>> num=[1 1]>> den=conv([1 0],[1 -3])>> sys=tf(num,den)>> rlocus(sys)根轨迹图:分析稳定的k的取值范围:由上图可知:当k>3的时候,根轨迹在左半平面,此时系统稳定。
阻尼分布情况由图可以看出与上题相同:在左边横轴上的线阻尼系数对应的为1;在左半平面(非横轴)对应的阻尼系数为0到1;在右半平面阻尼系数对应为小于0;在纵轴上对应的阻尼系数为0。
另外,在右边横轴上的阻尼系数为-1。
6-4、(1))12)(12.0)(11.0()1(5)()(++++=s s s s s H s G 源代码:>> num=[5 5]>> den=conv(conv([0.1 1],[0.2 1]),[2 1])>> sys=tf(num,den)>> nyquist(sys)奈氏曲线:奈氏曲线逆时针包围(-1,j0)点0次,右半平面开环极点数为0,由奈氏判据一可知该闭环系统稳定。
自动控制原理 matlab实验报告

自动控制原理实验(二)一、实验名称:基于MATLAB的控制系统频域及根轨迹分析二、实验目的:(1)、了解频率特性的测试原理及方法;(2)、理解如何用MATLAB对根轨迹和频率特性进行仿真和分析;(3)、掌握控制系统的根轨迹和频率特性两大分析和设计方法。
三、实验要求:(1)、观察给定传递函数的根轨迹图和频率特性曲线;(2)、分析同一传递函数形式,当K值不同时,系统闭环极点和单位阶跃响应的变化情况;(3)、K值的大小对系统的稳定性和稳态误差的影响;(4)、分析增加系统开环零点或极点对系统的根轨迹和性能的影响。
四、实验内容及步骤(1)、实验指导书:实验四(1)、“rlocus”命令来计算及绘制根轨迹。
会出根轨迹后,可以交互地使用“rlocfind”命令来确定点击鼠标所选择的根轨迹上任意点所对应的K值,K值所对应的所有闭环极点值也可以使用形如“[K, PCL] = rlocfind(G1)”命令来显示。
(2)、波特图:bode(G1, omga)另外,bode图还可以通过下列指令得出相位和裕角:[mag,phase,w] = bode(sys)(3)、奈奎斯特图:nuquist(G, omega)(2)课本:例4-1、4-2、4-7五实验报告要求(1)、实验指导书:实验四思考题请绘制下述传递函数的bode图和nyquist图。
1. 根据实验所测数据分别作出相应的幅频和相频特性曲线;2. 将思考题的解题过程(含源程序)写在实验报告中。
幅频特性曲线相频特性曲线Gs = zpk([10], [-5; -16; 9], 200)subplot(1, 2, 1)bode(Gs)gridsubplot(1, 2, 2)nyquist(Gs)grid(2)课本:例4-1、4-2、4-7图像结果:程序:Gs = zpk([-1], [0; -2; -3],1) rlocus(Gs)图像结果:程序:Gs = zpk([-2], [-1-j; -1+j],1) rlocus(Gs)程序:K=[0.5 1 2]for i=1:1:3num=[1,1,0,0]; den=[1,1,K(i)]; sys=tf(num,den); rlocus(sys); hold ongrid onend图像结果:目标:改变增益K和转折频率依次调节源程序:k1=[4.44,10,20];num=[1,2];den=conv([1,1],[1,2,4]);%一阶转折频率 1/T(wn1=2,wn2=1)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 num1=[1,1];den1=conv([1,2],[1,2,4]);%一阶转折频率 1/T(wn1=1,wn2=2)二阶转折频率 wn3=wn'=2,伊布西塔=1/2 t=[0:0.1:7]; %for i=1:3g0=tf(k1(i)*num,den);g=feedback(g0,1);[y,x]=step(g,t);c(:,i)=y;g1=tf(k1(i)*num1,den1);g(1)=feedback(g1,1);[y1,x]=step(g(1),t);c1(:,i)=y1;endplot(t,c(:,1),'-',t,c(:,2),'-',t,c(:,3),'-',t,c1(:,1),'-',t,c1(:,2), '-',t,c1(:,3),'-');gridxlabel('Time/sec'),ylabel('out')结果分析:在本题中(1)改变k值:k值越大,超调量越大,调节时间越长,峰值时间越短,稳态误差越小(2)改变转折频率:超调量,调节时间,峰值时间,稳态误差同样有相应的变化。
线性系统的根轨迹-自动控制原理实验报告

自动控制原理实验报告实验题目:线性系统的根轨迹班级:学号:姓名:指导老师:实验时间:一、实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、实验内容同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围。
2.1绘制下面系统的根轨迹曲线)136)(22()(22++++=s s s s s Ks G程序:G=tf([1],[1 8 27 38 26 0]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统 step(G_c) %绘制闭环系统的阶跃响应曲线-12-10-8-6-4-20246-10-8-6-4-20246810Root LocusReal AxisI m a g i n a r y A x i s0204060801001201400.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围:K>28.74252.2绘制下面系统的根轨迹曲线)10)(10012)(1()12()(2+++++=s s s s s K s G 程序:G=tf([1 12],[1 23 242 1220 1000]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统 step(G_c) %绘制闭环系统的阶跃响应曲线-60-50-40-30-20-100102030-50-40-30-20-1001020304050Root LocusReal AxisI m a g i n a r y A x i s01234560.0020.0040.0060.0080.010.012Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围: K>1.1202e+032.3绘制下面系统的根轨迹曲线)11.0012.0)(10714.0()105.0()(2++++=s s s s s K s G 程序:G=tf([5 100],[0.08568 1.914 17.14 100 0]); rlocus (G); %绘制系统的根轨迹[k,r]=rlocfind(G) %确定临界稳定时的增益值k 和对应的极点r G_c=feedback(G,1); %形成单位负反馈闭环系统step(G_c) %绘制闭环系统的阶跃响应曲线-60-50-40-30-20-10010203040-60-40-200204060Root LocusReal AxisI m a g i n a r y A x i s012345670.10.20.30.40.50.60.70.80.91Step ResponseTime (sec)A m p l i t u d e得出在单位阶跃负反馈下使得闭环系统稳定的K 值的范围:K> 7.8321根据实验结果分析根轨迹的绘制规则:⑴绘制根轨迹的相角条件与系统开环根轨迹增益 值的大小无关。
自动控制原理实验报告根轨迹分析法

相关根轨迹知识
根轨迹的概念 根轨迹是开环系统某一参数从零变化到无穷大时, 闭环系 统特征根在 s 平面上变化的轨迹。 增设零、极点对根轨迹的影响 (1)增加开环零点对根轨迹的影响 第一,加入开环零点,改变渐近线的条数和渐近线的倾角; 第二,增加开环零点,相当于增加微分作用,使根轨迹向左 移动或弯曲,从而提高了系统的相对稳定性。系统阻尼增加,过 渡过程时间缩短; 第三,增加的开环零点越接近坐标原点,微分作用越强,系 统的相对稳定性越好。 (2)增加开环极点对根轨迹的影响 第一,加入开环极点,改变渐近线的条数和渐近线的倾角; 第二,增加开环极点,相当于增加积分作用,使根轨迹向右 移动或弯曲,从而降低了系统的相对稳定性。系统阻 尼减小,过渡过程时间加长;
-4-
五、实验过程
第一题 Gc=1:
Gc=s+5:
Gc=(s+2)(s+3):
-5-
Gc=1/(s+5):
第二题 第 一 步 : 在 MATLAB 的 命 令 窗 口 中 键 入 “ num=[1 3];den=[1 2 0];rlocus(num,den)” ,得图如下:
第二步: 第三步:
第三题 第一步:由已知条件 ts(△=2%)≤4s,超调量≤40%得
s ( s 2)
1 。作 s5
确定系统具有最大的超调量时的根轨迹增益,并作时域 仿真验证;(2)确定系统阶跃响应无超调时的根轨迹取值 范围,并作时域仿真验证 3、已知一单位反馈系统的开环传递函数为 ss 0.8试加入一 个串联超前校正控制(其中,|z|<|p|) ,使得闭环系统 的 ts(△=2%)≤4s,超调量≤40%。
-7-
本为图标的切线与 K 的横坐标的交点所得的纵坐标再减去延迟时间。 随后按图慢慢调整数值,一定要有耐心。 第二题中,Step 的属性不能忘改,否则横轴(0,1)处恒为 1。 分母出 S 前的系数必须小于 1(阻尼比小于 1) ,之后改改分子,调整 调整 S 前的系数并保持 S^2 前的系数不变 (因为分子分母都可约分) , 曲线即可得出。
自控仿真实验报告根轨迹

自控仿真实验报告根轨迹《自动控制原理》MATLAB分析与设计仿真实验报告《自动控制原理》MATLAB分析与设计仿真实验任务书(2010)一.仿真实验内容及要求:1.MATLAB软件要求学生通过课余时间自学掌握MATLAB软件的基本数值运算、基本符号运算、基本程序设计方法及常用的图形命令操作;熟悉MATLAB仿真集成环境Simulink的使用。
2.各章节实验内容及要求1)第三章线性系统的时域分析法? 对教材P136.3-5系统进行动态性能仿真,并与忽略闭环零点的系统动态性能进行比较,分析仿真结果;? 对教材P136.3-9系统的动态性能及稳态性能通过的仿真进行分析,说明不同控制器的作用;在MATLAB环境下完成英文讲义P153.E3.3。
,在Ka?100时,试采? 对英文讲义中的循序渐进实例“Disk Drive Read System”用微分反馈使系统的性能满足给定的设计指标。
2)第四章线性系统的根轨迹法在MATLAB环境下完成英文讲义P157.E4.5;;? 利用MATLAB绘制教材P181.4-5-(3)? 在MATLAB环境下选择完成教材第四章习题4-10或4-18,并对结果进行分析。
3)第五章线性系统的频域分析法利用MATLAB绘制本章作业中任意2个习题的频域特性曲线; 4)第六章线性系统的校正利用MATLAB选择设计本章作业中至少2个习题的控制器,并利用系统的单位阶跃响应说明所设计控制器的功能。
5)第七章线性离散系统的分析与校正利用MATLAB完成教材P383.7-20的最小拍系统设计及验证。
利用MATLAB完成教材P385.7-25的控制器的设计及验证。
二.仿真实验时间安排及相关事宜1.依据课程教学大纲要求,仿真实验共6学时,教师可随课程进度安排上机时间,学生须在实验之前做好相应的准备,以确保在有限的机时内完成仿真实验要求的内容;2.实验完成后按规定完成相关的仿真实验报告;3.仿真实验报告请参照有关样本制作并打印装订;4.仿真实验报告必须在本学期第15学周结束之前上交授课教师。
自动控制原理--控制系统的根轨迹分析及特殊根轨迹

j1
s0
j1
jk
s sk
j1
jk
单位阶跃响应为
n
y(t) A0 Akeskt k 1
m
m
Ks zi Kzi
A0
i1 n
s sj
i1 n
GB(0)
sj
j1
s0
j1
m
m
K s zi
Ak
i1 n
s sj
1 s
K sk zi
i1 n
sk sk sj
jk
1
s2
100 8s 100
4 3
os1
1.5
1.7
可求得 0.4, ,n 10
s3
所以 % e 1 2 100% 25%,ts (s3.)5 n 3.5 4 0.9
j
0
利用根轨迹分析控制系统的性能
例11 分析K的变化对系统稳定性的影响
K (s 3) G(s)H (s) s(s 5)(s 6)(s2 2s 2)
增加开环极点的影响 增加极点对根轨迹形状的影响
增加开环零点的影响 增加零点对根轨迹形状的影响
例9 已知某系统闭环传递函数
GB (s) 0.67s 1
1 0.01s2
0.08s 1
试计算在单位阶跃输入时的系统输出超调量 % 和调节时间t。s
解:该闭环系统有三个极点,s1 1.5, s2,3 零4 、j9.2极点 分布如右图。
系统稳定的K的范围为: 0<K<35
例12 分析K的变化对系统的影响。设负反馈系统的开环传递函数为
K s z G(s)H(s) ss p
z p
求系统闭环根轨迹,并分析 p 2, 时z系 统4 的动态性能。
自动控制原理-线性系统的根轨迹实验报告

线性系统的根轨迹一、 实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、 实验容1. 请绘制下面系统的根轨迹曲线。
)136)(22()(22++++=s s s s s K s G )10)(10012)(1()12()(2+++++=s s s s s K s G )11.0012.0)(10714.0()105.0()(2++++=s s s s K s G 同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的围。
2. 在系统设计工具rltool 界面中,通过添加零点和极点方法,试凑出上述系统,并观察增加极、零点对系统的影响。
三、 实验结果及分析1.(1) )136)(22()(22++++=s s s s s K s G 的根轨迹的绘制: MATLAB 语言程序:num=[1];den=[1 8 27 38 26 0];rlocus(num,den)[r,k]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis') title('Root Locus')运行结果:选定图中根轨迹与虚轴的交点,单击鼠标左键得:selected_point =0.0021 + 0.9627ik =28.7425r =-2.8199 + 2.1667i-2.8199 - 2.1667i-2.3313-0.0145 + 0.9873i结论:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
由根轨迹图和运行结果知,当0<K<28.7425时,系统总是稳定的。
(2) )10)(10012)(1()12()(2+++++=s s s s s K s G 的根轨迹的绘制: MATLAB 语言程序:num=[1 12];den=[1 23 242 1220 1000];rlocus(num,den)[k,r]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis')title('Root Locus')运行结果:选定图中根轨迹与虚轴的交点,单击鼠标左键得:selected_point =k =1.0652e+003r=-11.4165 + 2.9641i-11.4165 - 2.9641i-0.0835 + 9.9528i-0.0835 - 9.9528i结论:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.5, 1.32 和 1.5, 1.32 ,阶跃响应如图 3.3 所示。
图 3.2
图 3.3
' (2)使 Z ' 3 Z , p1' 3 p1 , p2 4 p2 ,其根轨迹如图 3.4 所示。零
点为 3, 0 ,极点为 1.5, 1.32 和 1.5, 1.32 ,阶跃响应如图 3.5 所示。
图 2.1
(3)指出该类型根轨迹图形的特点,并在进一步实验中验证。
Z ' Z , Z ' Z ,绘出根轨迹,观察改变开
环零点位置对系统性能的影响;
图 2.2
' (3)取 Z ' Z ,改变 p1' 、 p 2 与 p1、p2 的大小关系,绘出根轨迹,观察改变
开环极点位置对系统性能的影响。 3.改变零极点个数对根轨迹的影响。 (1)输入参数 Z,观 察当增加一个开环零点时 根轨迹的变化, 零点位置变 化对根轨迹的影响, 对闭环 系统的响应的影响;
观察根据图 2.4 系统所绘制的根轨迹与一般根轨迹的区别,判断导致零度根 轨迹的原因。 观察根据图 2.5 系统所绘制的根轨迹,判断导致零度根轨迹的原因。 6.参数根轨迹。 绘制式(2-2)的根轨迹,并与计算机绘制图形比较。
s 3 K 2 s 2 K1 s K 1 0
(2-2)
其中 K1 及 K2 是可变参数,且其值都在 0 到∞之间。 7.绘制任意系统的根轨迹。
图 2.6
自由改变 a0、a1、a2、b0、b1、b2、b3 和 r 的值,观察绘制出的根轨迹图。
2
根轨迹仿真分析
实验报告
三、实验结果
1. 观察二极点一零点系统的 根轨迹。 如图 3.1 所示, 根轨迹始于开 环极点 1, 1.41 和 1, 1.41 , 终于开环零点 2, 0 及无穷远处, 有两条分支, 分离点为 3.73, 0 , 为一段圆弧。 2.改变开环零极点位置对根轨迹的影响。 (1)使 Z=2,p1=3,p2=4,则根轨迹如图 3.2 所示。零点为 2, 0 ,极点为
图 3.29
图 3.30
图 3.31
5.零度根轨迹。 图 2.4 所示系统根轨迹如图 3.32 所示, 图 2.5 所示系统根轨迹如图 3.33 所示。 引起零度根轨迹具有两种情况: (1)非最小相位系统中包含 s 最高次幂的系 数为负的因子; (2)控制系统中包含有正反馈内回路。由于在零度根轨迹绘制法 则中, 实轴上某一区域若右边开环实数零极点个数之和为偶数,则该区域必是根 轨迹, 故根轨迹图中在实轴上有某一点至正无穷为根轨迹时, 该图为零度根轨迹。
1, 2.83 。结果表明,引入开
环零点 3, 0 与原系统开环极点 对消,则根轨迹向左移,系统稳定性增强。 4.互逆系统的根轨迹。 式(2-1)中,G1 s H1 s 的根轨迹如图 3.30 所示,G2 s H 2 s 的根轨迹如图 3.31 所示,可以看出互逆系统的根轨迹图像除零极点位置交换外,图形无变化
s 1s 2s 3 ss 2s 3 ss 2s 3 G2 s H 2 s s 1s 2s 3
G1 s H 1 s
观察如式(2-1)描述的互逆系统根轨迹的异同。 5.零度根轨迹。
(2-1)
图 2.4
图 2.5
图 3.8
图 3.9
' 再使 Z ' 2 Z , p1' 2 p1 , p2 2 p2 ,其根轨迹如图 3.10 所示。零点
为 2, 0 ,极点为 1, 1.41 和 1, 1.41 ,阶跃响应如图 3.11 所示。
4
根轨迹仿真分析
实验报告
图 3.10
9
ቤተ መጻሕፍቲ ባይዱ
根轨迹仿真分析
实验报告
图 3.32
图 3.33
6.参数根轨迹。 绘制式(2-2)的根轨迹。 以 K1 为参量绘制根轨迹,传递函数为
Gs H s K1 s 1 s3
K 2 0
根轨迹如图 3.34 所示。 以 K2 为参量绘制根轨迹,传递函数为
Gs H s
8, 0 ,极点为 3, 0 , 1, 2.83 , 1, 2.83 , 9, 0 。
图 3.26
图 3.27
以上结果表明,增加开环偶极子前后的根轨迹几乎没有差别,开环偶极子对 系统动态性能和稳态性能的影响很小, 几乎可以略去。 ( 6 )若引入开环极点 2, 0 与原 系统零点对消,则其根轨迹如图 3.28 所 示。零点为 2, 0 ,极点为 3, 0 ,
图 3.4
3
图 3.5
根轨迹仿真分析
实验报告
' 再使 Z ' 1 Z , p1' 3 p1 , p2 4 p2 ,其根轨迹如图 3.6 所示。零点为
1, 0 ,极点为 1.5, 1.32 和 1.5, 1.32 ,阶跃响应如图 3.7 所示。
图 3.6
图 3.24
7
根轨迹仿真分析
实验报告
1, 0 , 1, 0 , 极 点 为 3, 0 , 1, 2.83 , 1, 2.83 。
若引入重极点 1, 0 ,则其根轨 迹如图 3.25 所示,零点为 2, 0 ,极 点为 3, 0 , 1, 2.83 , 1, 2.83 ,
图 3.11
实验结果表明所增加的开环极点越接近原点,积分作用越强,超调量越大, 系统的相对稳定性越差。 3.改变零极点个数对根轨迹的影响。 (1)先不改变零极点个数,其根轨迹如图 3.12 所示,阶跃响应如图 3.13。
图 3.12
图 3.13
若使 a=1,b=0,Z=1,P=0,则其根轨迹如图 3.14,零点为 1, 0 , 2, 0 , 极点为 3, 0 , 1, 2.83 , 1, 2.83 ,阶跃响应如图 3.15。
图 3.18
图 3.19
若使 a=0,b=1,Z=0,P=4,则其根轨迹如图 3.20,零点为 2, 0 ,极点为
3, 0 , 1, 2.83 , 1, 2.83 , 4, 0 ,阶跃响应如图 3.21。
6
根轨迹仿真分析
实验报告
图 3.20
图 3.21
上述实验结果表明,增加开环极点相当于增加积分环节,使根轨迹向右移动 或弯曲, 从而降低了系统的相对稳定性, 并使系统阻尼减小, 过渡过程时间加长。 增加的开环极点越接近坐标原点,积分作用越强,系统的相对稳定性越差。 (3) 若使 a=1, b=1, Z=1, P=4, 即同时引入开环零点 1, 0 和极点 4, 0 , 则其根轨迹如图 3.22,阶跃响应如图 3.23。
图 3.7
根据实验结果, 可以说明增加开环零点可以改善系统的稳定性,且所增加的 开环零点越接近坐标原点,微分作用越强,系统的相对稳定性越好
' (3)使 Z ' 2 Z , p1' 4 p1 , p2 5 p2 ,其根轨迹如图 3.8 所示。零
点为 2, 0 ,极点为 2, 2 和 2, 2 ,阶跃响应如图 3.9 所示。
根轨迹如图 3.35 所示。
K2s2 s 3 K1 s K1
图 3.34
图 3.35
7.绘制任意系统的根轨迹。 以《自动控制理论》 (夏超英编著,科学出版社,2010)第 161 页习题 4-3 (c)为例绘制根轨迹。 4-3(c) 设单位反馈控制系统的开环传递函数为
10
根轨迹仿真分析
实验报告
Gs
K s 5 ss 2s 3
试概略绘制出相应的 K 从 0 变化时的闭环根轨迹。 如图 3.36 所示。
图 3.36
11
1, 2.83 , 1, 2.83 , 2, 0 。结果
图 3.28
8
根轨迹仿真分析
实验报告
表明,引入开环极点 2, 0 与原系统零点对消,则根轨迹向右移,系统的稳定性 变差。 若引入开环零点 3, 0 与原 系统开环极点对消,则其根轨迹 如图 3.29 所示。零点为 2, 0 , 极点为 3, 0 , 3, 0 , 1, 2.83 ,
图 3.22
图 3.23
结果表明,同时引入开环零点和极 点对根轨迹的影响是:哪一个离原点更 近,则哪一个对根轨迹的影响越大。图 3.22 为零点距离原点较近,则根轨迹向 左移,系统地相对稳定性增强。 (4)若引入重零点 1, 0 ,则其根 轨迹如图 3.24 所示,零点为 2, 0 ,
以上结果表明, 增加开环零点相当于增加微分环节,使根轨迹向左移动或弯 曲,从而提高了系统的相对稳定性,并且使系统阻尼增加,过渡过程时间缩短。 零点越靠近原点,系统稳定性越好,但动态性能较差。 (2)若使 a=0,b=1,Z=0,P=2,则其根轨迹如图 3.18,零点为 2, 0 , 极点为 3, 0 , 1, 2.83 , 1, 2.83 , 2, 0 ,阶跃响应如图 3.19。
二、实验内容
1.观察二极点一零点系统的根轨迹。 (1)指出该根轨迹的起始点与终止点, 并说明它们与开环传函零、极点的关系; (2)指出根轨迹的分支数,在图上读出 分离点坐标; 2.改变开环零极点位置对根轨迹的影响。 (1)给定一组 Z,p1,p2 的值,绘出 它的根轨迹;
' ( 2 ) 取 p1' p1 , p 2 p2 , 分 别 使
1, 0 , 1, 0 。
图 3.25
(5)未增加开环偶极子时,其根轨迹如图 3.26 所示,零点为 2, 0 ,极点 为 3, 0 , 1, 2.83 , 1, 2.83 。 若增加一对开环偶极子
