根轨迹分析实验报告
自动控制根轨迹实验报告
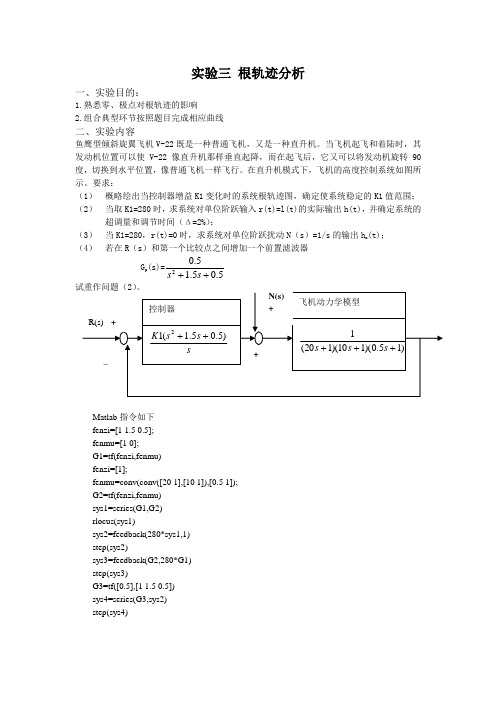
实验三 根轨迹分析一、实验目的:1.熟悉零、极点对根轨迹的影响2.组合典型环节按照题目完成相应曲线二、实验内容鱼鹰型倾斜旋翼飞机V-22既是一种普通飞机,又是一种直升机。
当飞机起飞和着陆时,其发动机位置可以使V-22像直升机那样垂直起降,而在起飞后,它又可以将发动机旋转90度,切换到水平位置,像普通飞机一样飞行。
在直升机模式下,飞机的高度控制系统如图所示。
要求:(1) 概略绘出当控制器增益K1变化时的系统根轨迹图,确定使系统稳定的K1值范围; (2) 当取K1=280时,求系统对单位阶跃输入r(t)=l(t)的实际输出h(t),并确定系统的超调量和调节时间(Δ=2%);(3) 当K1=280,r(t)=0时,求系统对单位阶跃扰动N (s )=1/s 的输出h n (t); (4) 若在R (s )和第一个比较点之间增加一个前置滤波器 G p (s)=5.05.15.02++s sMatlab 指令如下 fenzi=[1 1.5 0.5]; fenmu=[1 0];G1=tf(fenzi,fenmu) fenzi=[1];fenmu=conv(conv([20 1],[10 1]),[0.5 1]); G2=tf(fenzi,fenmu) sys1=series(G1,G2) rlocus(sys1)sys2=feedback(280*sys1,1) step(sys2)sys3=feedback(G2,280*G1) step(sys3)G3=tf([0.5],[1 1.5 0.5]) sys4=series(G3,sys2) step(sys4)(1)(3)(2)(4)三、结果分析1.根在左半平面,系统稳定;根在虚轴上临界稳定;根在右半平面系统不稳定。
2.当k>1时,特征方程为一对共轭复根,系统为欠阻尼系统,单位阶跃响应为阻尼振荡过程,振荡幅度或超调量随k值的增加而增大,但调整时间不会有显著变化。
根轨迹实验报告

根轨迹实验报告根轨迹实验报告引言:根轨迹是控制系统理论中的一个重要概念,它描述了系统在参数变化下的稳定性和响应特性。
本实验旨在通过实际操作和数据分析,深入理解根轨迹的原理和应用。
通过对比不同系统的根轨迹,可以更好地理解系统的稳定性和控制性能。
一、实验目的本实验的目的是通过实际操作和数据分析,加深对根轨迹的理解,掌握根轨迹的绘制方法和分析技巧。
同时,通过对比不同系统的根轨迹,分析系统参数对根轨迹的影响,进一步认识系统的稳定性和控制性能。
二、实验装置与方法实验所需的装置包括控制系统实验台、计算机和相应的控制软件。
实验过程中,首先将系统接入实验台,通过控制软件设置系统参数,然后进行数据采集和分析。
根据实验要求,可以改变系统参数、增加干扰等,观察根轨迹的变化。
三、实验结果与分析在实验过程中,我们分别绘制了不同系统的根轨迹,并进行了数据分析。
通过观察根轨迹的形状和位置,我们可以判断系统的稳定性和响应特性。
以一个简单的一阶系统为例,我们改变了系统的比例增益和时间常数,绘制了对应的根轨迹。
通过观察根轨迹的位置和形状,我们可以发现以下规律:当比例增益增大时,根轨迹向左移动,系统的稳定性增强;当时间常数增大时,根轨迹变得更加平缓,系统的响应速度变慢。
在另一个二阶系统的实验中,我们改变了系统的阻尼比和自然频率,绘制了对应的根轨迹。
通过观察根轨迹的形状和分布,我们可以得出以下结论:当阻尼比增大时,根轨迹变得更加收敛,系统的稳定性提高;当自然频率增大时,根轨迹变得更加散布,系统的响应速度增加。
通过对比不同系统的根轨迹,我们可以进一步分析系统的稳定性和控制性能。
例如,当两个系统的根轨迹重合或者相似,可以认为它们具有相似的稳定性和响应特性;而当根轨迹相交或者离散较大时,可能存在系统不稳定或者不良的控制性能。
四、实验总结通过本次实验,我们深入了解了根轨迹的原理和应用。
通过实际操作和数据分析,我们掌握了根轨迹的绘制方法和分析技巧。
自动控制理论实验报告-根轨迹仿真分析

1.5, 1.32 和 1.5, 1.32 ,阶跃响应如图 3.3 所示。
图 3.2
图 3.3
' (2)使 Z ' 3 Z , p1' 3 p1 , p2 4 p2 ,其根轨迹如图 3.4 所示。零
点为 3, 0 ,极点为 1.5, 1.32 和 1.5, 1.32 ,阶跃响应如图 3.5 所示。
图 2.1
(3)指出该类型根轨迹图形的特点,并在进一步实验中验证。
Z ' Z , Z ' Z ,绘出根轨迹,观察改变开
环零点位置对系统性能的影响;
图 2.2
' (3)取 Z ' Z ,改变 p1' 、 p 2 与 p1、p2 的大小关系,绘出根轨迹,观察改变
开环极点位置对系统性能的影响。 3.改变零极点个数对根轨迹的影响。 (1)输入参数 Z,观 察当增加一个开环零点时 根轨迹的变化, 零点位置变 化对根轨迹的影响, 对闭环 系统的响应的影响;
观察根据图 2.4 系统所绘制的根轨迹与一般根轨迹的区别,判断导致零度根 轨迹的原因。 观察根据图 2.5 系统所绘制的根轨迹,判断导致零度根轨迹的原因。 6.参数根轨迹。 绘制式(2-2)的根轨迹,并与计算机绘制图形比较。
s 3 K 2 s 2 K1 s K 1 0
(2-2)
其中 K1 及 K2 是可变参数,且其值都在 0 到∞之间。 7.绘制任意系统的根轨迹。
图 2.6
自由改变 a0、a1、a2、b0、b1、b2、b3 和 r 的值,观察绘制出的根轨迹图。
2
根轨迹仿真分析
实验报告
三、实验结果
1. 观察二极点一零点系统的 根轨迹。 如图 3.1 所示, 根轨迹始于开 环极点 1, 1.41 和 1, 1.41 , 终于开环零点 2, 0 及无穷远处, 有两条分支, 分离点为 3.73, 0 , 为一段圆弧。 2.改变开环零极点位置对根轨迹的影响。 (1)使 Z=2,p1=3,p2=4,则根轨迹如图 3.2 所示。零点为 2, 0 ,极点为
自动控制原理实验报告根轨迹分析法

相关根轨迹知识
根轨迹的概念 根轨迹是开环系统某一参数从零变化到无穷大时, 闭环系 统特征根在 s 平面上变化的轨迹。 增设零、极点对根轨迹的影响 (1)增加开环零点对根轨迹的影响 第一,加入开环零点,改变渐近线的条数和渐近线的倾角; 第二,增加开环零点,相当于增加微分作用,使根轨迹向左 移动或弯曲,从而提高了系统的相对稳定性。系统阻尼增加,过 渡过程时间缩短; 第三,增加的开环零点越接近坐标原点,微分作用越强,系 统的相对稳定性越好。 (2)增加开环极点对根轨迹的影响 第一,加入开环极点,改变渐近线的条数和渐近线的倾角; 第二,增加开环极点,相当于增加积分作用,使根轨迹向右 移动或弯曲,从而降低了系统的相对稳定性。系统阻 尼减小,过渡过程时间加长;
-4-
五、实验过程
第一题 Gc=1:
Gc=s+5:
Gc=(s+2)(s+3):
-5-
Gc=1/(s+5):
第二题 第 一 步 : 在 MATLAB 的 命 令 窗 口 中 键 入 “ num=[1 3];den=[1 2 0];rlocus(num,den)” ,得图如下:
第二步: 第三步:
第三题 第一步:由已知条件 ts(△=2%)≤4s,超调量≤40%得
s ( s 2)
1 。作 s5
确定系统具有最大的超调量时的根轨迹增益,并作时域 仿真验证;(2)确定系统阶跃响应无超调时的根轨迹取值 范围,并作时域仿真验证 3、已知一单位反馈系统的开环传递函数为 ss 0.8试加入一 个串联超前校正控制(其中,|z|<|p|) ,使得闭环系统 的 ts(△=2%)≤4s,超调量≤40%。
-7-
本为图标的切线与 K 的横坐标的交点所得的纵坐标再减去延迟时间。 随后按图慢慢调整数值,一定要有耐心。 第二题中,Step 的属性不能忘改,否则横轴(0,1)处恒为 1。 分母出 S 前的系数必须小于 1(阻尼比小于 1) ,之后改改分子,调整 调整 S 前的系数并保持 S^2 前的系数不变 (因为分子分母都可约分) , 曲线即可得出。
自动控制原理(系统根轨迹分析)
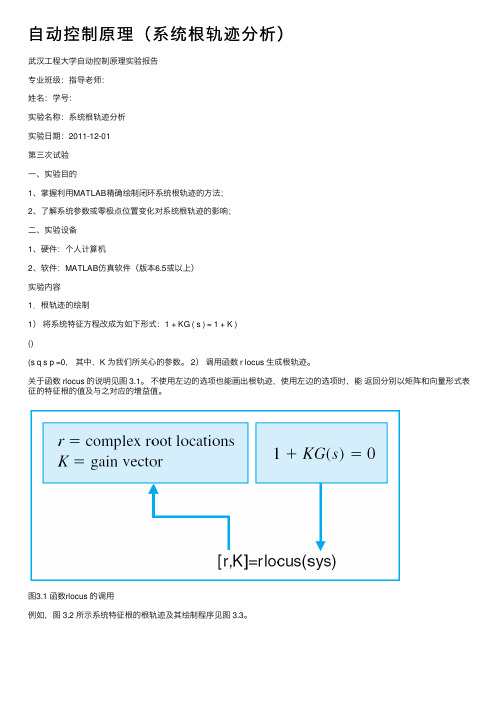
⾃动控制原理(系统根轨迹分析)武汉⼯程⼤学⾃动控制原理实验报告专业班级:指导⽼师:姓名:学号:实验名称:系统根轨迹分析实验⽇期:2011-12-01第三次试验⼀、实验⽬的1、掌握利⽤MATLAB精确绘制闭环系统根轨迹的⽅法;2、了解系统参数或零极点位置变化对系统根轨迹的影响;⼆、实验设备1、硬件:个⼈计算机2、软件:MATLAB仿真软件(版本6.5或以上)实验内容1.根轨迹的绘制1)将系统特征⽅程改成为如下形式:1 + KG ( s ) = 1 + K )()(s q s p =0,其中,K 为我们所关⼼的参数。
2)调⽤函数 r locus ⽣成根轨迹。
关于函数 rlocus 的说明见图 3.1。
不使⽤左边的选项也能画出根轨迹,使⽤左边的选项时,能返回分别以矩阵和向量形式表征的特征根的值及与之对应的增益值。
图3.1 函数rlocus 的调⽤例如,图 3.2 所⽰系统特征根的根轨迹及其绘制程序见图 3.3。
图3.2 闭环系统⼀图3.3 闭环系统⼀的根轨迹及其绘制程序注意:在这⾥,构成系统s ys 时,K 不包括在其中,且要使分⼦和分母中s最⾼次幂项的系数为1。
当系统开环传达函数为零、极点形式时,可调⽤函数 z pk 构成系统 s ys : sys = zpk([zero],[pole],1);当系统开环传达函数⽆零点时,[zero]写成空集[]。
对于图 3.2 所⽰系统,G(s)H(s)=)2()1(++s s s K *11+s =)3)(2()1(+++s s s s K . 可如下式调⽤函数 z pk 构成系统 s ys :sys=zpk([-1],[0 -2 -3],1)若想得到根轨迹上某个特征根及其对应的 K 的值,⼀种⽅法是在调⽤了函数 rlocus 并得到了根轨迹后调⽤函数 r locfind 。
然后,将⿏标移⾄根轨迹图上会出现⼀个可移动的⼤⼗字。
将该⼗字的中⼼移⾄根轨迹上某点,再点击⿏标左键,就可在命令窗⼝看到该点对应的根值和 K 值了。
根轨迹实验报告

根轨迹实验报告
《根轨迹实验报告》
根轨迹实验是一种常见的实验方法,用于研究植物根系的生长和发育。
通过这种实验,我们可以观察和记录植物根系在不同环境条件下的生长情况,从而更好地了解植物的生长规律和适应能力。
在进行根轨迹实验时,首先需要选择一种适合的植物种类,并在适当的条件下培养植物。
然后,我们将植物的根系放置在透明的介质中,如琼脂或琼脂糖,使其根系在介质中生长。
随着时间的推移,我们可以观察到根系在介质中的生长情况,并记录下根系的生长轨迹。
通过根轨迹实验,我们可以研究植物根系在不同环境条件下的生长速度、生长方向以及根系的分枝情况。
这些研究结果不仅可以帮助我们更好地了解植物根系的生长规律,还可以为植物栽培和种植提供参考,以及为植物生长环境的改善提供科学依据。
在进行根轨迹实验时,我们需要注意保持实验条件的稳定性,避免外界因素对实验结果的影响。
同时,我们还需要精确记录实验过程中的数据和观察结果,以便后续的数据分析和研究。
总的来说,根轨迹实验是一种重要的植物生长研究方法,通过这种实验,我们可以更好地了解植物根系的生长规律和适应能力,为植物栽培和种植提供科学依据。
希望通过我们的努力,可以为植物生长领域的研究和实践做出贡献。
线性系统的根轨迹法实验报告

线性系统的根轨迹法实验报告实验二线性系统的根轨迹法一,实验目的1,掌握matlab绘制根轨迹的方法。
2,观察k值变化对系统稳定性的影响。
3,掌握系统临界稳定情况下k值得求取。
4,了解增设零点对系统稳定的影响以及改善系统稳定性的方法。
二,实验原理根轨迹的概念:所谓根轨迹就是当开环系统某一参数从零变到无穷大时,闭环系统特征方程式的根在s平面上变化的轨迹。
根轨迹与系统性能:有了根轨迹就可以分析系统的各种性能了,稳定性的判定,当开环增益从零变到无穷大时,根轨迹不会越过虚轴进入s平面的右半平面,此时K的范围为系统稳定的范围,根轨迹与虚轴的交点处的K值,为系统的临界开环增益,开根轨迹进入s平面的右半平面时所对应的K值为系统不稳定的情况。
三,实验内容A、设单位负反馈系统的开环传递函数为G(s)=K/(s*(s+1)(s+5)) (1) 绘制系统的根轨迹,并将手工绘制结果与实验绘制结果比较; (2) 从实验结果上观察系统稳定的K 值范围;(3) 用simulink 环境观察系统临界稳定时的单位阶跃响应分析:绘制根轨迹的matlab文本为clfnum=1;den=conv([1 1 0],[1 5]); rlocus(num,den) %绘制系统根轨迹1,得到如图的根轨迹图:2,用鼠标点击根轨迹与虚轴处的交点可得到临界稳定的开环增益K=30,所以系统稳定的K值范围为0―30。
3,在simulink环境下按下图连接电路:取增益为30的时候在示波器下观察单位节约响应,输出波形为:由图可以看出单位阶跃响应的输出为等幅的震荡输出,所以此时系统为临界稳定状态。
当改变开环增益为50和20时观察示波器,得到输出波形分别为:由图可知当增益K为50时输出为不稳定的震荡输出,此时系统不稳定,当增益K为20时输出的波形震荡越来越缓慢,最后趋于稳定,所以此时的系统是稳定的。
B,设单位反馈控制系统的开环传递函数为G(S)=K(s+3)/s(s+1)(s+2)(1) 仿照上题绘制系统的根轨迹,并判断系统的稳定性; 参照第一题得到matlab命令文本为:clfnum=1;den=conv([1 1 0],[1 2]); rlocus(num,den) %绘制系统根轨迹得到如图的根轨迹图:1,由图可知根轨迹没有进入s平面右半平面,所以系统在K=0到K=?都是稳定的。
自动控制原理-线性系统的根轨迹实验报告

线性系统的根轨迹一、 实验目的1. 熟悉MATLAB 用于控制系统中的一些基本编程语句和格式。
2. 利用MATLAB 语句绘制系统的根轨迹。
3. 掌握用根轨迹分析系统性能的图解方法。
4. 掌握系统参数变化对特征根位置的影响。
二、 实验容1. 请绘制下面系统的根轨迹曲线。
)136)(22()(22++++=s s s s s K s G )10)(10012)(1()12()(2+++++=s s s s s K s G )11.0012.0)(10714.0()105.0()(2++++=s s s s K s G 同时得出在单位阶跃负反馈下使得闭环系统稳定的K 值的围。
2. 在系统设计工具rltool 界面中,通过添加零点和极点方法,试凑出上述系统,并观察增加极、零点对系统的影响。
三、 实验结果及分析1.(1) )136)(22()(22++++=s s s s s K s G 的根轨迹的绘制: MATLAB 语言程序:num=[1];den=[1 8 27 38 26 0];rlocus(num,den)[r,k]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis') title('Root Locus')运行结果:选定图中根轨迹与虚轴的交点,单击鼠标左键得:selected_point =0.0021 + 0.9627ik =28.7425r =-2.8199 + 2.1667i-2.8199 - 2.1667i-2.3313-0.0145 + 0.9873i结论:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
由根轨迹图和运行结果知,当0<K<28.7425时,系统总是稳定的。
(2) )10)(10012)(1()12()(2+++++=s s s s s K s G 的根轨迹的绘制: MATLAB 语言程序:num=[1 12];den=[1 23 242 1220 1000];rlocus(num,den)[k,r]=rlocfind(num,den)gridxlabel('Real Axis'),ylabel('Imaginary Axis')title('Root Locus')运行结果:选定图中根轨迹与虚轴的交点,单击鼠标左键得:selected_point =k =1.0652e+003r=-11.4165 + 2.9641i-11.4165 - 2.9641i-0.0835 + 9.9528i-0.0835 - 9.9528i结论:根轨迹与虚轴有交点,所以在K 从零到无穷变化时,系统的稳定性会发生变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程名称: 控制理论乙 指导老师: 成绩: 实验名称: 控制系统的根轨迹分析 实验类型: 同组学生姓名:
一、实验目的和要求(必填) 二、实验内容和原理(必填)
三、主要仪器设备(必填) 四、操作方法和实验步骤
五、实验数据记录和处理 六、实验结果与分析(必填)
七、讨论、心得
一、实验目的和要求
1. 掌握用计算机辅助分析法分析控制系统的根轨迹
2. 熟练掌握Simulink 仿真环境
二、实验内容和原理
1. 实验内容
一开环系统传递函数为
22)
34()2()(+++=s s s k s G 绘制出此闭环系统的根轨迹,并分析系统的稳定性。
2. 实验原理
根轨迹是指,当开环系统某一参数(一般来说,这一参数选作开环系统的增益k )从零变到无穷大时,死循环系统特征方程的根在s 平面上的轨迹。
因此,从根轨迹,可分析系统的稳定性、稳态性能、动态性能。
同时,对于设计系统可通过修改设计参数,使闭环系统具有期望的零极点分布,因此根轨迹对系统设计也具有指导意义。
在MATLAB 中,绘制根轨迹有关的函数有:rlocus ,rlocfind ,pzmap 等。
3. 实验要求
(1)编制MA TLAB 程序,画出实验所要求根轨迹, 求出系统的临界开环增益,并用闭环系统的冲击响应证明之。
(2)在Simulink 仿真环境中,组成系统的仿真框图,观察临界开环增益时系统单位阶跃响应曲线并记录之。
三、主要仪器设备
计算机一台以及matlab 软件,simulink 仿真环境
四、实验源代码
>> A=[1 2];
>> B=conv([1 4 3],[1 4 3]);
>> G=tf(A,B)
G =
s + 2
-------------------------------
s^4 + 8 s^3 + 22 s^2 + 24 s + 9
Continuous-time transfer function.
>> figure
>> pzmap(G)
>> rlocus(G)
>> x=solve('s^4-22*s^2+9+2*k=0','-8*s^3+(24+k)*s=0')
x =
k: [5x1 sym]
s: [5x1 sym]
>> x0=x.k
x0 =
-9/2
-32*3^(1/2)
32*3^(1/2)
-32*3^(1/2)
32*3^(1/2)
>> x1=x0(3)
x1 =
32*3^(1/2)
>> G1=G*32*3^(1/2)
G1 =
55.43 s + 110.9
-------------------------------
s^4 + 8 s^3 + 22 s^2 + 24 s + 9
Continuous-time transfer function.
>> G2=G1/(1+G1)
G2 =
55.43 s^5 + 554.3 s^4 + 2106 s^3 + 3769 s^2 + 3159 s + 997.7
-----------------------------------------------------------------------------------
s^8 + 16 s^7 + 108 s^6 + 455.4 s^5 + 1440 s^4 + 3306 s^3 + 4741 s^2 + 3591 s + 1079 Continuous-time transfer function.
>> impulse(G2) >> xlim([0 20])
2.simulink仿真
(1)新建一个simulink仿真文件,然后按照框架图连接如下图所示
(2)分别带入不同的K值,运行仿真,得到最终的波形如下图所示(其中K=32*3^(1/2)=55.425为临界开环增益)
K=32
K=55.425
K=65
五、心得、体会
1.通过本次实验,学会了如何用MATLAB程序来实现根轨迹分析,包括根轨迹图的绘制、根轨迹的临界开环增益求解方法、临界与非临界冲激响应的实现方法等,并且进一步掌握了simulink方法的应用,对我们在课上学习根轨迹更有着促进作用。
2.在根轨迹求解函数中,我们运用了s=solve(‘方程’,’方程’)的方法来求解,实际上还有两种其他方法可以求解方程。
一种是用s=roots(‘方程’),这种方法和上述方法基本一样,只是调用的时候有些差别;另一种方法是直接用复数方程来替代原来的实数多项式方程,这种方法较为直接,且减少了人为计算量,不过最终的根也是用复数形式来表示,当你需要引用的时候,可能也需要real()函数和imag()函数来求实部和虚部,也会比较麻烦。
3.另外,在求临界开环增益的过程中,我们同样应用了rlocfind()函数,可以在图上直观地求解临界开环增益。
不过,这时的临界开环增益只能是准确值的一种近似,而且这种方法需要提前实现rlocus()函数,让根轨迹图显示出来,然后再用鼠标指向根轨迹与y轴交点,可能会存在一定误差,不过实验证明这点误差并不影响整体结果,而且交点指示也比较明确。
4.在求出临界开环增益之后,我们在用simulink仿真过程中,为了比较开环临界增益5
5.425的准确性,我们分别取了一个大于临界开环增益的数和一个小于临界开环增益的数,结果显示我们的计算是正确的。
5.在根轨迹的开环临界冲激响应时,由于自动求出来的x在0-70之间,等幅振荡波形非常密集,无法观察图像,所以加一条语句xlim([0 20]),减少横坐标的最大范围,来保证实验波形的美观。
