广东工业大学线性代数试卷A卷1(含答案)
线性代数试题线性代数试卷及答案大全(173页大合集)

属于 对应的特征向量为 ,单位化: ,
属于 对应的特征向量为 ,单位化: ,
取 ,则有 。
八、(本题8分)证明:由
得 的特征值 ,
,
故 的最大特征值是 。
试卷2
闭卷考试时间:100分钟
一、填空题(本题15分,每小题3分)
1、若n阶行列式零元素的个数超过n(n-1)个,则行列式为。
三、(本题8分)解:从第一行开始,每行乘 后逐次往下一行加,再按最后一行展开得:
原式= 。
四、(本题12分)解:由 ,得: ,
可逆,故 ;
由于 , 。
五、(本题14分)解:(1)令 , ,
则 线性无关,故 是向量组 的一个极大无关组;
(2)由于4个3维向量 线性相关,
若 线性无关,则 可由 线性表示,与题设矛盾;
A:矩阵A必没有零行
B:矩阵A不一定是阶梯形矩阵
C:矩阵A必有零行
D:矩阵A的非零行中第一个不等于零的元素都是1
非齐次线性方程组Ax=b中,系数矩阵A和增广矩阵(A b)的秩都等于3,A是3×4矩阵,则▁▁▁。【A】
A:方程组有无穷多解
B:无法确定方程组是否有解
C:方程组有唯一解
D:方程组无解
试卷1
4、若 阶实方阵 , 为 阶单位矩阵,则( )。
(A) (B)
(C) (D)无法比较 与 的大小
5、设 , , , ,其中 为任意常数,则下列向量组线性相关的为( )。
(A) ( B) (C) (D)
三、(10分)计算 阶行列式 , 的主对角线上的元素都为 ,其余位置元素都为 ,且 。
四、(10分)设3阶矩阵 、 满足关系: ,且 ,求矩阵 。
B:Ax=0的基础解系中的解向量的个数不可能为n-r
广东工业大学考试试卷2020年高数A1考试卷

广东工业大学试卷用纸,共2页,第1页广东工业大学考试试卷(B )考试时间:2020年1月4日(第18周星期五)一.填空题:(每小题4分,共20分)1 .极限 lim? =2 .曲线y = 21nx + ;i 的拐点坐标为4 .反常积分「72公=5 .微分方程/满足y x二.选择题:(每小题4分,共20分)f sint 2dt2.函数y = xsinx + cosx (0 W x W 4)的单调递减区间是((A) 3 :(B );:(C) 2:(D)- 2(A) 0,?(C) (D)7t 2课程名称:等数学A (1) 试卷满分100分1 -COSX3.若函数/«=仄7_1r 0 ''在x = 0处连续,则”x = 0)o3.「吧叫& = :( )oJ1 X(A) --1:[B) — + 1 ;(C)-;(D) 12 2 24.曲线),=:—渐近线的条数为()o厂-1(A) 0:(B) 1:(C) 2:(D) 35.设函数/w在(-8,+ 8)上可微,且= 则函数y = /(/'(x))在x = 0处的微分 "丁3=()。
(A)2dx:(B)-2dx ;(C)4dx :(D)-4dx三.计算题:(共37分)1.(7分)函数y = y(x)由参数方程= 确定,求二。
y = 2cosZ dx1(2 + 3 吓2.(7分)求极限:lim -- 0 T 33.(7分)求不定积分:f tan \ dx.J 1 + cosr4.(8分)求圆,d+y2—2), = o绕x轴旋转一周而形成的旋转体的体积。
5.(8分)求微分方程〉,"-2y'-3y = Yx"的通解。
四 .(8分)求介于x = 0和x = l之间的由两条曲线G :/=),,。
2:/=4¥(0<〃<1)所困成的图形面积的最小值。
五.(7 分)证明:当x 2 0时,arctan^f + x > lii(x + Vl + x2) o六.(8分)已知函数/⑴在L㈤上连续,在(a,力内可导,且/(〃)=劝,/(切=",其中尤为不等于0的常数,证明:(1)存在ge(a,b),使得了《) =有;(2)存在两个不同的点小4 使得(0)・/'(4)=矛。
三、2009-6-15线性代数A卷

广东工业大学试卷用纸,共3页,第1页广东工业大学试卷用纸,共3页,第2页2、设行列式1534780311113152−−−==A D ,则2=+−+4443424135A A A A .(A )0(B )1(C )-1(D )-163、设A 、B 是n 阶方阵,下列等式正确的是.(A )AB=BA (B )))((22B A B A B A −+=−(C )22AA =(D )111)(−−−+=+B A B A 4、设0α是非齐次方程组b AX =的一个解,r ααα,,,21⋯是0=AX 的基础解系,则.(A)01,,,r ααα⋯线性相关。
(B )01,,,r ααα⋯线性无关。
(C )01,,,r ααα⋯的线性组合是b AX =的解。
(D )01,,,r ααα⋯的线性组合是0=AX 的解。
5、n 阶方阵A 与对角阵相似的充要条件是.(A)A 是实对称阵;(B)A 有n 个互异特征值;(C)A 的特征向量两两正交.(D)A 有n 个线性无关的特征向量;三、(10分)设na a a A +++=111111111||21⋯⋯⋯⋯⋯⋯⋯,021≠n a a a ⋯其中.求A .四、(10分)设4阶方阵C B A ,,满足方程11)2(−−=−C A B C E T ,试求矩阵A ,其中123212010*******,0012001200010001B C −−⎛⎞⎛⎞⎜⎟⎜⎟−⎜⎟⎜⎟==⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎜⎟⎝⎠⎝⎠五、(10分)讨论λ为何值时,方程组⎪⎩⎪⎨⎧=+++=+++=+++λλλλ321321321)1(3)1(0)1(x x x x x x x x x广东工业大学试卷用纸,共3页,第3页(1)有唯一解?(2)无解?(3)有无穷多解?并在此时求出其通解。
六、(10分)已知R 3中的向量组321,,ααα线性无关,向量组112223,b k b αααα=−=+,331b k αα=+线性相关,求k 值。
(完整版)广东工业大学线性代数试卷A卷1(含答案)

第三步将特征向量正交化
第四步将特征向量单位化
……………………………………9分
……………………………………………………11分
八、证明题(每小题7分,共14分)
1、证明:反证法
假设 ,
又:
从而: ,………………………………4分
由于特征值各不相等,所以
线性无关,
四、(10分)解:由 ,
两边同时左乘C,得 ………………………………………………2分
而 …………………………………………………………3分
两边再同时左乘 ,得到
或者对
…………………………………………7分
……………………………………………………8分
即 ……………………………………………………10分
五、(10分)解:
2、设行列式
,则2 .
(A)0(B)1(C)-1(D)-16
3、设A、B是 阶方阵,下列等式正确的是.
(A)AB=BA(B)
(C) (D)
4、设 是非齐次方程组 的一个解, 是 的基础解系,则
.
(A) 线性相关。
(B) 线性无关。
(C) 的线性组合是 的解。
(D) 的线性组合是 的解。
5、 阶方阵 与对角阵相似的充要条件是.
所以的 ,矛盾。………………7分
2、证明:因为线性方程组 ,当秩 时,基础解系为 个,由
则有 ,…………………………………………………3分
即B的列均为 的解,这些列的极大线性无关组的向量个数≤
即秩( ,
从而秩 。……………………………………………………7分
注:本题方法不唯一,酌情给分。
…………………………………………3分
线性代数习题1(附答案)

线性代数复习题1(广工卷)一.填空题(每小题4分,共20分) 1.设五阶矩阵 123230,2A A A A A ⎡⎤=⎢⎥⎣⎦是3阶方阵,122,1A A ==,则 A = .2.设 123,,a a a 线性无关,若 112223331,,b a ta b a ta b a ta =+=+=+ 线性无关,则 t 应满足条件 .3.向量组112α⎛⎫⎪= ⎪⎪⎝⎭,⎪⎪⎪⎭⎫ ⎝⎛-=113β,⎪⎪⎪⎭⎫ ⎝⎛-=201γ线性 关4.如果矩阵 14000400x x x x A x xx ⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭是不可逆的, 则 x = . 5.设 n 阶(3n ≥)矩阵 1111a a a a a a A aa a a aa⎛⎫ ⎪⎪⎪= ⎪ ⎪ ⎪⎝⎭的秩为 1n -, 则 a 必为 二.单项选择题(每小题4分,共20分)1. 设 ,A B 为同阶可逆矩阵, 则 ( ) (A) .A B B A = (B) 存在可逆矩阵 ,P 使 1.P AP B -= (C) 存在可逆矩阵,C 使 .TC AC B = (D)存在可逆矩阵P 和,Q 使 .PAQ B = 2.设A,B 都是n 阶非零矩阵,且 0A B =,则A 与B 的秩是 ( ). (A) 必有一个等于零. (B) 都小于n.(C) 都等于n. (D) 一个小于n, 一个等于n.3. 设n 元齐次线性方程组 0A x =中 ()R A r =, 则0A x = 有非零解的充要条件是 ( )(A) r n =. (B) r n ≥. (C) .r n < (D) .r n >4. 若 向量组,,a b c 线性无关,,,a b d 线性相关, 则 ( )(A) a 必可由 ,,b c d 线性表示. (B) b 必不可由 ,,a c d 线性表示. (C) d 必可由 ,,a b c 线性表示. (D) d 必不可由 ,,a b c 线性表示.5. 设⎪⎪⎭⎫ ⎝⎛=1011A ,则12A 等于 ( ) (A ) ⎪⎪⎭⎫ ⎝⎛1101111 (B ) ⎪⎪⎭⎫ ⎝⎛10121 (C ) ⎪⎪⎭⎫ ⎝⎛11121(D ) ⎪⎪⎭⎫⎝⎛1201212三.(14分) 设 3521110513132413D --=----D 的(,)i j 元的余子式和代数余子式依次记作,,ij ij M A 求11121314112131.A A A A M M M M ++++++及 四. (10分) 已知 21311122,20,13225A B --⎡⎤⎡⎤⎢⎥⎢⎥=-=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦求 X AX B =使.五.(10分) 判定下列向量组的线性相关性, 求出它的一个极大线性无关组, 并将其余向量用极大线性无关组线性表示.()()()()()123451,1,2,4,0,3,1,2,3,0,7,141,2,2,0,2,1,5,10a a a a a =-===-=六.(10分) 用基础解系表示下面方程组的全部解:12341234123422124522x x x x x x x x x x x x a+-+=⎧⎪+++=⎨⎪++-=⎩七(16分) 已知A 是n 阶方阵,且满足 220(A A E E +-=是n 阶单位阵). (1) 证明 A E + 和 3A E - 可逆,并求逆矩阵; (2) 证明 2A E +不可逆线性代数复习题1(广工卷)一.填空题(每小题4分, 共24分) 1.144。
线性代数试题(附参考答案)

《 线性代数 》课程试题(附答案)一、 填空。
(3×8=24分)1.设A 为四阶方阵,且3=A ,则=-A 22.设⎪⎪⎪⎭⎫⎝⎛=003020100A ,则=-1A3.设⎪⎪⎭⎫⎝⎛=4321A ,则A 的伴随矩阵=*A 4.设CB A ,,为n 阶方阵,若0≠A ,且C AB =,则=B 5.矩阵A 可逆的充要条件为6.齐次线性方程组01=⨯⨯n n m X A 有非零解的充要条件为7.设n 维向量组321,,∂∂∂线性无关,则向量组32,∂∂ (填“线性相关”或“线性无关”)8.设n 元齐次线性方程组0=Ax ,且n r A r <=)(,则基础解系中含有 个解向量。
二、 计算行列式的值。
(10分)321103221033210=D三、 已知矩阵⎪⎪⎪⎭⎫ ⎝⎛---=145243121A ,求1-A 。
(10分)四、 设矩阵⎪⎪⎭⎫ ⎝⎛=1112A ,求矩阵X ,使E A AX 2+=。
(10分)五、 问K 取什么值时下列向量组线性相关(10分) T k )1,2,(1=α,T k )0,,2(2=α,T )1,1,1(3-=α。
六、 设A ,B 为n 阶矩阵且2B B =,E B A +=,证明A 可逆并求其逆(6分)七、 设矩阵⎪⎪⎪⎭⎫⎝⎛----=979634121121112A ,求矩阵A 的列向量组的秩及一个极大线性无关组,并把其余向量用极大线性无关组表示。
(15分)八、 求非齐次线性方程组⎪⎩⎪⎨⎧=--+=+--=--+0895443313432143214321x x x x x x x x x x x x 的通解。
(15分)《线性代数》课程试题参考答案一、 填空。
(3×8=24分)1.设A 为四阶方阵,且3=A ,则=-A 2482.设⎪⎪⎪⎭⎫ ⎝⎛=003020100A ,则=-1A ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛001021031003.设⎪⎪⎭⎫⎝⎛=4321A ,则A 的伴随矩阵=*A ⎪⎪⎭⎫ ⎝⎛--1324 4.设C B A ,,为n 阶方阵,若0≠A ,且C AB =,则=B C A 1- 5.矩阵A 可逆的充要条件为0≠A6.齐次线性方程组01=⨯⨯n n m X A 有非零解的充要条件为n A r <)(7.设n 维向量组321,,∂∂∂线性无关,则向量组32,∂∂线性无关(填“线性相关”或“线性无关”)8.设n 元齐次线性方程组0=Ax ,且n r A r <=)(,则基础解系中含有r n -个解向量。
线性代数试卷2014A

A. ;B. ;
C. ;D. .
5.设矩阵 ,则 的对应于特征值 的特征向量 为( ).
A. B. C. D.
二、填空题(每小题5分,共计30分)
1.已知三阶矩阵 的行列式 , 则 _____________.
2.行列式=
3.设A为4阶方阵, 且 是 的两个解向量,则 的一个基础解
六.(12分) 设线性方程组为 ,问 取何值时,方程组无解、有唯一解、有无穷多解? 在有无穷多解时求出其通解。
七、(12分)设矩阵 ,试判断它是否可对角化?若可以,写出可逆阵P及相应的对角阵 .
系为______________.
4.设 的秩为1,则
5.已知向量组 线性无关,而向量组 , 线性相关,则
6.设 , ,三维向量 与 正交,则
三.(8分)、已知 ,满足 ,求矩阵 .
四.(8分)设 是 的一个基础解系, 是非齐次线性方程 的解,证明:向量组 是 的线性无关解。
五.(10分)设 请问a,b为何值时,向量组 的秩为2。
(完整word版)线性代数考试题及答案解析
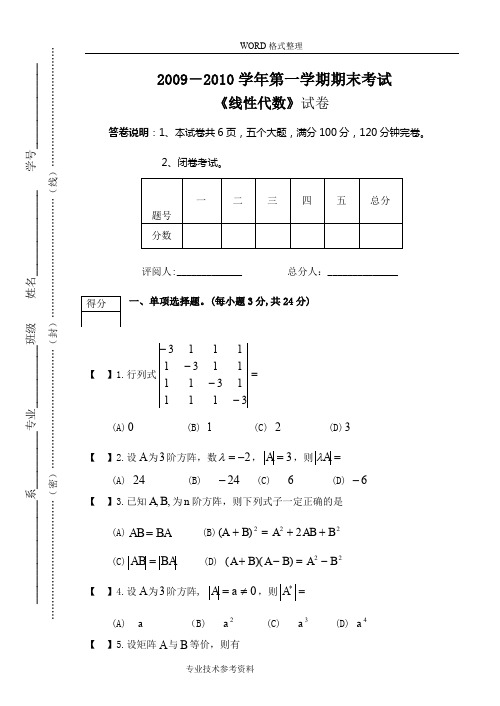
WORD 格式整理 2009-2010学年第一学期期末考试 《线性代数》试卷 答卷说明:1、本试卷共6页,五个大题,满分100分,120分钟完卷。
2、闭卷考试。
评阅人:_____________ 总分人:______________ 一、单项选择题。
(每小题3分,共24分) 【 】1.行列式=----3111131111311113 (A)0 (B) 1 (C) 2 (D)3 【 】2.设A 为3阶方阵,数2-=λ,3=A ,则=A λ (A) 24 (B) 24- (C) 6 (D) 6- 【 】3.已知,,B A 为n 阶方阵,则下列式子一定正确的是 (A)BA AB = (B)2222B)(A B AB A ++=+(C)BA AB = (D) 22))((B A B A B A -=-+ 【 】4.设A 为3阶方阵, 0≠=a A ,则=*A (A) a (B) 2a (C) 3a (D) 4a__________________系__________专业___________班级姓名_______________学号_______________………………………………(密)………………………………(封)………………………………(线)………………………………(A) )()(B R A R < (B) )()(B R A R >(C) )()(B R A R = (D) 不能确定)(A R 和)(B R 的大小【 】6.设n 元齐次线性方程组0=Ax 的系数矩阵A 的秩为r ,则0=Ax 有非零解的充分必要条件是(A) n r = (B) n r ≥ (C) n r < (D) n r >【 】7. 向量组)2(,,,21≥m a a a m 线性相关的充分必要条件是(A) m a a a ,,,21 中至少有一个零向量(B) m a a a ,,,21 中至少有两个向量成比例(C) m a a a ,,,21 中每个向量都能由其余1-m 个向量线性表示(D) m a a a ,,,21 中至少有一个向量可由其余1-m 个向量线性表示【 】8. n 阶方阵A 与对角阵相似的充分必要条件是(A)n A R =)( (B)A 有n 个互不相同的特征值(C)A 有n 个线性无关的特征向量 (D)A 一定是对称阵二、填空题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、证明:因为线性方程组 ,当秩 时,基础解系为 个,由
则有 ,…………………………………………………3分
即B的列均为 的解,这些列的极大线性无关组的向量个数≤
即秩( ,
从而秩 。……………………………………………………7分
注:本题方法不唯一,酌情给分。
,…………3分
由 线性无关,
得 ,
因为 相关,所以 有非零解,………………………………7分
故系数行列式=0,得 。………………………………………………10分
七、(11分)解:
第一步求A的特征值
=0
…………………………………………………………3分
解之得基础解系 ………………………………4分
解之得基础解系 ………………………………………5分
线性相关,求k值。
七、(11分)设 ,求一个正交矩阵 ,使 为一个对角矩阵。
八、证明题(每小题7分,共14分)
1、设 是 阶方阵 的3个特征向量,它们的特征值不相等,记 ,
证明 不是 的特征向量。
2、设 为 阶方阵,若 ,则r r 。
………………………………………………………………10分
注:本题方法不唯一,根据学生的做题步骤酌情给分。
…………………………………………3分
当 时,方程组有唯一解………………………………………………5分
当 时,增广矩阵为
,方程组无解…………………………………………………………7分
当 时,增广矩阵为
,
方程组有无穷多解,
解为 ,(c为任意常数)…………………………10分
六、(10分)解:设存在三个实数 ,使
四、(10分)解:由 ,
两边同时左乘C,得 ………………………………………………2分
而 …………………………………………………………3分
两边再同时左乘 ,得到
或者对
…………………………………………7分
……………………………………………………8分
即 ……………………………………………………10分
五、(10分)解:
解之得基础解系 ……………………………………6分
第三步将特征向量正交化
第四步将特征向量单位化
……………………………………9分
……………………………………………………11分
八、证明题(每小题7分,共14分)
1、证明:反证法
假设 ,
又:
从而: ,………………………………4分
由于特征值各不相等,所以
线性无关,
(A) 是实对称阵; (B) 有 个互异特征值;
(C) 的特征向量两两正交.(D) 有 个线性无关的特征向量;
三、(10分)设 , .求 .
四、(10分)设4阶方阵 满足方程 ,试求矩阵 ,其中
五、(10分)讨论 为何值时,方程组
(1)有唯一解?(2)无解?(3)有无穷多解?并在此时求出其通解。
六、(10分)已知R3中的向量组 线性无关,向量组 ,
2、设行列式
,则2 .
(A)0(B)1(C)-1(D)-16
3、设A、B是 阶方阵,下列等式正确的是.
(A)AB=BA(B)
(C) (D)
4、设 是非齐次方程组 的一个解, 是 的基础解系,则
.
(AБайду номын сангаас 线性相关。
(B) 线性无关。
(C) 的线性组合是 的解。
(D) 的线性组合是 的解。
5、 阶方阵 与对角阵相似的充要条件是.
