结构力学§5-5_图乘法
合集下载
结构力学第05章 虚功原理与结构位移计算-3

6、把复杂图形分为简单图形 、 使其易于计算面积和判断形心位置) (使其易于计算面积和判断形心位置)
•
取作面积的图形有时是不规则图形, 取作面积的图形有时是不规则图形,面积 的大小或形心的位置不好确定。 的大小或形心的位置不好确定。可考虑把图形 分解为简单图形(规则图形) 分解为简单图形(规则图形)分别图乘后再叠 加。
FP
⊿CV
l/2 l/2 AP FP l
3、正确的作法 、
AP1=1/2×FP l×l/2=FP l2/4 AP2=1/2×FP l/2×l/2=FP l2/8 AP3=1/2×FP l/2×l/2=FP l2/8 y1=l/3 y2=l/6 FP y3 = 0
⊿CV=∑AP·yC/EI
=(FP l2/4×l/3+ FP l2/8×l/6 × +FP l2/8 ×0) / EI =5FP l3/48EI (↓)
32
32
• θC=2[(1/2·80·5)·(2/3·5/8)+(1/2·80·5)·(2/3·5/8+1/3·1) • -(2/3·32·5)·(1/2·5/8+1/2·1)]/EI • kN·m m kN/m2 • =0.005867 (弧度) • 方向与虚拟力方向一致。
思考题:判断下列图乘是否正确?
由此可见,当满足上述三个条件时, 由此可见,当满足上述三个条件时,积分式 的值⊿就等于M 图的面积A乘其形心所对应 乘其形心所对应M 的值⊿就等于 P图的面积 乘其形心所对应 图上的竖标y 再除以EI。 图上的竖标 C,再除以 。 正负号规定: 正负号规定: A与yC在基线的同一侧时为正,反之为负。 与 在基线的同一侧时为正,反之为负。
第五章
虚功原理与结构位移 计算
谈结构力学图乘法应用中复杂图形的图乘技巧

基金项目:辽宁工程技术大学应用创新型人才培养立项课题资助项目(YB083033)。 作者简介:孙庆巍,男,辽宁阜新人,硕士,j工宁工程技术大学建筑与工程学院讲师。
2009年第ll卷
孙庆巍
谈结构力学图乘法应用中复杂图形的图乘技巧
-27・
狰衄+狰—一弘
E岛一
图l圈乘法示意图
解法一:将原结构中的荷载分解,如图4。
算的求解过程,大大减少求解的计算量。
譬睑
【1)
相应地嗨图也分解为两个,见图5。
+
(b)
3复杂问题的图乘技巧
从图乘法公式可知,要想顺利采用图乘法求出 位移,必须要知道Mp的面积和形心位置,对于简单
图S
这时原来的Mi图与M,图进行图乘的过程转
变为丽。图分别与(a)、(b)的%图进行图乘再将结
果相加的过程。此时(a)弯矩图是标准的二次抛物 线,其面积公式与形心位置都已知,(b)弯矩图为三 角形,其面积公式与形心位置自然也已知,所以,将
求出原题中的位移。 总之,遇到复杂图形进行图乘时,均可参考上面 的思路,想办法把原来的复杂图形分解为可确定面
弘2
2
积与形心位置的标准图形,或将原结构的复杂荷载 分解为单一荷载分别与单位力作用下的M图进行
+
图乘再求和,这样,就可解决复杂图形的图乘问题。
图9
2∞9年第ll卷
孙庆巍
谈结构力学图乘法应用中复杂图形的图乘技巧
解法一:根据分段叠加法对AC段的M,图分
解,分解为直线(两端截面弯矩纵坐标的连线)与曲 线(AC段的简支梁形式在均布荷载作用下的弯矩 图)相叠加,见图9。
声 譬p 卜j譬仁爿 卜j)T红一) 一)孚p)
荷载形式 弯矩图 圈11
6.5 图形相乘法 结构力学

C A0 ql2/8 A2
B A C y0
1
B 1
M 2图
MP图
将MP图与 M 2 图相乘,则得 A0 y 0 ql 2 1 2 l qB ( l ) EI EI 3 8 2 ( ql )3 24EI
All Rights Reserved 重庆大学土木工程学院®
【例6-8】试求图示悬臂梁跨中截面C的挠度DCV。已知EI=常数。
其中
M图
l
All Rights Reserved
当MP或图的竖标a、b或c、 d不在基线同侧时,如图619b所示,处理原则仍和上 面一样,可将MP分解为位 于基线两侧的两个三角形 (其中A1在上侧,A2在下 侧),按上述方法,分别图 乘,然后叠加。
1 1 A1 al, A2 bl 2 2 2 1 2 1 y01 c d , y02 d c 3 3 3 3
二梁杆 竖杆
All Rights Reserved
1 qa2 2 a 1 qa2 1 a a) ( ) 2 ( a) ( ) 0 2 ( 2 4 3 2 2 4 3 2 3qa4 () 24EI 1 EI
重庆大学土木工程学院®
All Rights Reserved 重庆大学土木工程学院®
如果结构上所有各杆段均可图乘,则位移计算公式可写 为
Ay0 MM P Δ ds EI EI
三、应用图乘法的注意事项
(6-17)
1)y0只能取自直线图形,而A应取自另一图形。
2)当A与y0在弯矩图的基线同侧时,其互乘值应取正号;在 异侧时,应取负号。
y03 y 04
MP图 y01
1
5结构力学图乘法.

(1)常见图形面积和形心:
矩 形
a
l
A al
xc 1 l 2 xc 1 3l
xc 1 4l
3 xc 8 l
三角形
a
l
A 1 2 al A 1 3 al A 2 3 al
l
a
l
标准二次 抛物线
a
l
a
A 2 3 al
xc 1 l 2
(2) 梯形相乘
A1
A2
M M
i
K
dx A1 y1 A2 y 2
1 M M P dx EI
(M x tanα)
yc
xc x
M
x
图乘法是Vereshagin于1925年 提出的,他当时为莫斯科铁路 运输学院的学生。
4、 注意事项
KP AP yc EI
还记得 吗?
(1)必须符合图乘法的适用条件; (2) 必须取自直线图形; (3)同侧弯矩图相乘为正,反之为负; (4)拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解; (5)应用图乘法首先熟练掌握常用图形面积及形心 位置。
如果将AC段的 M P图如下图那样分块,就比 16 较麻烦。 4kN 4 2kN/m 8 M P图 4 A C C A 2m 4kN.m 例2 求 B, EI等于常数。 12kN.m 4kN C 4m
2kN/m
4kN.m 4m B 7kN
A
5kN
解: 作 M 图 M P 图,如下页图所示。
12
c
y2
d
M图
(3)一般形式的二次抛物线图形相乘 (4)曲线图形与折线图形相乘
M M
i
K
矩 形
a
l
A al
xc 1 l 2 xc 1 3l
xc 1 4l
3 xc 8 l
三角形
a
l
A 1 2 al A 1 3 al A 2 3 al
l
a
l
标准二次 抛物线
a
l
a
A 2 3 al
xc 1 l 2
(2) 梯形相乘
A1
A2
M M
i
K
dx A1 y1 A2 y 2
1 M M P dx EI
(M x tanα)
yc
xc x
M
x
图乘法是Vereshagin于1925年 提出的,他当时为莫斯科铁路 运输学院的学生。
4、 注意事项
KP AP yc EI
还记得 吗?
(1)必须符合图乘法的适用条件; (2) 必须取自直线图形; (3)同侧弯矩图相乘为正,反之为负; (4)拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解; (5)应用图乘法首先熟练掌握常用图形面积及形心 位置。
如果将AC段的 M P图如下图那样分块,就比 16 较麻烦。 4kN 4 2kN/m 8 M P图 4 A C C A 2m 4kN.m 例2 求 B, EI等于常数。 12kN.m 4kN C 4m
2kN/m
4kN.m 4m B 7kN
A
5kN
解: 作 M 图 M P 图,如下页图所示。
12
c
y2
d
M图
(3)一般形式的二次抛物线图形相乘 (4)曲线图形与折线图形相乘
M M
i
K
第五节图乘法
4m C 4m
MP图(kN·m)
须注意两点:一是对于斜杆CD, 解:求解本题∆DV时,须注意两点:一是对于斜杆 ,应以杆 轴为基线计算;二是对于阶形住AC,应按EI不同分段图乘 不同分段图乘。 轴为基线计算;二是对于阶形住 ,应按 不同分段图乘。 (1)作MP图 作
A1 = 2 × 12.65 × 45 = 379.5 3
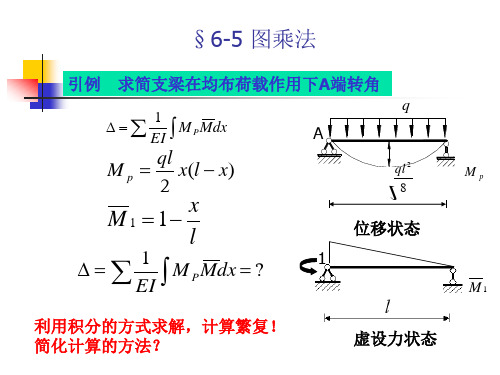
§6-5 图乘法
求简支梁在均布荷载作用下A端转角 引例 求简支梁在均布荷载作用下 端转角
1 ∆=∑ ∫ M P Mdx EI
q
A
ql 2 8
ql M p = x(l − x) 2
Mp
x M 1 = 1− l
1 ∆=∑ ∫ M P Mdx = ? EI
利用积分的方式求解,计算繁复! 利用积分的方式求解,计算繁复! 简化计算的方法? 简化计算的方法? 1
2.5kN/m D 2EI (12.65m) 3EI B 8m 4EI A 12m
20kN 100 A2 C A3 20 B A4 A A5
(45)
A1
D
4m C 4m
140
MP图(kN·m)
1 A2 = × 12.65 × 100 = 632.5 2
A4 =
A5 =
1 × 8 × 20 = 80 2
A q B l/2 l
ql 2 ( ) 32
ql
C l/2
并按A 作MP图,并按 1、A2、A3、A4四部 分划分,如图6-22b所示 分划分,如图 所示
∆CV 1 = ( A1 y01 + A2 y02 + A3 y03 − A4 y04 ) EI 1 = EI 1 l ql 2 l l ql 2 3 )× + ( × )× l ( × × 3 2 2 4 2 2 2
静定结构的位移计算-图乘法

这种利用内力图相乘代替积分的方法称为图乘法。
如果两个图形均为直线,则可取其中任一图形面积和 另一图形纵距相乘;如果两个图形都为曲线,则不能用图 乘法。
利用图乘法应注意:
(1)要满足3个条件;
(2)形心的纵距需取自直线图形; (3)正、负号规定:两个内力图在基线同侧时,乘 积为正。
例 1 计算图示结构 C 点转角
FP
FP B
C
0.5EI
a
EI A
a
C
5FP a 2 2EI
(
)
例 2 :计算图示结构 B 点转角。
A
B
EI
20kN
m 10m40kN
m
B
500 3EI
(
)
当内力图是由迭加得到时,图乘也可用迭加法。
对于两个图形都是梯形的情况(同侧)
1
2
Mp M dx 1 y1 2 y 2
y1
(2c 3
d)
FP
EI
A
C
B
l/2 l/2
例 8: 计算图示结构A点竖向位移
FP=0.5qL q
A
EI B
L
例 9(课后完成) : 计算图示结构 C点竖向位移 q
A l/2C l/2 B
作业: 5—20、5—23
第五章 静定结构的位移计算
§5-5 图乘法
目的:用弯矩图面积乘积代替积分 条件:
(1)各杆为等直杆 (2)各杆截面物理参数(EI、EA、GA)为常数 (3)内力图Mp、MK中至少有一个是直线
K
M P M ds Mp M C
EI
EI
(d )
公式(d)的意义在于:当两个内力图形中有一条为 直线时,其积分结果为曲线图形积分段内的面积ω与其形 心相对应的直线图形中纵距的乘积。
结构力学I-第五章 虚功原理与结构位移计算(荷载位移,图乘法)

局部变形时静定结构的位移计算
⑴ 在要求的位移处,施加相应的单位荷载; ⑵ 利用力平衡条件,求出局部变形处对应的 内力M,FN,FQ; ⑶ 由虚力方程解出拟求位移: dΔ = ( Mκ + FNε + FQγ0 ) ds
Page 7
Δ A 1
B M
θ
14:32
LOGO
结构体位移计算的单位荷载法
真实荷载 弯曲 剪切
A
x
虚设荷载
B
b 截面参数 1 bh3 I=— 12 A =bh,k = 1.2
ql 4 1 2 qx dx 1.5 0 x Ebh3 2
l
变形类型
M P 0.5qx2
M x
FQP qx
F Q 1
MM P 1 ⑴ 弯曲变形引起的位移 M ds EI EI
Page 12
14:32
LOGO
荷载作用下的位移计算及举例
k F Q FQP F N FNP MM P ds ds ds EI EA GA
弯曲变形 拉伸变形 剪切变形
各类结构的位移公式
各类结构中三种变形的影响所占比重各不相同,故可简化; 例5-3 试求图示悬臂梁在A端的竖直 位移 Δ ,并比较弯曲变形和剪切变 形对位移的影响。设梁的截面为矩 形,泊松比1/3。 解:应用单位荷载法 A 1 q A x B
单位荷载法
单位荷载法求刚体体系位移
虚力原理
⑴ 虚力方程,实质为几何方程;
⑵ 虚力与实际位移状态无关,故可设 单位广义力 P = 1;单位荷载法 ⑶ 关键是找出找出虚力状态的静力平
衡关系。
Page 6
14:32
结构力学图乘法详述

6
Pl 2 16 EI
积分常可用图形相乘来代替
§6-5 图乘法
直杆 EI C
位移计算举例
MiMk MiMk 1 EI ds EI dx EI M i M k dx M i是直线 B B 1 1 tg xM k dx M k xtgdx A EI EI A tg B 1 1 y w ×w x0 y tg xd w 0 EI EI EI A
适用范围与特点: 1) 适于小变形,可用叠加原理。 2) 形式上是虚功方程,实质是几何方程。 关于公式普遍性的讨论: (1)变形类型:轴向变形、剪切变形、弯曲变形。 (2)变形原因:荷载与非荷载。 (3)结构类型:各种杆件结构。 (4)材料种类:各种变形固体材料。
2
三、位移计算的一般步骤: K
t1 t2
MP EI
NP EA
QP k GA
10 9
k--为截面形状系数 (3) 荷载作用下的位移计算公式
1.2
A
A1
MM P NN P kQ QP ds ds ds EI EA GA
4
二、各类结构的位移计算公式
(1)梁与刚架
MM P ds EI
1 1 ql 2 3 ql 4 B l l EI 3 2 4 8EI
⑥当图乘法的适用条件不满足时的处理方法: a)曲杆或 EI=EI(x)时,只能用积 分法求位移; 9 b)当 EI 分段为常数或 M、MP 均非直线时,应分段图乘再叠加。
例:求图示梁中点的挠度。
1 1 3a 3a Pa EI 2 4
求B点的竖向位移。
ql2/2
4
1 1 ql 3l ql B l EI 3 2 4 8 EI 1 1 3ql 2 l B y 0 L 2 EI 3 8 2
Pl 2 16 EI
积分常可用图形相乘来代替
§6-5 图乘法
直杆 EI C
位移计算举例
MiMk MiMk 1 EI ds EI dx EI M i M k dx M i是直线 B B 1 1 tg xM k dx M k xtgdx A EI EI A tg B 1 1 y w ×w x0 y tg xd w 0 EI EI EI A
适用范围与特点: 1) 适于小变形,可用叠加原理。 2) 形式上是虚功方程,实质是几何方程。 关于公式普遍性的讨论: (1)变形类型:轴向变形、剪切变形、弯曲变形。 (2)变形原因:荷载与非荷载。 (3)结构类型:各种杆件结构。 (4)材料种类:各种变形固体材料。
2
三、位移计算的一般步骤: K
t1 t2
MP EI
NP EA
QP k GA
10 9
k--为截面形状系数 (3) 荷载作用下的位移计算公式
1.2
A
A1
MM P NN P kQ QP ds ds ds EI EA GA
4
二、各类结构的位移计算公式
(1)梁与刚架
MM P ds EI
1 1 ql 2 3 ql 4 B l l EI 3 2 4 8EI
⑥当图乘法的适用条件不满足时的处理方法: a)曲杆或 EI=EI(x)时,只能用积 分法求位移; 9 b)当 EI 分段为常数或 M、MP 均非直线时,应分段图乘再叠加。
例:求图示梁中点的挠度。
1 1 3a 3a Pa EI 2 4
求B点的竖向位移。
ql2/2
4
1 1 ql 3l ql B l EI 3 2 4 8 EI 1 1 3ql 2 l B y 0 L 2 EI 3 8 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
L M P M ds L FNP F N ds FNP F N L
o EI
o EA
EA1
(曲杆)
(曲杆)
(拉杆)
§5-5 图乘法
1.图乘原理公式
——将积分转变为图形相乘
y
dω
形心
积分式: L MP M ds
o EI
等直杆EI常数: 1
EI
L
o M P M ds
A
C dx
MP图 B
EI
L o
M
P
M
ds
1 EI
yC
乘积“+、-”规定—— 与 yC 同侧为+,不同侧为-
其中:
— M P 图的面积 (教材用A表示)
yC — M P 图形心位置所对应的 M 图中的竖标
2.图乘注意事项
1)杆件是直杆,EI必须是常数;
2) yC必须取自直线图 ( M P 均M为直线时可互换);
3)M 图为折线或 M P 在基线两侧时都需分段图乘;
MM P EI
dx
1 EI
Ay0
1 2 ql 2 1
ql 3
EI
3
8
l
2
24 EI
Cy
1 EI
(
2 l 1 ql 2 38
)
l 4
B
Cy
1 EI
(
2 3
l 2
1 8
ql 2 )
(85
4l )
2
5 ql4 () 384 EI
分段图乘
[例2] 计算悬臂梁在集中荷载作用下的C点的竖向位移 C 。
o EI
o GA
o EA
2. 各种静定结构位移的计算公式 (1)梁、刚架 —只考虑弯曲变形
l M P M ds
o EI
(2)桁架 —只有轴向变形
FNP F N L EA
(3)组合结构
l M P M ds FNP F N L
o EI
EA
(受弯构件)
(链杆)
(4)三铰拱 — 曲杆要考虑弯曲变形和轴向变形,拉杆只有轴向变形。
2 3
q 2
m2
2m
——(二次抛物线)
y3
1m
1 EI
2 A1 y1 A2 y2 A3 y3
q EI
4 15
m4
结束
(第二版)作业:5—17, 19, 24
感谢下 载
1 ql 2
ql 3
A1 2 2 l 4
ql 3 A2 4
2 ql 2
ql 3
A3 3 8 l 12
2 y1 3 l
2 y2 3 l
l y3 2
MM P EI
ds
1 EI
A1 y1
A2 y2 A3 y3
3ql 4 8 EI
[例5] 试求图示刚架在水压力作用下C、D两点的相对水 平
4)图形的 或 y很C 难计算时,不宜用图乘法。
技巧:恰当运用叠加原理
3.常用图形的 面积及形心
注意: “顶点”切线与基线平行,
若不是则公式无效。
4. 图乘的分段
示例(1): M为图折线
MP图
L
o MP Mds A1y1 A2 y2 A3 y3
M图
C1 C2
MP图
y1
M图
y2=0
示例(2): M为图特殊折线
位移。设各杆解EI:为1常) 数作。荷载作用下的弯矩图
MP图
MA
1q 0
x
dx
1
x
1
0 q
x
1
x
dx
q 6
2) 在C、D两点加一对反 向的单位水平力,并
M图
作弯矩图
MP图
M图
A1
1 4
1m
q 6
m2
——(三次抛物线)
4
4
y1 5 1m 5 m
A2
q 6
m2
2m
——(矩形)
y2 1m
A3
考察MP和M图
MP ——曲线 M ——直线
由图可见: M x tg
0α xA xC
M yC
代入积分式有:
M图
B
B
Bx
A MP Mdx
A x tg MPdx B
d
MP图对Poy的xc面积矩
tg A x MPdx
B
tg A x d
yc
tg xc P
yc P
得图乘法公式: 1
L
o MP Mds A1y1 0
5. 图乘的叠加
MP图 M图
(1) 两个直线图形图乘的叠加法
L
o MP Mds A1y1 A2 y2
其中
y1
2 3
c
1 3
d
y2
2 3
d
1 3
c
6. 举例
1
C
A l 4
[例1] 试用图乘法计算简支梁在均布
荷载q作用下的B端转角
B,
移。
解:
B
以及AB梁中点的竖向位
第5章 结构位移计算与虚功-能量法
§5-1 §5-2 §5-3 §5-4 §5-5 §5-6 §5-9
刚体体系的虚功原理与位移计算 结构位移计算的一般公式 荷载作用下的位移计算 荷载作用下的位移计算举例 图乘法 温度变化时的位移计算 互等定理
1.荷载作用下的位移计算公式:
回顾
位移计算的一般公式:
力场(虚)
叠加图乘
1
CV
300 2
6
2 3
6
2
1
2 6 45 3 3
6660
10kN/m 20kN
B 300
C 6m
45 不是顶点
MP图
MA图
6
1
MC图
[例4] 计算图示刚架在分布荷载作用下的B点的水平位移 。
各杆截面为矩形bh,惯性矩相等。只考虑弯曲变形的
影响。
ql 2
ql
MP图
M图
ql
2
解: MP图面积可分为三块: A1、A2 、 A3lBiblioteka ll1 [
M d
0
F Qd
0
0 F N d ] F RkCk
(弯曲)
(剪切) (轴向) (已知支座移动)
仅考虑荷载作用,Ck 0
位移场(实)
由材料力学可知 :
d M P ds
EI 代入得 :
d k FQP ds
GA
d FNP ds
EA
1 l M P M ds l k FQP F Q ds l FNP F N ds
解: yc取自MP图
1 l l l2 A
222 8
C
MM P EI
dx
1 EI
Ayc
1 EI
l2 8
5 6
FP
l
5FPl 3 48 EI
[例3] 求A点的转角和C点的竖向位移。 (EI=1)
解:(1)求A点的转角
A
300 6 2
1 1 3
300
A 6m
(2)求C点的竖向位移
