初中数学重庆南开中学初级(下)半期考试.docx
文档:南开中学初2013级11-12学年(下)半期试题——数学

南开中学初2013级八下数学期中题库题卷(全卷共32个小题,时间120分钟,满分150分)一、选一选,慧眼识金(下列各小题均给出四个备选答案,其中只有一个正确答案。
本大题10个小题,每小师4分,共40分)1、如果分式12x -有意义,则x 满足( ) A 、2x ≠ B 、2x =C 、2x >D 、0x >2、下列分解因式正确的是( )A 、()321a a a a -+=-+B 、()24222a b a b -+=-C 、()22211a a a -+=-D 、()()1a b ma mb m a b --+=+-3、下列说法正确的是( )A 、为了解全国中学生的心理健康情况,应采用普查B 、要调查人们对“低碳生活”的了解程度,应采用普查C 、对即将升空的“神州九号”各零部件的检查,应采用抽样调查D 、妈妈为了解菜品的咸淡是否适合,应采用抽样调查4、若分式()()211x x x -+-的值为零,则x 的取值应为( )A 、21x x ==-或B 、1x =-C 、1x =±D 、2x =5、二胡要获得最佳音色,需将其“千金” C 放在琴弦AB 的黄金分割点上,如图所示,已知60,,AB cm AC BC AC =<=则( ) A 、()3051-B 、()3051+C 、()3035-D 、()3035+6、如果3a -是多项式229a ma -+的一个因式,则m 的值为( ) A 、0 B 、6 C 、9 D 、12 7、如图,小芳和爸爸正在散步,爸爸身高1.8m ,他在地面上的影长为2.4m 。
若小芳比爸爸矮0.3m ,则她的影长为( ) A 、1.5m B 、2m C 、2.1m D 、2.8m8、已知:()1101a x x x =+≠≠-且,()()213211,11,a a a a =÷-=÷-()1201111,n n a a a -=÷-则等于( ) A 、1x +B 、xC 、1x-D 、1x x +9、已知关于x 的不等式组0213x a x -<⎧⎪+⎨≥⎪⎩只有三个整数解,则实数a 的取值范围是( )A 、34a ≤<B 、34a <≤C 、34a <<D 、34a ≤≤10、如图,在正方形纸片ABCD 中,对角线AC 、BD 交于点O ,折叠正方形纸片ABCD ,使AD 落在BD 上,点A 恰好与BD 上的点F 重合,展开后折痕DE 分别交AB 、AC 于点E 、G ,连接GF 。
重庆市南开中学校2022-2023学年七年级下学期入学数学考试试题

重庆市南开中学校2022-2023学年七年级下学期入学数学考试试题学校:___________姓名:___________班级:___________考号:___________一、单选题A..C...单项式-3x2y的次数是.13.下列调查中,调查方式选择合理的是().为了解重庆市初中生每天做作业所用的时间,选择全面调查.为了解NBA篮球队的队员身高情况,选择抽样调查A.14-B.14C.164-D8.下列说法中正确的是()A.64B.72C.73D.8110.某班组每天需生产50个零件才能在规定的时间内完成一批零件任务,实际上该班组每天比计划多生产了6个零件,结果比规定的时间提前3天并超额生产120个零件,二、填空题26.已知点C为直线的中点,则MN=27.将长方形纸片ABCD后的对应点分别为点28.小南帮同学小开点了一份外卖(售价小于心将支付金额的整数部分与小数部分数字看倒置了并按看错的数字将钱转给了小南,小南收到后加上原有余额的5倍,于是将多收的金额退还给了小开.若售价的整数部分是一位数,小数部分数字三、解答题请根据图中提供的信息,解答下列问题:(1)此次调查中,共调查了___________名顾客,图2中(2)将图1的条形统计图补充完整;(3)根据调查结果,请你估计新年期间4000名顾客中有多少顾客购买35.如图,同一直线上有A,B,C,D四点,已知DB=求AB的长.36.某中学准备将库存中若干套桌凳修理后支援贫困山区学校,现有甲、乙两木工组,甲每天修桌凳21套,乙每天修桌凳比甲多7套,甲单独修完这些桌凳比乙单独修完多用7天,学校每天付甲组80元修理费,付乙组120元修理费.(1)请问该中学库存中有多少桌凳?(2)在修理过程中,学校要派一名工人进行质量监督,学校负担他每天(1)如图1,若10AOD ∠=︒,则AOM ∠=___________,CON ∠=___________(2)如图2,探究MON ∠与BON ∠的数量关系,并说明理由;(3)在(2)的条件下,若5BON ∠=︒,将AOB ∠绕点O 以每秒2︒的速度顺时针旋转,同时将COD ∠绕点O 以每秒3︒逆时针旋转,若旋转时间为t 秒()090t <<,当∠时,直接写出t 的值.。
重庆南开中学 2017-2018学年 七年级下 半期测试卷

重庆南开(融侨)中学 2017-2018 学年度下学期期中考试初 2020 级数 学 试 题(时间:120 分钟 满分:150 分)一、选择题(本大题共 12 个小题,每小题 4 分,共 48 分)在每个小题的下面,都给出了代号为 A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将正确答案填入答卷对应的表格中.1. 计算(x 2)2 的结果是( ▲ ).A .x 2B .x 4C .x 6D .x 82. 如图,在所标识的角中,互为对顶角的两个角是( ▲ ).A .∠1 和∠2B .∠1 和∠4C .∠2 和∠3D .∠3 和∠43. 如图,O 是直线 AB 上一点,若∠1=26°,则∠AOC 为( ▲ ).A .154°B .144°C .116°D .26°或 154°2 题图3 题图4. 王师傅想做一个三角形的框架,他有两根长度分别为 15cm 和 16cm 的细木条,需要将其中一根木条分为两段,如果不考虑损耗和接头部分,那么他可以把( ▲ )分为两截.A .15c m 的木条B .16c m 的木条C .两根都可以D .两根都不行5. 若(2a +3b )()=4a 2-9b 2,则括号内应填的代数式是( ▲ ).A .-2a -3bB .2a +3bC .2a -3bD .3b -2a6. 如图,将一副三角板如图放置,∠E =45°,∠C =30°,若 A E ∥B C ,则 ∠AFD =( ▲ ).A .90°B .85°C .75°D .65°6 题图7. 一列火车匀速通过隧道(隧道长大于火车的长),火车在隧道内的长度 y 与火车进入隧道的时间 x 之间的关系用图象描述正确的是( ▲ ).ABCD8. 下列选项所给条件能画出唯一△ABC 的是( ▲ ).A .∠A =50°,∠B =30°,AB =2 B .AC =4,AB =5,∠B =60° C .∠C =90°,AB =9D .AC =3,AB =4,BC =89. 小明用某种材料制成的框架如图所示,已知∠B=∠E,A B=D E,BF=EC,其中框架△ABC 的周长为24c m,C F=3c m,则整个框架所需这种材料的长度为(▲).A.51c m B.49c m C.47c m D.45c m9 题图10. 长为a,宽为b 的长方形的周长为14,面积为10,则a2+b2 的值为(▲).A.7 B.15 C.29 D.3611. 下列是用火柴棒拼成的一组图形,第①个图形中有3 根火柴棒,第②个图形中有9 根火柴棒,第③个图形中有18 根火柴棒,…,按此规律排列下去,第⑥个图形中火柴棒的根数是(▲).……12 题图A.63 B.60 C.56 D.4512. 如图,已知四边形ABCD 中,A B∥D C,连接BD,BE 平分∠ABD,BE⊥AD,∠EBC 和∠DCB 的角平分线相交于点F,若∠ADC=110°,则∠F 的度数为(▲).A.115°B.110°C.105°D.100°二、填空题(本大题共12个小题,每小题3分,共36分)请将每小题的答案直接填在答卷中对应的横线上.13. PM2.5 是大气压中直径小于或等于0.0000025m的颗粒物,将数0.0000025 用科学记数法表示为▲.14. 如图,已知A C⊥B C,C D⊥A B,其中A C=6,B C=8,A B=10,C D=4.8,那么点B到A C 的距离是▲.15. 三角形的两个内角分别为60°和80°,则它的第三个内角的度数是▲°.16. 声音在空气中传播的速度y(米/秒)(简称音速)与气温x(℃)之间的关系如下.一辆汽车停在路边,其正前方有一座山崖,驾驶员按响喇叭,4s后听到回声,若当时的气温为25℃,则由此可知,汽车距山崖▲米.17. 如图,∠A=70°,O 是AB 上一点,直线OD 与AB 所夹角∠BOD=82°,要使OD∥A C,直线OD 绕点O 按逆时针方向至少旋转▲°.18. 计算:2008×2010-20092=▲ .19. 若 x +2y -2=0,则 5x ·25y =▲.14 题图17 题图22 题图23 题图20. 某工厂年产值为 150 万元,经测算每增加 100 万元的投资,年产值可增加 250 万元,设新增加的投资为 x 万元,增加投资后的年产值为 y 万元,则 y 与 x 的关系式为▲.21. 若 m 2 + 4n 2 - 4m + 4n + 5 = 0 ,则 n m =▲ .22. 如图,Rt △ABC 中,∠ACB =90°,∠A =55°,将其折叠,使点 A 落在边 CB 上点 A ′处,折痕为 CD ,则∠A ′DB =▲.23. 如图,E 是△ABC 中 BC 边上的一点,且 B C =3B E ,点 D 是 AC 边上一点,且 AD =14A C ,S △ABC =36, 则 S △B E F -S △AD F =▲.24. 如图,在△ABC 中,AD 平分∠BAC ,过点 C 作 CD ⊥AD ,AD 交 BC 于点 G ,DE ∥AB 交 AC 于点 E ,作∠BCA 的平分线 CF 交 AD 于点 P ,交 AB 于 点 F ,且∠EDC =∠ECD , ∠PCD =30°,下列结论:①∠B =60°;② FP =GP ③B G =A E ;④S △A P F +S △C PG =S △A P C ,其中正确的是▲ (请填写序号)三、计算题(本大题共 5 小题,25-28 题每小题 5 分,29 题 8 分,共 28 分)解答时每小题必须给出必要的演算过程或推理步骤. 25.230123()( 3.1415)2π--+-⨯+-26. 2 x (3 - 2 x ) - (2 x + 3)(3x - 4)27. (-2x 2 y )3 + 8( x 2 )2 ⋅ (-x 2 ) ⋅ (- y )3 28.2222()()22m n m n +--29.化简求值:[(x+2y)2 -(x +y)(3x -y)-5y2 ]÷(2x),其中x=-2,y=12.四、解答题(本大题共5个小题,30题4分、31题6分,32题8分,33题10分,34题10分,共38分)解答时每小题必须给出必要的演算过程或推理步骤.30.尺规作图,不写作法,但要保留作图痕迹.王师傅开车在一条公路上经过点B 和点C 处两次拐弯后,仍在原来的方向上平行行驶.已知第一次的拐角为∠ABC,请利用尺规作出第二次拐弯的拐角∠BCD.31.如图,点A,B,C,D 在同一条直线上,CE∥DF,EC=BD,AC=FD,∠FBD=25°,试求∠E 的度数.32.已知点E、F 在线段BD 上,BF=DE,点A、C 在线段BD 的两侧且AB=CD,AE=CF ,连结AC 交BD 于点O.求证:AO=CO.33.甲、乙两人分别居住在A、C 两地,B 地在A、C 两地之间.甲、乙两人驾车分别从A、C 两地同时出发,匀速行驶,甲从A 地经B 地去C 地,乙从C 地送货到B 地,交货后立即以原速返回C 地(交货时间不计),甲、乙两人离B 地的距离y(千米)与行驶时间x(小时)之间的关系图象如图所示,观察图象:(1)填空:①A、C 两地之间的路程为千米;②乙比甲每小时多走千米;③点P 表示甲、乙两人离B 地千米;(2)在乙停止运动前,求甲出发后经过多少小时与乙相遇.34.已知△ADC 中,∠ACD=90°,AC=DC.以DC 为斜边作Rt△DEC,其中∠DEC=90°,连接AE 并延长,与CD 的延长线交于点B,∠AEC=∠ACE.(1)如图1,求证:∠ECD=∠BED;(2)如图1,求证:CE=2DE;(3)如图2,F 为线段AC 上一点,连接BF,与EC 相交于点G,分别过点D、C 作DM⊥BF 于点M,CN⊥BF 于点N,若BG=GC,试判断MD、DE、CN 三者间的数量关系,并证明你的结论.图1 图2。
重庆市南开(融侨)中学初级九年级数学下学期半期考试试题(无答案)

重庆南开(融侨)中学初2018级九年级下半期考试数学试卷(本试卷共五大题,满分150分,考试时间120分钟)一、选择题:(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A 、B 、C 、D 的四个答案,其中只有一个是正确的,请将答题卡上对应题目的正确答案标号涂黑。
1.下列各数中,最小的实数是()A.1B.0C.-3D.-12.如果∆ABC ∽∆DEF ,且∆ABC 与∆DEF 的面积比为4:9,那么∆ABC 与∆DEF 的相似比为()A2:3 B.4:9 C.3:2 D.9:43.计算的结果是()A.52xB. 62xC. 54xD. 54x4.下列调查中,是和全面调查(普查)方式的是()A.调查全市中小学生玩网游的情况B.调查我校初三某班的中考体育成绩C.调查央视《中国诗词大会》节目的收视率D.调查一批华为手机的使用寿命5.函数2x y +=中,自变量x 的取值范围是() A.2x ≥- B.x ≠3 C. 2x -f 或x ≠3 D. 2x ≥-或x ≠36.下列命题是假命题的是()A.四边相等的四边形是菱形B.有一个角是直角的平行四边形是矩形C.一组对边平行另一组对边相等的四边形是平行四边形D.对角线互相平分的四边形是平行四边形7.估计22183+⨯÷的运算结果应在下列哪两个数之间()A.4.5和5.0B.5.0和5.5C.5.5和6.0D.6.0和6.58.如图,在Rt ∆ABO 中,∠AOB=90°,AO=BO=2,以O 为圆心,AO 为半径作半圆,以A 为圆心,AB 为半径作BD,则图中阴影部分的面积为()A.2B.112π+C. 122π+D. 324π+9.下列图形都是由同样大小的●和○按照一定规律组成的 ,其中第①个图形中一共有6个●,第二个图形中一共有13个●,第③个图形中一共有25个●,…….按此规律排列下去,第⑦个图形中●的个数为()A.91B.112C.123D.16010.鹅岭公园内的小山坡上有一观景楼AB (如图),山坡BC 的坡度为i=1:2.4,为了测量观景楼AB 的高度,小楚在山脚C 处测得观景楼顶部A的仰角为45°,然后从山脚C 沿山坡CB 向上行走26米到达E 处,测得观景楼顶部A 的仰角为72°(A 、B 、C 、E 、D 在同一平面内),则观景楼AB 的高度约为()A.15.6B.18.1C.19.2D.22.511.如图,已知四边形OABC 是平行四边形,反比例函数(0)k y k x=≠的图像经过点C ,且与AB 交于点D ,连接OD ,CD ,若AB=3AD ,∆OCD 的面积是10,则k 的值为()A.10B.-5C.83-D. 163- 12.若关于x 的不等式212213147x a x +⎧⎪-⎨≥⎪⎩p 无解,且关于x 的分式方程6322a y y y --=--有正解数集,则满足条件的所有整数a 的个数为()A.2B.3C.4D.5二、填空题(本大题共6个小题,每小题4分,共24分)请将每小题的答案直接填在答题卡中对应的横线上。
重庆南开中学初2022级七(下)数学期中模拟(3)试题卷

甲、乙、丙三种方式搭配的盒数之比为 2:1:6 时,则销售的总利润率为 ▲ .
三、计算题(本大题共 2 小题,25 题每小题 4 分,26 题 7 分,共 31 分)解答时每小题必须给出必
要的演算过程或推理步骤.
25.(1)
2
Байду номын сангаас
20
1 2
2
1 2020
(2)
1
2 5
8
0.255
5 7
8
分∠FGD. 若∠EFG = 90o,∠E = 35o,求∠EFB 的度数.
解:在 Rt△EFG 中,∠EFG = 90o(已知)
∵ ▲ E 90 (
▲
)
∴ EGF 90 E 90 35 55 (等式的性质)
∵ GE 平分∠FGD(已知)
∴ ▲ = EGF 55 (
▲
)
又∵ AB ∥ CD (已知)
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两 车之间的路程不超过 25 千米,请通过计算说明,按图像所表示的 走法是否符合约定.
31.我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图 1,可得等式:
(a 2b)(a b) a2 3ab 2b2 .
(1)由图 2,可得等式:
y/千米
y/千米
y/千米
y/千米
0
x/时
0
x/时
0
A.
B.
C.
9. 已知 x2 y 3 ,则 2xy x5 y2 3x3 y 4x 的值为( ▲ )
A. 24
B. -24
C. -60
x/时 0 D. 60
初 2022 级半期模拟(3)数学试题卷 第 1 页 共 4 页
重庆市南开中学校2023-2024学年七年级下学期期末数学试题
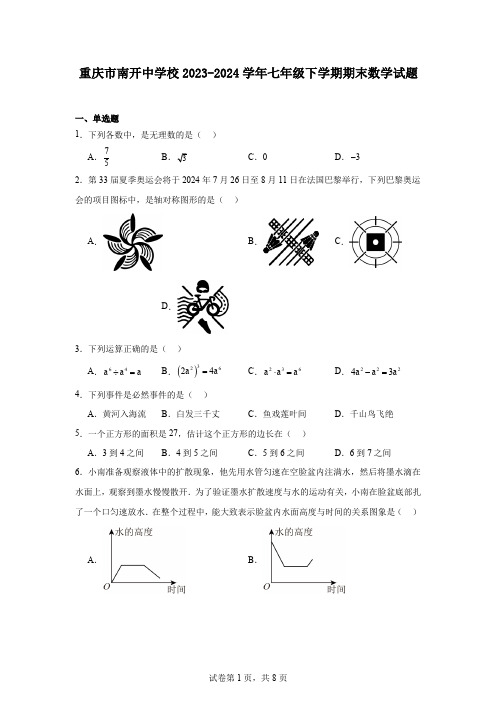
重庆市南开中学校2023-2024学年七年级下学期期末数学试题一、单选题1.下列各数中,是无理数的是( )A .75 B C .0 D .3-2.第33届夏季奥运会将于2024年7月26日至8月11日在法国巴黎举行,下列巴黎奥运会的项目图标中,是轴对称图形的是( )A .B .C .D .3.下列运算正确的是( )A .64a a a ÷=B .()32624a a =C .236a a a ⋅=D .22243a a a -= 4.下列事件是必然事件的是( )A .黄河入海流B .白发三千丈C .鱼戏莲叶间D .千山鸟飞绝 5.一个正方形的面积是27,估计这个正方形的边长在( )A .3到4之间B .4到5之间C .5到6之间D .6到7之间 6.小南准备观察液体中的扩散现象,他先用水管匀速在空脸盆内注满水,然后将墨水滴在水面上,观察到墨水慢慢散开.为了验证墨水扩散速度与水的运动有关,小南在脸盆底部扎了一个口匀速放水.在整个过程中,能大致表示脸盆内水面高度与时间的关系图象是( ) A . B .C .D .7.下列说法正确的是( )A .等腰三角形一边上的中线也是这条边上的高B .面积相等的两个三角形全等C .三角形三条角平分线的交点一定在三角形的内部D .两直线平行,内错角互补8.如图,某段河流的两岸是平行的,小开想出了一个不用涉水过河就能测得河的宽度的方案,首先在岸边点B 处,选对岸正对的一棵树A ,然后沿河岸直行20m 到达树C ,继续前行20m 到达点D 处,再从点D 处沿河岸垂直的方向行走.当到达树A 正好被树C 遮挡住的点E 处时,停止行走,此时DE 的长度即为河岸AB 的宽度.小开这样判断的依据是( )A .SSSB .SASC .AASD .ASA9.如图1,90ACB ∠=︒,4AC =,3BC =,以这个直角三角形两直角边为边作正方形.图2由图1的两个小正方形向外分别作直角边之比为4:3的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形,…,按此规律,则图6中所有正方形的面积和为( )A .200B .175C .150D .12510.如图,在Rt ABC △中,90ABC ∠=︒,BD 平分ABC ∠交AC 于点D ,点E 为BC 边上靠近点C 的三等分点,且AB BE =,若阴影部分面积为4,则ABC V 的面积为( )A .6B .8C .10D .1211.如图,已知AB CD ∥,BAC ∠的角平分线与CD 交于点E ,F 为射线AB 上的一个动点,连接EF ,过点C 作CG EF ⊥,且FG EG =.若AEF α∠=,则ECG ∠的度数为( )A .452α︒- B .30α︒+ C .45α︒- D .2α12.在整式()231a -,()254a a -+,()28419a a -+前添加“+”或“-”,先求和,再求和的绝对值的操作,称为“优绝对值”操作,将操作后的化简结果记为M .例如:()()()22222231548419618618618a a a a a a a a ----+--+=--=+=+,则2618M a =+,当1a =时,M 的化简求值结果为:2611824M =⨯+=.下列说法正确的个数为( ) ①至少存在一种“优绝对值”操作,使得操作后的化简结果为常数;②把所有可能的“优绝对值”操作后的式子化简,共有8种不同的结果;③在所有可能的“优绝对值”操作中,若操作后的化简求值的结果为17,则满足条件的a 有且只有一个,此时14a =-. A .0 B .1 C .2 D .3二、填空题13.世界上最小的鱼是生活在澳大利亚东海岸的胖婴鱼,它的质量约为0.0000012千克,将数据0.0000012用科学记数法表示为.14x 的取值范围是.15.已知8的立方根是x ,16的算术平方根是y ,则y x =.16.为了提高学生劳动能力,学校举行了“躬身劳动,悦享春光”活动.初一某班栽种红薯幼苗,栽种的幼苗总数量y (棵)与参与活动人数x (人)的变化关系如下表所示:观察表中数据可知,该班有人栽种幼苗时,栽种幼苗总数量为32棵.17.一个不透明口袋中装有红,黄,绿三种颜色的玻璃球共16个,每个球除颜色外完全相同,其中黄球和绿球一共12个,若从袋中任意摸出一球恰好摸到红球的概率是. 18.已知ABC V 两边长分别为4与5,第三边的长为奇数,则第三边的长的最大值为. 19.如图,将长方形ABCD 沿AE 折叠,点D 恰好落在BC 边的F 点上,已知4CF =,8AB =,则AD =.20.如图,在等边ABC V 中,点D 为线段AB 上一点,4BD AD =,连接CD ,点E 为线段AC下方一点,连接CE ,且C D C E =,BDC ACE ∠=∠,连接BE 交AC 于点M ,点F 为线段AC延长线上一点,AD CF =,连接EF .已知2AD =,则CM 的长为.21.如图,在ABC V 中,AB BC =,90ABC ∠=︒,BAC ∠与BCA ∠的角平分线交于点D ,延长AD 交BC 于点E ,过点E 作EF AC ⊥于点F ,过点E 作EH CD ⊥交AC 于点H ,则下列结论:①135ADC ∠=︒;②HF GF =;③2222AC CE AE +=;④DEC HEF S S ∆∆=,正确的有.(填序号)22.对于任意一个三位自然数M ,若它的各数位上的数字均不为0,且满足十位数字与百位数字之差等于个位数字与十位数字之差的2倍,则称M 为“2阶等差中项数”,将这个三位自然数M 的百位数字和个位数字互换位置,得到M ',规定()99M M F M '-=.已知A 、B 均为“2阶等差中项数”,其中31010A x y =++,10070B m n =++(18x ≤≤,1y ≤,m ,9n ≤,且x ,y ,m ,n 均为正整数).令()()F A k F B =,当()()303F A F B --为完全平方数时,则满足条件的所有k 之和为.三、解答题23.计算:(1)())2020241113-⎛⎫-+-- ⎪⎝⎭; (2)()3263272372a a a a a a ⋅+⋅÷+;(3)()()222525m n m n --+;(4)()()3131x y x y +--+.24.先化简,再求值:()()()()24332253a b a b a b a b b a ⎡⎤-+--++÷⎣⎦,其中4a =,23b =-. 25.如图,在ABC V 中,AB AC =,D 为BC 延长线上一点.(1)用直尺和圆规完成以下基本作图:作线段BD 的垂直平分线,与边AC ,BC 分别交于点E ,F ,在线段AB 上截取AH ,使得AH AE =,连接EH ;(保留作图痕迹,不写作法和结论) (2)在(1)所作图形中,连接BE ,DE ,求证:HE CD =.(请补全下面的证明过程) 证明:∵AB AC =,AH AE =,∴AB AH AC AE -=-,∴①______.∵EF 是BD 的垂直平分线,∴______②,∴EBD EDC ∠=∠.∵AB AC =,∴③______.在ECD V 中,CED ACB EDC ∠=∠-∠,HBE ABC EBD ∠=∠-∠,∴CED HBE ∠=∠.在EBH △和DEC V 中,()()BH EC BE ED ⎧=⎪⎨⎪=⎩已证④已证 ∴()SAS EBH DEC V V ≌.∴HE CD =.26.“五月五是端阳,插艾叶戴香囊,吃粽子撒白糖,龙船下水喜洋洋.”端午是我国传统节日,也是集拜神祭祖,祈福辟邪,欢庆娱乐和饮食为一体的民俗大节.某校为了更好地调动学生参与端午活动的积极性,采取抽样调查的方法,调查了学生感兴趣的四项端午习俗项目:插艾叶,戴香囊,吃粽子,赛龙舟,并将调查结果绘制成下面两幅不完整的统计图,请你根据图中提供的信息解答下列问题:(1)在这次调查中,一共调查了______名学生,扇形统计图中m 的值为______;(2)补全条形统计图;(3)若该校共有3000名学生,请估计该校对插艾叶项目感兴趣的学生有多少人? 27.在Rt ABC △中,90BAC ∠=︒,过点A 作AD CB ⊥于点D ,延长DA 至点E ,使得DE AC =,过点E 作EF AB ∥,交CB 的延长线于点F ,连接CE .(1)求证:ACB DEF V V ≌;(2)若50FCE ∠=︒,70CEF ∠=︒,求FCA ∠的度数.28.利用整体思想解题,运用代数式的恒等变形,使不少依照常规思路难以解决的问题找到简便解决方法.请阅读材料:例题:计算()()()()234188345189234189345188+++⋅⋅⋅+⨯+++⋅⋅⋅+-+++⋅⋅⋅+⨯+++⋅⋅⋅+的值.解:设34188M =++⋅⋅⋅+,则原式()()()21892189378M M M M =++-++=. 请解决下列问题:(1)计算:()()()()2342024345202523420253452024______---⋅⋅⋅-⨯+++⋅⋅⋅+----⋅⋅⋅-⨯++++=L;(2)已知23a b a b-=+,求42332a b a b a b a b -+---的值;(3)证明:若n 为正整数,则代数式()()()223581n n n n +++++的值一定是某个整数的平方.29.如图1,已知八边形ABCDEFGH 相邻的两边互相垂直,且AB AH =,DC DE =,动点P 从八边形顶点A 出发,沿着八边形的边以每秒cm a 的速度逆时针运动,当P 运动到点E 时调头,以原来的速度原路返回,到A 点处停止运动.PAH V 的面积为()2cm S ,运动时间为t (秒),S 与t 的图象如图2所示,请回答以下问题:(1)AB =______cm ,DE =______cm ,=a ______cm/s ;(2)当点P 第一次在边CD 上运动时,求S 与t 的关系式;(3)点P 在返回过程中,当时间t 为何值时,AHP △为等腰三角形?请直接写出t 的值.。
重庆南开中学八年级下学期半期.docx
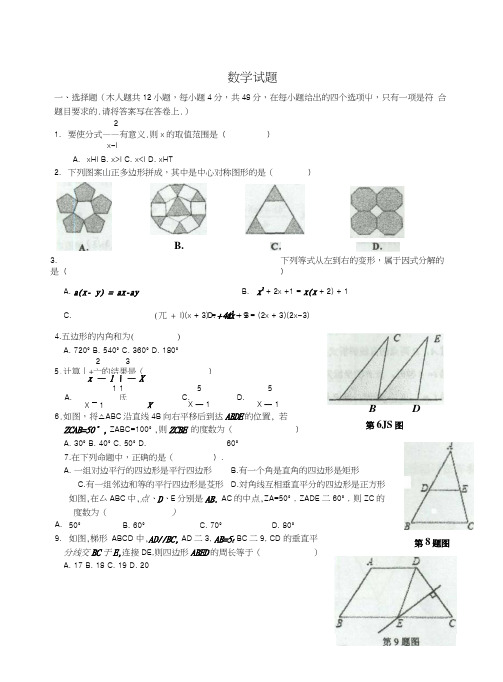
x — 1 \ — X1 15 5A. 氏C.D.X — 1 XX — 1X — 16.如图,将△ABC 沿直线4B 向右平移后到达ABDE 的位置, 若ZCAB=50° , ZABC=100° ,则ZCBE 的度数为()A. 30°B. 40°C. 50°D. 7.在下列命题中,正确的是().A. 一组对边平行的四边形是平行四边形C.有一组邻边和等的平行四边形是芟形 60° A. 9. BD第6JS 图B.有一个角是直角的四边形是矩形D.対角线互相垂直平分的四边形是正方形如图,在厶ABC 中,点、D 、E 分别是AB. AC 的中点,ZA=50° , ZADE 二60° , 则ZC 的度数为()50°B.60°C. 70°D. 80°如图,梯形 ABCD 中,AD//BC, AD 二3, AB=5f BC 二9, CD 的垂直平分线交BC 于E,连接DE,则四边形ABED 的周长等于()A. 17B. 18C. 19D. 20数学试题一、选择题(木人题共12小题,每小题4分,共48分,在每小题给出的四个选项屮,只有一项是符 合题目要求的.请将答案写在答卷上.)21. 要使分式——有意义.则x 的取值范围是()x-lA. xHlB. x>lC. x<lD. xHT2. 下列图案山正多边形拼成,其中是中心对称图形的是()3. 下列等式从左到右的变形,属于因式分解的是()B. x 2+ 2x +1 = x(x + 2) + 1B.A. a(x- y) = ax-ay C.(兀 + l)(x + 3) = + 4x + 3D. 4x 2- 9 = (2x + 3)(2x-3) 4.五边形的内角和为( )A. 720°B. 540°C. 360°D. 180°2 3 5.计算丄+亠的结果是() 第8题图二、填空题(本大题共6小题,每小题4分,共24分.请将答案写在答卷匕)13.因式分解2/—4°= _____________________14. 如图,在矩形ABCD 中,对角线AC. BD 和交于点D,点E 、F 分别是AO. AD的小点,若人B 二6cm, BC 二8cm,则厶4£尸的周长二 _______ cm.x 2 _115. 当兀二 ________ 时,分式一的值为0.X + 1x m16. 己知关于x 的方程 一- 2 = —^无解,则" ___________________ •x ~3 x — 3r 217. 若〒一3兀一1 = 0,则-------- :—二X 4+3X 2+118. 如图,在正方形ABCD 屮,E 为正方形ABCD 内一点,且ZAEB=90° , AE=2EB, 将△ABE 绕点B 逆时针旋转90°得到连接EF 、AC. CE 、G 为4E 的中点 连接CG.有下列结论:①ABEF 为等腰直角三角形;②AE 丄CF ;③CG=AD,10. 如图,△ABC 是斜边AB 的长为3的等腰直角三角形,在AABC 内作第1个正方形A I BQ I Q (。
重庆南开中学初2007级初一数学(下)半期考试试卷

重庆南开中学初2007级初一(下)半期考试数学试卷一、精心选一选(每题2分,共24分) 1、下列说法中正确的是( ) A 、34a 不是整式B 、34a 是单项式C 、2a +是单项式D 、2r π是多项式 2、下列说法正确的是( )A 、4.3万精确到千位B 、0.010有一个有效数字C 、近似数2.8与2.80表示的意义相同D 、由四舍五入得近似数43.0,精确到个位3、如图,要得到a ∥b ,则需要条件( ) A 、24∠=∠ B 、13180∠+∠= C 、12180∠+∠= D 、23∠=∠4、下列运算正确的是( ) A 、5510a a a += B 、6424a a a ⨯=C 、01a a a -÷=D 、440a a a-=5、如图,已知AB ∥DE ,80,140ABC C D E ∠=∠=,则C ∠=( )A 、20B 、30C 、40D 、50 6、式子n m -与()n m -的正确判断是( )A 、这两个式子互为相反数B 、这两个式子是相等的C 、当n 为奇数时,它们互为相反数;n 为偶数时它们相等D 、当n 为偶数时,它们互为相反数;n 为奇数时它们相等 7、23,24mn==,则322m n-等于( )A 、1B 、98C 、278D 、27168、下列各题中正确的个数有( )个(1)两个角和其中一角的对边对应相等的两个三角形全等; (2)两条边和其中一边的对角对应相等的两个三角形全等; (3)两条边和其中一边的对角对应相等的两个三角形一定不全等;(4)三个角对应相等的两个三角形全等;(5)三角形的最大角不小于60度,最小角不大于60度。
A 、1 B 、2 C 、3 D 、4 9、已知:11,2x y ==,则20332()x x y -的值等于( )A 、3544--或 B 、3544或 C 、34D 、54-10、小明有两根5cm 、8cm 的木棒,他想以这两根木棒为边做一个等腰三角形,还需再选用一根( )长的木棒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
xx 学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:3的倒数是( )A.3 B. C.-3 D.试题2:的结果是( )A. B. C. D.试题3:如图,直线分别与相交,则为( )A. 150° B.140° C.130° D.120°试题4:下列事件是确定事件的是( )A.阴天一定会下雨B.黑暗中从5把不同的钥匙中随意摸出一把,用它打开了门C.打开电视机,任选一个频道,屏幕上正在播放新闻联播D.在学校操场上向上抛出的篮球一定会下落试题5:如图,是的直径,则长为( )A.2 B. C.4D.试题6:分式方程的解是( )A. B. C . D.试题7:右图是一个由相同小正方体搭成的几何体的俯视图,小正方形中的数字表示该位置上的小正方体的个数,则这个几何体的主视图是( )试题8:如图,房间地面的图案是用大小相同的黑、白正方形镶嵌而成.图中,第1个黑色形由3个正方形组成,第2个黑色形由7个正方形组成,……那么组成第个黑色形的正方形个数是( )A. B.C.D.试题9:如图,梯形中,为中点,点在梯形的边上沿运动,速度为1cm/s,则的面积与点经过的路程cm 之间的函数关系用图象表示大致是下图中的( )试题10:如图,在中,是斜边上两点,且将绕点顺时针旋转90°后,得到连接下列结论:①②③的面积等于四边形的面积;④⑤其中正确的是( )A .①②④B .③④⑤ C.①③④ D.①③⑤试题11:从重庆市国资委获悉,截至2010年2月末,重庆农商行涉农贷款余额达339亿元,那么339亿元用科学计数法表示为____________________元.试题12:分解因式:___________________.试题13:已知与的半径分别为和,圆心距,则两圆的位置关系为_____.试题14:五张分别写有数字-1,0,1,3,4的卡片背面完全相同.现把它们洗匀后背面向上摆放在桌面上,从中任取一张,所得的数字同时作为一个点的横纵坐标,这个点在函数的图象上侧平面内的概率是______________.试题15:已知:如图,在平面直角坐标系中,为坐标原点,四边形是矩形,点的坐标分别为点的坐标为点在边上运动. 当是腰长为5的等腰三角形时,点的坐标为___________________.试题16:如图,用铆枪把铆钉垂直压入设备时,每压一次,铆枪要短暂休息,铆枪每次压铆钉时的作用力是相同的. 随着铆钉的深入,铆钉所受的阻力也越来越大. 当铆钉进入设备部分长度足够时,每次进入设备的铆钉长度是前一次的已知这个铆钉被铆枪作用3次后全部进入设备(设备足够厚),且第一次作用后,铆钉进入设备的长度是2cm,若铆枪总长度为则的取值范围是_________.试题17:计算:试题18:解方程组:试题19:已知一个三角形的两边分别为线段并且边上的中线为线段求作此三角形.(要求:用尺规作图,写出已知、求作,保留作图痕迹,不写作法,要写结论)已知:求作:结论:试题20:如图,在大树前的平地上选一点测得由点看大树顶端的仰角为35°,在点和大树之间选择一点(在同一直线上),测得由点看大树顶端的仰角为45°,再量得两点间的距离为5.43米,求大树的高度(结果保留两个有效数字). (测角器的高度忽略不计. 参考数据:)试题21:先化简,再求值:其中试题22:如图,一次函数的图象与反比例函数的图象交于两点,已知点的坐标为(1)求反比例函数的解析式和一次函数的解析式;(2)观察图象,直接写出使函数值成立的自变量的取值范围.试题23:在我校举办的课外活动中,有一项是小制作评比.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1. 第三组的件数是12. 请你回答:(1)本次活动共有__________件作品参赛;各组作品件数的中位数是_________件.(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?(3)小制作评比结束后,组委会决定从4件最优秀的作品A、B 、C、D中选出两件进行全校展示,请用树状图或列表法求出刚好展示B、D的概率.试题24:如图,在直角梯形中,与延长线交于点是延长线上一点,于(1)求证:(2)连接若求的长.试题25:为推进节能减排,发展低碳经济,深化“宜居重庆”的建设,我市某“用电大户”用480万元购得“变频调速技术”后,进一步投入资金1520万元购买配套设备,以提高用电效率达到节约用电的目的.已知该“用电大户”生产的产品“草甘磷”每件成本费为40元.经过市场调研发现:该产品的销售单价,需定在100元到300元之间较为合理.当销售单价定为100元时,年销售量为20万件;当销售单价超过100元,但不超过200元时,每件新产品的销售价格每增加10元,年销售量将减少0.8万件;当销售单价超过200元,但不超过300元时,每件产品的销售价格在200元的基础上每增加10元,年销售量将减少1万件.设销售单价为(元),年销售量为(万件),年获利为(万元).(年获利=年销售额-生产成本-节电投资)(1)直接写出与之间的函数关系式;(2)求第一年的年获利与间的函数关系式,并说明投资的第一年,该“用电大户”是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?(3)若该“用电大户”把“草甘磷”的销售单价定在超过100元,但不超过200元的范围内,并希望到第二年底,除去第一年的最大盈利(或最小亏损)后,两年的总盈利为1842万元,请你确定此时销售单价.在此情况下,要使产品销售量最大,销售单价应定为多少元?试题26:已知:二次函数的图象与轴交于两点(点在点的左侧),与轴交于点对称轴是直线且图象向右平移一个单位后经过坐标原点(1)求这个二次函数的解析式;(2)直线交轴于点,为抛物线顶点.若求的值.(3)在(2)问的前提下,为抛物线对称轴上一点,且满足在轴右侧的抛物线上是否存在点使得的面积等于若存在,求出点的坐标;若不存在,请说明理由.B试题2答案: B试题3答案: C试题4答案: D试题5答案: B试题6答案: A试题7答案: A试题8答案: C试题9答案: D试题10答案: C试题11答案:试题12答案:相交试题14答案:试题15答案:或试题16答案:试题17答案:解:原式………………………………5分………………………………………………………6分试题18答案:解:②×3得由①+③得:∴…………………………………………………………2分将代入②得:∴………………………………………………………4分∴原方程组的解为……………………………………6分已知:线段………………………………………………………1分求作:使是的中点,且……2分(或:求作使边上的中线)结论:如图,即为所求.…………………………………………6分试题20答案:解:由题知米设大树的高为米∵∴∴………………………………………………2分∵在中,∴解得…………………………………………5分∵∴答:大树的高度为13米. ……………………………………6分解:原式…………………………………2分…………………………………………4分……………………………………………………6分当时…………………………………………………7分………………………………………………8分………………………………………………………10分试题22答案:解:(1)过点作轴于∴在中,∴设(其中)∴在中,又∴∴∴∴………2分将代入反比例函数中∴∴∴反比例函数解析式为………………………4分将代入中∴∴……………6分将代入中,得解之得∴…………………………………………8分(2)由图像知,当或时,……………………10分试题23答案:(1) 6010.5 ………………………………2分(2)解:第四组有作品(件)第六组有作品(件)∴第四组的获奖率为第六组的获奖率为∴第六组的获奖率较高.…………………………………5分(3)解:画树状图如下或列表如下A B C DA (A,B) (A,C) (A,D)B(B,A) (B,C) (B,D)C (C,A) (C,B) (C,D)D (D,A) (D,B) (D,C)…………………………8分由图(表)知,所有等可能的结果有l2种,其中刚好是(B,D)的有2种,所以刚好展示B、D的概率为……………………10分试题24答案:(1)证明:连接…………………………1分∴∴∴……………3分∴∴∴……………………5分(2)解:由(1)知,∴∴∴在中,∴在中,……………………7分法一:由(1)知,∴∴分别是垂直平分线上的点,∴………………………………………………8分在中,∴…………………………9分∴…………………………10分法二:在中,在中,∴∴∴∴……………………………………9分∴即∴………………………………………………10分试题25答案:解:(1)当时,.(略解:) 当时,(略解:把代入得,∴)………………………………2分(2)当时,,当时,…………………………………………4分当时,∴对称轴是直线[来源:]∴…………………………………………6分∴投资的第一年该“用电大户”是亏损的,最少亏损为78万元.……………7分(3)依题意可知,当时,第二年与之间的函数关系为[来源:学*科*网]当总利润刚好为1842万元时,依题意可得……8分整理,得解得,∴要使两年的总盈利为1842万元,销售单价可定为190元或200元.……………9分对随的增大而减小∴使销售量最大的销售单价应定为190元.………………………………10分试题26答案:解:(1)由题意,对称轴是直线∴……………………………………………………………………1分把,分别代入得……………2分解得∴这个二次函数的解析式为………………………………3分(2)直线与轴交于,∴由得连接过作轴于(如图1),则抛物线与轴交于∴∴,∴[来源:]∴∴……∴∴(3)设`∴即解得∴∴………………………………8分法一:设存在符合条件的点则①当在直线上侧时,连接(如图1),则即整理,得解得(舍去),把代入得∴……………………………………10分②当在直线下侧时,不妨叫连接(如图1),则即整理,得解得(舍去)把代入得∴综上所述,存在符合条件的点其坐标为或. ………………………………………………………………12分法二:设存在符合条件的点则①当在直线上侧时,过作轴,交于(如图2)设到距离分别为则即整理,得解得(舍去),把代入得∴……………………………………10分②当在直线下侧时,不妨叫过作轴,交于(如图2) 设到距离分别为则即整理,得解得(舍去)把代入得∴综上所述,存在符合条件的点其坐标为或.…………12分法三:①当在直线上侧时,过作交轴于连接(如图3)则,即∴∴∴直线解析式为联立得或在轴右侧, ∴坐标为…………………………………………10分②当在直线下侧时,不妨叫过作,交轴于连接(如图3),同理可得∴∴直线解析式为联立得或在轴右侧,∴坐标为综上所述,存在符合条件的点其坐标为或.。
