力矩、力偶与力的平移分析
关于力的平移定理

关于力的平移定理力的平移定理: 将力从物体上的一个作用点,移动到另外一点上,额外加上一个力偶矩,其大小等于这个力乘以2点距离,方向为移动后的力与移动前力的反向力形成的力偶的反方向刚体受力是不会发生形变的,而变形体就不一样了。
力的概念形成简史推拉物体时,可以直觉意识到“力”的模糊概念。
被推拉的物体发生运动以及物体滑行时,由于摩擦而逐渐变慢,最后停止下来,都反映了力的作用。
中国古代文献《墨经》就把这个概念总结为“力,形之所由奋也。
”就是说,力是使物体奋起运动的原因。
所以,力是那样自然地反映到人的意识中来的。
但是人们从直觉意识到“力”的概念到获得“力”的严格科学定义,却经历了长期的斗争。
力的概念在牛顿力学中占有最根本的位置。
牛顿在1664年就提出了力的定义是动量的时间变率(动量等于质量乘速度)。
牛顿第一定律(惯性定律)是力的定性的定义,它给出力在什么条件下存在和什么条件下不存在的定性条件。
牛顿第二定律给出了力的定量的定义,即力等于动量的时间变率,如果质量不变,力也等于质量乘加速度。
牛顿第三定律指出,对于每一个力而言,必有一大小相等方向相反的反作用力存在。
它指出所有的力都是成对的,只在两个物体相互作用时才能实现(见牛顿运动定律)。
牛顿的万有引力理论的惊人成就,使超距作用力的概念推广到物理学的其他分支中去。
但是,牛顿并不能从物理上说清超距作用的实质,所以长期受到各方的严厉批评,直到A,爱因斯坦于1905年提出狭义相对论,指出一切物理作用传播的最大速度是光速以后,人们才认识到牛顿有关超距作用力的概念有极大的局限性。
爱因斯坦1915年在他的广义相对论里明确指出,万有引力的传播速度不可能大于光速。
力矩

汽 车 机 械 基 础
x
3
2
1
例
解:
阳台(简化为悬臂梁)。求:固定端约束力
2、列平衡方程、
0,
F F
x
FAx 0
y
0,
FAy ql F 0
ql 2 M A 0, M A 2 Fl 0 3、解方程
FAx 0, FAy ql F ql MA Fl 2
F
F
d
F
F
O
A
=
O
d A
=
M
O A
F
汽 车 机 械 基 础
F ' = F " = F ,
M= Fd = MO ( F )
3
2
1
4 力系向给定点O的简化
F2 F3 F1 F’3 F’2 F’1
简化中心0
平面汇交力系
平面一般力系 F1、F2…Fn
F1’= F1 F2’= F2 Fn’ =Fn
汽 车 机 械 基 础
2m
x
3
2
1
R0 y F y F1 F2 sin 60 F4 sin 30 3 1 1 2 3 0.768kN 2 2
2m y A
F2
60°
B
F3
R0
2 2 R0 R x 0 y 0.794 kN R0 x cosR 0 、 x 0.614 R0
3
2
1
例 在长方形平板的O、A、B、C 点上分别作用着有 四个力:F1=1kN,F2=2kN,F3=F4=3kN(如图),试 求以上四个力构成的力系对点O 的简化结果,以及 该力系的最后的合成结果。
1-2力矩力偶力的平移

力矩为零的情形:
1)力等于零;
2)力臂等于零。
应当注意:一般来说,同一个力对不同点产生的力矩是不同的,因此不指明矩心而求力矩是无任何意义的。在表示力矩时,必须标明矩心。即力矩与矩心的位置有关。
推论一:力偶可在其作用面内任意转移,而不改变它对刚体的作用效果。
推论二:只要保持力偶矩的大小和转向不变,可以同时改变力偶中力的大小和力偶臂的长短,而不改变其对刚体的作用效果。
三、力的平移定理
力的平移定理——若将作用在刚体某点(A点)的力(F)平行移到刚体上任意点(O点)而不改变原力的作用效果,则必须同时附加一个力偶,这个力偶的力偶矩等于原来的力对新作用点之矩。
力偶矩是代数量,一般规定:使物体逆时针转动的力偶矩为正,反之为负。力偶矩的单位是N•m,读作“牛米”。
4.力偶的性质
性质1:力偶中的两个力在其作用面内任意坐标轴上的投影的代数和等于零,因而力偶无合力,也不能和一个力平衡,力偶只能用力偶来平衡。
性质2:力偶对其作用面内任一点之矩恒为常数,且等于力偶矩,与矩心的位置无关。
作业
教学反思
2.合力矩定理
3.力矩的平衡条件
二、力偶的概念
1.定义:
大小相等、方向反向、作用线平行但不共线的两个力。用符号(F,F′)表示。
两个力作用线之间的垂直距离d称为力偶臂;
两力作用线所确定的平面称为力偶的作用面。
2.力偶的作用效应
使刚体产生转动效应。
3.力偶矩
力偶矩是力偶中的一个力的大小和力偶臂的乘积并冠以正负号。用来表示力偶在其作用面内使物体产生转动效应的度量,用M或M(F,F′)表示。
1.2力矩力偶与力的平移教案
课题 1.2力矩力偶与力的平移
课时 1 班级21机电3/4班课型新课时间2021年10月19日
教学目标知识目标:熟记力矩、力偶的概念
能力目标:应用力矩、力偶,力的平移定理解题德育目标:提高合作探究能力,增强合作意识
教学重点力的平移定理
教学难点力的平移定理
教法直观教学法
学法小组合作探究
教学评价师生互评,小组互评
教具多媒体课件,教具,动画
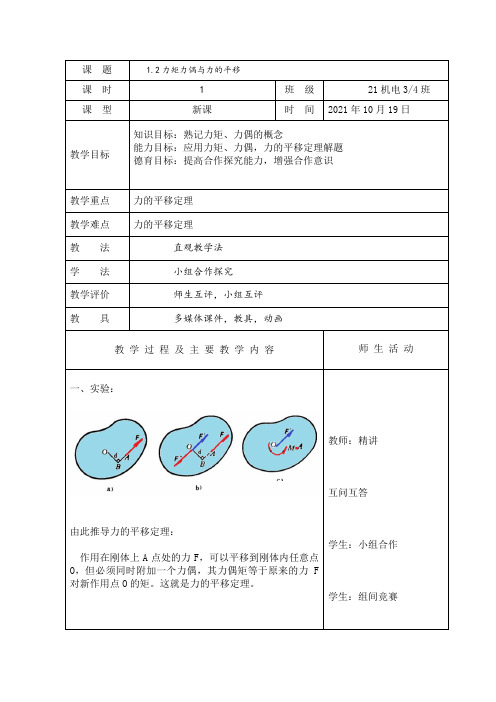
教学过程及主要教学内容师生活动一、实验:
由此推导力的平移定理:
作用在刚体上A点处的力F,可以平移到刚体内任意点O,但必须同时附加一个力偶,其力偶矩等于原来的力F 对新作用点O的矩。
这就是力的平移定理。
教师:精讲
互问互答
学生:小组合作学生:组间竞赛。
第一章 力矩力偶力的平移

力F 对任一点之矩,不会因该力沿其作用线移动而
改变,因为此时力臂和力的大小均未改变;
力的作用线通过矩心时,力矩等于零;
力矩的平衡条件
日常生活中,常会遇到绕定点转动的物体,我们在生活中最常见的定点转动如 下:
力矩的平衡条件
力矩的平衡条件
力矩平衡的条件是: 各力对转动中心O点的力矩的代数和等于零
力偶
(1) 力偶的概念
力偶 大小相等,方向相反,作用线不重合的 平行的两个力,称为力偶。并记为(F, F´)。 力偶作用面 力偶中两个力所在的平面。 力臂
两个力作用线间的垂直距离
实验表明,力偶对物体只能产生转动 效应,且当力越大或力偶臂越大时, 力偶使物体转动的就越显著
力偶
公式:
M
力偶矩的单位:
生活中的力矩
力矩
F 使物体 绕O点转动
矩心
O称为力矩中心。
F
O点到力的作用线的垂直距离称
力臂
为力臂。
力矩是一个代数量,它的绝对值大小等于力与力臂的乘积.
符号规定:力使物体绕矩心逆时针转动为正,反之为负。
力矩记:
mo(F)= ±Fd
+_
单位:牛顿米(N·m) 或 千牛顿米(kN·m)
力矩的特点:
力F 对O点之矩不仅取决于力的大小,同时还与矩
牛顿米(N·m)或千牛顿米(kN·m)
(2)力偶的性质
① 力偶无合力
力偶对刚体只有转动效应,没有移动效应
② 力偶可以在作用面内任意转移,而不影 响它对物体的作用效应;
③在保持力偶矩的大小和转向不改变的条件下, 可以任意改变力和力偶臂的大小,而不影响它 对物体的作用。
在同一平面内的两个力偶,只要它们的力偶矩 大相等、转动方向相同,则两力偶必等效。
工程力学6 力的平移定理

M F d
F
F′
d F′
A
F
O d
A
三、力的平移定理的应用
假设在一块钢板上O点钉一个钉子, 用四根绳子用力拉,钢板将会如何 运动呢?钉子将如何受力?
F1
F2 O
F4 F3
Y
F1
Y
F2
X
O
F3 图① F4 Y R′ Mo
O 图③
根据力的平移定理 F2
M1 F1
M2 X
O
M2 M3
F4
F3 图②
根据平面汇交力系和
d
OM
F′
d
FA
A
M F,F F d M O F
因此:作用于刚体上的力,可平移到刚体上的任意一点, 但必须附加一力偶,其附加力偶矩等于原力对平移点的 力矩。图中O称为简化中心。
1.力的平移定理
F1
F2
F3
O
F4
例题1:如图所示,假设每个方格是边长为1m的 正方形,F1=10KN、F2=10KN、F3=30KN、 F4=30KN,试求:将四个力平移至O点的结果。
B Od
b
A
F=
M B
F
O d M MO F F d
A B
O b
A
逆时针为正
M M O F F b
M 顺时针为负 F
2.力的平移定理性质
(2)力的平移定理只适用于刚体,对变形体不适用, 并且力的作用线只能在同一刚体内平移,不能平移到另 一刚体。
(3)力的平移定理的逆定理也成立。
OM
X
平面力偶系的合成
R′=F1+F2+F3+F4(矢量和) MO=M1+M2+M3+M4 (代数和)
机械基础课件力矩力偶力的平移
杠杆
在杠杆中,力矩是用来平衡力的,使 得杠杆两端受力平衡。力矩的计算公 式是力乘以力臂,通过调整力臂的长 度可以改变力矩的大小,从而实现重 物的升降或旋转。
门和窗户
门和窗户的开闭需要用到力矩原理, 通过转动把手来施加力矩,使门窗绕 着轴心转动。同样地,通过调整施加 在把手上的力和力臂的长度,可以控 制门窗的开关速度。
力偶在实际机械中的应用
传送带
传送带在运输物品时,需要用到力偶原理。 通过在传送带的一端施加一个力偶,可以使 传送带转动起来,从而将物品从一个地方运 输到另一个地方。
车辆转向系统
车辆的转向系统也是利用力偶原理,通过施 加一个与车轮转向相反的力偶,使车轮产生 回转效应,实现车辆的转向。
力的平移在实际机械中的应用
滑轮组
滑轮组是利用力的平移原理,通 过将施加在滑轮上的力平移到绳 索上,从而实现重物的升降或移 动。
杠杆式千斤顶
杠杆式千斤顶也是利用力的平移 原理,通过将施加在杠杆上的力 平移到支撑杆上,从而将重物顶 起。
THANKS FOR WATCHING
感谢您的观看
总结词
力偶矩等于力与力偶臂的乘积。
详细描述
力偶矩是衡量力偶作用效果的物理量,其计算公式为 M = F * d,其中 F 是组 成力偶的两个力的大小,d 是力偶臂的长度。力偶矩是一个代数量,其大小等 于两个分力的代数和乘以力偶臂的长度。
力偶的平衡条件
总结词
当一个物体上所受的各力偶矩的代数和为零时,该物体处于平衡状态。
力矩的计算
根据给定的力和力臂,利用公式计算力矩。
特殊情况
当力垂直于力臂时,力矩为零。
力矩的平衡条件
力矩平衡条件
平衡条件的计算方法
力矩、力偶与力的平移分析
F asin bcos
oa
b
Fx
§2-2 力矩、力偶与力的平移
例2-2 已知 a、b、l、F、 ,求力F 对O点的矩。
l
O
解: (1)由力矩定理计算力矩: d
F Fx Fy
Fy
F
ba
Fx
MO(F) =MO(Fx)+ MO(Fy)=Fy(l+a)+Fxb
证明从略22力矩力偶与力的平移只要保持力偶矩的大小和转向不变力偶可以在作用面内任意移转不改变对刚体的作用效果
§2-2 力矩、力偶与力的平移
一、力对点之矩(力矩)
力对点之矩(力矩)是指力使物体绕某点转动效应 的量度。
矩心O
力臂d
力矩:力的大小(F)与力臂(d)的乘积再冠以适当的正负号(±)来
表示力F 使物体绕O点转动的效应,称为力F 对O 点的矩,简称力矩。
§2-2力矩、力偶与力的平移
(a)只要保持力偶矩的大小和转向不变,力偶可以在 作用面内任意移转,不改变对刚体的作用效果。
=
=
§2-2力矩、力偶与力的平移
(b)只要保持力偶矩的大小和转向不变,可以同时 改变力偶中力的大小和力偶臂的长短,而不改变 力偶对刚体的作用效果。
M
M
M
§2-2力矩、力偶与力的平移
二、力偶 力偶实例
F1 F2
§2-2 力矩、力偶与力的平移
力偶实例
§2-2 力矩、力偶与力的平移
1.力偶
力偶——两个大小相等、方
A
F d
向相反且不共线的平行力组
C 成的力系。(Fˊ、F)
F
力偶臂——力偶的两力之间的
B
1.2力矩、力偶、力的平移(课件)-高一《机械基础》pptx
第1章 杆件的静力分析
正负规定:力使物体绕矩心逆时针方向转动时,力矩为 正,反之为负。力矩的单位名称为牛顿·米,符号为N·m。
力矩为零的两种情况:(1)力等于零;(2)力的作 用线通过矩心,即力臂等于零。
应当注意:一般来说,同一个力对不同点产生的力矩 是不同的,因此不指明矩心而求力矩是无任何意义的。在 表示力矩时,必须标明矩心。 也就是说力矩与矩心的位置 有关。
○为力偶(F,F′)作用平面内
任意一点。
M○(F,F′)=-F′·x+F(x+d )= -F′·x+Fx+Fd)
=+F·d
图1-24力偶对其平面内任意点之矩
=M(F,F′)
第1章 杆件的静力分析
·推论1: 力偶可在其作用面内任意转移,而不改变它对刚体的作 用效果(图1-25)。
拧瓶盖时,可将力夹在A、B
的力偶矩为正,反之为负。力偶矩的单位是N•m,读作
“牛米”。
第1章 杆件的静力分析
4.力偶的性质 性质1:力偶中的两个力在其作用
面内任意坐标轴上的投影的代数和等于 零,如图1-23所示,因而力偶无合力, 也不能和一个力平衡,力偶只能用力偶 来平衡。
图1-23力偶的投影
·性质2:力偶对其作用面内任一点之矩恒为常数,且等于力偶矩,与 矩心的位置无关(图1-24)。
图(c) Mo(F)=-Fd=200×200×10-3 =-40(N·m)
第1章 杆件的静力分析
1.2.2力偶的概念 1.什么是力偶 大小相等、方向反向、作用线平行但不共线的两个力 。 用符号(F,F′)表示。 两个力作用线之间的垂直距离d称为力偶臂; 两力作用线所确定的平面称为力偶的作用面。
力偶和力偶矩与力的平移,载荷与应力,零件的失效与工作能力
【课题编号】4—1.4【课题名称】力偶和力偶矩与力的平移,载荷与应力,零件的失效与工作能力准则。
【教学目标与要求】一、知识目标1.复习力偶、力偶矩与力的平移的基本知识。
2.了解载荷对零件的作用及应力的分类。
3.了解机械零件的主要失效形式及工作能力准则。
二、能力目标1.会求力偶和力偶矩与力的平移产生的附加力偶。
2.会分析载荷作用下零件的应力状态。
3.会分析零件失效的原因及强度计算准则。
三、素质目标1. 能应用力学知识分析零件的应力状态。
2. 能分析失效的原因。
四、教学要求1. 能熟悉力偶及会力偶矩的计算方法,会作力的平移。
2.了解常见的四种应力状态与产生原因,及失效的四种形式与设计准则。
【教学重点】1.静力学知识的复习。
2.应力的四种状态,失效的四种形式。
【难点分析】应力的四种状态分析是难点,应当举例说明,注意对称循环变化应力和脉动循环应力的区别。
力矩与力偶矩的区别是难点。
【分析学生】力的性质是旧知识的复习,应当充分调动学生为主体的积极性,从实例计算达到复习基本公理的目的。
失效的形式应多举例说明。
【教学思路设计】通过习题的计算,总结出力、力矩与力偶矩的区别,达到复习的目的。
应力的分类应选择恰当的实例。
【教学安排】2学时(90分钟)【教学过程】一、力偶和力偶矩力偶—一对等值、反向且不共线的平行力组成的力系,它是二个力的作用,如开汽车双手控制方向盘为力偶;用手扭动圆形门把为力偶,力偶是左右两个力作用产生的;如果用手压单门把,是单力对轴的矩,称为力矩,不是力偶。
两者作用效果一样,但含义不同。
在表达方式上也不一样,力矩表达式为M0﹝F﹞;力偶表达式为M0﹝F,F ¹﹞。
力偶对物体产生转动效应的三要素是力偶矩的大小、转向和作用平面。
力偶与力矩有以下两点区别:1)力偶无合力。
其两力的大小相反且等值,但不在一条线上;而力矩可以分别求各力对点的矩后再求合力矩,也可以先求各力的合力后再求合力对点的矩。
2)力偶可以在平面内任意移动或转动,对物体的转动效应不变,与矩心的位置无关。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2-2 力矩、力偶与力的平移
2.力偶的性质
①力偶在任意坐标轴上的投影等于零。力偶不能合成 为一个力,也不能用一个力来平衡,力偶只能由力偶 来平衡。
F
AF
B
Fx F cos Fcos 0
力和力偶是静力学的两个 基本要素。力偶对刚体只 有转动效应,而无移动效 x 应。
§2-2 力矩、力偶与力的平移
§2-2 力矩、力偶与力的平移
1.力偶
力偶——两个大小相等、方
A
F d
向相反且不共线的平行力组
C 成的力系。(Fˊ、F)
F
力偶臂——力偶的两力之间的Leabharlann B垂直距离。(d)
力偶矩:
力偶的作用面——力偶中两力 所在平面。
M Fd 2ABC
两个要素:
a.大小:力与力偶臂乘积;
b.方向:转动方向。
②力偶对任意点取矩都等于力偶矩,不因矩心的改变
而改变。
M Fd
AF
MO F,F MO F MO F F x Fd x Fd M
F d
Bx
力矩的符号 MO F
力偶矩的符号 M
O
③同平面两个力偶的等效条件:在同平面内的两个力 偶,如果力偶矩相同(大小相等,转向相同),则两力 偶彼此等效。(证明从略)
例2-3已知Fn、、r,
求力 Fn 对于轮心O的力矩。
解:利用力矩定理计算
MO (Fn ) MO (Fr ) MO (Fτ ) MO (Fτ )
Fnr cos
r
O
d Fτ
Fn Fr
§2-2 力矩、力偶与力的平移
二、力偶 力偶实例
F1 F2
§2-2 力矩、力偶与力的平移
力偶实例
§2-2力矩、力偶与力的平移
(a)只要保持力偶矩的大小和转向不变,力偶可以在 作用面内任意移转,不改变对刚体的作用效果。
=
=
§2-2力矩、力偶与力的平移
(b)只要保持力偶矩的大小和转向不变,可以同时 改变力偶中力的大小和力偶臂的长短,而不改变 力偶对刚体的作用效果。
M
M
M
§2-2力矩、力偶与力的平移
三、力的平移定理
作用于刚体上的力,可平移至 该刚体内任一点,但须附加一力偶, 其力偶矩等于原力对平移点之矩。
MB MB (F ) Fd
(加) F
F
B
Bd F
A
F A
F' = -F" = F
仅适应于同一刚体。
F
MB
B A
§2-2力矩、力偶与力的平移 力的平移定理的应用:
§2-2 力矩、力偶与力的平移
正负号表示两种不同的转向,使物体逆转,正值;顺转,负值
“+ ”—— 使物体逆时针转时力矩为 正;
“-” —— 使物体顺时针转时力矩 为负。
由力矩的定义可知:
(1)当力的大小等于零或力的作用线通过矩心(力臂
d=0)时,力矩等于零;
(2)当力沿其作用线移动时,力矩不变。
oa
b
Fx
§2-2 力矩、力偶与力的平移
例2-2 已知 a、b、l、F、 ,求力F 对O点的矩。
l
O
解: (1)由力矩定理计算力矩: d
F Fx Fy
Fy
F
ba
Fx
MO(F) =MO(Fx)+ MO(Fy)=Fy(l+a)+Fxb
=F(lsin+bcos+asin)
§2-2 力矩、力偶与力的平移
§2-2 力矩、力偶与力的平移
一、力对点之矩(力矩)
力对点之矩(力矩)是指力使物体绕某点转动效应 的量度。
矩心O
力臂d
力矩:力的大小(F)与力臂(d)的乘积再冠以适当的正负号(±)来
表示力F 使物体绕O点转动的效应,称为力F 对O 点的矩,简称力矩。
MO (F ) Fd
MO(F)——代数量(标量),单位:N·m。
§2-2 力矩、力偶与力的平移
例2-1 已知 a、b、F、,求力F对O点的矩。
解: F Fx Fy
Fx Fcos Fy Fsin
Fy F
MO F MO Fx MO Fy
Fxb Fya
Fbcos Fasin
F asin bcos
