第一章函数练习题1

合集下载

高等数学课后习题答案--第一章

《高等数学》习题参考资料第一篇一元函数微积分第一章极限与连续§1 函数习题1.确定下列初等函数的定义域：(1) 21)(2−−+=x x x x f ；(2)4)(2−=x x f ；(3) 21arcsin )(−=x x f ；(4)2)5lg()(x x x f −=；(5) 4lg )5lg()(2−−=x x x f ；(6)x x x f cos sin )(−=。

1．【答案】(1) )},2()2,1()1,(|{:+∞∪−∪−−∞∈=x x D (2) )},2[]2,(|{:+∞∪−−∞∈=x x D (3) ]}3,1[|{:;−∈=x x D (4) )}5,0()0,(|{:∪−∞∈=x x D (5) ]}4,1[|{:∈=x x D (6)+ +∈=+∞−∞=U k k k x x D ππ452,412|:.2. 作出下列函数的图象：（1）|sin |sin )(x x x f −=；(2)|1|2)(−−=x x f ；（3）+−−=,1,1,21)(x x x x f .12,21,1||−<<−<<≤x x x 2 【答案】 (1)2(2)2 (3)3.判断下列函数的奇偶性：（1）x x x f ++−=11)(；（2）xxx f x x +−+−=11lg110110)(；（3）x x a a x f x x sin )(++=−；（4）)1lg()(2x x x f ++=。

3. 【答案】 (1) 偶函数; (2) 偶函数; (3) 偶函数; (4) 奇函数 .4.证明:两个奇函数的乘积是偶函数;一个奇函数与一个偶函数的乘积是奇函数。

4．【答案】设)(x f ,)(x h 是奇函数, )(x g 是偶函数,)()()(x h x f x f =,)()()(x g x f x G =, 于是)()()(x h x f x F −−=−))())(((x h x f −−=)()()(x F x h x f ==, 因此)(x F 是偶函数.)()()(x g x f x G −−=−)()(x g x f −=)(x G −=, 因此)(x G 是奇函数.5．设函数f 满足：D （f ）关于原点对称，且()xc x bf x af =+1)(，其中a ,b ,c 都是常数，||||b a ≠,试证明f 是奇函数。

经济数学第一章练习题

经济数学第一章练习题一、函数与极限1. 判断下列函数的单调性：(1) f(x) = 2x + 3(2) f(x) = x^2 + 4x + 1(3) f(x) = e^x 2x2. 求下列极限：(1) lim(x→0) (sin x / x)(2) lim(x→1) (x^2 1) / (x 1)(3) lim(x→+∞) (1 + 1/x)^x3. 讨论下列函数在指定区间内的连续性：(1) f(x) = |x|，区间为[1, 1](2) f(x) = sqrt(4 x^2)，区间为[2, 2]二、导数与微分1. 求下列函数的导数：(1) f(x) = 3x^2 2x + 1(2) f(x) = ln(x + 1)(3) f(x) = e^x sin x2. 计算下列函数的微分：(1) f(x) = x^3 2x^2 + 3x 4(2) f(x) = arcsin(x/2)3. 求下列隐函数的导数：(1) y = e^(x + y)(2) x^2 + y^2 = 4三、高阶导数与微分方程1. 求下列函数的二阶导数：(1) f(x) = x^4 3x^3 + 2x^2(2) f(x) = ln(x^2 + 1)2. 求下列微分方程的通解：(1) y' + y = x(2) y'' 2y' + y = e^x3. 求下列微分方程的特解：(1) y' = 2x + y，初始条件为y(0) = 1(2) y'' + y = sin x，初始条件为y(0) = 0，y'(0) = 1四、泰勒公式与应用1. 将下列函数在指定点处展开成泰勒级数：(1) f(x) = e^x，展开点为x = 0(2) f(x) = sin x，展开点为x = π/22. 利用泰勒公式求下列极限：(1) lim(x→0) (1 cos x) / x^2(2) lim(x→0) (e^(x^2) 1 x^2) / x^43. 计算下列函数的近似值：(1) f(x) = sqrt(1 + x)，当x = 0.01时(2) f(x) = ln(1 + x)，当x = 0.1时五、多元函数微分法1. 计算下列多元函数的偏导数：(1) z = x^2 + y^2，对x和y求偏导数(2) u = sin(xy) + e^z，对x、y和z求偏导数2. 求下列函数的全微分：(1) z = x^2y + y^2x(2) u = ln(xyz)3. 验证下列函数是否满足拉格朗日中值定理：(1) f(x, y) = x^2 + y^2，在直线y = x上(2) f(x, y) = e^(x^2 + y^2)，在圆x^2 + y^2 = 1上六、极值与条件极值1. 求下列函数的极值：(1) f(x) = x^3 3x^2 + 2(2) f(x, y) = x^2 + y^2 2x 4y + 52. 求下列函数在给定区间上的最大值和最小值：(1) f(x) = x^2 + 4x，区间为[0, 3](2) f(x, y) = x^2 + y^2，在圆x^2 + y^2 = 4内3. 求下列条件极值问题：(1) max f(x, y) = x + y，约束条件为x^2 + y^2 = 1(2) min f(x, y, z) = x + y + z，约束条件为x^2 + y^2 + z^2 = 4，x + y + z = 1七、积分与定积分的应用1. 计算下列不定积分：(1) ∫(3x^2 2x + 1)dx(2) ∫(e^x sin x)dx2. 计算下列定积分：(1) ∫_{0}^{1} (x^2 + 1)dx(2) ∫_{π/2}^{π/2} (cos x)dx3. 利用定积分求解下列实际问题：(1) 计算由曲线y = x^2与直线x = 1，y = 0围成的平面图形的面积(2) 计算由曲线y = e^x，直线x = 0，y = e及y轴围成的平面图形的体积八、多元积分1. 计算下列二重积分：(1) ∬_D (x^2 + y^2)dxdy，其中D为圆x^2 + y^2 ≤ 1(2) ∬_D (e^(x + y))dxdy，其中D为矩形区域0 ≤ x ≤ 1，0 ≤ y ≤ 22. 计算下列三重积分：(1) ∭_E (x + y + z)dV，其中E为长方体0 ≤ x ≤ 1，0 ≤ y ≤ 2，0 ≤ z ≤ 3(2) ∭_E (xyz)dV，其中E为球体x^2 + y^2 + z^2 ≤ 13. 利用二重积分求解下列实际问题：(1) 计算由抛物线y = x^2与直线x = 1，y = 0围成的平面图形绕x轴旋转一周所形成的旋转体的体积(2) 计算由曲面z = x^2 + y^2与平面z = 4围成的立体图形的体积答案一、函数与极限1. (1) 单调递增(2) 单调递减(3) 单调递增2. (1) 1(2) 2(3) e3. (1) 在[1, 1]上连续(2) 在[2, 2]上连续，但在x = ±2处不连续二、导数与微分1. (1) f'(x) = 6x 2(2) f'(x) = 1 / (x + 1)(3) f'(x) = e^x sin x + e^x cos x2. (1) df(x) = (6x^2 4x + 3)dx(2) df(x) = (1 / sqrt(1 (x/2)^2))dx3. (1) y' = (e^(x + y) y') / e^(x + y)(2) y' = x / y三、高阶导数与微分方程1. (1) f''(x) = 12x^2 12x(2) f''(x) = 2 / (x^2 + 1)^22. (1) y = C e^(x) + x(2) y = C1 e^x + C2 e^(x)3. (1) y = x + 1(2) y = (1/2) sin x (1/2) cos x四、泰勒公式与应用1. (1) e^x = 1 + x + x^2/2! + x^3/3! +(2) sin x = 1 (x π/2)^2/2! + (x π/2)^4/4!2. (1) 1/2(2) 1/23. (1) f(0.01) ≈ 1.005(2) f(0.1) ≈ 0.09516五、多元函数微分法1. (1) ∂z/∂x = 2x，∂z/∂y = 2y(2) ∂u/∂x = y cos(xy)，∂u/∂y = x cos(xy)，∂u/∂z = e^z2. (1) dz = (2xy + y^2)dx + (x^2 + 2xy)dy(2) du = (1/x + 1/y + 1/z)dx + (1/x + 1/y + 1/z)dy + (1/x + 1/y + 1/z)dz3. (1) 满足(2) 满足六、极值与条件极值1. (1) 极大值f(1) = 0，极小值f(2/3) = 4/27(2) 极小值f(1, 2) = 52. (1) 最大值f(3) = 3，最小值f(1) = 1(2) 最大值f(0, 2) = 4，最小值f(0, 2) = 03. (1) 最大值f(√2/2, √2/2)= √2(2) 最小值f(1, 0, 0) = 1七、积分与定积分的应用1. (1) (x^3 x^2 + x) + C(2) (e^x + cos x) + C2. (1) 5/3(2) 23. (1) 1/3 π(2) (e^2 e)π八、多元积分1. (1) π(2) e^2 12. (1) 3(2) 0（因为积分区域关于y轴对称，被积函数关于x为奇函数）3. (1) (2/3)π(2) (π/6)。

《高等数学一》第一章-函数--课后习题(含答案解析)

第一章函数历年试题模拟试题课后习题（含答案解析）[单选题]1、设函数，则f(x)=（）A、x(x+1)B、x(x-1)C、(x+1)(x-2)D、(x-1)(x+2)【正确答案】B【答案解析】本题考察函数解析式求解.，故[单选题]2、已知函数f(x)的定义域为[0，4]，函数g(x)=f(x+1)+f(x-1)的定义域是（）.A、[1，3]B、[-1，5]C、[-1，3]D、[1，5]【正确答案】A【答案解析】x是函数g(x)中的定义域中的点，当且仅当x满足0≤x+1≤4且0≤x-1≤4即-1≤x≤3且1≤x≤5也即1≤x≤3，由此可知函数g(x)的定义域D(g)={x|1≤x≤3}=[1,3]. [单选题]3、设函数f（x）的定义域为[0，4]，则函数f（x2）的定义域为（）.A、[0，2]B、[0，16]C、[-16，16]D、[-2，2]【正确答案】D【答案解析】根据f(x)的定义域，可知中应该满足：[单选题]4、函数的定义域为（）.A、[-1,1]B、[-1,3]C、(-1,1)D、(-1,3)【正确答案】B【答案解析】根据根号函数的性质，应该满足：即[单选题]写出函数的定义域及函数值（）.A、B、C、D、【正确答案】C【答案解析】分段函数的定义域为各个分段区间定义域的并集，故D=(－∞，-1]∪（-1，＋∞）.[单选题]6、设函数,则对所有的x，则f(-x)=（）.A、B、C、D、【正确答案】A【答案解析】本题考察三角函数公式。

.[单选题]7、设则=（）.A、B、C、D、【正确答案】B【答案解析】令则，故[单选题]8、则（）.A、B、C、D、【正确答案】D【答案解析】[单选题]9、在R上，下列函数中为有界函数的是（）.xA、eB、1＋sin xC、ln x【正确答案】B【答案解析】由函数图像不难看出在R上e x,lnx,tanx都是无界的，只有1+sinx可能有界，由于|sinx|≤1,|1+sinx|≤1+|sinx|≤2所以有界.[单选题]10、不等式的解集为（）.A、B、C、D、【正确答案】D【答案解析】[单选题]11、（）.A、B、C、D、【正确答案】A【答案解析】根据二角和公式，[单选题]12、函数的反函数是（）.A、B、C、D、【正确答案】A【答案解析】由所以，故.[单选题]13、已知则（）.A、B、C、D、【正确答案】C【答案解析】[单选题]14、已知为等差数列，，则（）.A、-2B、1C、3D、7【正确答案】A因为同理可得：故d=a4－a3=－2.[单选题]15、计算（）.A、B、C、D、【正确答案】A【答案解析】根据偶次根式函数的意义，可知，故[单选题]16、计算（）.A、0B、1C、2D、4【正确答案】C【答案解析】原式=[单选题]将函数|表示为分段函数时，=（）.A、B、C、D、【正确答案】B【答案解析】由条件[单选题]18、函数f(x)=是（）.A、奇函数B、偶函数C、有界函数D、周期函数【正确答案】C【答案解析】易知不是周期函数，,即不等于，也不等于，故为非奇、非偶函数.，故为有界函数.[单选题]19、函数,则的定义域为（）.A、[1,5]C、(1,5]D、[1,5)【正确答案】A【答案解析】由反正切函数的定义域知：，故定义域为[1,5].[单选题]20、下列等式成立的是()A、B、C、D、【正确答案】B【答案解析】A中(e x)2=，C中，D中[单选题]21、下列函数为偶函数的是()A、y=xsinxB、y=xcosxC、y=sinx+cosxD、y=x(sinx+cosx)【正确答案】A【答案解析】sinx是奇函数，cosx是偶函数。

高数第一次课随堂练习函数与极限

随堂练习一第一章函数与极限一、填空题1、432lim23=-+-→x kx x x ，则k= 。

2、函数xxy sin =有间断点，其中为其可去间断点。

3、若当0≠x 时，xxx f 2sin )(= ，且0)(=x x f 在处连续，则=)0(f 。

4、=++++∞→352352)23)(1(limx x x x x x 。

5、3)21(lim -∞→=+e nknn ，则k= 。

6、函数23122+--=x x x y 的间断点是。

7、当+∞→x 时，x1是比3-+x 8、当0→x 时，无穷小x --11与x 相比较是无穷小。

9、函数xe y 1=在x=0处是第类间断点。

10、设113--=x x y ，则x=1为y 的间断点。

11、已知33=⎪⎭⎫⎝⎛πf ，则当a 为时，函数x x a x f 3sin 31sin )(+=在3π=x 处连续。

12、设⎪⎩⎪⎨⎧>+<=0)1(02sin )(1x ax x xxx f x 若)(lim 0x f x →存在，则a= 。

13、设⎩⎨⎧>≤+=0,cos 0,)(x x x a x x f 在0=x 连续，则常数a= 。

二、计算题1、计算下列极限（1）)2141211(lim n n ++++∞→ ；（2）2)1(321lim nn n -++++∞→ ；（3）35lim 22-+→x x x ；（4）112lim 221-+-→x x x x（5）)12)(11(lim 2xx x -+∞→ ；（6）x x x 1sin lim 20→ ；（7）xx x x +---→131lim21；（8）)1(lim 2x x x x -++∞→ ；2、计算下列极限（1）x wx x sin lim0→ ；（2）xxx 5sin 2sin lim 0→ ；（3）x x x cot lim 0→ ；（4）x x x x )1(lim +∞→ ；（5）1)11(lim -∞→-+x x x x ；（6）x x x 1)1(lim -→ ； 3、比较无穷小的阶（1）32220x x x x x --→与，时；（2）)1(21112x x x --→与，时； (3)当0→x 时， 232-+xx与x 。

第一章习题 1-8 函数的连续性与间断点

2
lim
( x 1)( x 1) ( x 1)( x 2 )
x 1
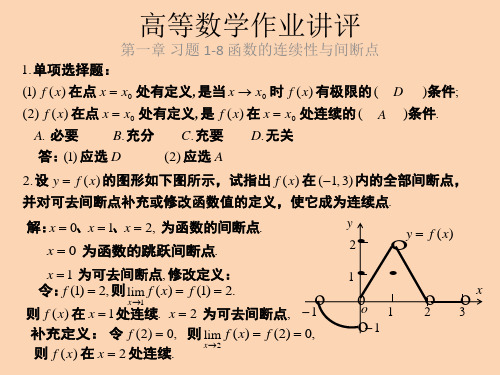
lim
x 1 x2
x 1
2.
所以 x 1 为函数的第一类可去间
断点 . 补充定义： f (1) 2 .
在 x 2 处 , 因为 lim
x 1
2
x 2
x 3x 2
2

所以 x 2 为函数的第二类无穷间
解： f ( 0 ) lim
x 0
x0 x0; x0 在 x 0 处连续？
1 x
sin x 1 .
1 f ( 0 ) lim x sin 1 1 . x x 0

欲使 f ( x ) 在 x 0 处连续 , 应 f ( 0 ) f ( 0 ) f ( 0 ).
( 第 4 题的函数图形 )
5 . 下列函数在指出点处间
断 , 说明这些间断点属于哪义使它连续：
一类？如是可去间断
点 , 则补充或改变函数的定
(1) y
x 1
2
x 3x 2
2
,
x 1, x 2 ;
x 1
2
解：在 x 1 处 , 因为 lim
x 1
x 3x 2

f ( x ) 在 x 1 处不连续 .
在 x 3 处
f ( 3 ) lim

x

x 3
x
1;

f ( x ) 在 x 3 处右连续 .
f ( 3 ) lim
x3
在 x 3处
x x
.

《经济数学--微积分》第一章函数练习题

第一章函数一、填空题1．()x y 32log log =的定义域。

2．523arcsin 3x x y -+-=的定义域。

3．xx y +-=11的反函数。

4．已知31122++=⎪⎭⎫ ⎝⎛+x x x x f ，则=)(x f 。

二、计算题1. 设⎪⎪⎩⎪⎪⎨⎧≥<=3x , 0 3 , sin )(ππϕx x x ，求()2,6-⎪⎭⎫ ⎝⎛ϕπϕ。

2. 指出下列函数的复合过程。

（1）e y 1= ；（2）x ey 3sin = ；（3）()[]12ln arcsin +=x y3. 设()⎩⎨⎧<≥=0, 10 , x x x x f （1）求()1-x f ；（2）求()()1-+x f x f ，（写出最终的结果）4. 某运输公司规定货物的吨公里运价为：在a 公里内，每公里k 元；超过a 公里，超过部分每公里54k 元，求运价m 和里程s 之间的函数关系，并作出此函数的图形。

5. 某商店年销售某种产品800件，均匀销售，分批进货。

若每批订货费为60元，每件每月库存费为0.2元，试列出库存费与进货费之和p 与批量x 之间的函数关系。

三、简单经济问题1. 某车间设计最大生产力为月生产100台机床，至少要完成40台方可保本，当生产x 台时的总成本函数()x x x c 102+=（百元），按市场规律，价格为x p 5250-=（x 为需求量），可以销售完，试写出月利润函数。

2. 某工厂生产某种产品年产量为x 台，每台售价为250元，当年产量在600台内时，可全部售出，当年产量超过600台时，经广告宣传后又可再多出售200台，每台平均广告费为20元，生产再多，本年就售不出去了。

试建立本年的销售收入R 与年产量x 的关系。

3. 当某商品价格为P 时，消费者对此商品的月需求量为D （P ）= 12×103-200P.（1）画出需求函数的图形；（2）将月销售额（即消费者购买此商品的支出）表达为价格P 的函数（3）画出月销售额的图形，并解释其经济意义。

北大版高等数学第一章函数及极限答案第一章总练习题

第一章总练习题221.:581 2.3|58|1422.|58|6,586586,.3552(2)33,52333,015.5(3)|1||2|1(1)(2),2144,.22|2|,.2,2,4,2;2,3x x x x x x x x x x x x x x x x x y x x x y x y x y x y x y x -≥-≥-≥-≥-≤-≥≤-≤-≤-≤≤≤+≥-+≥-+≥-+≥=+-≤=+≤=->=求解下列不等式（）或或设试将表示成的函数当时当时解解解2.解222312312,4,(2).32,41(2), 4.313.1.22,4(1)44,0.1,0.4.:1232(1)2.222221211,.22123222n n y x y y y x y y x x x x x x x x x x n n n n ->=--≤⎧⎪=⎨->⎪⎩<+≥-<++<++>≥-≠+++++=-+==++的全部用数学归纳法证明下列等式当时,2-等式成立设等式对于成立,则解证1231111121211222112312222222124(1)(1)3222,22221..1(1)(2)123(1).(1)1(11)1(1)1,(1)(1)n n n n n n n n n n n n n n n n n n n n n x nx x x nxx x x x x n x x ++++++-+++++=++++++++-+++=-+=-=-+-++++++=≠--++-===--即等式对于也成立故等式对于任意正整数皆成立当时证1,1212.1(1)123(1)(1)(1)n n n nnn n x nx x x nxn x n x x +--++++++++=++-等式成立设等式对于成立,则122122112211221221(1)(1)(1)(1)1(1)(12)(1)(1)1(1)(2)(1)(1)1(1)(2)(1)(1)1(2)(1),(1)1n n n n n n n n n n n n n n n n n n n x nx x n x x n x nx x x n x x n x nx x x x n x n x nx x x x n x n x n x x n ++++++++++-+++-+=--+++-++=--+++-++=--+++-++=--+++=-+即等式对于成立.,.|2|||25.()(1)(4),(1),(2),(2);(2)();(3)0()(4)224211222422(1)(4)1,(1)2,(2)2,(2)0.41224/,2(2)()x x f x xf f f f f x x f x x f f f f x x f x +--=---→→----------==--==-====----≤-=由归纳原理等式对于所有正整数都成立设求的值将表成分段函数当时是否有极限:当时是否有极限?解00022222222;2,20;0,0.(3).lim ()2,lim ()0lim ().(4).lim ()lim (4/)2,lim ()lim 22lim (),lim () 2.6.()[14],()14(1)(0),x x x x x x x x x x x f x f x f x f x x f x f x f x f x x f x x f →-→+→-→--→--→-+→-+→--→-⎧⎪-<≤⎨⎪>⎩==≠=-======--无因为有设即是不超过的最大整数.求003,;2(2)()0?(3)()?391(1)(0)[14]14,1467.[12]12.244(2).lim ()lim[14]14(0).(3).()12,()x y x x f f f x x f x x f f f f x y f f x f x →→+⎛⎫⎪⎝⎭==⎛⎫⎡⎤⎡⎤=-=-=-=-+=-=-=- ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦=-=-==-的值在处是否连续在连续因为不连续因为解111111.7.,0,,:(1)(1);(2)(1).n n n n n n a b a b n b a b a n b n a b a b a++++=-≤<--<++<--设两常数满足对一切自然数证明1111111()()(1),(1).118.1,2,3,,1,1.:{},{}..111,1,7,111n n n n n n n n n n n n nn n n n n n n b a b a b b a a b b b b n b b a b a b a n a b an a b n n a b a b a b n nn ++--+++--+++=<+++=+--->+-⎛⎫⎛⎫==+=+ ⎪ ⎪⎝⎭⎝⎭<+=++⎛+ ⎝类似有对令证明序列单调上升而序列单调下降,并且令则由题中的不等式证证=11111111111(1)1,111111111(1)11(1)1111111,11111.1111(1)11n n nn n nn nn nn n n n n n n n n n n n n n n n n n n n n n +++++++⎫⎛⎫-+⎪ ⎪+⎛⎫⎭⎝⎭<++ ⎪⎝⎭-+⎛⎫⎛⎫⎛⎫+-+<++ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+-+<+ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫+<+ ⎪ ⎪+⎝⎭⎝⎭⎛⎫+ ⎛⎫⎝⎭++< ⎪+⎝⎭111111121111111111(1)1111(1)11111111111111111.1111111.111n n nn n nn n n n n n n n n n n n n n n n n n nn n n n n +++++++⎛⎫-+⎪ ⎪+⎝⎭-+⎛⎫⎛⎫⎛⎫++<+-+ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+<+-+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫+++<+ ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭⎛⎫++>+ ⎪++⎝⎭⇔我们证明22111211111(1)11..(1)(1)1111,1,1,11.nn n n n n n n n n n n e e e n n n n ++++>+++++⇔>++⎛⎫⎛⎫⎛⎫⎛⎫→∞+→+→+<<+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭最后不等式显然成立当时故9.求极限22222222221111lim 1111234111111112341324351111().2233442210.()lim (00, ()lim n n n n n n n n n n n n nxf x a nx ax nxf x nx a →∞→∞→∞⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫---- ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭++==→→∞=≠+===+作函数)的图形.解解0;1/,0.x x ⎧⎨≠⎩1111.?,()[,]|()|,[,].,(),[,],max{||,||}1,|()|,[,].,|()|,[,],(),[,].12.f x a b M f x M x a b M N f x N x a b M M N f x M x a b M f x M x a b M f x M x a b <∀∈≤≤∀∈=+<∀∈<∀∈-<<∀∈1在关于有界函数的定义下证明函数在区间上为有界函数的充要条件为存在一个正的常数使得设存在常数使得M 取则有反之若存在一个正的常数使得则证12121212:()()[,],()()()()[,].,,|()|,|()|,[,].|()()||()||()|,|()()||()||()|,[,].113.:()cos 0y f x y g x a b f x g x f x g x a b M M f x M g x M x a b f x g x f x g x M M f x g x f x g x M M x a b f x x x xπ==+<<∀∈+≤+<+=<∀∈==证明若函数及在上均为有界函数则及也都是上的有界函数存在证明在的任一证,0().11(,),00,,,(),1()(,)0,()(21/2)cos(21/2)0,21/20().n x f x M n n M f n M n nf x f x n n n x f x δδδδδδπ→->><>=>-=→=++=→∞+→n 邻域内都是无界的但当时不是无穷大量任取一个邻域和取正整数满足和则故在无界.但是x 故当时不是无穷大量证11111000114.lim (1)ln (0).1ln 1,ln ln(1),.lim lim 10.ln(1)ln(1)lim lim ln(1)ln lim(1)ln 1,ln (1)ln ().ln(1)15.()()nn nn n n n n y y y y y n nn n x x x xx y x y n y x n y y y y e y y xn x x n y f x g x →∞→∞→∞→→→-=>-==+==-=++=+=+==-=→→∞+证明令则注意到我们有设及在实轴上有证00002022222220000.:()(),,()lim ()lim ()().1cos 116.lim.22sin 1cos 2sin 1sin 12lim lim lim lim 1422n n n n n x x x y y f x g x x x x f x f x g x g x x x x x y y x x y y →∞→∞→→→→→→===-=⎛⎫-==== ⎪⎝⎭定义且连续证明若与在有理数集合处处相等,则它们在整个实轴上处处相等.任取一个无理数取有理数序列证明证证0011000000001.2ln(1)17.:(1)lim 1;(2)lim .ln(1)(1)lim lim ln(1)ln lim(1)ln 1.(1)11(2)lim lim lim lim ln(1)ln(1)lim1.1x a xa y x y y y y y x a a a x x aa ax x x y y a a y e e e y x y y y e ye e e e e y e e e y x x x y ye e +→→→→→+→→→→→=+-==+=+=+==---====++==证明证0111018.()lim ()0,()lim ()()0.|()|,0||.0,0,0|||()|/.min{,},0||,|()()||()||()|,li x ax ay f x a f x y g x a f x g x g x M x a x a f x M x a f x g x f x g x M Mδεδδεδδδδεε→→====<<-<>><-<<=<-<=<=设在点附近有定义且有极限又设在点附近有定义,且是有界函数.证明设对于任意存在使得当时令则时故证m ()()0.x af xg x →=19.()(,),,()()|()|() () ()(),()(,).y f x c g x f x f x c g x c f x cc f x c g x g x =-∞+∞≤⎧⎪=>⎨⎪-<-⎩-∞+∞设在中连续又设为正的常数定义如下当当当试画出的略图并证明在上连续0000000000000|()|,0,||lim ()lim ()()().(),0,||()lim ()lim ().(),().0,,0,x x x x x x x x f x c x x g x f x f x g x f x c x x f x c g x c c g x f x c g x c c δδδδεεδ→→→→<>-<===>>-<>=====><>一若则存在当时|f(x)|<c,g(x)=f(x),若则存在当时,g(x)=c,若则对于任意不妨设存在使证()0000121212|||()|.||.(),()(),|()()||()|,(),(),|()-()|0.()()min{(),}max{(),}().max{(),()}(|()()|()())/2.min x x f x c x x f x c g x f x g x g x f x c f x c g x c g x g x g x f x c f x c f x f x f x f x f x f x f x δεδεε-<-<-<≤=-=-<>==<=+--=-++得当时设若则若则二利用证121212123123123111123{(),()}(|()()|(()())/2.120.()[,],[()()()],3,,[,].[,],().()()(),(),.()min{(),(),()},f x f x f x f x f x f x f x a b f x f x f x x x x a b c a b f c f x f x f x f x c x f x f x f x f x f ηηη=--++=++∈∈======设在上连续又设其中证明存在一点使得若则取即可否则设证31231313000000()min{(),(),()},()(),[,],,[,],().21.()(),()g(),,.0()g()()g()x f x f x f x f x f x f x x c a b f c y f x x g x x x kf x l x x k l l kf x l x x kf x l x x ηη=<<∈==+=+≠+在连续根据连续函数的中间值定理存在一点使得设在点连续而在点附近有定义但在不连续问是否在连续其中为常数如果在连续;如果在解,l 0,000000||()[[()lg()]()]/.22.Dirichlet ..,()1;,()0;lim (),()11(1)lim 0;(2)lim (arctan )sin 12n n n n x x x x x g x kf x x kf x l x x x x D x x x D x D x D x x x x x →→∞→+∞=+-''→→→→+⎛⎫= ⎪+⎝⎭不连续,因否则将在连续证明函数处处不连续任意取取有理数列则取无理数列则故不存在在不连续.23.求下列极限:证222001/112132100;2tan 5tan 5/5(3)lim lim 5.ln(1)sin [[ln(1)]/]sin /1lim(1).24.()[0,),0().0,(),(),,().{x x y x y n n x x x x x x x x x x x y e y f x f x x a a f a a f a a f a π→→→→+=====++++=+==+∞≤≤≥===设函数在内连续且满足设是一任意数并假定一般地试证明11},lim .lim ,(),().(),{}()0(1,2,),{}n n n n n n n n n n n n a a l a l f x x f l l a f a a a a f a n a →∞→∞++====≤=≥=单调递减且极限存在若则是方程的根即单调递减.又单调递减有下界,证111lim ,lim lim ()(lim )().25.()(,),:(0)1,(1),()()().()((,)).()()().()()n n n n n n n n n x n n a l a l a f a f a f l y E x E E e E x y E x E y E x e x E x x E x E x E nx E x +→∞→∞→∞→∞======-∞+∞==+==∀∈-∞+∞++==故有极限.设则设函数在内有定义且处处连续并且满足下列条件证明用数学归纳法易得于是证11.,()(11)(1).1(0)(())()()(),().().1111,(1)()()()(),().11()()().,n n n n n n nn mmm n n n E n E E e E E n n E n E n e E n E n e E n e n E E n E n E e E E e n n n n m E E m E e e r E n n n -=++====+-=-=--======⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭设是正整数则于对于任意整数对于任意整数即对于所有有理数lim ().,,(),()lim ()lim ().nn n r x x x x n n n r e x x E x E x E x e e e e →∞→∞→∞=→====n 对于无理数取有理数列x 由的连续性的连续性。

高等数学第一章函数例题及答案

高等数学第一章函数、极限、连续§1．1 函数一．求函数的定义域例1．求函数()2100ln ln ln x x x f -+=的定义域例2．求5ln 1-+-=x x x y 的定义域例3．设()x f 的定义域为[]()0,>-a a a ，求()12-x f 的定义域例4．设()⎩⎨⎧≤≤<≤=42 ,220 ,1x x x g 求()()()12-+=x g x g x f 的定义域，并求⎪⎭⎫ ⎝⎛23f 。

二．求函数的值域例1．求3311-=x ey 的值域例2．求()()⎪⎩⎪⎨⎧>--≤≤---<-==2,2122,52,323x x x x x x x f y 的值域，并求它的反函数三．求复合函数有关表达式 1．已知()x f 和()x g ，求()[]x g f 例1．已知()1-=x xx f ，求()⎥⎦⎤⎢⎣⎡-11x f f 例2．设()21x x x f +=，求()()[]()重复合n x f x f f f n =例3．设()⎩⎨⎧>≤-=2,02,42x x x x f ，求()[]x f f 2．已知()x g 和()[]x g f ，求()x f 例1．设()x e e e f x xx++=+21，求()x f例2．已知()xxxee f -='，且()01=f ，求()x f例3．设()x x fsin =，求()x f '例4．已知()x x f 2cos 3sin -=，求证()x x f 2cos 3cos += 3．已知()x f 和()[]x g f ，求()x g例．已知()()x x f +=1ln ，()[]x x g f =，求()x g 解：()[]x fx g 1-=实际上为求反函数问题()[]()[]x x g x g f =+=1ln ，()x e x g =+1 ()1-=x e x g 4．有关复合函数方程例．设()x x f x x f 2311-=⎪⎭⎫⎝⎛-+，求()x f 四．有关四种性质例1．设()()x f x F ='，则下列结论正确的是[ ]（A ）若()x f 为奇函数，则()x F 为偶函数。

高中数学必修一函数练习题及答案

高中数学必修一函数试题一、选择题： 1、若()f x =(3)f = （）A 、2B 、4 C、 D 、10 2、对于函数()y f x =，以下说法正确的有（）①y 是x 的函数；②对于不同的,x y 的值也不同；③()f a 表示当x a =时函数()f x 的值，是一个常量；④()f x 一定可以用一个具体的式子表示出来。

A 、1个B 、2个C 、3个D 、4个 3、下列各组函数是同一函数的是（）①()f x =与()g x =；②()f x x =与2()g x =；③0()f x x =与01()g x x =；④2()21f x x x =--与2()21g t t t =--。

A 、①②B 、①③C 、③④D 、①④4、二次函数245y x mx =-+的对称轴为2x =-，则当1x =时，y 的值为（） A 、7- B 、1 C 、17 D 、25 5、函数y =（）A 、[]0,2B 、[]0,4C 、(],4-∞D 、[)0,+∞ 6、下列四个图像中，是函数图像的是（）A 、（1）B 、（1）、（3）、（4）C 、（1）、（2）、（3）D 、（3）、（4） 7、)(x f 是定义在R 上的奇函数，下列结论中，不正确．．．的是( ) A 、()()0f x f x -+= B 、()()2()f x f x f x --=- C 、()()0f x f x -≤ D 、()1()f x f x =-- 8、如果函数2()2(1)2f x x a x =+-+在区间(],4-∞上是减少的，那么实数a 的取值范围是（） A 、3a -≤ B 、3a -≥ C 、a ≤5 D 、a ≥5 9、设函数()(21)f x a x b =-+是R 上的减函数，则有（）（1）（2）（3）（4）A 、12a >B 、12a <C 、12a ≥D 、12a ≤ 10、下列所给4个图象中，与所给3件事吻合最好的顺序为（）（1）我离开家不久，发现自己把作业本忘在家里了，于是立刻返回家里取了作业本再上学；（2）我骑着车一路以常速行驶，只是在途中遇到一次交通堵塞，耽搁了一些时间；（3）我出发后，心情轻松，缓缓行进，后来为了赶时间开始加速。

自测题(1-7章附参考答案)-高等数学上册

第一章函数与极限一、选择题：1．函数1arccos 2x y +=的定义域是（）(A)1x ≤； (B)31x -≤≤； (C)(3,1)-； (D){}{}131x x x x <⋂-≤≤.2.函数23,401,03x x x x --≤≤⎧⎨+<≤⎩的定义域是（）(A)40x -≤≤；(B)3≤;(C)(4,3)-; (D){}{}4003x x x x -≤≤⋃<≤. 3、函数cos sin y x x x =+是（） (A)偶函数； (B)奇函数；(C)非奇非偶函数；(D)奇偶函数. 4、函数()1cos2f x x π=+的最小正周期是（）(A)2π； (B)π； (C) 4 ； (D)12. 5、函数21xx +在定义域为（）(A)有上界无下界； (B)有下界无上界； (C)有界，且 1122()f x ≤≤；(D)有界，且 2221xx -≤≤+ . 6、与()f x =）(A) x ；(B) 2；(C) 3； (D) x . 7、当0x →时，下列函数哪一个是其它三个的高阶无穷小（）（A ）2x ；（B ）1cos x -；（C ）tan x x -；（D ）ln(1)x +.8、设00,0,a b ≠则当（）时有10101010........lim .........m m m n n x na x a x a ab x b x b b --→∞+++=+++ . (A)m n > ； (B)m n = ；(C)m n < ； (D),m n 任意取 . 9、设1,10,01x x x x --<≤⎧⎨<≤⎩,则0lim ()x f x →=( )(A)-1 ； (B)1 ； (C)0 ； (D)不存在 . 10、0limx xx→（） (A)1； (B)-1；(C)0； (D)不存在. 二、求下列函数的定义域：1sin(21)arctan ;y x x =++、2、()x φ=三、设2(1)231g x x x -=-- （1）试确定,,a b c 的值使2(1)(1)(1)g x a x b x c -=-+-+ ；（2）求(1)g x +的表达式 .四、求2()(1)sgn f x x x =+的反函数1()f x -.五、求极限：1、2221lim (1)n n n n →∞++- ； 2、3x → ； 3、2lim(1)xx x →+ ； 4、1lim (1)xx x e →∞- ；5、当0x ≠时，limcoscos ........cos 242n n x x x→∞； 6、21sinlimx x六、设有函数sin ,1()(1)1,1ax x f x a x x <⎧=⎨--≥⎩试确定a的值使()f x 在1x =连续 .七、讨论函数1arctan1()sin 2x x f x xπ-=的连续性，并判断其间断点的类型 . 八、证明奇次多项式：2120121()n n n P x a x a x a ++=+++ 0(0)a ≠至少存在一个实根 .第二章导数与微分一、选择题：1、函数()f x 在点0x 的导数0()f x '定义为（）（A ）00()()f x x f x x+∆-∆；（B ）000()()limx x f x x f x x →+∆-∆；（C ）00()()limx x f x f x x→-∆；（D ）000()()limx x f x f x x x →--；2、若函数()y f x =在点0x 处的导数0()0f x '=，则曲线()y f x =在点(00,()x f x )处的法线（）（A ）与x 轴相平行；（B ）与x 轴垂直；（C ）与y 轴相垂直；（D ）与x 轴即不平行也不垂直：3、若函数()f x 在点0x 不连续，则()f x 在0x ( ) （A ）必不可导；（B ）必定可导；（C ）不一定可导；（D ）必无定义.4、如果()f x =（），那么()0f x '=. (A) arcsin 2arccos x x +； (B) 22sec tan x x +； (C) 22sin cos (1)x x +-；(D) arctan x +arc cot x .5、如果2,0()(1),0ax e x f x b x x ⎧≤⎪=⎨->⎪⎩处处可导，那末（）（A ）1a b ==；（B ）2,1a b =-=-；（C ）1,0a b ==；（D ）0,1a b ==. 6、已知函数()f x 具有任意阶导数，且 []2()()f x f x '=,则当n 为大于2的正整数时， ()f x 的n 阶导数()()n f x 是（）（A ）1![()]n n f x +；（B ） 1[()]n n f x +；（C ） 2[()]nf x ；（D ）2![()]nn f x .7、若函数()x x t =,()y y t =对t 可导且()0x t '≠,又()x x t =的反函数存在且可导，则dydx=（）（A ）()()y t x t '；（B ）()()y t x t '-'；（C ）()()y t x t ''；（D ）()()y t x t '. 8、若函数()f x 为可微函数，则dy （）（A ）与x ∆无关；（B ）为x ∆的线性函数；（C ）当0x ∆→时为x ∆的高阶无穷小；（D ）与x ∆为等价无穷小.9、设函数()y f x =在点0x 处可导，当自变量x 由0x 增加到0x x +∆时，记y ∆为()f x 的增量，dy 为()f x 的微分，0limx y dyx∆→∆-∆等于（）（A ）-1；（B ）0；（C ）1；（D ）∞.10、设函数()y f x =在点0x 处可导，且0()0f x '≠，则 0lim x y dyx∆→∆-∆等于（）.（A ）0；（B ）-1；（C ）1；（D ）∞ . 二、求下列函数的导数：1、2sin ln y x x =；2、cosh x y a = （0a >）；3、2sec (1)x y x =+ ；4、2ln[cos(103)]y x =+；5、设y 为x的函数是由方程arctany x=确定的；6、设2x y y =+，322()u x x =+，求dydu.三、证明sin tx e t =，cos ty e t =满足方程222()2()d y dyx y x y dx dx+=- . 四、已知()cos ,0(),0g x xx f x xa x -⎧≠⎪=⎨⎪=⎩其中()g x 有二阶连续导数，且(0)1g =，1、确定a 的值，使()f x 在0X =点连续；2、求()f x '五、设ln ,y x x =求()(1)n f ..七、一人走过一桥之速率为4公里/小时，同时一船在此人底下以8公里/小时之速率划过，此桥比船高200米，问3分钟后人与船相离之速率为多少？第三章微分中值定理一、选择题：1、一元函数微分学的三个中值定理的结论都有一个共同点，即（）（A ）它们都给出了ξ点的求法 . （B ）它们都肯定了ξ点一定存在，且给出了求ξ的方法。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二章函数练习题1
一选择题
1设M={x ︱02≤≤x },N={y ︱02≤≤y },给出图中的四个图形，其中能表示集合M 到集
合N 的函数关系的有( )
A 0个
B 1个
C 2个
D 3个
2下列各组中的函数图像相同的是( )
A f(x)=1, g(x)=0x
B f(x)=1, g(x)=x
x C f(x) =3
)3(2
++x x g(x)=(x+3)0)3(+x D f(x)=|x| ， g(x)={x x - )0()0(<>x x 3函数y=x 111
+的定义域是（）
A x>0
B x>0或x ≤—1
C x>0或x ＜—1
D 0＜x ＜1
4已知f （x ）=a 3x +cx+5，满足f （—3）=—3，则f （3）的值等于（）
A 13
B 10
C 7
D 3
5设集合A ，B 都是正整数N +,映射f ：A →B 是把A 中的元素n 映射到集合B 中的元素n 2+n ，
则在映射f 下，象20的原象是（）
A 2
B 3
C 4
D 5
6设f ：A →B 是集合A 到集合B 的映射，下列结论正确的是（）
A A 中不同的元素必有不同的象
B B 中每一个元素在A 中必有原象
C A 中每一个元素在B 中必有象
D B 中每一元素在A 中的原象唯一
7给定f ：（x ，y ）→（x+2y ，2x —y ），在映射f 下，（3，1）的原象为（） A (1,3) B (1,1) C (3,1) D (21,
21,) 8已知f （x —x 1）=2x +21x
，则f （x+1）=（）
A 2)1(+x +2)1(1+x
B 2)1(x x -+2
)1(1x
x - C 2)1(+x +2 D 2)1(+x +1 9下列四个命题
（1）函数是其定义域到值域的映射（2）f （x ）=x x -+-23是函数
（3）函数y=2x （x ∈N ）的图像是一条直线（4）函数y={22
x x - )0)0( x x ≥的图像是抛物线，
其中正确的命题有（）
A 1个
B 2个
C 3个
D 4个
10已知f （x ）=a 2x ，g （x ）=x
2，且f （2）=g （2），M={x|f （x ）＞g （x ）}，则M 等于（）
A 〔—2,2〕
B (—2，2)
C （—∞，0）∪（2，+∞）
D （—∞，0〕∪（2，+∞）
二填空题
1 f （2x+1）=2x —2x ，则f （2）=＿＿。

2 若函数f （x 2）的定义域是〔—1,1〕，则函数f （log x
2）的定义域为＿＿。

3 已知f （x ）=1+x x 则f （1）+f （2）+f （3）+……+f （2003）+f （1）+f （21）+f （3
1）+……+f （2003
1）=＿＿。

4 已知对一切x ∈R ，都有f （x ）=f （2-x ），且方程f （x ）=0有五个不同的根，则这五个根
的和为＿＿。

5 已知f （x ）={
x x 212-+ )0()0( x x ≤若f （x ）=10，则x=＿＿。

三解答题
1已知函数f （x ）=
2
12)1(-x +1的定义域与值域都是{x|1b x ≤≤}（b>1）,求实数b 。

2（1）已知函数f （x ）的定义域是{x|0﹤x ﹤1}，求f （2
x —1）的定义域。

（2）已知f （x ）的定义域是{1≤x ≤5}。

求F （x ）=f （x+a ）+f （x —a ）的定义域，其中a ＞0.。

3求下列函数的值域（1） y=1122+-x x （2）y=2x —4x+6 x ∈〔1 ，5〕（3）y=312-+x x （4）y=3
452+-x x （5）y=2x —3—x 413- （6）y=
131+-x x
4已知函数f （x ）= lg )1(2++ax ax
（1）若f （x ）的定义域为R ，求实数a 的取值范围。

（2）若f （x ）的值域为R ，求实数a 的取值范围。

5求函数y=)01(4.322≤≤--+x x x 的值域
6若函数f （x ）=12++x b ax （x ∈R ）的值域为〔—1，4〕求a ，b。