专题一勾股定理(解析版)

合集下载

专题01探索勾股定理重难点专练(解析版)

学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图是两个全等的三角形纸片，其三边长之比为3: 4: 5，按图中方法分别将其对折，使折痕（图中虚线）过其中的一个顶点，且使该顶点所在两边重合，记折叠后不重叠部分面积分别为,A B S S ，已知15A B S S -=，则纸片的面积是（）A ．102B ．104C ．106D ．108【答案】D 【分析】设3AC FH x ==，则4BC GH x ==，5AB GF x ==，根据勾股定理即可求得CD 的长，利用x 表示出A S ，同理表示出B S ，根据15A BS S -=，即可求得x 的值，进而求得三角形的面积．【详解】解：设3AC FH x ==，则4BC GH x ==，5AB GF x ==．设CD y =，则4BD x y =-，DE CD y ==，在直角BDE ∆中，532BE x x x =-=，根据勾股定理可得：2224(4)x y x y +=-，解得：32y x =，2222A 同理可得：223B S x =，15A B S S -= ，∴22321523x x -=，解得：x =，∴纸片的面积是：213461082x x x ⨯== ，故选：D ．．【点睛】本题主要考查了翻折变换（折叠问题），三角形面积的计算，根据勾股定理求得CD 的长是解题的关键．2．七巧板是大家熟悉的一种益智玩具，用七巧极能拼出许多有趣的图案，小聪将一块等腰直角三角形硬纸板（如图①）切割成七块，正好制成一副七巧板（如图②），已知80cm AB =，则图中阴影部分的面积为（）2cm ．A ．200B ．2003C ．50D ．100【答案】A如图，设OF＝EF＝FG＝x cm，可得EH＝＝40cm，解方程即可解决问题．【详解】解：如图：设OF＝EF＝FG＝x（cm），∴OE＝OH＝2x，在Rt△EOH中，由勾股定理得：EH＝，∵AB＝80cm，∴由题意得EH＝40cm，∴40＝，∴x＝∴阴影部分的面积＝（2＝200（cm2）故选：A．【点睛】本题考查了正方形的性质、勾股定理、等腰三角形的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．3．下列四组数据，不是勾股数的是（）A．3，4，5B．5，6，7C．6，8，10D．9，40，41【答案】B根据勾股数的定义：满足222a b c +=的三个正整数，称为勾股数，根据定义即可求解．【详解】解：A 、因为32+42＝52，属于勾股数；B 、因为52+62≠72，不属于勾股数；C 、因为62+82＝102，属于勾股数；D 、因为92+402＝412，属于勾股数；故选：B ．【点睛】本题考查了勾股数的定义，注意：作为勾股数的三个数必须是正整数，一组勾股数扩大相同的整数倍得到的三个数仍是一组勾股数．4．ABC 在由边长为1的小正方形构成网格中的位置如图所示，则AC 边上的高是（）A ．135B ．145C ．165D ．175【答案】D 【分析】作BD AC ⊥于D ，根据勾股定理求出AC 的长，再利用三角形面积公式求ABC 中AC 边上的高即可．【详解】∵小正方形的边长都为1，∴5AC ==，∵11117451523342222ABC S =⨯-⨯⨯-⨯⨯-⨯⨯= ，∴11175222ABC S AC BD BD =⨯⨯=⨯⨯= ，解得：175BD =，故选：D ．【点睛】本题主要考查了勾股定理在网格中的应用以及三角形的面积，根据题意得出ABC 的面积等于矩形的面积减去三个小三角形的面积是解题的关键．5．如图，在Rt ABC 中，90,8,6ACB AC BC ∠=︒==，将边BC 沿CN 折叠，使点B 落在AB 上的点B ′处，再将边AC 沿CM 折叠，使点A 落在CB '的延长线上的点A '处，两条折痕与斜边AB 分别交于点N 、M ，则线段A M '的长为（）5555【答案】B 【分析】利用勾股定理求出AB =10，利用等积法求出CN ＝245，从而得AN ＝325，再证明∠NMC ＝∠NCM ＝45°，进而即可得到答案．【详解】解：∵90,8,6ACB AC BC ∠=︒==∴AB 10==，∵S △ABC ＝12×AB ×CN ＝12×AC ×BC∴CN ＝245，∵AN 325=，∵折叠∴AM ＝A'M ，∠BCN ＝∠B'CN ，∠ACM ＝∠A'CM ，∵∠BCN +∠B'CN +∠ACM +∠A'CM =90°，∴∠B'CN +∠A'CM ＝45°，∴∠MCN ＝45°，且CN ⊥AB ，∴∠NMC ＝∠NCM ＝45°，∴MN ＝CN ＝245，∴A'M ＝AM ＝AN −MN ＝325-245=85．故选B ．本题考查了翻折变换，勾股定理，等腰直角三角形的性质，熟练运用折叠的性质是本题的关键．6．有一个面积为1的正方形，经过一次“生长”后，在它的左右“肩”上“生出”两个小正方形，这3个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了如图所示的图形，如果继续“生长”下去，它将变得“枝繁叶茂”，则“生长”了2021次后形成的图形中所有正方形的面积和为（）A．2019B．2020C．2021D．2022【答案】D【分析】根据勾股定理求出“生长”了1次后形成的图形中所有的正方形的面积和，结合图形总结规律，根据规律解答即可．【详解】解：如图，设直角三角形的三条边分别是a，b，c，根据勾股定理，得222a b c，+=同理：正方形D 的面积+正方形E 的面积+正方形F 的面积+正方形G 的面积=正方形A 的面积+正方形B 的面积=正方形C 的面积1=，推而广之，“生长”了2021次后形成的图形中所有的正方形的面积和是202212022⨯=．故选：D 【解答】本题考查了勾股定理，熟练掌握勾股定理，理解“勾股树”的关系是解题关键．7．我们把梯形下底与上底的差叫做梯形的底差，梯形的高与中位线的比值叫做梯形的纵横比．如果一个腰长为5的等腰梯形，底差等于6，面积为24，那么这个等腰梯形的纵横比等于（）A ．54B ．56C ．23D ．35【答案】C 【分析】作AE ⊥BC 于E ，DF ⊥BC 于F ，根据BC-AD =6求出BE=CF =3，利用勾股定理求出高AE 的长，利用梯形面积公式求出AD 的长，由此得到梯形中位线的长，即可得到答案．【详解】解：如图，由题意得：AB=CD =5，BC-AD =6，作AE ⊥BC 于E ，DF ⊥BC 于F ，∴BE=CF =3，∴4AE DF ===，∵梯形面积11()(6)42422S AD BC AE AD AD =+⋅=⨯++⨯=，∴3AD =，22∴这个等腰梯形的纵横比=4263=，故选：C ．．【点睛】此题考查勾股定理，梯形面积公式及中位线公式，正确理解题意确定各线之间的数量及关系是解题的关键．8．如图，1OP =，过P 作1PP OP ⊥且11PP =，得1OP =再过1P 作122PP OP ⊥且121P P =，得2OP =；又过2P 作232PP OP ⊥且231PP =，得32OP =…依此法继续作下去，则20202021OP P △的面积为（）A B C D 【答案】B 【分析】根据勾股定理分别列式计算，找出被开方数的变化规律，最后用三角形的面积公式求解．123=12OP OP OP OP == ，4OP ∴==，…，n OP2020OP ∴202020211P P = ，2020OP 和20202021P P 相互垂直20202021OP P ∴ 的面积为1122S =⨯⨯=．故答案为：B ．【点睛】本题考查了勾股定理(在直角三角形中，两直角边的平方之和等于斜边的平方)，三角形面积公式(1=2S ⨯底⨯底边上的高)．根据题目观察出，被开方数比相应的序数大1是解题的关键．9．如图，有一张长方形纸片ABCD ，8cm AB =，10cm BC =，点E 为CD 上一点，将纸片沿AE 折叠，BC 的对应边B C ''恰好经过点D ，则线段CE 的长为（）cmA ．3B ．4C ．5D ．6【答案】A 【分析】由折叠的性质可得8cm AB AB '==，10cm BC B C ''==，CE C E '=，由勾股定理可求B D '的长，由勾股定理可求解．解：将纸片沿AE 折叠，BC 的对应边B C ''恰好经过点D ，8AB AB cm '∴==，10BC B C cm ''==，CE C E '=，6B D cm '∴=，4C D B C B D cm ''''∴=-=，222DE C D C E ''=+ ，2216(8)DE DE ∴=+-，5DE cm ∴=，∴3cmCE =故选：A ．【点睛】本题考查了翻折变换，矩形的性质，勾股定理，熟练运用折叠的性质是解决本题的关键．10．已知a 、b 为两正数，且12a b +=，则代数式+）A ．12B ．13C ．14D ．15【答案】B 【分析】如图所示，构造Rt △BEA 和Rt △AFC 使得BE =a ，EA =2，AF =3，FC =b ，然后根据勾股定理构可得AB 和AC ，当A ，B ，C 三点共线时有最小值，在根据勾股定理计算即可．【详解】解：如图所示，构造Rt △BEA 和Rt △AFC 使得BE =a ，EA =2，AF =3，FC =b ，根据勾股定理可得：AB 和AC所以：AB AC BC +≥，∴当A ，B ，C 三点共线时+AB AC 有最小值，即BC ，在Rt △BDC 中13BC ===．故选：B 【点睛】本题主要考查勾股定理，能够根据二次根式的特点，数形结合，构造出直角三角形表示所求式子是解题的关键．11．如图，在Rt ABC 中，90ACB ∠=︒，分别以AB ，AC ，BC 为斜边作三个等腰直角ABD △，ACE ，BCF △，图中阴影部分的面积分别记为1S ，2S ，3S ，4S ，若已知Rt ABC 的面积，则下列代数式中，一定能求出确切值的代数式是（）A ．4S B ．143S S S +-C ．234S S S ++D ．123S S S +-【答案】A 【分析】表示相应的面积，确定面积与m ，n ，S 之间的关系，从而作出判断．【详解】设AC =m ，BC =n ，ABC 的面积为S ，∵Rt ABC 中，90ACB ∠=︒，分别以AB ，AC ，BC 为斜边作三个等腰直角ABD △，ACE ，BCF △，∴S =1mn 2，AB∴AE =EC =m 2，BF =CF =2n ，AD =BD ，在直角三角形AED 中，ED ==2n ，∴DC =EC -ED =m 2-2n =()2m n -，∴4S =11111AE ED=2222222m n mn S ∙=⨯=，故4S 的值可以确定，∴A 选项符合题意；设AC ，BD 的交点为G ，则3S +ADG S =112222()22S CD AE m n =∙=⨯-⨯△ADC =24()1m mn -，1S +ADG S =222241S AD m n +==△ADB ，∴143S S S +-=224m n ++12S -24()1m mn -=2+4n S ，与n 有关系，故代数式的值不能确定，∴B 选项不符合题意；∵3S +ADG S =24()1m mn -，1S +ADG S =224m n +，∴13S S -=21+42n S ，∴234S S S ++=212BF +12S +1S -21-42n S =24n +12S +1S -21-42n S =1S ，无法确定，∴C 选项不符合题意；∵123S S S +-=21+42n S +24n =21+22n S ，与n 有关，∴D 选项不符合题意；故选A ．【点睛】本题考查了直角三角形的性质，等腰直角三角形的性质，勾股定理，图形面积的割补，灵活运用性质和勾股定理计算阴影的面积是解题的关键．12．如图，在ABC 中，点D 是边AB 上的中点，连接CD ，将BCD △沿着CD 翻折，得到ECD ，CE 与AB 交于点F ，连接AE ．若6,42AB CD AE ===,，则点C 到AB 的距离为（）A ．72B ．C ．3D ．【答案】C 【分析】连接BE ，延长CD 交BE 于G 点，过C 作CH ⊥AB 于H ，由折叠的性质及中点性质，可得△AEB 是直角三角形，且G 点是BE 的中点，从而CG ⊥BE ，由勾股定理可求得BE 的长，则根据△ABC 的面积相等一方面可表示为12AB CH ，另一方面其面积为△BCD 与△ACD 面积的和，从而可求得CH 的长．【详解】连接BE ，延长CD 交BE 于G 点，过C 作CH ⊥AB 于H ，如图所示由折叠的性质，得：BD =ED ，CB =CE∴CG 是线段BE 的垂直平分线∴BG =12BE∵D 点是AB 的中点∴BD =AD ，BCD ACDS S ∴AD =ED∴∠DAE =∠DEA∴∠DEB =∠DBE∵∠DAE +∠BEA +∠DBE =180°即∠DAE +∠DEA +∠DEB +∠DBE =180°∴2∠DEA +2∠DEB =180°∴∠DEA +∠DEB =90°即∠AEB =90°在Rt △AEB 中，由勾股定理得：BE =∴BG =∵BCD ACD ABCS S S += ∴11222CD BG AB CH ⨯=∴224863CD BG CH AB ⨯⨯==故选：C ．【点睛】本题考查了直角三角形的判定、勾股定理、线段垂直平分线的判定，利用面积相等求线七巧板拼成的，则这四个图形的周长从大到小排列正确的是（）A．乙＞丙＞甲＞丁B．乙＞甲＞丙＞丁C．丙＞乙＞甲＞丁D．丙＞乙＞丁＞甲【答案】A【分析】设最小的直角三角形的直角边长为1，根据勾股定理，分别表示出七块七巧板各边的长度，计算每个图形中重合的线段和，和越大，周长越小．【详解】解：设七巧板中最小的边长为1根据勾股定理，可以得出其余的边长分别为2，分别求出各图中重合的线段的长度和，和越大，则周长越小；甲图中重叠的线段和为：；乙图中重叠的线段和为：；丙图中重叠的线段和为丁图中重叠的线段和为：；+>+>+>+∵6755∴乙＞丙＞甲＞丁本题考查了勾股定理，不规则图形的周长，解题关键是明确总周长一定，重叠的线段和越大，则周长越小．二、填空题14．如图，点A ，B 在直线MN 的同侧，A 到MN 的距离8AC =，B 到MN 的距离5BD =，已知4CD =，P 是直线MN 上的一个动点，记PA PB +的最小值为a ，||PA PB -的最大值为b ，则22a b -=_______．【答案】160【分析】作点A 关于直线L 的对称点A ′，连接A ′B 交直线L 于点P ，过点A ′作直线A ′E ⊥BD 的延长线于点E ，再根据勾股定理求出A ′B 的长就是PA +PB 的最小值；延长AB 交MN 于点P ′，此时P ′A -P ′B =AB ，由三角形三边关系可知AB ＞|PA -PB |，故当点P 运动到P ′点时|PA -PB |最大，作BE ⊥AM ，由勾股定理即可求出AB 的长就是|PA -PB |的最大值．进一步代入求得答案即可．【详解】解：如图，作点A关于直线L的对称点A′，连接A′B交直线L于点P，则点P即为所求点．过点A′作直线AE⊥BD的延长线于点E，则线段A′B的长即为PA+PB的最小值．∵AC=8cm，BD=5cm，CD=4cm，∴A′C=8cm，BE=8+5=13cm，A′E=CD=4cm，∴A′B=即PA+PB的最小值是a如图，延长AB交MN于点P′，∵P′A-P′B=AB，AB＞|PA-PB|，∴当点P运动到P′点时，|PA-PB|最大，∵BD=5，CD=4，AC=8，∴AB =5．∴|PA -PB |=5为最大，即b =5，∴a 2-b 2=185-25=160，故答案为：160．【点睛】本题考查的是最短线路问题及勾股定理，熟知两点之间线段最短及三角形的三边关系是解答此类问题的关键．15．在ABC 中，1520AB AC BC ==,,边上的高线为12，则ABC ∆的面积为________．【答案】150或42【分析】分两种情况：①B Ð为锐角；②B Ð为钝角；利用勾股定理求出BD 、CD ，即可求出BC 的长．【详解】解：分两种情况：①当B Ð为锐角时，如图1所示，在Rt △ABD 中，9BD ===，在Rt ADC 中，16CD ===，25BC BD CD ∴=+=，ABC ∆∴的面积为125121502⨯⨯=；②当B Ð为钝角时，如图2所示，在Rt △ABD 中，1697BC CD BD =-=-=，所以ABC ∆的面积为1712422⨯⨯=；故答案为：150或42．【点睛】本题主要考查了勾股定理；熟练掌握勾股定理，画出图形，分类讨论是解答此题的关键．16．在ABC 中，5AB =，AC =，BC 边上的高为3，则边BC 的长为__________．【答案】2或10【分析】分两种情况考虑：当△ABC 为锐角三角形，在直角三角形ABD 与直角三角形ACD 中，利用勾股定理求出BD 与DC 的长，由BD +DC 求出BC 的长即可；当△ABC 为钝角三角形，同理由CD -BD 求出BC 的长即可．【详解】解：分两种情况考虑：如图，此时△ABC为锐角三角形，==，在Rt△ABD中，根据勾股定理得：BD4在Rt△ACD中，根据勾股定理得：CD6，此时BC=BD+DC=4+6=10；如图，此时△ABC为钝角三角形，==；在Rt△ABD中，根据勾股定理得：BD4在Rt△ACD中，根据勾股定理得：CD6，=-=，此时BC=CD-BD642综上，BC的长为2或10．故答案为：2或10．【点睛】本题考查的是勾股定理，在解答此题时要注意进行分类讨论，不要漏解．17．如图，Rt△ABC，∠ACB=90°，AC=6，BC=8，将边AC沿CE翻折，使点A落在AB上的点D处；再将BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段CE的长等于_________，线段BF的长等于_________．【答案】24585【分析】先依据勾股定理求得AB 的长，然后在△ABC 中，利用面积法可求得CE 的长，然后依据勾股定理定理可求得AE 的长，证明△ECF 为等腰直角三角形可求得EF 的长，依据FB =AB -AF 求得FB 的长即可．【详解】解：由翻折的性质可知CE ⊥AD ，在Rt △ABC 中，AB ，∵S △ABC =12AC •BC =12AB •CE ，∴CE =6824105⨯=，在△AEC 中，依据勾股定理得：AE =185，由翻折的性质可知∠ECD =12∠ACD ，∠DCF =12∠DCB ，CE ⊥AD ，∴∠ECF =45°，∵CE ⊥AD ，∴CE =EF =245，∴FB =AB -AE -EF =10-185-245=85，故答案为：245，85．本题主要考查的是翻折的性质、勾股定理的应用，利用面积法求得CE 的长，然后再利用勾股定理和等腰三角形的性质求得AE 和EF 的长是解答问题的关键．18．如图，已知在Rt △ABC 中，∠ACB ＝90°，分别以AC ，BC ，AB 为直径作半圆，面积分别记为S 1，S 2，S 3，若S 3＝9π，则S 1+S 2等于_____．【答案】9π．【分析】根据勾股定理和圆的面积公式，可以得到S 1+S 2的值，从而可以解答本题．【详解】解：∵∠ACB ＝90°，∴AC 2+BC 2＝AB 2，∵S 1＝π（2AC ）2×12，S 2＝π（2BC ）2×12，S 3＝π（2AB ）2×12，∴S 1+S 2＝π（2AC ）2×12+π（2BC ）2×12＝π（2AB ）2×12＝S 3，∵S 3＝9π，∴S 1+S 2＝9π，故答案为：9π．【点睛】本题考查勾股定理，解答本题的关键是利用数形结合的思想解答．作A E BC '⊥，垂足为E ，若8AB =，5CE =，则BC 的长为__．【答案】【分析】过C 作CF AB ⊥，F 为垂足，通过已知条件可以求得()AFC CEA AAS D @D ¢，AF CE =，从而求得3BF =，再根据直角三角形的性质，即可求解．【详解】解：过C 作CF AB ⊥，F为垂足，ACE ABC A ∠=∠+∠Q ，又30ABC =︒∠ ，30ACE A \Ð=°+Ð，又30ACE A CE ��孝Q ，A A CE \�孝，在AFC ∆与CEA D ¢中，'90''AFC A EC A A CE AC CA ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，()AFC CEA AAS \D @D ¢，∴3BF AB AF =-=，在Rt BFC △中，30FBC ∠=︒，设FC x =，则2BC x=由勾股定理可得222BC FC BF =+即222(2)3x x =+解得x =BC =故答案为【点睛】此题主要考查了三角形全等的证明方法和直角三角形的有关性质，利用已知条件合理构造直角三角形是解决本题的关键．20．如图，在Rt ABC 中，AC BC =，点D 为AB 中点．90GDH ∠=︒，GDH ∠绕点D 旋转，DG ，DH 分别与边AC ，BC 交于E ，F 两点．下列结论：①AE BF AC +=；②222AE BF EF +=；③12ABC CEDF S =四边形△；④DEF 始终为等腰直角三角形．其中正确答案的序号有__________．【答案】①②③④【分析】连接CD 根据等腰直角三角形的性质就可以得出ADE CDF ∆≅∆，就可以得出AE CF =，进而得出CE BF =，就有AE BF AC +=，由勾股定理就即可求出结论．【详解】12AD CD BD AB ∴===．45A B ACD BCD ∠=∠=∠=∠=︒，90ADC BDC ∠=∠=︒．90ADE EDC ∴∠+∠=︒，90EDC FDC GDH ∠+∠=∠=︒ ，ADE CDF \Ð=Ð．在ADE ∆和CDF ∆中，A DCB AD CD ADE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩，()ADE CDF ASA ∴∆≅∆，AE CF ∴=，DE DF =，ADE CDF S S ∆∆=．AC BC = ，AC AE BC CF ∴-=-，CE BF ∴=．AC AE CE =+ ，AC AE BF ∴=+．①222AC BC AB +=，AC ∴=，2AE BF AB ∴+=．DEF ∴∆始终为等腰直角三角形．④222CE CF EF += ，222AE BF EF ∴+=．②EDC CDF CEDF S S S ∆∆=+ 四边形，12EDC ADE ABC CEDF S S S S ∆∆∆∴=+=四边形．③∴正确的有①②③④．故答案为：①②③④．【点睛】本题考查了等腰直角三角形的性质的运用，全等三角形的判定及性质的运用，勾股定理的运用，三角形的面积公式的运用，解答时证明ADE CDF ∆≅∆是关键．21．如图所示的网格是正方形网格，点A ，B ，C ，D ，E 是网格线交点，则BAC DAE ∠-∠的度数为_______．【答案】45°【分析】如图，连接CG 、AG ，根据勾股定理的逆定理可得∠CAG =90°，从而知△CAG 是等腰直角三角形，根据平行线的性质和三角形全等，可知：∠BAC -∠DAE =∠ACG ，即可得解．【详解】解：如图，连接CG 、AG ，设小正方形的边长为1，由勾股定理得：AC 2=AG 2=12+22=5，CG 2=12+32=10，∴AC 2+AG 2=CG 2，∴∠CAG =90°，∴△CAG 是等腰直角三角形，∴∠ACG =45°，∵CF ∥AB ，∴∠ACF =∠BAC ，在△CFG 和△ADE 中，∵90CF AD CFG ADE FG DE ⎧⎪∠∠︒⎨⎪⎩＝＝＝＝，∴△CFG ≌△ADE （SAS ），∴∠FCG =∠DAE ，∴∠BAC -∠DAE =∠ACF -∠FCG =∠ACG =45°，故答案为：45°．【点睛】本题考查了勾股定理的逆定理，勾股定理，三角形的全等的性质，等腰直角三角形的判定和性质，正确的作出辅助线是解题的关键．22．如图，在ABC 中，4AB =，135BAC ∠=︒，D 为边BC 的中点，若 1.5AD =，则AC 的长度为______．【答案】1+【分析】延长AD 到E ，使得AD =DE ，证明△ADB ≌△EDC ，得4CE AB ==，过点E 作EH AC ⊥于H ，分别求出CH 和AH 的长即可得到结论．【详解】解：延长AD 到E ，使得AD =DE，如图，∵D 为边BC 的中点，∴BD=CD在△ADB 和△EDC 中，AD DE ADB EDC BD CD =⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△EDC∴,4B DCE CE AB ∠=∠==∴//AB CE∴180BAC ACE ︒∠+∠=∴18013545ACE ︒︒︒∠=-=过点E 作EH AC ⊥于H∴CH EH ==在Rt AHE ∆中，23AE AD ==，HE =∴1AH ==∴1AC AH HC =+=故答案为：1．【点睛】此题主要考查了全等三角形的判定与性质，中线的性质，等腰直角三角形的性质以及勾股定理等知识，正确作出辅助线构造全等三角形是解答此题的关键．23．如图，四边形ABCD 中，AB AD =，90BAD ∠=︒，连接AC ，BD 交于点E ，90CBD ∠=︒，若点E 为AC 的中点，CD =ABCD 的面积为______．【答案】6【分析】过点A 作AF BD ⊥，可证得CBE AFE ≌△△，得到线段BC 和BD 的数量关系，即可求出BC 和BD 的长度，然后根据三角形面积公式即可求得．【详解】过点A 作AF BD ⊥，如图所示，在CBE △和AFE △中，CBE AFE BEC AEF EC EA ∠=∠⎧⎪∠=∠⎨⎪=⎩∴()CBE AFE AAS ≌△△，∴BC AF =，又∵2BD AF =，∴2BD BC =，∴在Rt BCD 中，222BC BD CD +=，()2222BC BC +=，解得：BC(负值舍去)，BD=AF∴四边形ABCD的面积11=622ABD CBD S S +=⨯=△△．故答案为：6．【点睛】此题考查了勾股定理，全等三角形的判定和性质，三角形面积的计算，正确的识别图形是解题的关键．24．我们规定：经过三角形的一个顶点且将三角形的周长分成相等的两部分的直线叫做3BC=，若直线l为Rt ABC的“等周线”，请直接写出ABC的所有“等周径”长为______________．【答案】5或【分析】分直线过顶点A、B、C三种情况，分别画出图形求解即可．【详解】解：分三种情况讨论：①当“等周线”经过点C时，直线1交AB于点E，设BE=x，则AE=5-x，作CH⊥AB于H，由题意：3+x=4+5-x，解得：x=3，∵125BC ACCHAB⋅==，∴95 BH==，∴96355 EH=-=，在Rt△ECH中，CE=∴“等周径”由题意得：4+3-x=5+x，解得：x=1，∴EC=2，在Rt△ACE中，AE==，∴“等周径”长为③当∴“等周径”经过点B时，直线l交AC于点E，设AE=x，则CE=4-x，由题意：3+4-x=5+x，解得：x=1，∴CE=3，在Rt△BCE中，BE==∴“等周径”长为本题考查了勾股定理的应用和分类讨论思想，关键是分三种情况进行讨论．25．把两个同样大小含45︒角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A ，且另外三个锐角顶点B ，C ，D 在同一直线上．若4AB =，则CD =____．【答案】【分析】作AF BC ⊥于F ，根据等腰直角三角形的性质求出AF ，BF ，CF ，在Rt ABC ∆中根据勾股定理求出BC ，得到AD ，在Rt ADF ∆中，根据勾股定理求出DF ，即可得CD ．【详解】过点A 作AF BC ⊥于点F ，在Rt ABC ∆中，45B ∠=︒，∴4AB AC ==，∴BC =，BF CF AF ===，∵两个同样大小的含45°角的三角尺，∴AD BC ==DF ==∴CD FD FC =-=，故答案为：【点睛】本题考查的是勾股定理，等腰直角三角形的性质，掌握勾股定理，正确作出辅助线是解本题的关键．26．如图，矩形ABCD 中，3AD =，2AB =．点E 是AB 的中点，点F 是BC 边上的任意一点（不与B 、C 重合），EBF △沿EF 翻折，点B 落在B '处，当DB '的长度最小时，BF 的长度为______．【答案】13+【分析】先确定当D ，B '，E 共线时，DB '的值最小，再根据勾股定理解题．【详解】如图，连接DE ，∴1DB '≥，∴当D ，B '，E 共线时，DB '的值最小，不妨设此时点B '落在DE 上的点B ''处，设BF F B x ''''==，∵22222F D CD F C B D B F '''''''=+=+，∴())2222231x x +-=-+，解得13x =．故答案为：13．【点睛】本道题考查了两点之间，线段最短、勾股定理(在直角三角形中，两直角边的平方之和等于斜边的平方)．解题的关键是确定当D ，B '，E 共线时，DB '的值最小．27．如图，矩形ABCD 中，6AB =，4=AD ，E ，F ，Q 分别是AD 和BC 、DC 的中点，P 是EF 上的点，则PD PQ +的最小值为________．【答案】5【分析】取AB 的中点为'Q ，连接'DQ 交EF 于点P'，则PD PQ +的最小值转为两点之间的距离最短，利用勾股定理求解．【详解】小值，如下图：由图可知，'''P Q P Q =，''''PD PQ DP P Q DQ ∴+=+=，在'Rt DQQ 中，13,'42DQ AB QQ AD ====，'5DQ ∴==，由两点之间的距离最短即，PD PQ +的最小值为5，故答案是：5．【点睛】本题考查了动点问题，涉及到勾股定理的使用，解题的关键是把PD PQ +转换为两点之间的距离最短来求解，运用转换的思想．28．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，点E 是AB 边上一点．将△CEB 沿直线CE 折叠到△CEF ，使点B 与点F 重合．当CF ⊥AB 时，线段EB 的长为_____．【分析】设CF 与AB 交于点H ，利用勾股定理求出AB ，利用面积法求出CH ，求出HF 和BH ，设BE =EF =x ，在△EHF 中利用勾股定理列出方程，解之即可．【详解】解：设CF 与AB 交于点H ，∵∠ACB =90°，AC =3，BC =4，∴AB =5，∴S △ABC =1122AC BC AB CH ⨯⨯=⨯⨯，即345CH ⨯=⨯，∴CH =125，由折叠可知：CF =CB =4，∴HF =CF -CH =85，在△BCH 中，BH 165=，设BE =EF =x ，则EH =165-x ，在△EHF 中，222EH FH EF +=，∴22216855x x ⎛⎫⎛⎫-+= ⎪ ⎪⎝⎭⎝⎭，解得：x =2，∴EB =2，故答案为：2．【点睛】本题考查了勾股定理，折叠的性质，解题的关键是利用折叠的性质得到相等线段，利用勾股定理列出方程．29．在平面直角坐标系中，己知y轴上一点B，A为x轴上的一动点，连接AB，的最小值是________．以AB为边作等边ABC如图所示，连接OC，则BC OC【答案】3【分析】作等边△BOD，构造出△BAO≌△BCD，从而得到∠BDC＝∠AOB＝90°，找到点C的运动轨迹为直线CD，延长BD交y轴于点B′，利用已知条件可证明直线CD就是线段BB′的中垂线，从而BC+OC=B'C+OC，而O、C、B'三点共线时，B'C+OC的值最小，最小值为OB'的长．【详解】解：如图所示，在第二象限以OB为边长作等边△BOD，连接OD，并作直线BD，延∵等边△ABC 、等边△BOD∴AB ＝BC ，BO ＝BD ，∠CBA ＝∠OBD ＝60°∴∠OBA ＝∠CBD在△BAO 和△BCD 中BO BD BA BC OBA DBC =⎧⎪=⎨⎪∠=∠⎩∴△BAO ≌△BCD （SAS ）∴∠AOB ＝∠BDC ＝90°∴CD ⊥BD∴点C 随着点B 的运动形成的图形是直线CD∵∠BOB '＝90°，∠OBD ＝60°∴∠BB 'O ＝30°∴OB ＝12BB '∴BD ＝OB ＝12BB '∴点D 是BB '的中点∴CD 是BB '的中垂线∴BC ＝B ′C∴BC +OC ＝B 'C +OC又∵点C 在直线CD 上运动，所以点O 、C 、B '三点共线时，B 'C +OC 的值最小，最小值为OB '的长．在R △BOB '中，∠BOB '＝90°，∠OBD ＝60°，OB BB，OB ′3=，∴BC +OC 的最小值为3．故答案为3．【点睛】本题主要考查等边三角形的性质、利用轴对称求最短线路．这里构造三角形全等找到点C 的运动轨迹是关键．30．如图，在ABC 中，90ACB ∠=︒，4BC AC ==，M 为AB 中点，D 是射线BC 上的一动点，连接AD ，将线段AD 绕点A 逆时针旋转90︒得到线段AE ，连接ED 、ME ，点D 在运动过程中ME 的最小值为_______．【答案】2【分析】连接EB ，过点M 作MG EB ⊥于点G ，过点A 作AK AB ⊥交BD 的延长线于点K ，则AKB △是等腰直角三角形．推出ADK ABE ≅△△，根据全等三角形的性质得到【详解】解：连接EB ，过点M 作MG EB ⊥于点G ，过点A 作AK AB ⊥交BD 的延长线于点K ，则AKB △是等腰直角三角形．在ADK △与ABE △中，AK AB KAD BAE AD AE =⎧⎪∠=∠⎨⎪=⎩，∴()ADK ABE ASA ≅ ，∴45ABE K ∠=∠=︒，∴BMG △是等腰直角三角形，∵4BC =，∴AB =∵M 为AB 中点，∴MB =∴2MG =，∵90G ∠=︒，∴ME MG ≥，∴当ME MG =时，ME 的值最小，∴2ME BE ==.故答案为：2．【点睛】本题考查了旋转的性质和等腰直角三角形的性质、三角形全等的性质和判定，证明线段最短有一定的难度．但通过构造全等三角形，利用全等三角形和等腰直角三角形的性质就变得容易．31．已知，有一个井泵如图1所示，它的一个纵向截面如图2，当活塞EF向上移动时，底面BC上的阀门打开，EF上的阀门关闭，外部液体被吸入活塞下方的空间内，活塞EF上方的液体被上推；当活塞EF向下移动时，BC上的阀门关闭，EF上的阀门打开，液体从活塞EF下方空间被压入活塞内EF上方空间．在图2中，点J在直径AD上，水泵底面直径BC＝10cm，活塞直径EF∥BC，G为EF中点．手柄IH支撑杆ID长cm，弧JI是直径为的半圆，连轴JG的长为25cm，（点C，D，F，I四点共线，J，I，H三点共线，水泵材质厚度忽略不计），则DF＝_____cm，当手柄IH从图2位置按压到与CD重合（如图3）过程中井泵的最大出水量是_____cm3．【答案】GM=DF，在直角△IJD中由勾股定理可计算出JD，从而可得MJ，然后在直角△GMJ 中，由勾股定理可求得GM，进而求得DF的长；当手柄IH从图2位置按压到与CD重合（如图3）过程中，点J上升的最大高度为JD=ID+IJ，从而EF的最大上升高度也为JD，此时最大出水量为一个圆柱的体积，圆柱的高为JD的长，底面直径为10cm，所以可求得其体积．【详解】（1）如图，连接AD，过点G作GM⊥AD于点M，则M为AD的中点，且四边形MGFD为矩形，所以有DF=MG，MD=GF=152EF=cm∵ID⊥AD，ID=cm，IJ=∴由勾股定理得：6JD===(cm)∴MJ=JD−MD=6-5=1(cm)在Rt△GMJ中，由勾股定理得：GM===(cm)∴DF=cm当手柄IH从图2位置按压到与CD重合（如图3）过程中，点J上升的最大高度为JD=ID+IJ==(cm)，相应地EF也随之上升的最大高度为cm，此时井泵的最大出水量是一个底面直径为10cm高为的圆柱的体积．2V π=⨯⨯= ⎪⎝⎭(cm 3)故答案为：；【点睛】本题主要考查了解直角三角形在实际中的应用，第二问的关键是明白点J 上升的最大垂直高度为图3中JD 的长度，即为EF 上升的最大高度，从而可求出此时的最大出水量，且这个出水量是底面直径为10cm ，高为JD 的圆柱的体积．32．如图，在等腰直角三角形ABC 中，∠ABC ＝90°．点E 是BC 上的一点，D 为AC 中点，连接ED ，将△CED 沿ED 翻折，得到△EDC ′，连接AC ′，BC ′．若DC ′⊥AB ，AC ′＝2，则△ABC 的面积为_____．【答案】4+【分析】设AB 与C′D 交于O 点，根据等腰直角三角形以及折叠找到三角形AOC ′的三边关系利用勾股定理计算即可.【详解】∴DB=DC=DA ，∠BAD =45°∵将△CED 沿ED 翻折，得到△EDC ′，∴DC=DC′设DB=DC=DA=DC′=x∵DC ′⊥AB∴△AOD 是等腰直角三角形∴22OA OD x ===∴C C O O D x x D ==''-在Rt △AOC ′中，222C OA O AC +=''∵AC ′＝2∴222())2x +=解得24x =+∴2142ABC S BD AC x =⋅==+V 故答案为4+【点睛】本题综合考察勾股定理与等腰直角三角形，解题过程中与二次根式有关的运算也是解题的关键.33．如图，在Rt ABC 的纸片中，∠C ＝90°，AC ＝7，AB ＝25．点D 在边BC 上，以AD 为折痕将 ADB 折叠得到ADB ' ，AB '与边BC 交于点E ．若DEB '△为直角三角形，则BD 的长是_____．【答案】17或754【分析】由勾股定理可以求出BC 的长，由折叠可知对应边相等，对应角相等，当DEB ∆'为直角三角形时，可以分为两种情况进行考虑，分别利用勾股定理可求出BD 的长．【详解】解：在Rt ABC ∆中，24BC =，（1）当90EDB ∠'=︒时，如图1，过点B ′作B F AC '⊥，交AC 的延长线于点F ，由折叠得：25AB AB ='=，BD B D CF ='=，设BD x =，则B D CF x '==，24B F CD x '==-，在Rt AFB ∆'中，由勾股定理得：222(7)(24)25x x ++-=，即：2170x x -=，解得：10x =（舍去），217x =，因此，17BD =．由折叠得：25AB AB ='=，则25718B C '=-=，设BD x =，则B D x '=，24CD x =-，在Rt △B CD ¢中，由勾股定理得：222(24)18x x -+=，解得：754x =，因此754BD =．故答案为：17或754．【点睛】本题考查了翻折变换，直角三角形的性质，勾股定理等知识，解题的关键是：分类讨论思想的应用注意分类的原则是不遗漏、不重复．34．如图，Rt ACB △中，90ACB ∠=︒，ACB △的角平分线AD ，BE 相交于点P ，过P 作PF AD ⊥交BC 的延长线于点F ，交AC 于点H ，则下列结论：①135APB ∠=︒；②DH =；③APH ADE S S =△△；④DH 平分CDE ∠；其中正确的结论是___________．（填正确结论的序号）【答案】①②③【分析】（ASA ）与△APH ≌△FPD （ASA ），结合90,HPD ∠=︒可判断②，由△ABP ≌△FBP ，△APH ≌△FPD ，可得S △APB =S △FPB ，S △APH =S △FPD ，再证明HD ∥EP ，可判断③，若DH 平分∠CDE ，推导DE ∥AB ，这个显然与条件矛盾，可判断④；【详解】解：在△ABC 中，∵∠ACB =90°，∴90BAC ABC ∠+∠=︒，又∵AD 、BE 分别平分∠BAC 、∠ABC ，∴∠BAD +∠ABE =190452窗=，∴∠APB =135°，故①正确．∴∠BPD =45°，又∵PF ⊥AD ，∴∠FPB =90°+45°=135°，∴∠APB =∠FPB ，又∵∠ABP =∠FBP ，BP =BP ，∴△ABP ≌△FBP （ASA ），∴∠BAP =∠BFP ，AB =FB ，PA =PF ，,BAD CAD ∠=∠ ,PAH PFD ∴∠=∠在△APH 和△FPD 中，90APH FPD PA PF PAH PFD ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩，。

3.1勾股定理(七大题型)(解析版)

（苏科版）八年级上册数学《第3章勾股定理》3.1 勾股定理●勾股定理：直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两条直角边长分别为a ，b ，斜边长为c ，那么a 2+b 2=c 2.◆1、勾股定理的应用条件：勾股定理只适用于直角三角形；◆2、勾股定理揭示的是直角三角形三边的关系，已知直角三角形中的任意两边可以求出第三边.◆3、勾股定理的几种变形式：勾股定理将“数”与“形”联系起来，体现了直角三角形三边之间的等量关系.如果直角三角形的两条直角边长分别为a ，b ，斜边长为c ，则a 2 + b 2 = c 2、 a 2 = c 2 - b 2、b 2 = c 2 - a 2；22b a c +=、22b c a -=、22a c b -=.【拓展】◎1、锐角三角形的三边关系是：在锐角三角形中，若三边长分别为a ，b ，c ，其中c 为最大边，则a 2+b 2＞c 2.◎2、钝角三角形的三边关系是：在钝角三角形中，若三边长分别为a ，b ，c ，其中c 为最大边，则a 2+b 2＜c 2.●通过拼图证明勾股定理的思路：（1）图形经过割补拼接后，只要没有重叠、没有空隙，面积就不会改变.（2）根据同一种图形的面积的不同表示方法列出等式.（3）利用等式性质变化验证结论成立，即拼出图形→写出图形面积的表达式→找出等量关系→恒等变形→推导命题结论.●下面列举几种证明方法：◆1、“赵爽弦图”证明：在图1中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和．即c2=12ab×4+（b﹣a）2，化简得：a2+b2＝c2．◆2、我国数学家邹元治的证明方法证明：在图2中，大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和．即（a+b）2＝c2+12ab×4，化简得：a2+b2＝c2．◆3、美国第二十任总统伽菲尔德的“总统证法”证明：在图3中，梯形的面积等于三个直角三角形的面积的和．即12（a+b）（a+b）=12ab×2+12c2，化简得：a2+b2＝c2．【例题1】在直角三角形中，两条直角边的长分别为9和12，则斜边的长为．【分析】根据勾股定理直接求出斜边的长即可．【解答】解：∵在直角三角形中，两条直角边的长分别为9和12，=15．故答案为：15．【点评】本题主要考查了勾股定理，解题的关键是熟练掌握勾股定理，如果直角三角形的两条直角边长为a、b，斜边长为c，那么a2+b2＝c2．【变式1-1】已知△ABC中，∠C＝90°，AB＝c，BC＝a，AC＝b．（1）如果a＝7，b＝24，求c；（2）如果a＝12，c＝13，求b．【分析】（1）利用勾股定理计算c=（2）利用勾股定理计算b=【解答】解：（1）在Rt△ABC中，∠C＝90°，由勾股定理得：c==＝25；（2）在Rt△ABC中，由勾股定理得：b==＝5．【点评】本题考查了勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．即：如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．注意勾股定理应用的前提条件是在直角三角形中．【变式1-2】（2022秋•东方期末）如图，在△ABC 中，AB ＝AC ＝10，BC ＝12，AD 平分∠BAC ，则AD 等于（）A ．6B ．7C ．8D ．9【分析】根据等腰三角形的三线合一得到AD ⊥BC ，BD ＝DC =12BC ＝6，根据勾股定理计算，得到答案．【解答】解：∵AB ＝AC ，AD 平分∠BAC ，∴AD ⊥BC ，BD ＝DC =12BC ＝6，在Rt △ABD 中，AD 8，故选：C ．【点评】本题考查的是勾股定理、等腰三角形的性质，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．【变式1-3】（2022秋•新泰市期末）如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，则点C 到直线AB 的距离是（）A ．185B ．3C ．125D ．2【分析】作CD⊥AB于点D，根据勾股定理可以求得AB的长，然后根据面积法，可以求得CD的长．【解答】解：作CD⊥AB于点D，如右图所示，∵∠C＝90°，AC＝3，BC＝4，∴AB=5，∵AC⋅BC2=AB⋅CD2，∴3×42=5CD2，解得CD＝2.4，故选：C．【点评】本题考查勾股定理、三角形的面积，解答本题的关键是明确题意，画出相应的图形，利用勾股定理和面积法解答．【变式1-4】（2021春•连州市期中）如图所示，AB⊥BC，DC⊥BC，E是BC上一点，∠BAE＝∠DEC＝60°，AB＝3，CE＝4，则AD等于（）A．10B．12C．24D．48【分析】本题主要考查勾股定理运用，解答时要灵活运用直角三角形的性质．【解答】解：∵AB⊥BC，DC⊥BC，∠BAE＝∠DEC＝60°∴∠AEB＝∠CDE＝30°∵30°所对的直角边是斜边的一半∴AE＝6，DE＝8又∵∠AED ＝90°根据勾股定理∴AD ＝10．故选：A ．【点评】解决此类题目的关键是熟练掌握运用直角三角形两个锐角互余，30°所对的直角边是斜边的一半，勾股定理的性质．【变式1-5】如图，在△ABC 中，∠ACB ＝90°，AC ＝3，BC ＝4，分别以点A 和点B 为圆心，以相同的长（大于12AB ）为半径作弧，两弧相交于点M 和点N ，作直线MN 交AB 于点D ，连接CD ，则CD 的长为．【分析】根据勾股定理可以求得AB 的长，然后根据线段垂直平分线的判定方法可以得到MN 为线段AB 的垂直平分线，再根据直角三角形斜边上的中线等于斜边的一半，即可得到CD 的长．【解答】解：∵∠ACB ＝90°，AC ＝3，BC ＝4，∴AB ==5，连接NA ，NB ，MA ，MB ，如图所示，∵分别以点A 和点B 为圆心，以相同的长（大于12AB ）为半径作弧，两弧相交于点M 和点N ，∴NA ＝NB ，MA ＝MB ，∴直线MN 垂直平分AB ，∵直线MN 交AB 于点D ，∴点D 为AB 的中点，∴CD 为Rt △ACB 斜边上的中线，∴CD =12AB =52，故答案为：52．【点评】本题考查勾股定理、线段垂直平分线的性质，解答本题的关键是明确题意，利用数形结合的思想解答．【变式1-6】（2022春•河北区期末）如图，在△ABC中，CD⊥AB于点D，AC＝20，CD＝12，BD＝9．求AB与BC的长．【分析】根据勾股定理求出BC即可；根据勾股定理求出AD，求出AB即可．【解答】解：∵CD⊥AB，AC＝20，CD＝12，BD＝9，∴∠ADC＝∠BDC＝90°，在Rt△CDB中，由勾股定理得：BC=15，在Rt△ADC中，由勾股定理得：AD=16，∴AB＝AD+DB＝16+9＝25．答：AB的长为25，BC的长为15．【点评】本题考查了勾股定理的应用，关键是对定理的掌握和运用．【变式1-7】如图，在△ABC中，AC＝8，BC＝6，CE是AB边上的中线，CD是AB边上的高，且AE＝5．（1）求CD的长；（2）求DE的长．【分析】（1）先证明三角形ABC是直角三角形，再根据等面积法即可求解；（2）根据勾股定理求出BD的长即可求解．【解答】解：（1）∵CE是AB边上的中线，∴AE＝BE＝5，∴AB＝10，又∵AC＝8，BC＝6，∴AC2+BC2＝82+62＝100＝AB2，∴△ABC是直角三角形，又∵CD是△ABC的高，∴S△ABC=12AC⋅BC=12AB⋅CD，∴CD=AC⋅BCAB=4.8；（2）在Rt△BDC中，由勾股定理得，BD=3.6，∴DE＝BE﹣BD＝5﹣3.6＝1.4．【点评】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．【例题2】勾股定理的验证方法很多，用面积（拼图）证明是最常见的一种方法．如图所示，一个直立的长方体在桌面上慢慢地倒下，启发人们想到勾股定理的证明方法，设AB＝c，BC＝a，AC＝b，证明中用到的面积相等关系是（）A．S△ABC+S△ABD＝S△AFG+S△AEFB．S梯形BCEF＝S△ABC+S△ABF+S△AEFC．S△BDH＝S△FGHD．S梯形BCEF＝S△ABC+S△ABF+S△AEF+S△FGH【分析】通过用两种方法计算梯形BCEF的面积即可证明勾股定理．【解答】解：∵矩形ACBD旋转得出矩形AGFE，∴△ABC≌△FAE，∴AB＝AF，∠BAC＝∠AFE，∵∠AFE+∠EAF＝90°，∴∠BAC+∠EAF＝90°，∴△ABF是等腰直角三角形，由题意知：S梯形BCEF =12（a+b）•（a+b）=12(a+b)2=12a2+ab+12b2，S△ABC+S△ABF+S△AEF=12ab+12ab+12c2=ab+12c2，∴12a2+ab+12b2=ab+12c2，∴a2+b2＝c2，故选：B．【点评】本题主要考查了勾股定理的证明，等腰直角三角形的判定，表示出图形面积的不同表达形式，建立等量关系是解题的关键．【变式2-1】（2022春•三门峡期末）我国是最早了解勾股定理的国家之一．据《周髀算经》记载，勾股定理的证明是在商代由商高发现的，故又称之为“商高定理”；三国时代的赵爽对《周髀算经》内的勾股定理作出了详细注释，又给出了另外一个证明．古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用．下面四幅图中，不能证明勾股定理的是（）A ．B ．C ．D ．【分析】由正方形面积公式、三角形面积公式以及梯形面积公式分别对各个选项进行判断即可．【解答】解：A 、大正方形的面积为：c 2，也可看作是4个直角三角形和一个小正方形组成，则其面积为：12ab ×4+（b ﹣a ）2＝a 2+b 2，∴a 2+b 2＝c 2，故A 选项能证明勾股定理；B 、大正方形的面积为：（a +b ）2，也可看作是2个矩形和2个小正方形组成，则其面积为：a 2+b 2+2ab ，∴（a +b ）2＝a 2+b 2+2ab ，∴B 选项不能证明勾股定理．C 、大正方形的面积为：（a +b ）2；也可看作是4个直角三角形和一个小正方形组成，则其面积为：12ab ×4+c 2＝2ab +c 2，∴（a +b ）2＝2ab +c 2，∴a 2+b 2＝c 2，故C 选项能证明勾股定理；D、梯形的面积为：12（a+b）（a+b）=12（a2+b2）+ab，也可看作是2个直角三角形和一个等腰直角三角形组成，则其面积为：12ab×2+12c2＝ab+12c2，∴12（a2+b2）+ab＝ab+12c2，∴a2+b2＝c2，故D选项能证明勾股定理；故选：B．【点评】本题考查了勾股定理的证明、正方形面积公式、三角形面积公式以及梯形面积公式，熟练掌握内弦图、外弦图是解题的关键．【变式2-2】“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b，若ab＝8，大正方形的面积为25，则小正方形的边长为（）A．9B．6C．4D．3【分析】分析题意，首先根据已知条件易得，中间小正方形的边长为：a﹣b；接下来根据勾股定理以及题目给出的已知数据即可求出小正方形的边长．【解答】解：由题意可知：中间小正方形的边长为：a﹣b，∵每一个直角三角形的面积为：12ab=12×8＝4，从图形中可得，大正方形的面积是4个直角三角形的面积与中间小正方形的面积之和，∴4×12ab+（a﹣b）2＝25，∴（a﹣b）2＝25﹣16＝9，∴a﹣b＝3．故选：D．【点评】本题考查勾股定理，解题的关键是熟练运用勾股定理以及完全平方公式．【变式2-3】（2022春•高安市期中）勾股定理被誉为“几何明珠”，如图是我国古代著名的“赵爽弦图”，它由4个全等的直角三角形拼成，已知大正方形面积为25，小正方形面积为1，若用a、b表示直角三角形的两直角边（a＞b），则下列说法：①a2+b2＝25，②a﹣b＝1，③ab＝12，④a+b＝7．正确的是（）A．①②B．①②③C．①②④D．①②③④【分析】根据勾股定理和大正方形面积为25，可以判断①；根据小正方形面积为1，可以判断②；根据大正方形面积为25，小正方形面积为1，可以得到四个直角三角形的面积，从而可以得到ab的值，即可判断③；根据完全平方公式可以判断④．【解答】解：由图可得，a2+b2＝c2＝25，故①正确；∵小正方形面积为1，∴小正方形的边长为1，∴a﹣b＝1，故②正确；∵大正方形面积为25，小正方形面积为1，∴12ab＝（25﹣1）÷4，解得ab＝12，故③正确；∵a2+b2＝25，ab＝12，∴（a+b）2＝a2+2ab+b2＝49，∴a+b＝7，故④正确；故选：D．【点评】本题考查勾股定理的证明、正方形的性质、直角三角形的面积，利用数形结合的思想解答是解答本题的关键．【变式2-4】如图1是我国古代著名的“赵爽弦图”的示意图，它是由四个全等的直角三角形围成的．若AC ＝6，BC＝5，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到如图2所示的“数学风车”，则这个风车的外围周长是（）A ．36B ．76C ．66D ．12【分析】由题意∠ACB 为直角，利用勾股定理求得外围中一条边，又由AC 延伸一倍，从而求得风车的一个轮子，进一步求得四个．【解答】解：依题意，设“数学风车”中的四个直角三角形的斜边长为x ，则x 2＝122+52＝169，所以x ＝13，所以这个风车的外围周长是：（13+6）×4＝76．故选：B ．【点评】此题考查了勾股定理的证明，本题是勾股定理在实际情况中的应用，并注意隐含的已知条件来解答此类题．【变式2-5】用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题，这种方法称为等面积法，这是一种重要的数学方法，请你用等面积法来探究下列三个问题：（1）如图1是著名的“赵爽弦图”，由四个全等的直角三角形拼成，请用它验证勾股定理c 2＝a 2+b 2．（2）如图2，在Rt △ABC 中，∠ACB ＝90°，CD 是AB 边上的高，AC ＝4，BC ＝3，求CD 的长度；（3）如图1，若大正方形的面积是13，小正方形的面积是1，求（a +b ）2的值（a ＜b ）．【分析】（1）根据大正方形的面积的两种表示方法求解即可；（2）根据直角三角形的面积公式求解即可；（3）根据小正方形的为1得出2ab ＝12，再结合c 2＝13即可求解．【解答】解：（1）如图1，大正方形的面积＝c 2＝4×12ab +(b ―a )2，整理得，c2＝a2+b2；（2）在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，∴AB=5，∵S△ABC=12AC⋅BC=12AB⋅CD，∴CD=AC⋅BCAB=125；（3）∵大正方形的面积是13，小正方形的面积是1，∴c2＝13，（b﹣a）2＝1，∴a2+b2﹣2ab＝1，∴2ab＝12，∴（a+b）2＝a2+b2+2ab＝13+12＝25，即（a+b）2的值为25．【点评】本题考查了勾股定理的证明，正确表示出大正方形的面积的两种表示方法是解题的关键．【变式2-6】（2022春•巢湖市校级期中）学习勾股定理之后，同学们发现证明勾股定理有很多方法．某同学提出了一种证明勾股定理的方法：如图1点B是正方形ACDE边CD上一点，连接AB，得到直角三角形ACB，三边分别为a，b，c，将△ACB裁剪拼接至△AEF位置，如图2所示，该同学用图1、图2的面积不变证明了勾股定理．请你写出该方法证明勾股定理的过程．【分析】连接BF，由图1可得正方形ACDE的面积为b2，由图2可得四边形ABDF的面积为三角形ABF 与三角形BDF面积之和，再利用正方形ACDE的面积与四边形ABDF的面积相等即可证明．【解答】证明：如图，连接BF，∵AC ＝b ，∴正方形ACDE 的面积为b 2，∵CD ＝DE ＝AC ＝b ，BC ＝a ，EF ＝BC ＝a ，∴BD ＝CD ﹣BC ＝b ﹣a ，DF ＝DE +EF ＝a +b ，∵∠CAE ＝90°，∴∠BAC +∠BAE ＝90°，∵∠BAC ＝∠EAF ，∴∠EAF +∠BAE ＝90°，∴△BAE 为等腰直角三角形，∴四边形ABDF 的面积为：12c 2+12（b ﹣a ）（a +b ）=12c 2+12（b 2﹣a 2），∵正方形ACDE 的面积与四边形ABDF 的面积相等，∴b 2=12c 2+12（b 2﹣a 2），∴b 2=12c 2+12b 2―12a 2，∴12a 2+12b 2=12c 2，∴a 2+b 2＝c 2．【点评】本题考查勾股定理的证明，解题的关键是熟练掌握勾股定理的证明方法，一般利用拼图的方法，再利用面积相等证明．【例题3】如图，当正方形B的面积为64，正方形C的面积为100时，正方形A的面积为（）A．36B．25C．16D．6【分析】直接根据勾股定理进行解答即可．【解答】解：由图可知，△DEF是直角三角形，∴DE2+DF2＝EF2，∵正方形B的面积＝DF2，正方形C的面积＝EF2，正方形A的面积＝DF2，正方形B的面积为64，正方形C的面积为100，∴正方形A的面积＝100﹣64＝36．故选：A．【点评】本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解题的关键．【变式3-1】（2022秋•渠县期末）如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A、C、D的面积依次为4、6、18，则正方形B的面积为（）A．8B．9C．10D．12【分析】根据勾股定理、正方形的面积公式计算即可．【解答】解：由勾股定理，得正方形E的面积＝正方形C的面积+正方形D的面积，正方形E的面积＝正方形A的面积+正方形B的面积，则正方形B的面积＝18﹣6﹣4＝8，故选：A．【点评】本题考查了勾股定理，要熟悉勾股定理的几何意义，知道直角三角形两直角边的平方和等于斜边的平方．【变式3-2】（2022秋•南京期末）如图，在等腰Rt△ACB中，∠ACB＝90°，AC＝BC，且AB＝AB、AC、BC为直径画半圆，其中所得两个月形图案AFCD和BGCE（图中阴影部分）的面积之和等于（）A．8B．4C．2D．【分析】由等腰三角形的性质及勾股定理可求解AC＝CB＝2，进而可求得S△ACB＝2，再利用阴影部分的面积＝以AC为直径的圆的面积+△ACB的面积﹣以AB为直径的半圆的面积计算可求解．【解答】解：在等腰Rt △ACB 中，∠ACB ＝90°，AC ＝BC ，AB ＝∴AC 2+BC 2＝AB 2＝8，∴AC ＝CB ＝2，∴S △ACB =12AC •BC ＝2，∴S 阴影＝π（AC 2）2+S △ACB ―12π（AB 2）2＝π+2﹣π＝2，故选：C ．【点评】本题主要考查等腰直角三角形，勾股定理，理清阴影部分的面积＝以AC 为直径的圆的面积+△ACB 的面积﹣以AB 为直径的半圆的面积是解题的关键．【变式3-3】如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中S A ＝4，S B ＝2，S c ＝2，S D ＝1，则S ＝（）A ．25B ．20C ．9D ．5【分析】根据正方形的性质和勾股定理的几何意义解答即可．【解答】解：如图，根据勾股定理的几何意义，可知：S＝S F+S G＝S A+S B+S C+S D＝4+2+2+1＝9；即S＝9；故选：C．【点评】本题考查了正方形的性质、勾股定理的几何意义，关键是掌握两直角边的平方和等于斜边的平方．【变式3-4】如图，Rt△ABC中，分别以这个三角形的三边为边长作正方形，面积分别记为S1、S2、S2．如果S2+S1﹣S3＝18，则阴影部分的面积为　．【分析】由勾股定理得出S2﹣S3＝S1，再根据S2+S1﹣S3＝18即可得出S1的值，即为图中阴影部分的面积．【解答】解：由勾股定理得，BC2﹣AC2＝AB2，即S2﹣S3＝S1，∵S2+S1﹣S3＝18，∴S 1＝9，由图形可知，阴影部分的面积=12S 1，∴阴影部分的面积=92，故答案为：92．【点评】本题考查了勾股定理，由勾股定理得出S 2﹣S 3＝S 1，是解题的关键．【变式3-5】（2022秋•绿园区校级期末）如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为16cm ，则正方形A ，B ，C ，D 的面积之和为 cm 2．【分析】如图根据勾股定理有S 正方形2+S 正方形3＝S 正方形1，S 正方形C +S 正方形D ＝S 正方形3，S 正方形A +S 正方形B ＝S 正方形2，等量代换即可求四个小正方形的面积之和．【解答】解：如右图所示，根据勾股定理可知，S 正方形2+S 正方形3＝S 正方形1，S 正方形C +S 正方形D ＝S 正方形3，S 正方形A +S 正方形B ＝S 正方形2，∴S 正方形C +S 正方形D +S 正方形A +S 正方形B ＝S 正方形2+S 正方形3＝S 正方形1＝162＝256（cm 2）．故答案为：256．【点评】本题考查了勾股定理的几何意义，关键是掌握两直角边的平方和等于斜边的平方．【变式3-6】如图，直角三角形ACB，直角顶点C在直线l上，分别过点A、B作直线l的垂线，垂足分别为点D和点E．（1）求证：∠DAC＝∠BCE；（2）如果AC＝BC．①求证：CD＝BE；②若设△ADC的三边分别为a、b、c，试用此图证明勾股定理．【分析】（1）根据直角三角形的定义和垂直的定义，可以证明结论成立；（2）①根据AAS可以证明结论成立；②根据S梯形ADEB＝S△ADC+S△ACB+S△CEB，代入字母计算即可证明结论成立．【解答】证明：（1）∵∠ACB＝90°，AD⊥DE于点D，∴∠DAC+∠ACD＝90°，∠ADC+∠BCE＝90°，∴∠DAC＝∠BCE；（2）①∵AD⊥DE于点D，BE⊥DE于点E，∴∠ADC＝∠CEB＝90°，由（1）知：∠DAC＝∠BCE，在△ADC和△CEB中，∠ADC=∠CEB∠DAC=∠ECB，AC=CB∴△ADC≌△CEB（AAS），∴CD＝BE；②由图可知：S 梯形ADEB ＝S △ADC +S △ACB +S △CEB ，∴(a b )(a b )2=ab 2+c 22+ab 2，化简，得：a 2+b 2＝c 2．【点评】本题考查勾股定理的证明，解答本题的关键是明确题意，利用数形结合的思想解答．【例题4】（2022秋•门头沟区期末）已知：如图，在△ABC 中，AB ＝AC ＝5，BC ＝8．求BC 边上的高的长．【分析】过点A 作AD ⊥BC 于点D ，根据等腰三角形的性质求出BD =12BC ＝4，根据勾股定理求出AD 的长即可．【解答】解：如图，过点A 作AD ⊥BC 于点D ，∵AB ＝AC ＝5，BC ＝8，AD ⊥BC ，∴BD ＝CD =12BC ＝4，∴AD==3，即BC 边上的高的长为3．【点评】此题考查了等腰三角形的性质、勾股定理等知识，熟练掌握等腰三角形的性质、勾股定理是解题的关键．【变式4-1】如图，在△ABC中，∠C＝90°，DE垂直平分AB，分别交AB，BC于D，E两点，若BE＝5，CE＝3，则AC的长为．【分析】先根据线段垂直平分线的性质可得BE＝AE＝5，然后在Rt△ACE中，利用勾股定理进行计算，即可解答．【解答】解：连接AE，∵DE垂直平分AB，∴BE＝AE＝5，∵∠C＝90°，CE＝3，∴AC==4，故答案为：4．【点评】本题考查了勾股定理，线段垂直平分线的性质，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．【变式4-2】（2021春•齐齐哈尔月考）已知：△ABC中，AC＝2，∠C＝30°，∠B＝45°，求AB和BC的长．【分析】作AD⊥BC，得∠ADC＝∠ADB＝90°，根据勾股定理和直角三角形30°所对的直角边是斜边的一半计算即可．【解答】解：作AD⊥BC，∴∠ADC＝∠ADB＝90°，∵∠C＝30°，∴AD=12AC＝1，在Rt△ACD，根据勾股定理得，CD=∵∠B＝45°，∴∠DAB＝∠B＝45°，∴BD＝AD＝1，则BC＝1∴AB=【点评】本题考查了解直角三角形，熟练掌握勾股定理和直角三角形中30°所对的直角边是斜边的一半，这两个定理的应用是解题关键．【变式4-3】（2022春•阳新县期末）△ABC中，AB＝13，AC＝15，高AD＝12，则BC的长为（）A．14B．4C．14或4D．以上都不对【分析】分两种情况讨论：锐角三角形和钝角三角形，根据勾股定理求得BD，CD，再由图形求出BC，在锐角三角形中，BC＝BD+CD，在钝角三角形中，BC＝CD﹣BD．【解答】解：（1）如图，锐角△ABC中，AB＝13，AC＝15，BC边上高AD＝12，在Rt△ABD中AB＝13，AD＝12，由勾股定理得BD2＝AB2﹣AD2＝132﹣122＝25，则BD＝5，在Rt△ABD中AC＝15，AD＝12，由勾股定理得CD2＝AC2﹣AD2＝152﹣122＝81，则CD＝9，故BC＝BD+DC＝9+5＝14；（2）钝角△ABC中，AB＝13，AC＝15，BC边上高AD＝12，在Rt△ABD中AB＝13，AD＝12，由勾股定理得BD2＝AB2﹣AD2＝132﹣122＝25，则BD＝5，在Rt△ACD中AC＝15，AD＝12，由勾股定理得CD2＝AC2﹣AD2＝152﹣122＝81，则CD＝9，故BC的长为DC﹣BD＝9﹣5＝4．故选：C．【点评】本题考查了勾股定理，把三角形边的问题转化到直角三角形中用勾股定理解答．【变式4-4】如图，Rt△ABC中，AC⊥CB，AC＝15，AB＝25，点D为斜边上动点．连接CD，在点D的运动过程中，当△ACD 为等腰三角形时，AD 的长为．【分析】分三种情况讨论，利用等腰三角形的性质，分别求解即可解决问题．【解答】解：①当AD ＝AC 时，△ACD 为等腰三角形，∵AC ＝15，∴AD ＝AC ＝15．②当CD ＝AD 时，△ACD 为等腰三角形，∵CD ＝AD ，∴∠DCA ＝∠CAD ，∵∠CAB +∠B ＝90°，∠DCA +∠BCD ＝90°，∴∠B ＝∠BCD ，∴BD ＝CD ，∴CD ＝BD ＝DA ＝12.5；③当CD ＝AC 时，△ACD 为等腰三角形，如图，作CH ⊥BA 于点H ，则12×AB ×CH =12×AC ×BC ，∵AC ＝15，BC ＝20，AB ＝25，∴CH ＝12，在Rt △ACH 中，AH =9，∵CD ＝AC ，CH ⊥BA ，∴DH ＝HA ＝9，∴AD ＝18，综上所述：AD 的值为15或12.5或18．故答案为：15或12.5或18．【点评】本题考查解直角三角形的应用，等腰三角形的判定和性质，勾股定理等知识，解题的关键是学会利用参数构建方程解决问题，属于中考常考题型．【例题5】如图，阴影部分表示以Rt △ABC 的各边为直径的三个半圆所组成的两个新月形，面积分别记作S 1和S 2．若S 1+S 2＝7，AB ＝6，则△ABC 的周长是（）A ．12.5B ．13C ．14D ．15【分析】根据勾股定理得到AC 2+BC 2＝AB 2，根据扇形面积公式、完全平方公式计算即可．【解答】解：由勾股定理得，AC 2+BC 2＝AB 2，∵S 1+S 2＝7，∴12×π×（AC 2）2+12×π×（BC 2）2+12×AC ×BC ―12×π×（AB 2）2＝7，∴AC ×BC ＝14，∴（AC +BC ）2＝AC 2+BC 2+2AC •BC ＝62+2×14＝64，∴AC +BC ＝8（负值舍去），∴△ABC 的周长＝AB +AC +BC ＝8+6＝14，故选：C ．【点评】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2．【变式5-1】如图，三角形ABC中，∠C=90°，∠BAC的平分线交BC于D，DE⊥AB于E，已知CD=3，BD=5，求三角形ABC的周长．【分析】根据角平分线的性质得到DE=CD=3，根据勾股定理求出BE的长，再根据勾股定理列出方程，解方程得到答案．【解答】解：∵AD是∠BAC的平分线，∠C=90°，DE⊥AB，∴DE=CD=3，AC=AE，∵DE⊥AB，DE=3，BD=5，根据勾股定理得，BE=4，∴AC2+82=（AE+4）2，解得AE=6，则AC=6，∴三角形ABC的周长=AC+AB+BC=24．【点评】本题考查的是角平分线的性质和勾股定理的应用，掌握角的平分线上的点到角的两边的距离相等是解题的关键．【变式5-2】如图，△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB于E，若AB＝10cm，AC＝6cm，则△BED周长为（）A．10cm B．12cm C．14cm D．16cm【分析】根据角平分线上的点到角的两边距离相等可得CD＝DE，再利用“HL”证明Rt△ACD和Rt△AED全等，根据全等三角形对应边相等可得AC＝AE，可求出BE，再利用勾股定理列式求出BC，最后根据三角形的周长列式计算即可得解．【解答】解：∵AD是∠CAB的平分线，∠C＝90°，DE⊥AB于E，∴CD＝DE，在Rt△ACD和Rt△AED中，AD=ADDC=DE，∴Rt△ACD≌Rt△AED（HL），∴AC＝AE＝6，∴BE＝AB﹣AE＝10﹣6＝4，由勾股定理得，BC==8，∴△BDE的周长＝BE+BD+CD＝BE+BD+CD＝BE+BC＝4+8＝12（cm）．故选：B．【点评】本题考查了角平分线上的点到角的两边距离相等的性质，全等三角形的判定与性质，勾股定理，熟记性质并求出三角形全等是解题的关键．【变式5-3】在四边形ABCD中，∠ABC＝∠ADC＝90°，连接AC，点E为AC的中点，连接BE，DE．若DE=132，BC＝12，则△ABE的周长为．【分析】根据直角三角形斜边上的中线等于斜边的一边得到AC＝2BE＝2DE＝2AE＝13，再利用勾股定理求出AB＝5即可得到答案．【解答】解：∵∠ABC＝∠ADC＝90°，点E为AC的中点，∴AC＝2BE＝2DE＝2AE＝13，∵BC＝12，∴AB=5，∴△ABE的周长为AE+BE+AB=5+2×132=18，故答案为：18．【点评】本题主要考查了直角三角形斜边上的中线的性质，勾股定理，熟知直角三角形斜边上的中线等于斜边的一半是解题的关键．【例题6】（2022春•范县期中）如图，正方形ABCD中，AE⊥BE，且AE＝3，AB＝5，则阴影部分的面积是（）A．13B．15C．18D．19【分析】利用正方形的面积减去三角形的面积即可求出阴影部分的面积．【解答】解：∵AE⊥BE，且AE＝3，AB＝5，∴BE=4，∴S△ABE=12AE⋅BE=12×3×4=6，∵四边形ABCD是正方形，AB＝5，∴S正＝5×5＝25，∴S阴影＝S正﹣S△ABE＝25﹣6＝19．故选：D．【点评】本题主要考查正方形的性质与勾股定理，解题的关键是用割补法求阴影部分的面积．【变式6-1】如图，在△ABC中，AC＝BC＝17，AB＝16，求△ABC的面积．【分析】过C作CD⊥AB于D，根据等腰三角形的性质和勾股定理，以及三角形的面积公式即可得到结论．【解答】解：过C作CD⊥AB于D，∵AC＝BC＝17，AB＝16，∴AD＝BD=12AB＝8，∵AD2+CD2＝AC2，∴CD=15，∴S△ABC =12AB•CD=12×16×15=120．【点评】本题考查了勾股定理，三角形的面积的计算，等腰三角形的性质，熟练掌握勾股定理是解题的关键．【变式6-2】（2022春•桐城市期末）如图2，在△ABC 中，AC ＝8，AB ＝4，∠BAC ＝120°，求△ABC 的面积．【分析】过点C 作CD ⊥AB ，交BA 的延长线于点D ，由勾股定理求出CD 的长，利用三角形面积公式可求出答案．【解答】解：过点C 作CD ⊥AB ，交BA 的延长线于点D ，∵∠BAC ＝120°，∴∠DAC ＝60°，∴∠ACD ＝30°，∵AC ＝8，∴AD =12AC ＝4，∴CD =∴S △ABC =12AB •CD =12×=【点评】此题主要考查了勾股定理，三角形面积公式，求得出AB ，CD 的长是解题的关键．【变式6-3】如图在四边形ABCD 中，∠ABC ＝120°，AB ⊥AD ，BC ⊥CD ，AB ＝4，CD ＝5，求该四边形的面积．【分析】延长DA 和CB 交于O ，求出∠O ＝30°，根据含30度角的直角三角形性质求出OB 和OD ，根据勾股定理求出OA 和OC ，根据三角形面积公式求出即可．【解答】解：延长DA 和CB 交于O ，∵AB ⊥AD ，BC ⊥CD ，∴∠DAB ＝∠C ＝∠OAB ＝90°，∵∠D ＝60°，∴∠O ＝30°，∵AB ＝4，DC ＝5，∴OB ＝2AB ＝8，OD ＝2DC ＝10，由勾股定理得：OA ==OC =∴四边形ABCD 的面积是:S △OCD ﹣S △OAB =12×OC ×CD ―12×OA ×AB =12×5―12×【点评】本题考查了含30度角的直角三角形性质，勾股定理，三角形的面积的应用，注意：在直角三角形中，两直角边的平方和等于斜边的平方．【变式6-4】如图，已知在四边形ABCD 中，∠BCD ＝90°，BD 平分∠ABC ，AB ＝4，BD ＝10，BC ＝8，求四边形ABCD 的面积．【分析】过点D 作DE ⊥BA 的延长线于点E ，利用勾股定理和角平分线的性质可得出DE ＝DC ＝6，再利用三角形的面积公式结合S 四边形ABCD ＝S △ABD +S △BCD 可求出四边形ABCD 的面积．【解答】解：过点D 作DE ⊥BA 的延长线于点E ，如图所示．∵∠BCD＝90°，BD＝10，BC＝8，∴BD=6，∵BD平分∠ABC，∴DE＝DC＝6，∴S四边形ABCD ＝S△ABD+S△BCD，=12AB•DE+12BC•CD，=12×4×6+12×8×6，＝36．【点评】本题考查了角平分线的性质以及三角形的面积，利用角平分线的性质，找出DE＝8是解题的关键．【例题7】如图，在四边形ABCD中，∠ABC＝90°，CD⊥AD，AD2+CD2＝2AB2．（1）求证：AB＝BC；（2）当BE⊥AD于E时，试证明：BE＝AE+CD．【分析】（1）根据勾股定理AB2+BC2＝AC2，得出AB2+BC2＝2AB2，进而得出AB＝BC；（2）首先证明CDEF是矩形，再根据△BAE≌△CBF，得出AE＝BF，进而证明结论．【解答】证明：（1）连接AC．∵∠ABC＝90°，∴AB2+BC2＝AC2．∵CD⊥AD，∴AD2+CD2＝AC2．∵AD2+CD2＝2AB2，∴AB2+BC2＝2AB2，∴BC2＝AB2，∵AB＞0，BC＞0，∴AB＝BC．（2）过C作CF⊥BE于F．∵BE⊥AD，CF⊥BE，CD⊥AD，∴∠FED＝∠CFE＝∠D＝90°，∴四边形CDEF是矩形．∴CD＝EF．∵∠ABE+∠BAE＝90°，∠ABE+∠CBF＝90°，∴∠BAE＝∠CBF，∴在△BAE与△CBF中∴∠AEB=∠BFC ∠BAE=∠CBF AB=BC，∴△BAE≌△CBF．（AAS）∴AE＝BF．∴BE＝BF+EF＝AE+CD．【点评】此题主要考查了勾股定理的应用以及三角形的全等证明，根据已知得出四边形CDEF是矩形以及△BAE≌△CBF是解决问题的关键．【变式7-1】已知AD是△ABC的中线，∠C＝90°，DE⊥AB于点E，试说明AC2＝AE2﹣BE2．【分析】根据直角三角形的性质和勾股定理可得AE2﹣BE2＝（AD2﹣DE2）﹣（BD2﹣DE2）＝AD2﹣BD2＝AD2﹣CD2＝AC2，从而证明结论．【解答】证明：∵AD是△ABC的中线，∴BD＝CD．∵∠C＝90°，DE⊥AB于E，∴AE2﹣BE2＝（AD2﹣DE2）﹣（BD2﹣DE2）＝AD2﹣BD2＝AD2﹣CD2＝AC2．故AC2＝AE2﹣BE2．【点评】考查了直角三角形的性质和勾股定理，注意线段相互间的转化．【变式7-2】已知，如图，△ABC中，AB＞AC，AD为BC边上的高，M是AD边上任意一点．求证：AB2﹣AC2＝MB2﹣MC2．。

2023年中考数学几何专题：勾股定理的应用(解析版)

2023中考数学几何专题：勾股定理的应用（解析版）1. 放学以后，小红和小颖从学校分手，分别沿东南方向和西南方向回家，若小红和小颖行走的速度都是40米/分，小红用15分钟到家，小颖20分钟到家，小红和小颖家的直线距离为（）A ．600米 B. 800米 C. 1000米 D. 不能确定【解析】速度一定且相同，路程比=时间比.再用勾股定理，直线距离应该是25分钟的路程.选C.【答案】C2. 一架25分米长的梯子，斜立在一竖直的墙上，这时梯足距离墙底端7分米.如果梯子的顶端沿墙下滑4分米，那么梯足将滑动( )A. 9分米B. 15分米C. 5分米D. 8分米【解析】在初始和结束两个状态下,选定直角三角形,应用勾股定理. 初始时,经计算,可知,梯顶距墙底端24分米.结束时,经计算,可知,梯足距离墙底端15分米.选D. 【答案】D3. 如图,点P 是AOB ∠的角平分线上一点，过点P 作//PC OA 交OB 于点C .若60,4AOB OC ∠==,则点P 到OA 的距离PD 等于__________.【解析】过P 点作PE OB ⊥，并交OB 于点E .∵60,AOB OP ∠=是AOB ∠的角平分线， ∴630BOP ∠==. 又∵//PC OA ，∴60PCB AOB ∠=∠=.∴30OPC BOP BPC ∠==∠=∠.∴14,22PC OC EC PC ====.∴PB =.【答案】4. 将一根长为24cm 的筷子，置于底面直径为5cm ，高为12cm 的圆柱形水杯中，设筷子露在杯子外边的长度为cm h ，则h 的取值范围为PODC B A EP ODC BA【答案】2.3cm5. 如图，是一块直角三角形的土地，现在要在这块地上挖一个正方形蓄水池AEDF ，已知剩余的两直角三角形（阴影部分）的斜边长分别为20cm 和30cm ，则剩余的两个直角三角形（阴影部分）的面积和．．．为 2cm ．【解析】cm AE x =，cm BE a =，cm CF b =，在Rt BDE ∆中，22230900a x +== ① 在Rt CDF ∆中，22220400b x +== ②在Rt ABC ∆中，()()222502500a x b x +++==，即2222222500a ax x b bx x +++++= ③③-①-②得，221200ax bx +=，3002ax bx+=最简单的方法为两个小的直角三角形旋转合并成一个大的直角三角形（正方形的边重合）故130203002⨯⨯=．【答案】3006. 如图，学校有一块长方形花铺，有极少数人为了避开拐角走“捷径”，在花铺内走出了一条“路”．他们仅仅少走了步路（假设2步为1米），却踩伤了花草．【解析】直接应用勾股定理可知,少走了5m.又知2步为1米,所以少走了10步. 【答案】107. 蚂蚁沿图中的折线从A 点爬到D 点，一共爬了多少厘米？（小方格的边长为1厘米）【解析】把折线从A 到D,分三段计算.第1段长为5,第2段长为13,第3段长为10,进行加法计算,所以蚂蚁一共爬了28cm .【答案】28cm8. 在Rt ABC ∆中，90C ∠=︒，若54a b c +==，，则ABC S ∆= . 【解析】在Rt ABC ∆中,由勾股定理得，222a b c +=. 又有()2222a b a b ab +=++, 所以 ()222a b c ab +-=所以1924ABC S ab ∆==.【答案】94ABC S ∆=9. 如图，Rt ABC ∆中，90CAB ∠=︒，AB AC =，E 、F 为BC 上的点，且45EAF ∠=︒，求证：222EF BE FC =+．【解析】过点A 作线段AD ，使CAF BAD ∠=∠，且AD AF =．在ACF ∆和ABD ∆中， AC AB CAF BAD AF AD =⎧⎪∠=∠⎨⎪=⎩∴ACF ABD ∆∆≌ ∴CF BD =，DBA FCA ∠=∠90DBE DBA ABE FCA ABE ∠=∠+∠=∠+∠=︒ 在ADE ∆和AFE ∆中， 45AE AE EAF EAD AD AF =⎧⎪∠=∠=︒⎨⎪=⎩∴ADE AFE ∆∆≌ ∴ED EF =在Rt BDE ∆中，222DE BD BE =+，∴222EF BE FC =+．【答案】见解析F E C B ADF E CB ACBAD10. 如图，已知Rt △ABC 的周长为26+，其中斜边2AB =，求这个三角形的面积.【解析】在Rt △ABC 中，根据勾股定理，得2222a b +=，即2()24a b ab +-=。

勾股定理(讲义及答案)及解析

一、选择题1．已知长方体的长2cm 、宽为1cm 、高为4cm ，一只蚂蚁如果沿长方体的表面从A 点爬到B′点，那么沿哪条路最近，最短的路程是（）A ．29cmB ．5cmC ．37cmD ．4.5cm2．如图，在平行四边形ABCD 中，∠DBC=45°，DE ⊥BC 于E ，BF ⊥CD 于F ，DE ，BF 相交于H ，BF 与AD 的延长线相交于点G ，下面给出四个结论:①2BD BE =； ②∠A=∠BHE ； ③AB=BH ； ④△BCF ≌△DCE ，其中正确的结论是( )A ．①②③B ．①②④C ．②③④D ．①②③④3．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由三角形较长直角边长为a ，较短直角边长为b ，若（a ＋b ）2＝21，大正方形的面积为13，则小正方形的面积为（）A ．3B ．4C ．5D ．64．如图，在Rt ABC 中，90BAC ︒∠=，以Rt ABC 的三边为边分别向外作等边三角形'A BC ，'AB C △，'ABC △，若'A BC ，'AB C △的面积分别是10和4，则'ABC △的面积是( )A ．4B ．6C ．8D ．95．如图中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为10cm ，正方形A 的边长为6cm 、B 的边长为5cm 、C 的边长为5cm ，则正方形D 的边长为( )A ．3cmB ．14cmC ．5cmD ．4cm6．如图，正方形ABCD 的边长为8，M 在DC 上，且DM=2，N 是AC 上的一动点，则DN+MN 的最小值是（）A ．8B ．9C ．10D ．127．勾股定理是“人类最伟大的十个科学发现之一”．我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的，他用来证明勾股定理的图案被称为“赵爽弦图”.2002年在北京召开的国际数学大会选它作为会徽．下列图案中是“赵爽弦图”的是（）A ．B ．C ．D ．8．小明学了在数轴上画出表示无理数的点的方法后，进行练习：首先画数轴，原点为O ，在数轴上找到表示数2的点A ，然后过点A 作AB ⊥OA ，使AB=3(如图)．以O 为圆心，OB 的长为半径作弧，交数轴正半轴于点P ，则点P 所表示的数介于( )A ．1和2之间B ．2和3之间C ．3和4之间D ．4和5之间 9．一个直角三角形的两条边的长度分别为3和4，则它的斜边长为（） A ．5 B ．4 C 7D ．4或5 10．下列条件中，不能．．判定ABC 为直角三角形的是（） A ．::5:12:13a b c =B ．A BC ∠+∠=∠ C ．::2:3:5A B C ∠∠∠=D ．6a =，12b =，10c =二、填空题11．如图，RT ABC ，90ACB ∠=︒，6AC =，8BC =，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B '处，两条折痕与斜边AB 分别交于点E 、F ，则B FC '△的面积为______．12．如图，这是由八个全等的直角三角形拼接而成，记图中正方形ABCD ，正方形EFGH ，正方形MNKT 的面积分别为 1S ，2S ，3S ，若123144S S S ++=，则2S 的值是__________．13．如图，有一个圆柱，它的高等于12厘米，底面半径等于3厘米．在圆柱的下底面A 点有一只蚂蚁，它想吃到上底面上与A 点相对的C 点处的食物，需要爬行的最短路程是___________________（π的值取3）．14．如图，Rt ABC 中，90A ∠=︒，8AC =，6AB =，DE AC ⊥，13CD BC =，13CE AC =，P 是直线AC 上一点，把CDP 沿DP 所在的直线翻折后，点C 落在直线DE 上的点H 处，CP 的长是__________15．在△ABC 中，AB ＝6，AC ＝5，BC 边上的高AD ＝4，则△ABC 的周长为__________.16．如图，在Rt ABC ∆中，90ABC ∠=，DE 垂直平分AC ，垂足为F ，//AD BC ，且3AB =，4BC =，则AD 的长为______．17．如图,在四边形ABCD 中,∠A=60°,∠B=∠D=90°,AD=4,AB=3,则CD=_________18．如图，在△ABC 中，∠C =90°，∠ABC =45°，D 是BC 边上的一点，BD =2，将△ACD 沿直线AD 翻折，点C 刚好落在AB 边上的点E 处.若P 是直线AD 上的动点，则△PEB 的周长的最小值是________．19．如图，△ABC 中，∠ACB=90°，AB=2，BC=AC ，D 为AB 的中点，E 为BC 上一点，将△BDE 沿DE 翻折，得到△FDE ，EF 交AC 于点G ，则△ECG 的周长是___________．20．如图，在Rt ABC ∆中，90ACB ∠=，2AC BC ==，D 为BC 边上一动点，作如图所示的AED ∆使得AE AD =，且45EAD ∠=，连接EC ，则EC 的最小值为__________．三、解答题21．（1）计算：1312248233⎛⎫-+÷ ⎪ ⎪⎝；（2）已知a 、b 、c 满足2|23|32(30)0a b c +-+--=．判断以a 、b 、c 为边能否构成三角形？若能构成三角形，说明此三角形是什么形状？并求出三角形的面积；若不能，请说明理由．22．如图，△ABC 中AC =BC ，点D ，E 在AB 边上，连接CD ，CE ．(1)如图1，如果∠ACB =90°，把线段CD 逆时针旋转90°，得到线段CF ，连接BF ， ①求证：△ACD ≌△BCF ；②若∠DCE =45°，求证：DE 2=AD 2+BE 2；(2)如图2，如果∠ACB =60°，∠DCE =30°，用等式表示AD ，DE ，BE 三条线段的数量关系，说明理由．23．如图，在ABC ∆中，90ACB ∠=︒，2BC AC =.(1)如图1，点D 在边BC 上，1CD =，5AD =ABD ∆的面积.(2)如图2，点F 在边AC 上，过点B 作BE BC ⊥，BE BC =，连结EF 交BC 于点M ，过点C 作CG EF ⊥，垂足为G ，连结BG .求证：2EG BG CG =+.24．我国古代数学家赵爽曾用图1证明了勾股定理，这个图形被称为“弦图”.2002年在北京召开的国际数学家大会(ICM 2002)的会标(图2)，其图案正是由“弦图”演变而来.“弦图”是由4个全等的直角三角形与一个小正方形组成，恰好拼成一个大正方形请你根据图1解答下列问题:(1)叙述勾股定理(用文字及符号语言叙述);(2)证明勾股定理;(3)若大正方形的面积是13,小正方形的面积是1,求()2a b +的值.25．定义：在△ABC 中，若BC ＝a ，AC ＝b ，AB ＝c ，若a ，b ，c 满足ac +a 2＝b 2，则称这个三角形为“类勾股三角形”，请根据以上定义解决下列问题：（1）命题“直角三角形都是类勾股三角形”是命题（填“真”或“假”）；（2）如图1，若等腰三角形ABC 是“类勾股三角形”，其中AB ＝BC ，AC ＞AB ，请求∠A 的度数；（3）如图2，在△ABC 中，∠B ＝2∠A ，且∠C ＞∠A ．①当∠A ＝32°时，你能把这个三角形分成两个等腰三角形吗？若能，请在图2中画出分割线，并标注被分割后的两个等腰三角形的顶角的度数；若不能，请说明理由； ②请证明△ABC 为“类勾股三角形”．26．如图1, △ABC 和△CDE 均为等腰三角形，AC=BC, CD=CE, AC>CD, ∠ACB=∠DCE=a ，且点A 、D 、E 在同一直线上，连结BE.(1)求证: AD=BE.(2)如图2,若a=90°，CM ⊥AE 于E.若CM=7, BE=10, 试求AB 的长.(3)如图3,若a=120°, CM ⊥AE 于E, BN ⊥AE 于N, BN=a, CM=b,直接写出AE 的值(用a, b 的代数式表示).27．如图，在平面直角坐标系中，点O 是坐标原点，ABC ∆，ADE ∆，AFO ∆均为等边三角形，A 在y 轴正半轴上，点0()6,B -，点(6,0)C ，点D 在ABC ∆内部，点E 在ABC ∆的外部，32=AD 30DOE ∠=︒，OF 与AB 交于点G ，连接DF ，DG ，DO ，OE .（1）求点A的坐标；（2）判断DF与OE的数量关系，并说明理由；的周长.（3）直接写出ADG28．已知：四边形ABCD是菱形，AB＝4，∠ABC＝60°，有一足够大的含60°角的直角三角尺的60°角的顶点与菱形ABCD的顶点A重合，两边分别射线CB、DC相交于点E、F，且∠EAP＝60°．（1）如图1，当点E是线段CB的中点时，请直接判断△AEF的形状是．（2）如图2，当点E是线段CB上任意一点时（点E不与B、C重合），求证：BE＝CF；（3）如图3，当点E在线段CB的延长线上，且∠EAB＝15°时，求点F到BC的距离．29．（已知：如图1，矩形OACB的顶点A，B的坐标分别是（6，0）、（0，10），点D 是y轴上一点且坐标为（0，2），点P从点A出发以每秒1个单位长度的速度沿线段AC﹣CB方向运动，到达点B时运动停止．（1）设点P运动时间为t，△BPD的面积为S，求S与t之间的函数关系式；（2）当点P运动到线段CB上时（如图2），将矩形OACB沿OP折叠，顶点B恰好落在边AC上点B′位置，求此时点P坐标；（3）在点P运动过程中，是否存在△BPD为等腰三角形的情况？若存在，求出点P坐标；若不存在，请说明理由．30．如图1，已知△ABC是等边三角形，点D，E分别在边BC，AC上，且CD＝AE，AD与BE相交于点F．（1）求证：∠ABE＝∠CAD；（2）如图2，以AD为边向左作等边△ADG，连接BG．ⅰ）试判断四边形AGBE的形状，并说明理由；ⅱ）若设BD＝1，DC＝k（0＜k＜1），求四边形AGBE与△ABC的周长比（用含k的代数式表示）．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】要求长方体中两点之间的最短路径，最直接的作法，就是将长方体展开，然后利用两点之间线段最短解答．【详解】解：根据题意，如图所示，最短路径有以下三种情况：（1）沿AA'，A C''，C B''，B B'剪开，得图1:22222AB AB BB'=+'=++=；(21)425（2）沿AC，CC'，C B''，B D''，D A''，A A'剪开，得图2:22222'=+'=++=+=；AB AC B C2(41)42529DD，B D''，C B''，C A''，AA'剪开，得图3:（3）沿AD，'22222'=+'=++=+=；AB AD B D1(42)13637综上所述，最短路径应为（1）所示，所以225AB '=，即5cm AB '=．故选：B ．【点睛】此题考查最短路径问题，将长方体从不同角度展开，是解决此类问题的关键，注意不要漏解．2．A解析：A【分析】先判断△DBE 是等腰直角三角形，根据勾股定理可推导得出BE ，故①正确；根据∠BHE 和∠C 都是∠HBE 的余角，可得∠BHE=∠C ，再由∠A=∠C ，可得②正确；证明△BEH ≌△DEC ，从而可得BH=CD ，再由AB=CD ，可得③正确；利用已知条件不能得到④，据此即可得到选项.【详解】解：∵∠DBC=45°，DE ⊥BC 于E ，∴在Rt △DBE 中，BE 2+DE 2=BD 2，BE=DE ，∴BE ，故①正确；∵DE ⊥BC ，BF ⊥DC ，∴∠BHE 和∠C 都是∠HBE 的余角，∴∠BHE=∠C ，又∵在▱ABCD 中，∠A=∠C ，∴∠A=∠BHE ，故②正确；在△BEH 和△DEC 中，BHE C HEB CED BE DE ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△BEH ≌△DEC ，∴BH=CD ，∵四边形ABCD 为平行四边形，∴AB=CD ，∴AB=BH ，故③正确；利用已知条件不能得到△BCF ≌△DCE ，故④错误，故选A.【点睛】本题考查了平行四边形的性质、等腰直角三角形的判定与性质、勾股定理、全等三角形的判定与性质等，熟练掌握相关性质与定理是解题的关键.3．C解析：C【分析】观察图形可知，小正方形的面积=大正方形的面积-4个直角三角形的面积，利用已知2()a b + =21，大正方形的面积为13，可以得以直角三角形的面积，进而求出答案。

中考数学考点大串讲(北师大版)：勾股定理必刷基础30题(解析版)

专题01勾股定理（基础30题3种题型）一、探索勾股定理1．（2023春·黑龙江佳木斯·八年级校考期中）在Rt ABC △中，90C ，12a ，16b ，则c 的长为（）A ．26B ．18C ．20D ．21【答案】C【分析】根据勾股定理222 a b c ，即可．【详解】∵在Rt ABC △中，90C ，12a ，16b ∴2222121620c a b 故选：C ．【点睛】本题考查勾股定理的知识，解题的关键是掌握勾股定理的运用．2．（2022秋·江苏扬州·八年级仪征市第三中学校考阶段练习）下列各组数中，是勾股数的为（）A ．1，2，3B ．4，5，6C ．6，8，10D ．7，8，9【答案】C【分析】根据勾股定理的逆定理分别进行分析，从而得到答案．【详解】解：A 、221236 ∵，这组数不是勾股数；B 、222456+¹Q ，这组数不是勾股数；C 、2226810 ∵，这组数是勾股数；D 、222789 ∵，这组数不是勾股数，故选：C ．【点睛】此题主要考查了勾股数的定义，解答此题要用到勾股定理的逆定理：已知三角形ABC 的三边满足222 a b c ，则ABC 是直角三角形．3．（2023春·河北廊坊·八年级廊坊市第四中学校考期中）如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A 、B 、C 、D 的边长分别是3、5、2、3，则正方形E 的面积是（）A ．47B ．37C ．34D ．13【答案】A 【分析】根据勾股定理：两条直角边的平方和等于斜边的平方，而正方形的面积等于边长的平方，故可得到以斜边为边长的正方形的面积等于两个以直角边为边长的面积之和．【详解】解：由勾股定理得：正方形F 的面积正方形A 的面积正方形B 的面积223534 ，同理，正方形G 的面积正方形C 的面积正方形D 的面积222313 ，∴正方形E 的面积正方形F 的面积正方形G 的面积341347 ．故选：A ．【点睛】此题考查的是勾股定理，掌握以直角三角形斜边为边长的正方形的面积等于两个以直角边为边长的正方形面积之和是解决此题的关键．4．（2023春·福建福州·八年级统考期中）在ABC 中，90C ，若3AB ，则222AB BC AC ．【答案】6【分析】利用勾股定理得222BC AC AB ，再代入计算即可．【详解】解：在ABC 中，90C ∵，222BC AC AB ，2222222(3)6AB BC AC AB ，故答案为：6．【点睛】本题主要考查了勾股定理，熟练掌握勾股定理解题的关键．5．（2023·北京丰台·二模）如图所示，正方形网格中，三个正方形A ，B ，C 的顶点都在格点上，用等式表示三个正方形的面积A B C S S S ，，之间的关系．【答案】A B CS S S 【分析】根据勾股定理以及正方形的面积公式即可得到结论．【详解】解：239A S ，2525B S ，正方形C 的边长为223534 ，∴ 23434C S ，∴A B C S S S ，，之间的关系为A B C S S S ，故答案为：A B C S S S ，【点睛】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．6．（2022秋·七年级单元测试）数组3、4、5；5、12、13；7、24、25；9、40、41；……都是勾股数，若n 为直角三角形的一较长直角边，用含n 的代数式表示斜边为．【答案】1n /1n【分析】首先确定各勾股数中的较长直角边、斜边，认真观察，总结规律，不难得出．【详解】解：因为3、4、5中较长直角边是4、斜边是541 ；5、12、13中较长直角边是12、斜边是13121 ；7、24、25中较长直角边是24、斜边是25241 ；9、40、41中较长直角边是40、斜边是41401 ；…∴若n 为直角三角形的一较长直角边，用含n 的代数式表示斜边为1n ．【点睛】此题考查勾股数之间的规律，认真观察是关键．7．（2023春·陕西安康·八年级统考期末）已知在ABC 中，906cm 2cm ACB AC BC ，，，求AB 的长．【答案】210cm【分析】利用勾股定理进行求解即可．【详解】解：∵在ABC 中，906cm 2cm ACB AC BC ，，，∴由勾股定理得222262210cm AB AC BC ．【点睛】本题主要考查了勾股定理，熟知勾股定理是解题的关键．8．（2023春·山东聊城·八年级统考期中）如图，某人从A 地到B 地共有三条路可选，第一条路是从A 地沿AB 到达B 地，AB 为10米，第二条路是从A 地沿折线AC CB 到达B 地，AC 为8米，BC 为6米，第三条路是从A 地沿折线AD DB 到达B 地共行走26米，若,,C B D 刚好在一条直线上．(1)求证：90C ；(2)求AD 和BD 的长．【答案】(1)见解析(2)AD 的长为17米，BD 的长为9米【分析】（1）通过计算得出222AC BC AB ，再根据勾股定理的逆定理即可证明．（2）先设一条线段长x ，根据已知条件及勾股定理可列出关于x 的方程，然后求解即可．【详解】（1）证明：∵8AC 米，6BC 米，10AB 米，∴222AC BC AB ，∴ABC 是直角三角形，即90C ；（2）解：设AD x 米，则 26BD x 米，∴ 62632CD BC BD x x （米），在Rt ACD 中，由勾股定理得：2228(32)x x ，解得：17x ，则2626179x ．答：AD 的长为17米，BD 的长为9米．【点睛】本题考查了勾股定理及其逆定理的应用，设未知数、运用方程解题是本题的关键所在．9．（2022秋·吉林长春·八年级统考期中）如图①、图②均为43 的正方形网格，每个小正方形的顶点称为格点，边长均为1．在图①、图②中按下列要求各画一个三角形．(1)与ABC 全等，以点B 为一个顶点，另外两个顶点也在格点上．(2)与ABC 全等，且不与ABC 重合．【答案】(1)见解析(2)见解析【分析】（1）根据题意画出符合题意的格点三角形即可；（2）根据题意画出对应的全等三角形即可．【详解】（1）解：如图①中，BCE 即为所求，（2）解：如图②所示，BFK 即为所求；【点睛】本题主要考查了画格点三角形，画全等三角形，正确理解题意是解题的关键．10．（2022春·黑龙江哈尔滨·八年级哈尔滨市虹桥初级中学校校考阶段练习）如图所示，在△ABC 中，CD ⊥AB 于D ，AC ＝4，BC ＝3，165AD ，求CD 、BD 的长．【答案】CD 的长为125，BD 的长为95【分析】在Rt △ACD 中，利用勾股定理列式求出CD ，在Rt △BCD 中，利用勾股定理列式计算即可求出BD ．【详解】解：∵CD ⊥AB ，∴∠ADC ＝∠BDC ＝90°，∴△ADC 和△BDC 是直角三角形，在Rt △ACD 中，222AC AD CD ，∴22221612455CD AC AD ，在Rt △BCD 中，222BC CD BD ，∴2222129355BD BC CD ，答：CD 的长为125，BD 的长为95．【点睛】本题考查了勾股定理，根据图形判断出所求的边所在的直角三角形是解题的关键．11．（2023·山西忻州·统考模拟预测）如图是3世纪我国汉代的赵爽在注解《周髀算经》时给出的“赵爽弦图”．他通过对图形的切割、拼接，巧妙地利用面积关系证明的重要数学定理是（）A ．三角形内角和定理B ．勾股定理C ．勾股定理的逆定理D ．斜边、直角边定理【答案】B 【分析】“赵爽弦图”通过对图形的切割、拼接，巧妙地利用面积关系证明了勾股定理．【详解】解：由勾股定理相关的数学背景可知：“赵爽弦图”是对勾股定理的验证故选：B【点睛】本题考查了勾股定理的数学背景．熟知相关数学史即可．12．（2023春·山西吕梁·八年级统考期末）如图，毕达哥拉斯用图1，图2证明了．个重要的数学定理，他的思路是图1中拼成的正方形与图2中拼成的正方形面积相等，通过面积相等可以得到：222114422a b ab c ab ，整理得222 a b c ．证明的这个定理是（）A ．勾股定理B ．勾股定理的逆定理C ．祖暅原理D ．费马定理【答案】A 【分析】根据勾股定理作答即可．【详解】解：由222114422a b ab c ab ，整理得222 a b c ．而a 、b 、c 是直角三角形的三边，∴证明的定理是勾股定理，故选：A ．【点睛】本题主要考查了勾股定理，熟记勾股定理的内容是解题的关键．13．（2023春·河南驻马店·八年级统考期中）我国是最早了解勾股定理的国家之一．早在三千多年前，周朝数学家商高就提出，将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于下列哪部著名数学著作中（）A ．《周髀算经》B ．《九章算术》C ．《海岛算经》D ．《几何原本》【答案】A【分析】加强教材的阅读，熟记相关知识的来源与出处．【详解】解：早在三千多年前，我国周朝数学家商高就提出：将一根直尺折成一个直角，如果勾等于三，股等于四，那么弦就等于五，即“勾三、股四、弦五”．它被记载于我国古代著名数学著作《周髀算经》中．故选：A ．【点睛】本题考查了勾股定理的历史渊源，仔细阅读教材，熟记知识是解题的关键．14．（2023春·黑龙江绥化·八年级校考期中）如下图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7cm ，则正方形A ，B ，C ，D 的面积之和为2cm .【答案】49【分析】根据勾股定理计算即可【详解】解：最大的正方形的面积为22749cm ，由勾股定理得，正方形E 、F 的面积之和为249cm ，∴正方形A 、B 、C 、D 的面积之和为249cm ，故答案为49．【点睛】本题考查的是勾股定理，如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么222 a b c ．15．（2023秋·全国·八年级专题练习）公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”，它是由四个全等的直角三角形和一个小正方形密铺构成的大正方形.如图，设勾3a ，弦5c ，则小正方形ABCD 的边长．．是.【分析】根据勾股定理计算即可解题．【详解】解：根据勾股定理可得2222534b c a ，∴小正方形ABCD 的边长为431 ，故答案为：1．【点睛】本题考查勾股定理，掌握勾股定理是解题的关键．16．（2023春·湖北宜昌·八年级校考期中）如图，数轴上点A 所表示的数为a ，求 a ．【答案】15 /51【分析】根据勾股定理算出斜边长度解题即可，注意是从-1开始．【详解】解：如图，由勾股定理得221115BC CA ．∵点C 表示-1，∴点A 表示的数是15a ．故答案为：15 ．【点睛】本题主要考查了数轴的意义和勾股定理，理解数轴的意义的是解答关键．17．（2023秋·全国·八年级专题练习）如图，将两个全等的直角三角形按照如下的位置摆放，使点A ，E ，D 在同一条直线上，90A D ，AE CD a ，AB ED b ，BE CE c ．(1)填空：BEC ______ ，根据三角形面积公式，可得BEC 的面积 ______；根据割补法，由梯形的面积减去阴影部分的面积，可得BEC 的面积 ______．(2)求证：222 a b c ．【答案】(1)90，212c ，212c【分析】（1）根据全等三角形的判定和性质以及三角形的面积公式即可得到结论；（2）用两种不同的方法表示梯形ABCD 的面积，计算化简后，即可得出222 a b c ．【详解】（1）解：AE CD a ∵，AB ED b ，BE CE c ，BAE ≌ SSS EDC ，ABE DEC ，90ABE AEB ∵，90AEB DEC ，90BEC ，BEC 的面积21122BE CE c，由梯形的面积减去阴影部分的面积，可得BEC 的面积22222111112222222a b a b ab a ab b ab a b ab ab c ，故答案为：90，212c ，212c ；（2）证明：Rt ABE ∵ ≌Rt DEC △，AEB DCE ，BE EC c ，90D ∵，90DCE DEC ，90AEB DEC ，90BEC ，BEC 是等腰直角三角形，Rt ABE Rt CDE Rt BEC ABCD S S S S ∵梯形，2222AB CD AD AE AB ED DC BE EC，即2222a b a b ab ba ca ，2222222a ab bc ab ，222a b c ．【点睛】本题考查了梯形，勾股定理的证明，用两种不同的方法表示同一个图形的面积是解决问题的关键．18．（2021秋·黑龙江绥化·八年级校考阶段练习）已知某开发区有一块四边形空地ABCD ，如图所示，现计划在空地上种植草皮，经测量∠A =90°，∠CBD =90°，DB =5m ，CD =13m ，DA =4m ，若每平方米草皮需要200元，问需要多少投入【答案】需要投入资金为7200元【分析】仔细分析题目，需要求得四边形的面积才能求得结果，连接BD，在直角三角形CBD中由勾股定理可求BC的长，在直角三角形ABD中可求得BA的长，由此看，四边形ABCD由Rt△ABD和Rt△DBC 构成，则容易求解．【详解】证明：连接BD∵∠A=90°，∠CBD=90°，∴△CBD，△ABD为直角三角形，在Rt△CBD中，BC2=CD2-BD2∴222213512BC CD BDm在△ABD中，AB2=BD2-AD2∴AB=2222543BD ADm∴四边形ABCD面积=S△BAD十S∆DBC=12∙AD∙AB+12∙DB∙BC=1143+512=6+30=3622m2，36×200=7200（元）所以需要投入资金为7200元．【点睛】此题主要考查了勾股定理的应用，得出△CBD，△ABD为直角三角形，用勾股定理求出BC，AB 的长是解题的关键．19．（2022春·八年级单元测试）洋洋想知道学校旗杆的高度，他发现旗杆顶端的绳子垂到地面还多2米，当他把绳子的下端拉开5米后，发现下端刚好接触地面，求旗杆的高度．【答案】214米【分析】因为旗杆、绳子、地面正好构成直角三角形，设旗杆的高度为x米，则绳子的长度为（x+2）米，根据勾股定理即可求得旗杆的高度．【详解】解：设旗杆的高度为x米，则绳子的长度为（x+2）米，根据勾股定理可得：x2+52=（x+2）2，解得，x=21 4．答：旗杆的高度为214米．【点睛】此题考查学生利用勾股定理解决实际问题的能力，关键是利用勾股定理即可求得AB的长．20．（2022秋·全国·八年级专题练习）如图，请在数轴上找到表示17的P点．（保留作图痕迹，不写作法）【答案】见解析【分析】因为17＝16＋1，则首先作出以1和4为直角边的直角三角形，则其斜边的长即是17，再以原点为圆心，以17为半径画弧，和数轴的正半轴交于一点即可．【详解】解：如图，点P即为所求．【点睛】本题考查运用数轴上的点来表示一个无理数，比较基础．21．（2023春·重庆忠县·八年级统考期末）把5米长的梯子斜靠在墙上，若梯子底端离墙4米，则梯子顶端到离地面（）A．2米B．3米C．4米D．4.5米【答案】B【分析】根据勾股定理求解即可．【详解】解：∵梯子的长度为5米，梯子底端离地面4米，将梯子长度看作直角三角形的斜边，梯子底端离地面距离看作一条直角边，梯子顶端到地面的距离为：22543 （米），故选B ．【点睛】本题考查勾股定理的实际应用，理解题意将实际问题转化为数字问题是解题的关键．22．（2023·浙江·八年级假期作业）如图，垂直地面的旗杆在离地3m 处断裂，旗杆顶部落地点离旗杆底部4m ，则旗杆折断前的高度为（）A ．6B ．7C ．8D ．9【答案】C 【分析】根据勾股定理两个直角边的平方和等于斜边的平方．此题要求斜边和直角边的长度，解直角三角形即可．【详解】解：旗杆折断后，落地点与旗杆底部的距离为4m ，旗杆离地面3m 折断，且旗杆与地面是垂直的，所以折断的旗杆与地面形成了一个直角三角形．根据勾股定理，折断的旗杆为 22345m ，所以旗杆折断之前高度为3m 5m 8m ．故选：C ．【点睛】本题考查了勾股定理在解实际问题中的运用，弄清勾股定理存在的条件是重点，解题的关键是理解文字语言的含义．23．（2023秋·八年级课前预习）如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离BC 为0.7m ，梯子顶端到地面的距离AC 为2.4m ．如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A D 为1.5m ，则小巷的宽为（）．A ．2.4mB ．2mC ．2.5mD ．2.7m【答案】D【分析】,ACB A BD △△是直角三角形，根据勾股定理即可求解．【详解】解：根据题意可知，,ACB A BD △△是直角三角形，在Rt ABC △中， 2.4AC ，0.7BC ，∴22222(2.4)(0.7) 5.760.49 6.25AB AC BC ， 2.5AB ，在Rt A BD 中， 2.5A B AB ， 1.5A D ，则2 2.25A D ，∴22 6.25 2.252BD A B A D，∴小巷的宽为0.72 2.7m CB BD ，故选：D ．【点睛】本题主要考查勾股定理的运用，掌握勾股定理的运算方法是解题的关键．24．（2023秋·八年级课前预习）如图，一个圆桶底面直径为5cm ，高12cm ，则桶内所能容下的最长木棒为cm ．【答案】13【分析】根据题意画出示意图，再根据勾股定理求解，即可．【详解】解：如图，AC 为圆桶底面直径，BC 为圆桶的高，∵5cm AC ，12cm BC ，∴2222512=13cm AB AC BC ，∴桶内所能容下的最长木棒为：13cm ．故答案为：13．【点睛】本题考查勾股定理的运用，解题的关键是将实际问题转化为数学问题，灵活运用勾股定理．25．（2023春·新疆乌鲁木齐·八年级校考期中）已知，一轮船以4海里/时的速度从港口A 出发向东北方向航行，另一轮船以3海里/时的速度同时从港口A 出发向东南方向航行，离开港口2小时后，两船相距海里．【答案】10【分析】根据方位角可知两船所走的方向正好构成了直角，然后根据路程=速度×时间，得两条船分别走了8海里和6海里，再根据勾股定理，即可求得两条船之间的距离．【详解】解：∵两船行驶的方向是东北方向和东南方向，∴90BAC ，两小时后，两艘船分别行驶了428 ，326 海里，根据勾股定理得：228610 （海里）．故答案为：10．【点睛】本题考查了勾股定理的应用，熟练运用勾股定理进行计算，基础知识，比较简单．26．（2023秋·全国·八年级专题练习）如图，台阶A 处的蚂蚁要爬到B 处搬运食物，则它爬行的最短距离为．【答案】13m/13米【分析】先将图形平面展开，再用勾股定理根据两点之间线段最短进行解答．【详解】解：如图所示，台阶平面展开图为长方形，5AC ，9312BC ，则蚂蚁沿台阶面爬行到B 点最短路程是此长方形的对角线长．由勾股定理得：222AB AC BC ，13AB ，故答案为：13m ．【点睛】本题主要考查了平面展开图—最短路径问题，用到台阶的平面展开图，只要根据题意判断出长方形的长和宽即可解答．27．（2023秋·全国·八年级专题练习）已知一架5m 长的梯子斜靠在一竖直的墙上，这时梯足距墙脚3m ，若梯子的顶端下滑1m ，则梯足将滑动多远？【答案】1米【分析】根据勾股定理求解即可．【详解】解：在直角三角形ABO 中，根据勾股定理可得，22534m OA ，如果梯子的顶度端下滑1米，则413m OA ．在直角三角形A B O 中，根据勾股定理得到：4m OB ，则梯子滑动的距离就是431m OB OB ．【点睛】本题考查的知识点是勾股定理的应用，掌握勾股定理是解题的关键．28．（2023春·河北廊坊·八年级统考期末）《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根三尺．问折高者几何？意思是：一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，其竹稍恰好抵地，抵地处离竹子底部3尺远，问折断处离地面的高度是多少？【答案】9120尺【分析】设折断处离地的高度为x 尺，利用勾股定理建立方程，解方程即可得．【详解】解：设折断处离地的高度为x 尺，由勾股定理得： 222310x x ，解得9120 x ，答：折断处离地的高度为9120尺．【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理是解题关键．29．（2023秋·全国·八年级专题练习）如图，点O是位于东西海岸线的一个港口，A，B两艘客轮从港口O 同时出发，A客轮沿北偏东75°航行，航速是每小时18海里，B客轮沿北偏西15°方向航行，航速是每小时24海里，请计算3小时之后两客轮之间的距离．【答案】90海里【分析】根据题意得：∠AOB=75°+15°=90°，OA=18×3=54（海里），OB=24×3=72（海里），再由勾股定理，即可求解．【详解】解：根据题意得：∠AOB=75°+15°=90°，OA=18×3=54（海里），OB=24×3=72（海里），根据勾股定理得：2222547290AB AO BO海里，即3小时之后两客轮之间的距离90海里．【点睛】本题主要考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．30．（2023秋·全国·八年级专题练习）如图是一个棱长为6cm的正方体的有盖纸盒，一只蚂蚁想从盒底的A 点爬到盒顶的B点，其中BC＝2cm，那么蚂蚁爬行的最短行程是多少？【答案】10cm【分析】将正方体侧面展开图展开，由勾股定理计算即可．【详解】解：如图所示．∵BC＝2cm，棱长为6cm，∴AD＝6+2＝8（cm），BD＝6cm由勾股定理得，AB＝2222＝10（cm），BD AD86答：蚂蚁爬行的最短行程是10cm．【点睛】此题考查了平面展开一最短路径问题，利用勾股定理是解题的关键．。

专题01 勾股定理的基本应用(解析版)

专题01 勾股定理的基本应用题型一求面积1．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设“赵爽弦图”中直角三角形较长直角边长为a ，较短直角边长为b ，若2()24a b +=，大正方形的面积为14，则小正方形的面积为( )A ．2B ．3C ．4D ．5【解答】解：设大正方形的边长为c ，则22214c a b ==+，2()24a b +=Q ，22224a ab b \++=，解得5ab =，\小正方形的面积是：1441425141042ab -´=-´=-=，故选：C ．2．如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A 、B 、D 的面积依次为6、10、24，则正方形C 的面积为( )A ．4B ．6C ．8D ．12【解答】解：由题意：A B E S S S +=正方形正方形正方形，D C E S S S -=正方形正方形正方形，A B D CS S S S \+=-正方形正方形正方形正方形Q 正方形A 、B 、D 的面积依次为6、10、24，24610C S \-=+正方形，8C S \=正方形．故选：C ．3．如图，点C 是线段AB 上的一点，分别以AC 、BC 为边向两侧作正方形．设6AB =，两个正方形的面积和1220S S +=，则图中BCD D 的面积为( )A ．4B ．6C ．8D ．10【解答】解：设AC a =，BC b =，由题意得：6a b +=，2220a b +=，222()2a b a b ab +=+-Q ，22062ab \=-，8ab \=，BCD \D 的面积118422ab ==´=．图中BCD D 的面积为4．故选：A ．4．正方形ABCD 的边长为1，其面积记为1S ，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积记为2S ，L 按此规律继续下去，则2022S 的值为( )A ．20221()2B ．20211()2C ．2022D ．2021【解答】解：在图中标上字母E ，如图所示．Q 正方形ABCD 的边长为1，CDE D 为等腰直角三角形，222DE CE CD \+=，DE CE =，221S S S \+=．观察，发现规律：2111S ==，211122S S ==，321124S S ==，431128S S ==，¼，11()2n n S -\=．当2022n =时，202212021202211()()22S -==，故选：B ．5．如图，以正方形ABCD 的边AD 为直径作一个半圆，点M 是半圆上一个动点，分别以线段AM 、DM 为边各自向外作一个正方形，其面积分别为1S 和2S ，若正方形的面积为10，随点M 的运动12S S +的值为( )A ．大于10B ．小于10C ．等于10D ．不确定【解答】解：AB Q 为半圆的直径，90AMD \Ð=°，22210AM DM AD \+==，21S AM =Q ，22S DM =，1210S S \+=．故选：C ．6．如图，在四边形ABDE 中，//AB DE ，AB BD ^，点C 是边BD 上一点，BC DE a ==，CD AB b ==，AC CE c ==．下列结论：①ABC CDE D @D ；②90ACE Ð=°；③四边形ABDE 的面积是21()2a b +；④22111()2222a b c ab +-=´；⑤该图可以验证勾股定理．其中正确的结论个数是( )A ．5B ．4C ．3D ．2【解答】解：//AB DE Q ，AB BD ^，DE BD \^，90B D \Ð=Ð=°．在ABC D 和CDE D 中，90AB CD B D BC DE =ìïÐ=Ð=°íï=î，()ABC CDE SAS \D @D，A DCE \Ð=Ð，ACB E Ð=Ð．90A ACB Ð+Ð=°Q ，90DCE ACB \Ð+Ð=°．180DCE ACB ACE Ð+Ð+Ð=°Q ，90ACE \Ð=°，故①②正确；//AB DE Q ，AB BD ^，\四边形ABDE 的面积是21()2a b +；故③正确；Q 梯形ABDE 的面积-直角三角形ACE 的面积=两个直角三角形的面积，\22111()2222a b c ab +-=´，222a b c \+=．故③④⑤都正确．故选：A ．7．如图，Rt ABC D 中，90C Ð=°，AD 平分BAC Ð，交BC 于点D ，6CD =，12AB =，则ABD D 的面积是( )A ．18B ．24C ．36D ．72【解答】解：作DH AB ^于D ，如图，AD Q 平分BAC Ð，DH AB ^，DC AC ^，6DH DC \==，1126362ABD S D \=´´=．故选：C ．8．如图，Rt ABC D 中，90C Ð=°，5AC =，12BC =，分别以AB 、AC 、BC 为边在AB 的同侧作正方形ABEF 、ACPQ 、BCMN ，四块阴影部分的面积分别为1S 、2S 、3S 、4S ，则1234S S S S +++等于( )A ．60B ．80C ．90D ．120【解答】解：连接PF ，过点F 作FD AK ^于点D ，AB EB =Q ，90ACB ENB Ð=Ð=°，而90CBA CBE EBN CBE Ð+Ð=Ð+Ð=°，CBA EBN \Ð=Ð，()CBA NBE AAS \D @D ，故4ABC S S D =；同理ADF ABC D @D ，AC DF AQ CP \===，90QAC KDF PCD Ð=Ð=Ð=°Q ，//AQ DF \，\四边形CDFP 是矩形，90CPF \Ð=°，180QPC CPF \Ð+Ð=°，Q \，P ，F 三点共线，又FA AB =Q ，90FDA ACB Ð=Ð=°，而90FAD CAB CAB ABC Ð+Ð=Ð+Ð=°，FAD ABC \Ð=Ð，()FAD ABC AAS \D @D ，同理可证ACT FDK D @D ，2FDA ABC S S S D D \==，同理可证TPF KME D @D ，AQF ABC D @D ，13ADF ABC S S S S D D \+==，综上所证：1234133125902ABC S S S S S D +++==´´´=．故选：C ．9．如图，直线l 上有三个正方形a ，b ，c ，若a ，c 的面积分别为4和10，则b 的面积为　14　．【解答】解：如图，a Q 、b 、c 都为正方形，BC BF \=，90CBF Ð=°，24AC =，210DF =，1290Ð+Ð=°Q ，2390Ð+Ð=°，13\Ð=Ð，在ABC D 和DFB D 中，13BAC FDB BC FB Ð=ÐìïÐ=Ðíï=î，ABC DFB \D @D ，AB DF \=，在ABC D 中，2222241014BC AC AB AC DF =+=+=+=，b \的面积为14．故答案为14．10．勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，90BAC Ð=°，3AB =，4AC =，点D ，E ，F ，G ，H ，I 都在矩形KLMJ 的边上，则空白部分的面积为 60　．【解答】解：如图，延长AB 交KF 于点O ，延长AC 交GM 于点P ，所以，四边形AOLP 是正方形，90BAC Ð=°Q ，3AB =，4AC =，347AO AB AC \=+=+=，3710KL \=+=，4711LM =+=，因此，矩形KLMJ 的面积为1011110´=，\空白部分的面积为22211034560---=，故答案为：60．11．我国古代著作《周髀算经》中记载了“赵爽弦图”．如图，若勾6AE =，弦10AD =，则小正方形EFGH 的面积是　4　．【解答】解：如图，Q 勾6AE =，弦AD =弦10AB =，\股8BE ==，\小正方形的边长862=-=，\小正方形的面积224==．故答案是：4．12．如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A 、C 、D 的面积依次为4、6、18，则正方形B 的面积为　8　．【解答】解：由题意：A B E S S S +=正方形正方形正方形，D C E S S S -=正方形正方形正方形，A B D CS S S S \+=-正方形正方形正方形正方形Q 正方形A 、C 、D 的面积依次为4、6、18，4186B S \+=-正方形，8B S \=正方形．故答案为：8．13．如图，在同一平面内，直线l 同侧有三个正方形A ，B ，C ，若A ，C 的面积分别为9和4，则阴影部分的总面积为 6　．【解答】解：如图，作LM FE ^交FE 的延长线于点M ，交JI 的延长线于点N ，Q 四边形A 、B 、C 都是正方形，且正方形A 、C 的面积分别为9、4，90EKI EDR IHG \Ð=Ð=Ð=°，29DE =，24HI =，3DE \=，2HI =，1809090EDK KHI Ð=Ð=°-°=°Q ，90DKE KHI HIK \Ð=°-Ð=Ð，在EDK D 和KHI D 中，EDK KHI DKE HIK EK KI Ð=ÐìïÐ=Ðíï=î，()EDK KHI AAS \D @D ，2DK HI \==，3DE HK ==，13232EDK KHI S S D D \==´´=；90DEF HIJ Ð=Ð=°Q ，18090DEM DEF \Ð=°-Ð=°，18090HIN HIJ Ð=°-Ð=°，90KEL KIL Ð=Ð=°Q，90MEL DEK KEM \Ð=Ð=°-Ð，90NIL HIK KIN Ð=Ð=°-Ð，//EF l Q ，//IJ l ，//EF IJ \，90EML EMN N \Ð=Ð=Ð=°，在EML D 和EDK D 中，MIL DEK EML EDK EL EK Ð=ÐìïÐ=Ðíï=î，()EML EDK AAS \D @D ，EM ED EF \==，3EFL EML EDK S S S D D D \===；在LNI D 和KHI D 中，NIL HIK N KHI IL IK Ð=ÐìïÐ=Ðíï=î，()LNI KHI AAS \D @D ，IN IE IJ ==Q ，3LJI LNI KHI S S S D D D \===，336EFL LJI S S D D \+=+=，\阴影部分的总面积为6．14．如图，正方形ABDE 、CDFI 、EFGH 的面积分别为25、9、16，AEH D 、BDC D 、GFI D 的面积分别为1S 、2S 、3S ，则123S S S ++=　18　．【解答】解：DF DC =Q ，DE DB =，且180EDF BDC Ð+Ð=°，过点A 作AJ EH ^，交HE 的延长线于点J ，90J DFE \Ð=Ð=°，90AEJ DEJ DEJ DEF Ð+Ð=Ð+Ð=°Q ，AEJ DEF \Ð=Ð，AE DE =Q ，()AEJ DEF AAS \D @D ，AJ DF \=，EH EF =Q ，AHE DEF S S D D \=，同理：BDC GFI DEF S S S D D D ==，1233AHE BDC GFI DEF S S S S S S S D D D D ++=++=´，13462DEF S D =´´=，12318S S S \++=．故答案为：18．题型二求线段长15．一个大正方形，被两条线段分割成两个小正方形和两个小长方形，若两个小正方形的面积分别为10和6，则小长方形的对角线AB 的长为( )A ．4B ．6C ．10D ．16【解答】解：如图，Q 两个小正方形的面积分别为10和6，26AC \=，210BC =，由勾股定理得，4AB ===．故选：A ．16．如图，在Rt ABC D 中，90ABC Ð=°，以AB 为边在ABC D 外作正方形，其面积为9，以BC 为斜边在ABC D 外作等腰直角三角形，其面积为4，过点B 作BD AC ^交AC 于点D ，则(AD = )A ．85B ．94C ．95D ．2【解答】解：Q 以AB 为边的正方形的面积为9，29AB \=，Q 以BC 为斜边的等腰直角三角形的面积为4，\等腰直角三角形的腰长为216BC \=，在Rt ABC D 中，90ABC Ð=°，则5AC ===，1122ABC S AB AC AC BD D =´´=´´Q ，\1134522BD ´´=´´，解得：125BD =，由勾股定理得：95AD ===，故选：C ．17．如图，在Rt ABC D 中，90ACB Ð=°，CD AB ^于D ．已知15AB =，Rt ABC D 的周长为15+，则CD 的长为( )A ．5BC ．D ．6【解答】解：如图所示：Rt ABC D Q 的周长为15+，90ACB Ð=°，15AB =，AC BC \+=，222215225AC BC AB +===，22()AC BC \+=，即222405AC AC BC BC +´+=，2405225180AC BC \´=-=，90AC BC \´=，Q 1122AB CD AC BC ´=´，90615AC BC CD AB ´\===；故选：D ．18．若ABC=，高24=，则BC的长为( )cm．AD cmAC cmD中，30AB cm=，26A．28或8B．8C．28D．以上都不对Q为边BC上的高，【解答】解：AD\Ð=Ð=°．90ADB ADCBD===，在Rt ABDD中，18CD===．在Rt ACDD中，10当点D在线段BC上时，如图1，181028=+=+=；BC BD CD当点D在线段CB的延长线上时，如图2，18108=-=-=．BC BD CD\的长为28或8．BC故选：A．19．如图，在ABCBC=，6AB=，4AC=，则DE的^于D，且5D中，CE是AB边上的中线，CD AB长　2　．【解答】解：设BD x=-，=，则5AD x在Rt ACD D 中，222CD AC AD =-，在Rt BCD D 中，222CD BC BD =-，2222AC AD BC BD \-=-，即22226(5)4x x --=-，解得，12x =，则12BD =，2DE BE BD \=-=，贵答案为：2．20．如图，锐角三角形ABC 中，2C B Ð=Ð，AB =，8BC CA +=，则ABC D 的面积为　【解答】解：过A 作AE BC ^于E ，延长BC 到D 使CD AC =，则CAD D Ð=Ð，ACB D CAD Ð=Ð+ÐQ ，2ACB D \Ð=Ð，2C B Ð=ÐQ ，B D \Ð=Ð，AB AD \=，BE DE \=，8BC CA +=Q ，8BD BC CD BC AC \=+=+=，4BE \=，AE \==，222AE CE AC \+=，即228(4)(8)BC BC +-=-，解得：5BC =，ABC \D 的面积11522BC AE ==´´=g故答案为：．21．如图所示，ABC D 的顶点A 、B 、C 在边长为1的正方形网格的格点上，BD AC ^于点D ，则BD 的长为　3　．【解答】解：由图形可知，5BC =，BC 边上的高为3，ABC \D 的面积1155322=´´=，由勾股定理得，5AC ==，则115522BD ´´=，解得，3BD =，故答案为：3．22．如图，在Rt ABC D 中，90B Ð=°，3AB =，6BC =，AC 的中垂线DE 交AC 于点D ，交BC 于点E ．延长DE 交AB 的延长线于点F ，连接CF ．（1）求出CD 的长；（2）求出CF 的长．【解答】解：（1）在Rt ABC D 中，90B Ð=°，3AB =，6BC =，则AC ===，DE Q 是AC 的中垂线，12CD AC \==（2）DF Q 是AC 的中垂线，FA FC \=，3AB =Q ，33FB FA CF \=-=-，在Rt FBC D 中，222CF BC FB =+，即2226(3)CF CF =+-，解得：152CF =．23．如图，在ABC D 中，AB AC =，AD BC ^于点D ，45CBE Ð=°，BE 分别交AC ，AD 于点E 、F ．（1）如图1，若13AB =，10BC =，求AF 的长度；（2）如图2，若AF BC =，求证：222BF EF AE +=．【解答】（1）解：如图1，AB AC =Q ，AD BC ^，BD CD \=，10BC =Q ，5BD \=，Rt ABD D 中，13AB =Q ，12AD \==，Rt BDF D 中，45CBE Ð=°Q ，BDF \D 是等腰直角三角形，5DF BD \==，1257AF AD DF \=-=-=；（2）证明：如图2，在BF 上取一点H ，使BH EF =，连接CF 、CH 在CHB D 和AEF D 中，Q 45BH EFCBH AFE BC AF=ìïÐ=Ð=°íï=î，()CHB AEF SAS \D @D ，AE CH \=，AEF BHC Ð=Ð，CEF CHE \Ð=Ð，CE CH \=，BD CD =Q ，FD BC ^，CF BF \=，45CFD BFD \Ð=Ð=°，90CFB \Ð=°，EF FH \=，Rt CFH D 中，由勾股定理得：222CF FH CH +=，222BF EF AE \+=．24．如图，在ABC D 中，AD BC ^，垂足为点D ，13AB =，5BD =，15AC =．（1）求AD 的长；（2）求BC的长．【解答】解：（1）AD BC ^Q ，90ADB CDA \Ð=Ð=°．在Rt ADB D 中，90ADB Ð=°Q ，222AD BD AB \+=，222144AD AB BD \=-=．0AD >Q ，12AD \=．（2）在Rt ADC D 中，90CDA Ð=°Q ，222AD CD AC \+=，22281CD AC AD \=-=．0CD >Q ，9CD \=．5914BC BD CD \=+=+=．题型三通过勾股定理设方程25．如图，四个全等的直角三角形围成正方形ABCD 和正方形EFGH ，即赵爽弦图．连接AC ，分别交EF 、GH 于点M ，N ，连接FN ．已知3AH DH =，且21ABCD S =正方形，则图中阴影部分的面积之和为( )A ．214B ．215C ．225D ．223【解答】解：21ABCD S =Q 正方形，221AB \=，设DH x =，则33AH DH x ==，22921x x \+=，22110x \=，根据题意可知：AE CG DH x ===，3CF AH x ==，32FE FG CF CG x x x \==-=-=，2FGN CGNS S D D \=AEM CGN S S D D =Q ，FGN AEM CGN S S S D D D \=+，\阴影部分的面积之和为：()12NGFM S NG FM FG =+×梯形1()2EM MF FG =+×12FE FG =×21(2)2x =´22x =215=．故选：B ．26．如图，在ABC D 中，90C Ð=°，点M 是AB 的中点，点N 在AC 上，MN AB ^．若8AC =，4BC =，则NC 的长为( )A ．3B ．4C ．5D ．【解答】解：如图，连接BN ，AB Q 的垂直平分线交AB 、AC 于点M 、N ，AN BN \=，设NC x =，则8AN BN x ==-，在Rt BCN D 中，由勾股定理得：222BN BC CN =+，即222(8)4x x -=+，解得：3x =，即3NC =，故选：A ．27．如图，由四个全等的直角三角形拼成的图形，设CE a =，HG b =，则斜边BD 的长是()A B C ．a b +D ．a b-【解答】解：设CD x =，则DE a x =-，HG b =Q ，AH CD AG HG DE HG a x b x \==-=-=--=，2a bx -\=，22a b a bBC DE a -+\==-=，2222222()()222a b a b a b BD BC CD +-+\=+=+=，BD \=，故选：B ．28．在长方形ABCD 中，52AB =，4BC =，CE CF =，延长AB 至点E ，连接CE ，CF 平分ECD Ð，则BE =　76　．【解答】解：如图，延长CF ，BA 交于点G ，连接EF ，过点F 作FH CE ^于H ，过点E 作EM CF ^于M ，Q 四边形ABCD 是矩形，且52AB =，4BC =，//AB CD \，52AB CD ==，90D ABC CBE Ð=Ð=Ð=°，DCF G \Ð=Ð，CF Q 平分ECD Ð，DCF FCE \Ð=Ð，FH DF =，G ECF \Ð=Ð，EC EG \=，ECG \D 是等腰三角形，CM MG \=，CE CF =Q ，ECF \D 是等腰三角形，EM CF ^Q ，FH CE ^，EM \和FH 是等腰三角形腰上的高，EM FH DF \==，Rt CDF Rt CME(HL)\D @D ，52CM CD \==，5CG \=，Rt CBG D 中，3BG ===，设BE x =，则3EC EG x ==+，Rt CBE D 中，222(3)4x x +=+，解得：76x =，76BE \=．故答案为：76．29．如图是“赵爽弦图”， ABH D ，BCG D ，CDF D 和DAE D 是四个全等的直角三角形，四边形ABCD 和EFGH 都是正方形，如果10AB =，且:3:4AH AE =．那么AH 等于　6　．【解答】解：10AB =Q ，:3:4AH AE =，设AH 为3x ，AE 为4x ，由勾股定理得：222222(3)(4)(5)AB AH AE x x x =+=+=，510x \=，2x \=，6AH \=，故答案为：6．30．[阅读理解]如图，在ABC D 中，4AB =，6AC =，7BC =，过点A 作直线BC 的垂线，垂足为D ，求线段AD 的长．解：设BD x =，则7CD x =-．AD BC ^Q ，90ADB ADC \Ð=Ð=°．在Rt ABD D 中，222AD AB BD =-，在Rt ACD D 中，222AD AC CD =-，2222AB BD AC CD \-=-．又4AB =Q ，6AC =，222246(7)x x \-=--．解得2914x =，2914BD \=．AD \==．[知识迁移]（1）在ABC D 中，13AB =，15AC =，过点A 作直线BC 的垂线，垂足为D ．)i 如图1，若14BC =，求线段AD 的长；)ii 若12AD =，求线段BC 的长．（2）如图2，在ABC D 中，AB =，AC =，过点A 作直线BC 的垂线，交线段BC 于点D ，将ABD D 沿直线AB 翻折后得到对应的ABD D ¢，连接CD ¢，若252AD =，求线段CD ¢的长．【解答】解：（1）)i 设BD x =，则14CD x =-，AD BC ^Q ，90ADB ADC \Ð=Ð=°，在Rt ABD D 中，222AD AB BD =-，在Rt ACD D 中，222AD AC CD =-，2222AB BD AC CD \-=-，13AB =Q ，15AC =，22221315(14)x x \-=--，5x \=，5BD \=，12AD \===；)ii 在Rt ABD D 中，5BD ===，在Rt ACD D 中，9CD ===，当ABC Ð为锐角时，如图11-，5914BC BD CD =+=+=，当ABC Ð为钝角时，如图12-，954BC BD CD =-=-=；（2）如图2，连接DD ¢交AB 于点N ，则DD AB ¢^，过点D ¢作D H BD ¢^于H ，在Rt ABD D 中，254BD ==；在Rt ACD D 中，5CD ==，AB Q 垂直平分DD ¢，254D B DB ¢\==，2D D DN ¢=，1122ABD S AD BD AB DN D =×=×Q ，\252524DN ´=，DN \=2D D DN ¢\==，设HB m =，则254HD HB BD m =+=+，22222D H D D HD D B HB ¢¢¢=-=-Q ，22222525(()44m m \-+=-，154m \=，154HB \=，152541544HC HB BD CD \=++=++=，5D H ¢===，D C ¢\===．。

专题01 用勾股定理解三角形(解析版)

专题01 用勾股定理解三角形一、单选题1．如图，在ABC 中，90C ∠=︒，13AB =，5AC =，D 、E 分别是AC 、AB 的中点，则DE 的长是（）A ．6.5B ．6C ．5.5D ．2【答案】B 【分析】根据勾股定理可先求出BC ，然后结合中位线定理得出结论．【解析】由勾股定理得：12BC =，∵D 、E 分别是AC 、AB 的中点， ∵DE 是ABC 的中位线，则162DE BC ==，故选：B ．【小结】本题考主要考查三角形的中位线定理，熟记并灵活运用基本定理是解题关键． 2．直角三角形的直角边长分别为3，4，则直角三角形的周长为（）A ．5B ．12C ．12或7D ．7【答案】B 【分析】先根据勾股定理求出直角三角形的斜边，继而即可求出三角形的周长．【解析】根据勾股定理可知：斜边=5，∵三角形周长=3+4+5=12，故选：B．【小结】本题考查的是勾股定理的应用，难度适中，解题关键是根据勾股定理求出斜边的长．3．如图，在∵ABC中，∵ACB=90°，CD是高，∵A=30°，AB=4，则下列结论中不正确的是（）A．BC=2B．BD=1C．AD=3D．CD=2【答案】D【分析】根据含30°角的直角三角形的性质及勾股定理求出各线段的长度，即可判断．【解析】∵∵ACB=90°，∵A=30°，∵BC=12AB=2，∵B=60°，∵CD∵AB，∵∵CDB=∵CDA=90°，∵BCD=30°，∵BD=12BC=1，∵AD=AB-BD=4-1=3，CD==∵不正确的是D．故选：D．【小结】本题考查的是直角三角形的性质，勾股定理，掌握直角三角形中，30°角所对的直角边等于斜边的一半是解题的关键．4．如图是2002年8月在北京召开的国际数学大会的会标，它是由四个相同的直角三角形与中间一个小正方形拼成的一个大正方形，若大正方形的边长是13cm，每个直角三角形较短的一条直角边的长是5cm，则小正方形的边长为（）A．4cm B．5cm C．6cm D．7cm【答案】D【分析】先设直角三角形的两直角边分别是a cm、b cm（a＞b），斜边是c cm，于是有a2+b2=c2，即a2+52=132，易得a=12 cm，a-b即可得小正方形的边长．【解析】设大直角三角形的两直角边分别是a cm、b cm（a＞b），斜边是c cm，那么有a2+b2=c2，∵大正方形的边长是13cm，每个直角三角形较短的一条直角边的长是5cm，∵a2+52=132，解得a= 12（舍去负值），即a=12 cm，∵小正方形的边长为：a-b=12-5=7 cm．故选：D．【小结】本题考查了勾股定理，解题的关键是知道小正方形的边长等于直角三角形较长直角边减去较小直角边．5．已知一个直角三角形三边的平方和为800，则这个直角三角形的斜边长为（）A．20B．40C．80D．100【答案】A【分析】直角三角形中两直角边的平方和等于斜边的平方，已知三边的平方和可以求出斜边的平方，根据斜边的平方可以求出斜边长．【解析】∵在直角三角形中斜边的平方等于两直角边的平方和，又∵已知三边的平方和为800，则斜边的平方为三边平方和的一半，即斜边的平方为，800÷2=400，∵斜边长，故选：A ．【小结】本题考查了勾股定理在直角三角形中的灵活应用，考查了勾股定理的定义，本题中正确计算斜边长的平方是解题的关键．6．如图，O 的直径AB 垂直于弦,CD 垂足为,22.5,2E A OC ∠=︒=，则CD 的长为（）A B ．2C ．D ．4【答案】C 【分析】由垂径定理可得出CD=2CE ，∵CEO=90°，由∵A=22.5°，利用圆周角定理可求出∵COE=45°，进而可得出∵CEO 为等腰直角三角形，再利用等腰直角三角形的性质及OC=2可求出CE 的长（或通过解直角三角形求出CE 的长），结合CD=2CE 可求出CD 的长．【解析】∵∵O 的直径AB 垂直于弦CD ， ∵CD=2CE ，∵CEO=90°，又∵∵COE=2∵A=45°， ∵∵CEO 为等腰直角三角形，∵CD=2CE= 故选：C ．【小结】本题考查了圆周角定理、垂径定理以及等腰直角三角形，利用等腰直角三角形的性质求出CE的长是解题的关键．7．菱形的边长是5cm，一条对角线的长为6cm，则另一条对角线的长为（）A．6cm B．C．8cm D．10cm【答案】C【分析】根据菱形性质得出OB＝OD＝3cm，OA＝OC，AC∵BD，由勾股定理求出OA，即可得出答案．【解析】如图所示：∵四边形ABCD是菱形，∵AB＝5cm，OB＝OD＝12BD＝3cm，AC∵BD，∵∵AOB＝90°，由勾股定理得：OA=4cm，∵AC＝2OA＝8cm，故选：C．【小结】本题考查了菱形的性质和勾股定理，熟练掌握菱形的对角线互相垂直平分是解题的关键．8．若直角三角形中，斜边的长为17，一条直角边长为15，则另一条直角边长为（）A．7B．8C．20D．65【答案】B【分析】根据勾股定理解答即可．【解析】∵直角三角形中，斜边的长为17，一条直角边长为15， ∵另一条直角边222171456=-=， ∵另外一边为8．故选：B ．【小结】此题主要考查了勾股定理，正确把握勾股定理是解题关键． 9．边长为2的正方形的对角线长是（）A B ．2C ．D ．4【答案】C 【分析】根据勾股定理，可得对角线的长，根据开方运算，可得答案．【解析】对角线平方的长是8，边长为2的正方形的对角线长是故选：C ．【小结】本题考查了算术平方根，利用了开方运算．10．如图，菱形ABCD 的周长为32，60ABC ∠=，点E 、F 分别为AO 、AB 的中点，则EF 的长度为（）A ．B ．3C D ．4【答案】A 【分析】首先根据菱形的性质得出8,,AB AC BD =⊥1302ABO ABC =∠=∠︒，然后利用含30°的直角三角形的性质和勾股定理求出BO 的长度，最后利用三角形中位线的性质求解即可．【解析】∵菱形ABCD 的周长为32，60ABC ∠=︒8,,AB AC BD ∴=⊥1302ABO ABC =∠=∠︒． 142AO AB ∴==，BO ∴==．∵点E 、F 分别为AO 、AB 的中点，12EF BO ∴== 故选：A ．【小结】本题主要考查菱形的性质，含30°的直角三角形的性质和三角形中位线的性质，熟练掌握这些性质是关键． 11．若直角三角形两边长分别是6，8，则它的斜边为（） A ．8 B ．10C ．8或10D ．以上都不正确【答案】C 【分析】分两种情况：∵6和8都是直角边，利用勾股定理求解即可；∵6是直角边，8是斜边，从而可确定答案．【解析】∵6和810=； ∵8是斜边，综上所述，斜边为8或10，故选：C ．【小结】本题主要考查勾股定理，分情况讨论是关键．12．如图，长为12cm 的橡皮筋放置在水平面上，固定两端A 和B ，然后把中点C 垂直向上拉升4.5cm 至点D ，则拉升后橡皮筋伸长了（）A．2cm B．3cm C．4cm D．5cm【答案】B【分析】根据勾股定理，可求出AD、BD的长，则AD BD+即为拉长后橡皮筋的长，从而减去原来的长度即可得到答案．【解析】Rt△ACD中，16cm2AC AB==， 4.5cmCD=；根据勾股定理，得：7.5cmAD=；215cmAD BD AD∴+==；15123cm∴-=；故选：B．【小结】此题主要考查了等腰三角形的性质以及勾股定理的应用．关键是根据勾股定理，可求出AD、BD的长．13．如图，AB为∵O的直径，点C为∵O上一点，连接CO，作AD//OC，若CO＝52，AC＝2，则AD＝（）A．3B．C．72D．175【答案】D【分析】根据题意，作出合适的辅助线，然后可以求得OG的长，再利用勾股定理即可得到AG的长，从而可以得到AD的长．【解析】作AE∵OC于点E，作OF∵CA于点F，作OG∵AD于点G，则EA∵OG，∵AD∵OC，∵四边形OEAG是矩形，∵OG ＝EA ，∵OF ∵AC ，OA ＝OC ＝52，AC ＝2， ∵CF ＝1，∵OF2=， ∵22AC OF OC AE⋅⋅=，∵522222AE ⋅=，解得5AE =， ∵OG， ∵OG ∵AD ，∵AG1710==， ∵AD ＝2AG ＝175，故选：D ．【小结】本题考查圆的性质，矩形的判定与性质，勾股定理，面积等积式，掌握圆的性质，矩形的判定与性质，勾股定理，面积等积式是解题关键．14．如图，在正方形网格中，以格点为顶点的ABC 的面积等于3，则点A 到边BC 的距离为（）A B ．C ．4 D ．3【答案】D 【分析】根据勾股定理表示出BC 的长，再根据三角形的面积为3，求出BC ，即可求出点A 到边BC 的距离．【解析】设单位方格的边长为a ，BC a ==，ABC 的面积等于3，()211222322a a a a a ∴-⨯⨯⨯-⨯⨯=，解得a =，2BC ===， ∴点A 到边BC 的距离为2632ABC S BC ==．故答案为：D ．【小结】此题考查了三角形的面积勾股定理的运用，关键是根据图形列出求三角形面积的算式． 15．等腰三角形底边上的高为4cm ，周长为16cm ，三角形的面积为（） A ．214cm B ．212cm C ．210cm D ．28cm【答案】B 【分析】设等腰三角形的底边长为2x ，则有腰长为8-x ，然后根据勾股定理可得()22248x x +=-，进而问题可求解．【解析】如图，由题意得：AD =4cm ，设等腰三角形的底边长为2x cm ，由周长为16cm 可得()8cm AB x =-， ∵在Rt ∵ADB 中，由勾股定理得()22248x x +=-，解得：3x =， ∵6BC cm =， ∵21122ABCSBC AD cm =⋅=；故选B ．【小结】本题主要考查等腰三角形的性质及勾股定理，熟练掌握等腰三角形的性质及勾股定理是解题的关键． 16．在ABC 中，AB =AC =5，BC =6，M 是BC 的中点，MN ∵AC 于点N ．则MN =（） A ．125B ．61C ．6D ．11【答案】A 【分析】连接AM ，根据等腰三角形三线合一的性质得到AM ∵BC ，根据勾股定理求得AM 的长，再根据在直角三角形的面积公式即可求得MN 的长．【解析】如图，连接AM ，∵AB =AC ，点M 为BC 中点， ∵AM ∵CM ，BM =CM =12BC =3，在Rt ∵ABM 中，AB =5，BM =3，∵AM4==，又∵S∵AMC=12MN•AC=12AM•MC，∵MN=AM CMAC=125故选：A．【小结】本题考查三角形的面积，等腰三角形的性质，勾股定理，掌握相关性质定理正确推理计算是解题关键．17．两个直角三角形拼成如图所示的图形，则2x的值为（）A B．3C D．5【答案】B【分析】可设直角边都是1的直角三角形的斜边为y，根据勾股定理可求出y2＝2，则再利用勾股定理可求出2x的值．【解析】在直角边都是1的直角三角形中，设斜边为y，则由勾股定理得：y2＝12+12＝2，同理可得：x2＝y2+12＝2+1＝3．故选：B．【小结】此题考查了勾股定理，掌握勾股定理的应用条件及方法是解题的关键．18．一直角三角形的斜边长比其中一直角边长大3，另一直角边长为9，则斜边长为（）A．15B．12C．10D．9【答案】A【分析】设斜边长为x，则一直角边长为x-3，再根据勾股定理求出x的值即可．【解析】设斜边长为x ，则一直角边长为x -3，根据勾股定理得92+(x -3)2=x 2，解得x=15．故选：A ．【小结】本题考查了勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．19．如图，在Rt ABC △中，90C ∠=︒，D 为AC 上一点．若12DA DB ==，ABD △的面积为60，则CD 的长是（）A ．5B ．C ．8D ．10【答案】B 【分析】根据Rt ∵ABC 中，∵C =90°，可证BC 是∵DAB 的高，然后利用三角形面积公式求出BC 的长，再利用勾股定理即可求出DC 的长．【解析】∵∵C =90°，DA =12， ∵S ∵DAB =12DA BC ⋅=60， ∵BC =10，在Rt ∵BCD 中，CD ²+BC ²=BD ²，即CD ²+10²=12²，解得：CD =，故选：B ．【小结】本题主要考查勾股定理，解题的关键是掌握勾股定理：在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．20．一等腰三角形底边长为10cm，腰长为13cm，则腰上的高为（）A．12cm B．60cm13C．12013cm D．13cm5【答案】C【分析】过点A作AD∵BC于D，过点B作BE∵AC于E，根据勾股定理求出AD，根据三角形的面积公式计算即可．【解析】如下图，在等腰三角形ABC中，底边长为BC=10cm，腰长为AB=13cm，过点A作AD∵BC于D，过点B作BE∵AC于E，∵AD∵BC于D，∵BD=DC，∵BC=10cm，∵BD=DC=5cm，在Rt∵ABD中，12AD==cm，由于1122BC AD AC BE⋅=⋅，∵10121201313BE⨯==cm，故选：C．【小结】本题考查的是勾股定理、等腰三角形的性质，如果直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2+b2=c2．21．如图，在长方形ABCD中，AB=3，BC=6，对角线AC的垂直平分线分别交AD、AC于点M，N，连接CM，则CM的长为（）A．154B．153C．-154D．-153【答案】A【分析】由线段垂直平分线的性质求出AM=CM，在Rt∵DMC中，由勾股定理得出DM2+DC2=CM2，得出方程（6-CM）2+32=CM2，求出CM即可．【解析】∵四边形ABCD是矩形，∵∵D=∵B=90°，AD=BC=6，AB=DC=3，∵MN是AC的垂直平分线，∵AM=CM，∵DM=AD-AM=AD-CM=6-CM，在Rt∵DMC中，由勾股定理得：DM2+DC2=CM2，（6-CM）2+32=CM2，解得：CM=154，故选：A．【小结】本题考查了矩形性质，勾股定理，线段垂直平分线性质的应用，关键是能得出关于CM的方程．22．如图，已知∵ABC中，∵ABC=90°，AB=BC，过∵ABC的顶点B作直线l，且点A到l的距离为2，点C到l的距离为3，则AC的长是()A B．C D．5【答案】C【分析】分别过A 、C 作AD ∵l 于D ，CE ∵l 于E ，根据锐角互余可得∵ABD =∵BCE ，∵DAB =∵CBE ，利用ASA 可证明∵ABD ∵∵CBE ，即可得BD =CE ，根据勾股定理可求出AB 的长，再利用勾股定理求出AC 的长即可．【解析】作AD ∵l 于点D ，作CE ∵l 于点E ， ∵∵ABC =90°， ∵∵ABD +∵CBE =90°，又∵DAB +∵ABD =90°， ∵∵BAD =∵CBE ，在∵ABD 和∵BCE 中，ADB BEC BAD CBE AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩，，， ∵∵ABD ∵∵BCE (AAS )， ∵BE =AD =2，DB =CE =3，在Rt ∵BCE 中，根据勾股定理，得BC在Rt ∵ABC 中，根据勾股定理，得AC=．故选：C ．【小结】本题考查全等三角形的判定与性质及勾股定理，根据三角形全等得出BD =CE 是解题关键．23．如图1，点P 从ABC 的顶点A 出发，沿A B C →→匀速运动到点,C 图2是点P 运动时线段CP 的长度y 随时间x 变化的关系图象，其中点Q 为曲线部分的最低点，则ABC 的边AB 的长度为（）A ．12B ．8C ．10D ．13【答案】C 【分析】根据图2中的曲线可得，当点P 在∵ABC 的顶点A 处，运动到点B 处时，图1中的AC ＝BC ＝13，当点P 运动到AB 中点时，此时CP ∵AB ，根据图2点Q 为曲线部分的最低点，可得CP ＝12，根据勾股定理可得AP ＝5，再根据等腰三角形三线合一可得AB 的长．【解析】根据图2中的曲线可知：当点P 在∵ABC 的顶点A 处，运动到点B 处时，图1中的AC ＝BC ＝13，当点P 运动到AB 中点时，此时CP ∵AB ，根据图2点Q 为曲线部分的最低点，得CP ＝12，所以根据勾股定理，得此时AP 5．所以AB ＝2AP ＝10．故选：C ．【小结】本题考查了动点问题的函数图象，解决本题的关键是综合利用两个图形给出的条件．24．如图，在ABC 中，90C ∠=︒，D 是边BC 上一点，ADC 2B ∠=∠，5AD =，4AC =，则AB 的长为（）A ．B ．C ．6D ．8【答案】A 【分析】根据勾股定理求出CD ，根据三角形的外角的性质得到∵B ＝∵BAD ，求出BD ，计算即可．【解析】∵∵C ＝90°，AC ＝4，AD ＝5， ∵CD ＝3，∵∵ADC ＝2∵B ，∵ADC ＝∵B +∵BAD ， ∵∵B ＝∵BAD ， ∵DB ＝AD ＝5， ∵BC ＝BD +CD ＝8，在Rt∵ABC 中，∵C ＝90°，AC ＝4，BC ＝8，∵AB ===故选：A ．【小结】本题考查的是勾股定理、等腰三角形判定的应用，掌握如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么a 2+b 2＝c 2是解题的关键．25．菱形CD AB 的边20AB =，面积为320，D 90∠BA <，∵O 与边AB 、D A 都相切，10AO =，则∵O 的半径长等于（）A ．5B ．6C ．D ．【答案】C 【分析】如图作DH∵AB 于H ，连接BD ，延长AO 交BD 于E ．利用菱形的面积公式求出DH ，再利用勾股定理求出AH ，BD ，由∵AOF∵∵DBH ，可得=OA OFBD BH，即可解决问题．【解析】如图作DH∵AB 于H ，连接BD ，延长AO 交BD 于E ．∵菱形ABCD 的边AB=20，面积为320， ∵AB•DH=320， ∵DH=16，在Rt∵ADH 中，12=，∵HB=AB -AH=8，在Rt∵BDH 中，=设∵O 与AB 相切于F ，与AD 相切于J ，连接OF ，OJ ，则OF∵AB ，OJ∵AD ，OF=OJ ， ∵OA 平分∵DAB ， ∵AD=AB ， ∵AE∵BD ，∵∵OAF+∵ABE=90°，∵ABE+∵BDH=90°， ∵∵OAF=∵BDH ，∵∵AFO=∵DHB=90°， ∵∵AOF∵∵DBH ， ∵=OA OFBD BH，8OF=，∵OF= 故选：C ．【小结】本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．26．如图，在Rt ABC △中，90C ∠=︒，BD 平分,5cm,3cm ABC AB BC ∠==，则AD 的长等于（）A ．2.5cmB ．2cmC ．1.5cmD ．3cm【答案】A 【分析】如图（见解析），先根据角平分线的性质可得CD DE =，再根据直角三角形全等的判定定理与性质可得3cm BE BC ==，从而可得2cm AE =，然后利用勾股定理可得4cm AC =，最后在Rt ADE △中，利用勾股定理即可得．【解析】如图，过点D 作DE AB ⊥于点E ，BD 平分ABC ∠，90C ∠=︒，DE AB ⊥， CD DE ∴=，在Rt BCD 和Rt BED 中，CD DEBD BD =⎧⎨=⎩，()Rt BCD Rt BED HL ∴≅，3cm BE BC ∴==， 5cm AB =，2cm AE AB BE ∴=-=，在Rt ABC 中，90,5cm,3cm C AB BC ∠=︒==，4cm AC ∴==，设cm AD x =，则(4)cm DE CD AC AD x ==-=-，则在Rt ADE △中，222AE DE AD +=，即2222(4)x x +-=，解得 2.5(cm)x =，即 2.5cm AD =，故选：A ．【小结】本题考查了角平分线的性质、直角三角形全等的判定定理与性质、勾股定理等知识点，通过作辅助线，利用到角平分线的性质是解题关键．27．如图，∵ABCD 的对角线AC 与BD 相交于点O ，AB ∵AC ，若AB ＝4，AC ＝6，则BO 的长为（）A ．5B ．8C ．10D ．11【答案】A 【分析】根据平行四边形的性质可得AO ＝CO ＝12AC ＝3，再利用勾股定理可得BO 的长．【解析】∵四边形ABCD 是平行四边形， ∵AO ＝CO ＝12AC ＝3， ∵AB ∵AC ，AB ＝4，∵BO 5，故选：A ．【小结】此题主要考查了平行四边形的性质和勾股定理，解题关键是掌握平行四边形的对角线互相平分．28．如图，在矩形ABCD 中，AB ＝5，AD ＝12，对角线BD 的垂直平分线分别与AD ，BC 边交于点E 、F ，则四边形BFDE 的面积为（）A．84524B．84512C．16912D．82513【答案】A【分析】根据矩形的性质和菱形的判定得出四边形BEDF是菱形，进而利用勾股定理和菱形的面积公式解答即可．【解析】∵四边形ABCD是矩形，∵AD∵BC，∵∵DEO＝∵BFO，∵EDO＝∵FBO，∵对角线BD的垂直平分线分别与AD，BC边交于点E、F，∵BO＝DO，EF∵BD，∵∵DEO∵∵BFO（AAS），∵EO＝FO，∵BO＝DO，∵四边形BEDF是平行四边形，∵EF∵BD，∵平行四边形BEDF是菱形，∵BE＝DE，∵AB＝5，AD＝12，∵A＝90°，∵BD＝13，设DE＝x，则AE＝12﹣x，在Rt∵AEB中，AB2+AE2＝BE2，即52+（12﹣x）2＝x2，∵x 16924=， ∵BE ＝DE 16924=，在Rt∵BEO 中，OE 6524===， ∵EF ＝2EO 6512=， ∵菱形BEDF 的面积116584513221224BD EF =⋅⋅=⨯⨯=，故选：A ．【小结】此题考查矩形的性质、菱形的性质和判定以及勾股定理，关键是根据矩形的性质和菱形的判定和性质解答． 29．如图，D 是ABC 内一点，BD CD ⊥，6AD =，4BD =，3CD =，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，则四边形EFGH 的周长是（）A ．7B ．9C ．10D ．11【答案】D 【分析】先根据勾股定理求出线段BC 的长度，再根据三角形中位线的性质定理求出 2.5EF HG ==，3EH GF ==，即可求出四边形的周长．【解析】∵BD CD ⊥，4BD =，3CD =，由勾股定理得：5BC ==，∵E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点， ∵12HG BC EF ==，12EH FG AD ==，∵6AD =，∵ 2.5EF HG ==，3EH GF ==，∵四边形EFGH 的周长是()2 2.5311EF FG HG EH +++=⨯+=．故选：D ．【小结】此题考查勾股定理的应用，三角形中位线的性质定理，熟记定理并正确应用是解题的关键．30．如图，在∵ABC 中，∵ACB =90°，AC =3、BC =4、P 、Q 两点分别在AC 和AB 上．且CP =BQ =1，在平面上找一点M ．以A 、P 、Q 、M 为顶点画平行四边形，这个平行四边形的周长的最大值为（）A ．12B ．4C ．6+D ．8+【答案】D 【分析】先依据勾股定理以及相似三角形的性质，即可得到PQ 的长，再分三种情况，即可得到以A 、P 、Q 、M 为顶点的平行四边形的周长，进而得出周长的最大值．【解析】由勾股定定理得：5AB =，则4AQ =；过点Q 作QN AC ⊥，垂足为N ，则//QN BC ，则::4AN NC AQ QB ==，则125AN =， 122255PN ∴=-=，由::NQ BC AQ AB =，得165NQ =，再由勾股定理得：PQ =如图1：周长2()4PA PQ =+= 如图2：周长2()12PA PM =+=；如图3：周长2()8AQ PQ =+=∵84>88>即814.412>>，故周长的最大值是8故选：D ．【小结】本题主要考查了平行四边形的性质以及勾股定理的运用，关键是作辅助线构造直角三角形，利用勾股定理计算得到PQ 的长．31．如图，在Rt ABC ∆中，90,BAC BA CA ∠=︒==D 为BC 边的中点，点E 是CA 延长线上一点，把CDE ∆沿DE 翻折，点C 落在C '处，EC '与AB 交于点F ，连接BC '．当43FA EA =时，BC '的长为（）AB ．CD ．【答案】D 【分析】如图，连接CC ′，过点C ′作C ′H ∵EC 于H ．设AB 交DE 于N ，过点N 作NT ∵EF 于N ，过点D 作DM ∵EC 于M ．证明∵CC ′B =90°，求出CC ′，BC 即可解决问题．【解析】如图，连接CC′，过点C′作C′H∵EC于H．设AB交DE于N，过点N作NT∵EF于N，过点D作DM∵EC 于M．∵∵F AE=∵CAB=90°，43 FAAE，∵EF：AF：AE=5：4：3，∵C′H∵AF，∵∵EAF∵∵EHC′，∵EC′：C′H：EH=EF：AF：AE=5：4：3，设EH=3k，C′H=4k，EC′=EC=5k，则CH=EC=EH=2k，由翻折可知，∵AEN=∵TEN，∵NA∵EA，NT∵ET，∵∵NAE=∵NTE，∵NE=NE，∵∵NEA∵∵NET（AAS），∵AN=NT，EA=ET，设AE=3m，AF=4m，EF=5m，AN=NT=x，则AE=ET=3m，TF=2m，在Rt∵FNT中，∵FN2=NT2+FT2，∵（4m-x）2=x2+（2m）2，解得x=32 m，∵AC=AB，∵CAB=90°，∵BC∵CD=BD∵DM∵CM，∵DCM=45°，∵CM=DM∵AN∵DM，∵AN EA DM EM=，∵31232mAN DMEA EM m===，∵EM，∵ECk，∵k=，∵CH C H'==，∵CC'===∵DC=DC′=DB，∵∵CC′B=90°，∵BC'===故选：D．【小结】本题考查翻折变换，解直角三角形，等腰直角三角形的性质，相似三角形的性质，全等三角形的性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程解决问题．32．如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∵DAM＝45°，点F在射线AM上，且AFBE，CF与AD相交于点G，连接EC、EF、EG．则下列结论：∵∵ECF＝45°；∵∵AEG的周长为a；∵BE2+DG2＝EG2；∵∵EAF的面积的最大值是a2；∵当BE=a时，G是线段AD的中点．其中正确的结论是（）A．∵∵∵B．∵∵∵C．∵∵∵D．∵∵∵【答案】D【分析】∵正确：如图1中，在BC上截取BH=BE，连接EH．证明∵FAE∵∵EHC（SAS），即可解决问题；∵∵错误：如图2中，延长AD到H，使得DH=BE，则∵CBE∵∵CDH（SAS），再证明∵GCE∵∵GCH（SAS），即可解决问题；∵正确：设BE=x，则AE=a-x，，构建二次函数，利用二次函数的性质解决最值问题；∵正确：当BE=13a时，设DG＝x，则EG＝x13+a，利用勾股定理构建方程可得x2a=，即可解决问题．【解析】如图1中，在BC上截取BH＝BE，连接EH，∵BE＝BH，∵EBH＝90°，∵EH，∵AF=，∵AF＝EH，∵∵DAM＝∵EHB＝45°，∵BAD＝90°，∵∵FAE＝∵EHC＝135°，∵BA＝BC，BE＝BH，∵AE＝HC，∵∵FAE∵∵EHC（SAS），∵EF＝EC，∵AEF＝∵ECH，∵∵ECH+∵CEB＝90°，∵∵AEF+∵CEB＝90°，∵∵FEC＝90°，∵∵ECF＝∵EFC＝45°，故∵正确，如图2中，延长AD到H，使得DH＝BE，则∵CBE∵∵CDH（SAS），∵∵ECB＝∵DCH，∵∵ECH＝∵BCD＝90°，∵∵ECG＝∵GCH＝45°，∵CG＝CG，CE＝CH，∵∵GCE∵∵GCH（SAS），∵EG＝GH，∵GH＝DG+DH，DH＝BE，∵EG＝BE+DG，故∵错误，∵∵AEG的周长＝AE+EG+AG＝AE+AH＝AD+DH+AE＝AE+EB+AD＝AB+AD＝2a，故∵错误，设BE＝x，则AE＝a﹣x，AF=，∵S∵AEF=12•（a﹣x）×x=1-2x2+12ax=1-2（x2﹣ax14+a214-a2）=1-2（x1-2a）218+a2，∵12-<0，∵x=12a 时，∵AEF 的面积的最大值为218a ，故∵正确，当BE=13a 时，设DG ＝x ，则EG ＝x 13+a ，在Rt∵AEG 中，则有（x 13+a ）2＝（a ﹣x ）2+（23a ）2，解得x 2a=， ∵AG ＝GD ，故∵正确，综上，∵∵∵正确，故选：D ．【小结】本题考查正方形的性质，全等三角形的判定和性质，二次函数的应用等知识，熟练掌握并灵活运用是解题的关键．33．如图，在ABC 中，AC BC =，90ACB ∠=︒，AE 平分BAC ∠交BC 于E ，BD AE ⊥于D ，DM AC ⊥交AC 的延长线于M ，连接CD ，给出四个结论：∵45ADC ∠=︒；∵12BD AE =；∵AC BE AB +=；∵2AB BC MC -=；其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个【答案】C 【分析】过E 作EQ ∵AB 于Q ，作∵ACN ＝∵BCD ，交AD 于N ，过D 作DH ∵AB 于H ，根据角平分线性质求出CE ＝EQ ，DM ＝DH ，根据勾股定理求出AC ＝AQ ，AM ＝AH ，根据等腰三角形的性质和判定求出BQ ＝QE ，进而可判断∵；根据三角形外角性质求出∵CND ＝45°，证∵ACN ∵∵BCD ，推出CD ＝CN ，进而可判断∵∵；证∵DCM ∵∵DBH ，得到CM ＝BH ，进一步变形即可判断∵，于是可得答案．【解析】如图，过E 作EQ ∵AB 于Q ， ∵∵ACB ＝90°，AE 平分∵CAB ，∵CE＝EQ，∵∵ACB＝90°，AC＝BC，∵∵CBA＝∵CAB＝45°，∵EQ∵AB，∵∵EQA＝∵EQB＝90°，由勾股定理得：AC＝AQ，∵∵QEB＝45°＝∵CBA，∵EQ＝BQ，∵AB＝AQ+BQ＝AC+CE，∵BE＞EQ=CE，∵∵错误；作∵ACN＝∵BCD，交AD于N，∵∵CAD＝12∵CAB＝22.5°＝∵BAD，∵∵ABD＝90°﹣22.5°＝67.5°，∵∵DBC＝67.5°﹣45°＝22.5°＝∵CAD，∵∵DBC＝∵CAD，∵AC=BC，∵ACN＝∵BCD，∵∵ACN∵∵BCD（ASA），∵CN＝CD，AN＝BD，∵∵ACN+∵NCE＝90°，∵∵NCB+∵BCD＝90°，∵∵CND＝∵CDA＝45°，∵∵ACN＝45°﹣22.5°＝22.5°＝∵CAN，∵AN＝CN，∵∵NCE＝∵AEC＝67.5°，∵CN＝NE，∵DCB=90°－67.5°=22.5°，∵BD＝AN＝EN＝12AE，∵ADC=180°－∵DAC－∵ACD=180°－22.5°－112.5°=45°，∵∵正确，∵正确；过D作DH∵AB于H，∵∵MCD＝∵CAD+∵CDA＝67.5°，∵DBA＝67.5°，∵∵MCD＝∵DBA，∵AE平分∵CAB，DM∵AC，DH∵AB，∵DM＝DH，在∵DCM和∵DBH中90 M DHB MCD DBA DM DH ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩，∵∵DCM∵∵DBH，∵BH＝CM，由勾股定理得：AM＝AH，∵AC AB AC AH BH AC AM CMAM AM AM+++++==＝2AMAM＝2，∵AC+AB＝2AM，即AC+AB＝2AC+2CM，∵AB﹣AC＝2CM，∵AC＝CB，∵AB﹣CB＝2CM，∵∵正确．综上，正确的有3个．故选：C．【小结】本题主要考查了等腰直角三角形的判定和性质、三角形的外角性质、三角形的内角和定理、等腰三角形的性质和判定、全等三角形的性质和判定以及勾股定理等知识，正确添加辅助线、能综合运用所学知识进行推理是解此题的关键．34．如图，在Rt ABC △中，90,30,ACB ABC CD ︒∠︒=∠=平分ACB ∠．边AB 的垂直平分线DE 分别交,CD AB 于点,D E ．以下说法错误的是（）A ．60BAC ∠=︒B ．2CD BE =C ．DE AC =D 12BC AB =+【答案】B 【分析】利用直角三角形的性质、三角形内角和定理、勾股定理、全等三角形的判定与性质等知识对各选项的说法分别进行论证，即可得出结论．【解析】如图，连接BD 、AD ，过点D 作DM∵BC 于M ，DN∵CA 的延长线于N ，A 、在Rt ABC △中，90ACB ∠=︒，30ABC ∠=︒， ∵60BAC ∠=︒．故此选项说法正确； B 、∵DM∵BC ，DN∵CA ∵∵DNC ＝∵DMC ＝90°， ∵CD 平分∵ACB ， ∵∵DCN ＝∵DCM ＝45°． ∵∵DCN ＝∵CDN ＝45°．∵CN=DN ．则∵CDN 是等腰直角三角形．同理可证：∵CDM 也是等腰直角三角形，．， ∵DM=DN= CM=CN ，∵MDN ＝90°． ∵DE 垂直平分AB ， ∵BD=AD ，AB=2BE ． ∵Rt∵BDM∵∵ADN ， ∵∵BDM=∵AND ．∵∵BDM+∵ADM =∵AND+∵ADM ＝∵MDN ． ∵∵ADB=90°．=．即．∵在Rt∵AND 中，AD 是斜边，DN 是直角边，∵AD ＞DN ． ∵2BE ＞CD ．故此选项说法错误． C 、∵BD=AD ，∵ADB=90°， ∵∵ABD 是等腰直角三角形． ∵DE=12AB ．在Rt ABC △中，90ACB ∠=︒，30ABC ∠=︒， ∵AC=12AB ． ∵DE=AC ．故此选项说法正确． D 、∵Rt∵BDM∵∵ADN ， ∵BM=AN ．∵CN=AC+AN=AC+BM=CM ． ∵BC=BM+CM=AC+2BM ．，．∵AC=12 AB，12AB+BC．故此选项说法正确．故选：B．【小结】本题属于三角形综合题，考查了直角三角形的性质，全等三角形的判定与性质，勾股定理等知识，难度较大，准确作出辅助线并灵活运用所学知识是解题的关键．35．如图，在平面直角坐标系中，O为坐标原点，直线y x=-+x轴交于B点，与y轴交于A点，点C D，在线段AB上，且22CD AC BD==，若点P在坐标轴上，则满足7PC PD+=的点P的个数是（）A．4B．3C．2D．1【答案】A【分析】作点C关于y轴的对称点'C，根据直线y x=-+x轴交于B点，与y轴交于A点，求出A，B两点的坐标，然后利用勾股定理求得'C D=，即'PD PC C D<+，可判断点P在x轴上，使得7PC PD+=的点P的个数是两个；作点D关于x轴的对称点'D，同理可判断点P在y轴上，使得7PC PD+=的点P 的个数是两个，据此求解即可．【解析】如图示，作点C关于y轴的对称点'C，直线y x =-+x 轴交于B 点，与y 轴交于A 点，则当0x =时，y =A 点坐标是：（0，，当0y =时，x =B 点坐标是：（0），∵OA OB ==∵8AB ，∵22CD AC BD ==，AB CD AC BD =++ ∵4CD =，2==AC BD ，由勾股定理可得：CE AE ==DF AF ==∵OE =OF =∵C 点坐标是：，D 点坐标是：（，则'C 点坐标是：（，∵'CD <∵'7CD<，即：'P D P C C D <+， ∵如下图示，点P 在y 轴上，使得7PC PD +=的点P 的个数是两个，如图示，作点D 关于x 轴的对称点'D ，同理可以求得'CD = 即：'P D P C C D <+，∵点P 在y 轴上，使得7PC PD +=的点P 的个数是两个，综上所述，点P 在坐标轴上，满足7PC PD +=的点P 的个数是4个，故选：A ．【小结】本题考查了一次函数的应用、轴对称的性质、勾股定理的应用，熟悉相关性质是解题的关键． 36．在∵ABC 中，∵BAC =90°，点D 在边BC 上，AD =AB ( )A ．若AC =2AB ，则∵C =30° B ．若AC =2AB ，则3BD =2CD C ．若∵B =2∵C ，则AC =2AB D ．若∵B =2∵C ，则S ∵ABD =2∵ACD 【答案】B 【分析】根据直角三角形30°角所对边是斜边的一半，可得BC =2AB ＞AC ，从而可判断选项A 、C ；作AE∵BC ，根据勾股定理和等面积法克求得BC 、BD 和DC ，从而得出BD 和CD 的关系，可判断选项B ；可先得出AD 为中线，根据三角形中线平分三角形的面积可判断选项D ．【解析】由题，∵BAC=90°，点D 在BC 边上，AD=AB ，A.若AC =2AB ，则BC ==，若∵C=30°，BC=2AB ，故A 错误；B. 若AC =2AB ，则BC ，作AE∵BC ，则1122ABCSAB AC BC AE =⋅=⋅，可得AB AC AE AB BC ⋅===， ∵AD=AB ，∵5BE DE AB ===，∵,55BD AB DC BC AB AB ==-=， ∵3BD =2CD ，故B 正确；C. 若∵B =2∵C ， ∵∵BAC=90°， ∵∵B+∵C=90°， ∵∵C=30°，∵B=60°，∵BC=2AB ，AC ＜2AB ，故C 错误；D. 若∵B =2∵C ，由选项C 可得∵C=30°，∵B=60°， ∵AD=AB ，∵∵ABD 为等边三角形， ∵∵ADB=60°，∵∵DAC=∵ADB -∵C=30°=∵C ，∵AD=DC=BD ，即AD 为∵ABC 的中线， ∵S ∵ABD =S ∵ACD ，故D 错误．故选：B ．【小结】本题考查等边三角形的性质和判定，勾股定理，含30°角的直角三角形．熟练掌握这些定理，能借助已知条件，选择合适的定理分析是解题关键．37．在Rt ∵ABC 中，∵C =90°，点P 在边AB 上．BC =6， AC =8， ( ) A ．若∵ACP=45°，则CP=5 B ．若∵ACP=∵B ，则CP=5 C ．若∵ACP=45°，则CP=245 D ．若∵ACP=∵B ，则CP=245【答案】D【分析】四个选项，A、C选项CP为顶角的平分线，B、D选项CP为底边上的高线，根据直角三角形斜边上的中线可得斜边上的中线等于5，利用等面积法可得底边上的高线等于245，易得三角形不是等腰三角形，所以它斜边上的高线、中线和直角的角平分线不是同一条，可得正确的为D选项．【解析】∵∵C=90°，点P在边AB上．BC=6，AC=8，∵10AB==，当CP为AB的中线时，152CP AB==，若∵ACP=45°，如图1，则CP为直角∵ACB的平分线，∵BC≠AC，∵CP与中线、高线不重合，不等于5，故A选项错误；若∵ACP=∵B，如图2∵∵ACB=90°,∵∵A+∵B=90°，∵∵A+∵ACP =90°，∵∵APC=90°，即CP为AB的高线，∵BC≠AC，∵CP与中线不重合，不等于5，故B选项错误；当CP为AB的高线时，1122ABCS AC BC AB PC =⋅=⋅△,即11861022PC⨯⨯=⨯⋅，解得245PC=,故D选项正确，C选项错误．故选：D ．【小结】本题考查直角三角形斜边上的中线，等腰三角形三线合一，勾股定理等．能根据等面积法算出斜边上的高线的长度是解题关键．38．如图，在等腰Rt ABC 中，90ACB ∠=︒，点P 是ABC 内一点，且1CP =，BP =2AP =，以CP 为直角边，点C 为直角顶点，作等腰Rt DCP ，下列结论：∵点A 与点D ∵AP PC ⊥；∵AB =∵2APBS=，其中正确结论有是（）A ．∵∵∵B ．∵∵C ．∵∵D ．∵∵∵【答案】C 【分析】连结AD ，由等腰Rt ABC ，可得AC=BC ，等腰Rt DCP ，可得CD=CP ，由余角性质可∵DCA=∵PCB ，可证∵ADC∵∵BPC （SAS ）AD BP ==∵，由勾股定理22222AD +DP =+=4=AP ，可证∵ADP 为等腰直角三角形，可判断∵，由PB 与PD 可求由勾股定理，可判断∵，由面积112122APBS PB AD ===可判断∵即可【解析】连结AD ，在等腰Rt ABC 中，90ACB ∠=︒， ∵AC=BC ，∵Rt DCP 是等腰三角形， ∵CD=CP ，∵∵ACD+ACP=90°，∵ACP+∵PCB=90°，。

专题01第一章勾股定理(中等类型,10大类型)(解析版)

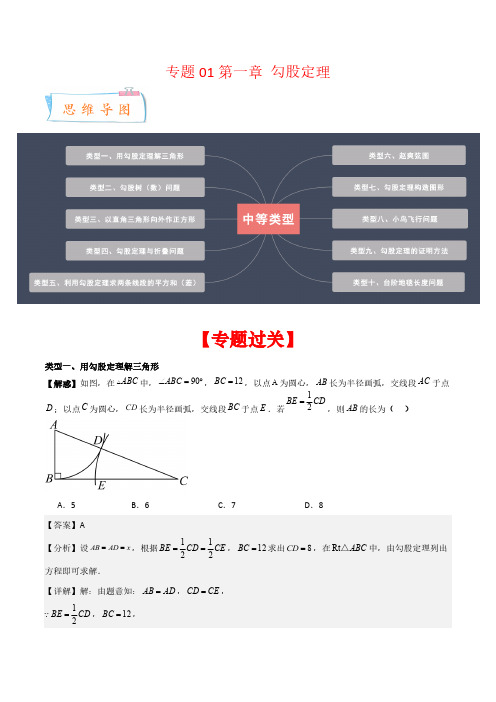
专题01第一章勾股定理【专题过关】类型一、用勾股定理解三角形【解惑】如图，在ABC V 中，90ABC Ð=°，12BC =，以点A 为圆心，AB 长为半径画弧，交线段AC 于点D C CD BC E 12BE CD =ABA ．5B ．6【答案】A 【分析】设AB AD x ==，根据12BE CD =方程即可求解．【融会贯通】B．A．8013【答案】45【分析】如图，作22,AE l CF l ^^，垂足分别为勾股定理求出2BC 即可．【详解】解：如图，作2,AE l CF ^^则90AEB BFC Ð=Ð=°，ABE BAE Ð+Ð∵点A 到直线2l 的距离是3，点C 到直线2l 的距离是6，∴3,6BF AE CF ===，∴222223645BC BF CF =+=+=，∴正方形ABCD 的面积为45；故答案为：45【点睛】本题考查了点到直线的距离、勾股定理和全等三角形的判定和性质等知识，正确理解题意、证明ABE BCF △△≌是解题的关键．4．（2023春·黑龙江黑河·八年级校考期中）如图，四边形ABCD 中，90A B Ð=Ð=°，25AB =，15AD =，10BC =，点E 是AB 上一点，且DE CE =，求AE 的长．【答案】10【分析】设AE x =，则25BE x =-，分别在Rt AED △和Rt BCE V 中，利用勾股定理求解即可．【详解】解：设AE x =，则25BE x =-，∵90A B Ð=Ð=°∴AED △、BCE V 都为直角三角形，在Rt AED △中，由勾股定理可得：2222215DE AE AD x =+=+在Rt BCE V 中，由勾股定理可得：()222222510CE BE BC x =+=-+∵DE CE=∴()2222152510x x +=-+解得10x =(1)求证：ABD △△≌(2)若3AD =，DE =【答案】(1)见解析(2)10类型二、勾股树（数）问题【解惑】如图是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形．若正方形A 、B 、C 、D 的边长分别是3、5、5、7，则最大正方形E 的面积是（）A ．14B ．108C ．58D ．72【答案】B 【分析】由勾股定理可得，直角三角形中，以斜边为边的正方形的面积等于分别以两个直角边为边的正方形的面积的和，据此求解即可．【详解】解：如图所示，由勾股定理，得22223557108E M N A B C D S S S S S S S =+=+++=+++=，故选：B ．【点睛】本题考查了勾股树，掌握勾股树的特征是解题的关键．【融会贯通】1．（2023春·重庆忠县·八年级校考阶段练习）如图所示的图形中，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm ，则正方形A 、B 、C 、D 的面积的和是（）A ．249cm B ．225cm C ．236cm D ．211cm 【答案】A 【分析】如图，设正方形A 、B 、C 、D 、E 、F 的边长分别为a 、b 、c 、d 、e 、f ，根据勾股定理可得222e a b =+，222f c d =+，2227e f +=，即可得出正方形A 、B 、C 、D 的面积之和等于最大正方形G 的面积，根据正方形面积公式即可得答案．【详解】如图，设正方形A 、B 、C 、D 、E 、F 的边长分别为a 、b 、c 、d 、e 、f ，∵所有的四边形都是正方形，所有的三角形都是直角三角形，∴222e a b =+，222f c d =+，∴正方形E 、F 的面积和为正方形A 、B 、C 、D 面积的和，∵最大的正方形的边长为7，∴222497e f =+=，【答案】25【答案】26【分析】标记正方形F 210y =，222z x y =+，代入计算出【详解】解：如下图，标记正方形则由勾股定理得：26x =即最大正方形E 的面积为：则最大正方形E 的边长为故答案为：26．【答案】22【分析】根据正方形的面积公式，结合勾股定理，能够导出正方形面积．【详解】设正方形A，B，C，DQ正方形A，B，C，D的面积分别为【答案】2024【分析】根据勾股定理可得第一代勾股树中所有正方形的面积为2，再一次求出第二代、第三代勾股树中所有三角形的面积，总结出一般规律，即可进行解答．【详解】解：设第一代勾股树中间三角形的两直角边长为a 和b ，斜边长为c ，根据勾股定理可得：222+=a b c ，∵21c =,∴第一代勾股树中所有正方形的面积为222222a b c c c =++=+=；同理可得：第二代勾股树中所有正方形的面积为22222233a b c c =++==；第三代勾股树中所有正方形的面积为244c ==；第n 代勾股树中所有正方形的面积为()211n c n =+=+；∴第2023代勾股树中所有正方形的面积为2024．故答案为：2024．【点睛】本题主要考查了勾股定理，解题的关键是仔细观察图形，根据勾股定理总结出变化的一般规律．类型三、以直角三角形向外作正方形【解惑】如图，在四边形ABCD 中，90ABC ADC Ð=Ð=°，分别以四边形的四条边为边向外作四个正方形，面积依次为1S ，2S ，3S ，4S ，下列结论正确的是（）A ．()34124S S S S +=+B ．1234S S S S =--C ．4231S S S S -=-D ．241333S S S S -=-【答案】B 【分析】利用勾股定理，分别得出同一直角三角形的两直角边上的两个正方形面积和都是2AC ，即可得到答案．【详解】解：如图，连接AC ，根据勾股定理，得222222AC AB BC AC AD CD =+=+，，∴221423AC S S AC S S ++＝，＝，\1423S S S S +=+，\1234S S S S =--故选：B ．【点睛】本题考查了勾股定理的应用，关键是发现两个直角三角形的斜边是公共边．【融会贯通】1.（2023春·新疆阿克苏·八年级校联考阶段练习）如图，以Rt ABC △的三边向外作正方形，其面积分别为123S S S ，，，且13615S S ==，，则2S = ( )A．21B【答案】C【分析】根据勾股定理求出【详解】解：由勾股定理得，A．22023B【答案】C【分析】根据勾股定理和正方形的面积公式，知面积和等于以斜边为边长的正方形的面积，即所有正方形的面积和是【点睛】本题主要考查了勾股定理在几何图形中的应用，能够根据勾股定理发现每一次得到新正方形的面积和与原正方形的面积之间的关系是解本题的关键．3．（2023春·河北保定·八年级统考期中）如图，以直角三角形的三边为边向外作正方形，其面积分别为2S 、3S ，且17S =，2S =A ．3B 【答案】B 【分析】利用勾股定理易得【详解】解：Q 直角三角形的三边为边向外作正方形，其面积分别为【答案】14【分析】根据勾股定理即可求解．【详解】解：根据勾股定理可得：由图可知：26,AB AC =∴x 所在的正方形的面积为【答案】284cm 【分析】根据勾股定理得出空白正方形的面积，进而得出其边长，再根据勾股定理求出度，最后根据三角形面积公式即可求解．【详解】解：∵②为直角三角形，阴影部分是两个正方形，【点睛】本题主要考查了勾股定理，解题的关键是掌握直角三角形两直角边平方和等于斜边平方．类型四、勾股定理与折叠问题【解惑】如图，有一块直角三角形纸片，两直角边6cm AC =，8cm BC =，现将直角边AC 沿AD 折叠，使它落在斜边AB 上，则BD 等于（）A ．2cmB ．【答案】D 【分析】先根据勾股定理求出后利用勾股定理解Rt DEB △Q由折叠的性质，可得()8cm DE CD x ==-，90AED ACD Ð=Ð=°，在Rt DEB △中，222DE BE BD +=，\()22284x x -+=，解得5x =，\BD 等于5cm ．故选D ．【点睛】本题考查勾股定理与折叠的性质，解题的关键是掌握折叠前后对应边相等，对应角相等．【融会贯通】【答案】2或5/5或2【分析】当90B ED Ð¢=°时，先求出时，作AH BC ^，证明出ADH V 【详解】解：当90B ED Ð¢=°时，如图，AB AC =Q ，AE BC ^，8BE CE \==，10AB =Q ，90Q，Ð¢=°B DEADB ADB\Ð=Ð¢=°，135ADH\Ð=°，45\==，6DH AHCD AB \^，=90ACB Ð°Q ，AC =223AB AC BC \=+=1122AB CD AC BC ××=Q 1153422CD \´´´=，12作DG BC ^于点G ，1122AC DH BC DG ×+×Q【答案】25cm 4【分析】根据折叠的性质，则【详解】由题意得，DB=DE=【答案】5【分析】由四边形用勾股定理求出BDx类型五、利用勾股定理求两条线段的平方和（差）【解惑】在△ABC 中，∠C ＝90°，AB ＝3，则AB 2+BC 2+AC 2的值为（）A ．6B ．9C ．12D ．18【答案】D【分析】根据90C Ð=°，利用勾股定理可得222AB BC AC =+，据此求解即可．【详解】解：如图示，90C Ð=°∴在Rt ABC V 中，222AB BC AC =+∴222222222318AB BC AC AB AB AB =+==+=+´，【点睛】本题主要考查了勾股定理的性质，掌握直角三角形中，三角形的三边长a ，b ，c 满足222+=a b c 是解题的关键．【融会贯通】【答案】8【分析】根据常见的“手拉手全等模型【详解】解：连接BD因为ABC V 和ECD V 都是等腰直角三角形，,ACB ECD E \Ð=ÐÐ=90Ð=Ð=°Q ACB ECD【答案】69【点睛】此题考查了勾股定理的知识，解题的关键是熟练掌握勾股定理，分别两次运用勾股定理求出(1)求证：22AF BE +=(2)若7AC =，5BC =【答案】(1)见解析(2)177AF =【分析】（1）延长EDAG AC ^Q ，90CAG °\Ð=，9090180CAG ACB °°°\Ð+Ð=+=，AG BE \P ，AGD DEB \Ð=Ð，在AGD △和BED V 中，AGD DEB ADG BDE AD BD Ð=ÐìïÐ=Ðíï=î，()AGD BED AAS \△≌△，AG BE \=，DG DE =，DF EG ^Q ，FG EF \=，90FAG °Ð=Q ，222AF AG FG \+=，222AF BE EF \+=，（2）解：设AF x =，7AC =Q ，5BC =，1CE =，则7CF AC AF x =-=-，4BE BC CE =-=，90C Ð=°Q ，222CF CE EF \+=，即：22(7)1EF x =-+，由（1）知：MF EF =，90BAF Ð=°，AM BE =，类型六、赵爽弦图【解惑】如图是我国古代著名的“赵爽弦图”，它由4个全等的直角三角形拼成，已知大正方形面积为25，小正方形面积为1，若用a ，b 表示直角三角形的两直角边（a b >），c 表示斜边，则下列说法中错误的是（）A ．5c =B ．1a b -=C ．6ab =D ．7a b +=【答案】C 【分析】根据正方形的面积得出5c =，1a b -=，根据勾股定理得出22525a b c +==，进而根据完全平方公式变形求得,ab a b +的值，即可求解．【详解】解：∵大正方形面积为25，∴5c =，故A 选项正确，不合题意；∴22525a b c +==∵小正方形面积为1，∴1a b -=，故B 选项正确，不合题意；∴()22222521a b a ab b ab -=-+=-=∴12ab =，故C 选项错误，符合题意；∴()2222252449a b a b ab +=++=+=∴7a b +=（负值舍去），故D 选项正确，不合题意；故选：C ．【点睛】本题考查了勾股定理的应用，完全平方公式的变形求值，熟练掌握勾股定理是解题的关键．【融会贯通】1．（2023春·安徽·八年级统考期末）“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a ，较短直角边长为b ，若168ab =，大正方形的面积为625，则小正方形的边长为（）A ．7B ．24C ．17D ．25【答案】C 【分析】勾股定理得：22625a b +=，又222()26252168289a b a b ab -=+-=-´=，由此即可求出17()a b a b -=>，因此小正方形的边长为17．【详解】解：由题意知小正方形的边长是a b -，由勾股定理得：22625a b +=，222()26252168289a b a b ab -=+-=-´=Q ，17()a b a b \-=>，\小正方形的边长为17．故选：C ．【点睛】本题考查了勾股定理的证明，正方形的性质，全等三角形的性质，熟练掌握勾股定理是解题的关键．2．（2023春·北京·八年级统考期末）如图，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，如果图中勾3a =，弦5c =，则小正方形的面积为（）A ．1B ．2C ．3D ．4【答案】2【分析】根据含【详解】在Rt△∴2=，AB AE【答案】4【分析】由图1可知，图2中正方形ABCD的边长为直角三角形长和宽的差，即可求解．-=，【详解】解：由图1可知，图2中正方形ABCD的边长为642´=，∴图2中小正方形ABCD的面积为224故答案为：4．【点睛】本题考查勾股定理，正方形的面积．正确识图是解题的关键．【答案】2【分析】根据边长求出中间小正方形的边长，再根据勾股定理即可求解．【详解】解：如图所示，根据题意可得，AD BC AC ==∵四边形CDEF 是正方形，∴43CD DE EF FC ====-=∴在Rt CDE △中，2CE CD =故答案为：2．【点睛】本题主要考查勾股定理的运用，掌握勾股定理的计算方法是解题的关键．类型七、勾股定理构造图形【解惑】为预防新冠疫情，民生大院入口的正上方A 处装有红外线激光测温仪（如图所示），测温仪离地面的距离 2.4AB =米，测温仪就会自动测温并报告人体体温．当身高为1.8米的市民CD 正对门缓慢走到离门0.8米的地方时（即0.8BC =米），测温仪自动显示体温（）A ．1.0米B ．1.2米C ．1.25米D ．1.5米【答案】A 【分析】过点D 作DE AB ^于点E ，构造Rt ADE △，利用勾股定理求得AD 的长度即可．【详解】解：如图，过点D 作DE AB ^于点E ，AB=米，∵ 2.4=-∴AE AB BE△中，由勾股定理得到：在Rt ADE2=AD AE DE+故选：A．【点睛】本题考查了勾股定理的应用，解题的关键是作出辅助线，构造直角三角形，利用勾股定理求得线【融会贯通】A．2m B．3m【答案】D【分析】根据勾股定理求得AB【答案】101【分析】过D 作DE AB ^于E ，构建直角三角形，根据勾股定理计算求解即可．【详解】解：过D 作DE AB ^于E ，设OA OB AD BC r ====，则10DE =，112OE CD ==，1AE r =-，在Rt ADE △中，可有222AE DE AD +=，即【详解】解：如图，两人同时从A 地出发，甲向南行走10步后到达C 地后，偏离原方向．设x 秒两人在B 处相遇，这时乙行驶3AB x =，甲共行驶7AC BC x +=，∵10AC =，∴710BC x =-，∵90A Ð=°，由勾股定理得：()()222710103x x -=+，故答案为：()()222710103x x -=+．【点睛】本题主要考查了勾股定理的应用，解题的关键是从实际问题中抽象出直角三角形，利用勾股定理是解决问题的关键．4．（2023秋·全国·八年级专题练习）暑假中，小明到某海岛探宝，如图，他到达海岛登陆点后先往东走8km ，又往北走2km ，遇到障碍后又往西走3km ，再折向北走6km 处往东一拐，仅1km 就找到宝藏，问登陆点到埋宝藏点的直线距离是多少？【答案】登陆点到宝藏处的距离为10千米【分析】通过行走的方向和距离得出对应的线段的长度，构造直角三角形利用勾股定理求解．【详解】解：过点B 作BD AC ^于点D ，根据题意可知，8316AD =-+=千米，268BD =+=千米，【点睛】本题考查了矩形的性质以及勾股定理的应用，解题的根据是结合图形，读懂题意，根据题意找到需要的数量关系，运用勾股定理求线段的长度．2022秋·七年级单元测试）如图，小丽荡秋千，秋千架高时，坐位离地0.8米．此时小红荡出的水平距离是多少？（荡到秋千架两边的最高点之间的距离）【答案】2.4米【分析】画出秋千的侧面图，根据勾股定理即可求出【详解】解：如图为秋千侧面图，座位最低点为则 2.40.42OA OB ==-=，过B 点作OA 的垂线，垂足为则0.80.40.4AC =-=，OC 由勾股定理得：22BC =【点睛】本题考查了勾股定理的运用，属于基础题，关键是正确理解题意．类型八、小鸟飞行问题【解惑】如图，有一只喜鹊在一棵2m高的小树AB上觅食，它的巢筑在与该树水平距离（BD）为8m的一棵9m高的大树DM上，喜鹊的巢位于树顶下方1m的C处，当它听到巢中幼鸟的叫声，立即飞过去，如果2.5m/sA．1s B．3s C．4s【答案】C【分析】过A作AE MD^于E，如图所示，由勾股定理求出最短路径长即可得到答案．【详解】解：过A作AE MD^于E，如图所示：=由题意可知，AB DE根据两点之间线段最短，则它要飞回巢中所飞的最短路径为222=+=AC AE CE6\它要飞回巢中所需的时间至少是【融会贯通】1．（2023春·重庆云阳·八年级校考阶段练习）如图，有两棵树，一棵高10米，另一棵高4米，两树相距8米，一只小鸟从一棵树的树稍飞到另一棵树的树稍，问小鸟至少要飞行（）【答案】10【分析】根据“两点之间线段最短定理可将两点之间的距离求出．，为树，且【详解】如图所示，AB CD【点睛】本题主要考查了勾股定理的的实际运用和两点之间，线段最短等知识点，熟练掌握其性质是解决此题的关键．4．（2023秋·全国·八年级专题练习）如图，有两棵树，一棵高鸟从一棵树的树梢飞到另一棵树的树梢，问小鸟至少飞行【答案】10【答案】一只小鸟从一棵树的树梢飞到另一棵树的树梢，则它至少要飞行【分析】根据题意画出对应的几何图形，的长度，在Rt BDE △中利用勾股定理即可求解．【详解】解：根据题意画出图形如下：其中6AB =米，3CD =米，过点D 作DE AB ^，则四边形∴3AE CD ==米，DE =∴3=-=BE AB AE 米，在Rt BDE △中，BD BE =答：一只小鸟从一棵树的树梢飞到另一棵树的树梢，则它至少要飞行类型九、勾股定理的证明方法【解惑】意大利著名画家达·芬奇用如图所示（四边形ABCD ，四边形CEFG ，四边形PQMN 都为正方形，设图①中空白部分的面积为1S ，图③中空白部分的面积为2S ）的方法验证了勾股定理，步骤如下所示，则下列判断不正确的是（）A ．★表示2b ab+B ．●表示22c ab +C ．◆表示=D ．▲表示22a b +【答案】B 【分析】根据图形表示出12S S 、，即可求解．【详解】解：由图①可得22221122S a a b b a ab b =+´´´+=++，【融会贯通】1．（2023春·河南周口·八年级校考期中）数学兴趣小组的同学用火柴盒研究证明勾股定理的新方法．如图，火柴盒的一个侧面ABCD 倒下到CEFG 的位置，连接AF ，此时90ABC Ð=°，BC a =，AB b =，AC c =．Q BC a =，AB b =，AC =()12ABEF S EF AB BE \=+×梯形()()12a b a b =´++(2)以图甲中的直角三角形为基础，可以构造出以你利用图乙验证勾股定理．【答案】(1)在直角三角形中，两条直角边的平方和等于斜边的平方；(2)验证见解析【分析】（1）根据题意分别用文字和符号描述出勾股定理即可；（2）根据题意可知()Rt Rt SAS ABE ECD V V ≌，可得Rt Rt Rt ABE DEC AED ABCD S S S S =++V V V 梯形整理可得验证出勾股定理．【详解】（1）文字语言叙述：在直角三角形中，两条直角边的平方和等于斜边的平方，(1)如图1是一个重要公式的几何解释，请你写出这个公式____________；(2)如图2所示，90B D Ð=Ð=°，且B ，C ，D 在同一直线上，试说明，90ACE Ð=°；(3)伽菲尔德（1881年任美国第20届总统）利用（1）中的公式和图2证明了勾股定理（发表在1876年4月1日的《新英格兰教育日志》上），请你写出验证过程．【答案】(1)()2222a b a ab b +=++；(2)见解析；(3)见解析．【分析】（1）用面积分割法证明：大正方形的面积等于小正方形和两个长方形的面积之和，从而推出平方和公式；（2）先证明ABC CDE △≌△，利用全等三角形对应角相等，直角三角形的两个锐角互余，推出直角；（3）用面积分割法法证明勾股定理：梯形ABDE 的面积=三角形ABC 的面积+三角形CDE 的面积+三角形ACE 的面积．【详解】（1）解：这个公式是完全平方公式：()2222a b a ab b +=++；理由如下：∵大正方形的边长为a b +，∴大正方形的面积()2a b =+，又∵大正方形的面积＝两个小正方形的面积＋两个矩形的面积，22222a b ab ab a ab b =+++=++，∴222()2a b a ab b ×+=++．故答案为：()2222a b a ab b +=++．（2）证明：∵在ABC V 和CDE V 中，∴222=+．c a b【点睛】本题主要考查了勾股定理的证明，掌握数形结合思想是解答本题的关键．类型十、台阶地毯长度问题【解惑】如图在一个高为3米，长为5米的楼梯表面铺地毯，则地毯至少需要（）．A．3米B．4米C．【答案】D【分析】当地毯铺满楼梯时的长度是楼梯的水平宽度与垂直高度的和，根据勾股定理求得水平宽度，即可求得地毯的长度．【融会贯通】1．（2023春·辽宁抚顺·八年级统考期中）如图，在高为5m，坡面长为13m的楼梯表面铺地毯，地毯的长度至少需要（）A．13m B．17m C．18m D．26m【答案】BA．5米B．6【答案】C【分析】先根据直角三角形的性质求出【答案】1020【分析】地毯的长是楼梯的竖直部分与水平部分的和，即即可求得AB的长，地毯的长与宽和积就是面积，再乘地毯每平方米的单价即可求解．【详解】解：由勾股定理得：AB【答案】13AC=´【分析】先根据图形求得51可．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级北师大版上册第一章勾股定理培优专题一、勾股定理的应用（最短路径）1．如图是放在地面上的一个长方体盒子，其中AB=18，BC=12，BF=10，点M在棱AB上，且AM=6，点N是FG的中点，一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N，它需要爬行的最短路程的平方为（）A．400B．424C．136D．324【答案】A【解析】【分析】利用平面展开图有两种情况，画出图形利用勾股定理求出MN的长即可．【详解】解：如图1，∵AB=18cm，BC=GF=12cm，BF=10cm，∵BM=18-6=12，BN=10+6=16，∵MN2=122+162=400如图2，∵AB=18cm，BC=GF=12cm，BF=10cm，∵PM=18-6+6=18，NP=10，∵MN2=182+102=424．∵因为400<424，所以蚂蚁沿长方体表面从点M爬行到点N的最短距离的平方为400.故选：A．【点睛】此题主要考查了平面展开图的最短路径问题和勾股定理的应用，利用展开图有两种情况分析得出是解题关键．2．如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为_______cm．【答案】15.【分析】过C作CQ∵EF于Q，作A关于EH的对称点A′，连接A′C交EH于P，连接AP，则AP+PC就是蚂蚁到达蜂蜜的最短距离，求出A′Q，CQ，根据勾股定理求出A′C即可．【详解】沿过A的圆柱的高剪开，得出矩形EFGH，过C作CQ∵EF于Q，作A关于EH的对称点A′，连接A′C交EH于P，连接AP，则AP+PC就是蚂蚁到达蜂蜜的最短距离，∵AE=A′E，A′P=AP，∵AP+PC=A′P+PC=A′C，∵CQ=12×18cm=9cm，A′Q=12cm-4cm+4cm=12cm，在Rt∵A′QC中，由勾股定理得：，故答案为15．3．有一个如图所示的长方体的透明鱼缸，假设其长AD＝80 cm，高AB＝60 cm，水深AE＝40 cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG＝60 cm.一小虫想从鱼缸外的点A处沿缸壁爬到鱼缸内G处吃鱼饵．(1)小虫应该走怎样的路线才可使爬行的路程最短？请画出它的爬行路线，并用箭头标注；(2)试求小虫爬行的最短路程．【答案】(1)如图所示见解析，AQ→QG为最短路线；(2)小虫爬行的最短路程为100 cm.【分析】(1)根据轴对称性质,通过作对称点将折线转化成两点之间线段距离最短.(2)根据AE＝40cm,AA′＝120cm,可得:A′E＝120－40＝80(cm),再根据EG＝60cm,可得:A′G2＝A′E2＋EG2＝802＋602＝10000,A′G＝100cm,进而可得:AQ＋QG＝A′Q＋QG＝A′G＝100cm.【详解】(1)如图所示,AQ→QG为最短路线,(2)因为AE＝40cm,AA′＝120cm,所以A′E＝120－40＝80(cm),因为EG＝60cm,所以A′G2＝A′E2＋EG2＝802＋602＝10000,所以A′G＝100cm,所以AQ＋QG＝A′Q＋QG＝A′G＝100cm,所以小虫爬行的最短路程为100cm.【点睛】本题主要对称性质和勾股定理的应用,解决本题的关键是要熟练掌握利用轴对称性质和勾股定理解决实际问题的方法.勾股定理的实际应用4．有一辆装满货物的卡车，高2.5米，宽1.6米，要开进如图所示的上边是半圆，下边是长方形的桥洞，已知半圆的直径为2米，长方形的另一条边长是2.3米.（1）这辆卡车能否通过此桥洞？试说明你的理由.（2）为了适应车流量的增加，想把桥洞改为双行道，并且要使宽1.2米，高为2.8米的卡车能安全通过，那么此桥洞的宽至少应增加到多少米？【答案】(1)能通过，理由见解析；(2) 桥洞的宽至少应增加到2.6米.【分析】（1）如图①，当桥洞中心线两边各为0.8米时，由勾股定理得方程2220.81x +=，解出x 的值，再用x +2.3与卡车的高2.5作比较即可；（2）如图②，在直角三角形AOB 中，已知OB =1.2，AB =2.8－2.3=0.5，由此可求OA 的长，即桥洞的半径，再乘以2即得结果.【详解】解：（1）能通过.理由如下：如图①所示，当桥洞中心线两边各为0.8米时，由勾股定理得2220.81x +=，解得0.6x =，∵2.5 2.30.6<+，∵卡车能通过.（2）如图②所示，在直角三角形AOB 中，已知OB =1.2，AB =2.8－2.3=0.5，由勾股定理得：22221.20.5 1.3OA =+=，∵ 1.3OA =，∵桥洞的宽至少应增加到1.32 2.6⨯=（米）.① ②【点睛】本题考查了勾股定理的应用，解题的关键是正确理解题意，画出图形，弄清相关线段所表示的实际数据. 5．如图，公路MN 和公路PQ 在点P 处交会，公路PQ 上点A 处有学校，点A 到公路MN 的距离为80m ，现有一拖拉机在公路MN上以18km/h的速度沿PN方向行驶，拖拉机行驶时周围100m以内都会受到噪音的影响，试问该校受影响的时间为多长？【答案】24s.【解析】试题分析：设拖拉机开到C处刚好开始受到影响，行驶到D处时结束，在Rt∵ACB中求出CB，继而得出CD，再由拖拉机的速度可得出所需时间．试题解析：设拖拉机开到C处刚好开始受到影响，行驶到D处时结束了噪声的影响．则有CA=DA=100m，在Rt∵ABC中，CB60(m)，∵CD=2CB=120m，∵18km/h=18000m/3600s=5m/s，∵该校受影响的时间为：120÷5=24（s）．答：该校受影响拖拉机产生的噪声的影响时间为24秒．6.如图是某体育广场上的秋千，秋千静止时，其下端离地面0.7m，秋千荡到最高位置时，其下端离地面1.2 m，此时秋千与静止位置时的水平距离为1.5 m，请你根据以上数据计算秋千摆绳的长度．【答案】2.5m ．【分析】根据题意画出图形，表示出图形中相关线段的长，再利用勾股定理得出答案．【详解】解：如图，作BE∵OA ，垂足为E ，由题意得，0.7m AC =， 1.2m BD =， 1.5m BE =，∵ 1.2m CE BD ==， 1.20.70.5(m)AE =-=．设m OA OB x ==，则(0.5)m OE x =-．在Rt OBE 中，由勾股定理得，222OE O E B B -=，即222(0.5) 1.5x x --=，解得 2.5x =．答：秋千摆绳的长度为2.5m ．二、勾股定理与几何问题的应用7．如图，把长方形纸条ABCD 沿EF ，GH 同时折叠，B ，C 两点恰好落在AD 边的P 点处，若∵FPH ＝90°，PF ＝8，PH ＝6，则长方形ABCD 的边BC 的长为( )A ．20B ．22C ．24D ．30【答案】C【详解】由折叠得： ,,FP BF CH PH ==在Rt PHF ∆ 中，∵FPH ＝90°，PF ＝8，PH ＝6，则10.FH == 故BC=BF+FH+HC=6+8+10=24. 故选C.8．如图，在四边形ABCD 中，AD∵BC ，∵ABC+∵DCB=90°，且BC=2AD ，分别以AB 、BC 、DC 为边向外作正方形，它们的面积分别为S 1、S 2、S 3．若S 2=48，S 3=9，则S 1的值为（）A．18B．12C．9D．3【答案】D【分析】过A作AH∵CD交BC于H，根据题意得到∵BAE=90°，根据勾股定理计算即可．【详解】∵S2=48，∵BC A作AH∵CD交BC于H，则∵AHB=∵DCB．∵AD∵BC，∵四边形AHCD是平行四边形，∵CH=BH=AD AH=CD=3．∵∵ABC+∵DCB=90°，∵∵AHB+∵ABC=90°，∵∵BAH=90°，∵AB2=BH2﹣AH2=3，∵S1=3．故选D．【点睛】本题考查了勾股定理，正方形的性质，平行四边形的判定和性质，正确的作出辅助线是解题的关键．9．如图，在∵ABC中，AB=AC=m，P为BC上任意一点，则PA2+PB•PC的值为（）A．m2B．m2+1C．2m2D．（m+1）2【答案】A【分析】如图，作AD∵BC交BC于D，根据勾股定理得AB2=BD2+AD2，AP2=PD2+AD2，再根据D是BC的中点，整理得到AB2﹣AP2=PB•PC，再把AB=m代入求解即可.【详解】解：如图，作AD∵BC交BC于D，AB2=BD2+AD2 ①，AP2=PD2+AD2 ②，①﹣②得：AB2﹣AP2=BD2﹣PD2，∵AB2﹣AP2=（BD+PD）（BD﹣PD），∵AB=AC，∵D是BC中点，∵BD+PD=PC，BD﹣PD=PB，∵AB2﹣AP2=PB•PC，∵PA2+PB•PC=AB2=m2．故选A.10．如图，点E 是正方形ABCD 内一点，将ABE ∆绕点B 顺时针旋转90到CBE '∆的位置，若1,2,3AE BE CE ===，求BE C '∠的度数．【答案】135︒【分析】连接EE`,如图,根据旋转的性质得BE=B E'=2,AE=C E'=1,∵EBE`=90°,则可判断∵BEE`为等腰直角三角形,根据等腰直角三角形的性质得在∵CE E'中,由于CE`2 +E E'2=CE 2,根据勾股定理的逆定理得到∵CEE`为直角三角形,即∵EE`C=90°,然后利用∵B E'C=∵B E'E+∵C E'E 求解【详解】连接EE`,如图,∵∵ABE 绕点B 顺时针旋转90°得到∵CBE`∵BE=BE'=2,AE=CE'=1,∵EB E'=90°∵∵BE E'为等腰直角三角形在∵CEE`中∵122=32∵CE 2+E E'2= CE 2∵∵CE E'为直角三角形∵∵E E'C=90°∵∵B E'C=∵B E'E+∵C E'E=135°【点睛】此题考查了等腰直角三角形，勾股定理的逆定理，正方形的性质和旋转的性质，利用勾股定理证明三角形是直角三角形是解题关键11．我国汉代数学家赵爽为了证明勾股定理，创制了一副“弦图”，后人称其为“爽弦图”（如图1）．图2由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD ，正方形EFGH ，正方形MNKT 的面积分别为1S ，2S ，3S ，若12315S S S ++=，则2S 的值是__________．【答案】5【分析】根据图形的特征得出四边形MNKT 的面积设为x ，将其余八个全等的三角形面积一个设为y ，从而用x ，y 表示出1S ，2S ，3S ，得出答案即可．【详解】解：将四边形M TKN 的面积设为x ，将其余八个全等的三角形面积一个设为y ，正方形ABCD ，正方形EFGH ，正方形MNKT 的面积分别为1S ，2S ，3S ，12310S S S ++=， ∴得出18S y x ，24S y x ，3S x =， 12331215S S S x y ，故31215x y， 154=53x y ，所以245S x y ，故答案为：5．【点睛】此题主要考查了图形面积关系，根据已知得出用x ，y 表示出1S ，2S ，3S ，再利用12315S S S ++=求出是解决问题的关键．12．如图，P 是等边三角形ABC 内的一点，连接PA ，PB ，PC ，以BP 为边作60PBQ ∠=︒，且BQ=BP ，连接CQ.若::3:4:5PA PB PC =，连接PQ ，试判断PQC △的形状，并说明理由.【答案】PQC △是直角三角形,理由详见解析【解析】【分析】先利用SAS 证明∵ABP ∵∵CBQ ，得到AP=CQ ；设PA =3a ，PB =4a ，PC =5a ，由已知可判定∵PBQ 为正三角形，从而可得PQ =4a ，再根据勾股定理的逆定理即可判定∵PQC 是直角三角形．【详解】解：PQC △是直角三角形. 理由如下：在ABP △与CBQ △中，∵AB CB =，BP BQ =，60ABC PBQ ∠=∠=︒，∵ABP ABC PBC PBQ PBC CBQ ∠=∠-∠=∠-∠=∠.∵ABP CBQ ≌△△.∵AP CQ =.∵::3:4:5PA PB PC =，∵设3PA a =，4PB a =，5.PC a =在PBQ △中，由于4PB BQ a ==，且60PBQ ∠=︒，∵PBQ △为等边三角形.∵4PQ a =.在PQC △中，∵22222216925PQ QC a a a PC +=+==，∵PQC △为直角三角形.【点睛】此题考查了等边三角形的性质、勾股定理逆定理和全等三角形的判定与性质，解题的关键是通过证明ABP CBQ≌△△得出AP=CQ.13．已知：如图，∵ABC中，AB=AC=10，BC=16，点D在BC上，DA∵CA于A．求：BD的长．【答案】7 2【分析】先根据等腰三角形的性质和勾股定理求出AE=6，设BD=x，则DE=8﹣x，DC=16﹣x．在Rt∵ADE和Rt∵ADC中利用勾股定理得：AD2=AE2+DE2=DC2﹣AC2，继而代入求出x的值即可．【详解】如图,过点A作AE∵BC于点E，∵AB=AC=10，BC=16，∵BE=CE=8，在Rt∵ACE中，利用勾股定理可知：AE=6，设BD=x，则DE=8﹣x，DC=16﹣x，又DA∵CA，在Rt∵ADE和Rt∵ADC中分别利用勾股定理得：AD2=AE2+DE2=DC2﹣AC2，代入为：62+（8﹣x）2=（16﹣x）2﹣102，解得：x=72．即BD=72．【点睛】本题考查了勾股定理及等腰三角形的性质，解题的关键是在Rt∵ADE和Rt∵ADC中分别利用勾股定理，列出等式AD2=AE2+DE2=DC2﹣AC2．14．已知：AB=AC，且AB∵AC，D在BC上，求证：2222BD CD AD+=．【答案】证明见解析【分析】作AE∵BC于E，由于∵BAC=90°，AB=AC，得到∵BAC是等腰直角三角形，再由等腰直角三角形的性质得到BE=AE=EC，进而得到BD= AE－DE，DC= AE+DE，代入BD2+CD2计算，结合勾股定理，即可得到结论．【详解】作AE∵BC于E，如图所示．∵AB=AC，且AB∵AC，∵∵BAC是等腰直角三角形．∵AE∵BC，∵BE=AE=EC，∵BD=BE －DE=AE－DE，DC=EC+DE= AE+DE，∵BD2+CD2= （AE－DE）2+（AE+DE）2= AE2+DE2-2AE•DE+ AE2+DE2+2AE•DE= 2AE2+2DE2= 2（AE2+DE2）=2AD2．【点睛】本题主要考查勾股定理及等腰直角三角形的性质，关键在于得出BD= AE－DE，DC= AE+DE．三、动点问题15．已知，如图，在Rt∵ABC中，∵C=90°，∵A=30°，BC=18cm．动点P从点A出发，沿AB向点B运动，动点Q从点B出发，沿BC向点C运动，如果动点P以2cm/s，Q以1cm/s的速度同时出发，设运动时间为t(s)，解答下列问题：(1)t为______时，∵PBQ是等边三角形？(2)P，Q在运动过程中，∵PBQ的形状不断发生变化，当t为何值时，∵PBQ是直角三角形？说明理由．【答案】(1)12；(2)当t为9或725时，∵PBQ是直角三角形，理由见解析.【分析】（1）根据等边三角形的性质解答即可；（2）分两种情况利用直角三角形的性质解答即可．【详解】(1)要使，∵PBQ是等边三角形，即可得：PB=BQ，∵在Rt∵ABC中，∵C=90°，∵A=30°，BC=18cm．∵AB=36cm，可得：PB=36-2t，BQ=t，解得：t=12故答案为；12(2)当t为9或725时，∵PBQ是直角三角形，理由如下：∵∵C=90°，∵A=30°，BC=18cm∵AB=2BC=18×2=36(cm)∵动点P以2cm/s，Q以1cm/s的速度出发∵BP=AB-AP=36-2t，BQ=t∵∵PBQ是直角三角形∵BP=2BQ或BQ=2BP当BP=2BQ时，36-2t=2t解得t=9当BQ=2BP时，t=2(36-2t)解得t=72 5所以，当t为9或725时，∵PBQ是直角三角形．【点睛】此题考查了等边三角形的判定和含30°角的直角三角形的性质，关键是含30°角的直角三角形的性质的逆定16．如图1，Rt∵ABC 中，∵ACB =90．，直角边AC 在射线OP 上，直角顶点C 与射线端点0重合，AC =b ，BC =a ，30a -=．（1）求a ，b 的值；（2）如图2，向右匀速移动Rt∵ABC ，在移动的过程中Rt∵ABC 的直角边AC 在射线OP 上匀速向右运动，移动的速度为1个单位／秒，移动的时间为t 秒，连接OB ．①若∵OAB 为等腰三角形，求t 的值；②Rt∵ABC 在移动的过程中，能否使∵OAB 为直角三角形？若能，求出t 的值：若不能，说明理由．【答案】（1）a =3，b =4（2）①t =4或t =1；②能．t =94．【分析】（1）根据两个非负数的和为零则每一个数都为零，得出b -4=0 ,a -3=0 ,求解即可得出a ,b 的值；（2） ①首先根据勾股定理算出AB 的长及用含t 的式子表示出OA ,OB 2 ，然后分三类讨论：当OB =AB 时；当AB =OA 时；当OB =OA 时；一一列出方程求解即可得出t 的值； ②能．由于t ＞0，点C 在OP 上，∵ACB = 90，故只能是∵OBA =90°，根据勾股定理得出关于t 的方程求出t 的值即可. 【详解】（1）解0≥,30a -≥， 30a -=，0=， 30a -=∵a=3，b=4（2）解:①∵AC=4，BC=3，∵AB，∵OC=t∵OB2=t2+32=t2+9，OA=t+4，当OB=AB时，t2+9=25，解得t=4或t=﹣4（舍去）；当AB=OA时，5=t+4，解得t=1；当OB=OA时，t2+9=（t+4）2，解得t=-78（舍去）．综上所述，t=4或t=1；②能．∵t＞0，点C在OP上，∵ACB ∵只能是∵OBA=90°，∵OB2+AB2=OA2，即t2+9+25=（t+4）2，解得t=94．∵Rt∵ABC在移动的过程中，能使∵OAB为直角三角形，此时t=94．【点睛】本题考查了非负数的性质，勾股定理的应用，等腰三角形的定义及分类讨论的数学思想.掌握非负数的性质是解（1）的关键，掌握勾股定理及分类讨论的数学思想是解（2）的关键.四、分类讨论的思想17．阅读：能够成为直角三角形三条边长的三个正整数a，b，c，称为勾股数．世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》，其勾股数组公式为：22221()21()2a m n b mnc m n ⎧=-⎪⎪=⎨⎪⎪=+⎩其中m ＞n ＞0，m ，n 是互质的奇数．应用：当n=1时，求有一边长为5的直角三角形的另外两条边长．【答案】12，13或3，4．【详解】试题分析：由n=1，得到a= （m 2﹣1）①，b=m②，c=（m 2+1）③，根据直角三角形有一边长为5，分情况，列方程即可得到结论．试题解析：当n=1，a=12（m 2﹣1）①，b=m②，c=12（m 2+1）③， ∵直角三角形有一边长为5，∵∵、当a=5时，12（m 2﹣1）=5，解得：（舍去）， ∵、当b=5时，即m=5，代入①③得，a=12，c=13，∵、当c=5时，12（m 2+1）=5，解得：m=±3， ∵m ＞0，∵m=3，代入①②得，a=4，b=3，综上所述，直角三角形的另外两条边长分别为12，13或3，4．18．∵ABC 中，AB=15，AC=13，高AD=12，则∵ABC 的周长为（）A ．42B ．32C ．42或32D ．37或33 【答案】C【分析】存在2种情况，∵ABC是锐角三角形和钝角三角形时，高AD分别在∵ABC的内部和外部【详解】情况一：如下图，∵ABC是锐角三角形∵AD是高，∵AD∵BC∵AB=15，AD=12∵在Rt∵ABD中，BD=9∵AC=13，AD=12∵在Rt∵ACD中，DC=5∵∵ABC的周长为：15+12+9+5=42情况二：如下图，∵ABC是钝角三角形在Rt∵ADC中，AD=12，AC=13，∵DC=5在Rt∵ABD中，AD=12，AB=15，∵DB=9∵BC=4∵∵ABC的周长为：15+13+4=32故选：C【点睛】本题考查勾股定理，解题关键是多解，注意当几何题型题干未提供图形时，往往存在多解情况.18．如图是某商品的商标，由七个形状、大小完全相同的正六边形组成．我们称正六边形的顶点为格点，已知∵ABC的顶点都在格点上，且AB边位置如图所示，则∵ABC是直角三角形的个数有（）A．6个B．8个C．10个D．12个【答案】C【分析】根据正六边形的性质，分AB是直角边和斜边两种情况确定出点C的位置即可得解．【详解】如图所示：AB是直角边时，点C共有6个位置，即有6个直角三角形，AB是斜边时，点C共有4个位置，即有4个直角三角形，综上所述，∵ABC是直角三角形的个数有6+4=10个.故答案选：C.【点睛】本题考查的知识点是正多边形和圆, 勾股定理的逆定理，解题的关键是熟练掌握正多边形和圆, 勾股定理的逆定理.。