(完整版)复数知识点归纳及习题

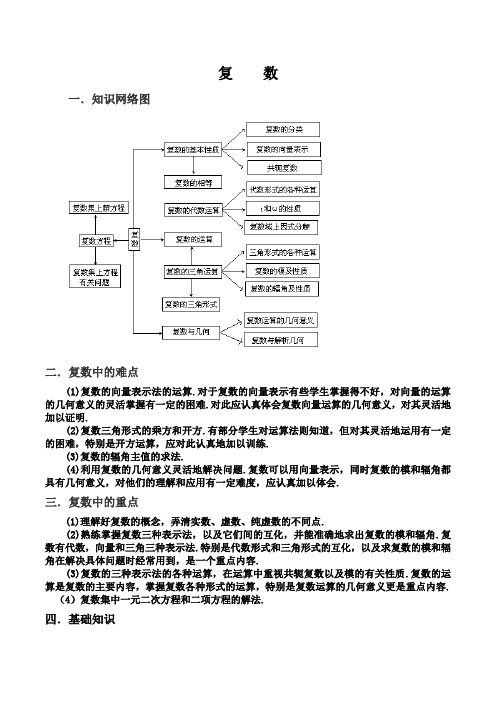
复数
一．知识网络图
二．复数中的难点
(1)复数的向量表示法的运算.对于复数的向量表示有些学生掌握得不好，对向量的运算的几何意义的灵活掌握有一定的困难.对此应认真体会复数向量运算的几何意义，对其灵活地加以证明.
(2)复数三角形式的乘方和开方.有部分学生对运算法则知道，但对其灵活地运用有一定的困难，特别是开方运算，应对此认真地加以训练.
(3)复数的辐角主值的求法.
(4)利用复数的几何意义灵活地解决问题.复数可以用向量表示，同时复数的模和辐角都具有几何意义，对他们的理解和应用有一定难度，应认真加以体会.
三．复数中的重点
(1)理解好复数的概念，弄清实数、虚数、纯虚数的不同点.
(2)熟练掌握复数三种表示法，以及它们间的互化，并能准确地求出复数的模和辐角.复数有代数，向量和三角三种表示法.特别是代数形式和三角形式的互化，以及求复数的模和辐角在解决具体问题时经常用到，是一个重点内容.
(3)复数的三种表示法的各种运算，在运算中重视共轭复数以及模的有关性质.复数的运算是复数的主要内容，掌握复数各种形式的运算，特别是复数运算的几何意义更是重点内容.
（4）复数集中一元二次方程和二项方程的解法.
四．基础知识
1．复数的定义：设i 为方程x 2=-1的根，i 称为虚数单位，由i 与实数进行加、减、乘、除等运算。

便产生形如a+bi （a,b ∈R ）的数，称为复数。

所有复数构成的集合称复数集。

通常用C 来表示。

(1) z =a +bi ∈R ⇔b =0 (a,b ∈R )⇔z=z ⇔ z 2≥0； (2) z =a +bi 是虚数⇔b ≠0(a ,b ∈R )；
(3) z =a+b i 是纯虚数⇔a =0且b ≠0(a,b ∈R )⇔z ＋z ＝0（z≠0）⇔z 2<0； (4) a +b i=c +di ⇔a =c 且c =d (a,b,c,d ∈R )； 2．复数的几种形式。

对任意复数z=a+bi （a,b ∈R ），a 称实部记作Re(z),b 称虚部记作Im(z). z=ai 称为代数形式，它由实部、虚部两部分构成；若将(a,b)作为坐标平面内点的坐标，那么z 与坐标平面唯一一个点相对应，从而可以建立复数集与坐标平面内所有的点构成的集合之间的一一映射。

因此复数可以用点来表示，表示复数的平面称为复平面，x 轴称为实轴，y 轴去掉原点称为虚轴，点称为复数的几何形式；如果将(a,b)作为向量的坐标，复数z 又对应唯一一个向量。

因此坐标平面内的向量也是复数的一种表示形式，称为向量形式
3．共轭与模，若z=a+bi ，（a,b ∈R ）,则=z a-bi 称为z 的共轭复数。

模与共轭的性质有：（1）
2121z z z z ±=±；（2）2121z z z z ⋅=⋅；（3）2||z z z =⋅；（4）2
12
1
z z z
z =⎪⎪⎭⎫ ⎝⎛；（5）||||||2121z z z z ⋅=⋅；（6）|
||
|||
2121z z z z =
；（7）||z 1|-|z 2||≤|z 1±z 2|≤|z 1|+|z 2|；（8）|z 1+z 2|2+|z 1-z 2|2=2|z 1|2+2|z 2|2；（9）若|z|=1，则z
z 1=。

4．复数的运算法则：（1）按代数形式运算加、减、乘、除运算法则与实数范围内一致，运算结果可以通过乘以共轭复数将分母分为实数；（2）按向量形式，加、减法满足平行四边形和三角形法则；
复数的代数形式及其运算：设z 1= a + bi , z 2 = c + di (a,b,c,d ∈R )，则： (1) z 1±z 2 = (a + b )± (c + d )i ；
(2) z 1.z 2 = (a +bi )·(c +di )＝（ac -bd ）+ (ad +bc )i ； (3) z 1÷z 2 =
=-+-+))(())((di c di c di c bi a i d
c a
d bc d c bd ac 2222+-+++ (z 2≠0) ; 几个重要的结论：
(1) i i 2)1(2±=±(2) i 性质：T=4；i i i i i i n n n n -=-===+++3424144,1,,1；;03424144=++++++n n n i i i i
(3) z z z z z 1
11=
⇔=⇔=。

；⑷;11;11i i
i i i i -=+-=-+ 运算律：（1）);,())(3(;))(2(;2121N n m z z z z z z z z z m
m
m
mn n m n m n m ∈=⋅==⋅+
共轭的性质：⑴2121)(z z z z ±=± ；⑵2121z z z z ⋅= ；⑶2
121)(
z z
z z = ；⑷ z z =。

模的性质：⑴||||||||||||212121z z z z z z +≤±≤-；⑵||||||2121z z z z =；⑶|
||
|||
2121z z z z =；⑷
n n z z ||||=；
5.复数相等的充要条件：两个复数实部和虚部分别对应相等。

6．复数z 是实数的充要条件是z=z ;z 是纯虚数的充要条件是：z+z =0（且z ≠0）.
五．习题
1．已知a ∈R ，若(1－ai )(3＋2i )为虚数，则a 的值为( )
A ．－32 B.32 C ．－23 D.23
2．复数
i 1＋2i
(i 是虚数单位)的实部是( )
A.25 B ．－25 C.15 D ．－15
3．复数z 是实数的充要条件是（ ） Ａ．z z =
Ｂ．z z =
Ｃ．2z 为实数
Ｄ．z z +为实数
4．若复数z 满足10
12z z i
-=-，则z 等于（ ） Ａ．34i -+ Ｂ．34i -- Ｃ．34i - Ｄ．34i +
5．
2
13(3)
i i -+等于（ ）
Ａ．1
344
i +
Ｂ．134
4i --
Ｃ．1322
i + Ｄ．1322
i --
6．z ∈C ，若{}
2
2(1)1M z z z =-=-|，则（ ） Ａ．{}M =实数
Ｂ．{}M =虚数
Ｃ．{}{}M
实数复数苘 Ｄ．{}M ϕ=
7．已知复数1z a bi =+，21()z ai a b =-+∈R ，，若12z z <，则（ ） Ａ．1b <-或1b >
Ｂ．11b -<< Ｃ．1b >
Ｄ．0b >
8．(32)(1)i i +-+表示（ ）
Ａ．点(32)，与点(11)，之间的距离 Ｂ．点(32)，与点(11)--，之间的距离 Ｃ．点(32)，与原点的距离 Ｄ．点(31)，与点(21)，之间的距离 9．已知z ∈C ，21z -=，则25z i ++的最大值和最小值分别是（ ） 411411
Ｂ．3和1 Ｃ．523439 3
10．设0<θ<
π2
，(a ＋
22i )(1－i )＝cos θ＋2
2
i ，则θ的值为( )
A.
2π3 B.3π4 C.π3 D.π4
11．若x ∈C ，则方程13x i x =+-的解是（ ） Ａ．132
2
i +
Ｂ．1241x x ==-， Ｃ．43i -+
Ｄ．1322
i --
12．满足条件22z i z +-+=的复数z 在复平面内对应的点的轨迹是 （ ） Ａ．双曲线
Ｂ．双曲线的一支
Ｃ．两条射线
Ｄ．一条射线
13．设A ，B 为锐角三角形的两个内角，则复数(cot tan )(tan cot )z B A B A i =-+-对应的点位于复平面（ ） Ａ．第一象限
Ｂ．第二象限
Ｃ．第三象限
Ｄ．第四象限
14．已知复数)()65(1
672
2
2R a i a a a a a z ∈--+-+-=，那么当a=_______时，z 是实数；当a ∈__________时，z 是虚数；当a=______时，z 是纯虚数。

15．若()1()f z z z =-∈C ，已知123z i =+，25z i =-，则1
2z f z ⎛⎫
= ⎪ ⎪⎝⎭
．
16．复数22(32)(28)z m m m m i =-++--的共轭复数在复平面上的对应点在第一象限内，则实数m 的取范围是 ．
17．已知1z =，则复数234z i ω=+-，对应点的轨迹是 ．
18．设222log (33)log (3)()z m m i m m =--+-∈R ，若z 对应的点在直线210x y -+=上，则m 的值是 ．
19.已知向量1OZ 对应的复数是i 45-，向量2OZ 对应的复数是i 45+-， 则1OZ +2OZ 对应的复数是___________。

20．复数z 1＝3＋4i ，z 2＝0，z 3＝c ＋(2c －6)i 在复平面内对应的点分别为A ，B ，C 若∠BAC 是钝角，则实数c 的取值范围为________．
21．已知复数3z z -对应的点落在射线(0)y x x =-≤上，12z +=，求复数z ．
22．已知z 是复数，2z i +与2z
i
-均为实数，且复数2()z ai +在复平面上对应的点在第一象限，求实数a 的取值范围．。