热力学课后习题01答案
热力学统计物理 课后习题 答案

第一章 热力学的基本规律1.1 试求理想气体的体胀系数α,压强系数β和等温压缩系数κT 。
解:已知理想气体的物态方程为nRT pV =由此得到 体胀系数TpV nR T V V p 11==⎪⎭⎫ ⎝⎛∂∂=α, 压强系数T pV nR T P P V 11==⎪⎭⎫ ⎝⎛∂∂=β 等温压缩系数p p nRT V p V V T 1)(112=-⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛∂∂-=κ 1.2证明任何一种具有两个独立参量T ,P 的物质,其物态方程可由实验测量的体胀系数和等温压缩系数,根据下述积分求得()⎰-=dp dT V T καln ,如果P T T 1,1==κα,试求物态方程。
解: 体胀系数 pT V V ⎪⎭⎫ ⎝⎛∂∂=1α 等温压缩系数 TT p V V ⎪⎪⎭⎫ ⎝⎛∂∂-=1κ 以T ,P 为自变量,物质的物态方程为 ()p T V V ,=其全微分为 dp V dT V dp p V dT T V dV T Tp κα-=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= dp dT VdV T κα-= 这是以T ,P 为自变量的完整微分,沿一任意的积分路线积分,得()⎰-=dp dT V T καln 根据题设 , 若 pT T 1,1==κα ⎰⎪⎪⎭⎫ ⎝⎛-=dp p dT T V 11ln 则有 C pT V +=ln ln , PV=CT 要确定常数C ,需要进一步的实验数据。
1.4描述金属丝的几何参量是长度L ,力学参量是张力£,物态方程是(£,L,T)=0,实验通常在大气压下进行,其体积变化可以忽略。
线胀系数定义为FT L L ⎪⎭⎫ ⎝⎛∂∂=1α ,等温杨氏模量定义为TL F A L Y ⎪⎭⎫ ⎝⎛∂∂= ,其中A 是金属丝的截面。
一般来说,α和Y 是T 的函数,对£仅有微弱的依赖关系。
如果温度变化范围不大,可以看作常数。
假设金属丝两端固定。
第一章化学热力学习题参考答案
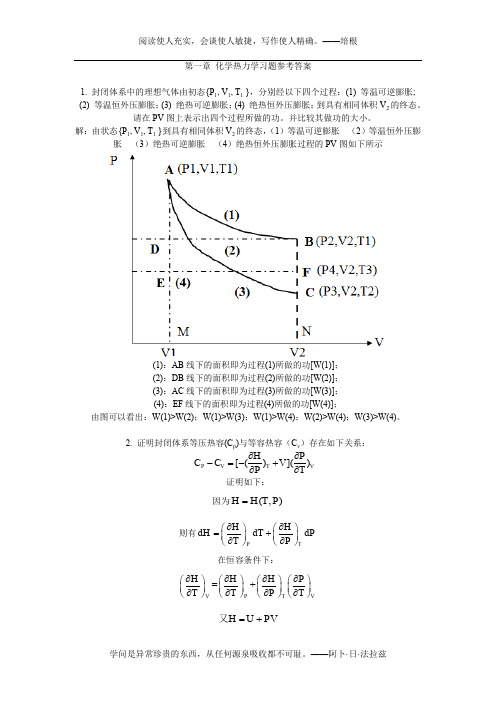
第一章 化学热力学习题参考答案1. 封闭体系中的理想气体由初态{P 1, V 1, T 1 },分别经以下四个过程:(1) 等温可逆膨胀;(2) 等温恒外压膨胀;(3) 绝热可逆膨胀;(4) 绝热恒外压膨胀;到具有相同体积V 2的终态。
请在PV 图上表示出四个过程所做的功。
并比较其做功的大小。
解:由状态{P 1, V 1, T 1 }到具有相同体积V 2的终态,(1)等温可逆膨胀 (2)等温恒外压膨胀 (3)绝热可逆膨胀 (4)绝热恒外压膨胀过程的PV 图如下所示(1):AB 线下的面积即为过程(1)所做的功[W(1)];(2):DB 线下的面积即为过程(2)所做的功[W(2)];(3):AC 线下的面积即为过程(3)所做的功[W(3)];(4):EF 线下的面积即为过程(4)所做的功[W(4)];由图可以看出:W(1)>W(2);W(1)>W(3);W(1)>W(4);W(2)>W(4);W(3)>W(4)。
2. 证明封闭体系等压热容(C p )与等容热容(C v )存在如下关系:[()]()P V T V H P C C V P T∂∂-=-+∂∂ 证明如下:因为(,)H H T P = 则有∂∂⎛⎫⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭P TH H dH dT dP T P 在恒容条件下:V =+P P T V H H H P T T T ∂∂∂∂⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭H U PV =+又U ()则 V V P T VPV H H P T T T P T ∂∂∂∂∂⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+ ⎪ ⎪ ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ U ()=+移项得: P V T V VH H P PV T T P T T ∂∂∂∂∂⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ =V P V T V H P C C P T ⎡⎤∂∂⎛⎫⎛⎫-=- ⎪ ⎪⎢⎥∂∂⎝⎭⎝⎭⎣⎦=V P V T VH P C C P T ⎡⎤∂∂⎛⎫⎛⎫-- ⎪ ⎪⎢⎥∂∂⎝⎭⎝⎭⎣⎦即3. 令 H = H(T, P) 和 S = S(T, P), 根据热力学关系式推导以下关系式:(1)2211[()]T P P P T P V H C dT T V dP T∂∆=+-+∂⎰⎰ (2)2211[()]T P P P T P C V S dT dP T T ∂∆=+-∂⎰⎰ 解答:(1)式证明:()()因为 p T H H dH dT dp T p∂∂=+∂∂ () (1)T H CpdT dp p ∂=+∂ dH TdS Vdp =+又()()T T H S T V p p∂∂=+∂∂则 (2) ()()T P S V p T ∂∂=-∂∂且有麦克斯韦关系式 (3) 将(2)和(3)式代入(1)式得:[()]p P V dH C dT T V dp T ∂=+-+∂ 积分得:2211[()]T P P P T P V H C dT T V dP T∂∆=+-+∂⎰⎰ (2)式证明:因为()()(4)P T S S dS dT dP T P∂∂=+∂∂ 将(3)式代入(4)式得:()[()](5)P p S V dS dT dP T T ∂∂=+-∂∂据dH TdS VdP =+得:()P H T S ∂=∂,即()()P P H T T T S∂∂=∂∂ 因而有:1()()(6)P P P C S H T T T T∂∂==∂∂ 将(6)式代入(5)式得:[()](7)P P C V dS dT dP T T∂=+-∂对(7)式积分得:2211[()]T P P P T P C V S dT dP T T∂∆=+-∂⎰⎰4. 证明卡诺循环中证明:卡诺循环P-V 图如下: Q 2卡诺循环经如下过程(理想气体)1、等温可逆膨胀22U 0T Q W ∆=+=,2222121ln V T V V Q W PdV nRT V =-==⎰ 2、绝热可逆膨胀1,112()Q V U Q W C T T ∆=+=-,,10,Q Q U W =∆=,113222311Q V V nRT V W PdV V γγ-⎡⎤⎛⎫⎢⎥==- ⎪-⎢⎥⎝⎭⎣⎦⎰3、等温可逆压缩Q 211U 0T Q W ∆=+=4411313ln VT V V Q W PdV nRT V =-==⎰ 4、绝热可逆压缩2,221()Q V U Q W C T T ∆=+=-220,,Q Q U W =∆=,214213411Q V V nRT V W PdV V -⎡⎤⎛⎫⎢⎥=-=- ⎪-⎢⎥⎝⎭⎣⎦⎰γγ 12,1,2,Q Q U U W W ∆=-∆=-可知则 12144323,V V V V V V V V ==则有即或:根据绝热可逆过程方程PV =常数可得:1423V V V V = 整个循环过程中:2,11,221T Q T Q T T W W W W W W W =+++=+2211,T T W Q W Q ==又2421131232221ln ln =ln V V nRT nRT V V Q Q W V Q Q nRT V η++==故有1423V V V V =又1221222=Q Q T T W Q Q T η+-==所以有5. 理想气体从始态(P 1, V 1, T 1)到终态 (P 2, V 2, T 2),设计三条不同路径,计算熵变,并证明三条路径所得结果一致。
大学物理化学1-热力学第一定律课后习题及答案

热力学第一定律课后习题一、是非题下列各题中的叙述是否正确?正确的在题后括号内画“√”,错误的画“⨯”。
1.在定温定压下,CO2由饱和液体转变为饱和蒸气,因温度不变,CO2的热力学能和焓也不变。
( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。
( )3. 一个系统从始态到终态,只有进行可逆过程才有熵变。
( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。
( )5. 稳定态单质的∆f H(800 K) = 0。
( )二、选择题选择正确答案的编号,填在各题后的括号内:1. 理想气体定温自由膨胀过程为:()。
(A)Q > 0;(B)∆U < 0;(C)W <0;(D)∆H = 0。
2. 对封闭系统来说,当过程的始态和终态确定后,下列各项中没有确定的值的是:( )。
( A ) Q;( B ) Q+W;(C ) W( Q = 0 );( D ) Q( W = 0 )。
3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是:( )(A)绝热过程;( B)理想气体绝热过程;( C )理想气体绝热可逆过程;(D)绝热可逆过程。
4. 在隔离系统内:( )。
( A ) 热力学能守恒,焓守恒;( B ) 热力学能不一定守恒,焓守恒;(C ) 热力学能守恒,焓不一定守恒;( D) 热力学能、焓均不一定守恒。
5. 从同一始态出发,理想气体经可逆与不可逆两种绝热过程:( )。
( A )可以到达同一终态;( B )不可能到达同一终态;( C )可以到达同一终态,但给环境留下不同影响。
6. 当理想气体反抗一定的压力作绝热膨胀时,则:( )。
( A )焓总是不变;(B )热力学能总是增加;( C )焓总是增加;(D )热力学能总是减少。
7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T),下列说法中不正确的是:()。
第01章热力学基本定律习题及答案

第01章热力学基本定律习题及答案第01章热力学基本定律习题及答案第一章热力学基本定律习题及答案§ 1. 1 (P10)1.“任何系统无体积变化的过程就一定不做功。
”这句话对吗?为什么?解:不对。
体系和环境之间以功的形式交换的能量有多种,除体积功之外还有非体积功,如电功、表面功等。
2. “凡是系统的温度下降就一定放热给环境,而温度不变时则系统既不吸热也不放热。
”这结论正确吗?举例说明。
答:“凡是系统的温度下降就一定放热给环境”不对:体系温度下降可使内能降低而不放热,但能量可以多种方式和环境交换,除传热以外,还可对外做功,例如,绝热容器中理想气体的膨胀过程,温度下降释放的能量,没有传给环境,而是转换为对外做的体积功。
“温度不变时则系统既不吸热也不放热”也不对:等温等压相变过程,温度不变,但需要吸热(或放热),如P?、373.15K下,水变成同温同压的水蒸气的汽化过程,温度不变,但需要吸热。
3. 在一绝热容器中,其中浸有电热丝,通电加热。
将不同对象看作系统,则上述加热过程的Q或W大于、小于还是等于零?(讲解时配以图示)解:(1)以电热丝为系统:Q<0,W>0(2)以水为系统:Q>0,W=0(忽略水的体积变化)(3)以容器内所有物质为系统:Q=0,W>0(4)以容器内物质及一切有影响部分为系统:Q=0,W=0(视为孤立系统)4. 在等压的条件下,将1mol理想气体加热使其温度升高1K,试证明所做功的数值为R。
解:理想气体等压过程:W = p(V2 -V1) = pV2 -PV1= RT2 -RT1= R(T2 -T1) = R5. 1mol 理想气体,初态体积为25dm 3, 温度为373.2K ,试计算分别通过下列四个不同过程,等温膨胀到终态体积100dm 3时,系统对环境作的体积功。
(1)向真空膨胀。
(2)可逆膨胀。
(3)先在外压等于体积50 dm 3时气体的平衡压力下,使气体膨胀到50 dm 3,然后再在外压等于体积为100dm 3时气体的平衡压力下,使气体膨胀到终态。
高中物理热力学第一定律课后习题答案及解析

高中物理热力学第一定律课后习题答案及解析练习与应用1.用活塞压缩汽缸里的空气,对空气做了900 J的功,同时汽缸向外散热210 J,汽缸里空气的内能改变了多少?解析:依题意可得:W=900J,Q=-210J由△U=W+Q得:△U=900+(-210)J=690J答:汽缸里空气的内增加了690J.2.如图3.2-4,在汽缸内活塞左边封闭着一定量的空气,压强与大气压相同。
把汽缸和活塞固定,使汽缸内空气升高一定的温度,空气吸收的热量为Q1。
如果让活塞可以自由滑动(活塞与汽缸间无摩擦、不漏气),也使汽缸内空气温度升高相同温度,其吸收的热量为Q2。
图 3.2-4(1)Q1和Q2哪个大些?(2)气体在定容下的比热容与在定压下的比热容为什么会有不同?解析:(1)题中两种不同情况下,质量的一定的气体升高相同的温度,气体内能增加量相同(温度是分子平均动能的标志),第一种情况气体对外不做功,W1=0第二种情况下,气体对外做功,W2<0。
由热力学第一定律可知,△U=W1+Q1,△U=W2+Q2,比较两式可知,Q2大些;(2)由于在一定量的空气升高相同温度的情况下,Q2>Q1,由根据比热容公式Q=Cm△t得:Q1=C1m△t,Q2=C2m△t,故C2>C1,即气体在定容下的比热容小于在定压下的比热容。
3.某风景区有一处约20层楼高的瀑布,甚为壮观。
请估计:瀑布上、下水潭的水温因瀑布的机械能转化成内能而相差多少?水的比热容c为4.2×103 J/(kg·℃)。
解析:设水的质量为m,上、下水潭的水温差为△t,由能量守恒定律有:mgh=Cm△t;△t=gℎ代入数据解得:△t≈0.14℃;C答:瀑布上、下水潭的水温因瀑布的机械能转化成内能而相差0.14℃。
4.奶牛的心脏停止跳动后,大约在1 h内体温由37.0 ℃降低到33.5 ℃。
请你由此估算,在这种环境下饲养奶牛,要维持一个体重400 kg奶牛的内能不变,每天喂养奶牛的食物至少要能为它提供多少热量?计算时,可以认为奶牛体内绝大部分是水。
热力学与统计物理课后习题答案第一章

1.1 试求理想气体的体胀系数α,压强系数β和等温压缩系数κT 。
解:已知理想气体的物态方程为,pV nRT = (1)由此易得11,p V nR V T pV Tα∂⎛⎫=== ⎪∂⎝⎭ (2) 11,V p nR p T pV Tβ∂⎛⎫=== ⎪∂⎝⎭ (3) 2111.T T V nRT V p V p pκ⎛⎫⎛⎫∂⎛⎫=-=--= ⎪ ⎪ ⎪∂⎝⎭⎝⎭⎝⎭ (4)1.2 证明任何一种具有两个独立参量,T p 的物质,其物态方程可由实验测得的体胀系数α及等温压缩系数κT ,根据下述积分求得:()ln T V =αdT κdp -⎰如果11,T T pακ==,试求物态方程。
解:以,T p 为自变量,物质的物态方程为(),,V V T p =其全微分为.p TV V dV dT dp T p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ (1) 全式除以V ,有11.p TdV V V dT dp V V T V p ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭根据体胀系数α和等温压缩系数T κ的定义,可将上式改写为.T dVdT dp Vακ=- (2) 上式是以,T p 为自变量的完整微分,沿一任意的积分路线积分,有()ln .T V dT dp ακ=-⎰ (3)若11,T T pακ==,式(3)可表为11ln .V dT dp Tp ⎛⎫=- ⎪⎝⎭⎰ (4)选择图示的积分路线,从00(,)T p 积分到()0,T p ,再积分到(,T p ),相应地体积由0V 最终变到V ,有000ln=ln ln ,V T pV T p - 即000p V pV C T T ==(常量), 或.pV CT = (5)式(5)就是由所给11,T T pακ==求得的物态方程。
确定常量C 需要进一步的实验数据。
1.3 在0C 和1n p 下,测得一铜块的体胀系数和等温压缩系数分别为51714.8510K 7.810.n p ακ----=⨯=⨯T 和T ακ和可近似看作常量,今使铜块加热至10C 。
(完整版)第一章热力学的基本规律课后作业及答案

解:已知理想气体的物态方程为 体胀系数1 VV T p压强系数1 PP T V等温压缩系数T1V pV nRTnR 1 pV T ,nR 1pV TV1 ’ n RT 、 1( 2 )p TV p p由此得到d PP T dTVp dT—dTTP 2 P 1___ T 2dTT 1—T 2 T_1TT11lnV(―dT d p)T P⑷积分pV CT1.3测得一块铜块的体胀系数和等 温压缩系数分别为4.85 10 5K 1和T 7.8*10 7P n 1,和T 可近似Q W 7.47 103 J1.5在25 C 下,压强在0至lOOOP n 之间,测得水的体积为3 6 2 3V (18.066 0.715 10 p 0.046 10 p )cm mol如果保持温度不变,将 1mol 的水从1 p n 加压至1000 p n ,求外界所做的功。
保持温度不变,将1mol 的水由1p n 加压至1000p n ,外界所做的功为在上述计算中我们已将过程近似看作准静态过程。
定容比热容可由所给定压比热容算出维持体积不变,将空气由 0 C 加热至20 C 所需热量Q v 为Q 口6仃2 T 1) 34.83 0.706 103 20J 4.920 105 J(b) 维持压强不变,将空气由 0 C 加热至20 C 所需热量Q p 为Q p m 1 c p (T 2 T 1) 34.83 0.996 1 03 20J 6.938 105 J(c) 若容器有裂缝,在加热过程中气体将从裂缝漏出,使容器内空气质量发生变化•根据理想气体的物 态方程解将题中给出的体积与压强关系记为 由此易得V a bp cp 2dV (b2cp)d p(1)V B V A P *V B V Ap(b2cp)d p1000 1,2 2 3-bp -cp 2 3“33.1J mol1.6在0 C 和15下,空气的密度为 今有27m 3的空气,试计算:(a) 若维持体积不变,将空气由 (b) 若维持压强不变,将空气由 (c) 若容器有裂缝,外界压强为 解(a)由题给空气密度可以算得1.29kg m 3。
工程热力学第一章课后答案

第一章 基本概念1-1 英制系统中采用华氏温标,它规定在标准大气压(101325Pa )下纯水的冰点是32F °,汽点是212F °,试推导华氏温度与摄氏温度的换算关系。
解:C F {}0{}32212321000t t °°−−=−−F C C 1809{}{}32{}321005t t t °°°=+=+1-2 英制系统中朗肯温度与华氏温度的关系为R F {}{}459.67T t °°=+。
已知热力学绝对温标及朗肯温标在纯水冰点的读数分别是273.15K 和491.67R °;汽点的读数分别是373.15K 和671.67R °。
(1)导出朗肯温度和开尔文温度的关系式;(2)开尔文温标上绝对零度在朗肯温标上是多少度?解:(1)若任意温度T 在朗肯温标上读数为(R)T °在热力学绝对温标上读数为T (K ), 则671.67491.67(R)491.67373.15273.15(K)273.15T T −°−=−−解得R K{} 1.8{}T T °=(2)据上述关系K {}0T =时,R {}0T °=1-3 设一新温标,用符号N °表示温度单位(它的绝对温标是用Q °表示温度单位)。
规定纯水的冰点和汽点100N °和1000N °。
试求:(1)该新温标与摄氏温标的关系;(2)若该温标的绝对零度与热力学温标零度相同,则该温标读数为0N °时,其绝对温标读数是多少Q °?解:(1)N C {}100{}010001001000t t °°−−=−−N C {}9{}100t t °°=+(2) Q N C K {}{}9{}1009[{}273.15]100T t C t C T C °°°=+=++=−++据题意,当K {}0T =时,Q {}0T °=,解得上式中2358.35C =,代回原式得Q N {}{}2358.35T t °°=+N {}0T °=时,2358.385Q T =°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章 基本概念
1-1 为了环保,燃煤电站锅炉通常采用负压运行方式。
现采用如图1-16所示的斜管式微压计来测量炉膛内烟气的真空度,已知斜管倾角α=30º,微压计中使用密度ρ=1000kg/m 3的水,斜管中液柱的长度l =220mm ,若当地大气压p b =98.85kPa ,则烟气的绝对压力为多少Pa ?
图1-16 习题1-1
解:大气压力98.85kPa 98850Pa b p ==
真空度3sin 1000kg/m 9.81N/kg 0.22m 0.51079.1Pa v p gl ρα==×××=
烟气的绝对压力98850Pa 1079.1Pa 97770.9Pa b v p p p =−=−=
1-2 利用U 形管水银压力计测量容器中气体的压力时,为了避免水银蒸发,有时需在水银柱上加一段水,如图1-17所示。
现测得水银柱高91mm ,水柱高20mm ,已知当地大气压p b =0.1MPa 。
求容器内的绝对压力为多少MPa ?
图1-17 习题1-2
解:容器内的压力高于大气压力,因此绝对压力b e p p p =+
表压力291mmHg+20mmH O 91133.3Pa 209.81Pa 0.0123MPa e p ==×+×≈
大气压力0.1MPa b p =
容器内的绝对压力0.1MPa 0.0123MPa 0.1123MPa b e p p p =+=+=
1-3 某容器被一刚性隔板分为两部分,在容器的不同部位安装有压力计,其中压力表B
放在右侧环境中用来测量左侧气体的压力,如图1-18所示。
已知压力表B 的读数为80kPa ,压力表A 的读数0.12MPa ,且用气压表测得当地的大气压力为99kPa ,试确定表C 的读数,及容器内两部分气体的绝对压力(以kPa 表示)。
如果B 为真空表,且读数仍为80kPa ,表C 的读数又为多少?
图1-18 习题1-3
解:(1)容器左侧(A )的绝对压力,99kPa 120kPa 219kPa b e A p p p =+=+=A
压力表B 的读数为容器左侧(A )的绝对压力A p 和容器右侧(C )的绝对压力C p 之差,因此,e B C p p p =−A ,得,219kPa 80kPa 139kPa C e B p p p =−=−=A
同时,b e C p p p =+C ,可得压力表C 的读数为,139kPa 99kPa 40kPa e C p =−=
(2)如果表B 为真空表,则,v B A p p p =−C ,得299kPa C p =,因此压力表C 的读数为,200kPa e C p =
1-4 如图1-19所示,容器A 放在B 中,用U 形管水银压力计测量容器B 的压力,压力计的读数为L =20cm ,测量容器A 的压力表读数为0.5MPa ,已知当地大气压力p b =0.1MPa ,试求容器A 和B 的绝对压力。
图1-19 习题1-4
解:容器B 的绝对压力6
,0.110Pa 200133.3Pa 0.127MPa b e B p p p =+=×+×≈B
测容器A 压力表的读数,e A p 为容器A 的绝对压力A p 和容器B 的绝对压力B p 之差,因此,e A B p p p =−A ,得容器A 的绝对压力0.5MPa 0.127MPa 0.627MPa p =+=A
1-5 凝汽器的真空度为710mmHg ,气压计的读数为750 mmHg ,求凝汽器内的绝对压
力为多少kPa ?若凝汽器内的绝对压力不变,大气压力变为760 mmHg ,此时真空表的读数有变化吗?若有,变为多少?
解:凝汽器内的绝对压力750mmHg 710mmHg 40mmHg 5.332kPa b v p p p =−=−==
凝汽器中的绝对压力保持不变,大气压力变化时,真空表读数有变化,
真空表读数变为760mmHg 40mmHg 720mmHg v b p p p =−=−=
1-6 在英、美等国在日常生活和工程技术上还经常使用华氏温标(英制单位)t F.。
.在1标
()2
1222411510J 2V V a W pdV aV b dV V bV ⎛⎞==+=+=−×⎜⎟⎝⎠∫∫ 在p -V 图上表示此压缩过程:。
