公差分析流程
进阶篇:5.1)公差分析的总流程

进阶篇:5.1)公差分析的总流程本章⽬标:了解公差分析的所有流程,按部就班就好。
1.前⾔如果现在结构设计能拿出⼀种挂在嘴上的技术的话,那⾮公差分析莫属。
(很多⼈不把画图当回事了)公差分析说难也⾮常难,深⼊研究就是⼀辈⼦的技术。
说简单也简单,⼊门时好好按照流程做⼏个项⽬实例,就能有⼀定的基础。
这⼀章作者就为⼤家梳理⼀下公差分析流程。
2.公差分析的总流程1)定义公差分析的⽬标尺⼨和判断标准;2)建⽴闭合尺⼨链;3)将⾮对称公差转成对称公差;4)判断尺⼨链中尺⼨的正负;5)计算⽬标尺⼨的名义值;6)选⽤公差分析的⽅法7)公差分析的计算;8)判断和优化;9)公差分析结果图纸标注,统计公差法标注对应符号。
2.1 公差流程要点讲解①定义公差分析的⽬标尺⼨和判断标准;--因为作者(mdmodule博主)要求是做完⼀整个产品的公差分析,所以这⼀条尤为重要。
甚⾄⼤部分时间不是花在做公差分析的计算上,因为作者提供表格辅助计算。
反⽽是定义公差分析的⽬标尺⼨和判断标准更花时间。
这⼀点作者会单独开⼀个分章书写。
②判断和优化--作者认为结构设计的优化⽐公差的优化更加能提升量产品的质量,简单来说,与其做公差优化,不如做DFMA来的划算;③选⽤公差分析的⽅法--选⽤统计法的话,理论上图纸是要特殊符号标注的。
作者推荐极值法为保底的⽅法,必须做。
但最后选定哪种⽅法,可以和质量管理⼈员沟通⼀下,最好在会议上提出。
④公差分析结果图纸标注,统计公差法标注对应符号--作者到底是⼀名结构设计师,设计师就要画图。
所以图纸上的尺⼨公差必须要和公差分析的结论相⼀致。
这⼀点的任务是最繁重的,⼜不得不做。
先要核算每⼀个公差在各种公差分析分析中处于最优解,然后修正对应的图纸尺⼨公差。
真的很累。
第4部分:公差分析

22
四. 公差分析的计算方法
DFMA
4. 极值法与均方根法的区别
当零件尺寸公差都是±0.1时,利用WC和RSS方法的计算结果区别如下: WC方法的累积公差更大,计算结果更大
23
四. 公差分析的计算方法
DFMA
4. 极值法与均方根法的区别
当产品装配公差要求是±0.5时,利用WC和RSS方法,对零件尺寸公差要 求的区别(假设尺寸链中的每个尺寸分配相同的公差)
减少尺寸链的长度,尺寸允许较大的公差
13
二. 公差分析
DFMA
C.使用定位特征
在零件的装配关系中增加可以定位的特征,例如定位柱等,定位特征能 够使得零件准确的装配在产品之中,产品设计只需要对定位特征相关的 尺寸公差进行制程管控,对其他尺寸就可以允许宽松的公差要求
D.使用点或线或小平面与平面配合代替平面与平面配合
DFMA
第4部分:公差分析 Tolerance Analysis
内容:
一.常见的公差分析做法 二.公差分析 三.公差分析的计算步骤 四.公差分析的计算方法 五.公差分析的三大原则 六.产品开发中的公差分析
DFMA
2
一. 常见的公差分析做法
DFMA
1. 产品详细设计完成后,在design review时,针对O-ring的压缩量进行
使用点或线与平面配合的方式代替平面与平面的配合方式,避免平面的 变形或者平面较高的粗糙度阻碍零件的顺利运动,从而可以对零件的平 面度和粗糙度允许宽松的公差
原始的设计
优化的设计
14
二. 公差分析
DFMA
4.公差分析的概念:
公差分析是指在满足产品功能、性能、外观和可装配性等要求的前提下, 合理定义和分配零件和产品的公差,优化产品设计,以最小的成本和最 高的质量制造产品
公差分析基础课件

根据分析结果,评估现有 公差方案的优劣,提出优 化方案,并进行实施。
在产品生命周期中持续进 行公差分析,不断优化公 差方案,提高产品质量和 降低制造成本。
02
公差分析的数学基础
概率论与数理统计
概率论
概率论是研究随机现象的数学学科,它为公差分析提供了理 论基础。概率论可以帮助我们理解随机变量的分布、期望值 、方差等概念,这些概念在公差分析中非常重要。
公差优化设计的方法与步骤
确定设计目标
明确产品性能要求,确定需要优化的关键公差项。
建立数学模型
根据实际需求,建立公差优化问题的数学模型,包括目标函数、约束条件等。
求解数学模型
采用适当的优化算法,求解数学模型以获得最优解。
分析结果
对优化结果进行分析,评估其对产品性能的影响,并据此进行必要的调整。
公差优化设计实例
VS
实例二
某箱体类零件的孔径为φ10H7,要求其 与轴类零件的配合精度为H8/s7。根据尺 寸公差的计算方法,我们可以计算出该孔 径的尺寸公差,并分析其对配合精度的影 响。
04
形位公差分析
形位公差的基本概念
形位公差
描述零件几何形状、尺寸和相对位置的允许变动范围 的参数。
形位公差包括
形状公差和位置公差。
公差分析的未来发展方向
跨学科融合
将公差分析与其他工程学科、数学、统计学 等学科进行交叉融合,推动公差分析理论和 方法的发展。
云平台与大数据技术
利用云平台和大数据技术,实现公差数据的存储、 处理和分析,提高分析效率和精度。
标准化与规范化
制定和完善公差分析的标准化和规范化体系 ,推动公差分析在工业界的广泛应用。
THANKS
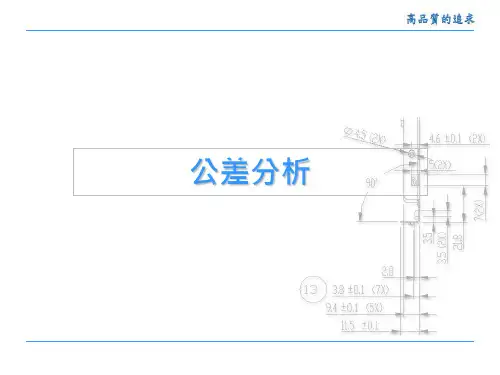
公差分析

0.52 (74) 2 (0.5) 2 (46) 2 (1) 2 (20) 2 48m
0 Ci i
0.5(67) (0.5)23 0 45m
L0 = L1/2 – L2/2 – L3 C1 =0.5 C2 =-0.5 C3 =-1
0.030 L1 80 f 9 80 0.104 0.046 L2 60H 8 600
20
/ 44
校核计算 例
如图所示的套筒,试判断套筒壁厚尺寸是否超过10mm。
第3步 RSS法计算
T1 = 74 μm μ1 = (ES1 + EI1 ) /2 = -67 μm
T2 = 46 μm μ2 = 23 μm T3 = 20 μm μ3 = 0 μm
L0 = L1/2 – L2/2 – L3 C1 =0.5 C2 =-0.5 C3 =-1
WC法 (完全互换)
T0 = 0.08 mm
0.005 10 0.085 mm
RSS法 (大数互换)
T0 = 0.048 mm
0.021 10 0.069 mm
23
/ 44
设计计算
24
/ 44
设计计算
已知封闭环的极限尺寸,求各组成环的极限偏差
L0 = f (L i) 例
如图所示的齿轮传动箱中,为了保证轴的顺利转动,要求装配以后的 轴向间隙X为1~1.75 mm。若已知A1=101mm、A2=50mm、A3=A5=5mm、 A4=140mm, 试设计A1、A2、A3、A4和A5各尺寸的公差和极限偏差。
L3 0 t / 2 0 0.01
19
/ 44
校核计算 例
如图所示的套筒,试判断套筒壁厚尺寸是否超过10mm。
公差分析
☆.產品設計變更的可行性評估. 產品設計變更的可行性評估.
設計變更後的組裝性的檢查,看部件的配合性. 設計變更後的組裝性的檢查,看部件的配合性.
BACK
公差分析--公差分析---做公差分析和方法和步驟 ★. 做公差分析方法和步驟
☆. 原始數據的收集. 原始數據的收集.
(規格,實際量測數據) 規格,實際量測數據)
☆.互換性的分類: 互換性的分類:
按照互換範圍的不同,可分為完全互換(絕對互換)和不完全互換(有限互換)。完全互換在機械製造中 按照互換範圍的不同,可分為完全互換(絕對互換)和不完全互換(有限互換)。完全互換在機械製造中 應用廣泛。但是,在單件生產的機器中(特重型、特高精度的儀器),往往採用不完全互換。這是因為在這種 情況下,完全互換將導致加工困難(甚至無法加工)或製造成本過高。為此,生產中往往把零、部件的精度適 當降低,以便於製造。然後再根據實測尺寸的大小,將製成的相配零、部件各分成若干組。使每組內尺寸差別 比較小。最後再把相應組的零、部件進行裝配。這樣既解決了零部件的加工困難,又保證了裝配的精度要求。
☆.Shielding Frame折彎角度從90設計變更性99的評估. Frame折彎角度從90設計變更性99的評估.
此設計變更的可行性評估,折彎角度變更後shielding Frame內空間能否容納高度增加後的電容,干涉 此設計變更的可行性評估,折彎角度變更後shielding Frame內空間能否容納高度增加後的電容,干涉 性的檢查。
☆.Shielding Frame折彎角度從90設計變更性99的評估. Frame折彎角度從90設計變更性99的評估.
BACK
公差分析--公差分析---結束 ★.結束
END
BACK
公差分析讲义PPT学习教案

RSS
4. 公差分析方法
确定 System的允许差后, 通过 Tolerance Analysis, 参考工程能力, 进行System的 工程能力分析, 最后确定CTQ的允许公差
Min/Max
最初的 设计构想图
✓ 目标尺寸 (Target)
❖ USL/LSL
- USL: Upper Spec Limit,规格上限 - LSL: Lower Spec Limit,规格下限。
❖ Tolerance (公差)
- 指顾客允许的限界尺寸 (USL 和 LSL) - 用数字确定 - 适用于组装品的特性和单位部品中
❖ Min / Max(极限公差法,即Worst Case法)
活用基准 Data
4.65 X σLT 6.15 X σST
假设是长期工程时 : 使用生产 Data 假设工程是在管理状态下 假设是短期工程Data时 : 使用新规模具
活用 Six Sigma 6.15 X σST 方法
以合理的 Subgroup收集Data Data 分为短期, 长期
第4页/共28页
良好的公差适用的优点
❖ 组装时的恰当性和机能向上 ❖ 可以对基本设计构成进行更好的
Sensitivity Analysis ❖ 减少模具修正的频度
对现 System的认识不足 会导致不完整的开发
第5页/共28页
1. 公差分析
7. 统计性公差分析的类型
1) 线性公差分析 ❖ 性能的函数式由构成部品尺寸的加减构成时, 称此式为线性的, 且性能的标准偏差用Root Sum of Square (RSS)求出.
Block Box(左 侧 )
公差分析
zemax公差分析步骤1、在zemax中editors中首先找到tolerance data,单击,出现如下图框。
2、在跳出来的图框中找到tools,从中找到default tolerances,单击,出现如下图框。
其中各个公差含义,可以查阅zemax指导书。
3、下面只对曲率半径公差对于结构的影响进行分析,作为事例。
首先设置曲率半径公差,其选择默认设置,0.2mm,实际设置时候可以比这个小。
Test wave按照结构设置为中心波长,然后点确定。
4、完成上一步后,第一步的表格变为如下。
5、然后点击tools中的,其有三个选项,选择第一个tolerancing。
跳出如下图框。
其中相关设置的意思,在zemax指导书中有相关解释,如公差分析模式,这多选用灵敏度分析法sensitivity。
这里面有相干蒙特卡罗分析设置。
6、到此公差分析的前期设置就好了,点击确定,zemax将对曲率半径公差为0.2mm进行分析,分析结果将跳出一个图框进行显示。
如下。
红框中显示的是我们前期的一些设置。
绿框中是灵敏度分析的结果,和统计分析,小框中即是那些曲率半径变化对成像质量影响较大的面。
Ps:此为zemax公差分析步骤,具体设置的含义,请参考zemax指导书。
20150528天光所附录:第十九章公差规定介绍ZEMAX 提供了一个使用简单,但灵活和强大的公差推导和灵敏度分析能力。
这个用于分析的公差包括了结构参数的变化,如曲率、厚度、位置、折射率、阿贝常数、非球面系数,以及其它更多的参数。
ZEMAX 也支持表面和镜头组的偏心分析,表面或镜头组在任意一点的倾斜分析,表面外形的不规则分析,以及参数或特殊数据的值的变化分析。
由于参数和特殊数据项可以说明非球面系数,梯度折射率系数,以及其它,因此这些数值的任意一个也都可以作为公差分析的一部分。
不同的公差可以被用在任意一个组合中来估计调整和装配误差对系统性能的影响。
公差也可以使用简单的操作数来定义,如TRAD,它定义了一个曲率半径的一个公差。
公差分析报告
公差分析报告1. 引言公差分析是制造过程中的重要环节,它用于确定产品在设计规格和制造能力范围内的变化范围。
本报告旨在对产品的公差进行分析,以便评估其设计和制造的可行性,并提供相应的决策依据。
2. 制造过程概述在进行公差分析前,我们首先需要了解产品的制造过程。
该制造过程包括以下几个主要步骤:1.设计:根据需求和规格,进行产品的设计和参数确定。
2.制造:使用合适的材料和工艺对产品进行加工和制造。
3.检验:对制造完成的产品进行检验和测试,确保其符合设计要求。
4.调整:根据检验结果,进行必要的调整和修正。
3. 公差分析方法公差分析是通过数学和统计方法来评估产品在设计和制造过程中的变异范围。
在本报告中,我们使用以下两种主要的公差分析方法:3.1. 极限公差分析极限公差分析是一种确定产品尺寸上限和下限的方法。
通过结合产品设计规格和制造能力,我们可以确定产品尺寸的变化范围,以确保产品的功能和质量。
3.2. 统计公差分析统计公差分析是一种基于统计学原理的公差分析方法。
通过对制造过程中的数据进行统计分析,我们可以评估产品的公差分布和控制能力,从而确定制造过程的优化方向。
4. 公差分析结果经过对产品的公差分析,我们得到以下结果:1.产品尺寸公差范围:–长度:±0.1mm–宽度:±0.05mm–高度:±0.2mm2.制造过程能力:–长度:CPK值为1.2,处于良好控制范围。
–宽度:CPK值为0.8,处于较差控制范围。
–高度:CPK值为1.5,处于优秀控制范围。
5. 公差分析结论基于以上结果,我们得出以下结论:1.产品的设计公差范围与制造能力相匹配,能够满足设计要求。
2.在制造过程中,需要进一步优化宽度的控制能力,以确保产品质量稳定性。
3.针对高度的控制能力,制造过程表现出优秀的稳定性。
4.建议在制造过程中加强对宽度的监控和控制,以提高产品一致性和稳定性。
6. 结论与建议根据公差分析的结果和结论,我们提出以下建议:1.在产品设计阶段,应合理确定公差范围,以准确反映产品功能和要求。
公差分析简介
§ 公差分析简介 §一、 前言于新产品之开发过程中,为确认组件可达到预期之功能,并做适当之公差订定及分配,应于开模前作公差分析,求出一功能尺寸(如于Inkjet printer 中之PPS ,pen to paper space )经一回路之公差累积后之最差尺寸(worst case )。
若该最差尺寸不符合规格之要求,则可考虑紧缩某些尺寸之公差,或重新设计,以缩短回路或使该功能尺寸可调整。
二、 方法2.1 为简化计算,先将极限尺寸改为平均尺寸,如:10 ± →(10+1/2)±1/2=10.5 ± 0.52.2 一回路中之公差可分为二类:各组件自身之制造公差及组件间之组装公差(即定位公差)。
参阅附图,该组件由Part A 及Part B 等二组件所组成,其中Part A 设有定位Boss 且Part B 设有定位孔。
Part A 之定位Boss 至基准面之距离,40±0.1,即为一制造公差。
而组装公差则由Part A 之Boss 之尺寸ψ10+0/-0.1及Part B 之孔之尺寸ψ10.2+0.1/-0所决定,说明如下:Boss ψ10+0/-0.1 →ψ9.95 ± 0.05 孔ψ10.2+0.1/-0 →ψ10.25 ± 0.05间隙之设计值=(10.25-9.95)÷ 2=0.15组装公差= ±(0.15+0.05/2+0.05/2)= ± 0.202.3以附图为例,于该组件中, Part B 之face X 与Part A 之reference face 之距离为一功能尺寸,欲知其最差尺寸,说明如下:○1以Part A 之reference face 为基准,该公差循环(tolerance loop )包括a , b , c , d , e , f 等6个尺寸,其中b , c , d 属于组装公差 ○2依序列出各尺寸之公称值及平均化后之公差,其中公称值应视为向量,故f 为负值○3求出各公称尺寸及公差之总合,其分别为0及0.4,其中公称值之总合可视为一验算。
机械制图机公差分析
机械制图机公差分析1. 简介机械制图中,公差是指产品实际大小与理论设计大小的偏差。
公差分析是机械制图过程中的一个重要环节,旨在确定产品各个部件之间的公差范围,以确保产品的质量和性能达到设计要求。
本文将介绍机械制图中的公差分析方法和应用。
2. 公差分析的意义公差分析是机械制图中的关键环节,它的意义主要体现在以下几个方面:•确定产品的功能性能:公差分析可以确定产品各个部件之间的尺寸偏差范围,以确保产品在装配和使用过程中的功能性能正常。
•优化产品结构:公差分析可以通过调整各个部件之间的公差范围,优化产品的结构设计,提高产品的性能、可靠性和经济性。
•降低生产成本:公差分析可以通过合理设置公差范围,降低产品的制造成本,提高生产效率。
•提高产品质量:公差分析可以帮助设计人员在设计初期就考虑到公差问题,从而减少产品出现质量问题的可能性,提高产品的质量。
3. 公差分析的方法3.1 传统公差分析方法传统公差分析方法主要包括以下几个步骤:1.制图:在机械制图软件中绘制产品的图形模型。
2.确定公差要求:根据产品的设计要求和功能性能要求,确定各个部件的公差要求。
3.确定公差链:根据产品的装配结构,在制图软件中确定各个部件之间的公差链,即公差依赖关系。
4.公差分配:根据公差链,将产品的公差进行逐级分配,确定各个部件的公差范围。
5.公差评估:根据公差范围,对产品的功能性能进行评估,确定是否满足设计要求。
6.优化调整:根据评估结果,对公差范围进行优化调整,以满足产品的设计要求。
3.2 计算机辅助公差分析方法随着计算机技术的不断发展,计算机辅助公差分析方法逐渐成为主流。
计算机辅助公差分析方法主要包括以下几个步骤:1.数字化模型建立:通过三维建模软件,将产品的三维模型进行数字化建模。
2.公差要求设置:在数字化模型中设定各个部件的公差要求。
3.公差分配:根据公差链和公差要求,通过计算机辅助公差分配软件,自动进行公差分配。
4.公差仿真:通过计算机辅助公差仿真软件,对产品进行公差仿真分析,评估产品的性能和质量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• •
•
Determine whether each dimension is “fixed” or “variable”. A fixed dimension is one in which we have no control, such as a vendor part dimension. A variable dimension is one that we can change to influence the outcome of the tolerance stack. (This will become important later, because we will be able to “adjust” or “resize” the variable dimensions and tolerances to achieve a desired assembly performance. We are not able to resize fixed dimensions or tolerance.)
4.Calculate the Mean Value for the Performance Requirement
5.Determine the Method of Analysis
6.Calculate the Variation for the Performance Requirement
• • • • • • •
Convert each requirement into an assembly gap requirement
• • • • • • •
Requirement 1. Gap1≥0 Requirement 2. Gap2≥0 Requirement 3. Gap3≥0.005 Requirement 4. Gap4≥0 Requirement 5. Gap5≥0.200 Requirement 6. Gap6≥0 Requirement 7. 0.020≥Gap7≥0
Fig1. Motor assembly
Loop diagram
• • • For horizontal dimension loops, start at the surface on the left of the gap. Follow a complete dimension loop, to the surface on the right. For vertical dimension loops, start at the surface on the bottom of the gap. Follow a complete dimension loop, to the surface on the top. Using vectors, create a “closed” loop diagram from the starting surface to the ending surface. Do not include gaps when selecting the path for the dimension loop. Each vector in the loop diagram represents a dimension. Use an arrow to show the direction of each “vector” in the dimension loop. Identify each vector as positive (+),or negative(-),using the following convention: – For horizontal dimensions: • Use a + sign for dimensions followed from left to right. • Use a – sign for dimensions followed from right to left. – For vertical dimensions: • Use a + sign for dimensions followed from bottom to top. • Use a – sign for dimensions followed from top to bottom. Assign a variable name to each dimension in the loop. (For example, the first dimension is assigned the variable name A, the second, B.) Record sensitivities for each dimension. The magnitude of the sensitivity is the value that the gap changes, when the dimension changes 1 unit. For example, if the gap changes 0.001 when the dimension changes 0.001,then the magnitude of the sensitivity is 1(0.001/0.001). On the other hand, if the gap changes 0.0005 for a 0.001change in the dimension, then the sensitivity is 0.5(0.0005/0.001). – If the dimension vector is positive (pointing to the right for horizontal loops, or up for vertical loops), enter a positive sensitivity. If a dimension with a positive sensitivity increases, the gap will also increase. – If the vector is negative (pointing to the left for horizontal loops, or down for vertical loops), enter a negative sensitivity. If a dimension with a negative sensitivity increase, the gap will decrease. All the sensitivities are equal to ±1
Methods of centering manufacturing processes
If the manufacture use the 3.019 or the 3.031 as the nominal dimensions, half of their products will be failed. So they will use the 3.025 as he nominal dimension to minimize their cost.
Tolerance analysis process
1.Establish the Performance Requirements
2.Draw a Loop Diagram
3.Convert All Dimensions to Mean Dimension with an Equal Bilateral Tolerance
Establishing Performance/Assembly Requirements Requirement 1. The gap between the shaft and the inner bearing cap must always be greater than zero to ensure that the rotor is clamped and the bearing are preloaded Requirement 2. The gap between the housing cap and the housing must always be greater than zero to ensure that the stator is clamped. Requirement 3.The mounting surface of the rotor and the stator must be within ±0.005 for the motor to operate. Requirement 4. The bearing outer race must always protrude beyond the main housing, so that the bearing stays clamped. Requirement 5. The thread of the bearing cap screw must have a minimum thread engagement of 0.200 inches. Requirement 6. The bottom of the bearing cap screw thread must never touch the bottom of the female thread on the shaft. Requirement 7. The rotor and stator must never touch. The maximum radial distance between the rotor and stator is 0.020.
Other examples of performance/assembly requirements are:
• • • • • • • •
Thermal requirements; Amount of “squeeze” on an o-ring; Amount of “preload” on bearing; Sufficient “material” for subsequent machining processes; Aerodynamic requirement; Interference requirement, such as when pressing pins into holes; Structural requirements; Optical requirements, such as alignment of optical elements
