机械原理第四章作业
机械原理习题_第四章

17
4-9 (1)解:系统的传递函数为: (1)解 系统的传递函数为:
100 100 G(s) = = (5s +1)(10s +1) 50s2 +15s +1
系统的频率特性为: 系统的频率特性为:
100 100(1 50ω2 ) 15ω G(jω) = = j 2 2 2 2 - 5ω +15jω +1 (1 50ω ) + 225ω (1 50ω2 )2 + 225ω2
11
25(0.1s +1) G(s) = 2 s (0.2s +1)
对数相频特性曲线 图中红色的曲线) (图中红色的曲线) 的画法: 的画法:实际上是 由两个积分环节 (绿色),一个惯 绿色),一个惯 ), 性环节(紫色), 性环节(紫色), 一个一阶微分环节 蓝色)叠加而成. (蓝色)叠加而成. 严格的说, 严格的说,应该使 用描点法画图. 用描点法画图.
|G 则: (jω) |=
100 (1 50ω2 )2 + 225ω2
15ω ∠G(jω) = arctan 1 50ω2
15ω Im ω) = ( (1 50ω2 )2 + 225ω2
18
100(1 50ω2 ) Re(ω) = (1 50ω2 )2 + 225ω2
当ω = 0时: | G(jω) |= 100
稳态输出的幅值: Y 稳态输出的幅值: (ω) = X A(ω) = 30.3
稳态输出的相位: 稳态输出的相位: (ω) = ∠G( jω) 72.5 =-
o
2
4-6 求当系统作用有以下输入信号时,系统的稳态输出. 求当系统作用有以下输入信号时,系统的稳态输出. 1 ) x(t)=sin(t+30) 2 ) x(t)=2cos(2t-45) 3 ) x(t)=sin(t+30)-2cos(2t-45)
机械原理典型例题(第四章连杆机构)10-12

CD为摆动副;2)找出极位夹角θ ,并判断慢行程方向;3)建立机构
最小传动角γ min与各构件长度之间的关系式,并求出γ min值。
慢行程
C
解:
C2
C1
1)Lmin+Lmax=a+b=85mm
B
γmin γ
<c+d=90mm
θ
满足杆长条件,且最短杆的
180+θ ω1
B2
D
A
邻边为机架 ,故为曲柄摇杆机 构,
(2)四杆机构的急回特性是针对主动件作___A_____而言的。
A. 等速转动 B. 等速移动 C. 变速转动或变速移动
(3)曲柄摇杆机构的极位夹角___B_____小于90°。
A. 一定
B. 不一定 C. 一定不
(4)对于双摇杆机构,最短构件与最长构件长度之和____B____大于
其它两构件长度之和。
A
(3)双摇杆机构:
①满足杆长条件,最短杆对边为机架,LBC<LAD(不满足) ②不满足杆长条件
LAB=Lmin LAB+LBC>LCD+LAD LAB=Lmax LAD+LAB>LCD+LAB LAD<LAB<LBC LAD+LBC>LCD+LAB
LAB>150 LAB>550 LAB<450
A . 一定 B. 不一定 C. 一定不
(5)如果铰链四杆运动链中有两个构件长度相等且均为最短,若另外
பைடு நூலகம்
两个构件长度也相等,则当两最短构件相邻时,有____B____整
转副。
A. 两个
B.三个
机械原理习题答案第四章

机械原理习题解答例4-1 绘制图4-2所示液压泵机构的机构运动简图。
解:该机构由机架1、原动件2和从动件3、4组成,共4个构件,属于平面四杆机构。
机构中构件1、2,构件2、3,构件4、1之间的相对运动为转动,即两构件间形成转动副,转动副中心分别位于A 、B 、C 点处;构件3、4之间的相对运动为移动,即两构件间形成移动副,移动副导路方向与构件3的中心线平行。
构件1的运动尺寸为A 、C 两点间距离,构件2的运动尺寸为A 、B 两点之间的距离,构件3从B 点出发,沿移动副导路方向与构件4在C 点形成移动副,构件4同时又在C 点与构件1形成转动副。
选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。
选择比例尺l μ=0.001m/mm ,分别量出各构件的运动尺寸,绘出机构运动简图,并标明原动件及其转动方向,如图4-2所示。
例4-2 绘制图4-3所示简易冲床的机构运动简图。
解:图示机构中已标明原动件,构件6为机架,其余构件为从动件。
需要注意的是,在区分构件时应正确判断图中各构件都包括哪些部分,例如:构件3就包括两部分,如图所示。
该机构中构件1与机架以转动副连接,转动副中心位于固定轴的几何中心A 点处;构件2除与构件1形成回转中心位于C 点的转动副外,又与构件3形成移动副,移动副导路沿BC 方向;构件3也绕固定轴上一点B 转动,即构件3与机架形成的转动副位于B 点,同时构件3与构件2形成移动副,又与构件4形成中心位于D 点的转动副;构件4与构件5形图4-3 简易冲床机构l μ=0.001m/mm成中心位于E 点的转动副;构件5与机架6形成沿垂直方向的移动副。
该机构属于平面机构,因此选择与各构件运动平面平行的平面作为绘制机构运动简图的视图平面。
选择比例尺l μ=0.001m/mm ,量出各构件的运动尺寸,绘出机构运动简图,并标明原动件及其转动方向,如图4-3所示。
4-3 题4-3图为外科手术用剪刀。
机械原理课后习题答案

第四章课后习题4—12图示为一曲柄滑块机构的三个位置,F为作用在活塞上的力转动副A及B上所画的小圆为摩擦圆,试决定在此三个位置时作用在连杆AB上的作用力的真实方向(构件重量及惯性力略去不计)。
解:上图中构件2受压力。
因在转动副A处2、1之间的夹角∠OAB在逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故FR12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA在逐渐增大,相对角速度ω23也沿顺时针方向,故FR32应切于摩擦圆的上方。
R32解:上图构件2依然受压力。
因在转动副A处2、1之间的夹角∠OAB逐渐减小,故相对角速度ω21沿顺时针方向,又因2受压力,故F R12应切于摩擦圆的下方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿逆时针方向,F R32应切于摩擦圆的下方。
解:上图构件2受拉力。
因在转动副A处2、1之间的夹角∠OAB在逐渐增大,故相对角速度ω21沿顺时针方向,又因2受拉力,故FR12应切于摩擦圆的上方;在转动副B处,2、3之间的夹角∠OBA逐渐减小,故相对角速度ω23沿顺时针方向,FR32应切于摩擦圆的下方。
4-13 图示为一摆动推杆盘形凸轮机构,凸轮1沿逆时针方向回转,F为作用在推杆2上的外载荷,试确定凸轮1及机架3作用给推杆2的总反力FR12及FR32方位(不考虑构件的重量及惯性力,解:经受力分析,FR12的方向如上图所示。
在FR12的作用下,2相对于3顺时针转动,故FR32应切于摩擦圆的左侧。
补充题1 如图所示,楔块机构中,已知γ=β=60°,Q =1000N 格接触面摩擦系数f =0.15,如Q 为有效阻力,试求所需的驱动力F 。
解:对机构进行受力分析,并作出力三角形如图。
对楔块1,R 21R310F F F ++=由正弦定理有21sin(602sin(90R F F ϕϕ+-=))o o ① 对楔块2,同理有R12R320Q F F ++=sin(90sin(602ϕϕ+-=))o o ②sin(602sin(602F Q ϕϕ+=⋅-))o o且有2112R R F F = ,8.53arctgf ϕ==o ③联立以上三式,求解得F =1430.65N2 如图示斜面机构,已知:f (滑块1、2与导槽3相互之间摩擦系数)、λ(滑块1的倾斜角)、Q (工作阻力,沿水平方向),设不计两滑块质量,试确定该机构等速运动时所需的铅重方向的驱动力F 。
机械原理--第4章--作业讲解

9
10
11
12
4-14
13
14
3
4
5
4-8 图示为手摇唧筒机构。已知各部分尺寸和接 触面的摩擦系数,转动副A、B、C处的虚线代表 摩擦圆。试画出在力作用下的各总反力作用线的 位置和方向(不考虑各构件的质量和转动惯量机构中,已知AB杆的长度为, 轴颈半径为,为驱动力,为生产阻力,设各构件 相互接触处的摩擦系数均为,若忽略各构件的重 力和惯性力,试求该机构的效率和自锁条件。
第4章 作业讲解
Synthese of Planar Linkages
1
本章作业
4-6、 4-8、 4-11、 4-14
2
4-6 在如图所示的曲柄滑块机构中,已知各构件尺寸, 作用在滑块上的水平驱动力F,各转动副处摩擦圆(图中 用虚线表示)及移动副的摩擦角,不计各构件的惯性力 和重力,试作出各构件的受力分析。
机械原理课件-第4章练习题
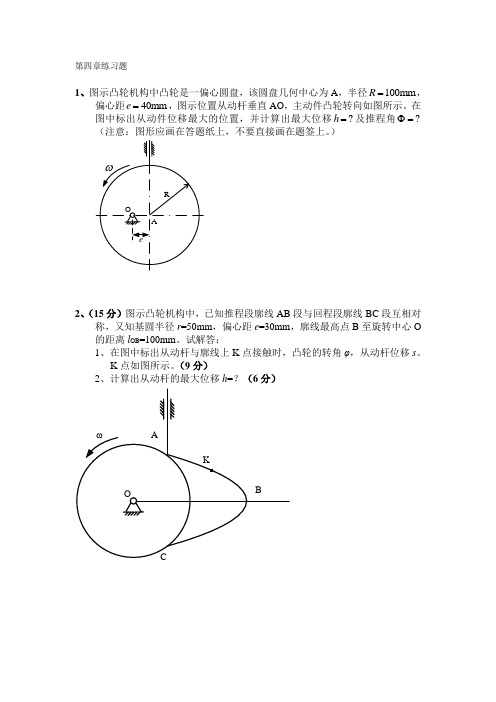
第四章练习题
1、图示凸轮机构中凸轮是一偏心圆盘,该圆盘几何中心为A,半径100mm
R=,偏心距40mm
e=,图示位置从动杆垂直AO,主动件凸轮转向如图所示。
在图中标出从动件位移最大的位置,并计算出最大位移?
Φ=
h=及推程角?
(注意:图形应画在答题纸上,不要直接画在题签上。
)
2、(15分)图示凸轮机构中,已知推程段廓线AB段与回程段廓线BC段互相对
称,又知基圆半径r=50mm,偏心距e=30mm,廓线最高点B至旋转中心O 的距离l OB=100mm。
试解答:
1、在图中标出从动杆与廓线上K点接触时,凸轮的转角φ,从动杆位移s。
K点如图所示。
(9分)
2、计算出从动杆的最大位移h=?(6分)
1、解:(15分)
图中从动件与凸轮在B 点接触时位移为最大的位置;(5分) 画出偏距圆3分、位移2分
89.44s mm =
(5分) 011040
40
(180cos )cos 205.21,
60140--Φ=-+= (5分)
2、解:(15分)
画出偏距圆、转角、位移各3分
(9分) 55.4h =
(6分)。
机械原理第四章作业

分度圆: d1= mz1 = 14*16 = 224mm d2= mz2 = 14*63 = 882mm 齿顶圆:
d a1 d1 2ha cos δ1 d 12mz 2 / z z
2 1
2 2
224 28 63 162 632 251.14mm
2 2 d a 2 d 2 2ha cos 2 d 22mz1 / z1 z2
题4-14:(1)
L r 32 mm v r , 1 16 0.0625 rad / s
(2)
L r xm 36.8mm v r , 1 16 0.0625 rad / s
rb r cos 30 .07 mm r f r h f xm 31 .8mm ra r ha xm 40 .8mm
《齿轮机构》作业
第1次:4-3、4-6、4-9、4-11、4-14 第2次: 4-18、4-19、 4-21、4-23、(4-32、4-35)
4-3 已知两个渐开线直齿圆柱齿轮的齿数z1=20,z2=40, 它们都是标准齿轮,而且m、、ha*、c*均相同。试用渐 开线齿廓的性质,说明这两个齿轮的齿顶厚度哪一个大, 基圆上的齿厚哪一个大。
延伸:m=2mm,z1=20,z2=40,a=61时,可有几种 办法实现无侧隙啮合? 1 解: 标准中心距 a= (z1+z2)=60mm 2
a=61>a
(1)采用正传动;
r1 =20.33mm, r2 =40.67mm
= arccos(acos/a) =22.44° (2)采用标准斜齿轮传动,
a mn ( z1 z2 ) / 2 cos 231 .9mm
机械原理作业答案(含相对运动图解法)

F
E D
A
C B 图7
以 EF 为原动件时,其基本杆组及驱动杆组如图 8 所示,为 II 级机构。
E
C
B
D
F
A 图8
16c 以 AB 为原动件和以 EF 为原动件时,均为 II 级机构,其基本杆组及驱动杆组分别如图 9、图
10 所示。
B
E
C
C
F
A
D
图9
B
D
C
C A
F E
图 10
16d 除去机构中局部自由度,高副低代后的机构示意图和其基本杆组及驱动杆组如图 11 所示,II 级 机构。
当 AB 为最长杆时,有 lAB+lAD>lBC+lCD,即 lAB+30>50+35,得到 lAB>55 mm;由于 AB 杆的最大长度不
能大于其余三杆长度之和,即 lAB< lBC+lCD+lAD=50+35=30=115 mm,得到 55 mm< lAB<115 mm。
综合以上分析,得到 AB 杆的取值为:15 mm<lAB<45 mm 或 55 mm< lAB<115 mm
图9
2.20 习题
2.21 习题
221 解 设计步骤为(参见图 11): 1)=180(K1)/(K+1)=180(1.51)/(1.5+1)=36 2)选择长度比例尺l,根据已知条件,作出机架 AD 和摇杆的一个极限位置 DC1,并以 D 为圆心, CD1 为半径画圆弧。连接 AC1;代表摇杆的一个极限位置; 3)根据极位夹角定义,作与 AC1 夹角为 的射线 AC,其与圆弧分别交于 C2 和 C2,则 DC2 和 DC2 均可作为摇杆 CD 的两个极限位置。 4)若将 AC2 视为连杆与曲柄拉伸共线位置,AC1 视为连杆与曲柄重叠共线位置,则 lAB=0.5l(AC2AC1)49.3 mm,lBC=0.5l(AC2+AC1)120 mm 若将 AC1 视为连杆与曲柄拉伸共线位置,AC2 视为连杆与曲柄重叠共线位置,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(5)两分度圆在连心线 O1O2的距离Δy
O1O2 ? r1? ? r2? ? 124.75mm ? y ? O1O2 ? (r1 ? r2 ) ? 2.75mm
4-14
? 用齿条型刀具加工一个齿数为 z=16 的齿轮 ,刀具参数
m具=的4m移m动, 速(? 度=2v0刀°=2,mmha/*s=.试1 ,求c:*=0.25 ),在加工齿轮时,刀
大,基圆上的齿厚哪一个大。
答: ? 模数相等的2 个标准齿轮,分度圆
上均的 等齿于厚?ms/12=。s 2与齿槽宽e1=e 2相等,
? 模数m相同,齿数越多的齿轮,基 圆半径rb也大;
? 根据渐开线性质,基圆半径越大, 相同展角?处渐开线的曲率半径也 大。因此,基圆大的齿轮2侧齿廓 渐度开 也线慢随。展因角此?齿k 增顶大厚相也互大靠。近的速
距a=60mm、a'=61mm 两种情况下,哪些尺寸不同。
a=60mm 时, r 2?=r 2 ?? = ?
r 1?=r 1
C=c*m
标准中心距: a= m(z 1+z2)/2=60mm
m=2mm,z=20 a=60 a?=61
a?=61mm 时,
m=2mm,z=40
r 1?= a?/(1+i12)=20.33mm, r 2?=40.67mm
rf ? r ? hf ? xm ? 31.8mm ra ? r ? ha ? xm ? 40.8mm
v ? r? ? mz ? ,?
2
z?
2v
m?
? 24
4-18 一对外啮合渐开线标准斜齿轮,已知:z1=16、
《齿轮机构》作业
第1次:4-3、4-6、4-9、4-11、4-14 第2次: 4-18、4-19、 4-21、4-23、(4-32、4-35)
4-3 已知两个渐开线直齿圆柱齿轮的齿数z1=20,z2=40, 它们都是标准齿轮,而且m、? 、ha*、c*均相同。试用
渐开线齿廓的性质,说明这两个齿轮的齿顶厚度哪一个
发生线 K
N rb
基圆 O
rk K0
?k
渐开线 k0k 的展角
? 同一理 个,齿随的展两角侧齿?k减廓小相,互大靠齿近轮的的速同 度也慢。因此基圆齿厚也较大。
4-6 一对已切制好的渐开线外啮合直齿圆柱标准齿轮,z1=20、
Z2=40、m=2mm、 ? =20o、ha*=1、c*=0.25。试说明在中心
计算重合度,并用重合度计算公式计算 进行对比校核。
题4-9:(1)画图:计算出标准中心距a、分 度圆直径d1( d2)、基圆直径db1 (db2)、齿 顶圆直径da1( da2)
d 1=mz 1=120mm; d 2=mz 2=240mm; a=(d1+d2)/2=180mm;
db1 =d1*cos α= 112.8mm; db2 =225.5mm; d a1=d+2h a*m=128mm; da2=248mm.
??
?B1B2 pn?Fra bibliotekB1B2
?mcos?
o1
ra1
rb1
N1
B1
B2
a
N2
rb2
ra2
o2
(2)用公式计算:
? ?? ?
cos ? a1
?
rb1 , ? ra 1
? a1 ? 28.2?
cos ? a 2
?
rb2 , ? ra 2
? a 2 ? 24.6?
? ? ?a
?
1 2?
z1(tg? a1 ? tg? ') ? z2(tg? a2 ? tg? ')
(1) 因为 : ?? ? B1B2 / pn ? 1 所以 : B1B2 ? pn ? ?m cos ? ? 11 .8mm
(2)d1=76mm, d2=168mm, db1 =71.42mm,db2 =157.87mm, da1=84mm, da2=176mm cos? a1 ? rb1 / ra1,? ? a1 ? 31.8? cos? a 2 ? rb2 / ra2 ,? ? a 2 ? 26.2?
? 1.73
4-11 若已知一对齿轮机构的安装位置,当采用一对标准直
齿圆柱齿轮,其z1=19, z2=42, m=4 mm, ? =20°,ha*=1, 此时刚好能保证连续传动,试求: (1) 实际啮合线B1B2的 长度;(2) 齿顶圆周上的压力角αa1 ,αa2;(3) 啮合角? ‘; (4) 两轮节圆半径r' 1, r‘2;(5) 两分度圆在连心线O1O2的距 离Δy。
?? = arccos(acos ? /a?) =22.44°
(2)采用标准斜齿轮传动,
a=
mn 2cos?
(z
1+z2)=61mm
? =10.38o
4-9
一对外啮合渐开线直齿圆柱标准齿轮,
已知z1=30,z2=60,m=4mm,α=20°,ha*=1,
试按比例精确作图画出无侧隙啮合时的
实际啮合线B1B2的长度,根据量得的B1B2
(1)欲加工成标准齿轮时 ,刀具中线与轮坯中心的距离 L 为多少?轮坯转动的角速度为多少?
(2)欲加工出 x=1.2的变位齿轮时 ,刀具中线与轮坯中心
的距离L为多少?轮坯转动的角速度为多少 ?并计算所加
工出的齿轮的齿根圆半径 ra;
r
f,基圆半径
rb
和齿顶圆半径
(3)若轮坯转动的角速度不变 ,而刀具的移动速度改为 V
刀=3mm/s,则加工出的齿轮齿数z为多少?
题4-14:(1)
L ? r ? 32mm
v ? r? , ? ? ? 1 16 ? 0.0625rad / s
(2) (3)
L ? r ? xm ? 36.8mm
v ? r? , ? ? ? 1 16 ? 0.0625rad / s
rb ? r ?cos? ? 30.07mm
(3)啮合角 ? '
? ? ?a
?
1
2?
z1(tg? a1 ? tg? ') ? z2 (tg? a 2 ? tg? ' ) ? 1
? ?? 23.2?
(4)两轮节圆半径 r1', r 2'
cos? ?? rb1 ? rb2 , ?
r1? r2?
r1? ? 38.86mm, r2? ? 85.89mm
?? = arccos(acos ? /a') =22.44°
c=c*m+(a ?–a) 为有侧隙传动
还有: 顶隙
延伸:m=2mm ,z1=20,z2=40,a?=61时,可有几种 办法实现无侧隙啮合?
解:
标准中心距
a=
1 2
(z
1+z2)=60mm
a ?=61>a
(1)采用正传动;
r 1?=20.33mm, r 2?=40.67mm
