310离散时间LTI系统单位脉冲响应
§3.1 LTI离散系统的响应

解为 yzi(k)=Czi1(– 1)k+Czi2(–2)k 将初始值代入 并解得 Czi1=1 , Czi2= – 2 yzi(k)=(– 1)k – 2(– 2)k , k≥0 (2)零状态响应yzs(k) 满足 yzs(k) + 3yzs(k –1) + 2yzs(k –2) = f(k) yzs(–1)= yzs(–2) = 0 递推求初始值 yzs(0), yzs(1), yzs(k) = – 3yzs(k –1) – 2yzs(k –2) + 2k , k≥0 yzs(0) = – 3yzs(–1) – 2yzs(–2) + 1 = 1 yzs(1) = – 3yzs(0) – 2yzs(–1) + 2 = – 1
Pm k m Pm1k m1 P 1 ) 1k P 0 (特征根均不为 k r ( Pm k m Pm1k m1 P1k P0 )(有r重为1的特征根)
Pak (a不等于特征根)
k (P k P ) a (a等于特征单根) 1 0
a
k
cosk 或 sin k
▲ ■ 第 14 页
零输入零状态举例
例:系统方程为 y(k) + 3y(k –1) + 2y(k –2) = f(k) 已知激励 f(k)=2k , k≥0 ,初始状态 y(–1)=0, y(–2)=1/2, 求系统的零输入响应、零状态响应和全响应。 解:(1)yzi(k)满足方程 yzi(k) + 3yzi(k –1)+ 2yzi(k –2)= 0 yzi(–1)= y(–1)= 0, yzi(–2) = y(–2) = 1/2 首先递推求出初始值yzi(0), yzi(1), yzi(k)= – 3yzi(k –1) –2yzi(k –2) yzi(0)= –3yzi(–1) –2yzi(–2)= –1 yzi(1)= –3yzi(0) –2yzi(–1)=3 特征根为λ1= –1 ,λ2= – 2
离散系统单位脉冲响应的物理含义

脉冲响应指的是:在一个输入上施加一个脉冲函数引起的时间响应。
单位脉冲响应(Unit impulse response)系统对单位脉冲输入的响应。
也称作记忆函数。
脉冲响应确定一个线性系统的特性,包含有与频率域中的传输函数相同的信息,而传输函数是脉冲响应的拉普拉斯变换。
线性系统的输出由系统的输入与它的脉冲响应的卷积给出。
单位脉冲响应是指一个无穷大的瞬时冲激,并且由于其在时间轴上的积分为1,而t又趋向于零,所以单位脉冲响应的大小应该是无穷大,但是要知道的是,无穷大量也有大小比较,所以单位脉冲响应可以用一个系数对之进行量度。
扩展资料
1、系统动态性能分析
动态性能是系统性能的一个十分重要的指标,通常用阶跃信号作用来测定系统的动态性能。
一般认为,阶跃信号对于系统来说是十分严峻的工作状态,因为阶跃信号中存在跃断点(不连续点)。
针对零初始状态系统在单位阶跃输入下的响应情况,定义了一系列动态性能指标,用以评判系统的动态性能,如超调量、衰减比、上升时间、调节时间、峰值时间等等。
2、建立系统响应模型
对于典型的输入信号,如冲激信号、阶跃信号、斜坡信号等,都建立有响应模型(在此即单位阶跃响应模型)。
根据模型,可以快速判断出实际系统的动态性能指标参数,只需要代入实际系统的相关测量参数,就可以定量分析其性能指标。
信号与系统_北京交通大学中国大学mooc课后章节答案期末考试题库2023年

信号与系统_北京交通大学中国大学mooc课后章节答案期末考试题库2023年1.某连续周期信号如题1图所示,该信号的频谱成分有( )【图片】参考答案:直流、奇次谐波的余弦分量2.已知描述某连续时间LTI系统的状态方程的矩阵分别为【图片】【图片】【图片】【图片】则该系统的系统函数【图片】为参考答案:3行3列矩阵3.关于连续非周期信号的频域表示,正确的说法是( )参考答案:将信号表示为不同频率正弦信号的线性组合4.连续非周期信号频谱的特点是( )参考答案:连续、非周期5.已知某线性连续时间系统,其在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】;该系统在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】试求初始状态为【图片】,激励为【图片】时系统的完全响应【图片】=( )。
参考答案:,6.连续非周期信号频谱的特点是参考答案:连续、非周期7.已知信号【图片】,其频谱【图片】在【图片】的值【图片】参考答案:88.连续周期信号【图片】是功率信号,其傅里叶变换【图片】都不存在。
参考答案:错误9.已知信号【图片】的最高频率分量为【图片】 Hz,若抽样频率【图片】,则抽样后信号的频谱一定混叠。
参考答案:错误10.连续时间周期信号【图片】的平均功率为( )参考答案:1111.利用状态变量分析法分析连续时间LTI系统时,输出方程【图片】可能与哪些因素有关参考答案:与输入和状态变量有关12.关于连续周期信号频谱的特性,正确的说法是( )参考答案:同时具有离散特性和幅度衰减特性。
13.若描述离散时间系统的差分方程为【图片】,该系统为( )。
参考答案:因果、线性时不变系统14.连续周期信号在有效带宽内各谐波分量的平均功率之和占整个信号平均功率的很大一部分。
参考答案:正确15.连续时间信号在时域展宽后,其对应的频谱中高频分量将增加。
参考答案:错误16.信号时域时移,其对应的幅度频谱不变,相位频谱将发生相移。
3_10离散时间LTI系统的单位脉冲响应

此方法称为等效初始条件法
2. 单位脉冲响应的求解
[例] 某离散因果LTI系统的差分方程为 y[k] 3y[k 1] 2y[k 2] x[k] 求系统的单位脉冲响应h[k]。
解:h[k]满足方程 h[k] 3h[k 1] 2h[k 2] d[k] (1) 确定h[k]的形式 特征方程为 r 2 3r 2 0 特征根为 r1 1, r2 2
(2) 求等效初始条件 对于因果系统有h[-1] = h[-2] = 0,代入上面方程可推出
h[0] d[0] 3h[1] 2h[2] 1
h[1] d [1] 3h[0] 2h[1] 3
二阶系统需要两个初始条件,可以选择h[0]和h[1]
2. 单位脉冲响应的求解
C1=-1,C2= 2
h[k ] [(1)k 2(2)k ]u[k ]
[例] 某离散因果LTI系统的差分方程为 y[k] 3y[k 1] 2y[k 2] x[k] 求系统的单位脉冲响应h[k]。
解:h[k]满足方程 h[k] 3h[k 1] 2h[k 2] d[k] (3) 确定齐次解的待定系数 代入初始条件
h[0] C1 C2 1, h[1] C1 2C2 3
h[k ] C1 (1) k C2 (2) k , k 0
2. 单位脉冲响应的求解
[例] 某离散因果LTI系统的差分方程为 y[k] 3y[k 1] 2y[k 2] x[k] 求系统的单位脉冲响应h[k]。
✓选择初始条件基本原则是必须将d[k]的作用体现在初始条件中 解:h[k]满足方程 h[k] 3h[k 1] 2h[k 2] d[k]
离散时间LTI系统零状态响应

x[k]* h[n] ( x[n])* h[k] y[n]
n
n
n
3. 卷积和的性质
[例]
计算
x[k]
{1,
0,
2,
4}与
h[k]
{1,
4,
5,
3}的卷积和。
解: x[k] [k 2] 2[k] 4[k 1]
利用分配律和位移特性
x[k]*h[k] {[k 2] 2[k] 4[k 1]}*h[k]
x[1] h[1]
x[1] h[2]
x[1] h[3]
对角斜线上各数值就 是 x[n]h[k-n]的值。
x[ 2 ] x[2] h[0]
x[ 3 ] x[3] h[0]
x[2] h[1] x[3] h[1]
x[2] h[2] x[3] h[2]
x[2] h[3] x[3] h[3]
对角斜线上各数值的 和就是y[k]各项的值。
h[k] h [ n ] 1
解:
n
n
0
3
k
02
k
y[k]
综上可知: 3
2 1
k 0 1 2 3 4 56
h[-n] 1
-2 0
n
两个信号的卷积和,卷积和结果仍为一个信号。该信号的起点 等于那两个信号起点之和,终点等于那两个信号的终点之和。
2. 卷积和的计算
列表法: 设x[k]和h[k]都是因果序列,则有
2. 卷积和的计算
[例]
计算x [ k ]
{1,
2,
0,
3,
2}
与h [ k ]
{1,
4,
2,
3 } 的卷积和。
解:
h [ -1 ] 1
离散时间LTI系统的单位脉冲响应

系统分析和设计
通过单位脉冲响应可以分析系统 的稳定性、频率响应和因果性等 特性,用于系统的设计和优化。
信号处理
单位脉冲响应可以用于信号的滤 波、预测和合成等处理,提高信 号的质量和性能。
控制工程
单位脉冲响应可以用于控制系统 的分析和设计,优化控制性能和 稳定性。
BIG DATA EMPOWERS TO CREATE A NEW ERA
IIR系统
系统的输出不仅与当前的输入有关, 还与过去的输入有关,因此其单位脉 冲响应在时间上是无限的。
系统的表示方法
差分方程
离散时间LTI系统的动态行为通常由差分方 程描述,如 $y(n) = f(n) + g(n)u(n)$。
传递函数
通过将差分方程转换为传递函数的形式,可以更方 便地分析系统的频率响应和稳定性。
仿真分析的步骤与过程
建立数学模型
根据系统定义,建立离散时间LTI系统的数学模型,包括差分方程或传递函数。
生成单位脉冲信号
在仿真中,生成一个单位脉冲信号,用于输入到离散时间LTI系统中。
计算单位脉冲响应
将单位脉冲信号输入到系统中,并记录系统的输出,即单位脉冲响应。
分析单位脉冲响应
对单位脉冲响应进行分析,包括幅度和相位特性,以及稳定性等。
性质
单位脉冲响应是线性时不变系统的内 部动态特性,具有稳定性、因果性和 可预测性。
单位脉冲响应的求解方法
直接法
根据系统函数或差分方程,直接计算单位脉冲响 应的数值解。
迭代法
根据系统函数或差分方程,通过迭代计算单位脉 冲响应的数值解。
逆系统法
通过求解系统的逆系统,得到单位脉冲响应的数 值解。
单位脉冲响应的应用
实验二_连续和离散时间LTI系统的响应及卷积
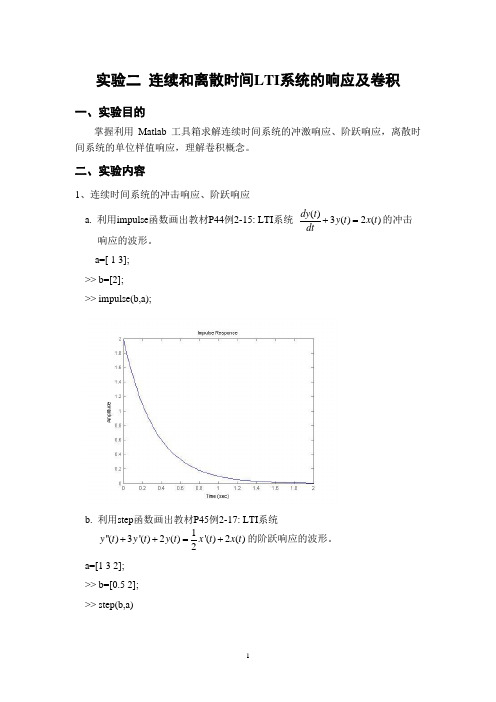
实验二 连续和离散时间LTI 系统的响应及卷积一、实验目的掌握利用Matlab 工具箱求解连续时间系统的冲激响应、阶跃响应,离散时间系统的单位样值响应,理解卷积概念。
二、实验内容1、连续时间系统的冲击响应、阶跃响应a. 利用impulse 函数画出教材P44例2-15: LTI 系统()3()2()dy t y t x t dt+=的冲击响应的波形。
a=[ 1 3];>> b=[2]; >> impulse(b,a);b. 利用step 函数画出教材P45例2-17: LTI 系统1''()3'()2()'()2()2y t y t y t x t x t ++=+的阶跃响应的波形。
a=[1 3 2];>> b=[0.5 2];>> step(b,a)2、离散时间系统的单位样值响应利用impz函数画出教材P48例2-21:--+---=的单位样值响应的图形。
[]3[1]3[2][3][]y n y n y n y n x na=[1 -3 3 -1];>> b=[1];>> impz(b,a)3、连续时间信号卷积画出函数f1(t)=(1+t)[u(t)-u(t-1)]和f2(t)=u(t-1)-u(t-2)的图形,并利用附在后面的sconv.m函数画出卷积积分f1(t)* f2(t)图形。
t=-1:0.01:3;f1=(1+t).*(0.5*sign(t)-0.5*sign(t-1));f2=(0.5*sign(t-1)-0.5*sign(t-2));subplot(2,2,1);plot(t,f1);subplot(2,2,2);plot(t,f2);sconv(f1,f2,t,t,0.01);4、画出教材P60例2-28中h[n]、x[n]的图形(图2-14(a)(b)),并利用conv函数求出卷积x[n]*h[n]并画出图形(图2-14(f))。
奥本海姆《信号与系统》配套题库【课后习题】(周期信号的傅里叶级数表示)

第3章周期信号的傅里叶级数表示基本题3.1 有一实值连续时间周期信号x(t),其基波周期了T=8,x(t)的非零傅里叶级数系数为a1=a-1=2,a3=a-3=4j。
试将x(t)表示成:解:3.2 有一实值离散时间周期信号x[n],其基波周期N=5,x[n]的非零傅里叶级数系数为,试将x[n]表示成:解:3.3 对下面连续时间周期信号求基波频率ω0和傅里叶级数系数a k,以表示成解:即非零的傅里叶级数系数为3.4 利用傅里叶级数分析式计算下连续时间周期信号(基波频率ω0=π)的系数a k:解:因ω0=π,故3.5 设x1(t)是一连续时间周期信号,其基波频率为叫ω1,傅里叶系数为a k,已知x2(t)=x1(1-t)十x1(t-1),问x2(t)的基波频率ω2与ω1是什么关系?求x2(t)的傅里叶级数系数b k与系数a k之间的关系。
解:x1(1-t)和x1(t-1)的基波频率都是ω1,则它们的基波周期都是T1=2π/π。
因为x2(t)是x1(1-t)和x1(t-1)的线性组合,所以x2(t)的基波周期,即ω2=ω1。
又故即3.6 有三个连续时间周期信号,其傅里叶级数表示如下:利用傅里叶级数性质回答下列问题:(a)三个信号中哪些是实值的?(b)哪些又是偶函数?解:(a)与式对照可知,对于x1(t),有由共轭对称性可知,若x1(t)为实信号,则有显然故x1(t)不是实信号。
同理,对于x2(t),对于x3(t),由于故可知x2(t)和x3(t)都是实信号。
(b)由于偶函数的傅里叶级数是偶函数,由上可知,只有x2(t)的a k是偶函数,故只有x2(t)是偶信号。
3.7 假定周期信号x(t)有基波周期为T,傅里叶系数为,的傅里叶级数系数为b k。
已知,试利用傅里叶级数的性质求a k用b k和T表达的表达式。
解:当k=0时,故3.8 现对一信号给出如下信息:(1)x(t)是实的且为奇函数;(2)x(t)是周期的,周期T=2,傅里叶级数为a k;(3)对|k|>1,a k=0;(4)试确定两个不同的信号都满足这些条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号处理课程组
离散时间LTI系统的单位脉冲响应
单位脉冲响应的定义 单位脉冲响应的求解
1. 单位脉冲响应的定义
在系统初始状态为零的条件下,以单位脉冲序列δ [k]激 励系统所产生的输出响应,称为系统的单位脉冲响应,以符 号h[k]表示。
d [k]
离散时间 LTI系统
(系统初始状态为零)
h[1] d [1] 3h[0] 2h[1] 3 二阶系统需要两个初始条件,可以选择 h[0]和h[1]
2. 单位脉冲响应的求解
[例] 某离散因果LTI系统的差分方程为 y[k ] 3 y[k 1] 2 y[k 2] x[k ] 求系统的单位脉冲响应h[k]。
解:h[k]满足方程 h[k ] 3h[k 1] 2h[k 2] d [k ]
(1) 确定h[k]的形式
特征方程为 特征根为
r 2 3r 2 0
r1 1, r2 2
h[k ] C1 (1) k C2 (2) k , k 0
2. 单位脉冲响应的求解
h [k]
1. 单位脉冲响应的定义
若描述离散时间LTI系统的常系数线性差分方程为
a y[k i ] b x[k j ]
i 0 i j 0 j
n
m
则离散时间LTI系统的单位脉冲响应h[k]应满足
i 0
nபைடு நூலகம்
ai h[k i ] b jd [k j ]
j 0
m
分析: 如何确定系统的初始条件?
由于d [k]信号在k>0后函数值都为零。对于因果系统, 将d [k]对系统的瞬时作用转化为系统的等效初始条件。
等效初始条件由差分方程和h[-1] = h[-2] = = h[-n] = 0 递推求出。
此方法称为等效初始条件法
2. 单位脉冲响应的求解
[例] 某离散因果LTI系统的差分方程为 y[k ] 3 y[k 1] 2 y[k 2] x[k ] 求系统的单位脉冲响应h[k]。
2. 单位脉冲响应的求解
[例] 某离散因果LTI系统的差分方程为 y[k ] 3 y[k 1] 2 y[k 2] x[k ] 求系统的单位脉冲响应h[k]。
分析: 当系统输入信号x[k]为d[k],输出信号y[k]则为h[k] 描述系统的差分方程为
h[k ] 3h[k 1] 2h[k 2] d [k ]
当k > 0时, d[k]=0,描述系统的差分方程为
h[k ] 3h[k 1] 2h[k 2] 0
因此,系统的单位脉冲响应具有齐次解形式
2. 单位脉冲响应的求解
[例] 某离散因果LTI系统的差分方程为 y[k ] 3 y[k 1] 2 y[k 2] x[k ] 求系统的单位脉冲响应h[k]。
[例] 某离散因果LTI系统的差分方程为 y[k ] 3 y[k 1] 2 y[k 2] x[k ] 求系统的单位脉冲响应h[k]。
选择初始条件基本原则是必须将d[k]的作用体现在初始条件中 解:h[k]满足方程 h[k ] 3h[k 1] 2h[k 2] d [k ] (2) 求等效初始条件 对于因果系统有h[-1] = h[-2] = 0,代入上面方程可推出 h[0] d [0] 3h[1] 2h[2] 1
解:h[k]满足方程 h[k ] 3h[k 1] 2h[k 2] d [k ] (3) 确定齐次解的待定系数 代入初始条件
h[0] C1 C2 1, h[1] C1 2C2 3
C1=-1,C2= 2
h[k ] [ (1) k 2(2) k ]u[k ]
