系统的单位阶跃响应为试求系统的传递函数和脉冲响应
《自动控制原理》典型考试试题
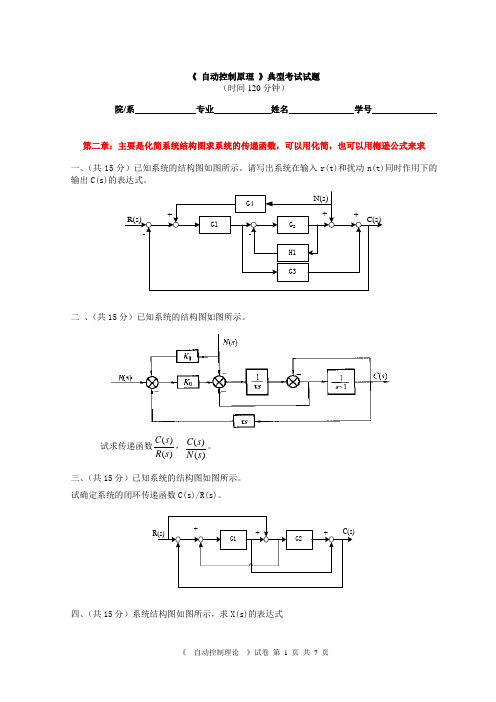
《 自动控制原理 》典型考试试题(时间120分钟)院/系 专业 姓名 学号第二章:主要是化简系统结构图求系统的传递函数,可以用化简,也可以用梅逊公式来求一、(共15分)已知系统的结构图如图所示。
请写出系统在输入r(t)和扰动n(t)同时作用下的输出C(s)的表达式。
G4H1G3G1G 2N(s)C(s)R(s)--+++二 、(共15分)已知系统的结构图如图所示。
试求传递函数)()(s R s C ,)()(s N s C 。
三、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)。
G1G2R(s)-++C(s)-+四、(共15分)系统结构图如图所示,求X(s)的表达式G4(s)G6(s)G5(s)G1(s)G2(s)N(s)C(s)R(s)--G3(s)X(s)五、(共15分)已知系统的结构图如图所示。
试确定系统的闭环传递函数C(s)/R(s)和C(s)/D(s)。
G1G2R(s)-++C(s)-+D(s)G3G4六、(共15分)系统的结构图如图所示,试求该系统的闭环传递函数)()(s R s C 。
七、(15分)试用结构图等效化简求题图所示各系统的传递函数)()(s R s C一、(共15分)某控制系统的方框图如图所示,欲保证阻尼比ξ=0.7和响应单位斜坡函数的稳态误差为ss e =0.25,试确定系统参数K 、τ。
二、(共10分)设图(a )所示系统的单位阶跃响应如图(b )所示。
试确定系统参数,1K 2K 和a 。
三、(共15分)已知系统结构图如下所示。
求系统在输入r(t)=t 和扰动信号d(t)=1(t)作用下的稳态误差和稳态输出)(∞C2/(1+0.1s)R(s)-C(s)4/s(s+2)E(s) D(s)四、(共10分)已知单位负反馈系统的开环传递函数为:2()(2)(4)(625)KG s s s s s =++++试确定引起闭环系统等幅振荡时的K 值和相应的振荡频率ω五、(15分)设单位反馈系统的开环传递函数为12 )1()(23++++=s s s s K s G α若系统以2rad/s 频率持续振荡,试确定相应的K 和α值第三章:主要包括稳、准、快3个方面稳定性有2题,绝对稳定性判断,主要是用劳斯判据,特别是临界稳定中出现全零行问题。
自动控制原理第三章答案

n
临界阻尼:ts 4.75T 4.75
1
4.75
n
1 0.95s 5
3-3 原系统传递函数为 G(s) 0.2s 1 , 现采用如题所示的负反馈方式,欲将反 馈系统的调节时间减小为原来的0.1倍, 并且保证原放大倍数不变,试确定参数 K0 , KH的值。 解:原系统传递函数 新系统传递函数
K 10
0
1 10K 10 (时间常数为
H
1 ) 10
K 0.9
H
问题 非标准形式 10K 0 1 1 10K H , 0 .2 s 1 Ts 1 1 10K H
3
3-4
已知系统的单位阶跃响应为 试求取系统的传递函数
y(t ) 1 e
t
e
2t
Y(s) X(s)
n
2
问题 1、没有完成 2、计算错误
0.146
8
1 KK
1
2
3-9 设题3-9图(a)所示的单位 阶跃响应如题3-9图(b)所示。 试确定系统参数K1,K2和a。
解:据题意
K K (s) s(s a ) K K K K s as K s 2 s 1 s(s a )
(s) s(0.1s 1)
K 1 s(0.1s 1) K 10K 0.1s s K s 10s 10K
2 2
对应二阶系统标准形式,取ζ=1,得
问题
1、没有求调节时间 2、临界阻尼,调节时间 计算错误
2 10 5
n n
5 10K K 2.5 10
t
p
0.1
1.1 1.0 100% 10% 1.1 根据二阶欠阻尼系统指标计算公式
哈工大机电系统控制基础秋-习题课第三章答案

第3章习题课答案3-1 设单位反馈系统的开环传递函数为4()(s 5)G s s =+,试求该系统的单位阶跃响应和单位脉冲响应。
解:系统闭环传递函数为24(s)44(s 5)4(s)54(s 1)(s 4)1(s 5)o i X s X s s s +===++++++ (1)当()1()i x t t =时,1()i X s s=41()41133()()()(4)(1)14o o i i X s X s X s X s s s s s s s ===-+++++则 441()1()1()1()33t tox t t e t e t --=-⋅+⋅ (2)当()()i x t t δ=时,()1i X s =44(s)433(s)(s)1(s)(s 4)(s 1)14o o i i X X X X s s ==⨯=-++++则 44()()1()3tt o x t e e t --=-⋅3-2 系统结构图如图3-70所示。
已知系统单位阶跃响应的超调量σ%3.16=%,峰值时间1=p t s 。
(1)求系统的开环传递函数)(s G ; (2)求系统的闭环传递函数)(s Φ;(3)根据已知的性能指标σ%、p t 确定系统参数K 及τ; (4)计算等速输入s t t r )(5.1)(︒=时系统的稳态误差。
解 (1) )110(10)1(101)1(10)(++=+++=ττs s K s s s s s K s G(2) 2222210)110(10)(1)()(nn n s s K s s Ks G s G s ωξωωτ++=+++=+=Φ (3)由 ⎪⎩⎪⎨⎧=-===--113.16212ξωπσςξπn p oooo t e 联立解出⎪⎩⎪⎨⎧===263.063.35.0τωξn由(2) 18.1363.31022===n K ω,得出318.1=K 。
(4) 63.31263.01018.1311010)(lim 0=+⨯=+==→τK s sG K s v 413.063.35.1===v ss K A e3-3 设图(a )所示系统的单位阶跃响应如图(b )所示。
第四章作业

第四章作业第一题:已知系统零初始条件下的单位阶跃响应分别如下,分别求它们脉冲响应与传递函数。
(1)y (t )=1+e -t –e -2t (2)y (t )=e -t -e -2t解:由单位阶跃响应与单位脉冲响应的关系,得单位脉冲响应为 (1)g (t )=δ(t)-e -t +2e -2t ,对应的传递函数为12()112G s s s =-+++ (2)g (t )=-e -t +2e -2t ,对应的传递函数为12()12G s s s =-+++第二题:已知单位负反馈系统结构图如图所示。
求 (1)K =50时系统单位阶跃响应的超调量;(4.3%)(2)K 取何值才能使系统单位阶跃响应的超调量为 10% ;(K =71.6) (3)K =50时系统的单位斜坡响应与单位抛物线响应。
解:(1)闭环系统特征多项式50102++s s,707.0,25==ζωn 。
代入p e100%σ=⨯得到πp e 100% 4.3%σ-=⨯=。
(2)由p e100%σ=⨯πln(/100)σ-=。
令βζcos =得到πtan ln(/100)βσ-=。
将p 10%σ=代入得到πarctan[]arctan1.3640.938ln(/100)βσ-===。
因此591.0=ζ。
闭环系统特征多项式K s s ++102,K K n /5,==ζω。
因此有591.0/5=K ,得到6.71=K 。
(3)斜坡响应22150()1050Y s s s s =++,反Laplace 变换,便可得。
抛物线响应32150()1050Y s s s s =++,反Laplace 变换,得可得。
第三题:某闭环系统如下图所示,控制器采用PI 控制,i n 0.6,0.7,2T ζω===,试分析计算该系统是否为欠阻尼,并在单位阶跃信号下计算上升时间、峰值时间、超调量、调节时间。
解:由题可得,系统的闭环传递函数为22i n n 32223232i n i i n n 2.444203()20.6 1.68 2.44 2.842034203( 2.32)(0.24 1.68i)(0.24 1.68i)T s s s s T s T s T s s s s s s s s s s s ωωζωωω+++Φ===++++++++++=++-++显然该系统存在主导极点,降阶为24(53) 2.88(0.61)() 2.32(0.24 1.68i)(0.24 1.68i)+0.48+2.88s s s s s s s +⨯+Φ==+-++这是一个含有零点的二阶系统,显然是一个欠阻尼系统,且有n 1.70,0.14ωζ==。
自动控制原理考试试题
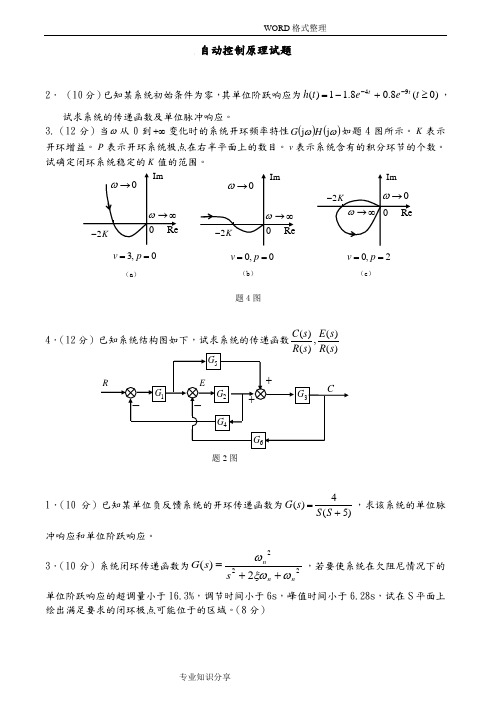
自动控制原理试题2. (10分)已知某系统初始条件为零,其单位阶跃响应为)0(8.08.11)(94≥+-=--t e e t h t t ,试求系统的传递函数及单位脉冲响应。
3.(12分)当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所示。
K 表示开环增益。
P 表示开环系统极点在右半平面上的数目。
v 表示系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的范围。
4.(12分)已知系统结构图如下,试求系统的传递函数)(,)(s E s C1.(10分)已知某单位负反馈系统的开环传递函数为)5(4)(+=S S s G ,求该系统的单位脉冲响应和单位阶跃响应。
3.(10分)系统闭环传递函数为2222)(nn n s s G ωξωω++=,若要使系统在欠阻尼情况下的单位阶跃响应的超调量小于16.3%,调节时间小于6s ,峰值时间小于6.28s ,试在S 平面上绘出满足要求的闭环极点可能位于的区域。
(8分)0,3==p v (a )0,0==p v (b ) 2,0==p v (c ) 题4图 题2图6. (15分)已知最小相位系统的对数幅频特性曲线如下图所示(分段直线近似表示)1、.(10分)已知某单位负反馈系统的开环传递函数为)5(6)(+=s s s G ,试求系统的单位脉冲响应和单位阶跃响应。
3、(10分)已知系统的结构图如下,试求: (1)开环的对数幅频和相频特性曲线;(2)单位阶跃响应的超调量σ%,调节时间ts ; (3)相位裕量γ,幅值裕量h 。
7.(15分)已知系统结构图如下图所示,试求传递函数)()(,)()(s R s E s R s C 。
3. (10分)已知某系统初始条件为零,其单位阶跃响应为)0(8.08.11)(94≥+-=--t e e t h t t ,试求系统的传递函数及单位脉冲响应。
8.(12分)已知系统结构图如下,试求系统的传递函数)()(s R s C 。
控制工程技术课后习题答案

1习题1-1 试列举几个日常生活中的开环和闭环控制系统的例子,并说明其工作原理。
1-2 根据题1-1图所示的电动机速度控制系统工作原理图:(1)将a ,b 与c ,d 用线连接成负反馈系统;(2)画出系统方框图。
1-3 下图是水位控制系统的示意图,图中1Q ,2Q 分别为进水流量和出水流量。
控制的目的是保持水位为一定的高度。
试说明该系统的工作原理并画出其方框图。
1-4 仓库大门自动控制系统如图1-3所示,试分析系统的工作原理,绘制系统的方框图,指出各实际元件的功能及输入、输出量。
2习题2-1 求下列函数的拉氏变换。
(1)t t t f 4cos 4sin )(+= (2)t e t t f 43)(+= (3)t te t f --=1)( (4)()cos3t f t e t -=2-2求下列函数的拉氏反变换。
(1))3)(2(1)(+++=s s s s F(2)()()()2114F s s s =++(3)()225sF s s s =-+(4)()221225s F s s s +=++(5) )3()1(2)(2=++=s s s s s G (6) ))()(()()(c s b s a s d s s G ++++=(7) 152122)(2+++=s s s s G2-3 解微分方程()()()22681d y t dy t y t dt dt++=,初始条件:(0)1y =,'(0)0y = 。
2-4 试证明图2-75所示电气系统与机械系统具有相同的传递函数。
图2-75 题2-4 图2-5 试分别写出图2-76中各有源网络的传递函数。
(1) (2)图2-76 题2-5图2-6系统的方框图如图2-77所示,试求该系统的输入输出传递函数。
图2-77 题2-6图2-7 系统的方框图如图2-78所示,试用梅逊公式求传递函数。
图2-78 题2-7图2-8 已知系统结构如图2-79所示。
自动控制原理模拟题及答案

学习中心 姓 名 学 号西安电子科技大学网络和继续教育学院《自动控制原理》模拟试题一一、简答题(共25分)1、简述闭环系统的特点,并绘制闭环系统的结构框图。
( 8分)2、简要画出二阶系统特征根的位置和响应曲线之间的关系。
( 10分)3、串联校正的特点及其分类?( 7分)二、已知某单位负反馈系统的开环传递函数为)42()(2++=s s s Ks G K ,试确定使系统产生持续振荡的K 值,并求振荡频率ω。
( 15分)三、设某系统的结构及其单位阶跃响应如图所示。
试确定系统参数,1K 2K 和a 。
( 15分)四、某最小相角系统的开环对数幅频特性如图示。
要求(20分)1)写出系统开环传递函数;2)利用相角裕度判断系统的稳定性;3)将其对数幅频特性向右平移十倍频程,试讨论对系统性能的影响。
五、设单位反馈系统的开环传递函数为)1()(+=s s Ks G试设计一串联超前校正装置,使系统满足如下指标:(25分) (1)在单位斜坡输入下的稳态误差151<ss e ; (2)截止频率ωc ≥7.5(rad/s);(3)相角裕度γ≥45°。
模拟试题一参考答案:一、简答题1、简述闭环系统的特点,并绘制闭环系统的结构框图。
解: 闭环系统的结构框图如图:闭环系统的特点:闭环控制系统的最大特点是检测偏差、 纠正偏差。
1) 由于增加了反馈通道, 系统的控制精度得到了提高。
2) 由于存在系统的反馈, 可以较好地抑制系统各环节中可能存在的扰动和由于器件的老化而引起的结构和参数的不确定性。
3) 反馈环节的存在可以较好地改善系统的动态性能。
2、简要画出二阶系统特征根的位置和响应曲线之间的关系。
解:113、串联校正的特点及其分类?答:串联校正简单, 较易实现。
设于前向通道中能量低的位置,减少功耗。
主要形式有相位超前校正、相位滞后校正、相位滞后-超前校正。
二、已知某单位负反馈系统的开环传递函数为)42()(2++=s s s Ks G K ,试确定使系统产生持续振荡的K 值,并求振荡频率ω。
机械工程控制基础——练习题及答案

一、计算题1 已知系统传递函数:求系统在单位阶跃信号、单位斜坡信号输入时的响应。
2 设系统处于静止状态,当输入单位阶跃函数时其输出响应为2()1t t y t e e --=-+ t>0试求该系统的传递函数和单位脉冲响应。
3 试化简图所示的系统结构图,求传递函数4已知系统结构如图2-7所示。
1)求传递函数C(S)/R(S)和C(S)/N(S)。
2)若要消除干扰对输出的影响 (即 C(S)/N(S)=0),问0()G s =?5 试用结构图等效化简求下图所示系统的传递函数)()(s R s C 。
11)(+=Ts S G6 系统结构图如图3-1所示。
(1)当r(t)=t,n(t)=t时,试求系统总稳态误差;(2)当r(t)=1(t),n(t)=0)时,试求M p,t p。
图3-1=sse7某控制系统如图所示。
其中控制器采用增益为K p的比例控制器,即G c(s)=K p试确定使系统稳定的K p值范围。
0<K p<158 控制系统的结构图如图所示,若系统以频率ω=2rad/s持续振荡,试确定相应的参数K 和τ的值0.75τ= K=29 系统如图所示,其中扰动信号n(t)=1(t)。
仅仅改变K1的值,能否使系统在扰动信号作用下的误差终值为-0.099?不能10已知系统特征方程为06363234=++++ssss,判断该系统的稳定性,若闭环系统不稳定,指出在s平面右半部的极点个数。
(要有劳斯计算表)S平面右半部有2个闭环极点,系统不稳定。
11 一控制系统的单位阶跃响应为tt eetc10602.12.01)(---+=,求1) 系统的闭环传递函数;2) 计算系统的无阻尼自然频率n ϖ和系统的阻尼比ξ。
12 已知闭环系统的特征方程如下: 1)01.023=+++K s s s 2)036134234=++++K s s s s 试确定系统稳定的K 值范围。
360;100<<<<K K14 一单位反馈控制系统的开环传递函数为)1.01(10)(s s s G +=1)求系统的静态误差系数p K 、v K 和a K ; 2)当输入221021)(t a t a a t r ++=时,求系统的稳态误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dt
(2) 对微分方程进行非零状态下的拉氏变换;
d 2c(t) dt 2
3
dc(t) dt
2c(t)
2r(t)
s2C(s) sc(0) c(0) 3{sC(s) c(0)} 2C(s) 2R(s)
(3) 代入初始条件,得到输出量的拉氏形式:
d 2c(t) 3 dc(t) 2c(t) 2r(t)
给定初始状态条件求系统的响应时,其步骤为: (1) 得到系统的微分方程; (2) 对微分方程进行非零状态下的拉氏变换; (3) 代入初始条件,得到输出量的拉氏形式; (4) 对输出量进行拉氏反变换
(1) 得到零初始条件下系统的微分方程;
d 2c(t) 3 dc(t) 2c(t) 2r(t)
dt 2
1 1
与前向通路的P2(增益= G3G4 )对应的余子式Δ2?
2 1
与前向通路的P3(增益=G2G4)对应的余子式Δ3?
3 1
(s)
1
n k 1
pk k
P11
P22
P33
G1G2G4 G3G4 G2G4 1 G2G4 G3G4
2-14(b) 试用梅森公式求下图的传递函数C(s)/N(s).
有无不互接触回路?
前向通路1个, 增益为G1G2 单独回路2个,增益分别为 –G1G2H1,-G1G2
无不互接触回路
流图特征式?
1 La 1 G1G2H1 G1G2
前向通路p1=G1G2对应的余子式Δ1?
1 1
(s)
1
n k 1
pk k
p11
G1G2
1 G1G2H1 G1G2
2-14(a) 试用梅森公式求下图的传递函数C(s)/N(s).
1 s
s
4 1
s
2
2
c(t) 1 4et 2e2t
2-11、试用结构图对下面的图示系统简化等效并求相 应的传递函数。
• 比较点后移遵循的原则是: 串接一个与所越过的方框有相同传递函数的方框。
• 比较点前移遵循的原则是: 串接一个与所越过的方框有相同传递函数成倒数的方框。
▪引出点前移遵循的原则是: 在分出支路中串接有相同传递函数的方框。
计算输入信号下的闭环传递函数,令 N(s)=0,则此时
前向通路个数为? 增益分别为? 前向通路3个, 增益为G1G2G4, G3G4, G2G4
单独回路个数?增益分别为?
单独回路2个,增益为 –G2G4,-G3G4
总增益Δ?
1 La 1 G2G4 G3G4
与前向通路的P1(增益= G1G2G4 )对应的余子式Δ1?
第一步:比较点后移
2-14(a) 试用梅森公式求下图的传递函数C(s)/R(s).
(s)
1
n k 1
pk k
P11
1
G1G2 G1G2H1 G1G2
2-14(a) 试用梅森公式求下图的传递函数C(s)/R(s). 计算输入信号下的闭环传递函数,令N(s)=0,则此时:
前向通路个数为? 增益? 单独回路个数? 1
pk k
P11
G4 1 G2G4 G3G4
2-14(b) 试用梅森公式求下图的传递函数C(s)/N(s).
计算扰动作用下的闭环传递函数,令R(s)=0,则此时
前向通路个数为? 增益分别为? 前向通路1个, 增益为G4
单独回路个数?增益分别为?
单独回路2个,增益为 –G2G4,-G3G4
dt 2
dt
s2C(s) sc(0) c(0) 3{sC(s) c(0)} 2C(s) 2R(s)
s2C(s) s 3sC(s) 3 2C(s) 2 s
C(s)
s2 3s 2 s(s2 3s 2)
1 s
s
4 1
s
2
2
(4) 对输出量进行拉氏反变换:
C(s)
s2 3s 2 s(s2 3s 2)
p11 p22
G3G2 1 G1G2H1 1 G1G2H1 G1G2
2-14(b) 试用梅森公式求下图的传递函数C(s)/R(s).
(s)
1
n k 1
pk k
P11
P22
P33
G1G2G4 G3G4 G2G4 1 G2G4 G3G4
2-14(b) 试用梅森公式求下图的传递函数C(s)/R(s).
(s)
1
n k 1
pk k
p11 p22
G3G2 1 G1G2H1 1 G1G2H1 G1G2
2-14(a) 试用梅森公式求下图的传递函数C(s)/N(s).
计 算 扰 动 作 用 下 的 闭 环 传 递 函 数 , 令 R(s)=0, 则此时
前向通路个数为? 增益? 单独回路个数?增益? 有无不互接触回路?
前向通路2个, 增益为-1,G3G2 单独回路2个,增益分别为 –G1G2H1,-G1G2
无不互接触回路
流图特征式Δ?
1 La 1 G1G2H1 G1G2
前向通路的p1=-1对应的余子式Δ1?
1 1 G1G2H1
前向通路的p2=G3G2对应的余子式Δ2?
2 1
(s)
1
n k 1
pk k
▪引出点后移遵循的原则是: 在分出支路中串接有相同传递函数倒数的方框。
第四步:写出传递函数的表达形式
第一步:引出点后移 第二步:比较点前移
和反馈等效
第三步:比较点合并 和并联等效
(e)
第一步:引出点后移和并联等效 第二步:反馈、串联等效
第四步:写出传递函数的表达形式
第三步:反馈等效
第二步:并联、反馈等效 第三步:写出传递函数的表达形式
G6 (1 G2G3H2 G3H1 G3G4H3 ) G1G2G3G4G5 1 G2G3H2 G3H1 G3G4H3
G6
1
G1G2G3G4G5 G2G3H2 G3H1
G3G4 H 3
前向通路个数为? 增益? 前向通路个数为n=2, 增益分别为G6 , G1G2G3G4G5 单独回路个数?增益? 单独回路3个,增益分别为 -G2G3H2, -G3H1, -G3G4H3
有无不互接触回路?
无不互接触回路
流图特征式Δ?
1 La 1 G2G3H2 G3H1 G3G4H3
总增益Δ?
1 La 1 G2G4 G3G4
与前向通路的P1(增益= G4 )对应的余子式Δ1?
(s)
1
n k 1
pk k
P11
1
G4 G2G4 G3G4
1 1
2-15(a) 试用梅森公式求下图的传递函数C(s)/R(s).
梅森公式求得的传递函数:
P
1
n k 1
pk k
p11 p22
