最速降线问题
用光的折射原理计算最速降落轨道

清风QQ123067087
最速降落问题
(在重力作用且忽略摩擦力的情况下,一个质点在一点A以速率为零开始,沿某条曲线,去到一点不高于A的B,怎样的曲线能令所需的时间最短呢?这就是最速降线问题,又称最短时间问题、最速落径问题。
)费马原理说明,两点间光线传播的路径是所需时间最少的路径。
约翰•伯努利利用该原理,通过假设光在光速以恒定竖直加速度(也就是重力加速度g)加速的介质中运动形成的轨迹来导出最速降线。
sinα/v==sin(α+▲α)/(v+▲v)==d(sinα)/dv ①
所以
v=v0/sinα0*sinα②
又v^2==2gy ③
令k= v0^2/(2gsin^2α0)
y== v0^2/(2gsin^2α0)*sin^2α=k cos^2θ④
又dy/dx=tanθ⑤
由以上整理得(令2t=θ)
x[t_]:=-k/2*(2t+Sin[2t]-Pi);
y[t_]:= k/2*(1+Cos[2t])
Mathematica画图
r[t_]:={x[t],y[t]};
ParametricPlot[r[t],{t,Pi/2,Pi},PlotStyle→{Red,AbsoluteThickness[ 3]},Ticks→{Range[-20,20,5],Range[-10,10,3]},PlotLabel→r r[t]] r2t sin2t,cos2t1
1。
牛顿对最速降线的推导

牛顿对最速降线的推导自1687年英国物理学家约翰牛顿发表他的著名著作《自然哲学的数学原理》后,他的力学原理便开始受到科学家们的研究与追求。
在当时,“最速降线”(least-time path,LTP)是科学家们极其关注的一个课题。
而经过一番努力之后,牛顿也发现了这一规律。
最速降线说明了一个物理体在同一力场作用下,从一点到另一点所经历的所有可能路径中,用最少的时间运动到达另一点的路径。
最速降线的途中的路径均经历了力的作用,最终到达终点。
他的发现令人称道,牛顿以自身努力将其解决得相当彻底,而自此以后,最速降线的推导也受到了牛顿的追随者们的不断探究。
在牛顿的推导当中,他首先指出,当一个物体从一个地点沿着一条路径移动到另一个地点时,它在路径上受到的力与它在另一个地点移动的距离成正比,而与运动速度及方向是无关的。
而物体在路径上经过的时间则与它在两个地点的距离之和成正比。
基于此,牛顿推导出了一个总的路径数学表达式来描述路径上时间的最短运动路径。
牛顿的路径表达式写作为:中O为起点,P为终点,x1,x2,…, xn 分别为路径上的位置点和s为路径总长度。
根据牛顿的推导,时间最短的路径必定满足以上表达式,即距离最短的路径也是时间最短的路径。
此外,牛顿还指出,若构建一条时间最短的路径,则可以将其划分为若干小块,每一小块的速度是固定的并且与其他小块的速度无关,这也就是牛顿对最速降线的推导。
牛顿的最速降线推导不仅仅在物理学上有所应用,它在航空、海洋和运输等多个领域也都有实际应用,其中在很多运输系统中都起到了核心作用。
最速降线的运用可以节省很多运输时间,这正是牛顿对最速降线推导的重要性所在。
最后,值得指出的是,牛顿对于最速降线的推导给科学界带来了极大的指导意义,它引领着科学家们前进,也助力了科学的发展。
牛顿为我们提供了一种有效的推导方法,我们可以根据此探索更多有关最速降线的研究,进一步开发出更加实用的结果,造福社会。
总之,英国物理学家约翰牛顿发表的《自然哲学的数学原理》首次提出了对最速降线研究的可能性。
最速降线问题的力学解法
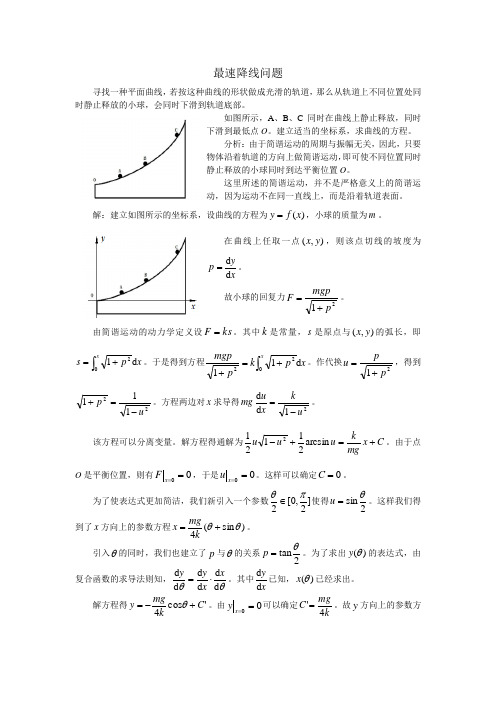
最速降线问题寻找一种平面曲线,若按这种曲线的形状做成光滑的轨道,那么从轨道上不同位置处同时静止释放的小球,会同时下滑到轨道底部。
如图所示,A 、B 、C 同时在曲线上静止释放,同时下滑到最低点O 。
建立适当的坐标系,求曲线的方程。
分析:由于简谐运动的周期与振幅无关,因此,只要物体沿着轨道的方向上做简谐运动,即可使不同位置同时静止释放的小球同时到达平衡位置O 。
这里所述的简谐运动,并不是严格意义上的简谐运动,因为运动不在同一直线上,而是沿着轨道表面。
解:建立如图所示的坐标系,设曲线的方程为)(x f y =,小球的质量为m 。
在曲线上任取一点),(y x ,则该点切线的坡度为xy p d d =。
故小球的回复力21pmgp F +=。
由简谐运动的动力学定义设ks F =。
其中k 是常量,s 是原点与),(y x 的弧长,即x p s xd 102⎰+=。
于是得到方程x p k pmgp xd 11022⎰+=+。
作代换21pp u +=,得到22111u p -=+。
方程两边对x 求导得21d d uk x u mg-=。
该方程可以分离变量。
解方程得通解为C x mgku u u +=+-arcsin 211212。
由于点O 是平衡位置,则有00==x F,于是00==x u 。
这样可以确定0=C 。
为了使表达式更加简洁,我们新引入一个参数]2,0[2πθ∈使得2sin θ=u 。
这样我们得到了x 方向上的参数方程)sin (4θθ+=kmgx 。
引入θ的同时,我们也建立了p 与θ的关系2tan θ=p 。
为了求出)(θy 的表达式,由复合函数的求导法则知,θθd d d d d d x x y y ⋅=。
其中x y d d 已知,)(θx 已经求出。
解方程得'cos 4C k mg y +-=θ。
由00==x y 可以确定kmg C 4'=。
故y 方向上的参数方程为)cos 1(4θ-=kmgy 。
最速降线曲线方程

最速降线曲线方程一、引言最速降线问题是数学中的一个研究领域,其研究的对象是质点在给定时刻从一点开始沿一根曲线下滑,经过时间t到达终点的轨迹。
最速降线问题在物理学、工程学和自然科学中有广泛的应用,因此研究最速降线曲线方程具有重要的理论和实际价值。
二、最速降线问题的基本概念最速降线问题的核心是求解质点在给定重力场中的最速降线曲线方程。
为了方便研究,我们假设空气阻力和其他外力对质点的影响可以忽略不计。
在这种情况下,质点沿最速降线曲线下滑时,其机械能守恒。
三、最速降线曲线的参数方程最速降线曲线的参数方程可以表达如下:x = f(t) y = g(t)其中,t表示时间,x和y分别表示质点在给定时刻t处的横坐标和纵坐标。
参数方程的求解需要满足两个条件:机械能守恒和速度最小。
四、求解最速降线曲线方程的方法求解最速降线曲线方程的常用方法有牛顿-拉夫逊迭代法和变分法。
下面分别介绍这两种方法的具体步骤:4.1 牛顿-拉夫逊迭代法1.假设最速降线曲线方程为y=f(x),其中x为横坐标,y为纵坐标。
2.根据机械能守恒和速度最小的条件,建立拉格朗日函数L(x, y, ),其中表示y的导数。
3.使用欧拉-拉格朗日方程消去,得到一个只包含x和y的微分方程。
4.通过对微分方程进行适当的变换,将其转化为获得y关于x的高阶导数的方程。
5.应用牛顿-拉夫逊迭代法,不断逼近y的解,直到满足给定条件。
4.2 变分法1.假设最速降线曲线方程为y=f(x),其中x为横坐标,y为纵坐标。
2.根据机械能守恒和速度最小的条件,建立变分问题。
3.将变分问题转化为欧拉-拉格朗日方程,并确定边界条件。
4.求解欧拉-拉格朗日方程,得到y关于x的方程。
5.应用适当的边界条件,解出y的表达式。
五、最速降线问题的应用最速降线问题在自然科学和工程学中有广泛的应用。
以下是一些具体的应用场景:1.地质勘探:最速降线曲线可以帮助地质学家确定地下岩层的形状和厚度。
2.工程设计:如何确定坡道、滑道和滚动体的形状是工程设计中的重要问题,最速降线曲线可以提供参考。
最速降线实验报告

最速降线实验报告实验目的,通过实验,验证最速降线的运动规律,并利用实验数据进行分析和计算。
实验仪器,小车、斜面、计时器、尺子、直尺、手机。
实验原理,最速降线是指物体在斜面上沿着特定角度的斜线运动,其速度在垂直方向上最小。
根据斜面的倾角和高度差,可以计算出小车在斜面上的加速度。
实验步骤:1. 在水平地面上放置斜面,并测量斜面的倾角和高度差。
2. 将小车放置在斜面的顶端,释放小车并启动计时器。
3. 观察小车沿着斜面运动的过程,并记录下小车到达底部所用的时间。
4. 重复实验多次,取平均值作为最终结果。
实验数据:斜面倾角,30°。
斜面高度差,1m。
小车到达底部所用时间,2.5s、2.3s、2.4s、2.6s、2.5s。
实验结果:根据实验数据和斜面参数,可以计算出小车在斜面上的加速度。
利用公式 a = gsinθ,其中g为重力加速度,θ为斜面倾角,可以求得小车在斜面上的加速度为a = 9.8m/s² sin30° = 4.9m/s²。
实验分析:通过实验数据和计算结果可以得出,小车在斜面上的加速度与斜面的倾角有关,倾角越大,加速度越大。
这符合最速降线的运动规律,即物体在斜面上运动时,其速度在垂直方向上最小。
实验结论:本实验验证了最速降线的运动规律,通过实验数据和计算分析,得出小车在斜面上的加速度为4.9m/s²。
实验结果与理论预期基本吻合,实验过程中未发现明显误差。
实验总结:最速降线实验是一项简单而有趣的物理实验,通过实验可以深入理解物体在斜面上的运动规律。
在实验过程中,要注意测量斜面参数的准确性,以及记录实验数据的精确性。
通过多次实验取平均值,可以减小误差,得到更可靠的实验结果。
通过本次实验,我对最速降线的运动规律有了更深入的理解,也掌握了实验操作的技巧和注意事项。
希望通过今后的实验学习,能够进一步提高实验技能,深化对物理知识的理解和应用。
最速降线问题

解 且y(0)=0,y(p)=q 这样 其E-L方程为 由于 所以有 则可得 上式对θ求导,所以 根据曲线过原点(0,0)及(p,q)可求出x0=0及r,这样,所求曲线为
应用
最速降线无论在数学上还是物理上都进行过严格的证明,对工程来说,其物理原理为在同一高度滚下的两个球, 两球下滚的原因都是受重力分力的作用,沿直线下滚的球,下滑的加速度保持不变,速度稳定地增加。沿着旋轮线 下滑时,开始的一段的坡度非常大,使得下滑的球在非常短的时间内取得的下滑速度非常大。虽然,在下滑的后半 阶段,坡度逐渐变小、速度增加变缓,但此时的下滑速度已经变得很大。所以,沿着旋轮线下滑在整个下滑阶段的 平均速度很大。即使旋轮线的长度比直线的长度大,沿着旋轮线下滑的时间也比直线短。
求解
列出表达式
最终解答
图1设 O, A是高度不同,且不在同一铅垂线上的两定点,如果不计摩擦和空气阻力,一质点 m在重力作用下 从 O点沿一曲线降落至。A(p,q) A点,问曲线呈何种形状时,质点降落的时间最短。
设曲线为 y=y(x),坐标如图1所示,质点由 O点开始运动,它的速度 v与它的纵坐标有关系 式中, g是重力加速度。 在曲线上点 (x, y)处,质点的运动速度为 式中, s表示曲线的弧长, t表示时间,于是 由于点 O, A的横坐标分别是 0, p,则质点 m从 O点运动到 A点所需时间为 这样,质点由 O点运动到 A点所需时间 t是 y(x)的函数,最速降线问题就是满足边界条件的 所有连续函数 y(x)中,求出一个函数 y使泛函式取最小值。 对泛函求极值的问题称为变分问题,使泛函取极值的函数称为变分问题的解,也称为极值函数。
旋轮线与1673年荷兰科学家惠更斯讨论的摆线相同。因为钟表摆锤作一次完全摆动所用的时间相等,所以摆 线(旋轮线)又称等时曲线。
最速降线原理

最速降线原理
最速降线原理指的是在自然界的各种运动中,物体在重力作用下,沿着一条路径从起点到终点,所经过的路径是使得时间最短的路径。
该原理可以用来解释光的传播、水流的流动、自由落体等现象。
在光的传播中,光线在不同介质中传播时会发生折射,而根据最速降线原理,光线会选择一条路径,使得光线的传播时间最短。
在水流的流动中,水会沿着地形自然流动,以最短的时间到达低处。
这可以解释河流的形成和水的正常流动。
而对于自由落体运动,物体受到重力的作用,在空气阻力不考虑的情况下,物体会选择纵向下降的路径,以最短的时间到达地面。
最速降线原理是自然界中普遍存在的规律,可以用来解释各种运动现象,并且在工程和科学研究中也有着广泛的应用。
最速下降曲线

最速下降曲线最速下降曲线是最大似然估计的一种重要形式,它可以在极少的计算代价下尽可能快地求出最大似然参数。
它是一种具有普适性的方法,用于估计未知的参数,广泛应用于统计学、机器学习、模式识别和深度学习中。
最速下降曲线也被称为梯度下降法,它的目的是用来求解无约束的最优化问题,它是根据梯度方法而得到的一种算法。
梯度方法是在求解最优化问题时通常使用的一种方法,它可以在非线性函数中有效地求解最优化问题。
最速下降曲线是基于梯度下降方法得到的,它可以有效地求解最大似然估计。
最大似然估计就是要从一堆测量数据中发现未知概率过程的参数,这些参数可以用于描述概率过程。
最大似然估计的结果可以用最速下降曲线来表示,最速下降曲线的直线是梯度的反方向,即最大似然估计的梯度方向。
最速下降曲线是基于梯度下降方法,梯度下降方法是求解无约束最优化问题的一种算法,它是基于参数的梯度(偏导数),而最速下降曲线是一条梯度下降曲线,它的方向是最大似然估计的梯度的反方向。
最速下降曲线的目的是找到最大似然参数,即求解最大似然参数,它把最大似然目标函数变换为一个凸函数,通过最速下降曲线,可以以最小的代价求出最大的似然参数。
在实际应用中,最速下降曲线可以用来估计参数,主要用于最大似然估计和贝叶斯估计,它们都是用来解决参数估计问题的有效方法。
最速下降曲线也被广泛应用于统计学、机器学习、模式识别和深度学习等领域,它可以非常快速准确地估计出参数,对于求解复杂问题,最速下降曲线可以提供有效的优化方法。
综上所述,最速下降曲线是一种重要的统计方法,用来估计参数,它在机器学习、模式识别、深度学习和统计学等领域都有着重要的作用,它的主要目的是求解最大似然参数,可以以最小的代价求出最大似然参数。
最速下降曲线的优点是求解时间短,精度高,可以非常有效的求解复杂的优化问题,它有助于提高估计模型的精度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最速降线问题
“想象一个小球,仅受重力,从点 A 出发沿着一条没有摩擦的斜坡滚至点 B。
怎样设计这条斜坡,才能让小球在最短的时间内到达点 B?”
这个在数学史上被称为“最速降线”的知名问题,最早是由著名的意大利科学家伽利略(Galileo Galilei)于 1630 年提出来的。
他在研究后认为最速降线应该是圆弧,但可惜的是这个答案并不是正确的。
时间又过了 60 多年,1696 年 6 月,来自瑞士巴塞尔(Barsel,这座城市不仅是数学世家伯努利的故乡,也是欧拉的故乡,有一个由欧拉解决的著名数论问题就是以这座城市命名的)的约翰・伯努利(Johann Bernoulli)在《教师学报》(Acta Eruditorum)上又重新提出这个问题,并向全欧洲的数学家提出公开挑战。
这个别出心裁却又十分容易理解的问题吸引了当时全欧洲的数学家,而最后给出了正确解答的人也都是数学史上赫赫有名的
巨人。
这也让这次挑战成为了数学史上最激动人心的一场公开挑战。
数学家之间公开挑战的传统要追溯到 16 世纪在意大利的博洛尼亚(Bologna)。
16 世纪初的博洛尼亚曾是欧洲数学思想的大熔炉,全欧洲的学生都会来到博洛尼亚大学。
他们甚至还“发明”了一项新的观赏运动——数学比赛。
这听起来有些匪夷所思,但在当时确实有大批的观众从各地涌来,围观数学家们互相之间用数学斗法。
其中最有名的一次,是在塔塔里亚(Tartaglia)和费奥(Fior)间上演的,是一场关于求出一元三次方程通解的世纪智力大战。
言归正传,在约翰・伯努利发出挑战后的半年里,他收到的唯一一份答案来自《教师学报》的主编,他的老师莱布尼茨(Gottfriend Wilhelm Leibniz)。
在莱布尼茨的要求下,他将接受答案的最后期限推迟到 1697 年的复活节,以便有更多的数学家能参与到这场挑战中来。
我们都知道,过两点的直线段是两点间的最短路径。
但使质点的运动时间最短的运动轨迹,却不是那么的显而易见。
这个问题和以往人们见过的那些求极值的问题是有本质区别的。
借助微积分,人们可以求出一个函数的极值;但最速降线问题要求的并不是某个传统函数的极值点,而是要在一簇曲线(过 A、B 两点的所有曲线)中,求出能让质点运动时
间最短的那条。
这是一个以函数(小球的运动轨迹)为自变量,以实数(小球运动的时间)为函数值的函数,也就是所谓的泛函。
我们要求的就是这样一个泛函的极值。
正如后文将要介绍的那样,这类问题形成了一个全新的数学分支——变分学。
1697 年的复活节很快就到了,约翰・伯努利一共收到了五份正确答案。
这五份答案分别来自他自己,他的老师莱布尼茨,他的哥哥雅各布・伯努利(Jakob Bernoulli),他的学生洛必达(Guillaume Francois Antonie de L'Hospital),还有一位来自英国的匿名数学家。
最后这份答案虽然没有署名,但显然出自赫赫有名的牛顿(Issac Newton)之手。
虽然五人的解法各不相同,但他们的答案全都一样——最速降线就是摆线。
同一个答案
所谓摆线(cycloid),就是当圆沿一条直线运动时,圆周上一定点所形成的轨迹。
其实当时的数学家对这种曲线并不陌生,帕斯
卡和惠更斯都曾研究过这一重要的曲线。
但大部分人都没有想到,这条线同时也是人们苦苦追寻的最速降线。
而我们大家对摆线也不陌生。
还记得小时候玩过的那种能够画出各种漂亮曲线的玩具吗?一块塑料板上开着几个圆形的大洞,还有几块较小的圆形塑料片,不同半径处留有一些孔。
把这些看似普通的小圆片放进大圆孔中,再将圆珠笔插在小孔里并带动小圆片沿着大圆的圆周运动,就能在纸上留下各种美丽的曲线。
这些曲线也都是摆线,只不过是另一种被称为“内摆线”(hypocycloid)的摆线。
它们是由给定圆在另一个圆内运动时,圆周上一定点形成的轨迹。
不同的解法
让我们回到众人给出的最速降线的解法上。
莱布尼茨、牛顿、洛比达都是用他们擅长的微积分来解决这个问题的。
伯努利
兄弟的解法就值得特别地说一说了。
约翰的解法应该是最漂亮的解法了。
他利用了费马原理(Fermat's principle),将小球的运动类比成光线的运动。
费马原理又叫做“最短光时”原理,说的是光线在传播时总会选择光程极短的那条路径。
那么,“最速降线”就是在光速随高度下降而增加(加速度恒为重力加速度 g)的介质里光线传播的路径。
用这样的类比思想,约翰成功地算出了这条曲线就是前面提到的摆线。
这种解法出人意料地用到了费马原理,实在是太巧妙了!在物理学中,费马原理被认为是“最小作用量原理”(principle of least action)在几何光学中的特例。
而最小作用量原理则是物理学定律普遍遵循的规律,甚至被称为“物理定律的定律”。
不知你想过没有,当我们将一个小球抛出后,它为什么会沿着所谓的抛物线运
动?你可能会说,因为小球只受重力作用,根据牛顿第一定律,它在水平方向上速度恒定不变;而根据牛顿第二定律,它在竖直方向上做匀变速运动。
这两个运动合起来就使得小球的运动轨迹成了一条抛物线。
这确实不错,但现在让我们换一个角度来考虑这个问题。
从整体的角度考虑,小球在被抛出后,为什么不沿着其他的路径运动,却总是沿着抛物线运动呢?同样,我们在考察了连接小球起点和终点的所有曲线后,会发现只有在沿着抛物线运动时,小球的动能和势能的差在运动过程中对时间的积分(这就是所谓的“作用量”)才是最小的。
注意,在这里我们同样是在一簇曲线中,求出一条曲线使得某个量达到极值。
这种在一簇曲线中,求出某条曲线使得函数取到极值的思想就是变分的核心思想。
也就是说,我们又是在用变分求泛函的极值。
再回过头来看看约翰・伯努利的哥哥——雅各布・伯努利的解法。
虽然雅各布的解法相对于约翰的解法来说更复杂更麻烦,但他的解法更具有一般性,体现了变分的思想。
约翰的学生,伟大的数学家欧拉吸收了这一思想,并从 1726 年开始发表相关的论文,最终于 1744 年首先给出了这类问题的解法,并创立了变分学这一新的数学分支。
投资者用它来计算最大利润,工程师用它来计算最小损耗,建筑师用它来
优化架构。
它成为了微积分理论中最强大的工具之一。
