寻找最速降线.ppt
最优化方法第二章_线搜索算法_最速下降法
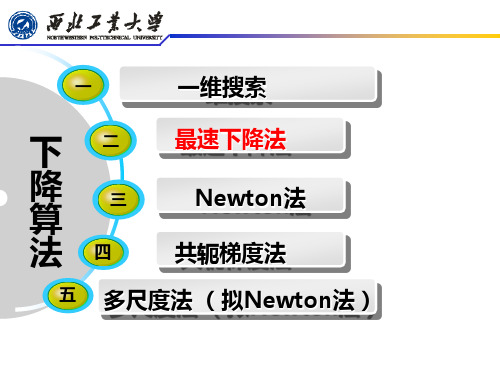
f x1 , x2 c, c>0,
2
改写为:
x12 2c 1
2 x2
2c 2
2
1
二、最速下降法
x2
这是以
2c
1
和
2c
2
为半轴的椭圆
2c
2c
2
2
从下面的分析可见 两个特征值的相对
x1
大小决定最速下降法的收敛性。
(1)当 1 2 时,等值线变为圆
2 2
4 f x , 2
2 x1 2 x2 4 f ( x) , 2 x1 +4x2
4 d = f x , 2
0 0
=40 2 20 3 令 0= ' ( ) 80 20, 得 0 =1/4,
一
一维搜索
二 三 四
下 降 算 法
五
最速下降法 Newton法 共轭梯度法
多尺度法 (拟Newton法)
二、最速下降法 假设 f 连续可微,取 线搜索方向
k
d f ( x )
k
步长k 由精确一维搜索得到。 从而得到第 k+1次迭代点,即
f ( x k k d k ) min f ( x k d k )
(推论)在收敛定理的假设下,若f (x)为凸函数,则最速下降 法或在有限迭代步后达到最小点;或得到点列 x k ,它的任 何聚点都是 f (x)的全局最小点。
二、最速下降法
最速下降法特征:相邻两次迭代的方向互相垂直。
令
( ) f ( x d ), 利用精确一维搜索,可得
最速降线推导过程

最速降线推导过程嘿,朋友们!今天咱来聊聊最速降线推导过程这个神奇的玩意儿。
你想想看啊,要是有个小球要从一个点快速地滚到另一个点,走什么样的路线才是最快的呢?这可不是随便说说就能明白的哟!咱先从最基本的开始。
就好比你要去一个地方,有好多条路可以走,那肯定得选最快的那条嘛。
最速降线就是这样一条神奇的路线。
假设现在有两个点,一个高一个低。
小球从高处往低处滚,那它可不能瞎滚呀。
它得找到那条最合适的路。
这就好像我们平时走路一样,有时候走直线不一定是最快的,可能得绕个弯,或者走个曲线。
最速降线就是这么个特别的存在。
咱再深入一点说。
要是光凭感觉去猜,那可不行。
得用一些数学的方法来推导。
就像解方程一样,一步一步地找到答案。
想象一下,把这个过程比作一场冒险。
小球就是勇敢的冒险者,它要在各种路线中找到那个最速降线这个宝藏。
数学家们就像是聪明的向导,他们通过各种计算和推理,帮小球找到那条正确的路。
他们会考虑很多因素呢,比如重力呀,摩擦力呀。
这些东西可都对小球的滚动速度有影响。
然后呢,经过一番复杂的推导和计算,终于找到了最速降线的秘密。
哎呀,这可真是不容易啊!这就好像是解开了一个超级难的谜题。
你说这神奇不神奇?原本看似很简单的一个小球滚动问题,背后竟然藏着这么多的学问和秘密。
最速降线的推导过程可不只是一堆数学公式和计算,它还让我们看到了数学的魅力和神奇。
它告诉我们,有时候看似简单的事情,背后可能有着非常复杂的原理。
就像生活中的很多事情一样,不能只看表面,要深入去了解,去探索。
所以啊,别小看了这个最速降线推导过程。
它可不仅仅是数学上的一个成果,更是让我们对世界有了更深的认识呢!这就是最速降线推导过程,一个充满奥秘和惊喜的领域。
是不是很有意思呢?你还不赶紧去研究研究!。
最速降线 原理

最速降线原理
最速降线原理是物理学中的一个重要概念,也是人们普遍生活中都能体验到的物理现象。
其原理主要包括重力及惯性力在物体运动过程中的作用以及在无阻力情况下物体在垂直方向上运动的规律等。
最速降线原理主要指的是在无阻力作用下,物体从一定高度自由落下时,其所经过的路径是一条曲线,这条曲线被称为最速降线。
最速降线原理主要的物理原理是重力的作用和惯性力的作用。
重力是地球对于物体的吸引力,其作用方向始终指向地心,其大小与物体的质量成正比,与物体所处的高度成反比。
惯性力是物体在运动过程中所受的惯性作用力,其大小与物体的质量成正比,与其运动速度的平方成正比。
在最速降线原理中,无论物体从什么高度自由落下,其所经过的路径都是一条曲线,这条曲线被称为最速降线。
其最大特点在于,物体在沿着这条曲线运动过程中,其速度是不断变化的,但其总能量保持不变。
这是因为,物体的动能和势能之和始终保持为定值。
最速降线的路径可以通过各种数学方法进行求解,其中最著名的是布鲁诺的卡西尼椭圆曲线。
这条曲线被称为“最优曲线”,因为它是物体自由落体运动中总时间最短的路径。
最速降线原理在实际生活中具有广泛的应用价值。
如,它可用于设计roller coaster(过山车)等娱乐设施,以及计算高空跳伞过程中的跳伞速度和轨迹等等。
总之,最速降线原理是物理学中的一个重要概念,对于人们理解和掌握物体运动过程中的规律具有重要意义。
最速降线问题的力学解法
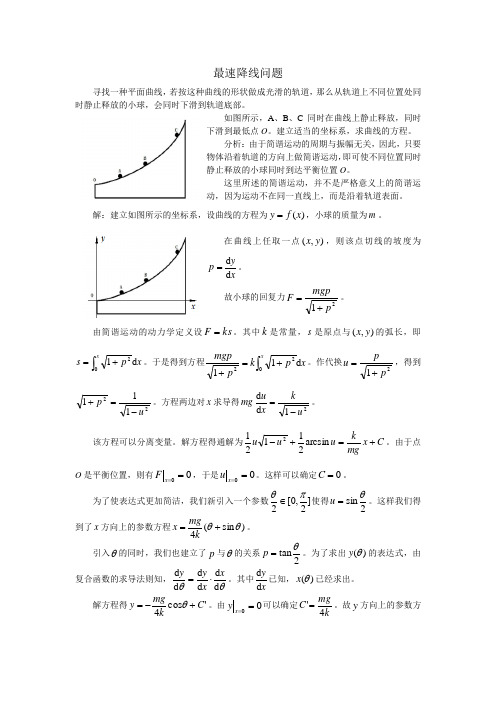
最速降线问题寻找一种平面曲线,若按这种曲线的形状做成光滑的轨道,那么从轨道上不同位置处同时静止释放的小球,会同时下滑到轨道底部。
如图所示,A 、B 、C 同时在曲线上静止释放,同时下滑到最低点O 。
建立适当的坐标系,求曲线的方程。
分析:由于简谐运动的周期与振幅无关,因此,只要物体沿着轨道的方向上做简谐运动,即可使不同位置同时静止释放的小球同时到达平衡位置O 。
这里所述的简谐运动,并不是严格意义上的简谐运动,因为运动不在同一直线上,而是沿着轨道表面。
解:建立如图所示的坐标系,设曲线的方程为)(x f y =,小球的质量为m 。
在曲线上任取一点),(y x ,则该点切线的坡度为xy p d d =。
故小球的回复力21pmgp F +=。
由简谐运动的动力学定义设ks F =。
其中k 是常量,s 是原点与),(y x 的弧长,即x p s xd 102⎰+=。
于是得到方程x p k pmgp xd 11022⎰+=+。
作代换21pp u +=,得到22111u p -=+。
方程两边对x 求导得21d d uk x u mg-=。
该方程可以分离变量。
解方程得通解为C x mgku u u +=+-arcsin 211212。
由于点O 是平衡位置,则有00==x F,于是00==x u 。
这样可以确定0=C 。
为了使表达式更加简洁,我们新引入一个参数]2,0[2πθ∈使得2sin θ=u 。
这样我们得到了x 方向上的参数方程)sin (4θθ+=kmgx 。
引入θ的同时,我们也建立了p 与θ的关系2tan θ=p 。
为了求出)(θy 的表达式,由复合函数的求导法则知,θθd d d d d d x x y y ⋅=。
其中x y d d 已知,)(θx 已经求出。
解方程得'cos 4C k mg y +-=θ。
由00==x y 可以确定kmg C 4'=。
故y 方向上的参数方程为)cos 1(4θ-=kmgy 。
最速降线曲线方程

最速降线曲线方程一、引言最速降线问题是数学中的一个研究领域,其研究的对象是质点在给定时刻从一点开始沿一根曲线下滑,经过时间t到达终点的轨迹。
最速降线问题在物理学、工程学和自然科学中有广泛的应用,因此研究最速降线曲线方程具有重要的理论和实际价值。
二、最速降线问题的基本概念最速降线问题的核心是求解质点在给定重力场中的最速降线曲线方程。
为了方便研究,我们假设空气阻力和其他外力对质点的影响可以忽略不计。
在这种情况下,质点沿最速降线曲线下滑时,其机械能守恒。
三、最速降线曲线的参数方程最速降线曲线的参数方程可以表达如下:x = f(t) y = g(t)其中,t表示时间,x和y分别表示质点在给定时刻t处的横坐标和纵坐标。
参数方程的求解需要满足两个条件:机械能守恒和速度最小。
四、求解最速降线曲线方程的方法求解最速降线曲线方程的常用方法有牛顿-拉夫逊迭代法和变分法。
下面分别介绍这两种方法的具体步骤:4.1 牛顿-拉夫逊迭代法1.假设最速降线曲线方程为y=f(x),其中x为横坐标,y为纵坐标。
2.根据机械能守恒和速度最小的条件,建立拉格朗日函数L(x, y, ),其中表示y的导数。
3.使用欧拉-拉格朗日方程消去,得到一个只包含x和y的微分方程。
4.通过对微分方程进行适当的变换,将其转化为获得y关于x的高阶导数的方程。
5.应用牛顿-拉夫逊迭代法,不断逼近y的解,直到满足给定条件。
4.2 变分法1.假设最速降线曲线方程为y=f(x),其中x为横坐标,y为纵坐标。
2.根据机械能守恒和速度最小的条件,建立变分问题。
3.将变分问题转化为欧拉-拉格朗日方程,并确定边界条件。
4.求解欧拉-拉格朗日方程,得到y关于x的方程。
5.应用适当的边界条件,解出y的表达式。
五、最速降线问题的应用最速降线问题在自然科学和工程学中有广泛的应用。
以下是一些具体的应用场景:1.地质勘探:最速降线曲线可以帮助地质学家确定地下岩层的形状和厚度。
2.工程设计:如何确定坡道、滑道和滚动体的形状是工程设计中的重要问题,最速降线曲线可以提供参考。
最速降线原理

最速降线原理
最速降线原理指的是在自然界的各种运动中,物体在重力作用下,沿着一条路径从起点到终点,所经过的路径是使得时间最短的路径。
该原理可以用来解释光的传播、水流的流动、自由落体等现象。
在光的传播中,光线在不同介质中传播时会发生折射,而根据最速降线原理,光线会选择一条路径,使得光线的传播时间最短。
在水流的流动中,水会沿着地形自然流动,以最短的时间到达低处。
这可以解释河流的形成和水的正常流动。
而对于自由落体运动,物体受到重力的作用,在空气阻力不考虑的情况下,物体会选择纵向下降的路径,以最短的时间到达地面。
最速降线原理是自然界中普遍存在的规律,可以用来解释各种运动现象,并且在工程和科学研究中也有着广泛的应用。
变分法解最速降线

变分法解最速降线
变分法是一种数学方法,可以用来求解优化问题。
在物理学和工程学中,变分法常用于研究最速降线问题。
最速降线问题是指一个物体从一点开始沿着一条曲线下滑,到达另一个点所需的时间最短。
变分法可以用来确定这条最速降线的方程。
具体来说,变分法的思路是先假设最速降线的方程形式,然后通过对这个假设方程进行微小的变化,求出这种变化对最终需要的时间的贡献。
通过对所有这样的微小变化求和,可以得到最终需要的总时间。
然后,通过对这个总时间进行求导,可以得到最速降线曲线的方程。
完整word版最速下降法求解线性代数方程组

最速下降法求解线性代数方程组要求:对于给定的系数矩阵、右端项和初值,可以求解线性代数方程组一、最速下降法数学理论PP?tX?Xf(X)的负梯中,在基本迭代公式每次迭代搜索方向取为目标函数kk1kkk?t)X??f(P?取为最优步长,由此确定的算法称为最速度方向,即,而每次迭代的步长kkk下降法。
X)Xminf(kk。
现在次,获得了第,假定我们已经迭代了为了求解问题个迭代点k X出发,可选择的下降方法很多,一个非常自然的想法是沿最速下降方向(即负梯度方从k X邻近的范围内是这样。
因此,去搜索方向为 )进行搜索应该是有利的,至少在向k P???f(X).kk P k?1进行一维搜索,由此得到第为了使目标函数在搜索方向上获得最多的下降,沿k个跌带点,即X?X?t?f(X),kk1k?k t按下式确定其中步长因子k f(X?t?f(X))?minf(X?t?f(X)),kkkkkk X?ls(X,??f(X)). ( 1)k1k?k X X,XX,, ,,?k0,12是初始点,由计算就可以得到一个点列,显然,令其中0210{X}f)X(X)(f 的满足一定的条件时,由式()所产生的点列必收敛于者任意选定。
当1k极小点。
二、最速下降法的基本思想和迭代步骤???,)(Xf(X)g. ,终止限已知目标函数及其梯度和321Xf?f(X),g?g(X)k?0.,计算;置(1)选定初始点00000X?ls(X,?g)f?f(X),g?g(X). (2)作直线搜索:;计算k?1kk1?k1k?kk?1?1(X,f(X))k?k?1,置,结束;用终止准则检验是否满足:若满足,则打印最优解否则,1k?1?k转(2)(3)最速下降法算法流程图如图所示.X结束三、最速下降法的matlab实现function [x,n]=twostep(A,b,x0,eps,varargin) %两步迭代法求线性方程组Ax=b的解if nargin==3eps= 1.0e-6;M = 200;elseif nargin<3errorreturnelseif nargin ==5M = varargin{1};endD=diag(diag(A)); %求A的对角矩阵L=-tril(A,-1); %求A的下三角阵U=-triu(A,1); %求A的上三角阵B1=(D-L)\U;B2=(D-U)\L;f1=(D-L)\b;f2=(D-U)\b;x12=B1*x0+f1;x =B2*x12+f2;n=1; %迭代次数while norm(x-x0)>=epsx0 =x;x12=B1*x0+f1;x =B2*x12+f2;n=n+1;if(n>=M)'); 迭代次数太多,可能不收敛! disp('Warning: return;endend的解最速下降法求线性方程组Ax=bfunction [x,n]= fastdown(A,b,x0,eps) %if(nargin == 3)eps = 1.0e-6;endx=x0;n=0;tol=1;以下过程 % while(tol>eps)可参考算法流程 r = b-A*x0;d = dot(r,r)/dot(A*r,r);x = x0+d*r;tol = norm(x-x0);x0 = x;n = n + 1;end四、最速下降法的算例实现A=[5 2 0;6 4 1;1 2 5];b=[10 18 -14]';eps=1.0e-6;x =-0.87507.1875-5.5000 k =60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
Dl
为a, b, OD =c, 质点经过l于C
O
C
2
OC =x 那么质点由A1到A2需时间
A2
14
t x2 a2 (c x)2 b2
v1
v2
dt
x
cx
dx v1 x2 a2 v2 (c x)2 b2
惟一驻点满足
x
cx
v1 x2 a2 v2 (c x)2 b2
i 1
vi
( yi 是已知的!)
(n -1元函数!)
求这个函数的极小值, 就得到问题的近似解 (为简单计,可取g =1000cm/s2)
可以使用数学软件来求极值,但所得曲线为 离散形式,无解析表达式
9
求解极值数值方法
令
T xi
vi [(xi
xi xi1
xi -1 ) 2
变,于是依辅助结论知
k+1
B
sin k sin k1
y
vk
vk 1
注意上式对任何k成立,
16
故导出
sink
vk
C1(常数)
令平行线的间距趋于零,我们就得到在曲线
上任何一点
A
cx
sin
v
C1
(常数)
其中 为该点切线与铅垂线
的夹角
B
y
17
导出微分方程
v 2gy
A
cx
y
R(1
cos
)
25
最速降线问题仿真方法Matlab程序
function cycloid(G,H,n) if nargin==2 %两个参数则默认n为100
n=100; end g=9.8; h=H/n; minc=0;maxc=1/sqrt(2*g*h*n); x=0;y=0;
while abs(G-x)>1e-4 x=0; c=(minc+maxc)/2; %二分法求c值 for j=1:n y=j*h; v=sqrt(2*g*y); x=x+c*v*h/sqrt(1-c^2*v^2);
32
5. 若求出最速降线的曲线方程,试将质点从曲线 上任何一点无摩擦地滑到最低点,试求下滑所 需时间 注:若选择本次实验,必须完成任务1、2
33
数学实验
谢谢各位!
上海交通大学数学科学学院
2019年8月26
34
35
27
取G=H=10,n=100
28
取G=H=10,精确解
29
取G=H=10,仿真方法与精确解
30
实验任务
1. 分别用数值方法和解析方法求出的最速降线 的曲线和下降时间,将两种结果比较 (设c=π/2, H=1)
2. 在一条直线 l 的上侧有两个点A,B,试找出一条从 A 到B的曲线,使得这曲线绕l 旋转所得的旋转面 的面积最小.设直线l与点A,B在xy 平面,l为x轴, A为(0,(e+e-1)/2), B为(3,(e2+e-2)/2)
那么
b
a f (x)g(x)dx 0
f (x) 0
19
另一种方法-变分法
设曲线为 y y(x), (x[0,c])
A
cx
满足 y(0)=0, y(c)=H
在曲线上P(x,y)处质点速度为
v 2gy
B
又设从A到P的弧长为s,则 y
ds 1 y2 dx
1 y2 dx
v
)
1 2 gC12
注意从降线定义可知 y 0, 故
y
C 1, y
其中C (2gC12 )1
解法
1)可求解析解
2)也可以用数值方法,例如欧拉法求解
24
求解析解提示:
由于在原点y = 0 ,可改写方程
dx y x 0 dy C y y0
解析解
x R( sin ),
12
利用数学软件求解得到的曲线
13
再作分析
质点要走最快的路线(曲线),应该如何变化?
依然用从质点速度变化的角度考虑
设质点从A1经直线 l 到达A2,质点速度在l 的 上侧为v1,下侧为v2,则质点如何运动才最省时?
如图,若A1,A2到l 的垂足分 A1
别为O,D, A1,A2 到l的距离分别
也即
sin 1 sin 2
v1
v2
A1
a
1
c-x D l
O x C 2
b
A2
这就是光学中的 Snell 折射定律
15
建立数学模型
分析:如图建坐标系,若用与x 轴平行的直线将
AB 分割成小段, 考虑在第k
A
cx
层与k +1层质点在曲线上的下 k
滑,依能量守恒律,可近似
认为质点在每层内的速度不
yk-1
0< y <H用平行于 x 轴的
yk
直线 y=yk=kH/n 把这区域
B
分成 n个带状小区域.
y
在带状域yk-1<y<yk ,可近似认为 vk 2gyk
而曲线段近似认为是直线段,其长度
(xi xi1)2 (yi )2
8
于是质点从A到B所需时间近似为
n
T
(xi xi1)2 (yi )2
dt
dt
dt
2gy
从而质点沿曲线由A到B需时间
T T ( y) 1 c 1 y2 dx 2g 0 y
20
设集合 E {y(x) y C1[0,c], y(0) 0, y(c) H}
那么我们的问题成为
求某个yˆ E, 使得
T (yˆ) min T (y) yE
注意第二项
c 0
f y ( yˆ, yˆ)dx
f y ( yˆ, yˆ )
c 0
c 0
d dx
[
f
y
(
yˆ,
yˆ)]
dx
22
0
于是导出
c 0
[
f
y
(
yˆ,
yˆ)
d dx
(
f
y
(
yˆ,
yˆ))]
dx
0,
E0
由 的任意性,
d dx
(
f y ( yˆ,
f ( y, y) 1 1 y2 2g y
那么对 F()
c
f (yˆ , yˆ )dx
0
依复合函数求导法
c
F() 0 [ fy ( yˆ , yˆ ) fy( yˆ , yˆ )]dx
c
F(0) 0 [ fy ( yˆ, yˆ) fy( yˆ, yˆ)]dx
历史
1697年5月号“教师学报”接收了5篇解答报告
5
贝努利 约翰 Bernoulli,Johann
欧洲著名科学家族 涉猎 微积分、微分方程、解析几
何、 概率论以及变分法 更贡献于物理、化学和天文学 谁发现 L’Hospital 法则 欧拉的指导者和老师 瑞士的骄傲
6
问题数学形式
引进集合E0 {(x) C1[0,c],(0) 0,(c) 0} 显然若 yˆ(x) 是最速曲线函数,则
yˆ(x) (x) E, R , E0
于是函数 F() T(yˆ ) 在 0 取得最小值
故得
dF 0
d 0
21
为了计算 F(0) ,记
31
3. 圆柱面方程为
x2 z2 1 ( y 0)
用曲线连接面上A(0,0,1), B(1,3,0)两点,求使得 AB 弧长最短的曲线(短程线)
4. 在第3题中,将曲面改为 z x2 y2
求在曲面上连接A(1,0,1),B(0,2,2)的最短弧线 (建议以数值和解析两种方法求解加以比较)
数学实验
寻找最速降线
上海交通大学数学科学学院
2019年8月26
1
数学给我们一个用之不竭,充满真理的宝库,这 些真理不是孤立的,而是以相互密切的关系并立着, 而且随着科学的每一成功进展,我们会不断发现这 些真理之间的新的接触点.
── C.F.Gauss
数学既不严峻,也不遥远,它和几乎所有的人 类活动有关,又对每个真心对它感兴趣的人有益.
A
cx
设曲线为 y y(x), (x[0,c])
满足 y(0)=0, y(c)=H
若 T T (y) {质点沿 y=y(x)
B
下滑的时间} y
我们要求的是怎样的函数y(x)
使得T(y) 取得最小值
minT(y)
7
近似方法
如图建立坐标系,设A为原 A xk-1 xk
cx
点, B为(c,H), 将带状区域
yˆ))
f y ( yˆ,
yˆ)
0
上式乘以 ˆy 可化为
d dx
[
yˆf
y
(
yˆ,
yˆ)
f
( yˆ,
yˆ)]
0
即 ˆy满足方程
yf y ( y, y) f ( y, y) C1
这里
23
f ( y, y) 1 1 y2 2g y
得到方程为
y(1
y2
又因 y tan cot
sin 1 1
y
B
cot2 1 y2 1
于是得到
