最速降线问题(数学模型概述)
微积分中10大经典问题
微积分中10大经典问题最初的想法来自大一，当时想效仿100个初等数学问题，整理出100个经典的高等数学问题（这里高等数学按广义理解）。
可惜的是3年多过去了，整理出的问题不足半百。
再用经典这把尺子一量，又扣去了一半。
这里入选原则是必须配得起“经典”二字。
知识范围要求不超过大二数学系水平，尽量限制在实数范围内，避免与课本内容重复。
排名不分先后。
1）开普勒定律与万有引力定律互推。
绝对经典的问题，是数学在实际应用中的光辉典范，其对奠定数学科学女皇的地位起着重要作用。
大家不妨试试，用不着太多的专业知识，不过很有挑战性。
重温下牛顿当年曾经做过的事，找找当牛人的感觉吧，这个问题是锻炼数学能力的好题！2）最速降线问题。
该问题是变分法中的经典问题，不少科普书上也有该问题。
答案是摆线（又称悬轮线），关于摆线还有不少奇妙的性质，如等时性。
其解答一般变分书上均有。
本问题的数学模型不难建立，即寻找某个函数，它使得某个积分取最小值。
这个问题往深层次发展将进入泛函领域，什么是泛函呢？不好说，一个通俗的解释是“函数的函数”，即“定义域”不是区间，而是“一堆”函数。
最速降线问题通过引入光的折射定律可以直接化为常微分方程，大大简化了求解过程。
不过变分法是对这类问题的一般方法，尤其在力学中应用甚广。
3）曲线长度和曲面面积问题。
一条封闭曲线，所围面积是有限的，但其周长却可以是无限的，比如02年高中数学联赛第14题就是这样一条著名曲线-----雪花曲线。
如果限制曲线是可微的，通过引入内折线并定义其上确界为曲线长度。
但把这个方法搬到曲面上却出了问题，即不能用曲面的内折面的上确界来定义曲面面积。
德国数学家H.A.Schwarz举出一个反例，说明即使像直圆柱面这样的简单的曲面，也可以具有面积任意大的内接折面。
4）处处连续处处不可导的函数。
长久以来，人们一直以为连续函数除了有限个或可数无穷个点外是可导的。
但是，魏尔斯特拉斯给出了一个函数表达式，该函数处处连续却处处不可导。
最速降线数学建模
最速降线数学建模最速降线是一种在数学建模中常用的方法，用于求解优化问题。
它的基本思想是通过确定一个下降方向，并在该方向上求解函数的最小值，从而找到全局最优解或局部最优解。
最速降线方法广泛应用于计算机科学、经济学、物理学等领域，能够有效地解决许多实际问题。
在最速降线方法中，首先需要确定一个初始点作为起点，然后选择一个下降方向。
下降方向的选择是关键，它决定了求解过程的收敛性和速度。
常见的选择方法包括梯度下降法、共轭梯度法等。
在确定下降方向后，需要通过一定的步长来沿着该方向进行下降，直到达到最小值或满足一定的停止条件为止。
最速降线方法的核心是在每一步迭代中，根据当前点的函数值和梯度信息来确定下降方向和步长。
梯度是一个向量，它的方向指向函数在该点上升最快的方向，梯度的反方向就是函数下降最快的方向。
因此，最速降线方法可以看作是在梯度方向上进行搜索的过程。
在每一步迭代中，通过计算梯度信息和选择合适的步长，最速降线方法能够快速地收敛到最优解。
最速降线方法的优点是简单易实现，并且能够在大多数情况下找到较好的解。
然而，它也存在一些缺点。
首先，最速降线方法可能陷入局部最优解，而无法找到全局最优解。
其次，最速降线方法的收敛速度可能较慢，特别是在函数存在高度非线性或非凸性的情况下。
为了解决这些问题，可以采用改进的最速降线方法，如共轭梯度法、牛顿法等。
最速降线方法在实际应用中具有广泛的用途。
例如，在机器学习中，最速降线方法常用于求解优化问题，如线性回归、逻辑回归、支持向量机等。
在工程设计中，最速降线方法可以用于求解最优控制问题，如最优路径规划、最优参数选择等。
此外，最速降线方法还可以用于求解经济学中的最优化问题，如最大化利润、最小化成本等。
最速降线是一种重要的数学建模方法，能够有效地求解优化问题。
它的基本思想是通过确定下降方向和步长，沿着梯度方向进行搜索，从而找到最优解。
最速降线方法广泛应用于各个领域，具有简单易实现、收敛速度较快等优点。
最速降线方程公式
最速降线方程公式人类探索自然规律的脚步永不停歇，而最速降线方程公式则是其中一道解谜的关键。
这个公式可以帮助我们理解物体在重力作用下的运动轨迹，揭示了自然界中诸多现象的背后原理。
让我们来看看最速降线方程公式的基本形式：y = f(x)。
这里，y代表物体的高度，x代表时间或者水平方向的位移。
通过这个公式，我们可以追踪物体在某个时刻的位置，进而推断出它在整个运动过程中的轨迹。
然而，最速降线方程公式的美妙之处并不仅限于此。
它还能帮助我们研究自由落体、抛体运动等多种物理现象。
通过改变方程中的各个参数，我们可以模拟出不同条件下的运动轨迹，从而更好地理解自然世界的运动规律。
例如，在最速降线方程公式中加入一个参数a，我们可以研究物体在斜坡上滑动的情况。
当a大于0时，物体将滑下斜坡；当a等于0时，物体将保持静止；而当a小于0时，物体将向上滑动。
通过调整a的数值，我们可以观察到物体在不同斜度的斜坡上的运动方式有何不同。
除此之外，最速降线方程公式还可以帮助我们解决一些实际问题。
比如，当我们需要计算一个物体从山顶滑下到山脚所需的时间时，可以利用最速降线方程公式来得出准确的结果。
这个公式成为了我们解决实际问题的得力工具。
最速降线方程公式的研究还有助于培养我们的科学思维能力。
通过观察、实验和推理，我们能够更深入地理解这个公式背后的物理原理，进而探索更多有趣的现象和问题。
最速降线方程公式是人类智慧的结晶，它揭示了自然界中物体运动的奥秘。
通过研究和应用这个公式，我们能够更好地理解自然规律，解决实际问题，并培养自己的科学思维能力。
让我们继续探索，揭开更多自然规律的面纱，为人类的进步贡献一份力量。
微积分的应用雨中行走 药物浓度 水流问题 最速降线
•前表面淋雨量
C2
(v cos
v
u
I )wh(L
/
u)
v cos u I是前面的降雨强度。
v
•总淋雨量(基本模型)
C
C1
C2
wdL [sin
u
h d
(v cos
v
u)]
因为考虑了降雨的方向，淋湿的部位只有顶部和前
面。分两部分计算淋雨量。
取参数v 4m / s, I 2cm / h
第五章 微积分的应用
本章通过用学习过的高等数学知识解决一些简单的问题， 以增加同学们学习数学的兴趣和应用数学的能力。同时，也 通过对其中一些问题的不断深入讨论来体会数学建模没有最 好、只有更好的精神。
1. 雨中行走问题 2. 体内药物浓度的变化 3. 水的流出问题 4. 最速降线问题
1. 雨中行走问题
16
2. 体内药物浓度的变化
医生给病人开处方时必须注明两点：服药的剂量 和服药的时间间隔。超剂量的药物会对患者产生不 良的后果，甚至死亡；剂量不足，则不能达到治疗 的效果。已知患者服药后，随时间推移，药物在体 内被逐渐吸收，发生化学反应，也就是体内药物的 浓度逐渐降低。药物浓度降低的速率与体内当时药 物的浓度成正比。当服药量为A、服药时间间隔为T 时，试分析体内药物的浓度随时间的变化规律。
2）在同样时间内，水从小孔流出的体积为 BS
--- S是从小孔流出的水时在时间段 内流t 经的距离
由质量守恒得
Ah BS
两端同除以 ，t 并令 t取极0 限得
25
可得一阶方程： dh B ds
dt
A dt
由于 ds v， 代入上式得 dt
最速降线问题的充分性
珒ｖ＝ ｄｄｔ珒ｒ（ｔ） ＝（ｘ′（ｔ），ｙ′（ｔ））
由动能势能守恒原理，可得
１２ｍ 珒ｖ２ ＝ｍｇ（ｙ１ －ｙ）
（１）
于是 珒ｖ ＝ 槡２ｇ（ｙ１ －ｙ）
由 ｄｓ＝ 珒ｒ′（ｔ） ｄｔ＝ 珒ｖｄｔ
得 ｄｄｓｔ＝ 槡２ｇ（ｙ１ －ｙ）
ｄｔ＝ １ ｄｓ
槡２ｇ槡ｙ１ －ｙ
当曲线 Ｌ的方程为 ｙ＝ｙ（ｘ）时，
槡ｙ１ －ｙ
当曲线 Ｌ的方程为 ｘ＝ｘ（ｙ）时，
（２）
ｄｓ＝ 槡（ｘ′（ｙ））２ ＋１ｄｙ＝
槡（ｘ′（ｙ））２ ＋１（－ｙ′（ｔ））ｄｔ
得
ｄｔ＝ １ ｄｓ ＝
槡２ｇ槡ｙ１ －ｙ
１ 槡（ｘ′（ｙ））２ ＋１（－ｙ′（ｔ））ｄｔ
槡２ｇ 槡ｙ１ －ｙ
∫ Ｔ（ｘ） ＝ １ ｙ１ 槡１＋（ｘ′（ｙ））２ｄｙ
槡２ｇ ｙ２
ｅｄｕ．ｃｎ； 杨义川（１９７０），男，甘肃天水人，教授，博士，主要从事逻辑代数、序代数、软计算及其应用方面的研究，（Ｅｍａｉｌ）ｙｃｙａｎｇ＠ｂｕａａ． ｅｄｕ．ｃｎ
第 ３２卷第 ４期 邢家省，等：最速降线问题的充分性
７７
ｘ１ ＜ｘ２，ｙ２ ＜ｙ１ 。 设曲线 Ｌ经过 Ａ点和 Ｂ点，曲线 Ｌ的方程为 ｙ＝
质点沿曲线 Ｌ由点 Ａ无摩擦地滑动到点 Ｂ，所需的 时间［１４］是
ｙ（ｘ），或者曲线 Ｌ的方程为 ｘ＝ｘ（ｙ）。
设有一质点沿某曲线 Ｌ由点 Ａ无摩擦地滑动到点
Ｂ，考察所需的滑动时间 Ｔ。
假设在时刻 ｔ质点已滑动了路程 ｓ，到达的位置为
（ｘ（ｔ），ｙ（ｔ）），
质点的运动方程为 珒ｒ＝珒ｒ（ｔ） ＝（ｘ（ｔ），ｙ（ｔ）），速度
也给出了表述公式。最速降线问题转化为求一个泛函的最小值问题。首先考虑最速降线问题的必要条
最速下降曲线——12071186余浩
最速下降曲线问题研究12071186-余浩问题的提出1696年，Johann Bernoulli(1667～1748)年提出最速下降曲线的问题：设有A 、B 两点，B 点的高低较A 点低，但不再A 点的正下方。
假定A 、B 之间连有一曲线轨道，而让一个刚性小球沿着轨道由A 点降到B点。
如果不考虑摩擦力，那么什么样的曲线会使得下降所需的时间最短？——这就是最速下降曲线问题( 也叫摆线问题) 。
最速下降曲线是一类求极值问题，但他与初等微积分求某个函数在自变量处取极值不同，它寻找的是众多函数中的一个，使得相应的数值为最大或最小。
它是一类自变量为函数的函数的极值问题，即变分问题。
经过查阅相关的资料，发现变分问题的求解较为复杂，本文从理论推导入手，得出求解该类问题的一种数值算法。
建立最速下降曲线的物理模型，在应用数学理论求解过程中得出最速下降曲线满足斯涅尔公式的结论；提出应用斯涅尔公式的求解最速下降曲线的数值算法。
最速下降曲线物理模型的求解过程题型模拟：A 点与B 点不在同一铅垂线上，有质量为m 的刚性小球，从A 点以零初始速度沿曲线路径下滑到B 点，忽略阻力。
求下滑时间最短的一条路径( 即最速下降曲线) 。
A 点坐标，B 点坐标如图1假设任意下降路径为(1)y ( x ) 满足条件y ( 0 ) = 0 ，y ( x n ) = y n，(2)当小球落到位置时所具有的速度为，重力加速度为(3)曲线微积分中有由公式(4)(5)得出(6)小球总下降时长T[y(x) ]有，(7)求特殊的一条曲线，使得取极小值，这条曲线就是我们要找的最速下降曲线。
要使泛函公式( 7 ) 在处取得极值，即变分为零(8)参考图二将连续的曲线离散化为n+1 个点，第i 点的坐标为(xi,yi)£¬i=0,1,1,2...n。
设定y0,y1⋯⋯yi⋯⋯yn为已知数x0,x1 ⋯⋯xi⋯⋯xn，只要计算未知数，即可确定曲线，将求曲线问题转换为求x0,x1⋯⋯xi⋯⋯xn问题。
最速降线问题的力学解法
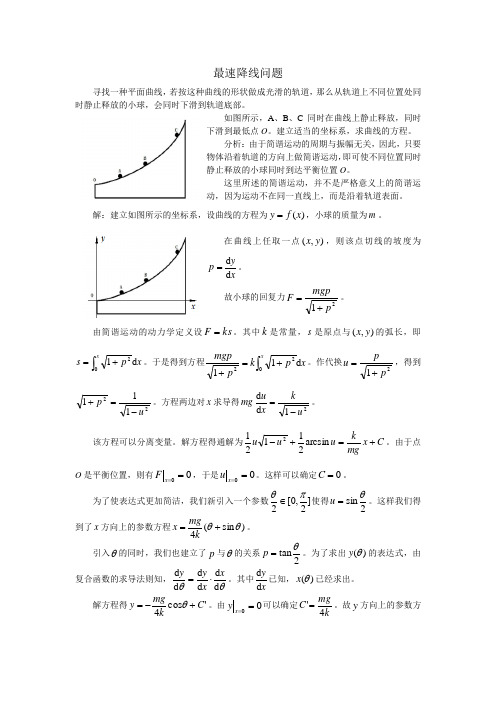
最速降线问题寻找一种平面曲线，若按这种曲线的形状做成光滑的轨道，那么从轨道上不同位置处同时静止释放的小球，会同时下滑到轨道底部。
如图所示，A 、B 、C 同时在曲线上静止释放，同时下滑到最低点O 。
建立适当的坐标系，求曲线的方程。
分析：由于简谐运动的周期与振幅无关，因此，只要物体沿着轨道的方向上做简谐运动，即可使不同位置同时静止释放的小球同时到达平衡位置O 。
这里所述的简谐运动，并不是严格意义上的简谐运动，因为运动不在同一直线上，而是沿着轨道表面。
解：建立如图所示的坐标系，设曲线的方程为)(x f y =，小球的质量为m 。
在曲线上任取一点),(y x ，则该点切线的坡度为xy p d d =。
故小球的回复力21pmgp F +=。
由简谐运动的动力学定义设ks F =。
其中k 是常量，s 是原点与),(y x 的弧长，即x p s xd 102⎰+=。
于是得到方程x p k pmgp xd 11022⎰+=+。
作代换21pp u +=，得到22111u p -=+。
方程两边对x 求导得21d d uk x u mg-=。
该方程可以分离变量。
解方程得通解为C x mgku u u +=+-arcsin 211212。
由于点O 是平衡位置，则有00==x F，于是00==x u 。
这样可以确定0=C 。
为了使表达式更加简洁，我们新引入一个参数]2,0[2πθ∈使得2sin θ=u 。
这样我们得到了x 方向上的参数方程)sin (4θθ+=kmgx 。
引入θ的同时，我们也建立了p 与θ的关系2tan θ=p 。
为了求出)(θy 的表达式，由复合函数的求导法则知，θθd d d d d d x x y y ⋅=。
其中x y d d 已知，)(θx 已经求出。
解方程得'cos 4C k mg y +-=θ。
由00==x y 可以确定kmg C 4'=。
故y 方向上的参数方程为)cos 1(4θ-=kmgy 。
微积分十大经典问题
这里入选原则是必须配得起“经典”二字。
知识范围要求不超过大二数学系水平，尽量限制在实数范围内，避免与课本内容重复。
排名不分先后。
1）开普勒定律与万有引力定律互推。
绝对经典的问题，是数学在实际应用中的光辉典范，其对奠定数学科学女皇的地位起着重要作用。
大家不妨试试，用不着太多的专业知识，不过很有挑战性。
重温下牛顿当年曾经做过的事，找找当牛人的感觉吧，这个问题是锻炼数学能力的好题！2）最速降线问题。
该问题是变分法中的经典问题，不少科普书上也有该问题。
答案是摆线（又称悬轮线），关于摆线还有不少奇妙的性质，如等时性。
其解答一般变分书上均有。
本问题的数学模型不难建立，即寻找某个函数，它使得某个积分取最小值。
这个问题往深层次发展将进入泛函领域，什么是泛函呢？不好说，一个通俗的解释是“函数的函数”，即“定义域”不是区间，而是“一堆”函数。
最速降线问题通过引入光的折射定律可以直接化为常微分方程，大大简化了求解过程。
不过变分法是对这类问题的一般方法，尤其在力学中应用甚广。
3）曲线长度和曲面面积问题。
一条封闭曲线，所围面积是有限的，但其周长却可以是无限的，比如02年高中数学联赛第14题就是这样一条著名曲线-----雪花曲线。
如果限制曲线是可微的，通过引入内折线并定义其上确界为曲线长度。
但把这个方法搬到曲面上却出了问题，即不能用曲面的内折面的上确界来定义曲面面积。
德国数学家H.A.Schwarz 举出一个反例，说明即使像直圆柱面这样的简单的曲面，也可以具有面积任意大的内接折面。
4）处处连续处处不可导的函数。
长久以来，人们一直以为连续函数除了有限个或可数无穷个点外是可导的。
但是，魏尔斯特拉斯给出了一个函数表达式，该函数处处连续却处处不可导。
这个例子是用函数级数形式给出的，后来不少人仿照这种构造方式给出了许多连续不可导的函数。
现在教材中举的一般是范德瓦尔登构造的比较简单的例子。
至于魏尔斯特拉斯那个例子，可以在齐民友的《重温微积分》中找到证明。
最优化方法-最速下降法
计算步骤
设f (X )是可微函数，精度要求为
X f ( ) K 1
，
X 0 为初始点。
(1)计算梯度
f
(
X
)
k
，初始k=0；
(2)
Pk
f
(
X
)
k
(3)求解 k
min f ( X k Pk)
s.t. 0
设 k 是一维搜索的最优解；
(4)求下一个点
评价
由例题中可以发现两次迭代的搜索方向满足：
P P P P T 0, T 0,...,
01
12
即相邻两个搜索方向 PK 与 PK1 正交，这是最速下降
法的搜索方向的基本形质。因此，最速下降法的迭代
路线呈锯齿形，尤其是在极小点附近，锯齿现象尤为
严重，从而影响了迭代速度。
评价
锯齿现象
最优化技术
第三章 7节 最速下降法
主要内容
1原 理
2 计算步骤
3 例题分析 4评 价
原理
定义：用来求解无约束多元函数 min f（x）
极小化问题的一种迭代算法。
拓展：
最速下降法又称梯度法，是 1847 年由著名数学家
Cauchy 给出的，它是解析法中最古老的一种，其他解析 方法或是它的变形，或是受它的启发而得到的，因此它是 最优化方法的基础。
X
)
0
(1,1)T
3-最优步长
2
X P ( ) f 5
0
0 2
1
0
应用一维搜索技术，解得函数最小值点 0 =0.2
举例分析
4-下一搜索点
X1
微积分中10大经典问题
微积分中10大经典问题最初的想法来自大一，当时想效仿100个初等数学问题，整理出100个经典的高等数学问题（这里高等数学按广义理解）。
可惜的是3年多过去了，整理出的问题不足半百。
再用经典这把尺子一量，又扣去了一半。
这里入选原则是必须配得起“经典”二字。
知识范围要求不超过大二数学系水平，尽量限制在实数范围内，避免与课本内容重复。
排名不分先后。
1）开普勒定律与万有引力定律互推。
绝对经典的问题，是数学在实际应用中的光辉典范，其对奠定数学科学女皇的地位起着重要作用。
大家不妨试试，用不着太多的专业知识，不过很有挑战性。
重温下牛顿当年曾经做过的事，找找当牛人的感觉吧，这个问题是锻炼数学能力的好题！2）最速降线问题。
该问题是变分法中的经典问题，不少科普书上也有该问题。
答案是摆线（又称悬轮线），关于摆线还有不少奇妙的性质，如等时性。
其解答一般变分书上均有。
本问题的数学模型不难建立，即寻找某个函数，它使得某个积分取最小值。
这个问题往深层次发展将进入泛函领域，什么是泛函呢？不好说，一个通俗的解释是“函数的函数”，即“定义域”不是区间，而是“一堆”函数。
最速降线问题通过引入光的折射定律可以直接化为常微分方程，大大简化了求解过程。
不过变分法是对这类问题的一般方法，尤其在力学中应用甚广。
3）曲线长度和曲面面积问题。
一条封闭曲线，所围面积是有限的，但其周长却可以是无限的，比如02年高中数学联赛第14题就是这样一条著名曲线-----雪花曲线。
如果限制曲线是可微的，通过引入内折线并定义其上确界为曲线长度。
但把这个方法搬到曲面上却出了问题，即不能用曲面的内折面的上确界来定义曲面面积。
德国数学家 H.A.Schwarz举出一个反例，说明即使像直圆柱面这样的简单的曲面，也可以具有面积任意大的内接折面。
4）处处连续处处不可导的函数。
长久以来，人们一直以为连续函数除了有限个或可数无穷个点外是可导的。
但是，魏尔斯特拉斯给出了一个函数表达式，该函数处处连续却处处不可导。
1-最速降线问题解析
这就是最速降线的微分方程数学模型。 3. 模型求解： 我们要求解上面微分方程，将上式变形为
1 2
y dx c y dy
y 令 c y tan t 从而，y c sin2 t , dy 2c sin t costdt
故 dx tantdy 2c sin2 tdt c1 cos2t dt 积分后得到 c x 2t sin 2t c1 2 这曲线过原点，故由上面第一式得， t 0 时， x y0 于是，c1 0 。这样 而
1 2 mv mgy 2
或 v 2gy
从这里的几何关系得
1 1 sin cos 2 sec 1 y
1 1 sin cos 2 sec 1 y
这些方程分别来自光学、力学、微积分，推导可得
2 y[1 y ] c y 0 0
丹尼尔.伯努利（Daniel Bernoulli 1700-1782）
起初也像他叔叔约翰.伯努利一样学医，写了一篇关于 肺的作用的论文获得医学学位，并且也像他父亲一样马 上放弃了医学而改攻他天生的专长。他在概率论、偏微分方程、物理 和流体动力学上都有贡献。而最重要的功绩是在流体动力学上，其中 的“伯努利定理”就是他的贡献。他曾经荣获法国科学院奖金１０次 之多。 ２５岁的丹尼尔在彼得堡解决了黎卡提方程的解。并发表了一系 列的科学论著。１７３３年回到巴塞尔，先后担任巴塞尔大学的植物 学、解剖学与物理学教授。以８２岁高龄离开人世，许多人认为他是 第一位真正的数学物理学家。
这就是著名的“最速降线”问题。它的难处在于和普通的极大极
小值求法不同，它是要求出一个未知函数（曲线），来满足所给的条 件。这问题的新颖和别出心裁引起了很大兴趣，罗比塔、伯努利兄弟、
最速降线问题
最速降线问题引言在古代建筑中屋顶为了雨水的下落速度最快常建设成一定的弧度，在科技馆里人们也常见到最速降线的模型，球体沿一定弧度的路线下落的时间却比直线短故宫屋顶科技馆里的最速降线模型1，历史背景：1696年，瑞士数学家Johann Bernoulli在《教师报》上发表了一封公开信。
信的内容是：请世界的数学家解决一个难题-“最速降线问题”此问题的提出一时轰动了欧洲。
引起了数学家的极大兴趣。
之后此问题由Newton,Lebeniz,Bernoulli兄弟所解决，从而产生了一门新的学科——变分学。
2，问题：确定一条连接两个定点A、B的曲线，使质点在这曲线上用最短的时间由A滑向B（介质的摩擦力和空气阻力忽略不计）。
3，建模3,1 模型假设：在垂直平面内存在两点A，B，A点速度为0，如图所示，假设存在一曲面C是质点由A运动到B所用的时间最短，忽略摩擦力和阻力。
3,2模型建立设质点质量为m 重力加速度为g,质点的速度为v根据能量守恒得： 12mv 2=mgy 则 v =√2gy =ds dtsecθ=ds dx tan θ=dy dx(sec θ)2−(tan θ)2=1得 ds =√1+(ẏ)2dxdt =ds v =√1+(y )22gy dxt =∫√1+(y )22gy dx a性能泛函 J (t )=√2g ∫√1+(y )2y dx a 0即： L=√1+(y )2y由欧拉方程的：y (1+ẏ2)=c令y =cot τ 得y =c (sin τ)2=c2(1-cos(2τ))所以： dx=dyy =2c sin τcos τcot τdτ=c (1−cos (2τ))dτx(0)=0所以： x =∫c(1−cos(2τ))τ0dτ=c2(2τ−sin(2τ))令t=2τ得：{x=12c(t−sin t) y=12c(1−cos t)其中c可由y(a)=b 确定因此可知：最速下降曲线是圆滚线即是半径为c/2的圆沿x 轴滚动时圆周上的一点所描出的曲线中的一段（旋轮线）。
最速降线
rn 意大利科学家伽利略在1630年提出一个分析学的基本问题──“一个质点在重力作用下，从一个给定点A到不在它垂直下方的另一点B，如果不计摩擦力，问沿着什么曲线滑下所需时间最短。
”这算是这个著名问题的起源了（为什么别人没有想起这个问题呢？所以说大科学家的素质就是思考、创新，要有思想，人没有思想，就和行尸走肉没有什么区别）。
可惜的是伽利略说这曲线是圆，但这却是一个错误的答案。
瑞士数学家约翰？伯努利在1696年再次提出这个最速降线的问题（problem of brachistochrone），向全欧洲数学家征求解答。
伯努利将此问题称为Brachistochrone，即希腊语中的“最短”（brochistos）和“时间”（chronos）合成而来。
人们当然会首先想到连接AB的直线。
伯努利说了：“虽然AB 间线段最短，但小球滚下来的时间不是最短。
如果在年底前（指1696年）没有人发现这条曲线，我将公布这条曲线。
”直线有可能不是最短时间的路径，因为小球从零速度开始滚下来，最初应该让路径陡一些，好更快地加速获得速度。
这有点像武侠小说中的挑战了，显然，伯努利自己是得出了答案，才敢下此战书的。
伯努利原定的截止期限是1696年年底，可是他只受到了一份解答，就是他的老师莱布尼兹（微积分的另一个独立发明人，也是个大数学家），莱布尼兹要求伯努利将截止期限延长到来年复活节（大致在3月下旬到4月下旬之间），以便让欧洲数学家们有更多时间来充分解决此道难题。
这个问题的难点在于，是求出一条曲线，实际就是求一个满足给出条件的未知函数，这在以前是前所未有的，有可能开创一个新的学科领域。
于是数学家们具有极大兴趣，纷纷开展研究。
有意思的是，伯努利在“战书”中还特别暗示了他的挑战对象，他写道：“……很少有人能解出我们的独特的问题，即使那些自称通过特殊方法……不仅深入探究了几何学的秘密、而且还以一种非凡的方式拓展了几何学领域的人，这些人自以为他们的伟大定理无人知晓，其实早已有人将它们发表过了”这简直是赤裸裸的指向伟大的伊萨克？牛顿了！伯努利提到的“定理”显然是指流数术（牛顿自己给微积分起的名字），而牛顿曾宣称自己早在莱布尼兹1684年发表微积分论文前就已经发现了这一理论。
3.最速降线问题(数学模型概述)
§数学模型分类 1）依数学模型功能分为：①定性的②定量的 2）依数学模型目的分为：①理论研究的②预知结果的 ③优化的. ③优化的. 3）依数学模型变量关系分为： ①代数的②几何的 ③积分的 4）依数学模型结构分为： ①分析的②非分析的 ③图论 5）依数学模型研究对象特征分为： ①确定的与随机的②静态的与动态的 ③连续的与离散的④线性的与非线性的
sec β
1 + tan β
2
1+ (2 ）（3 由（1）（2 ）（3） ，得：
y 1 + ( y ' ) 2 = c y (0) = 0
此为速降线的数学模型的DE. 此为速降线的数学模型的DE. 3.4 模型求解 c− y ' 2 把（4 把（4）变为 ( y ) = y
本章研究DE模型的建模方法： 本章研究DE模型的建模方法： 涉及：几何；力学；电学；化学；热学；扩散；医学；人 口；体育；社会经济等。
§4-1几何问题
建立几何问题的数学模型方法： 1）找出反映该问题的几何关系 2）把几何量的表达式代入该关系式 3）得到DE即几何问题的数学模型 ）得到DE即几何问题的数学模型
x1
1 + ( y ' ) 2 dx
（9）
f ( y, y ′) =
2 gy
由变分法知，（9 由变分法知，（9）的解所满足的欧拉方程为
即
∂f y ′ − f = c1 ∂y ′
(y )
' 2
y 1 + ( y ' )2
−
1 + ( y ' )2 y
= c2
y 1 + ( y ' ) 2 = c
最速降线问题
a
2
A2
这就是光学中的Snell折射定律
建立数学模型
若用与x 轴平行的直线将 分析；如图建坐标系， AB 分割成小段, 考虑在第k c x A 层与k+1层质点在曲线上的下 a 滑，依能量守恒律，可近似 k 认为质点在每层内的速度不 变，于是依辅助结论知
sin k sin k 1 vk vk 1
那么我们的问题成为
求某个 y ˆ E,使得
ˆ ) min T ( y ) T(y
yE
引进集合 E0 { ( x) C 1[0, c], (0) 0, (c) 0}
ˆ ( x) 是最速曲线函数,则 显然若 y ˆ ( x) ( x) E, R , E0 y
1
2
3
4
5
一个辅助结论
设质点从A1经直线 l 到达A2，质点速度在l 的 上侧为v1，下侧为v2，则质点如何运动才最省时？ 显然在l一侧质点应走直线，因此关键是质点 何时越过l ？ 如图，若A1,A2到l 的垂足分 A1 别为O,D, A1,A2 到l的距离分别 为a, b, OD =c, 质点经过l于C OC=x 那么质点由A1到A2需时间
E0
由于 的任意性,得到
d ˆ, y ˆ )) f y ( y ˆ, y ˆ ) 0 ( f y ( y dx
d ˆ y ˆ f y ( y ˆ, y ˆ ) f ( y ˆ, y ˆ )] 0 上式乘以 可化为 [y dx
ˆ 满足方程 也就是说 y
从而下降时间
T dt
0 T S 0
0 R 2(1 cos ) d ds 0 v 2 gy
T
0
有限元法20070706
对上式应用第一标量格林定理，得到
确定泛函的方法
L,
V [ ( *)]dV
S
*
n
*
n
dS
式中n 是S的外法向单位矢量。如果是实数或实函数，
则上式右边第一项可写成 , L。 第 二项是面积分。
0 0
0 0
确定泛函的方法
那么，通过求下式泛函的极小值
F() 1 L, 1 , f 1 f ,
2
2
2
即可求出原微分方程的解。
在上面的几个式子中，表示与满足相同边界条件的任
意函数。尖括号表示如下定义的内积
, *d
S r
所以，如果E和F均满足齐次狄利克雷边界条件
n E 0 ，在S1上
以及第三类齐次诺曼条件
1
r
n ( E) e n (n E)
0
在S2上
确定泛函的方法
那么，只要r和e是实数，上式中的面积分就为零。式 中，S=S1+S2。此外，如果r和r均为实数，则泛函式可
现令变分问题的解答(极值函数)为y=y(x)
设想函数y从极值解稍稍变动到y + y ，并把变分y改 记为(x) (是一个任意给定的微量实参数；(x)是定 义于区间[x1,x2]且满足齐次边界条件即有(x1) = (x1) =0的任意选定的可微函数)。这样，泛函J[y+]= J[y(x,)]=()成为参数的函数，因为参数的值确定了 y=y(x,)函数族里的曲线，所以同时也就确定了泛函 J[y(x,)]的值，而且当=0时泛函即获极值函数的解。
使用拉格朗日乘数法计算最速降线
使用拉格朗日乘数法计算最速降线一、引言在物理学和工程学中，我们经常需要研究物体在重力场中的运动规律。
而在研究物体在重力场中的运动问题时，经常需要求解最速降线的问题。
那么，如何使用拉格朗日乘数法来计算最速降线呢？接下来，我们将通过深入的探讨和分析，来揭示这一问题的解决方法。
二、什么是最速降线？最速降线是指在给定两点之间，一条曲线上一点到另一点的时间最短。
在重力场中，物体遵循最速降线原理，也就是物体在重力场中自由运动时，路径为最速降线。
对于给定两点之间的最速降线问题，我们需要找到一条曲线，使得物体从起点到终点所需的时间达到最小值。
三、拉格朗日乘数法的基本原理拉格朗日乘数法是一种求解约束条件下极值问题的方法。
它的基本思想是将原问题转化为一个无约束优化问题，通过引入拉格朗日乘子来构建一个拉格朗日函数，然后求解该函数的驻点。
在最速降线问题中，我们需要将最速降线的约束条件转化为拉格朗日乘数形式，然后应用拉格朗日乘数法来求解。
四、使用拉格朗日乘数法计算最速降线的步骤1. 建立参数方程我们需要建立最速降线的参数方程。
设最速降线为y=f(x)，起点为(x1,y1)，终点为(x2,y2)，则我们可以建立参数方程：x=x(t)，y=y(t)，a≤t≤b其中，参数t的范围为[a,b]。
2. 构建拉格朗日函数接下来，我们需要构建拉格朗日函数。
根据最速降线的约束条件，即起点和终点确定，我们可以建立拉格朗日函数：L(x,y,λ)=f(x,y)+λ(g(x,y)-k)其中，λ为拉格朗日乘子，g(x,y)为约束条件函数，k为约束条件的常数值。
3. 求解拉格朗日函数的偏导数我们需要求解拉格朗日函数关于x、y和λ的偏导数，并令其等于0，得到方程组：∂L/∂x=0∂L/∂y=0∂L/∂λ=0通过求解上述方程组，我们可以得到参数方程x=x(t)，y=y(t)的解。
4. 求解最速降线方程通过将参数方程带入原函数f(x,y)，我们可以求解出最速降线的方程，从而得到最速降线的数学表达式。
最速降线问题数学建模
最速降线问题数学建模最速降线问题是一个经典的数学问题，涉及到最优控制和变分法等领域。
下面是一个简单的数学建模过程：1.问题描述：给定一个高度为h的斜坡，一个物体从斜坡顶部释放，在重力作用下沿着斜坡滑下。
我们要找到一条路径，使得物体沿着这条路径滑到底部所需的时间最短。
2.变量定义：假设斜坡的高度为 h，物体的质量为 m，摩擦系数为μ，斜坡的角度为θ。
3.建立模型：(1) 物体沿着斜坡下滑时受到重力、摩擦力和斜坡的支持力的作用。
(2) 重力方向向下，大小为 mg；摩擦力方向与运动方向相反，大小为μmgcosθ；斜坡的支持力垂直于斜坡，大小为 mgcosθ。
(3) 物体的加速度 a = g - μgcosθ - gsinθ，其中 g 是重力加速度。
(4) 物体的速度 v = at，其中 t 是时间。
(5) 物体的位移 s = 1/2 at^2。
(6) 最速降线的目标是使得物体滑到底部所需的时间最短，即最小化t = sqrt(2h/a)。
4. 变分法求解：根据最速降线的定义，我们可以使用变分法求解这个最优化问题。
具体来说，我们可以通过求解以下变分问题来找到最速降线：(1) 定义一个参数化的路径函数 y(t)，表示物体在时间 t 时的位置。
(2) 定义一个泛函 F[y(t)]，表示物体沿着路径 y(t) 滑到底部所需的时间的平方，即 F = int [ (dy/dt)^2 dt ]。
(3) 求解 F[y(t)] 的极值问题，找到使得 F 最小的 y(t)。
5. 解的解析：经过一系列数学推导，我们可以得到最速降线的解析解。
在最速降线问题中，最速降线的形状是一条摆线。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
本章研究DE模型的建模方法： 涉及：几何；力学；电学；化学；热学；扩散；医学；人 口；体育；社会经济等。
§4-1几何问题
建立几何问题的数学模型方法： 1）找出反映该问题的几何关系 2）把几何量的表达式代入该关系式 3）得到DE即几何问题的数学模型
模型三、 最速降线问题
1.历史背景：1696年，瑞士数学家Johann Bernoulli在 《教师报》上发表了一封公开信。信的内容是：请世界 上的数学家解决一个难题- “最速降线问题” 此问题的 提出一时轰动了欧洲。引起了数学家的极大兴趣。之后 此问题由Newton，Lebeniz，Bernoulli兄弟所解决，从而 产生了一门新的学科-变分学。
•
Ch4. DE模型（ Ch5. 差分方程模型 Ch6. 工程系统中的模型）
在化工、仪表、通讯、交通、生物、经济、医学、 工程及社会等领域中，有大量的系统是DE模型。建 模的方法可归纳为： （1）由规律列方程：如数学定律、物理、力学、电学、 光学、生物学、药学、化学定律 （2）由微分法列方程：如微元法 dy f ( x)dx （3）模拟近似法：有些象生物，经济学科的实际问题， 规律性不清楚，建模时在不同的假设下去近似模拟 实际现象，得到DE。求出解来与实际对比。看其能 否刻划某些实际现象。
A 3.2 模型假设 设想质点由A滑到B的路径， 使所需时间为最短（像光学一样） 依光学原理（史奈尔折射定律）得 sin c （常数）（1） v y
x
p( x, y)
B
3.3 模型建立。 据能量守恒定律，质点在一定高度处的速度，完全由其 到达该高度处所损失的势能确定，而与路径无关。该质 点质量为m，重力加速度为g，质点由A滑到点 p( x, y )的 速度为v.则 1 2 mv mgy或 v 2 gy （2） 由几何关系，有 2 1 1 1 （3） sin cos
6）依数学模型所用方法分为： ①初等模型 ② DE模型 ③优化模型 ④统计模 ⑤控制论模型⑥逻辑模型⑦扩散模型 7）依数学模型的领域分为： ①人口模型②交通模型③生态模型④生理模型 ⑤经济模型⑥社会模型⑦工程系统模型以及电力模型 8）依数学模型对象的了解程度分为： ①白箱模型 ②灰箱模型 ③黑箱模型. §1-4建模步骤和原则 1）模型准备：了解问题的实际背景，明确建模的目的。 2）模型假设：由实际对象的特性和建模的目的，在掌握 必要资料基础上对问题进行必要的简化，并用精确的语 言作出假设。(关键一步)
1）选取走私船逃跑 R(0, at ) y 的方向为y 轴方向； y-at D ( x, y ) 2）缉私舰在（c，0） 处发现走私船在（0，0）处。 3）船舰视为两个质点。 4）设发现船的t时刻时，走 o 私船到达R（0，at）点，缉私舰到达D（ x， y ）. 3. 模型建立 因为直线DR与路径相切，所以由几何关系，有
作业 ：习题四 .4.3
问题3: 建立导弹攻击目标的数学模型。 问题4: 建立潜水艇的导弹攻击目标的数学模型。
x1
1 ( y ' )2 dx
（9）
f ( y, y )
2 gy
由变分法知，（9）的解所满足的欧拉方程为
即
f y f c1 y 1 ( y ' )2 ( y ' )2 c2 y y 1 ( y ' )2
' 2 y 1 ( y ) c
此即为（4）.
问题1: 建立我国海上人员缉私的实际模型。 问题2: 外摆线齿轮与圆渐开线齿轮数学模型的 区别研究
模型四、追线问题（追击模型）
1.问题描述（模型准备） 我海上缉私舰雷达发现，距c海里处有一艘走 私船正以匀速a沿直线行驶.缉私舰立即以最 大速度b追赶，若用雷达进行跟踪。保持船的 瞬时速度方向始终指向走私船，试求缉私舰 追逐路线和追上的时间。 2. 模型假设 （见下页图）
Ch1.数学模型概述
§数学模型分类 1）依数学模型功能分为：①定性的②定量的 2）依数学模型目的分为：①理论研究的②预知结果的 ③优化的. 3）依数学模型变量关系分为： ①代数的②几何的 ③积分的 4）依数学模型结构分为： ①分析的②非分析的 ③图论 5）依数学模型研究对象特征分为： ①确定的与随机的②静态的与动态的 ③连续的与离散的④线性的与非线性的
（14）
c 1 x k 1 1 x 1k ck y ( ) ( ) , 2 2 1 k c 1 k c 1 k ck abc y 2 , 2 2 当t=0时， 1 k b a
t a b a
2 2
abc 即走私船被缉私舰捕捉前所跑过的距离为 , 2 2 b a y bc 所用的时间为：
.
②若
ab
即
k 1 则由（14）可得：
（15）
1 x2 c2 x y c ln 2 2c c
③若 a b, 即 k 1, 显然，此时缉私舰也不可能追上 走私船。 1. 设飞机在半径为 a 的圆周上以等速v运动，导弹从 圆心出发追踪，当 t 0 时，飞机在 r , 0 ，导弹在圆 心，若导弹速度也是v，而且圆心、导弹、飞机总是在 一条直线上，证明当飞机飞行至 0, r 时，导弹正好追 上它。
ds 1 ( y)
所以
1 ( y ' ) 2 dx dd ds dt v 2 gy 2 gy
③整个下降时间是
dt
ds
的积分.故，需取最小值的积分
t y ( x) 是 ： 0 2 gy 此为求泛函 t y( x) 的极小值问题。 2 令 1 ( y ) ④
y y (c y ) c
2
（5）
y sin t
y c sin t ,
2
dy 2c sin t cos tdt
所以dx tan tdy 积分得： c
2c sin tdt c(1 2cos t ) d t
2
x
因为曲线过（0，0），所以当t=0时，有x=y=0.于是 c1 c =0.所以 （6） x 2t sin 2t 2 而 c 2 （7） y c sin t (1 cos 2t ) 若令
作业: 习题四4.1 1.如图所示，沿 y 轴及直线 是河的两岸，河水以 匀速 a 朝 y 轴方向流动， 小船从 (c, 0) 处入河相对 于河水的速度b直接朝原点行驶. 求船行路线，并确定a 与b须满足 什么条件才能使小船到达彼岸， 船在何处登岸？
xc
y
0
(c, 0)
y
( x, y )
xቤተ መጻሕፍቲ ባይዱ
a
• 2.问题：确定一条连接二定点A，B的曲线。使质点
•
在这曲线上用最短的时间由A滑向B点(介质的摩擦力 与空气阻力忽略不计）。 有人指出：连结A，B的直线段即为速度线。回答是 否定的。在1630年Newton实验：在铅垂平面内，取 两个球，其中一个沿圆弧从A滑到B。（先到达B） 另一个沿直线从A滑到B。（晚到达B） Galilei认为速降线是圆弧线（错了）。 3.建模 3.1 模型准备 选取直角坐标系 参看下页图
• •
• •
Ch2建模的常用方法
（1）理论分析法（2）模拟方法（3）类比分析法 （4）数据分析法（5）人工假设法（6）物理系统建模法 请作习题二，2.5 MP MO MS
M准备 M假设
M建立
M应用
分析 检验
M求解
MAP
MAN，MT
MF
• 简单方法建立问题的数学模型： • 1.代数法 • 此方法涉及到以下四个例题: • 1）例3.1.1 生小兔问题（Fabonacci问题） • 2）例3.1.2 椅子问题（战略核武器杀伤力问题） • 3）例3.1.3 雨中行走问题 • 4）例3.1.4 动物形体问题 • 2.图解法 • 1）例3.1 实物交换问题 • 2）例3.2.2 导弹核武器危机
2
2t sin 2t c1
c a , 2
2
2t
（8）
则(6)(7)变为
x a( sin 2t ) y a(1 cos 2t )
此为旋轮线（圆滚线，外摆线）的参数方程.（外摆线为齿轮线） 3.5 模型分析 3.6 模型检验 注1 只要适当选a，可使摆线过B点。 3.7 模型应用 a 注2 速降线的深远意义： （x,y） 1，由此产生了变分法——近代分析的一重要分支； 2，揭示了物理世界的心脏中包含着简单性. 注3 应用变分法。可同样得到模型（4）. ds ①设s为 AP 的弧长，则有 v 2 gy dt ②又由弧微分有 2
s
(c, 0)
x
dy y at dy tan t 或x y at dx x dx
两端对x求导，有 代入
（10） （11）
ds b, dt
d2 y dt x 2 a dx dx
（最大速度为b（缉私舰））
得到
dt dt ds 1 1 dy dx dx ds dx b
Ch3.初等模型
• 3.量纲分析法
• 1）单摆运动 • 2）开普勒第三定律 • 4.初等概率法 • 1）例3.4.1 Buffon问题（投针问题） • 2）例3.4.2 下赌注问题 • 3）例3.4.3 Banach火柴盒问题 • 4）例3.4.4生男生女问题 • 5）例3.4.5供电问题 • 另外还有 递推法 人狗鸡米渡河问题 • 夫妻过河问题 • 图形法 市场平衡问题
则上式可化为
所以
dx k 又 2 x 1 p
2
dp
p c 0
x k ln( p 1 p ) ln( ) c
所以 先确定k. ①若 a b,从而 k 1. 积分（14），有：
dy 1 x k c k p ( ) ( ) , y(c) 0. dx 2 c x