最速下降路线的确定--实验报告
最速降线最简单证明

最速降线最简单证明最速降线问题是数学中一个经典的优化问题。
在这个问题中,我们需要找到一个点,使得从该点触底后,到目标点的时间最短。
为了解决这个问题,我们可以设定一个二维坐标系,其中起始点为原点O (0, 0),目标点为P (x, y)。
同时,我们假设点P的横坐标x大于0,即目标点在原点的右侧。
我们需要找到这样一个点Q,使得从原点O出发经过Q点最短时间。
设点Q的横坐标为α,根据问题的对称性,我们可以假设点Q的纵坐标为0。
因此,点Q的坐标为(α, 0)。
我们假设点Q点处的切线,与横坐标轴的夹角为θ。
则根据三角函数的性质,我们可以得到:tanθ = y/α这表示切线的斜率为y/α。
我们知道,从点Q到点P所需的时间为t = √(α^2 + y^2) / V,其中V为垂直速度。
点Q处的切线斜率与速度向量的斜率相等。
假设速度向量的斜率为k,则有:k = tanθ = y/α由此可得:α = y/k将α的值代入到时间的表达式中,我们可以得到一个只涉及到k 和y的时间表达式:t = √(y^2+(y/k)^2) / V = √(y^2+k^2y^2)/Vk = y√(1+k^2) / Vk我们需要最小化时间t,即求极小值。
为了方便计算,我们可以对时间t取平方,即t^2。
由于t^2关于y的函数形式简单,我们可以通过求导数将其转化为极值的问题。
计算t^2的导数,我们可以得到:2t * dt/dy = 2y * √(1+k^2) / Vk + y * (1+k^2)^(-1/2) * 2k * dk/dy / Vk化简上式,我们可以得到:√(1+k^2) / k - k * (1+k^2)^(-1/2) * dk/dy = 0将上式中的k代入到之前的k = y/α中,我们可以得到:√(1+(y/α)^2) / y - (y/α) * (1+(y/α)^2)^(-1/2) * (1/α) * dy/dα = 0化简上式,我们可以得到:√(α^2+y^2)/α = 1/α * dy/dα移项并化简,我们可以得到:(α^2+y^2) / α^2 = dy/dα由于α = y/k,我们可以进一步化简上式,得到:(k^2y^2+y^2) / (y^2/k^2) = dy/dα化简上式,我们可以得到:(k^2+1) / k^2 = dy/dα上式左边是常数,因此dy/dα也是常数。
最优化方法实验报告(2)

最优化方法实验报告Numerical Linear Algebra And ItsApplications学生所在学院:理学院学生所在班级:计算数学10-1学生姓名:甘纯指导教师:单锐教务处2013年5月实验三实验名称:无约束最优化方法的MATLAB实现实验时间: 2013年05月10日星期三实验成绩:一、实验目的:通过本次实验的学习,进一步熟悉掌握使用MATLAB软件,并能利用该软件进行无约束最优化方法的计算。
二、实验背景:(一)最速下降法1、算法原理最速下降法的搜索方向是目标函数的负梯度方向,最速下降法从目标函数的负梯度方向一直前进,直到到达目标函数的最低点。
2、算法步骤用最速下降法求无约束问题n R()min的算法步骤如下:xxf,a )给定初始点)0(x ,精度0>ε,并令k=0;b )计算搜索方向)()()(k k x f v -∇=,其中)()(k x f ∇表示函数)(x f 在点)(k x 处的梯度;c )若ε≤)(k v ,则停止计算;否则,从)(k x 出发,沿)(k v 进行一维搜索,即求k λ,使得)(min )()()(0)()(k k k k v x f v x f λλλ+=+≥; d )令1,)()()1(+=+=+k k v x x k k k k λ,转b )。
(二)牛顿法1、算法原理牛顿法是基于多元函数的泰勒展开而来的,它将)()]([-)(1)(2k k x f x f ∇∇-作为搜索方向,因此它的迭代公式可直接写出来:)()]([)(1)(2)()(k k k k x f x f x x ∇∇-=-2、算法步骤用牛顿法求无约束问题n R x x f ∈),(min 的算法步骤如下:a )给定初始点)0(x ,精度0>ε,并令k=0;b )若ε≤∇)()(k x f ,停止,极小点为)(k x ,否则转c );c )计算)()]([,)]([)(1)(2)(1)(2k k k k x f x f p x f ∇∇-=∇--令;d )令1,)()()1(+=+=+k k p x x k k k ,转b )。
最速降线实验报告

最速降线实验报告最速降线实验报告引言:最速降线是物理学中的一个重要实验,通过探究物体在斜面上滑动的速度与角度的关系,可以帮助我们深入理解运动学和动力学的基本原理。
本实验旨在通过测量不同角度下物体滑动的时间和距离,验证最速降线的理论,并探讨其应用。
实验装置和步骤:实验装置包括一个倾斜角可调节的斜面,一个小球和一个计时器。
实验步骤如下:1. 将斜面调整到一个合适的角度,并固定好。
2. 在斜面的顶端放置小球,并用计时器记录小球从顶端滑到底端所经过的时间。
3. 重复以上步骤,分别记录不同角度下的滑动时间和距离。
实验结果:我们进行了多次实验,测量了不同角度下小球滑动的时间和距离。
结果如下表所示:角度(度)滑动时间(秒)滑动距离(米)30 2.5 1.245 1.7 0.960 1.2 0.775 1.0 0.690 0.8 0.5实验数据分析:根据实验结果,我们可以发现一个有趣的规律:随着角度的增加,小球的滑动时间和距离都减小。
这与最速降线的理论相吻合。
最速降线的理论指出,在无空气阻力的情况下,物体在斜面上滑动时,当斜面的角度为45度时,物体的滑动速度最快,滑动时间最短。
在实验中,我们可以看到,当斜面的角度为45度时,小球的滑动时间最短,滑动距离也相对较短。
而当角度小于45度或大于45度时,小球的滑动时间和距离都会增加。
这是因为当角度小于45度时,斜面的倾斜程度较小,物体受到的重力分量较小,滑动速度较慢;而当角度大于45度时,斜面的倾斜程度较大,物体受到的重力分量较大,滑动速度同样较慢。
只有当角度为45度时,物体的滑动速度达到最大值。
实验应用:最速降线的理论在现实生活中有着广泛的应用。
例如,设计滑道、滑雪场和过山车时,我们需要考虑最速降线的原理。
通过合理调整斜面的角度,可以使滑道、滑雪场和过山车的速度达到最佳状态,提供更好的体验和安全保障。
此外,最速降线的理论也可以应用于物体运动的优化问题。
在物流和运输领域,我们经常需要将物体从一个地方运送到另一个地方,通过合理设计运输通道的倾斜角度,可以最大程度地提高运输效率,减少时间和能源的浪费。
最速降线实验报告

最速降线实验报告实验目的,通过实验,验证最速降线的运动规律,并利用实验数据进行分析和计算。
实验仪器,小车、斜面、计时器、尺子、直尺、手机。
实验原理,最速降线是指物体在斜面上沿着特定角度的斜线运动,其速度在垂直方向上最小。
根据斜面的倾角和高度差,可以计算出小车在斜面上的加速度。
实验步骤:1. 在水平地面上放置斜面,并测量斜面的倾角和高度差。
2. 将小车放置在斜面的顶端,释放小车并启动计时器。
3. 观察小车沿着斜面运动的过程,并记录下小车到达底部所用的时间。
4. 重复实验多次,取平均值作为最终结果。
实验数据:斜面倾角,30°。
斜面高度差,1m。
小车到达底部所用时间,2.5s、2.3s、2.4s、2.6s、2.5s。
实验结果:根据实验数据和斜面参数,可以计算出小车在斜面上的加速度。
利用公式 a = gsinθ,其中g为重力加速度,θ为斜面倾角,可以求得小车在斜面上的加速度为a = 9.8m/s² sin30° = 4.9m/s²。
实验分析:通过实验数据和计算结果可以得出,小车在斜面上的加速度与斜面的倾角有关,倾角越大,加速度越大。
这符合最速降线的运动规律,即物体在斜面上运动时,其速度在垂直方向上最小。
实验结论:本实验验证了最速降线的运动规律,通过实验数据和计算分析,得出小车在斜面上的加速度为4.9m/s²。
实验结果与理论预期基本吻合,实验过程中未发现明显误差。
实验总结:最速降线实验是一项简单而有趣的物理实验,通过实验可以深入理解物体在斜面上的运动规律。
在实验过程中,要注意测量斜面参数的准确性,以及记录实验数据的精确性。
通过多次实验取平均值,可以减小误差,得到更可靠的实验结果。
通过本次实验,我对最速降线的运动规律有了更深入的理解,也掌握了实验操作的技巧和注意事项。
希望通过今后的实验学习,能够进一步提高实验技能,深化对物理知识的理解和应用。
最速下降法实验报告

竭诚为您提供优质文档/双击可除最速下降法实验报告篇一:最速下降法报告资料篇二:最优化方法实验报告最优化方法实验报告学生所在学院:理学院学生所在班级:信息1学生姓名:教务处20XX4年5月最优化方法实验报告书说明:1.下面程序在mATLAbR20XXa中均能正常运行。
程序之间有关联。
2.实验一熟悉mATLAb基本功能(2学时)实验的目的和要求:在本次实验中,通过亲临使用mATLAb,对该软件做一全面了解并掌握重点内容。
实验内容:1、全面了解mATLAb系统2、实验常用工具的具体操作和功能学习建议:本次实验在全面了解软件系统基础之上,学习和熟悉一些mATLAb的基础用途,重点掌握优化工具箱函数选用的内容。
重点和难点:优化工具箱函数选用。
数学模型:其中f,x,b,beq,lb和ub为向量,A和Aeq为矩阵。
语法:x=linprog(f,A,b,Aeq,beq)x=linprog(f,A,b,Aeq,beq,lb, ub)x=linprog(f,A,b,Aeq,beq,lb,ub,x0)x=linprog(f,A,b ,Aeq,beq,lb,ub,x0,options)[x,fval]=linprog(...)[x,fval,exitflag]=linprog(...)[x,fval,exitflag,outp ut]=linprog(...)[x,fval,exitflag,output,lambda]=lin prog(...)描述:x=linprog(f,A,b)求解问题minf*x,约束条件为A*x 篇三:实验2最速下降法和共轭梯度法的程序设计实验2最速下降法和共轭梯度法的程序设计一、实验目的1、熟悉无约束优化问题的最速下降算法和共轭梯度法。
2、培养matlab编程与上机调试能力。
二、实验课时:2个课时三、实验准备1、预习无约束优化问题的最速下降算法和共轭梯度法。
2、熟悉matlab软件的基本操作及程序编写。
实验数学十四:最速下降路线的确定
f y f C y 2 2 1 y y C y y 1 y 2
18
这可简化为
y[1 ( y) 2 ] C
与方程(16-2)是一致的。 2.5 内容小结 本次实验我们首先通过几个简单曲线的计算,排 除了直线是最快的下降曲线这一直觉结果,得出最快 的下降曲线应该是一条上凹的曲线这一猜想。然后根 据问题的实际意义得到相应的数学模型方程。先通过 求数值解的方法得到最快下降路径曲线,然后求出它 的理论解应是一条摆线。 14.3 实验任务
t
a 0
2 ( x ) 1 y 2
4
t
a 0
1 y 2 ( x ) 2 gy ( x)
dx
(16.1)
由此可见,质点从A点滑到B点依赖于曲线的形状, 不同的曲线下滑所用的时间不同。 下面我们分别用三种不同的曲线来计算质点所用的时间。 不妨假设B点的坐标为(1,1),如图14.3所示。
3
若设质点下降路程为s(t),则由
s(t )
可得
x
0
2 ( x) dx 1 y
d s(t ) dx 2 v(t ) 1 y ( x) dt dt
v(t ) 2 g y
dt 1 y2 ( x) 2g y dx
这样质点沿曲线从A点滑到B点所用的时间为
2
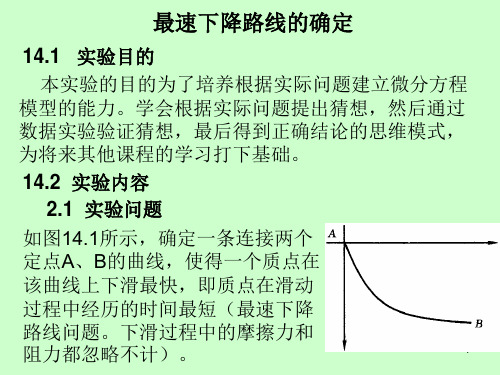
如图14.2所示,并选取相应的坐标系。
图中P(x,y)表示下降中的质点坐标,途经曲线设为 y=y(x),质点的质量设为m,重力加速度设为g,质点 下降的速度设为v(t),t为质点的下降时间。 则根据质点在下降过程中的能量守恒定律可知 1 2 mv (t ) m g y 2 由此可得
v(t ) 2 g y
因此按照史奈尔折射定律可得出
最速下降曲线实验

最速下降曲线实验作者:徐雷来源:《教育教学论坛》2018年第04期摘要:物理学是一门以实验为基础的学科。
物理实验是科学实验的先驱,体现了大多数科学实验的共性,而实验教学则是培养学生的一个非常重要的环节,它不仅可以培养学生的基本实验技能和素养,还可以培养其科学思维和创新意识,提高学生的综合能力和创新能力。
本文从理论模型出发,采用变分法推导出最速下降曲线的解并设计实验予以验证。
关键词:最速下降曲线;变分法;摆线中图分类号:O369 文献标志码:A 文章编号:1674-9324(2018)04-0190-02一、前言最速下降曲线问题在历史上具有显赫声名。
其问题的内容为:设有A、B两点通过一条曲线连接,让一个质点沿着此曲线由A点下滑到B点,那么质点沿着什么样的曲线下滑所需的时间最短(下滑过程中摩擦力和阻力均不考虑)?这就是著名的最速下降曲线问题(也叫摆线问题)[1,2]。
在很早以前,牛顿和伽利略都研究过这个问题,他们通过大量的实验研究发现,质点从A点滑到B点耗时最短的轨迹曲线是圆弧线。
直到1696年Johann Bernoulli采用了一种非常巧妙的方法解决了最速下降曲线问题,并就此问题向全欧洲发出挑战。
而到1697年时,牛顿、莱布尼茨以及Jakob Bernoulli(Johann Bernoulli的哥哥)都同时给出了此问题的解。
Jakob Bernoulli所提出的方法比较麻烦但是更具有普适性,也因此引发了他们兄弟俩长达数年的争执。
直到1744年,Leonhard Euler提出了曲线极值问题的微分方程并建立变分法,这一问题才画上圆满句号[3,4]。
二、实验原理最速下降曲线是求解泛函极值问题,可以通过变分法求解此类问题。
如图1所示,质点从A点滑到B点,并选取坐标系。
设质点滑过的曲线方程为y=y(x),质点的质量为m,重力加速度为g,质点的下滑的速度为v(t),其中t为质点下滑的时间。
根据能量守恒定律可知,在下滑过程中的任意一点P(x,y)都有:三、实验设计验证重力作用下的最速下降曲线。
消去法实验报告19

最速下降法最速下降法又称为梯度法,是1847 年由著名数学家Cauchy 给出的,它是解析法中最古老的一种,其他解析方法或是它的变形,或是受它的启发而得到的,因此它是最优化方法的基础。
作为一种基本的算法,他在最优化方法中占有重要地位。
其优点是工作量少,存储变量较少,初始点要求不高;缺点是收敛慢,效率不高,有时达不到最优解。
非线性规划研究的对象是非线性函数的数值最优化问题。
它的理论和方法渗透到许多方面,特别是在军事、经济、管理、生产过程自动化、工程设计和产品优化设计等方面都有着重要的应用。
而最速下降法正是n元函数的无约束非线性规划问题min f (x)的一种重要解析法,研究最速下降法原理及其算法实现对我们有着极其重要的意义。
最速下降法1.最速下降方向函数f(x)在点x处沿方向d的变化率可用方向导数来表示。
对于可微函数,方向导数等于梯度与方向的内积,即:Df(x;d) = ▽f(x)Td,因此,求函数f(x)在点x处的下降最快的方向,可归结为求解下列非线性规划:min ▽f(x)Tds.t. ||d|| ≤ 1当 d = -▽f(x) / ||▽f(x)||时等号成立。
因此,在点x处沿上式所定义的方向变化率最小,即负梯度方向为最速下降方向。
2.最速下降算法最速下降法的迭代公式是x(k+1) = x(k) + λkd(k) ,其中d(k)是从x(k)出发的搜索方向,这里取在x(k)处的最速下降方向,即d = -▽f(x(k)).λk是从x(k)出发沿方向d(k)进行一维搜索的步长,即λk满足f(x(k) + λkd(k)) = min f(x(k)+λd(k)) (λ≥0).计算步骤如下:(1)给定初点x(1) ∈ Rn,允许误差ε> 0,置k = 1。
(2)计算搜索方向d = -▽f(x(k))。
(3)若||d(k)|| ≤ε,则停止计算;否则,从x(k)出发,沿d(k)进行一维搜索,求λk,使f(x(k) + λkd(k)) = min f(x(k)+λd(k)) (λ≥0).(4)令x(k+1) = x(k) + λkd(k) ,置k = k + 1,转步骤(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
琼州学院
实验报告
课程名称:数学建模与实验_开课学期:2010—2011第二学期院(部):__理工学院_______开课实验室:_数学建模实验室学生姓名:__江秀菊_______ 专业班级:_09数学教育(1)班学号:_09110021________
最速下降路线的确定--实验报告
1实验目的:
通过数学实验掌握对MATlab 的使用,求解最速下降路线的确定问题
2实验内容:
如图1, 确定一条连接两个定点A 和B 的曲线, 使得一个质点在该曲线上下滑最快,即质点在滑动过程中经历的时间最短。
下滑过程中的摩檫力和阻力都可以忽略不计。
在最快的下滑路径曲线确定后,按照书上给出的数据进行检验。
并思考,将数据横坐标b x 看成一些点的纵坐标,而将纵坐标b y ,看成相应点的横坐标,分别用三次和四次多项式拟合的方法,做出这些数据点的多项式拟合曲线,将他们与原来求出的最佳下滑路线在同一坐标系下进行比较。
图1
3问题分析: 这个问题是书上P191页的思考题, 根据书上建立的模型可知,最
佳下滑路线的方程为:
2[1(')](I)(0)0y y c y ⎧+=⎨=⎩
,其中2
12c gd = 在取定0.07d =后,得到10.4123c =,代入到方程(I)中进行求解。
按照题目中的要求,我们可以借用书上的表达式和数据点进行画图。
并且为了使图形更接近实际,我们考虑将书上的图形向下翻转,即可得到和实际相统一的图形。
4 MATlab 求解:
实验程序: function y=shiyan(x,y) y=sqrt((10.4123-y)/y);
[xb,yb]=ode23('shiyan',[0,2],0.0001);
x=0:0.001:4;
p3=polyfit(yb,xb,3); %三次拟合
y3=polyval(p3,x);
p4=polyfit(yb,xb,4); % 四次拟合
y4=polyval(p4,x);
subplot(2,2,1),plot(xb,-yb),title('原图形');
subplot(2,2,2),plot(yb,-xb),title('新图形');
subplot(2,2,3),plot(x,-y3),title('三次拟合图形');
subplot(2,2,4),plot(x,-y4),title('四次拟合图形');
运行结果:
图2 四种情况比较图
问题重述:
按照书上P191页求最速下滑路线的解析解的模型,计算当质点从(0,0)下滑到(1,1) 所需的时间是多少?
问题分析:
由书上的模型可知:最速下降路径的方程为: (sin )
(II)(1cos )x a y a θθθ=-⎧⎨=-⎩,并且质点从(0,0)
到(1,1)的最速下降路径所对应的max 0.57292342212724, 2.4120a θ==,将这两个数据代入方程(II)可以画出最速下滑路径。
由书上公式可以知道:最速下滑路径所用时间
: 0
t =⎰
,
由方程(II)可知: sin '()1cos dy dy d y x dx dx d θ
θθθ
===
-,所以
: max
(1cos )t d θθθ=-⎰
将实际数据代入后进行计算即可. 实验程序:
function shiyan162 a=0.572923422127; t=0:0.001:2.412; for i=1:2413
x(i)=a*(t(i)-sin(t(i))); y(i)=a*(1-cos(t(i))); end
plot(x,-y) %最速下降路径 syms th;
f=(sqrt(1+(sin(th)/(1-cos(th)))^2))*a*(1-cos(th))/(sqrt(2*9.8*a*(1-cos(th)))); tmin=int(f,th,0,2.412)%最短时间
运行结果:
图3最速下降路径
最短时间为:0.5832秒
5总结体会:
通过实验我们发现,对于一个问题只有通过了实践过程才能发现问题的真实情况,也可以验证我们的猜想,对于该问题,在开始动手之前,从以往的经验中猜到结果可能是一般情况,但不肯定,通过实验,证实了结果和我的猜想有出入。
通过实验能让我们注重实践,也有助于发现自己处理问题中的失误。
总之,通过此次实验不仅让我们对MATlab又有了更进一步的了解,而且也让我学到了许多其他的知识。
学到了许多课外的知识和实践的理论。
希望能通过以后的实验让我获得更多的丰富知识,把理论和实践相结合是最大的收获。
