基于Matlab的机构运动仿真方法及其比较
基于matlab的四杆机构运动分析

基于matlab的四杆机构运动分析一、四杆机构基本概念四杆机构是一种通过变换连杆长度,改变机构运动形态的机械系统。
四杆机构通常由固定连杆、推动连杆、连接杆和工作连杆四个连杆组成,其中固定连杆和推动连杆固定不动,连接杆和工作连杆则沿固定轴线的方向做平动或旋转运动。
四杆机构的基本构造如下图所示:四杆机构的四个连杆的长度和构造参数,以及驱动机构的运动决定了机构的运动特性。
在进行四杆机构运动分析时,需要通过求解运动学关系式和动力学方程,得到连杆的运动规律和力学特性。
二、四杆机构运动学分析1.运动学基本方程四杆机构的运动学分析基本方程是连杆长度变化的定理,即:l₁²+l₂²-2l₁l₂cosθ₂=l₃²+l₄²-2l₃l₄cosθ₄其中,l₁,l₂分别为固定连杆和推动连杆长度;l₃,l₄分别为连接杆和工作连杆长度;θ₂,θ₄分别为推动连杆和工作连杆的夹角。
2.运动学求解方法根据四杆机构运动学基本方程,可以求解机构中任意连杆的角度和位置,从而分析机构运动规律。
在matlab程序中,运动分析可以采用分析法或图解法。
分析法通常采用向量法或坐标法,即将四杆机构中各连杆和运动副的运动量表示为向量或坐标,然后根据连杆长度变化的定理,求解四个未知角度θ₁、θ₂、θ₃、θ₄。
图解法则先通过画图确定机构的运动规律,在图上求解连杆的角度。
比如可以采用伯格(Bourgeois)图法或恰普利恩(Chaplygin)图法等。
四杆机构动力学分析基本方程包括平衡方程和力平衡方程。
平衡方程:当四杆机构处于平衡状态时,连杆的受力关系可以表示为:ΣF=0其中ΣF为各连杆受力的合力。
ΣF=m×a其中,m为每个连杆的质量,a为连杆的加速度。
四杆机构动力学求解方法以matlab为工具,可借助matlab的求解器完成求解。
具体可以利用matlab的优化工具箱、控制工具箱和系统动态学工具箱等,来实现机构模型的动态模拟、仿真和优化设计。
基于MATLAB的机构运动学分析

1. Movement analysis on materials flowing through a vertical pipe based on MATLAB2. Modeling and simulation of aircraft movement based on matlab/S-function3. Based on matlab electrically operated windshield wiper systems design method4. Optimum design of integral type steering mechanism based on MATLAB5. Analysis of assistant robotic leg on MATLABIEEE International Conference on Mechatronics and Automation, ICMA 2006Database: Compendex3.3 万方数据库3.3.1 检索式题名或关键词=机构运动与题名或关键词=Matlab 2005-20103.3.2 检索年限2003-20123.3.3 检索结果⑴【名称】基于CFD软件的数字船模平面运动机构实验方法【申请(专利)号】CN200810064057.2【申请人】哈尔滨工程大学.【发明人】张赫,李晔,庞永杰,徐玉如,秦再白,苏玉民,万磊,邹劲.【申请日期】2008-3-3【公告日期】2008-8-20【摘要】本发明提供的是一种基于计算流体动力学CFD软件FLUENT的数字船模平面运动机构实验方法。
包括应用FLUENT前处理软件GAMBIT建立研究对象模型及控制域;在模型表面布置三角形网格,进而在控制域内布置非结构化网格;设定边界条件,加入用户自定义函数UDF文件,引入动网格技术,采用基于完全非结构化网格的有限体积法,实现平面运动机构实验进行的纯横荡运动、纯升沉运动、纯摇首运动、纯俯仰运动和纯横滚运动;对FLUENT得到的力与力矩系数应用科学计算软件MATLAB傅立叶展开,EXCEL最小二乘法拟合,无因次化得到垂直面和水平面的水动力系数以及相关的流体动力分析。
基于Matlab的发动机连杆机构运动仿真及对比分析

根 据 所求 各 杆 长度 及 偏 置 量 可求 得 A 、 C杆 端 点和 重 心 的 坐 标 BB ( 这里 为 了研 究方 便 , 假设 A B B、 C杆 的质 量均 匀 分布 ) 。对于 对 称
单 ,不需要 进行 一些 高级 语 言编 程就 能很 直观 地观 察 到某 机构 的 运 动 状况 , 可通过 修 改各 构件 的仿 真参 数 , 到 不 同类 型 的运 动 还 得
补 了 在机 械 设 计 的教 学 实 践 和 科 研 中 , 果 不 够 准 确 和 耗 时 耗 力 的 缺 点 。通 过 对 比分 析 了 对 称 式 与 偏 置 式 2种 曲柄 迮 朴 机 构 的运 动 学 特 性 , 结 指
出 了 后 者 的 活 塞 冲 击 力 比前 者 要 小 些 。 关键 词 : 动 仿 真 ; 运 分析 ; a a M tb l
一
建立 发动 机 曲柄 连杆机 构 的数 学模 型 , 出各构 件位 置参 数 , 求 利 用 s lk s i i /i mu n mMehnc 中的模 块 ,建立 动态 仿 真系 统并对 其 cai s 进行 仿真 分 析 。可 以看 出, 与传 统 的 图解法 相 比, 种方 法非 常简 这
端 点及 其重 心 坐标 。如双 击 B d o yAB模 块 打开 属 性框 , A 端 将
图 4 发 动 机 曲 柄 连 杆 机 构 的 动 态 仿 真 图
3 仿 真 结 果
为 了 对 比研 究 偏 置 式 和对 称 式 曲柄 连杆 机 构 的活 塞冲 击 力 , 原 动件 ) 设其 初 始角 速度 为 0 加 速度 为 】 d/S, , , 0r a 根据 图 2所 示
基于MATLAB的双摇杆机构运动分析与仿真

基于MATLAB的双摇杆机构运动分析与仿真双摇杆机构是一种常见的机械系统,由两个摇杆组成,通过摇杆的运动来实现转换。
在本文中,我们将基于MATLAB对双摇杆机构进行运动分析与仿真。
首先,我们需要确定双摇杆机构的几何参数。
主要包括摇杆长度、连接点位置、连接点角度等。
假设双摇杆机构的摇杆长度分别为L1和L2,连接点之间的距离为d,连接点1的坐标(x1,y1)和连接点2的坐标(x2,y2),摇杆1和水平方向的夹角为θ1,摇杆2和水平方向的夹角为θ2根据几何原理,可以得到连接点位置之间的关系:x2 = x1 + L1 * sin(θ1) + L2 * sin(θ2)y2 = y1 + L1 * cos(θ1) + L2 * cos(θ2)接下来,我们可以使用MATLAB进行双摇杆机构的运动分析。
首先,我们需要定义一段时间内摇杆1和摇杆2的角度变化情况,可以使用一个时间向量t和对应的角度向量θ1和θ2来表示。
然后,根据上一步中得到的连接点坐标的关系式,可以计算出连接点的运动轨迹。
通过绘制连接点的运动轨迹,我们可以观察到双摇杆机构的运动情况。
以下是一个MATLAB代码示例,用于计算双摇杆机构的运动轨迹并进行绘制:```matlabL1=1;%摇杆1长度L2=2;%摇杆2长度d=0.5;%连接点之间的距离x1=0;%连接点1的横坐标y1=0;%连接点1的纵坐标t=0:0.01:10;%时间向量theta1 = pi/6*sin(t); % 摇杆1的角度变化theta2 = pi/4*sin(t); % 摇杆2的角度变化x2 = x1 + L1 * sin(theta1) + L2 * sin(theta2);y2 = y1 + L1 * cos(theta1) + L2 * cos(theta2);plot(x2, y2);xlabel('X');ylabel('Y');title('Double Crank Mechanism');```运行以上代码,即可得到双摇杆机构的运动轨迹图像。
基于MATLAB的四连杆机构运动分析

Abstract: In or der t o supply SD cards for low end embedded pr oducts, this paper pr esent s a design based on t he A RM 7 pr o cessor S 3C 44B 0X and taking W 86L 388D contr ol chip o f SD card as the co re . In this pa per , the har dw ar e circuit has been designed and the SD car d contr ol agr eement has been analy zed, the cor r esponding soft war e desig n metho d has been g iv en, and the dr iver pr og ra m has been co mpiled . F inally , the v iability of this pr oject has been analy zed thr ough actual testing . Key words: embedded systems; S3C44B0X; SD card; W 86L 388D
Design of SD Card Control System Based on ARM7
ZHANG Yu, ZHANG Yun-sheng, WANG Jian-ping
( Facult y of Inf or mat ion Engin eer ing and A ut omation , Ku nming U niversit y of Science and T echnol og y, K u nming 650051, China)
(完整)基于matlab的四杆机构运动分析

1平面连杆机构的运动分析1。
1 机构运动分析的任务、目的和方法曲柄摇杆机构是平面连杆机构中最基本的由转动副组成的四杆机构,它可以用来实现转动和摆动之间运动形式的转换或传递动力。
对四杆机构进行运动分析的意义是:在机构尺寸参数已知的情况下,假定主动件(曲柄)做匀速转动,撇开力的作用,仅从运动几何关系上分析从动件(连杆、摇杆)的角位移、角速度、角加速度等运动参数的变化情况。
还可以根据机构闭环矢量方程计算从动件的位移偏差。
上述这些内容,无论是设计新的机械,还是为了了解现有机械的运动性能,都是十分必要的,而且它还是研究机械运动性能和动力性能提供必要的依据.机构运动分析的方法很多,主要有图解法和解析法。
当需要简捷直观地了解机构的某个或某几个位置的运动特性时,采用图解法比较方便,而且精度也能满足实际问题的要求。
而当需要精确地知道或要了解机构在整个运动循环过程中的运动特性时,采用解析法并借助计算机,不仅可获得很高的计算精度及一系列位置的分析结果,并能绘制机构相应的运动线图,同时还可以把机构分析和机构综合问题联系起来,以便于机构的优化设计.1。
2 机构的工作原理在平面四杆机构中,其具有曲柄的条件为:a.各杆的长度应满足杆长条件,即:最短杆长度+最长杆长度≤其余两杆长度之和。
b。
组成该周转副的两杆中必有一杆为最短杆,且其最短杆为连架杆或机架(当最短杆为连架杆时,四杆机构为曲柄摇杆机构;当最短杆为机架时,则为双曲柄机构)。
在如下图1所示的曲柄摇杆机构中,构件AB为曲柄,则B点应能通过曲柄与连杆两次共线的位置。
1.3 机构的数学模型的建立1。
3。
1建立机构的闭环矢量位置方程在用矢量法建立机构的位置方程时,需将构件用矢量来表示,并作出机构的封闭矢量多边形。
如图1所示,先建立一直角坐标系.设各构件的长度分别为L1 、L2 、L3 、L4 ,其方位角为、、、.以各杆矢量组成一个封闭矢量多边形,即ABCDA。
其个矢量之和必等于零。
基于MATLAB的六杆机构动力学分析和仿真
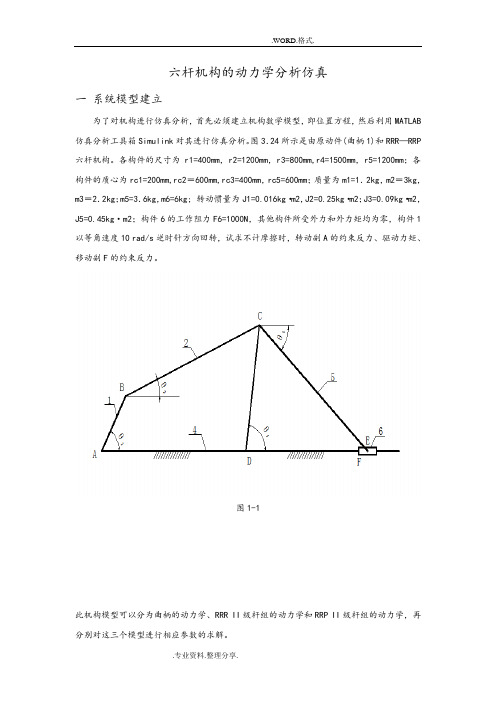
六杆机构的动力学分析仿真一系统模型建立为了对机构进行仿真分析,首先必须建立机构数学模型,即位置方程,然后利用MATLAB 仿真分析工具箱Simulink对其进行仿真分析。
图3.24所示是由原动件(曲柄1)和RRR—RRP 六杆机构。
各构件的尺寸为r1=400mm,r2=1200mm,r3=800mm,r4=1500mm,r5=1200mm;各构件的质心为rc1=200mm,rc2=600mm,rc3=400mm,rc5=600mm;质量为m1=1.2kg,m2=3kg,m3=2.2kg;m5=3.6kg,m6=6kg; 转动惯量为J1=0.016kg·m2,J2=0.25kg·m2;J3=0.09kg·m2,J5=0.45kg·m2;构件6的工作阻力F6=1000N,其他构件所受外力和外力矩均为零,构件1以等角速度10 rad/s逆时针方向回转,试求不计摩擦时,转动副A的约束反力、驱动力矩、移动副F的约束反力。
图1-1此机构模型可以分为曲柄的动力学、RRR II级杆组的动力学和RRP II级杆组的动力学,再分别对这三个模型进行相应参数的求解。
图1-2 AB 构件受力模型如上图1-2对于曲柄AB 由理论力学可以列出表达式:111XA Re R ∙∙=+-s m F R X XB 111y A Im R ∙∙=+-s m F R y yB1111111111111cos )(sin )(cos sin ∙∙=---+-++θθθθθJ r r R r r R r R r R M M c yB c XB c yA c XA F由运动学知识可以推得:)cos()2/cos(Re Re 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s )sin()2/sin(Im Im 12111111πθθπθθ++++=∙∙∙∙∙∙∙c c r r A s将上述各式合并成矩阵形式有,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++-+++++-++++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡∙∙∙∙∙∙∙∙∙∙g m R F r m r m A m R F r m r m A m M R R yB y c c XBX c c yA XA 111211111111112111111111)sin()2/sin(Im )cos()2/cos(Re πθθπθθπθθπθθ(1-21)如图1-3,对构件BC 的约束反力推导如下,图1-3 BC 构件受力模型222Re ∙∙=++s m R F R XC X XB 2222Im ∙∙=-++s m g m R F R yC y yB2222222222222cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yB c XB如图1-4,对构件BC 的约束反力推导如下,图 1-4 CD 构件受力模型333Re ∙∙=-+s m R F R XC X XD 3333Im ∙∙=-++s m g m R F R yC y yD3333333333333cos )(sin )(cos sin ∙∙=-----+θθθθθJ r r R r r R r R r R M c yC c XC c yD c XD由运动学可以推导得,)sin()2/sin(Im Im 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 22222222πθθπθθ++++=∙∙∙∙∙∙∙c c r r B s )cos()2/cos(Re Re 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s )sin()2/sin(Im Im 32333333πθθπθθ++++=∙∙∙∙∙∙∙c c r r D s将上述BC 构件,CD 构件各式合并成矩阵形式有,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------33333333332222222222cos sin cos )(sin )(0010100001010000cos )(sin )(cos sin 001010000101θθθθθθθθc c c c c c c c r r r r r r r r r r r r ⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡yD XD yC XC yB XB R R R R R R =⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-+-++++-++++-+-++++-++++∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙3333332333333333323333333322222222222222222222222222)sin()2/sin(Im )cos()2/cos(Re )sin()2/sin(Im )cos()2/cos(Re M J g m F r m r m D m F r m r m D m M J g m F r m r m B m F r m r m B m y c c X c c y c c X c c θπθθπθθπθθπθθθπθθπθθπθθπθθ (1-22)如图1-5 对构件5进行约束反力的推导如下,图1-5 CE 杆件受力模型∙∙=++s m R F R xE x xC Re 55 ∙∙=-++s m g m R F R yE y yC Im 5555555555555555cos )(sin )(cos sin ∙∙=-+-+--θθθθθJ r r R r r R r R r R M c yE c xE c yC c xC如图1-6 对滑块进行受力分析如下,滑块受力模型∙∙=--E m R R F F xE x Re sin 666θ ∙∙=-+-E m g m R R F F yE y Im cos 6666θ由运动学可推,)cos()2/cos(C Re Re 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s )sin()2/sin(C Re Im 5255555πθθπθθ∙∙∙∙∙∙∙+++=c c r r s66cos Re θ∙∙∙∙=s E 66sin Im θ∙∙∙∙=s E⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+---+-++++-++++=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-------∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙∙g m F s m F s m M J g m F r m r m m F r m r m m R R R R R r r r r r r y x y c c x c c F yE xE yC xC c c c c 66666666655555525555555555255555555665555555555sin cos )sin()2/sin(C Re )cos()2/cos(C Re cos 1000sin 01000cos )(sin )(cos sin 010*******θθθπθθπθθπθθπθθθθθθθθ(1-23)二编程与仿真利用MATLAB进行仿真分析,主要包括两个步骤:首先是编制计算所需要的函数模块,然后利用其仿真工具箱Simulink建立仿真系统框图,设定初始参数进行仿真分析。
基于MATLAB的平面四连杆机构运动仿真

12端 点 B运 动分析 .
在 复 数 坐标 系 中 ,端 点 B的位 置 可 表 示 为 B ri,则 =2 ̄ e2
6
』Brn02 I =c2 I 2si O R 2s e o mB=r
速度分别为 :
( 5 ) 一
。
4
2
分 别 对 上 式 求 一 次 、二 次 导 数 ,得 到 B点 的 速 度 、加
[ ] 孙 桓 , 陈作 模 . 械 原 理 [ ] . 京 : 高 等 教 育 出版 社 1 机 M 北
2 0 . 0 6
( 转第 8 下 4页 )
1 00
5 0
>
一
5 0
。
10 0
图 4 交 替 反相 层 叠 下 相 电 压 波形 及 对 应 频谱
1 0. 0 0
lve i v re sa d DTC o rd v p lc t n .I E a so e l n etr n mo r e a p i ai s EE Tr n n i o
[ ] 刘风 君 ,多 电平 逆 变技 术及 其 应 用 [ ] , 京 :机 械 工 业 出 4 M 北
1 00 0 .
8 . 0O
.
5 0 0.
≮ 0
一
S O 0.
一
1 0. 0 0 0
^ 1 j f
1 0 2 0 0. 0. 3 0 400 0. . 500 6 0 . 0。
越
0 20 . 40 . 60 . 80 . 1 0 0.
t / ms
0
~
.
ll1 斟 s2 v t c西 m o2 B j
l 『 Is 一s i I 一 c ].∞ o h1 I l +s c o j
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Matlab的机构运动仿真方法及其比较
发表时间:2015-12-18T16:19:30.760Z 来源:《基层建设》2015年16期供稿作者:严家炜
[导读] 广东伊之密精密机械股份有限公司运动学仿真对于机构设计研究有着非常重要的地位,它能够去除大量的复杂繁琐和重复的计算工作,对运动过程进行直观的表达。
严家炜
广东伊之密精密机械股份有限公司 528306
摘要:机构运动仿真在机构学研究中占有着非常重要的地位,本文依照仿真活动生命周期,总结概括了三种机构运动仿真方法,并进行对比研究深入分析。
基于MatLab平台,以曲柄摆杆机构为例探究这三种方法的实现途径。
关键词:Matlab;机构运动仿真;对比
前言
运动学仿真对于机构设计研究有着非常重要的地位,它能够去除大量的复杂繁琐和重复的计算工作,对运动过程进行直观的表达。
在机构运动仿真中,明确不同仿真方法及其特点,把握仿真方法的发展趋势,从而充分选择和利用不同仿真平台的功能,对于节约仿真费用,提高研究效率等方面有积极作用。
1.Matlab概述
Matlab是美国MathWorks公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。
2.机构运动仿真
机构仿真周期主要由建立模型,求解模型,展现结果,观察结果和调整模型等五部分构成,如图1所示。
建立模型即列出相关构件或关键点的运动方程,通过求解模型解算出相关点的位姿数据,基于这些数据建立直观的人机界面,将运动过程动态展现给用户。
通常仿真与优化配合使用,由于人机界面的直观性,通过观察常常可以获得优化方面的新信息,利用优化后的新参数调整仿真模型,开始一个新的仿真活动周期,直到获得满意结果为止。
根据对机构仿真中各阶段的侧重不同,可以将机构运动仿真方法基本归为三个大的类别。
第一类的核心是,对仿真模型进行数值求解,称之为基于模型解算的仿真方法。
第二类以提供建模支持手段为核心,利用一些辅助工具来提高建模效率,称之为基于辅助建模的仿真方法。
第三类方法中引进了虚拟现实技术,称之为基于虚拟现实的仿真方法。
以下以图1所示的曲柄摆杆机构为例,说明三种仿真方法的实现过程。
该机构的相关参数分别为l1=370,l2=1049.6,l3=524.7,(xd,yd)=(1080.3,-270)。
其中AB为曲柄,是原动件,以ω作匀速圆周运动,DC为摆杆。
图1:一个曲柄摆杆机构
3.运动仿真方法
3.1基于模型解算的运动仿真
基于模型解算的运动仿真方法属于传统的仿真方法,它以求解模型为核心,重点研究模型的求解方法,以及如何提高求解的效率。
也就是说,仿真效率的提高主要体现为模型求解效率的提高。
在MatLab中,具体表现为提供了大量的功能强大的函数,供求解模型时调用。
这种传统的机构仿真方法的另一个特点是,对仿真结果即运动轨迹的展现,除非用户满意字符界面,一般要用户本人利用图形函数绘制相关构件或关键点的轨迹。
对于图2所示机构,如果要在基于OpenGL的环境下,以图形方式展现运动轨迹,开发人员必须调用多个GDI 函数。
但在MatLab下,对于C点的位姿数据,只要调用plot函数即可获得运动图线。
3.2基于辅助建模的运动仿真
这种方法是以提高建模效率来提高仿真效率的,MatLab/Simulink就是以框图作为建立仿真模型的主要支持手段,框图成为描述模型的基本元素。
而且,MatLab还提供了一个机构系统仿真工具SimMechanics,它可以在Simulink环境下直接使用,使得仿真建模更为便捷。
3.3基于虚拟现实的仿真方法
虽然在SimMechanics下也可采用VR的显示方式,问题是由于构件模型不是三维的,不能得到虚拟环境下的效果。
尤其是对于空间机构,这种缺陷更为明显。
如果能够从不同的空间位置,观察机构的构件基于三维实体模型的动态运动过程,则可以得到更为逼真的仿真效果,这有助于人们对机构的直观理解,对于发现设计缺陷是非常重要的。
这可以利用MatLab中的VR工具箱[6]来实现。
以虚拟现实的方式展现仿真结果数据时,必须将仿真模型的数据实时传送到虚拟场景中,用仿真模型驱动三维场景。
4.方法比较
4.1模型解算方法
这类方法强调仿真模型的求解,以提高求解仿真模型的效率为核心。
主要优点是对软件平台的要求不高,比较灵活,不受制于仿真软件供应商。
可以在多个较为通用平台上开发,如选择VisualC++或BorlandC++,可以开发自主知识产权的仿真软件。
这类方法主要缺点是,通用性相对较差,当面临每一个具体机构时,都要开发一个单独的仿真引擎,因此工作量较大。
当要以图形方式展现仿真结果时,也必须进行额外的编程工作。
这类方法的另外一个缺点是,要求技术人员掌握较多的编程知识和仿真领域的知识,增
加了他们的负担,不能充分发挥他们在机构学领域的优势。
第三,解算的结果数据,与运动轨迹的展现是相对独立的两个部分,这两个部分没有集成起来。
另外,这种方法只适合于展现作平面运动的构件的轨迹。
4.2辅助建模方法
辅助仿真方法以提高建模效率为核心,以框图的形式提供通用的仿真模块,通过对仿真模块进行组装,建立框图之间的连接关系,来表达实际机构各杆件之间的逻辑关系。
由于仿真模型的表达更为直观,并且显著减少了编程工作量,所以,辅助仿真方法极大地扩大了仿真技术的应用领域,是仿真技术的一个飞跃,它使机构学研究人员可以轻易地对机构系统进行运动仿真分析。
仿真结果的实时动画展现,也是用MatLab辅助仿真方法的特点之一,这对于理解特别是平面机构是非常有利的。
4.3虚拟仿真方法
虚拟仿真技术以仿真结果的展现为核心,它采用虚拟现实技术,以三维动态的可视化形式,在一个虚拟场景中实时展现了运动过程,并且可以以多种交互形式从不同视角对场景进行浏览和观察,所以更适合于对空间机构进行运动仿真。
虚拟仿真方法的一个主要缺点是必须对各构件进行三维几何建模,但是由于工程实际中积累了大量可供利用的三维CAD模型,所以,三维几何建模不再成为虚拟仿真的主要制约因素。
三类仿真方法从“模型求解”到“辅助建模”再到“结果展现”的发展过程,实际上是从“人围着机器转”到“机器围着人转”的发展过程,它体现了仿真活动“以人为本”的思想,这也是仿真将来发展的趋势之一。
5.总结语
本文以曲柄摆杆机构为例,探讨了基于MatLab平台的三大机构运动仿真的实现过程。
探讨了三种仿真方法的特点,指出传统仿真方法以提高模型求解效率为核心,辅助仿真方法以提高建模效率为核心,而虚拟仿真方法则以提高仿真结果理解效率为核心的,指出虚拟仿真方法是机构运动仿真的主要趋势。
参考文献:
[1]王沫然.MatLab6.0与科学计算[M].北京.电子工业出版社,2011.
[2]薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2012.。
