系统辨识相关分析的一种改进
系统参数辨识与控制系统设计

系统参数辨识与控制系统设计一、系统参数辨识的概念与方法系统参数辨识是指通过对待辨识系统进行实验,对其动态特性进行分析,并通过所获得的实验数据推算出系统的参数。
对于控制系统的实现来说,系统参数的准确度是影响控制效果的主要因素之一,因此系统参数辨识是一项非常重要的技术。
系统参数辨识的方法主要有模型法和非模型法。
模型法是基于已知的系统模型进行参数拟合,包括参数估计和参数优化两部分。
而非模型法则是利用实验数据,通过数学分析提取系统参数信息,包括时域分析法和频域分析法。
常见的辨识算法包括最小二乘法、极大似然法、脉冲响应辨识法等。
二、常见的控制系统设计技术控制系统设计是指采用特定的方法和技术,对给定的控制要求进行设计和分析,以达到优化控制效果的目的。
常见的控制系统设计技术包括以下几种:1. PID控制器设计技术PID控制器是一种常用的控制器类型,由比例、积分和微分三个部分组成,其调节速度和精度都比较高。
PID控制器的设计涉及到参数的选择和调节,其中参数选择需要结合系统特性和控制要求,而参数调节则需要通过实验以及相关辨识算法中模型法的思想来完成。
2. 模糊控制技术模糊控制技术是一种新型的自适应控制方法,其主要特点是能够适应不确定和非线性系统,具有较好的鲁棒性和容错性。
模糊控制器的设计需要结合模糊规则的建立和优化,其中模糊规则的建立需要把握系统特点和控制需求,而优化则需要通过实验数据和非模型辨识算法来实现。
3. 自适应控制技术自适应控制技术是一种能够实现系统自动调节的控制方法,其主要思想是通过不断地更新控制器参数适应系统变化,从而达到优化控制效果的目的。
自适应控制器的设计需要结合算法的选用和参数的调节,其中算法的选用需要考虑算法的适应性和鲁棒性,而参数的调节则需要通过相关辨识算法以及实验数据来完成。
三、系统参数辨识与控制系统设计的关系系统参数辨识与控制系统设计是密切相关的。
在控制系统设计中,系统参数的准确性是影响整个设计效果的主要因素之一。
隐患排查治理不到位、岗位风险辨识管控不到位整改措施

隐患排查治理不到位、岗位风险辨识管控不到位整改措施隐患排查治理不到位、岗位风险辨识管控不到位是企业安全管理中非常重要的问题。
针对这种情况,需要采取一系列的整改措施,以有效地解决这些问题。
本文将就这些问题展开讨论,并提出相应的整改措施。
一、什么是隐患排查治理不到位和岗位风险辨识管控不到位问题?隐患排查治理不到位是指企业未能够对可能存在的安全隐患进行全面、系统的排查和治理,导致潜在的安全隐患未能够得到及时的发现和解决,进一步造成安全事故的发生。
岗位风险辨识管控不到位是指企业未能够对不同岗位的安全风险进行全面、系统的辨识和管控,导致岗位安全隐患未能够得到有效的控制,带来安全风险的潜在扩大。
二、隐患排查治理不到位和岗位风险辨识管控不到位的危害1.安全事故风险增加。
隐患排查治理不到位和岗位风险辨识管控不到位,会导致安全隐患得不到及时的发现和解决,进一步增加了安全事故的风险。
2.生产效率降低。
安全隐患可能导致生产线的停工,从而影响生产效率,降低企业的经济效益。
3.员工健康受损。
安全隐患未能得到有效的治理和管控,会对员工的身体健康产生潜在的危害。
三、隐患排查治理不到位和岗位风险辨识管控不到位的原因分析1.缺乏专业的隐患排查治理和岗位风险辨识管控人员。
企业可能没有专业的安全管理人员,导致隐患排查治理和岗位风险辨识工作的不到位。
2.缺乏有效的排查治理和辨识管控方法。
企业可能缺乏有效的排查治理和辨识管控方法,导致工作无法得到有效的开展。
3.缺乏足够的资金投入。
企业可能缺乏对隐患排查治理和岗位风险辨识管控工作的资金投入,导致工作难以正常展开。
四、整改措施1.建立健全的安全管理体系。
企业需要建立健全的安全管理体系,包括制定相应的安全管理制度和规范,明确相关责任人,确保隐患排查治理和岗位风险辨识管控工作得到有效的开展。
2.加强隐患排查治理和岗位风险辨识管控人员的培训。
企业需要加强对相关人员的培训,提高其隐患排查治理和岗位风险辨识管控的专业能力,确保安全管理工作得到有效的开展。
系统辨识实验报告30288
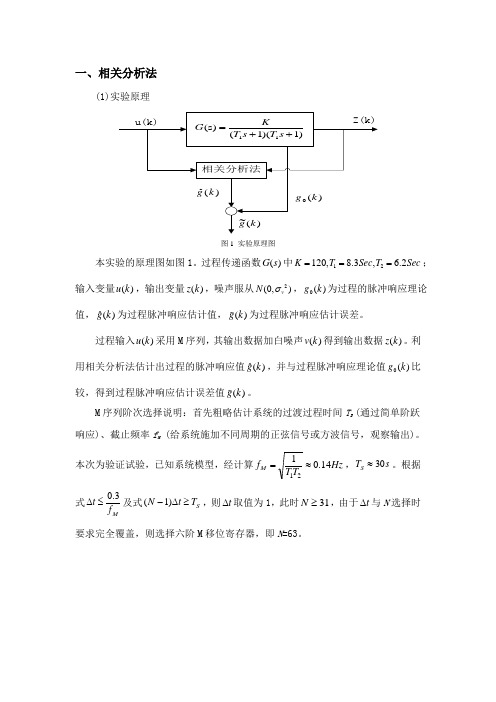
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===;输入变量()u k ,输出变量()z k ,噪声服从2(0,)v N σ,0()g k 为过程的脉冲响应理论值,ˆ()gk 为过程脉冲响应估计值,()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列,其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ,并与过程脉冲响应理论值0()g k 比较,得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明:首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号,观察输出)。
本次为验证试验,已知系统模型,经计算Hz T T f M 14.0121≈=,s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(,则t ∆取值为1,此时31≥N ,由于t ∆与N 选择时要求完全覆盖,则选择六阶M 移位寄存器,即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列:M 序列的循环周期63126=-=N ,时钟节拍1t Sec ∆=,幅度1a =,移位寄存器中第5、6位的内容按“模二相加”,反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下:② 生成白噪声序列: 程序如下:③ 过程仿真得到输出数据:如图2所示的过程传递函数串联,可以写成形如121211()1/1/K Gs TT s T s T =++,其中112KK TT =。
图2 过程仿真方框图程序如下:④ 计算脉冲响应估计值:互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=,互相关函数所用的数据是从第二个周期开始的,其中r 为周期数,取1-3之间。
系统辨识的经典方法

⎧T
⎨⎩τ
= 2(t2 − t1) = 2t1 − t2
对于以上结果,也可在
⎧⎪⎨tt34
≤τ,
= 0.8T
+τ
,
⎪⎩t5 = 2T +τ ,
y(t3 ) = 0 y(t4 ) = 0.55 y(t5 ) = 0.87
这几点上对实际曲线的拟合精度进行检验。
系统辨识的经典方法
频率响应法
频率响应法-1
; 阶跃响应法辨识原理
¾ 在系统上施加一个阶跃扰动信号,并测定出对象的响应随时间 而变化的曲线,然后根据该响应曲线,通过图解法而不是通过 寻求其解析公式的方法来求出系统的传递函数,这就是阶跃响 应法系统辨识。
¾ 如果系统不含积分环节,则在阶跃输入下,系统的输出将渐进 于一新的稳定状态,称系统具有自平衡特性,或自衡对象。
+ b1s + a1s
+ +
b0 a0
,
n>m
¾ 对应的频率特性可写成:
G(
jω)
=
bm ( an (
jω)m +" + b2 ( jω)2 + b1( jω)n +" + a2 ( jω)2 + a1(
jω) + b0 jω) + a0
=
(b0 − b2ω 2 (a0 − a2ω 2
+ b4ω 4 + a4ω 4
系统辨识的经典方法
肖志云
内蒙古工业大学信息工程学院自动化系
系统辨识的经典方法
1
引言
2
阶跃响应法
3
频率响应法
4
相关分析法
系统辨识

相关分析法通常采用类似白噪声的伪随机信号作为输入测试信号,这种信号对系统的正常工作干扰不大。
通常不加专门的输入测试信号,仅利用正常工作状态下测量的输入及输出信号,就可得到良好的辨识效果。
相关分析法辨识抗干扰能力强、数据处理简单、辨识精度高,因此应用比较广泛,尤其是在需要在线辨识的场合。
相关分析法辨识具有最小二乘法辨识的统计特性,即使在有色噪声干扰下,也可以得到无偏估计,这是它和一般最小二乘法相比最大的优点。
在采用相关分析法进行系统辨识时,系统的脉冲响应函数可由系统的输入及输出数据的相关函数来描述,因此,输入信号的选择及相关函数的估计是相关分析法的关键所在。
持续激励输入信号的要求。
更进一步的要求是输入信号必须具有较好的“优良性”,即输入信号的选择应能使给定问题的辨识模型精度最高。
在具体工程应用中,选择输入信号时还应考虑以下因素:输入信号的功率或幅度不宜过大,以免使系统工作在非线性区,但也不应过小,以致信噪比太小,直接影响辨识精度。
工程上要便于实现,成本低。
相关分析法是属于统计分析的方法,它的理论基础就是著名的维纳-霍甫积分方程。
这个方程为积分方程,不易求解,但如果采用白噪声作为系统输入,则可方便的求出系统的脉冲响应。
但是运用白噪声求系统响应,理论上需要无限长时间上的观测数据,这是不希望和不允许的,因此具有人工可以复制的、有规律的、周期性的伪随机信号是更适合应用的。
这种信号具有类似白噪声的性质,目前最常用的是伪随机二位式序列,它们主要有M序列和逆重复M序列,它们可由计算机或线性反馈寄存器产生。
用M序列和逆重复M序列对系统的脉冲响应进行辨识时,都是在离散的时间上进行的。
由它们获得的响应函数是原函数的一致性估计。
为了提高辨识精度,可采用多个周期输入伪随机序列的方法。
当对系统进行在线辨识时,可以采用脉冲响应的递推计算公式。
多变量系统的脉冲响应的辨识问题,最后要归结为用单变量系统辨识方法进行,所不同的只是较复杂。
系统辨识 相关分析法

3. 求解g(m)
RUZ (τ ) = ∫
∞ ∞
g (θ ) RU (τ θ )dθ
维纳-霍普方程
= nT0
τ = m, t = k , θ = j
N p 1 j =0
令 =1
离散形式
RUZ (m) =
∑ g ( j)R
U
(m j )
a2 , m = 0 RU (m) = a 2 , 1 ≤ m ≤ NP 1 NP
Np 1 j =0
∑ g ( j ) RU (m j )
m = 0,1, L , N p 1
r RUZ = [ RUZ (0), RUZ (1),L , RUZ ( Np 1)]T
r g = [ g (0), g (1),L, g ( Np 1)]T
r r r Ruz = Ru g
2 1 r 1 Np Ru = ( Np + 1)a 2 M 1 r r 1 r g = Ru Ruz 1 2 M 1
r Ru ≠ 0
谢谢观赏
�
1 Np 1 M 1 Np
= a
2
1 Np 1 Np M 1
N p*N p
四,对测试信号的要求 对输入信号的最低要求是:信号必须是持续激励的. 在辨识时间内,输入信号能持续激励被辨识系统的状 态或充分激励被辨识系统的所有模态. 从谱分析的角度来讲,输入信号的频谱必须足以覆盖 系统的频谱.
“安全风险分级管控”工作制度(四篇)

“安全风险分级管控”工作制度各专业、科室、单位:为全面辨识、管控矿井在生产过程中,针对各系统、各环节可能存在的安全风险、危害因素以及重大危险源,将风险控制在隐患形成之前,把可能导致的后果限制在可防、可控范围之内,提升安全保障能力,根据集团公司要求并结合我矿实际,特制定本制度。
一、总则安全风险分级管控是指在安全生产过程中,针对各系统、各环节可能存在的安全风险、危害因素以及重大危险源,进行超前辨识、分析评估、分级管控的管理措施。
各单位主要负责人是本单位安全风险分级管控工作实施的责任主体,各业务科室是本专业系统的安全风险分级管控工作实施的责任主体。
二、“安全风险分级管控”组织机构(一)成立“安全风险分级管控”工作领导组:组长:矿长常务副组长:安全矿长、总工程师副组长:生产矿长、通风矿长、机电矿长、基建矿长成员:各专业副总工程师及科室和单位主要负责人。
领导组下设办公室,办公室设在安全监察科。
办公室主任由安监科科长兼任,主要负责检查、督促“安全风险分级管控”工作的实施。
(二)领导组职责1、制定“安全风险分级管控”工作制度,制定实施方案,明确辨识程序、评估方法、管控措施以及层级责任、考核奖惩等内容。
2、制定安全风险辨识的程序和方法(通过对系统的分析、危险源的调查、危险区域的界定、存在条件及触发因素的分析、潜在危险性分析)。
3、指导、督促各专业及科室和单位开展“安全风险分级管控”工作。
(三)办公室职责1、办公室负责“安全风险分级管控”检查、督促“安全风险分级管控”工作的实施。
2、组织相关人员对全矿“安全风险分级管控”实施情况进行检查、考核。
3、承办上级部门和矿“安全风险分级管控”工作领导组交办的其他工作。
(四)职责分工1、矿长是安全风险分级管控第一责任人,对安全风险管控全面负责。
对安全风险分级辨识评估工作进行总体牵头和安排,并按照矿井安全风险评估辨识结果应用于确定年度安全生产重点工作,指导和完善年度生产计划、灾害预防和处理计划、应急救援预案,对安全风险评估辨识的危险因素,按管控措施要求,进行安全管控措施的安排。
系统辨识调研报告

北京工商大学《系统辨识》课程调研报告题目类别:系统建模的分类现代辨识方法报告题目:基于神经网络与模糊控制的辨识方法调研目录第一章系统辨识理论综述 21.1系统辨识的基本原理 21.2系统辨识的经典方法 21.3神经网络系统辨识综述 21.3.2神经网络在非线性系统辨识中的应用 2 1.4模糊系统辨识综述 31.4.1模糊系统的结构辨识 31.4.2参数优化的方法 31.4.3模糊规则库的化简 31.5小结 4第二章模糊模型辨识方法的研究 42.1模糊模型辨识流程 42.2模糊模型结构辨识方法 52.3模糊模型参数辨识方法 52.4模糊系统辨识中的其它问题 62.4.1衡量非线性建模方法好坏的几个方面 62.4.2模糊辨识算法在实际系统应用中的几个问题 62.4.3模糊模型的品质指标 62.5小结 7第三章基于两种模型的自行车机器人系统辨识 73.1基于ARX模型的自行车机器人系统辨识 73.2基于ANFls模糊神经网络的自行车机器人系统辨识 73.3 展望 7第一章系统辨识理论综述1.1系统辨识的基本原理根据LA.zadel的系统辨识的定义(1962):系统辨识就是在输入和输出数据的基础上,从一组给定的模型类中,确定一个与所测系统等价的模型"系统辨识有三大要素:(1) 数据。
能观测到的被辨识系统的输入或输出数据,他们是辨识的基础。
(2) 模型类。
寻找的模型范围,即所考虑的模型的结构。
(3) 等价准则。
等价准则一辨识的优化目标,用来衡量模型接近实际系统的标准。
1.2系统辨识的经典方法1、阶跃响应法系统辨识;2、频率响应法系统辨识;3、相关分析法系统辨识;4、系统辨识的其他常用方法;1.3神经网络系统辨识综述1.3.1神经网络在线性系统辨识中的应用自适应线性(Adallne一MadaLine)神经网络作为神经网络的初期模型与感知机模型相对应,是以连续线性模拟量为输入模式,在拓扑结构上与感知机网络十分相似的一种连续时间型线性神经网络。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
I.
4 结束语 ( Conclusion)
本文给出了系统辨识相关分析的一种改进试验 作为计算 及计算方法 , 所用的 M 序列长度和待辨识系统脉冲 传递函数离散样值个数的选取相互独立 , M 序列长 度可以大于脉冲传递函数离散样值个数 , 随着 M 序 列长度的增大 , 辨识结果中的恒偏大大减小 , M 序 列更接近于最优试验信号 , 在不增加计算复杂性的 前提下 , 提高了辨识精度 , 增加了参数选择的灵活 性 . 对一个二阶系统的辨识结果表明 , 这种改进方法 可以明显改善系统的辨识精度 . 参考文献 ( References )
… 1 … 1 ω … … N - p +1
<xy ( 0) <xy ( 1) … <xy ( p)
( 2 . 7) ,
在已有的试验设计方中[1 ,2 ] ,固定取 N = p + 1 , 则:
2 1 2
Φ
-1 x
N = 2 a ( N + 1)
1
… … 1 1
… … ω …
1 1
~ N 1 { <xy ( k ) + 2 a Δ T ( N + 1) N - p k = 0
2
Φx =
-
a N
…2
a N 为 M 序列的自相关阵 ,
2
…
2
… ω
…
~
a a N N
~
… a2
~
Φxy = [ <xy ( 0) <xy ( 1) … <xy ( p) ] T 是 M 序列和 输出的互相关阵 . 这里 , <xy ( i ) =
1
p+M
M + 1m= p
x( m ∑
- i) y ( m) ( i = 0 , 1 ,
p
∑
~
… 2
~
, ( 2 . 3)
<xy ( i ) } ( i = 0 , 1 , …, p) .
( 2 . 8)
得到 :
2 1
H ^ =
1
a Δ T ( N + 1)
2
… 1
… … … ω 1 …
1 2
1 1
<xy ( 0)
~
由式 ( 2 . 7) 或式 ( 2 . 8) 可以看出 , 改进的方法有 下述几个特点 : 1) N , p 相互独立 , 可独立选择 , 而式 ( 2 . 3) 是式 ( 2 . 6) 在 p = N - 1 时的特例 ; 1 2) 对于式 ( 216) 有 : lim Φ-x 1 = 2 I , I 是 ( p + 1)
A n I mp r ove m e nt of Cor r el a ti o n A n al ysis i n S ys t e m I d e ntif ic a ti o n
ZHAO Zhengmin 1 and REN Guiyong2
( 1 . Department of Electrical Engineering , Huaiyin Institute of Technology ・ Jiangshu Huaiyin , 223001 , P. R. China ;
© 1994-2008 China Academic Journal Electronic Publishing House. All rights reserved.
116
p
控制理论与应用
19 卷
N N - p 足够大时 ,恒偏 2 <xy ( k) 将 a Δ T ( N + 1) ( N - p) k =0 变得很小 , 可以忽略不计 , 估计将变为无偏估计 ; 4) 若系统干扰信号 v ( t ) 为白噪声 , ^ h ( i ) 的误
∑
2 表 1 是三组随机试验的定量分析结果 , σ =
1
p +1
p
i =0
[^ h ( i) ∑
- h ( i ) ] , h ( i ) 是理论值 , ^ h ( i) 是
2
差协方差阵为 :
1+ 1
N- P
1
N- P
… … ω
1
N- P
辨识结果 . 从表中的数据可以看出 , 改进方法对辨识 精度的改善是明显的 . 2 表 1 N 不同时 , 系统的辨识误差 σ
N →∞
<xy ( 1) …
~
a
… 2
,
阶单位阵 , 这表明就自相关矩阵而言 , 当信号长度趋 于无穷时 , M 序列趋向于理想白噪声信号 ;
N 3) lim 2 N →∞ a Δ T ( N + 1) ( N - p)
p k =0
<xy ( p)
( 2 . 4)
∑<
~
xy ( k)
= 0 , 表明
H ^ = [^ h ( 0) ^ h ( 1) … ^ h ( p) ] 是脉冲响应函数
T
或
^ h ( i) = N Δ T ( N + 1) a2
p
k =0
∑<
xy
( k ) + <xy ( i ) ( i = 0 , 1 , …, p) . ( 2 . 5)
的离散序列 ,
a
2 2
a
a2 a2 …N N
pulse response of control . An improvement of this method , i . e. , increasing the length of M sequence after fixing the number of discrete values of impulse response to improve the precision , is presented. Simulation results demonstrate the validity of this means .
2 . Department of Automatic Control , Harbin Institute of Technology ・Harbin , 150001 , P. R. China)
Abstract : Correlation analysis , using pseudo- random binary sequence as input , is an effective method to identify the im2
收稿日期 : 1999 - 10 - 14 ; 收修改稿日期 : 2000 - 07 - 17 .
其脉冲响应函数 h ( t ) , n > m 时 , lim h ( t ) = 0 ;
t →∞
当 n - m = 1 时 , h ( 0) ≠0 ; 当 n - m ≥2 时 , h ( 0) = 0 . 对这类系统的相关分析试验系统结构如图 1 所 示 , 设输入信号 M 序列长度为 N ,Δ T 为 M 序列的时 钟周期 , 也等于系统的采样周期 , y ( t ) 为待辨识系 统的有噪输出信号 , v ( t ) 为干扰信号 , 是 A/ D 量化 噪声及系统其它噪声在输出端的等效 , p + 1 为待辨 识脉冲响应函数离散样值的个数 , 观测 M + p + 2 组 数据 , M + 1 = qN , 整数 q 是 M 序列重复周期数 , 求
N = 1023 , p = 126 , M = 2048 , q = 2
5 . 2213e - 08 5 . 8070e - 08 7 . 6499e - 08
1 . 2620e - 08 1 . 7474e - 08 1 . 5008e - 08
显然 , lim Ψ =
N - p →∞
σv
a2
2
Table 1 System identification error σ for different N
2
Ψ =
σv N
a ( N + 1)
2
2
1
N- P
1+
1
N- P
1
N- P .
实验 序号
1 2 3
… 1
N- P
… 1
N- P
… 1+
… 1
N- P ( 2 . 9)
N = 127 , p = 126 , M = 2031 , q = 16
第 19 卷第 1 期 2002 年 2 月
控制理论与应用
CON TROL THEORY AND APPLICA TIONS
Vo1 . 19 No. 1 Feb. 2002
文章编号 : 1000 - 8152 ( 2002) 01 - 0114 - 03
系统辨识相关分析的一种改进 3
赵正敏1 任贵勇2
( 11 淮阴工学院电气工程系・ 江苏淮阴 , 223001 ; 21 哈尔滨工业大学控制工程系・ 哈尔滨 , 150001)
摘要 : 用伪随机二进制序列 ( PRBS ) 进行相关分析是辨识系统脉冲响应函数的有效方法 , 本文给出了相关分析 法的一个改进型 : 首先确定脉冲响应函数离散值的个数 , 然后独立增加 M 序列的长度以提高系统的辨识精度 , 仿真 表明了这种算法的有效性 . 关键词 : 伪随机二进制序列 ; 相关分析 ; M 序列 文献标识码 : A
( 2 . 1)
于其易于产生 , 易于处理并具有类似于白噪声的性 质 , 在系统辨识中 , M 序列常作为试验输入信号 , 并 已有成熟的理论与应用结果 . 提高系统脉冲响应函 数精度的方法主要有 : 减小 M 序列的时钟周期和增 大其长度 ; 用高精度的方法求解 Wiener- Hopf 方程 ; 提高互相关函数的计算精度等 . 随着计算机技术的发展 , 给出一个长度很大的 M 序列用于系统辨识已变得非常方便 . 针对 M 序列 长度大于待辨识脉冲响应函数离散值个数的情况 ,
