正弦三角函数的图像与性质
正弦函数的性质与图像

x
sin x
1 s in x
0 0
π 2
π
0
3π 2
2 π
1 2
1
0
1
1
0
1
描点作图
y
2 1
-
y 1 sin x , x [ 0, 2 π ]
π 2
o
1-
π
3π 2
2π
x
y sin x , x [ 0, 2 π ]
用“五点法”画出下列函数在区间[0,2π]的图。 (1)y=2+sin x; (2)y=sin x-1; (3)y=3sin x.
y
1
p (c o s x , s in x )
o
M
1
x
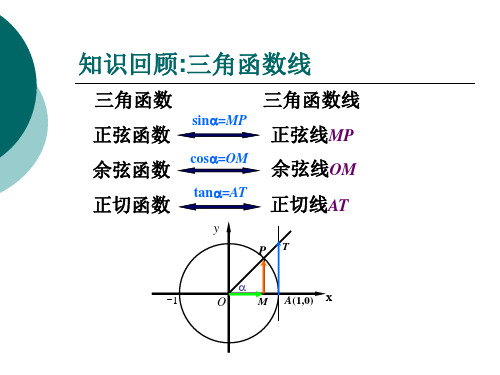
正弦线 MP
三角函数 问题
几何问题
正弦函数的图象
利用正弦线作出 y sin x , x 0, π 的图象. 2
y
作法: (1) 等分; (2) 作正弦线;
/
1P1
p1
(3) 平移; (4) 连线.
π 3
π 2
6
-
-
o1
M
-1 A
π 2
,1 );
与 x 轴的交点: ( 0 , 0 ), ( π , 0 ), ( 2 π , 0 ); 图象的最低点:
( 3π 2 , 1) .
五点 作图法
五 点 作 图 法
列表:列出对图象形状起关键作用的五点坐标.
描点:定出五个关键点.
连线:用光滑的曲线顺次连结五个点.
例 用“五点法”画出下列函数在区间[0,2π]的简图。 (1)y=-sin x; (2)y=1+sin x.
三角函数的图象与性质 (共44张PPT)

(
)
3 3 A.-2,2 3 3 3 3 C. - , 2 2
解析: 当 故
π π 1 π π 5π x∈0,2 时, 2x- ∈- 6, 6 , sin2x-6 ∈-2,1, 6
上是减函数 - π , 0 C.在[0,π]上是增函数,在
)
π π π π D.在2,π和-π,-2上是增函数,在-2,2 上是减函数
3.(2015· 皖南八校模拟)函数 f(x)=cos 2x+2sin x 的最大值与最小值 的和是 A.-2 3 C.- 2
4.求函数 y=cos x+sin
2
π x|x|≤4 的最大值与最小值.
π 2 2 解:令 t=sin x,∵|x|≤ ,∴t∈- , . 4 2 2
∴y=-t
2
1 2 5 +t+1=-t-2 + , 4
1- 2 1 5 2 ∴当 t= 时,ymax= ,当 t=- 时,ymin= . 2 4 2 2 ∴函数 y=cos x+sin
sin 2x>0, 解析:由 2 9-x ≥0,
π kπ<x<kπ+ ,k∈Z, 2 得 -3≤x≤3.
π π ∴-3≤x<- 或 0<x< . 2 2 ∴函数 y=lg(sin 2x)+ 9-x
2
π π 的定义域为-3,2 ∪0,2 .
2
π 1- 5 x通法]
1.三角函数定义域的求法 求三角函数定义域实际上是构造简单的三角不等式(组),常借 助三角函数线或三角函数图象来求解.
2.三角函数值域的不同求法 (1)利用 sin x 和 cos x 的值域直接求;
正弦和余弦的图像和性质
y sin x, x [0, 2 ]的图象 作法: (1) 等分
(2) 作正弦线
问题:如何作出比较精确的正弦函数图象? (3) 平移
途径:利用单位圆中正弦线来解决。
(4) 连线
y
B
1
用光滑曲线将这些正弦线 的终点连结起来!
A
O1
O 2 5 7 4 3 5 11 22
2
(
,1)
(
2 ,1)
(
2
,1)
(
2
,1)
( 2( ,21),1) ( 2 ,1)
,0) 3
(
2
( ,0) 2
(
((((((,,0,00),)0,),(003)2))(32,(-312,(1)32),1(33,)(212(3(323)2,21-,1,-),-1)-11)))
2 ,0) x
2 ,0)
解: x
3
0
2
2
2
sinx
0
1
0
-1
0
1+sinx
1
2
1
0
1
y
2
y=1+sinx,x[0, 2]
1
o
2
-1
2
3
2
x
2
典型例题:
例1(2) 画出函数y= -cosx,x[0, 2]的简图:
x
0
2
3
2
2
cosx
1
0
-1 0
1
-cosx
-1
0
1
0
-1
y
1
y=-cosx,x[0, 2]
正弦函数和余弦函数的图像与性质.ppt

, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式:cos x sin x, x [ , ]
-2
五个关键点:(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时, -6
余弦函数取得最大值1;-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时,
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值,及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
正弦型函数的图像性质

相位是正弦波在时间轴上的偏移量,决定了波形开始的时间点。当 $varphi > 0$ 时,图像向右位移;当 $varphi < 0$ 时,图像向左位移。相位的变化不会 改变波形周期和振幅,但会影响波形在时间轴上的位置。
03 正弦型函数的奇偶性
奇函数性质
奇函数性质
正弦型函数是奇函数,因为对于任意x,都有f(-x) = -f(x)。这意 味着正弦型函数的图像关于原点对称。
对称轴
正弦函数图像关于y轴对称
正弦函数$y = sin x$的图像关于y轴对称,即当$x$取正值和负值时,$y$的值相 同。
余弦函数图像关于x轴对称
余弦函数$y = cos x$的图像关于x轴对称,即当$y$取正值和负值时,$x$的值相 同。
对称中心
要点一
正弦函数图像关于点$(kpi, 0)$对 称
通过调整A、ω、φ的值,可以获 得不同振幅、周期和相位偏移的 正弦型函数。
单位圆与三角函数关系
单位圆是指在平面直角坐标系中, 以原点为圆心、半径为1的圆。
三角函数与单位圆密切相关,单 位圆上的点可以用三角函数来表
示。
在单位圆上,正弦和余弦函数的 值等于点的纵坐标和横坐标的比 值,正切函数的值等于点的纵坐
图像特点
偶函数的图像关于y轴对称,即当 x=0时,y达到最大或最小值。在 x>0和x<0的区间内,函数值相等。
应用实例
偶函数性质在电磁学中有广泛应用, 例如磁场分布等。
既非奇又非偶函数性质
既非奇又非偶函数
性质
正弦型函数既不是奇函数也不是 偶函数。虽然它的图像关于原点 和y轴都有对称性,但它不符合奇 偶函数的严格定义。
振幅与图像高度
常见三角函数图像及性质

常见三角函数图像及性质三角函数在数学中具有重要的作用,主要有正弦函数、余弦函数和正切函数。
这些三角函数的图像及性质对理解三角函数在不同角度下的变化规律至关重要。
1. 正弦函数(Sine Function)正弦函数可以表示为 $y = \\sin(x)$,其中x表示自变量(角度),x表示函数值。
正弦函数的图像是一条波浪形状的曲线,在 $[-\\pi, \\pi]$ 区间内,正弦函数的图像在原点(0,0)处达到最大值1和最小值−1,且图像在x轴上对称。
正弦函数的主要性质包括:•周期性:正弦函数的周期是 $2\\pi$,即 $f(x+2\\pi) = f(x)$。
•奇函数:正弦函数是奇函数,即x(−x)=−x(x)。
•范围:正弦函数的值域为[−1,1]。
•正负性:在第一和第二象限,正弦函数为正;在第三和第四象限,正弦函数为负。
2. 余弦函数(Cosine Function)余弦函数可以表示为 $y = \\cos(x)$,余弦函数的图像是一条类似正弦函数的波浪形状曲线,不过余弦函数的图像在x轴上下移了 $\\frac{\\pi}{2}$。
余弦函数的性质包括:•周期性:余弦函数的周期也是 $2\\pi$,即$f(x+2\\pi) = f(x)$。
•偶函数:余弦函数是偶函数,即x(−x)=x(x)。
•范围:余弦函数的值域为[−1,1]。
•正负性:在第一和第四象限,余弦函数为正;在第二和第三象限,余弦函数为负。
3. 正切函数(Tangent Function)正切函数可以表示为 $y = \\tan(x)$,正切函数的图像是一条周期性的曲线,其在某些角度处会出现无穷大的值。
正切函数的图像在 $x=k\\pi + \\frac{\\pi}{2}$ 时,即 $x =\\frac{\\pi}{2}, \\frac{3\\pi}{2}, \\frac{5\\pi}{2}$ 等,会出现垂直渐近线。
正切函数的性质包括:•周期性:正切函数的周期是 $\\pi$,即 $f(x+\\pi) = f(x)$。
正弦函数的图像和性质

1定义编辑数学术语正弦函数是三角函数的一种.定义与定理定义:对于任意一个实数x都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的正弦值sin x,这样,对于任意一个实数x都有唯一确定的值sin x与它对应,按照这个对应法则所建立的函数,表示为f(x)=sin x,叫做正弦函数。
正弦函数的定理:在一个三角形中,各边和它所对角的正弦的比相等,即a/sin A=b/sin B=c/sin C在直角三角形ABC中,∠C=90°,y为一条直角边,r为斜边,x为另一条直角边(在坐标系中,以此为底),则sin A=y/r,r=√(x^2+y^2)2性质编辑图像图像是波形图像(由单位圆投影到坐标系得出),叫做正弦曲线(sine curve)正弦函数x∈&定义域实数集R值域[-1,1] (正弦函数有界性的体现)最值和零点①最大值:当x=2kπ+(π/2),k∈Z时,y(max)=1②最小值:当x=2kπ+(3π/2),k∈Z时,y(min)=-1零值点:(kπ,0) ,k∈Z对称性既是轴对称图形,又是中心对称图形。
1)对称轴:关于直线x=(π/2)+kπ,k∈Z对称2)中心对称:关于点(kπ,0),k∈Z对称周期性最小正周期:y=sinx T=2π奇偶性奇函数(其图象关于原点对称)单调性在[-π/2+2kπ,π/2+2kπ],k∈Z上是单调递增.在[π/2+2kπ,3π/2+2kπ],k∈Z上是单调递减.3正弦型函数及其性质编辑正弦型函数解析式:y=Asin(ωx+φ)+h各常数值对函数图像的影响:φ(初相位):决定波形与X轴位置关系或横向移动距离(左加右减)ω:决定周期(最小正周期T=2π/|ω|)A:决定峰值(即纵向拉伸压缩的倍数)h:表示波形在Y轴的位置关系或纵向移动距离(上加下减)作图方法运用“五点法”作图“五点作图法”即当ωx+φ分别取0,π/2,π,3π/2,2π时y的值.单位圆定义图像中给出了用弧度度量的某个公共角。
正弦函数、余弦函数的图像和性质

图象的最高点 图象的最高点 与x轴的交点 轴的交点
x
1-
( 0 ,1 ) (2π ,1)
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
π ( π ,0 ) (32 ,0) 2π 2 图象的最低点 (π ,−1) 图象的最低点
-
应用“ 例1.应用“五点法”作图。 应用 五点法”作图。
π
π
例2.分别利用函数的图像和三角函数 先两种方法,求下列不等式的解集:
1 (1) sin x ≥ ; 2 1 5π (2) cos x ≤ (0 < x ≤ ); 2 2
例3.判断y = cos x + 1, x ∈ [0,2π ]与下列 直线交点的个数: 3 ( )y = 2; (2) y = ; (3) y = 0. 1 2
图
y
1-
数、 图
数
图象的最高点 ( ,1) 图象的最高点 2 与x轴的交点 轴的交点
( 0 , 0 ) (π , 0 ) (2π ,0)
x
π
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
图象的最低点 (32 ,−1 图象的最低点 π )
简图作法 (1) 列表 列出对图象形状起关键作用的五点坐标) 列表( (2) 描点 定出五个关键点) 描点( y (3) 连线 用光滑的曲线顺次连结五个点) 连线(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
问题提出
t
p
1 2
5730
1.正弦函数和余弦函数的图象分别是什
么?二者有何相互联系?
y 1
y=sinx
-6π
-4π
-2π -π π
O
-5π -3π
-1
y
2
2
1 22
3π 5π x
2π
4π
6π
y=cosx
2
2
x
2
O
2
2
-1
2
2
2
t
2.
世
界
上
有
许
多事 p
1 2
5730
y
1
ysinx,x[0,2
3
π
2
2π
O
x
2
-1
思考4:观察函数y=sinx在[0,2π]内的图 象,其形状、位置、凸向等有何变化规 律?
思考5:在函数y=sinx,x∈[0,2π]的图 象上,起关键作用的点有哪几个?
y 1
O
-12Leabharlann 3π22π x
思考6:当x∈[2π,4π], [-2π,0],… 时,y=sinx的图象如何?
例1 用“五点法”画出下列函数的 简图:
(1)y=1+sinx,x∈[0,2π]; (2)y=-cosx,x∈[0,2π] .
x
02
3
22
sinx 0 1 0 -1 0
1+sinx 1 2 1 0 1
y
2
y=1+sinx
1
3
π
2
2π
O
x
-1
2
x
02
cosx 1 0
-cosx -1 0
3
22 -1 0 1 1 0 -1
y 1
O
π
-1
2π x
知识探究(二):余弦函数的图象
思考1:观察函数y=x2与y=(x+1)2 的图 象,你能发现这两个函数的图象有什么内 在联系吗?
y
-1
o
x
思 考 2: 一 般 地 , 函 数 y=f(x + a)(a>0) 的 图象是由函数y=f(x)的图象经过怎样的 变换而得到的?
向左平移a个单位.
y
y=-cosx
1
3
2 2π
O
π
x
-1
2
例2 当x∈[0,2π]时,求不等式
co s x 1 的解集.
2
y
1
O
-1
2
y
1
2
π
2π x
2
[0, ] [5 ,2 ]
3
3
小结作业
1.正、余弦函数的图象每相隔2π个单位 重复出现,因此,只要记住它们在[0, 2π]内的图象形态,就可以画出正弦曲 线和余弦曲线.
思考3:设想由正弦函数的图象作出余弦 函数的图象,那么先要将余弦函数y=cosx 转化为正弦函数,你可以根据哪个公式 完成这个转化?
思考4:由诱导公式可知,y=cosx与 y sin(2 x) 是同一个函数,如何作函 数 y sin(2 x)在[0,2π]内的图象?
y
1
y=sinx
2
O -1
2
4.一个函数总具有许多基本性质,要直观、 全面了解正、余弦函数的基本特性,我 们应从哪个方面人手?
知识探究(一):正弦函数的图象 思考1:作函数图象最原始的方法是什么?
思考2:用描点法作正弦函数y=sinx在 [0,2π]内的图象,可取哪些点?
思考3:如何在直角坐标系中比较精确地 描出这些点,并画出y=sinx在[0,2π]内 的图象?
2.作与正、余弦函数有关的函数图象,是 解题的基本要求,用“五点法”作图是 常用的方法.
3.正、余弦函数的图象不仅是进一步研 究函数性质的基础,也是解决有关三角 函数问题的工具,这是一种数形结合的 数学思想.
作业:P34练习:2 P46习题1.4 A组: 1
1.4.2 正弦函数、余弦函数的性质 第一课时
-6π -4π -2π -5π -3π
y 1
-π
O
-1
π
3π 5π
2π 4π
6πx
思考7:函数y=sinx,x∈R的图象叫做正弦 曲线,正弦曲线的分布有什么特点?
-6π -4π -2π -5π -3π
y 1
-π
O
-1
π
3π 5π
2π 4π
6πx
思考8:你能画出函数y=|sinx|, x∈[0,2π]的图象吗?
π
2π x
思考5:函数y=cosx,x∈[0,2π]的图象 如何?其中起关键作用的点有哪几个?
y 1
O
-1
2
π
2π x
2
思考6:函数y=cosx,x∈R的图象叫做余弦 曲线,怎样画出余弦曲线,余弦曲线的 分布有什么特点?
y
2
2
1 22
2
O
2
2
-1
2
2
2
x
2
2
理论迁移
知识探究(二):周期概念的拓展
思 考 1: 函 数 f(x)=sinx ( x≥0 ) 是 否 为 周期函数?函数f(x)=sinx(x≤0)是否 为周期函数?
思考2:函数f(x)=sinx(x>0)是否为周 期函数?函数f(x)=sinx(x≠3kπ)是 否为周期函数?
思 考 3: 函 数 f(x)=sinx,x∈[0 , 10π] 是 否为周期函数?周期函数的定义域有什么 特点?
思考4:周期函数的周期是否惟一?正弦函 数的周期有哪些?
思考5:如果在周期函数f(x)的所有周期 中存在一个最小的正数, 则这个最小正 数叫做f(x)的最小正周期.那么, 正弦函 数的最小正周期是多少?为什么?
思考6:就周期性而言,对正弦函数有什 么结论?对余弦函数呢?
正 、 余 弦 函 数 是 周 期 函 数 ,2kπ (k∈Z, k≠0)都是它的周期,最小 正周期是2π.
思考2:设f(x)=sinx,则sin(x2k)sinx
可以怎样表示?其数学意义如何?
思考3:为了突出函数的这个特性,我们把 函数f(x)=sinx称为周期函数,2kπ为这 个函数的周期.一般地,如何定义周期函 数?
对于函数f(x),如果存在一个非零 常数T,使得当x取定义域内的每一个 值 时 , 都 有 f(x+T)=f(x), 那 么 函 数 f(x)就叫做周期函数,非零常数T就叫 做这个函数的周期.
1.4 三角函数的图象与性质 1.4.1正弦函数、余弦函数的图象
问题提出
t
p
1 2
5730
1.在单位圆中,角α的正弦线、余弦线分
别是什么?
y
sinα=MP
P(x,y)
cosα=OM
OM x
2.任意给定一个实数x,对应的正弦值 (sinx)、余弦值(cosx)是否存在?惟一?
3.设实数x对应的角的正弦值为y,则对应 关系y=sinx就是一个函数,称为正弦函 数;同样y= cosx也是一个函数,称为余 弦函数,这两个函数的定义域是什么?
物
都
呈
现
“
周
而
复
始
”
的变化规律,如年有四季更替,月有阴晴
圆缺.这种现象在数学上称为周期性,在
函数领域里,周期性是函数的一个重要
性质.
知识探究(一):周期函数的概念
思考1:由正弦函数的图象可知, 正弦曲 线每相隔2π个单位重复出现, 这一规律 的理论依据是什么?
. s in (x 2 k) s in x (k Z )
