2024届成都市零诊考试范围
2024届成都七中高二零诊模拟考试试卷(全科)24届高二文科数学零诊模拟考试试卷答案
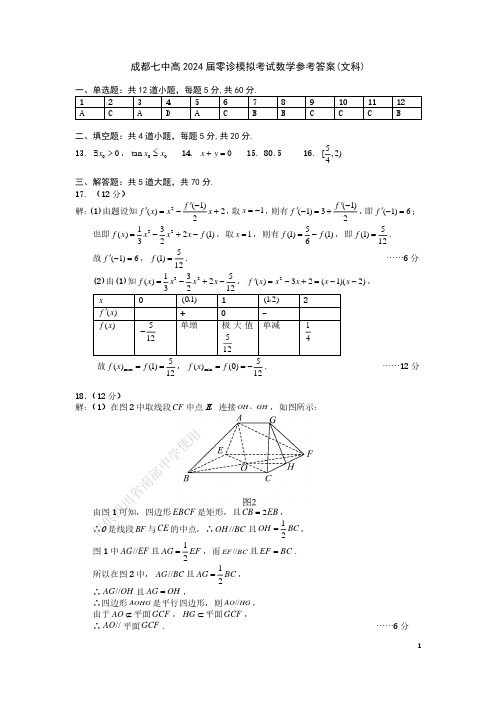
1成都七中高2024届零诊模拟考试数学参考答案(文科)二、填空题:共4道小题,每题5分,共20分.13. 00x ∃>,00tan x x ≤ 14. 0x y += 15. 80.5 16. 5[,2)4三、解答题:共5道大题,共70分. 17. (12分)解:(1)由题设知2(1)()22f f x x x '−'=−+,取1x =−,则有(1)(1)32f f '−'−=+,即(1)6f '−=; 也即3213()2(1)32f x x x x f =−+−,取1x =,则有5(1)(1)6f f =−,即5(1)12f =.故(1)6f '−=,5(1)12f =. ……6分(2)由(1)知32135()2f x x x x =−+−,2()32(1)(2)f x x x x x '=−+=−−,故max ()(1)12f x f ==,min ()(0)12f x f ==−. ……12分CF 中点H ,连接OH GH 、,如图所示:EBCF 是矩形,且2CB EB =,的中点,∴//OH BC 且12OH BC =,12EF ,而//EF BC 且EF BC =.BC 且12AG BC =,,是平行四边形,则//AO HG , HG ⊂平面GCF ,学使用四川省南部中学使用仅供2224t tt−=+,解得2,1()3t t==或舍去.故t的取值为23. ……12分21.(12分)解:(1)由()xf x e ax=−知()xf x e a'=−,1)当a e≤时,且有[1,)x∈+∞,()0f x'≥,()f x单增,故无极值;2)当a e>时,有(1,ln)x a∈,()0f x'<,()f x单减,而(ln,)x a∈+∞,()0f x'>,()f x单增,故()(ln)lnf x f a a a a==−极小值,()f x无极大值.综上,当a e≤时,()f x无极值;当a e>时,()f x极小值为lna a a−,()f x无极大值. ……4分(2)由(1)可知()1xf x e'=−,即有1111lntt t tλλ+>+−−,整理可令得(1)(1)()ln01tF t ttλλ+−=−>+, ……6分而22221(1)(1)(1)()(1)(1)t tF tt t t tλλλλ+−−'=−=++,……7分 1)当1λ≥时,且(1,)t∈+∞,有22(1)()0(1)tF tt tλ−'≥>+,()F t单增,()(1)0F t F>=,满足题设;……9分 2)当01λ<<时,且21(1,)tλ∈,有()0F t'<,()F t单减,()(1)0F t F<=,不满足题设;……11分综上,λ的取值范围为[1,)+∞. ……12分22.(10分)解:(1)由2sin2cosaρθθ=+,得22sin2cosaρρθρθ=+,故曲线的直角坐标方程为,即222()(1)1x a y a−+−=+;由sin()4πρθ−=,得sin cos2ρθρθ−=,故直线的直角坐标方程为. ……4分(2)点P的直角坐标为(2,0)−,在直线上,而直线的标准参数方程为(t为参数),将其代入,整理可得.由题设知222(3)4(44)2(1)0a a a∆=+−+=−>,解得.又,.当1,1a a>−≠且时,有12,0t t>,则1212||||||||3)PM PN t t t t a+=+=+=+=解得2a=;当1a≤−时,有12t t≤,则1212||||||||||1|PM PN t t t t a+=+=−==−=,解得4a=−.故a的值为2或-4. ……10分C2222x y y ax+=+l2y x=+ll22xy⎧=−⎪⎪⎨⎪=⎪⎩2222x y y ax+=+()2440t t a−+++=1a≠12t t+=1244t t a=+仅供四川省南部中学使用3。
四川省成都市2024-2024学年高二下学期零诊模拟物理高频考点试题(一)(基础必刷)

四川省成都市2024-2024学年高二下学期零诊模拟物理高频考点试题(一)(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图,小滑块以初速度从倾角的固定光滑斜面底端A沿斜面向上滑动,同时从以初速度斜向上抛出一个小球,经滑块滑到斜面顶端B,恰好被小球水平击中。
滑块和小球均视为质点,空气阻力忽略不计,已知,,。
则下列说法正确的是( )A.小滑块的初速度B.小球的初速度C.小球从抛出到离斜面最远处所经历的时间为D.斜面AB的长度为第(2)题一个负电荷从电场中的B点由静止释放,只受电场力作用,沿电场线运动到A点,它运动的速度—时间图像,如图所示,则A、B两点所在区域的电场线分布情况可能是图中的( )A.B.C.D.第(3)题如图甲所示为一玩具起重机的电路示意图。
变压器为理想变压器,原、副线圈的匝数比为,电动机的内阻为,a、b两端输入如图乙所示的电压,电动机正常工作,使质量为的物体恰好以的速度匀速上升,此时灯泡正常发光。
理想电流表的示数为,忽略一切阻力,。
下列说法正确的()A.原线圈输入电压瞬时值的表达式为B.灯泡的功率为C.电动机消耗的电功率为D.若电动机被卡住,灯泡会变亮第(4)题从1907年起,美国物理学家密立根就开始以精湛的技术测量光电效应中几个重要的物理量。
他通过如图甲所示的实验装置测量某金属的遏止电压U e与入射光频率,作出如图乙所示的图像,图像与横轴的交点坐标为(a,0),其反向延长线与纵轴的交点坐标为(0,-b),由此算出普朗克常量h。
并与普朗克根据黑体辐射测出的h相比较,以检验爱因斯坦光电效应方程的正确性。
下列说法正确的是( )A.入射光的频率越大,a的值越大B.入射光的频率越大,b的值越大C.图甲中极板A连接电源的正极D.由乙图可求出普朗克常量第(5)题如图所示,实线是沿x轴传播的一列简谐横波在t=0时刻的波形图,虚线是这列波在时刻的波形图。
四川省成都市2024-2024学年高二下学期零诊模拟全真演练物理试题(一)(基础必刷)

四川省成都市2024-2024学年高二下学期零诊模拟全真演练物理试题(一)(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图甲所示为家用燃气灶点火装置的电路原理图,转换器将直流电压转换为图乙所示的正弦交流电加在理想变压器的原线圈上,设变压器原、副线圈的匝数分别为n1、n2。
当两点火针间电压大于5000V就会产生电火花进而点燃燃气,闭合S,下列说法正确的是( )A.电压表的示数为50VB.在正常点燃燃气的情况下,两点火针间电压的有效值一定大于5000VC.当时,才能点燃燃气D.当时,点火针每个周期的放电时间为第(2)题如图所示,真空中一束复色光a沿AO方向射入半圆形玻璃柱体横截面的顶端O,经玻璃折射成b、c两束光。
下列说法正确的是( )A.玻璃对b光的折射率比c大B.在玻璃中,b光的传播速度比c大C.b光的光子能量比c小D.逐渐增大a光的入射角,b光先发生全反射第(3)题如图所示,正方形四个顶点各固定一个点电荷,等量同种负电荷固定在两点;等量同种正电荷固定在两点,是正方形的中心。
现将点处电荷沿方向移至无穷远处,规定无穷远处电势为零,则( )A.移动前,点的电势大于零B.移动过程中,点电场强度一直减少C.移动过程中,点处电荷所受静电力先减小后增大D.移到无穷远处时,点的电势小于零第(4)题2018年12月27日,北斗三号基本系统已完成建设,开始提供全球服务。
其导航系统中部分卫星运动轨道如图所示:a为低轨道极地卫星,b为地球同步卫星,c为倾斜轨道卫星,其轨道平面与赤道平面有一定的夹角,c的周期与地球自转周期相同。
下列说法正确的是( )A.卫星a的线速度比卫星c的线速度小B.卫星b的向心加速度比卫星c的向心加速度大C.卫星b和卫星c的线速度大小相等D.卫星a的机械能一定比卫星b的机械能大第(5)题物理学中有一些经典实验通过巧妙的设计使用简陋的器材揭示了深刻的物理本质。
四川省成都市2024-2024学年高二下学期零诊模拟全真演练物理试题(一)

四川省成都市2024-2024学年高二下学期零诊模拟全真演练物理试题(一)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题某静止的原子核发生核反应且释放出能量Q。
其方程为,并假设释放的能量全都转化为新核Y和Z的动能,其中Z的速度为v,以下结论正确的是( )A.Y原子核的动能是Z原子核的动能的倍B.Y原子核的速度大小为C.Y原子核和Z原子核的质量之和比X原子核的质量大(为光速)D.秦山核电站产生的核能与该核反应属于同种类型第(2)题中科院近代物理所将原子核加速后轰击原子核,成功合成了超重元素并同时释放出某种粒子,该粒子为( )A.中子B.质子C.电子D.氦核第(3)题我国空降部队在抗震救灾过程中多次建立功勋,这与伞兵们平时严格的训练是分不开的。
一伞兵从高空悬停的直升机上无初速度下落,5s后打开降落伞。
规定竖直向下为正方向,其沿竖直方向运动的图像如图所示,下列说法正确的是( )A.0~5s内伞兵处于完全失重状态B.5~9s内,伞兵处于超重状态C.伞兵下落50m时速度小于D.5~9s内伞兵所受的合力越来越大第(4)题如图所示,是边长为L的等边三棱镜,一束单色光照射在边上的D点,入射角为45°,折射光线在面的反射光照射到面的E点(图中未标出)。
不考虑光在面的反射,已知三棱镜对该光的折射率为,光在真空中的传播速度为c,则下列说法正确的是( )A.光有可能在面上发生全反射B.光从D点传播到E点所用时间为C.保持入射方向不变,入射点从D点向下移,光从D点传播到面所用时间一定不变D.保持入射点不变,将入射角略增大一些,光从D点传播到面所用时间可能变短第(5)题在农田灌溉中往往需要扩大灌溉面积,常用的方法是在水管的末端加装一段细管,如图所示。
保持细管水平且高度不变,农田水平,不考虑空气阻力的影响,单位时间内的进水量不变,下列说法正确的是( )A.加装细管后,单位时间内的出水量将显著增加B.加装细管后,喷出的水的出口速度不变C.加装细管后,喷出的水在空中运动的时间将变长D.加装细管后,喷出的水的水平射程将变大第(6)题如图所示,在第IV象限内有垂直坐标平面向外的匀强磁场,一对比荷之比为的正、负带电粒子在坐标平面内以相同的速率沿与x轴成角的方向从坐标原点射入磁场。
四川省成都市2024-2024学年高二下学期零诊模拟全真演练物理试题(一)(基础必刷)
四川省成都市2024-2024学年高二下学期零诊模拟全真演练物理试题(一)(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
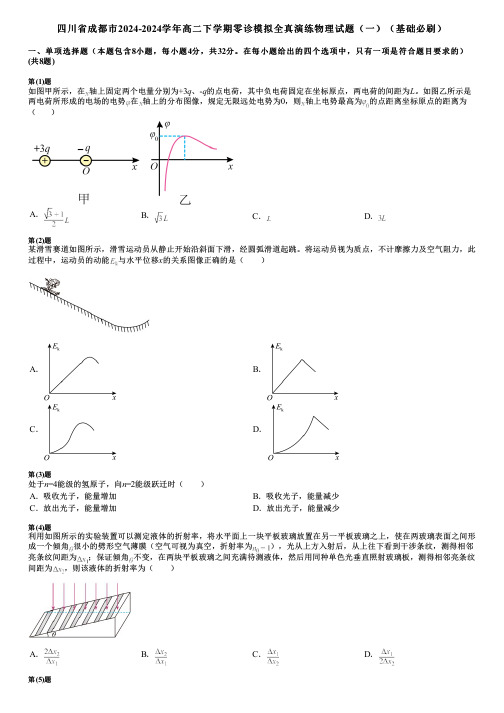
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题如图甲所示,在轴上固定两个电量分别为+3q、-q的点电荷,其中负电荷固定在坐标原点,两电荷的间距为L。
如图乙所示是两电荷所形成的电场的电势在轴上的分布图像,规定无限远处电势为0,则轴上电势最高为的点距离坐标原点的距离为()A.B.C.D.第(2)题某滑雪赛道如图所示,滑雪运动员从静止开始沿斜面下滑,经圆弧滑道起跳。
将运动员视为质点,不计摩擦力及空气阻力,此过程中,运动员的动能与水平位移x的关系图像正确的是( )A.B.C.D.第(3)题处于n=4能级的氢原子,向n=2能级跃迁时( )A.吸收光子,能量增加B.吸收光子,能量减少C.放出光子,能量增加D.放出光子,能量减少第(4)题利用如图所示的实验装置可以测定液体的折射率,将水平面上一块平板玻璃放置在另一平板玻璃之上,使在两玻璃表面之间形成一个倾角很小的劈形空气薄膜(空气可视为真空,折射率为),光从上方入射后,从上往下看到干涉条纹,测得相邻亮条纹间距为;保证倾角不变,在两块平板玻璃之间充满待测液体,然后用同种单色光垂直照射玻璃板,测得相邻亮条纹间距为,则该液体的折射率为( )A.B.C.D.第(5)题核电站发电原理是核裂变反应所释放的能量通过热力产生电能.铀235是核电站的主要核燃料,核反应堆在工作时,铀235既发生裂变,也发生衰变.铀235裂变方程为:,衰变方程为:,则下列说法正确的是()A.衰变产生的新核Y不再具有放射性B.的比结合能小于的比结合能C.衰变过程是通过吸收裂变过程释放的能量进行的D.反应堆中镉棒插入深一些将会加快核反应速度第(6)题2023年10月6日,杭州第19届亚运会艺术体操个人全能资格赛暨个人团体决赛在黄龙体育中心体育馆举行,中国队获团体铜牌。
2024届成都七中高二零诊模拟考试试卷(全科)24届高二理科数学零诊模拟考试试卷
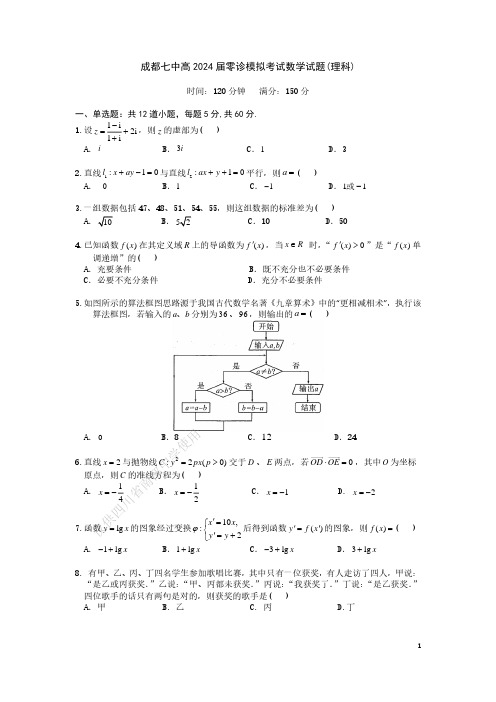
1成都七中高2024届零诊模拟考试数学试题(理科)时间:120分钟 满分:150分一、单选题:共12道小题,每题5分,共60分.1.设1i 2i 1iz −=++,则z 的虚部为( ) A .i B .3i C .1 D .32.直线1:10l x ay +−=与直线2:10l ax y ++=平行,则a =( )A . 0B .1C .1−D .11−或3.一组数据包括47、48、51、54、55,则这组数据的标准差为( )AB. C .10 D .504.已知函数()f x 在其定义域R 上的导函数为()f x ',当x R ∈ 时,“()0f x '>”是“()f x 单调递增”的( )A .充要条件B .既不充分也不必要条件C .必要不充分条件D .充分不必要条件5.如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减相术”,执行该算法框图,若输入的a b 、分别为36、96,则输出的a =( )A .0B .8C .12D .246.直线2x =与抛物线2:2(0)C y px p =>交于D 、E 两点,若0OD OE ⋅=,其中O 为坐标原点,则C 的准线方程为( ) A .14x =− B .12x =− C .1x =− D. 2x =−7.函数lg y x =的图象经过变换10,:2x x y y ϕ'=⎧⎨'=+⎩后得到函数()y f x ''=的图象,则()f x =( ) A .1lg x −+ B .1lg x + C .3lg x −+ D .3lg x +8. 有甲、乙、丙、丁四名学生参加歌唱比赛,其中只有一位获奖,有人走访了四人,甲说:“是乙或丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖.”四位歌手的话只有两句是对的,则获奖的歌手是( )A .甲 B. 乙 C. 丙 D.丁仅供四川省南部中学使用四川省南部中学使用仅供3三、解答题:共5道大题,共70分.17. (12分)设函数321(1)()2(1)34f f x x x x f '−=−+−, (1)求(1)f '−、(1)f 的值;(2)求()f x 在[0,2]上的最值.419.(12分)如图,三棱柱111ABC A B C −中,侧面11ACC A 为矩形,AB AC ⊥且2,AB AC D ==为11B C的中点,11AA B C ==.(1)证明:1AC //平面1A BD ;(2)求平面1AB C 与平面1AA D 所成锐二面角的余弦值.20. (12分)椭圆2222:1(0)x y C a b a b+=>>上顶点为B ,左焦点为F ,中心为O .已知T 为x 轴上动点,直线BT 与椭圆C 交于另一点D ;而P 为定点,坐标为(2,3)−,直线PT 与y 轴交于点Q .当T 与F 重合时,有||||PB PT =,且2BT BP BQ =+.(1)求椭圆C 的标准方程;(2)设T 的横坐标为t ,当(0,2)t ∈时,求△DTQ 面积的最大值.21.(12分)设函数()x f x e ax =−,其中a R ∈.(1)讨论函数()f x 在[1,)+∞上的极值;(2)若函数()f x 有两零点1x ,2x (1x <2x ),且满足1211x x λλ+>+,求正实数λ的取值范围.22.(10分)在平面直角坐标系中,以为极点,轴的正半轴为极轴,建立极坐标系,曲线和直线的极坐标方程分别为2sin 2cos a ρθθ=+和sin()4x πρ−=.且二者交于两个不同点.(1)写出曲线和直线的直角坐标方程; (2)若点的极坐标为,,求的值.xOy O x C l ,M N C l P ()2,πPM PN +=a 仅供四川省南部中学使用。
四川省成都市2024-2024学年高二下学期零诊模拟物理高频考点试题(一)(基础必刷)

四川省成都市2024-2024学年高二下学期零诊模拟物理高频考点试题(一)(基础必刷)一、单项选择题(本题包含8小题,每小题4分,共32分。
在每小题给出的四个选项中,只有一项是符合题目要求的)(共8题)第(1)题一列简谐横波沿x轴传播,图(a)是t=1.0s时的波形图,图(b)是x=3.0m处质点的振动图像,a、b两质点在x轴上平衡位置分别为x a=0.5m、x b=2.5m,下列说法正确的是( )A.波沿x轴正方向传播B.波的传播速度为0.5m/sC.t=1.0s时,a、b两质点加速度方向相反D.从t=1.0s到t=1.5s,质点a的路程10cm第(2)题2023年5月30日9时31分,搭载神舟十六号载人飞船的长征二号F遥十六运载火箭在酒泉卫星发射中心发射升空,飞船入轨后,于北京时间2023年5月30日16时29分,成功对接于空间站天和核心舱径向端口,18时22分,翘盼已久的神舟十五号航天员乘组顺利打开“家门”,欢迎远道而来的神舟十六号航天员乘组入驻“天宫”。
如图所示,已知空间站在距地球表面约400千米的高空绕地球做匀速圆周运动,地球半径约为6400km,地球同步卫星距地面高度约为36000km。
下列说法正确的是( )A.空间站绕地球做圆周运动的线速度略大于第一宇宙速度B.航天员在空间站中每天大约能看到6次日出C.空间站运行的向心加速度与地球表面附近重力加速度之比约为162:172D.空间站与地球同步卫星的线速度大小之比约为1:4第(3)题2023年12月15日我国在文昌航天发射场使用长征五号遥六运载火箭,成功将遥感四十一号卫星发射升空,卫星顺利进入预定轨道,该星是高轨光学遥感卫星.已知遥感四十一号卫星在距地面高度为h的轨道做圆周运动,地球的半径为R,自转周期为,地球表面的重力加速度为g,引力常量为G,忽略地球自转的影响,下列说法正确的是()A.遥感四十一号卫星绕地球做圆周运动的速度大于7.9km/sB.遥感四十一号卫星绕地球做圆周运动的向心加速度大于地球表面的重力加速度C.遥感四十一号卫星运行的周期为D.地球的密度为第(4)题原子核的比结合能是原子核稳定程度的量度,原子核的比结合能曲线如图所示,根据该曲线,下列说法正确的是( )A.原子核的结合能越大,原子核就越稳定B.核的结合能约为14 MeVC.一个重原子核衰变成α粒子和另一原子核,衰变产物的结合能之和一定大于原来重核的结合能D.核中核子的比结合能比核中核子的比结合能小第(5)题太阳放出的能量来自于()A.重核裂变B.天然衰变C.轻核聚变D.人工转变第(6)题某处地下有水平埋设的长直导线,现用图所示的闭合线圈和电流传感器探测导线的位置及其走向。
2024届四川省成都市高三零诊模拟考试数学(文)试题【含答案】

高2024届零诊模拟考试数学试题(文科)一、单选题:共12道小题,每题5分,共60分.1.直线1l :210x y +-=与直线2l:20ax y ++=平行,则=a ()A.12B.12-C.2D.2-A【分析】由两直线平行得到方程和不等式,求出答案.【详解】由题意得1120120a a ⨯-=⎧⎨⨯+≠⎩,解得12a =.故选:A 2.设1i2i 1iz -=++,则z 的虚部为()A.i B.3iC.1D.3C【分析】利用复数的除法及加减运算求解作答.【详解】依题意,(1i)(1i)2i2i=2i i 2i i (1i)(1i)2z ---=++=-+=+-,所以复数z 的虚部为1.故选:C3.一组数据包括47、48、51、54、55,则这组数据的标准差为() A.10 B.52C.10D.50A【分析】根据平均数、方差公式计算可得.【详解】依题意这组数据的平均数为4748515455515++++=,所以方差为()()()()()22222147514851515154515551105⎡⎤-+-+-+-+-=⎣⎦,则标准差为10.故选:A4.已知函数()f x 在其定义域R 上的导函数为()f x ',当x ∈R 时,“()0f x '>”是“()f x 单调递增”的()A.充要条件B.既不充分也不必要条件C.必要不充分条件D.充分不必要条件D【分析】根据充分条件、必要条件的定义判断即可.【详解】因为函数()f x 在其定义域R 上的导函数为()f x ',若当x ∈R 时,()0f x '>,则()f x 单调递增,故充分性成立;若()f x 在R 上单调递增,则()0f x '≥,如()3f x x =,显然函数()f x 在R 上单调递增,但是()230f x x '=≥,故必要性不成立;故“()0f x '>”是“()f x 单调递增”的充分不必要条件.故选:D5.圆C :22(1)(1)1x y -+-=与直线l :143x y+=的位置关系为()A.相切 B.相交C.相离D.无法确定A【分析】求出圆心坐标与半径,再将直线方程化为一般式,根据圆心到直线的距离即可判断.【详解】圆C :22(1)(1)1x y -+-=的圆心为()1,1C ,半径1r =,直线l :143x y+=即34120x y +-=,则圆心到直线的距离223412134d r +-===+,所以直线l 与圆C 相切.故选:A6.如图所示的算法框图思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该算法框图,若输入的a 、b 分别为36、96,则输出的=a ()A.0B.8C.12D.24C【分析】根据题意,由程序框图,逐步运算,即可得出结果.【详解】第一步:初始值36a =,96b =;此时a b ¹;进入循环;第二步:3696a =<,计算963660b =-=,此时3660≠,进入循环;第三步:3660a =<,计算603624b =-=,此时3624≠,进入循环;第四步:3624a =>,计算362412a =-=,此时1224≠,进入循环;第五步:1224a =<,计算241212b =-=,此时1212=,结束循环,输出12a =.故选:C.本题主要考查循环程序框图求输出值,属于基础题型.7.直线2x =与抛物线()2:20C y px p =>交于D 、E 两点,若0OD OE ⋅=,其中O 为坐标原点,则C 的准线方程为()A.14x =- B.12x =-C.=1x -D.2x =-B【分析】求出点D 、E 的坐标,根据0OD OE ⋅=求出p 的值,即可得出抛物线C 的准线方程.【详解】不妨设点D 在第一象限,则点E 在第四象限,联立222x y px =⎧⎨=⎩可得22x y p=⎧⎪⎨±⎪⎩,则点()2,2D p 、()2,2E p -,所以,440OD OE p ⋅=-= ,解得1p =,因此,C 的准线方程为122p x =-=-.故选:B.8.函数lg y x =的图象经过变换10:2x xy y ϕ''=⎧⎨=+⎩后得到函数()y f x ''=的图象,则()f x =()A.1lg x -+ B.1lg x+ C.3lg x-+ D.3lg x+B【分析】由已知可得出102x x y y ''⎧=⎪⎨⎪=-⎩,代入lg y x =可得出()f x '的表达式,即可得出()f x 的表达式.【详解】由已知可得102x x y y ''⎧=⎪⎨⎪=-⎩,代入lg y x =可得2lg lg 110x y x '''-==-,则lg 1y x ''=+,即()lg 1f x x ''=+,因此,()lg 1f x x =+.故选:B.9.有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或是丙获奖.”乙说:“甲、丙都未获奖.”丙说:“我获奖了.”丁说:“是乙获奖了.”四位歌手的话只有两句是对的,则获奖歌手是()A.甲 B.乙C.丙D.丁C【分析】逐一验证即可.【详解】若甲是获奖的歌手,则都说假话,不合题意若乙是获奖的歌手,则甲、乙、丁都说真话,丙说假话,不符合题意若丁是获奖的歌手,则甲、丁、丙都说假话,乙说真话,不符合题意故获奖的歌手是丙故选:C10.点A 、B 在以PC 为直径的球O 的表面上,且AB BC ⊥,2AB BC ==,已知球O 的表面积是12π,下列说法中正确的个数是()①BC ⊥平面PAB ;②平面PAC ⊥平面ABC ;③PB AC ⊥.A.0B.1C.2D.3C【分析】利用线面垂直的判定定理可判断命题①;取线段AC 的中点M ,连接OM ,利用球体的几何性质可得出OM ⊥平面ABC ,再利用中位线的性质结合面面垂直的判定定理可判断②;利用反证法可判断③.【详解】对于①,因为PC 为球O 的直径,B 为球O 上异于P 、C 的一点,所以,BC PB ⊥,又因为BC AB ⊥,PB AB B ⋂=,PB 、AB ⊂平面PAB ,所以,BC ⊥平面PAB ,①对;对于②,取线段AC 的中点M ,连接OM ,因为AB BC ⊥,则M 为ABC 外接圆的圆心,由球的几何性质可知OM ⊥平面ABC ,因为O 、M 分别为PC 、AC 的中点,则//OM PA ,则PA ⊥平面ABC ,又因为PA ⊂平面PAC ,因此,平面PAC ⊥平面ABC ,②对;对于③,因为PA ⊥平面ABC ,AC ⊂平面ABC ,所以,PA AC ⊥,若PB AC ⊥,且PA PB P = ,PA 、PB ⊂平面PAB ,则AC ⊥平面PAB ,因为AB ⊂平面PAB ,则AC AB ⊥,事实上,因为AB BC ⊥,且2AB BC ==,则ABC 为等腰直角三角形,且45BAC ∠= ,这与AC AB ⊥矛盾,假设不成立,故PB 与AC 不垂直,③错故正确命题为①②.故选:C.11.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请100名同学每人随机写下一个x ,y 都小于1的正实数对(),x y ;再统计两数能与1构成钝角三角形三边的数对(),x y 的个数m ;最后再根据统计数m 估计π的值,假如某次统计结果是28m =,那么本次实验可以估计π的值为().A.227B.4715C.7825D.5317C【分析】根据约束条件22110x y x y +>⎧⎨+-<⎩画出可行域,得到面积,根据几何概型得到答案.【详解】∵0101x y <<⎧⎨<<⎩而满足构成钝角三角形,则需22110x y x y +>⎧⎨+-<⎩画出图像:弓形面积:28π110042=-,∴78π25=.故选C本题考查了几何概型,画出图像是解题的关键,意在考查学生的综合应用能力.12.函数()25πlog sin f x x x =-零点个数为()A.4B.3C.2D.1B【分析】作出函数25πlogy x =、sin y x =的图象,观察两个函数图象的公共点个数,可得出结论.【详解】令()0f x =可得25πlog sin x x =,作出函数25πlogy x =、sin y x =的图象如下图所示:当5π2x >时,225π5π5πlog log 12x <=-,又因为1sin 1x -≤≤,所以,函数25πlog y x =、sin y x =在5π,2⎛⎫+∞ ⎪⎝⎭上的图象没有交点,观察图象可知,函数25πlogy x =、sin y x =的图象有三个交点,因此,函数()f x 的零点个数为3.故B.二、填空题:共4道小题,每题5分,共20分.13.命题“0x ∀>,tan x x >”的否定为________.00x ∃>,00tan x x ≤【分析】根据全称量词命题的否定为特称量词命题,即可得解.【详解】命题“0x ∀>,tan x x >”为全称量词命题,其否定为:00x ∃>,00tan x x ≤.故00x ∃>,00tan x x ≤14.函数()cos xf x x=的图象在πx =处的切线方程为________.0x y +=【分析】求出函数的导函数,即可求出切线的斜率,再利用点斜式求出切线方程.【详解】因为()cos xf x x=,则()πππcos πf ==-,2cos s ()cos in x x x x f x +'=,则()21cos si ππππc n os πf +'==-,所以切线方程为()()ππy x --=--,整理得0x y +=.故0x y +=15.某区为了解全区12000名高二学生的体能素质情况,在全区高二学生中随机抽取了1000名学生进行体能测试,并将这1000名的体能测试成绩整理成如下频率分布直方图.根据此频率分布直方图,这1000名学生平均成绩的估计值为________.80.5【分析】根据所有矩形面积之和为1求出a 的值,将每个矩形底边的中点值乘以对应矩形的面积,相加可得这1000名学生平均成绩.【详解】由于频率分布直方图中所有矩形面积之和为1,可得()0.0050.0220.04101a ++⨯+⨯=,解得0.015a =,由频率分布直方图可知,这1000名学生平均成绩的估计值为550.05650.15750.2850.4950.280.5⨯+⨯+⨯+⨯+⨯=分.故答案为80.516.双曲线H :22221(,0)x y a b a b -=>其左、右焦点分别为1F 、2F ,倾斜角为3π的直线2PF 与双曲线H 在第一象限交于点P ,设双曲线H 右顶点为A ,若226PF AF ≥,则双曲线H 的离心率的取值范围为________.5,24⎡⎫⎪⎢⎣⎭【分析】设2PF m =,则12PF a m =+,然后在12PF F △中利用余弦定理列方程可表示出m ,再由226PF AF ≥可求出离心率的范围【详解】设2PF m =,则12PF a m =+,因为直线2PF 的倾斜角为3π,所以212π3PF F ∠=,在12PF F △中,由余弦定理得2221212212212cos PF PF F F PF F F PF F =+-∠,2222π(2)(2)22cos3a m m c m c +=+-⋅,22224442a am m m c mc ++=++得22222c a m a c-=-,因为226PF AF ≥,所以22226()2c a c a a c-≥--得32c a a c +≥-,4502c aa c -≥-,所以(45)(2)020c a a c a c --≥⎧⎨-≠⎩,所以(45)(2)020e e e --≥⎧⎨-≠⎩,解得524e ≤<,即双曲线H 的离心率的取值范围为5,24⎡⎫⎪⎢⎣⎭故5,24⎡⎫⎪⎢⎣⎭关键点睛:此题考查求双曲线的离心率的范围,考查直线与双曲线的位置关系,解题的关键是根据题意在12PF F △中利用余弦定理表示出2PF ,然后代入已知条件中可求得结果,考查数学转化思想,属于较难题.三、解答题:共5道大题,共70分.17.设函数321(1)()2(1)34f f x x x x f '-=-+-,(1)求(1)f ¢-、(1)f 的值;(2)求()f x 在[0,2]上的最值.(1)(1)6f '-=,5(1)12f =(2)max 5()12=f x ,min 5()12=-f x 【分析】(1)求出函数的导函数,令=1x -求出(1)f ¢-,再令1x =求出()1f ;(2)由(1)可得32135()23212f x x x x =-+-,利用导数求出函数的单调性,即可求出函数的极值,再由区间端点的函数值,即可得解.【小问1详解】因为321(1)()2(1)34f f x x x x f '-=-+-,所以2(1)()22f f x x x '-'=-+,取=1x -,则有(1)(1)32f f '-'-=+,即(1)6f '-=;所以3213()2(1)32f x x x x f =-+-,取1x =,则有5(1)(1)6f f =-,即5(1)12f =.故(1)6f '-=,5(1)12f =.【小问2详解】由(1)知32135()23212f x x x x =-+-,[]0,2x ∈,则2()32(1)(2)f x x x x x '=-+=--,所以x 、()f x '与()f x ,[]0,2x ∈的关系如下表:x(0,1)1(1,2)2()f x '+-()f x 512-单调递增极大值512单调递减14故max 5()(1)12f x f ==,min 5()(0)12f x f ==-.18.如图1,E 、F 、G 分别是边长为4的正方形的三边AB 、CD 、AD 的中点,先沿着虚线段FG 将等腰直角三角形FDG 裁掉,再将剩下的五边形ABCFG 沿着线段EF 折起,连接AB 、CG 就得到了一个空间五面体,如图2.(1)若O 是四边形EBCF 对角线的交点,求证://AO 平面GCF ;(2)若2π3AEB ∠=,求三棱锥A BEF -的体积.(1)证明见解析(2)433【分析】(1)在图2中取线段CF 中点H ,连接OH 、GH ,证明出四边形AOHG 是平行四边形,可得出//AO HG ,再利用线面平行的判定定理可证得结论成立;(2)证明出EF ⊥平面ABE ,计算出ABE 的面积,利用锥体的体积公式可求得三棱锥A BEF -的体积.【小问1详解】证明:在图2中取线段CF 中点H ,连接OH 、GH ,如图所示:由图1可知,四边形EBCF 是矩形,且2CB EB =,因为O 是线段BF 与CE 的中点,所以,//OH BC 且12OH BC =,在图1中,//AG EF 且12AG EF =,而//EF BC 且EF BC =.所以在图2中,//AG BC 且12AG BC =,所以,//AG OH 且AG OH =,所以,四边形AOHG 是平行四边形,则//AO HG ,由于AO ⊄平面GCF ,HG ⊂平面GCF ,所以,//AO 平面GCF .【小问2详解】解:翻折前,EF AE ⊥,EF BE ⊥,翻折后,则EF AE ⊥,EF BE ⊥,AE 、BE ⊂面ABE ,AE BE E =I ,所以,EF ⊥平面ABE ,因为12π13sin 2232322ABE S AE BE =⋅⋅=⨯⨯⨯=△,所以114334333A BEF F ABE ABE V V S EF --==⋅=⨯⨯=,即三棱锥A BEF -的体积为433.19.信创产业即信息技术应用创新产业,是一条规模庞大、体系完整的产业链,是数字经济的重要抓手之一.在政府、企业等多方面的共同努力下,中国信创产业市场规模不断扩大,市场释放出前所未有的活力.下表为2018—2022年中国信创产业规模(单位:千亿元),其中2018—2022年对应的代码依次为1~5.年份代码x12345中国信创产业规模y /千亿元8.19.611.513.816.7(1)从2018—2022年中国信创产业规模中任取2个数据,求这2个数据都大于10的概率.(2)由上表数据可知,可用指数型函数模型x y a b =⋅拟合y 与x 的关系,请建立y 关于x 的回归方程(a ,b 的值精确到0.01),并预测2023年中国信创产业规模能否超过20千亿元.参考数据:v51i ii x v=∑ 1.919e 0.177e 61.192.4538.526.811192.84其中ln i i v y =,5115i i v v ==∑.参考公式:对于一组数据()11,u w ,()22,u w ,…,(),n n u w ,其回归直线 wu αβ=+的斜率和截距的最小二乘估计公式分别为 1221ni ii ni i u w nuwu nu β==-=-∑∑, w u αβ=+.(1)310(2) 6.811.19x y =⨯,不会超过20千亿元.【分析】(1)根据古典概型概率计算公式,利用列举法可得2个数据都大于10的概率为310;(2)将指数型函数模型x y a b =⋅两边取对数可得ln ln ln y a x b =+,即ln ln v a x b =+,再利用参考数据可得回归方程为 6.811.19x y =⨯,将2023年的年份代码6代入可得19.3420y ≈<$,即可得出结论.【小问1详解】从2018—2022年中国信创产业规模中任取2个数据有()8.1,9.6,()8.1,11.5,()8.1,13.8,()8.1,16.7,()9.6,11.5,()9.6,13.8,()9.6,16.7,()11.5,13.8,()11.5,16.7,()13.8,16.7,共10种情况.其中这2个数据都大于10的有()11.5,13.8,()11.5,16.7,()13.8,16.7,共3种情况,所以2个数据都大于10的概率310P =.【小问2详解】x y a b =⋅两边同时取自然对数,得()ln ln ln ln xy a ba xb =⋅=+,则ln ln v a x b =+.因为3x =, 2.45v =,52155ii x==∑,所以5152221538.5253 2.45ln 0.17755535i i i ii x v xvb xx==--⨯⨯===-⨯-∑∑,ln ln 2.450.1773 1.919a v x b =-⋅=-⨯=,所以 1.9190.177vx =+ ,即 ln 1.9190.177y x =+,所以 1.9190.177e 6.81 1.19x x y +==⨯$,即y 关于x 的回归方程为 6.811.19x y =⨯.2023年的年份代码为6,把6x =代入 6.811.19x y =⨯,得 66.811.19 6.81 2.8419.3420y =⨯=⨯≈<,所以预测2023年中国信创产业规模不会超过20千亿元.20.椭圆()2222:10x y C a b a b+=>>上顶点为B ,左焦点为F ,中心为O .已知T 为x 轴上动点,直线BT与椭圆C 交于另一点D ;而P 为定点,坐标为()2,3-,直线PT 与y 轴交于点Q .当T 与F 重合时,有PB PT = ,且2BT BP BQ =+.(1)求椭圆C 的标准方程;(2)设T 的横坐标为t ,且(0,1)t ∈,当DTQ △面积等于35时,求t 的取值.(1)22143x y +=(2)23【分析】(1)由2BT BP BQ =+结合平面向量的坐标运算可求得c 的值,由PB PT = 结合平面内两点间的距离公式可求出b 的值,进而可求得a 的值,由此可得出椭圆C 的标准方程;(2)将直线BT 的方程与椭圆C 的方程联立,求出点D 的纵坐标,写出直线PT 的方程,可得出点Q 的纵坐标,由()33DTQ Q D PTBS y y S ⋅-=⋅△△可得出22234DTQt t S t -=⋅+△,再结合DTQ △面积等于35可求得t 的值.【小问1详解】解:设(,0)F c -,由2BT BP BQ =+知2202c -=-+=-,即1c =,由PB PT =知2222(20)(3)[2(1)](30)b --+-=---+-,即3b =,则222a b c =+=,故椭圆C 的标准方程为22143x y +=.【小问2详解】解:直线BT 的方程为(3)3t x y =--,联立22(3)3143t x y x y ⎧=--⎪⎪⎨⎪+=⎪⎩联立可得()22224233120t y t y t +-+-=,且()()42212443121920t t t ∆=-+-=>,,所以,2231234D t y t -⋅=+,即()22344D t y t -=+,直线PT 的方程为22(3)3t x y ++=--,令0x =,可得32Q ty t =+,由()sin sin 33DTQ Q D PTBS y y QT DT DTQ QT DT S PT BT BTPPT BT⋅-⋅⋅∠⋅===⋅⋅∠⋅⋅△△知3Q D DTQ PTBy y S S =-△△,即22234DTQt t S t -=⋅+△,(0,1)t ∈,而2223345t t t -⋅=+,解得23t =,或1t =(舍去),故t 的取值为23.21.设函数()e x f x ax =-,其中R a ∈.(1)讨论函数()f x 在[1,)+∞上的极值;(2)若1a =,设()f x '为()f x 的导函数,当1t >时,有11(ln )(ln )ln f t f t tλλ+>+''-,求正实数λ的取值范围.(1)答案见解析(2)[1,)+∞【分析】(1)求出函数的导函数,分e a ≤、e a >两种情况讨论,分别求出函数的单调性,即可得到函数的极值;(2)依题意可得1111ln t t t t λλ+>+--,整理得(1)(1)ln 01t t t λλ+-->+,令(1)(1)()ln 1t F t t t λλ+-=-+,()1,t ∈+∞,求出函数的导函数,分1λ≥、01λ<<两种情况讨论,结合函数的单调性,即可得解.【小问1详解】由()e x f x ax =-知()e '=-x f x a ,①当e a ≤时,且有[1,)x ∈+∞,()0f x '≥,()f x 单调递增,故无极值;②当e a >时,有(1,ln )x a ∈,()0f x '<,()f x 单调递减,而(ln ,)x a ∈+∞,()0f x '>,()f x 单调递增,故()(ln )ln f x f a a a a ==-极小值,()f x 无极大值.综上,当e a ≤时,()f x 无极值;当e a >时,()f x 极小值为ln a a a -,()f x 无极大值.【小问2详解】当1a =时由(1)可知()e 1x f x '=-,即有1111ln t t t tλλ+>+--,由1t >整理可得(1)(1)ln 01t t t λλ+-->+,令(1)(1)()ln 1t F t t t λλ+-=-+,()1,t ∈+∞,所以()22221(1)1(1)()(1)(1)t t F t t t t t λλλλ--+'=-=++,①当1λ≥时,且(1,)t ∈+∞,有22(1)()0(1)t F t t t λ-'≥>+,()F t 单调递增,()(1)0F t F >=,满足题设;②当01λ<<时,且当211,t λ⎛⎫∈ ⎪⎝⎭,有()0F t '<,()F t 单调递减,()(1)0F t F <=,不满足题设;综上,λ的取值范围为[1,)+∞.22.在平面直角坐标系xOy 中,以O 为极点,x 轴的正半轴为极轴,建立极坐标系,曲线C 和直线l 的极坐标方程分别为2sin 2cos a ρθθ=+和:πsin 24x ρ⎛⎫-= ⎪⎝⎭.且二者交于M ,N 两个不同点.(1)写出曲线C 和直线l 的直角坐标方程;(2)若点P 的极坐标为(2,π),||||52PM PN +=,求a 的值.(1)()()2221+1-+-=x a y a ,2y x =+(2)2或4-【分析】(1)利用极坐标与平面直角坐标方程互化公式进行求解;(2)先判断出P 的直角坐标为(2,0)-,在直线l 上,写出直线l 的标准参数方程,代入曲线的普通方程中,得到1a ≠,分1a >-且1a ≠,1a ≤-两种情况,列出方程,求出答案.【小问1详解】由2sin 2cos a ρθθ=+,得22sin 2cos a ρρθρθ=+,故曲线C 的直角坐标方程为2222x y y ax +=+,即222()(1)1x a y a -+-=+;由πsin 24ρθ⎛⎫-= ⎪⎝⎭,得sin cos 2ρθρθ-=,故直线l 的直角坐标方程为2y x =+.【小问2详解】因为π2,2sin π02cos =-=,所以点P 的直角坐标为(2,0)-,在直线l 上,而直线l 的标准参数方程为22222x t y t ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数),将其代入2222x y y ax +=+,整理可得2(322)440t a t a -+++=.由题设知222(3)4(44)2(1)0a a a ∆=+-+=->,解得1a ≠.又12322t t a +=+,1244t t a =+.当1a >-,且1a ≠时,有1t ,20t >,则1212||||2(3)52PM PN t t t t a +=+=+=+=,解得2a =,满足要求;当1a ≤-时,有120t t ≤,则()()212122121||||21524PM PN t t t t t t t a t +=+==--+-==,解得4a =-,满足要求.故a 的值为2或4-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、语文
课内外兼顾,课内涉及教材的内容以必修1至必修5(侧重必修4、5的内容)、选修IA(《中外传记作品选读》)所学内容为限。
2、数学(理)
人教A版必修1 2 3、4 5;选修2-1,选修2-2,选修4-4。
其中高一内容只涉及集合、函数、立体几何、解析几何相关部分。
3、数学(文)
人教A版必修1、2、3、4、5;选修1-1,选修1-2,选修4-4。
其中高一内容只涉及集合、函数、立体几何,解析几何相关部分。
4、英语
外研版新标准高中英语Book1至Book6Module6的内容。
5、物理
《普通高中课程标准实验教科书》选修3-1、3-2:3-3或3-4;选修3-5的第二、
三、四章。
6、化学
人教版课标教材《化学1》、《化学2》及《化学反应原理》(选生物题6的全部课题,专题5中的课题3。
人教版必修1全部内容,选修1中的专题1、专题2、专题4、专修4)全册。
7、历史
人民版课标教材《历史》必修1、2、3中的世界历史部分和选修1、3、4中的世界历史部分的内容。
8、政治
《生活与哲学》、《文化生活》,以《生活与哲学》为主。
9、地理
中国地理、世界地理;高中地理必修一:1、2单元;选修地理:旅游地理。
