(完整版)导数解曲线公切线问题
如何用导数解决与切线有关的问题

即:a=4
4.已知曲线 C: y=x3-3x2+2x, 直线 l: y=kx, 且直线 l 与 曲线
C 相切于点 (x0, y0)(x00), 求直线 l 的方程及切点坐标. y0 解: 由直线 l 过点(x0, y0),其斜率 k= x , 0 ∵点 (x0, y0) 在曲线 C 上, ∴y0=x03-3x02+2x0. y0 ∴ x =x02-3x0+2. 又 y=3x2-6x+2, 0 ∴在点 (x0, y0) 处曲线 C 的切线斜率 k=y|x=x0. ∴x02-3x0+2=3x02-6x0+2. 整理得 2x02-3x0=0. 解得 x0= 3 (∵x00). 2 3 1 这时 y0=- 8 , k=- 4 . 3 , - 3 ). 切点坐标是 ( ∴直线 l 的方程为 y=- 1 x , 8 2 4
曲线的切线问题,是高考的常见题型之 一,主要有以下几类问题: 一、求过曲线上某个定点处的切线
x 例1(2009全国卷Ⅱ理)曲线y= 在点 2x-1 (1,1)处的切线方程为 .
解
点(1,1)在曲线上. -1 因为y′= 2,在点(1,1)处的切线斜率 (2x-1) k=-1,所以切线方程为x+y-2=0.
2.导数运算及切线的理解应注意的问题
一是利用公式求导时要特别注意除法公式中分
子的符号,防止与乘法公式混淆. 二是直线与曲线公共点的个数不是切线的本质, 直线与曲线只有一个公共点,直线不一定是曲 线的切线,同样,直线是曲线的切线,则直线 与 曲 线 可 能 有 两 个 或 两 个 以 上 的 公 共 点 ,如 (4). 三是复合函数求导的关键是分清函数的结构形 式.由外向内逐层求导,其导数为两层导数之 积,如(9).
(完整版)利用导数求曲线的切线和公切线

利用导数求曲线的切线和公切线一.求切线方程【例1】.已知曲线f(x)=x3-2x2+1.(1)求在点P(1,0)处的切线l1的方程;(2)求过点Q(2,1)与已知曲线f(x)相切的直线l2的方程.提醒:注意是在某个点处还是过某个点!二.有关切线的条数【例2】.(2014•北京)已知函数f(x)=2x3﹣3x.(Ⅰ)求f(x)在区间[﹣2,1]上的最大值;(Ⅱ)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;(Ⅲ)问过点A(﹣1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)【解答】解:(Ⅰ)由f(x)=2x3﹣3x得f′(x)=6x2﹣3,令f′(x)=0得,x=﹣或x=,∵f(﹣2)=﹣10,f(﹣)=,f()=﹣,f(1)=﹣1,∴f(x)在区间[﹣2,1]上的最大值为.(Ⅱ)设过点P(1,t)的直线与曲线y=f(x)相切于点(x0,y),则y0=2﹣3x,且切线斜率为k=6﹣3,∴切线方程为y﹣y0=(6﹣3)(x﹣x),∴t﹣y0=(6﹣3)(1﹣x),即4﹣6+t+3=0,设g(x)=4x3﹣6x2+t+3,则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,等价于“g(x)有3个不同的零点”.∵g′(x)=12x2﹣12x=12x(x﹣1),∴g(0)=t+3是g(x)的极大值,g(1)=t+1是g(x)的极小值.∴g(0)>0且g(1)<0,即﹣3<t<﹣1,∴当过点过点P(1,t)存在3条直线与曲线y=f(x)相切时,t的取值范围是(﹣3,﹣1).(Ⅲ)过点A(﹣1,2)存在3条直线与曲线y=f(x)相切;过点B(2,10)存在2条直线与曲线y=f(x)相切;过点C(0,2)存在1条直线与曲线y=f(x)相切.【例3】.已知函数f(x)=lnax(a≠0,a∈R),.(Ⅰ)当a=3时,解关于x的不等式:1+e f(x)+g(x)>0;(Ⅱ)若f(x)≥g(x)(x≥1)恒成立,求实数a的取值范围;(Ⅲ)当a=1时,记h(x)=f(x)﹣g(x),过点(1,﹣1)是否存在函数y=h(x)图象的切线?若存在,有多少条?若不存在,说明理由.【解答】解:(I)当a=3时,原不等式可化为:1+e ln3x+>0;等价于,解得x,故解集为(Ⅱ)∵对x≥1恒成立,所以,令,可得h(x)在区间[1,+∞)上单调递减,故h(x)在x=1处取到最大值,故lna≥h(1)=0,可得a=1,故a的取值范围为:[1,+∞)(Ⅲ)假设存在这样的切线,设切点T(x,),∴切线方程:y+1=,将点T坐标代入得:即,①设g(x)=,则∵x>0,∴g(x)在区间(0,1),(2,+∞)上是增函数,在区间(1,2)上是减函数,故g(x)极大=g(1)=1>0,故g(x)极,小=g(2)=ln2+>0,.又g()=+12﹣6﹣1=﹣ln4﹣3<0,由g(x)在其定义域上的单调性知:g(x)=0仅在(,1)内有且仅有一根,方程①有且仅有一解,故符合条件的切线有且仅有一条.【作业1】.(2017•莆田一模)已知函数f (x )=2x 3﹣3x+1,g (x )=kx+1﹣lnx . (1)设函数,当k <0时,讨论h (x )零点的个数;三.切线与切线之间的关系 【例4】.(2018•绵阳模拟)已知a ,b ,c ∈R ,且满足b 2+c 2=1,如果存在两条互相垂直的直线与函数f (x )=ax+bcosx+csinx 的图象都相切,则a+c的取值范围是 .23a b c ++=则23b c +,∵b 2+c 2=1,∴sin ,cos b a ββ==设,∴235sin()b c βϕ+=+,故a+c ∈[﹣,],【例5】.已知函数f (x )=lnx ﹣a (x ﹣1),g (x )=e x ,其中e 为自然对数的底数. (Ⅰ)设,求函数t (x )在[m ,m+1](m >0)上的最小值;(Ⅱ)过原点分别作曲线y=f (x )与y=g (x )的切线l 1,l 2,已知两切线的斜率互为倒数,求证:a=0或.【解答】(Ⅰ)解:,令t'(x)>0得x>1,令t'(x)<0得x<1,所以,函数t(x)在(0,1)上是减函数,在(1,+∞)上是增函数,∴当m≥1时,t(x)在[m,m+1](m>0)上是增函数,∴当0<m<1时,函数t(x)在[m,1]上是减函数,在[1,m+1]上是增函数,∴t(x)min=t(1)=e.(Ⅱ)设l2的方程为y=k2x,切点为(x2,y2),则,∴x2=1,y2=e∴k2=e.由题意知,切线l1的斜率,∴切线l1的方程为,设l1与曲线y=f(x)的切点为(x1,y1),∴,∴,,又y1=lnx1﹣a(x1﹣1),消去y1,a后整理得,令,则,∴m(x)在(0,1)上单调递减,在(1,+∞)上单调递增,若x1∈(0,1),∵,,∴,而,在单调递减,∴.若x1∈(1,+∞),∵m(x)在(1,+∞)上单调递增,且m(e)=0,∴x1=e,∴综上,a=0或.【作业2】.(2017•黄山二模)已知函数f(x)=(ax2+x﹣1)e x+f'(0).(1)讨论函数f(x)的单调性;(2)若g(x)=e﹣x f(x)+lnx,h(x)=e x,过O(0,0)分别作曲线y=g(x)与y=h(x)的切线l1,l2,且l1与l2关于x轴对称,求证:﹣<a <﹣.四.求公切线的方程【例6】.(2018•安阳一模)已知函数,g(x)=3elnx,其中e为自然对数的底数.(Ⅰ)讨论函数f(x)的单调性.(Ⅱ)试判断曲线y=f(x)与y=g(x)是否存在公共点并且在公共点处有公切线.若存在,求出公切线l的方程;若不存在,请说明理由.【解答】解:(Ⅰ)由,得,令f′(x)=0,得.当且x≠0时,f′(x)<0;当时,f′(x)>0.∴f(x)在(﹣∞,0)上单调递减,在上单调递减,在上单调递增;(Ⅱ)假设曲线y=f(x)与y=g(x)存在公共点且在公共点处有公切线,且切点横坐标为x>0,则,即,其中(2)式即.记h(x)=4x3﹣3e2x﹣e3,x∈(0,+∞),则h'(x)=3(2x+e)(2x﹣e),得h(x )在上单调递减,在上单调递增,又h(0)=﹣e3,,h(e)=0,故方程h(x0)=0在(0,+∞)上有唯一实数根x=e,经验证也满足(1)式.于是,f(x0)=g(x)=3e,f′(x)=g'(x)=3,曲线y=g(x)与y=g(x)的公切线l的方程为y﹣3e=3(x﹣e),即y=3x.【作业3】.已知函数f (x)=lnx,g(x)=2﹣(x>0)(1)试判断当f(x)与g(x)的大小关系;(2)试判断曲线 y=f(x)和 y=g(x)是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;(3)试比较(1+1×2)(1+2×3)…(1+2012×2013)与 e4021的大小,并写出判断过程.五.与公切线有关的参数取值范围问题【例7】.已知函数f(x)=blnx,g(x)=ax2﹣x(a∈R).(Ⅰ)若曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,求实数a、b的值;(Ⅱ)当b=1时,若曲线f(x)与g(x)在公共点P处有相同的切线,求证:点P唯一;(Ⅲ)若a>0,b=1,且曲线f(x)与g(x)总存在公切线,求正实数a的最小值.【解答】解:(Ⅰ)f′(x)=,g'(x)=2ax﹣1.∵曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,∴,解得a=b=1.(Ⅱ)设P(x0,y),则由题设有lnx=ax2﹣x…①,又在点P有共同的切线,∴f′(x0)=g′(x),∴,∴a=,代入①得lnx0=x,设h(x)=lnx ﹣+x,则h′(x)=+(x>0),则h′(x)>0,∴h(x)在(0,+∞)上单调递增,所以 h(x)=0最多只有1个实根,从而,结合(1)可知,满足题设的点P只能是P(1,0).(Ⅲ)当a>0,b=1时,f(x)=lnx,f′(x)=,f(x)在点(t,lnt)处的切线方程为y﹣lnt=(x﹣t),即y=x+lnx﹣1.与y=ax2﹣x,联立得ax2﹣(1+)x﹣lnt+1=0.∵曲线f(x)与g(x)总存在公切线,∴关于t(t>0)的方程△=+4a(lnt﹣1)=0,即=4a(1﹣lnt)(*)总有解.若t>e,则1﹣lnt<0,而>0,显然(*)不成立,所以 0<t<e,从而,方程(*)可化为4a=.令H(t)=(0<t<e),则H′(t)=.∴当0<t<1时,h'(t)<0;当1<t<e时,h'(t)>0,即 h(t)在(0,1)上单调递减,在(1,e)上单调递增.∴h(t)在(0,e)上的最小值为h(1)=4,∴要使方程(*)有解,只须4a≥4,即a≥1.∴正实数a的最小值为1.【例8】.(2017•韶关模拟).已知函数f(x)=ae x(a≠0),g(x)=x2(Ⅰ)若曲线c1:y=f(x)与曲线c2:y=g(x)存在公切线,求a最大值.(Ⅱ)当a=1时,F(x)=f(x)﹣bg(x)﹣cx﹣1,且F(2)=0,若F(x)在(0,2)内有零点,求实数b的取值范围.【解答】解:(Ⅰ)设公切线l与c1切于点(x1,a)与c2切于点(x2,),∵f′(x)=ae x,g′(x)=2x,∴,由①知x2≠0,①代入②:=2x2,即x2=2x1﹣2,由①知a=,设g(x)=,g′(x)=,令g′(x)=0,得x=2;当x<2时g′(x)>0,g(x)递增.当x>2时,g′(x)<0,g(x)递减.∴x=2时,g(x)max =g(2)=,∴amax=.(Ⅱ)F(x)=f(x)﹣bg(x)﹣cx﹣1=e x﹣bx2﹣cx﹣1,∵F(2)=0=F(0),又F(x)在(0,2)内有零点,∴F(x)在(0,2)至少有两个极值点,即F′(x)=e x﹣2bx﹣c在(0,2)内至少有两个零点.∵F″(x)=e x﹣2b,F(2)=e2﹣4b﹣2c﹣1=0,c=,①当b≤时,在(0,2)上,e x>e0=1≥2b,F″(x)>0,∴F″(x)在(0,2)上单调增,F′(x)没有两个零点.②当b≥时,在(0,2)上,e x<e2≤2b,∴F″(x)<0,∴F″(x)在(0,2)上单调减,F′(x)没有两个零点;③当<b<时,令F″(x)=0,得x=ln2b,因当x>ln2b时,F″(x)>0,x<ln2b时,F″(x)<0,∴F″(x)在(0,ln2b)递减,(ln2b,2)递增,所以x=ln2b时,∴F′(x)最小=F′(ln2b)=4b﹣2bln2b﹣+,设G(b)=F′(ln2b)=4b﹣2bln2b﹣+,令G′(b)=2﹣2ln2b=0,得2b=e,即b=,当b<时G′(b)>0;当b>时,G′(b)<0,当b=时,G(b)最大=G()=e+﹣<0,∴G(b)=f′(ln2b)<0恒成立,因F′(x)=e x﹣2bx﹣c在(0,2)内有两个零点,∴,解得:<b <,综上所述,b 的取值范围(,).【作业4】.已知函数f(x)=a(x ﹣)﹣blnx(a,b∈R),g(x)=x2.(1)若a=1,曲线y=f(x)在点(1,f(1))处的切线与y轴垂直,求b的值;(2)若b=2,试探究函数f(x)与g(x)在其公共点处是否有公切线,若存在,研究a的个数;若不存在,请说明理由.六.公切线的条数问题【例9】.已知函数f(x)=lnx,g(x)=e x.(1)确定方程f(x)=实数根的个数;(2)我们把与两条曲线都相切的直线叫作这两条曲线的公切线,试确定曲线y=f (x),y=g(x)公切线的条数,并证明你的结论.【解答】解:(1)由题意得lnx==1+,即lnx﹣1=.分别作出y=lnx﹣1和y=的函数图象,由图象可知:y=lnx﹣1和y=的函数图象有两个交点,∴方程f(x)=有两个实根;(2)解:曲线y=f(x),y=g(x)公切线的条数是2,证明如下:设公切线与f(x)=lnx,g(x)=e x的切点分别为(m,lnm),(n,e n),m≠n,∵f′(x)=,g′(x)=e x,∴,化简得(m﹣1)lnm=m+1,当m=1时,(m﹣1)lnm=m+1不成立;当m≠1时,(m﹣1)lnm=m+1化为lnm=,由(1)可知,方程lnm=有两个实根,∴曲线y=f(x),y=g(x)公切线的条数是2条.【作业5】.已知函数f(x)=x2+2(1﹣a)x﹣4a,g(x)=﹣(a+1)2,则f (x)和g(x)图象的公切线条数的可能值是.【作业1解答】解:(1)f′(x)=(2x+1)(x﹣1)2=0,x=﹣或1,∴x=﹣是h(x)的零点;∵g′(x)=k﹣,k<0,g′(x)<0,g(x)在[1,+∞)上单调递减,g(x)的最大值为g(1)=k+1.k<﹣1,g(1)<0,g(x)在[1,+∞)上无零点;k=﹣1,g(1)=0,g(x)在[1,+∞)上有1个零点;﹣1<k<0,g(1)>0,g(e1﹣k)=ke1﹣k+k<0,g(x)在[1,+∞)上有1个零点;综上所述,k<﹣1时,h(x)有1个零点;﹣1≤k<0时,h(x)有两个零点;(2)设切点(t,f(t)),f′(x)=6x2﹣6x,∴切线斜率f′(t)=6t2﹣6t,∴切线方程为y﹣f(t)=(6t2﹣6t)(x﹣t),∵切线过P(a,﹣4),∴﹣4﹣f(t)=(6t2﹣6t)(a﹣t),∴4t3﹣3t2﹣6t2a+6ta﹣5=0①由题意,方程①有3个不同的解.令H(t)=4t3﹣3t2﹣6t2a+6ta﹣5,则H′(t)=12t2﹣6t﹣12at+6a=0.t=或a.a=时,H′(t)≥0,H(t)在定义域内单调递增,H(t)不可能有两个零点,方程①不可能有两个解,不满足题意;a时,在(﹣),(a,+∞)上,H′(t)>0,函数单调递增,在(,a)上,H′(t)<0,函数单调递减,H(t)的极大值为H(),极小值为H (a);a时,在(﹣∞,a),(,+∞)上,H′(t)>0,函数单调递增,在(a,)上,H′(t)<0,函数单调递减,H(t)的极大值为H(a),极小值为H ();要使方程①有三个不同解,则H()H(a)<0,即(2a﹣7)(a+1)(2a2﹣5a+5)>0,∴a>或a<﹣1.【作业2解答】解:由已知得f'(x)=[ax2+(2a+1)x]e x,f'(0)=0,所以f (x)=(ax2+x﹣1)e x.(1)f'(x)=[ax2+(2a+1)x]e x=[x(ax+2a+1)]e x.①若a>0,当或x>0时,f'(x)>0;当时,f'(x)<0,所以f(x)的单调递增区间为;单调递减区间为.②若a=0,f(x)=(x﹣1)e x,f'(x)=xe x,当x>0时,f'(x)>0;当x<0时,f'(x)<0,所以f(x)的单调递增区间为(0,+∞);单调递减区间为(﹣∞,0).③若,当或x<0时,f'(x)<0;当时,f'(x)>0,所以f(x)的单调递增区间为;单调递减区间为.④若,故f(x)的单调递减区间为(﹣∞,+∞).⑤若,当或x>0时,f'(x)<0;当时,f'(x)>0,所以f(x)的单调递增区间为;单调递减区间为.当a>0时,f(x)的单调递增区间为;单调递减区间为.当a=0时,f(x)的单调递增区间为(0,+∞);单调递减区间为(﹣∞,0).,当时,f(x)的单调递增区间为;单调递减区间为.当时,f(x)的单调递减区间为(﹣∞,+∞);当时,f(x)单调递增区间为;单调递减区间为,(0,+∞);(2)证明:g(x)=e﹣x f(x)+lnx=﹣e﹣x(ax2+x﹣1)e x+lnx=ax2+x﹣1+lnx,设l2的方程为y=k2x,切点为(x2,y2),则,所以x2=1,y2=e,k2=e.由题意知k1=﹣k2=﹣e,所以l1的方程为y=﹣ex,设l1与y=g(x)的切点为(x1,y1),则.又,即,令,在定义域上,u'(x)>0,所以(0,+∞)上,u(x)是单调递增函数,又,所以,即,令,则,所以,故.【作业3解答】解:(1)证明:设F(x)=f(x)﹣g(x),则F′(x)=﹣,由F'(x)=0,得x=3,当0<x<3时,F'(x)<0,当x>3时F'(x)>0,可得F(x)在区间(0,3)单调递减,在区间(3,+∞)单调递增,所以F(x)取得最小值为F(3)=ln3﹣1>0,∴F(x)>0,即f(x)>g(x);(2)假设曲线f(x)与g(x)有公切线,切点分别为P(x0,lnx)和Q(x1,2﹣).因为f′(x)=,g′(x)=,所以分别以P(x0,lnx)和Q(x1,2﹣)为切线的切线方程为y=+lnx﹣1,y=+2﹣.令,即2lnx1+﹣(3+ln3)=0.令h(x)=2lnx1+﹣(3+ln3).所以由h′(x)=﹣=0,得x1=3.显然,当0<x1<3时,h'(x)<0,当x1>3时,h'(x)>0,所以h(x)min=ln3﹣1>0,所以方程2lnx1+﹣(3+ln3)=0无解,故二者没有公切线.所以曲线y=f(x)和y=g(x)不存在公切线;(3)(1+1×2)(1+2×3)•…•(1+2012×2013)>e4021.理由:由(1)可得lnx>2﹣(x>0),可令x=1+n(n+1),可得ln(1+n(n+1))>2﹣>2﹣=2﹣3(﹣),则ln(1+1×2)+ln(1+2×3)+…+ln(1+2012×2013)>2×2012﹣3(1﹣+﹣+…+﹣)=4024﹣3+>4021.即有(1+1×2)(1+2×3)…(1+2012×2013)>e4021.【作业4解答】解:(Ⅰ)∵f(x)=x﹣﹣blnx,∴f′(x)=1+﹣,由于曲线y=f(x)在点(1,f(1))处的切线垂直于y轴,故该切线斜率为0,即f′(1)=0,即1+1﹣b=0,∴b=2;(2)假设f(x),g(x)的图象在其公共点(x0,y)处存在公切线,由f(x)=a(x﹣)﹣2lnx,得f′(x)=,g′(x)=2x,由f′(x0)=g′(x),得=2x,即2x3﹣ax2+2x﹣a=0,即(x02+1)(2x﹣a)=0,则x=,又函数的定义域为(0,+∞),当a≤0时,x0=≤0,则f(x),g(x)的图象在其公共点(x,y)处不存在公切线;当a>0时,令f()=g(),﹣2ln﹣2=,即=ln,令h(x)=﹣ln(x>0),h′(x)=x﹣=,则h(x)在(0,2)递减,(2,+∞)递增.且h(2)=﹣<0,且当x→0时,h(x)→+∞;当x→+∞时,h(x)→+∞,∴h(x)在(0,+∞)有两个零点,∴方程=ln在(0,+∞)解的个数为2.综上:当a≤0时,函数f(x)与g(x)的图象在其公共点处不存在公切线;当a>0时,函数f(x)与g(x)的图象在其公共点处存在公切线,a的值有2个.在导数的练习中,常见这一类题型:已知含有的一个不等式,以及的一些其他性质,让解不等式或者比较大小。
导数中的公切线问题--2024年新高考数学一轮复习题型归纳与方法总结 解析版
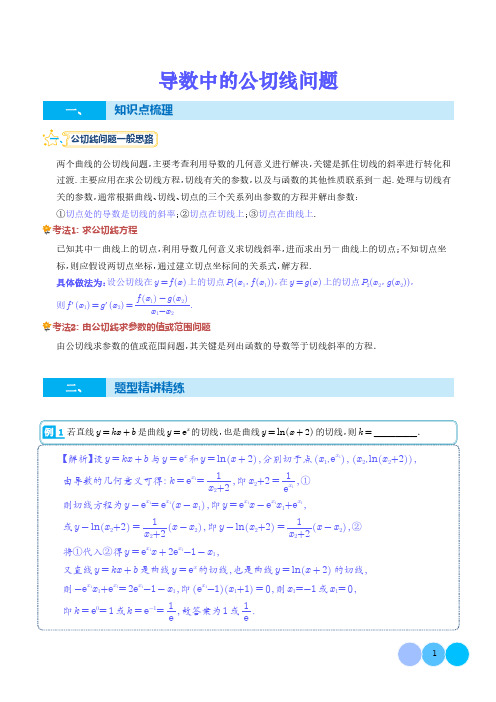
导数中的公切线问题知识点梳理一、公切线问题一般思路两个曲线的公切线问题,主要考查利用导数的几何意义进行解决,关键是抓住切线的斜率进行转化和过渡.主要应用在求公切线方程,切线有关的参数,以及与函数的其他性质联系到一起.处理与切线有关的参数,通常根据曲线、切线、切点的三个关系列出参数的方程并解出参数:①切点处的导数是切线的斜率;②切点在切线上;③切点在曲线上.考法1:求公切线方程已知其中一曲线上的切点,利用导数几何意义求切线斜率,进而求出另一曲线上的切点;不知切点坐标,则应假设两切点坐标,通过建立切点坐标间的关系式,解方程.具体做法为:设公切线在y =f (x )上的切点P 1(x 1,f (x 1)),在y =g (x )上的切点P 2(x 2,g (x 2)),则f ′(x 1)=g ′(x 2)=f x 1 -g x 2x 1-x 2.考法2:由公切线求参数的值或范围问题由公切线求参数的值或范围问题,其关键是列出函数的导数等于切线斜率的方程.题型精讲精练1若直线y =kx +b 是曲线y =e x 的切线,也是曲线y =ln x +2 的切线,则k =______.【解析】设y =kx +b 与y =e x 和y =ln x +2 ,分别切于点x 1,e x 1,x 2,ln x 2+2 ,由导数的几何意义可得:k =e x 1=1x 2+2,即x 2+2=1ex 1,①则切线方程为y -e x 1=e x 1x -x 1 ,即y =e x 1x -e x 1x 1+e x 1,或y -ln x 2+2 =1x 2+2x -x 2 ,即y -ln x 2+2 =1x 2+2x -x 2 ,②将①代入②得y =e x 1x +2e x 1-1-x 1,又直线y =kx +b 是曲线y =e x 的切线,也是曲线y =ln x +2 的切线,则-e x 1x 1+e x 1=2e x 1-1-x 1,即e x 1-1 x 1+1 =0,则x 1=-1或x 1=0,即k =e 0=1或k =e -1=1e ,故答案为1或1e.2已知直线y =kx +b 与函数y =e x 的图像相切于点P x 1,y 1 ,与函数y =ln x 的图像相切于点Q x 2,y 2 ,若x 2>1,且x 2∈n ,n +1 ,n ∈Z ,则n =______.【解析】依题意,可得e x 1=k =1x 2y 1=e x 1=kx 1+by 2=ln x 2=kx 2+b,整理得x 2ln x 2-ln x 2-x 2-1=0令f x =x ln x -ln x -x -1x >1 ,则f x =ln x -1x在1,+∞ 单调递增且f 1 ⋅f 2 <0,∴存在唯一实数m ∈1,2 ,使f m =0f x min =f m <f 1 <0,f 2 =ln2-3<0,f 3 =2ln3-4<0,f 4 =3ln4-5<0,f 5 =4ln5-6>0,∴x 2∈4,5 ,故n =4.【题型训练】1.求公切线方程一、单选题1(2023·全国·高三专题练习)曲线y =1x与曲线y =-x 2的公切线方程为()A.y =-4x +4B.y =4x -4C.y =-2x +4D.y =2x -4【答案】A【分析】画出图象,从而确定正确选项.【详解】画出y =1x,y =-x 2以及四个选项中直线的图象如下图所示,由图可知A 选项符合.故选:A2(2023·全国·高三专题练习)对于三次函数f (x ),若曲线y =f (x )在点(0,0)处的切线与曲线y =xf (x )在点(1,2)处点的切线重合,则f ′(2)=()A.-34B.-14C.-4D.14【答案】B【分析】由f(0)=0得d=0,然后求得f (x),由f (0)=2-01-0求得c=2,设g(x)=xf(x),由g(1)=2得f(1)=2及a+b=0,再由g (1)=2得3a+2b+2=0,解得a,b后可得f (2).【详解】设f(x)=ax3+bx2+cx+d(a≠0),∵f(0)=d=0,∴f(x)=ax3+bx2+cx,∴f′(x)=3ax2+2bx+c∴f′(0)=c=2-01-0=2,设g(x)=xf(x),则g(1)=f(1)=a+b+2=2,即a+b=0⋯⋯①又∵g′(x)=f(x)+xf′(x),∴g′(1)=f(1)+f′(1)=2,∴f′(1)=0,即3a+2b+2=0⋯⋯②由①②可得a=-2,b=2,c=2,∴f′(2)=-14.故选:B.3(2023·全国·高三专题练习)已知函数f x =x ln x,g x =ax2-x.若经过点A1,0存在一条直线l与曲线y=f x 和y=g x 都相切,则a=()A.-1B.1C.2D.3【答案】B【分析】先求得f(x)在A(1,0)处的切线方程,然后与g x =ax2-x联立,由Δ=0求解【详解】解析:∵f x =x ln x,∴f x =1+ln x,∴f 1 =1+ln1=1,∴k=1,∴曲线y=f x 在A1,0处的切线方程为y=x-1,由y=x-1y=ax2-x得ax2-2x+1=0,由Δ=4-4a=0,解得a=1.故选:B4(2023·全国·高三专题练习)已知函数f(x)=x2-4x+4,g(x)=x-1,则f(x)和g(x)的公切线的条数为A.三条B.二条C.一条D.0条【答案】A【分析】分别设出两条曲线的切点坐标,根据斜率相等得到方程8n3-8n2+1=0,构造函数f x =8x3-8x2+1,f x =8x3x-2,研究方程的根的个数,即可得到切线的条数.【详解】设公切线与f x 和g x 分别相切于点m,f m,n,f n,f x =2x-4,g x =-x -2,gn =fm =g n -f m n -m ,解得m =-n -22+2,代入化简得8n 3-8n 2+1=0,构造函数f x =8x 3-8x 2+1,f x =8x 3x -2 ,原函数在-∞,0 ↗,0,23 ↘,23,+∞ ↗,极大值f 0 >0,极小值,f 23<0故函数和x 轴有交3个点,方程8n 3-8n 2+1=0有三解,故切线有3条.故选A .【点睛】这个题目考查了利用导数求函数在某一点处的切线方程;步骤一般为:一,对函数求导,代入已知点得到在这一点处的斜率;二,求出这个点的横纵坐标;三,利用点斜式写出直线方程.考查了函数零点个数问题,即转化为函数图像和x 轴的交点问题.5(2023·全国·高三专题练习)已知函数f x =x 2-2m ,g x =3ln x -x ,若y =f x 与y =g x在公共点处的切线相同,则m =()A.-3B.1C.2D.5【答案】B【分析】设曲线y =f x 与y =g x 的公共点为x 0,y 0 ,根据题意可得出关于x 0、m 的方程组,进而可求得实数m 的值.【详解】设函数f x =x 2-2m ,g x =3ln x -x 的公共点设为x 0,y 0 ,则f x 0 =g x 0 f x 0 =g x 0 ,即x 20-2m =3ln x 0-x 02x 0=3x 0-1x 0>0,解得x 0=m =1,故选:B .【点睛】本题考查利用两函数的公切线求参数,要结合公共点以及导数值相等列方程组求解,考查计算能力,属于中等题.6(2023·全国·高三专题练习)函数f (x )=ln x 在点P (x 0,f (x 0))处的切线与函数g (x )=e x 的图象也相切,则满足条件的切点的个数有A.0个B.1个C.2个D.3个【答案】C【分析】先求直线l 为函数的图象上一点A (x 0,f (x 0))处的切线方程,再设直线l 与曲线y =g (x )相切于点(x 1,e x 1),进而可得ln x 0=x 0+1x 0-1,根据函数图象的交点即可得出结论.【详解】解:∵f (x )=ln x ,∴f ′(x )=1x ,∴x =x 0,f ′(x 0)=1x 0,∴切线l的方程为y-ln x0=1x0(x-x0),即y=1x0x+ln x0-1,①设直线l与曲线y=g(x)相切于点(x1,e x1),∵g (x)=e x,∴e x1=1x0,∴x1=-ln x0.∴直线l也为y-1x0=1x0(x+ln x0)即y=1x0x+ln x0x0+1x0,②由①②得ln x0=x0+1 x0-1,如图所示,在同一直角坐标系中画出y=ln x,y=x+1x-1的图象,即可得方程有两解,故切点有2个.故选:C二、填空题7(2023·吉林长春·长春吉大附中实验学校校考模拟预测)与曲线y=e x和y=-x24都相切的直线方程为.【答案】y=x+1【分析】分别设出直线与两曲线相切的切点,然后表示出直线的方程,再根据切线是同一条直线建立方程求解.【详解】设直线与曲线y=e x相切于点x1,e x1,因为y =e x,所以该直线的方程为y-e x1=e x1x-x 1,即y=e x1x+e x11-x1,设直线与曲线y=-x24相切于点x2,-x224,因为y =-x2,所以该直线的方程为y+x224=-x22x-x2,即y=-x22x+x224,所以e x1=-x22e x11-x1=x224,解得x1=0,x2=-2,所以该直线的方程为y=x+1,故答案为:y=x+1.8(2023·全国·高三专题练习)已知f x =e x-1(e为自然对数的底数),g x =ln x+1,请写出f x 与g x 的一条公切线的方程.【答案】y=ex-1或y=x【分析】假设切点分别为m,e m-1,n,ln n+1,根据导数几何意义可求得公切线方程,由此可构造方程求得m,代入公切线方程即可得到结果.【详解】设公切线与f x 相切于点m,e m-1,与g x 相切于点n,ln n+1,∵f x =e x,g x =1x,∴公切线斜率k=e m=1n;∴公切线方程为:y-e m+1=e m x-m或y-ln n-1=1nx-n,整理可得:y=e m x-m-1e m-1或y=1nx+ln n,∴e m=1nm-1e m+1=-ln n,即m=-ln nm-1e m +1=-ln n,∴m-1e m+1-m=m-1e m-1=0,解得:m=1或m=0,∴公切线方程为:y=ex-1或y=x.故答案为:y=ex-1或y=x.9(2023春·安徽·高三合肥市第六中学校联考开学考试)已知直线l与曲线y=e x、y=2+ln x都相切,则直线l的方程为.【答案】y=x+1或y=ex【分析】分别求出两曲线的切线方程是y=e x1x+e x11-x1和y=1x2x+1+ln x2,解方程e x1=1x2,e x11-x1=1+ln x2,即得解.【详解】解:由y=e x得y =e x,设切点为x1,e x1,所以切线的斜率为e x1,则直线l的方程为:y=e x1x+e x11-x1;由y =2+ln x 得y =1x ,设切点为x 2,2+ln x 2 ,所以切线的斜率为1x 2,则直线l 的方程为:y =1x 2x +1+ln x 2.所以e x 1=1x 2,e x 11-x 1 =1+ln x 2,消去x 1得1x 2-11+ln x 2 =0,故x 2=1或x 2=1e,所以直线l 的方程为:y =x +1或y =ex .故答案为:y =x +1或y =ex 10(2023春·浙江金华·高三浙江金华第一中学校考阶段练习)已知直线y =kx +b 是曲线y =ln 1+x 与y =2+ln x 的公切线,则k +b =.【答案】3-ln2【分析】分别设两条曲线上的切点,写出切线方程,建立方程组,解出切点,计算k +b .【详解】设曲线y =ln 1+x 上切点A x 1,ln 1+x 1 ,y =11+x,切线斜率k =11+x 1,切线方程y -ln 1+x 1 =11+x 1x -x 1 ,即y =11+x 1x -x 11+x 1+ln 1+x 1同理,设曲线y =2+ln x 上切点B x 2,2+ln x 2 ,y =1x,切线斜率k =1x 2,切线方程y -2+ln x 2 =1x 2x -x 2 ,即y =1x 2x +1+ln x 2,所以11+x 1=1x 2-x11+x 1+ln (1+x 1)=1+ln x 2,解得x 1=-12x 2=12,所以k =2,b =1-ln2,k +b =3-ln2.故答案为:3-ln2.2.公切线中的参数问题一、单选题1(2023·陕西渭南·统考一模)已知直线y =ax +b (a ∈R ,b >0)是曲线f x =e x 与曲线g x =ln x +2的公切线,则a +b 等于()A.e +2B.3C.e +1D.2【答案】D【分析】由f x 求得切线方程,结合该切线也是g x 的切线列方程,求得切点坐标以及斜率,进而求得直线y =ax +b ,从而求得正确答案.【详解】设t ,e t 是f x 图象上的一点,f x =e x ,所以f x 在点t ,e t 处的切线方程为y -e t =e t x -t ,y =e t x +1-t e t ①,令g x =1x=e t ,解得x =e -t ,g e -t=ln e -t+2=2-t ,所以2-t -e te -t-t=e t ,1-t =1-t e t ,所以t =0或t =1(此时①为y =ex ,b =0,不符合题意,舍去),所以t =0,此时①可化为y -1=1×x -0 ,y =x +1,所以a +b =1+1=2.故选:D2(2023·陕西榆林·校考模拟预测)若直线l 与曲线y =e x 相切,切点为M x 1,y 1 ,与曲线y =x +32也相切,切点为N x 2,y 2 ,则2x 1-x 2的值为()A.-2B.-1C.0D.1【答案】B【分析】根据导数求出切线的斜率,得到切线方程,根据两切线方程即可得解.【详解】因为直线l 与曲线y =e x 相切,切点为M x 1,y 1 ,可知直线l 的方程为y =e x 1x -x 1 +e x 1=e x 1x +1-x 1 e x 1,又直线l 与曲线y =x +3 2也相切,切点为N x 2,y 2 ,可知直线l 的方程为y =2x 2+3 x -x 2 +x 2+3 2=2x 2+3 x -x 22+9,所以e x 1=2x 2+3 1-x 1 e x 1=-x 22+9,两式相除,可得21-x 1 =3-x 2,所以2x 1-x 2=-1.故选:B3(2023春·河南·高三校联考阶段练习)已知曲线y =x 在点x 0,x 0 0<x 0<14处的切线也与曲线y =e x 相切,则x 0所在的区间是()A.0,14e 4B.14e 4,14e 2C.14e 2,14eD.14e ,14【答案】C【分析】设切线l与曲线y=e x的切点为m,e m,通过导数分别写出切线方程,由两条切线重合得出方程,再通过此方程有解得出结果.【详解】设该切线为l,对y=x求导得y =12x,所以l的方程为y-x0=12x0x-x0,即y=12x0x+x02.设l与曲线y=e x相切的切点为m,e m,则l的方程又可以写为y-e m=e m x-m,即y=e m x+1-me m.所以e m=12x0,x02=1-me m.消去m,可得x0=1+ln2x0,0<x0<1 4,令t=2x0∈0,1,则ln t-t24+1=0.设h t =ln t-t24+1,当0<t<1时,h t =1t-t2>0,所以h t 在0,1上单调递增,又h1e=-14e2<0,h1e=12-14e>0,所以t0=2x0∈1e,1e,所以x0∈14e2,14e.故选:C.4(2023·全国·高三专题练习)若函数f x =2a ln x+1与g x =x2+1的图像存在公共切线,则实数a的最大值为()A.eB.2eC.e22D.e2【答案】A【分析】分别设公切线与g x =x2+1和f(x)=2a ln x+1的切点x1,x21+1,x2,2a ln x2+1,根据导数的几何意义列式,再化简可得a=2x22-2x22ln x2,再求导分析h(x)=2x2-2x2⋅ln x(x >0)的最大值即可【详解】g x =2x,f x =2a x,设公切线与g x =x2+1的图像切于点x1,x21+1,与曲线f(x)=2a ln x+1切于点x2,2a ln x2+1,所以2x1=2ax2=2a ln x2+1-x21+1x2-x1=2a ln x2-x21x2-x1,故a=x1x2,所以2x1=2x1x2ln x2-x21x2-x1,所以x1=2x2-2x2⋅ln x2,因为a=x1x2,故a=2x22-2x22ln x2,设h(x)=2x2-2x2⋅ln x(x>0),则h (x)=2x(1-2ln x),令h (x)=0⇒x=e当h (x)>0时,x∈(0,e),当h (x)<0时,x∈(e,+∞),所以h x 在(0,e)上递增,在(e,+∞)上递减,所以h(x)max=h(e)=e,所以实数a的最大值为e,故选:A.5(2023·湖南郴州·统考模拟预测)定义:若直线l与函数y=f x ,y=g x 的图象都相切,则称直线l为函数y=f x 和y=g x 的公切线.若函数f x =a ln x a>0和g x =x2有且仅有一条公切线,则实数a的值为()A.eB.eC.2eD.2e【答案】C【分析】设直线与g x =x2的切点为x1,x21,然后根据导数的几何意义可推得切线方程为y=2x1x-x21,y=ax2x+a ln x2-1.两条切线重合,即可得出a=4x22-4x22ln x2有唯一实根.构造h x =4x2-4x2ln x x>0,根据导函数得出函数的性质,作出函数的图象,结合图象,即可得出答案.【详解】设直线与g x =x2的切点为x1,x21,因为g x =2x,根据导数的几何意义可知该直线的斜率为2x1,即该直线的方程为y-x21=2x1x-x1,即y=2x1x-x21.设直线与f x =a ln x的切点为(x2,a ln x2),因为f x =ax,根据导数的几何意义可知该直线的斜率为ax2,即该直线的方程为y-a ln x2=ax2x-x2,即y=ax2x+a ln x2-1.因为函数f x =a ln x a>0和g x =x2有且只有一条公切线,所以有2x1=ax2a ln x2-1=-x21 ,即a=4x22-4x22ln x2有唯一实根.令h x =4x2-4x2ln x x>0,则h x =8x-8x ln x-4x=4x1-2ln x.解h x =0,可得x= e.当4x1-2ln x>0时,0<x<e,所以h x 在0,e上单调递增;当4x1-2ln x<0时,x>e,所以h x 在e,+∞上单调递减.所以h x 在x=e处取得最大值h e=4e-4e×12=2e.当x→0时,h x →0,h e =4e2-4e2ln e=0,函数h x 图象如图所示,因为a>0,a=4x2-4x2ln x有唯一实根,所以只有a=2e.故选:C6(2023春·广东汕头·高三汕头市潮阳实验学校校考阶段练习)已知函数f x =2+ln x,g x = a x,若总存在两条不同的直线与函数y=f x ,y=g x 图象均相切,则实数a的取值范围为()A.0,1B.0,2C.1,2D.1,e【答案】B【分析】设函数y=f x ,y=g x 的切点坐标分别为x1,2+ln x1,x2,a x2,根据导数几何意义可得a2=4ln x1+4x1,x1>0,即该方程有两个不同的实根,则设h x =4ln x+4x,x>0,求导确定其单调性与取值情况,即可得实数a的取值范围.【详解】解:设函数f x =2+ln x上的切点坐标为x1,2+ln x1,且x1>0,函数g x =a x 上的切点坐标为x2,a x2,且x2≥0,又f x =1x,g x =a2x,则公切线的斜率k=1x1=a2x2,则a>0,所以x2=a24x21,则公切线方程为y-2+ln x1=1x1x-x1,即y=1x1x+ln x1+1,代入x 2,a x 2 得:a x 2=1x 1x 2+ln x 1+1,则a 22x 1=1x 1⋅a 24x 21+ln x 1+1,整理得a 2=4ln x 1+4x 1,若总存在两条不同的直线与函数y =f x ,y =g x 图象均相切,则方程a 2=4ln x 1+4x 1有两个不同的实根,设h x =4ln x +4x,x >0,则h x =4x⋅x -4ln x +4x2=-4ln xx,令h x =0得x =1,当x ∈0,1 时,h x >0,h x 单调递增,x ∈1,+∞ 时,h x <0,h x 单调递减,又h x =0可得x =1e,则x →0时,h x →-∞;x →+∞时,h x →0,则函数h x 的大致图象如下:所以a >00<a 2<4,解得0<a <2,故实数a 的取值范围为0,2 .故选:B .【点睛】本题考查了函数的公切线、函数方程与导数的综合应用,难度较大.解决本题的关键是,根据公切线的几何意义,设切点坐标分别为x 1,2+ln x 1 ,且x 1>0,x 2,a x 2 ,且x 2≥0,可得k =1x 1=a 2x 2,即有x 2=a 24x 21,得公切线方程为y =1x 1x +ln x 1+1,代入切点x 2,a x 2 将双变量方程a x 2=1x 1x 2+ln x 1+1转化为单变量方程a 22x 1=1x 1⋅a 24x 21+ln x 1+1,根据含参方程进行“参变分离”得a 2=4ln x 1+4x 1,转化为一曲一直问题,即可得实数a 的取值范围.7(2023·全国·高三专题练习)若曲线y =ln x +1与曲线y =x 2+x +3a 有公切线,则实数a 的取值范围()A.2ln2-36,3-ln22B.1-4ln212,3-ln22C.2ln2-36,+∞ D.1-4ln212,+∞【答案】D【分析】分别求出两曲线的切线方程,则两切线方程相同,据此求出a 关于切点x 的解析式,根据解析式的值域确定a 的范围.【详解】设x 1,y 1 是曲线y =ln x +1的切点,设x 2,y 2 是曲线y =x 2+x +3a 的切点,对于曲线y =ln x +1,其导数为y =1x ,对于曲线y =x 2+x +3a ,其导数为y =2x +1,所以切线方程分别为:y -ln x 1+1 =1x 1x -x 1 ,y -x 22+x 2+3a =2x 2+1 x -x 2 ,两切线重合,对照斜率和纵截距可得:1x 1=2x 2+1ln x 1=-x 22+3a,解得3a =ln x 1+x 22=ln 12x 2+1+x 22=-ln 2x 2+1+x 22x 2>-12 ,令h x =-ln 2x +1 +x 2x >-12,hx =-22x +1+2x =4x 2+2x -22x +1=2x +1 2x -1 2x +1=0,得:x =12,当x ∈-12,12时,h x <0,h x 是减函数,当x ∈12,+∞时,h x >0,h x 是增函数,∴h min x =h 12 =14-ln2且当x 趋于-12时,,h x 趋于+∞;当x 趋于+∞时,h x 趋于+∞;∴3a ≥14-ln2,∴a ≥1-4ln212;故选:D .8(2023·河北·统考模拟预测)若曲线f (x )=3x 2-2与曲线g (x )=-2-m ln x (m ≠0)存在公切线,则实数m 的最小值为()A.-6eB.-3eC.2eD.6e【答案】A【分析】求出函数的导函数,设公切线与f x 切于点x 1,3x 21-2 ,与曲线g x 切于点x 2,-2-m ln x 2 ,x 2>0 ,即可得到m =-6x 1x 2,则x 1=0或x 1=2x 2-x 2ln x 2,从而得到m =12x 22ln x 2-12x 22,在令h x =12x 2ln x -12x 2,x >0 ,利用导数求出函数的最小值,即可得解;【详解】因为f (x )=3x 2-2,g (x )=-2-m ln x (m ≠0),所以f (x )=6x ,g (x )=-mx,设公切线与f x 切于点x 1,3x 21-2 ,与曲线g x 切于点x 2,-2-m ln x 2 ,x 2>0 ,所以6x 1=-m x 2=-2-m ln x 2-3x 21-2 x 2-x 1=-m ln x 2-3x 21x 2-x 1,所以m =-6x 1x 2,所以6x 1=6x 1x 2ln x 2-3x 21x 2-x 1,所以x 1=0或x 1=2x 2-x 2ln x 2,因为m ≠0,所以x 1≠0,所以x 1=2x 2-x 2ln x 2,所以m =-62x 2-x 2ln x 2 x 2=12x 22ln x 2-12x 22,令h x =12x 2ln x -12x 2,x >0 ,则h x =12x 2ln x -1 ,所以当0<x <e 时h x <0,当x >e 时h x >0,所以h x 在0,e 上单调递减,在e ,+∞ 上单调递增,所以h x min =h e =-6e ,所以实数m 的最小值为-6e.故选:A【点睛】思路点睛:涉及公切线问题一般先设切点,在根据斜率相等得到方程,即可找到参数之间的关系,最后构造函数,利用导数求出函数的最值.二、多选题9(2023·湖北·统考模拟预测)若存在直线与曲线f x =x 3-x ,g x =x 2-a 2+a 都相切,则a 的值可以是()A.0B.-24C.log 27D.e π+πe【答案】ABC【分析】设该直线与f x 相切于点x 1,x 31-x 1 ,求出切线方程为y =3x 21-1 x -2x 31,设该直线与g x 相切于点x 2,x 22-a 2+a ,求出切线方程为y =2x 2x -x 22-a 2+a ,联立方程组,得到-a 2+a =94x 41-2x 31-32x 21+14,令h x =94x 4-2x 3-32x 2+14,讨论h x 的单调性,从而得到最值,则可得到-a 2+a ≥-1,解出a 的取值范围,四个选项的值分别比较与区间端点比较大小即可判断是否在区间内.【详解】设该直线与f x 相切于点x 1,x 31-x 1 ,因为f x =3x 2-1,所以f x 1 =3x 21-1,所以该切线方程为y -x 31-x 1 =3x 21-1 x -x 1 ,即y =3x 21-1 x -2x 31.设该直线与g x 相切于点x 2,x 22-a 2+a ,因为g x =2x ,所以g x 2 =2x 2,所以该切线方程为y -x 22-a 2+a =2x 2x -x 2 ,即y =2x 2x -x 22-a 2+a ,所以3x 21-1=2x 2-2x 31=-x 22-a 2+a ,所以-a 2+a =x 22-2x 31=3x 21-122-2x 31=94x 41-2x 31-32x 21+14,令h x =94x 4-2x 3-32x 2+14,∴h x =9x 3-6x 2-3x ,所以当x ∈-∞,-13 ∪0,1 时,hx <0;当x ∈-13,0 ∪1,+∞ 时,h x >0;∴h x 在-∞,-13和0,1 上单调递减;在-13,0 和1,+∞ 上单调递增;又h -13 =527,h 1 =-1,所以h x ∈-1,+∞ ,所以-a 2+a ≥-1,解得1-52≤a ≤1+52,所以a 的取值范围为1-52,1+52,所以A 正确;对于B ,-24-1-52=25-2+2 4>0,所以1-52<-24<0,所以B 正确;对于C ,因为0<log 27<log 222=32<1+52,所以C 正确;对于D ,因为e π+πe>2e π⋅πe=2>1+52,所以D 不正确.故选:ABC10(2023·全国·高三专题练习)函数f x =ln x +1,g x =e x -1,下列说法正确的是( ).(参考数据:e 2≈7.39,e 3≈20.09,ln2≈0.69,ln3≈1.10)A.存在实数m ,使得直线y =x +m 与y =f x 相切也与y =g x 相切B.存在实数k ,使得直线y =kx -1与y =f x 相切也与y =g x 相切C.函数g x -f x 在区间23,+∞ 上不单调D.函数g x -f x 在区间23,+∞上有极大值,无极小值【答案】AB【分析】对AB ,设直线与y =f x 、y =g x 分别切于点P x 1,y 1 ,Q x 2,y 2 ,利用点在线上及斜率列方程组,解得切点即可判断;对CD ,令h x =g x -f x ,由二阶导数法研究函数单调性及极值.【详解】对AB ,设直线l 与y =f x 、y =g x 分别切于点P x 1,y 1 ,Q x 2,y 2 ,f x =1x,gx =ex,则有y1=f x1=ln x1+1y2=g x2=e x2-1y1-y2x1-x2=1x1=e x2⇒ln x1+1-e x2-1x1-x2=e x2⇒-x2+1-e x2-11e x2-x2=e x2⇒e x2-1x2-1=0,解得x2=0或x2=1.当x2=0,则y2=0,x1=1,y1=1,公切线为y=x,此时存在实数m=0满足题意;当x2=1,则y2=e-1,x1=1e,y1=0,公切线为y=e x-1e=ex-1,此时存在实数k=1满足题意,AB对;对CD,令h x =g x -f x =e x-ln x-2,x∈0,+∞,则m x =h x =e x-1 x,由m x =e x+1x2>0得h x 在0,+∞单调递增,由h23=e23-32=e2-278e232+32e23+94>0得,x∈23,+∞时,h x >0,h x 单调递增,CD错.故选:AB.三、填空题11(2023·全国·高三专题练习)若曲线y=ax2与y=ln x有一条斜率为2的公切线,则a= .【答案】1ln2e【分析】根据导数的几何意义以及切线方程的求解方法求解.【详解】设公切线在曲线y=ax2与y=ln x上的切点分别为A(x1,y1),B(x2,y2),由y=ln x可得y =1x,所以1x2=2,解得x2=12,所以y2=ln x2=-ln2,则B12,-ln2 ,所以切线方程为y+ln2=2x-1 2,又由y=ax2,可得y =2ax,所以2ax1=2,即ax1=1,所以y1=ax21=x1,又因为切点A(x1,y1),也即A(x1,x1)在切线y+ln2=2x-1 2上,所以x1+ln2=2x1-1 2,解得x1=ln2+1,所以a =1x 1=1ln2+1=1ln2e .故答案为:1ln2e.12(2023·河北唐山·统考三模)已知曲线y =ln x 与y =ax 2a >0 有公共切线,则实数a 的取值范围为.【答案】12e,+∞【分析】设公切线与曲线的切点为x 1,ln x 1 ,x 2,ax 22 ,利用导数的几何意义分别求y =ln x 和y =ax 2上的切线方程,由所得切线方程的相关系数相等列方程求参数关系,进而构造函数并利用导数研究单调性求参数范围.【详解】设公切线与曲线y =ln x 和y =ax 2的切点分别为x 1,ln x 1 ,x 2,ax 22 ,其中x 1>0,对于y =ln x 有y =1x ,则y =ln x 上的切线方程为y -ln x 1=1x 1x -x 1 ,即y =xx 1+ln x 1-1 ,对于y =ax 2有y =2ax ,则y =ax 2上的切线方程为y -ax 22=2ax 2x -x 2 ,即y =2ax 2x -ax 22,所以1x 1=2ax 2ln x 1-1=-ax 22,有-14ax21=ln x 1-1,即14a=x 21-x 21ln x 1x 1>0 ,令g x =x 2-x 2ln x ,g x =x -2x ln x =x 1-2ln x ,令gx =0,得x =e 12,当x ∈0,e12时,g x >0,g x 单调递增,当x ∈e 12,+∞ 时,g x <0,g x 单调递减,所以g x max =g e12=12e ,故0<14a ≤12e ,即a ≥12e.∴正实数a 的取值范围是12e,+∞.故答案为:12e,+∞.13(2023·浙江金华·统考模拟预测)若存在直线l 既是曲线y =x 2的切线,也是曲线y =a ln x 的切线,则实数a 的最大值为.【答案】2e【分析】设切线与两曲线的切点分别为(n ,n 2),(m ,a ln m ),根据导数的几何意义分别求出切线方程,可得a4m2=1-ln m,由题意可知a4=m2(1-ln m)有解,故令g(x)=x2(1-ln x),(x>0),利用导数求得其最值,即可求得答案.【详解】由题意知两曲线y=x2与y=a ln x,(x>0)存在公切线,a=0时,两曲线y=x2与y=0,(x>0),不合题意;则y=x2的导数y =2x,y=a ln x的导数为y =a x,设公切线与y=x2相切的切点为(n,n2),与曲线y=a ln x相切的切点为(m,a ln m),则切线方程为y-n2=2n(x-n),即y=2nx-n2,切线方程也可写为y-a ln m=am(x-m),即y=amx-a+a ln m,故2n=am-n2=-a+a ln m,即a24m2=a-a ln m,即a4m2=1-ln m,即a4=m2(1-ln m)有解,令g(x)=x2(1-ln x),(x>0),则g (x)=2x(1-ln x)+x2-1 x=x(1-2ln x),令g (x)=0可得x=e,当0<x<e时,g (x)>0,当x>e时,g (x)<0,故g(x)在(0,e)是增函数,在(e,+∞)是减函数,故g(x)的最大值为g(e)=e 2,故a4≤e2,所以a≤2e,即实数a的最大值为2e,故答案为:2e。
(完整版)高考导数题型归纳

高考压轴题:导数题型及解题方法(自己总结供参考)一.切线问题题型1 求曲线)(x f y =在0x x =处的切线方程。
方法:)(0x f '为在0x x =处的切线的斜率。
题型2 过点),(b a 的直线与曲线)(x f y =的相切问题。
方法:设曲线)(x f y =的切点))(,(00x f x ,由b x f x f a x -='-)()()(000求出0x ,进而解决相关问题。
注意:曲线在某点处的切线若有则只有一,曲线过某点的切线往往不止一条。
例 已知函数f (x )=x 3﹣3x .(1)求曲线y=f (x )在点x=2处的切线方程;(答案:0169=--y x )(2)若过点A )2)(,1(-≠m m A 可作曲线)(x f y =的三条切线,求实数m 的取值范围、 (提示:设曲线)(x f y =上的切点()(,00x f x );建立)(,00x f x 的等式关系。
将问题转化为关于m x ,0的方程有三个不同实数根问题。
(答案:m 的范围是()2,3--)练习 1. 已知曲线x x y 33-=(1)求过点(1,-3)与曲线x x y 33-=相切的直线方程。
答案:(03=+y x 或027415=--y x )(2)证明:过点(-2,5)与曲线x x y 33-=相切的直线有三条。
2.若直线0122=--+e y x e 与曲线x ae y -=1相切,求a 的值. (答案:1)题型3 求两个曲线)(x f y =、)(x g y =的公切线。
方法:设曲线)(x f y =、)(x g y =的切点分别为()(,11x f x )。
()(,22x f x );建立21,x x 的等式关系,12112)()(y y x f x x -='-,12212)()(y y x f x x -='-;求出21,x x ,进而求出切线方程。
解决问题的方法是设切点,用导数求斜率,建立等式关系。
两曲线的公切线问题解题方法

两曲线的公切线问题解题方法
1. 嘿,先找到两条曲线的导数呀!就像找宝藏先确定地图一样。
比如说曲线 y=x^2 和 y=x^3,它们的导数能帮我们找到切线的斜率呢。
通过求导,我们就能知道在哪些地方可能存在公切线哦。
2. 接下来,假设公切线存在呀!这就像是假设我们能找到宝藏一样。
还是用刚才那两个例子,设出公切线的方程,然后带入到两条曲线中去看看是否满足呀。
这一步是不是很有趣呢?
3. 然后呢,建立方程组呀!这就好像搭积木一样,一块块把条件凑起来。
根据公切线与两条曲线的关系列出等式,通过解方程来确定公切线的具体情况呢。
比如求解上面的例子,不就能知道公切线到底存不存在啦!
4. 还要注意特殊情况呢!千万可别漏了呀,这就像是注意路上的小坑一样重要。
有时候可能会有一些不太明显的情况,得仔细想想,像一些渐近线之类的地方。
哎呀,可别掉进坑里啦!比如有的曲线在某个点看起来像是有公切线,但实际上不是哦。
5. 别忘了检验答案呀!就像检查作业一样仔细。
看看求出的公切线是不是真的满足条件,可不能马虎呢。
一旦不小心,就可能出错呀!
6. 嘿嘿,不断练习才是王道呀!就像练功一样,多练才能厉害。
多找些题目来做做,熟练掌握方法,以后遇到任何两曲线的公切线问题都能轻松搞定啦!就像大侠闯荡江湖一样轻松!总之呢,只要按照这些办法去做,两曲线的公切线问题就不再难啦!。
高考总复习一轮数学精品课件 第4章 导数及其应用 素能培优(四) 公切线问题

函数 y=g(x)在点 Q 处的切线方程为 y-ln
比较①和②得
e
1 -1
=
1
③,
2
1
x2= (x-x2),整理得
2
1
y= x+ln x2-1②,
2
(1-1 )e 1 -1 = ln 2 -1④,
两曲线公切线的条数即为该方程组解的组数,
2 -1
' = e ,
21 = e 2 ,
即
4(2 -1)
a= e2 ,设
4(-1)
f(x)= e ,则
4(2-)
f'(x)= e ,令
ae 2 =4x2-4,
f'(x)=0,解得 x=2,
所以 f(x)在(1,2)内单调递增,在(2,+∞)内单调递减,所以
B.3
C.e+1
D.2
解析 设(t,et)是 f(x)图象上的一点,f'(x)=ex,
所以 f(x)在点(t,et)处的切线方程为 y-et=et(x-t),y=etx+(1-t)et①,
令
1 t
g'(x)==e ,解得
-t
-t
-t
2--e
x=e ,所以 g(e )=ln e +2=2-t,所以
[对点训练1](2024·福建南平模拟)已知曲线y=aln x和曲线y=x2有唯一公共
点,且这两条曲线在该公共点处有相同的切线l,则l的方程为__________.
2 ex-y-e=0
解析 设曲线 g(x)=aln x 和曲线 f(x)=x2 在公共点(x0,y0)处的切线相同,
第5讲利用导数研究函数的公切线问题 高考数学

试卷讲评课件
练2
若曲线f x = acosx与曲线g x = x 2 + bx + 3在交点 0, m 处有
6
公切线,则a + b + m =___.
【分析】若曲线 与曲线 在交点 , 处有公切线,则切点的
坐标相等且切线的斜率(切点处的导函数值)均相等,由此构造关于,
当 , 不是 的切点时,
设切点为 , − + ≠ ,
则 ′ = − + ,
试卷讲评课件
− +
所以
= − + ,得 = ,
所以
= − ,所以直线的方程为 = − .
=
+
= .
故选:
− = + − +
,则
= +
,即
试卷讲评课件
例2
已知f x =1 lnx,g x = x a ,若f x 与g x 的图象在交点处的切
−1
/e
线重合,则a =______.
e
【分析】设 与 的图象交点为 , ,再根据导数的几何意义
第5讲 利用导数求解函数的切线(3)
主讲人:某某某老师
某某学校
知识点一 利用导数求解公切线问题
知识点二 与公切线有关的参数问题
知识点一 利用导数求解公切线问题
试卷讲评课件
例1
若直线y = kx + b是曲线y = lnx + 2的切线,也是曲线
y = ln x + 1 的切线,则k =(
(完整版)导数解决切线问题的习题.doc

导数复习专题——切线问题例一:求曲线 y x33x21在点(1,1)处的切线方程变式一:已知函数变式二:已知函数y x33x ,过点A(0,16)作曲线y f ( x) 的切线,求此切线方程.y x33x ,过点A(2,2)作曲线y f ( x) 的切线,求此切线方程.例二:已知函数 f(x)=x3+3ax2-3b, g(x)=-2x2+2x+3(a ≠ 0)(1) 若 f(x)的图象与 g(x)的图象在 x=2 处的切线互相平行,求 a 的值;(2)若函数 y=f(x)的两个极值点 x=x1,x=x2恰是方程 f(x)=g(x)的两个根,求 a、b 的值;并求此时函数y=f(x)的单调区间.变式二:设函数 y x3 ax2 9x 1 a 0 ,若曲线 y=f(x)的斜率最小的切线与直线12 x y 6 平行,求:(Ⅰ) a 的值; (Ⅱ)函数 f ( x) 的单调区间.例三:已知函数 y x3ax b a, b R(Ⅰ)若f ( x)的图像在 2 x 2 部分在 x 轴的上方,且在点(2, f 2 ) 处的切线与直线9x y 50 平行,求b的取值范围;(Ⅱ)当 x1 , x20,3,且x1x2时,不等式 f x1 f x2x1x2恒成立,求的3取值范围。
变式三:已知函数 f(x)=ax ,在 x=1 处取得极值为 2.2x b(1)求函数 f(x)的解析式;(2)若函数 f(x)在区间( m, 2m+ 1)上为增函数,求实数m 的取值范围;(3)若P( x0,y0)为 f(x)=axl 与 f(x)=ax的图象相切于x 2图象上的任意一点,直线2b x b点 P,求直线l 的斜率的取值范围.课后练习:一:选择题1. 曲线 y 1 x2 2x 在点(1, 3 )处切线的倾斜角为 ( )2 2A. 1B. 45C. 45D.1352. 过点(- 1, 0)作抛物线y x2 x 1 的切线,则其中一条切线为()A.2 x y 2 0B. 3x y 3 0C. x y 1 0D. x y 1 0 3.已知函数f ( x) x2 (ax b)(a,b R) 在x=2时有极值,其图象在点(1,f(1)) 处的切线与直线 3x+y=0 平行,则函数f(x) 的单调减区间为()A. ,0B.( 0, 2)C. 2,D. ,4. 曲线 y x( x 1)( x 2)...( x 50) 在原点处的切线,方程为()A、y 1275 xB、y 50 2 x C. y 100x D、y 50! x曲线 y 1 x5. e2在点 (4, e2 ) 处的切线与坐标轴所围三角形的面积为()A. 9 e2B. 4e2C. 2e2D. e226. 设点 P 是曲线:y x3 3x b (b 为实常数 )上任意一点, P 点处切线的倾斜角为α,则α的取值范围是()A. 2 ,B.2 ,5C.[0, ]∪[ 5 , π]D.[ 0,2)∪[ 2 , π)3 6 2 6 37. 函数 y ax2 1的图象与直线y x 相切,则 a =( )1 1 1A.8 B.4 C.2 D. 1二:填空题nx) 在x 2 处的切线与a n1.正整数n,y x (1 y 轴交点的纵坐标为a n,则数列n 1 的前 n 项和的公式是2曲线ysin x在点 M ( ,0) 处的切线方程为.x3. 函数 y f ( x) 的图象在点P处的切线方程是y x 8,则 f (5) f (5) =.94. 点 P 是曲线y x 2 ln x 上任意一点,则P 到直线y x 2 的距离的最小值为三:解答题1. 求曲线 ( x 1)2 ( y 3 )2 5 的切线,使该切线平行于直线 2 x y 82 41 2与 C2 2 1 2都相切,求直线l 的方程 .2. 已知曲线 C :y=x :y=- (x-2) ,直线 l 与 C 、C3.已知函数(1)求曲线f (x) x3x .y f (x) 在点 M (t, f (t)) 处的切线方程;(2)设a0,如果过点(a,b)可作曲线y f (x) 的三条切线,证明: a b f (a) .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数解公切线专题
3 215
1. (2009年江西文12)若存在过点(1,0)的直线与曲线y X和y ax x 9都相切,
4
则a等于25亠217亠257亠A. 1或B. 1或C. 或-D.—或7
6444644
2.(2016年全国II理16)若直线y kx b是曲线y ln x2的切线,也是曲线y In (x1)的切线,则b .
3•求曲线y=x3+x2- 2X在点A(1,0)处的切线方程•
变式:求曲线y=x3+x2—2x过点A(1,0)的切线方程
【答案】1 In2
【解析】
试题分析;对因数y=lnx+2求导得y (=-f 对> =ln (x+l )求导得#=丄,设直线y =
与圉数
X x+1
y=}nx+2相切于点号口小),与函埶y = ln (x +1)相切于点占(花jJ :则时=Ln 珂+ 2= In 任+1),
则点的g'J 在切线上得$-(1口珂+2)=丄(工-珂),由Eg/J 在切线上得
3•求曲线y=x 3+x 2— 2x 在点A(1,0)处的切线方程• 解:T y ' =x 2+2x — 2,
•••切线斜率 k= y'x =1=3. •••切线方程为y=3(x — 1), 即 3x — y — 3=0.
变式:求曲线y=x 3+x 2— 2x 过点A(1,0)的切线方程.
y-ln (^ + 1) = —-—(x-x,),这两芳立绫表示同一牛世戈,所以
“ ja + 1
ln(x n +1) =1口
叫
’解之得
X ; 叼+1
3
1. (2009年江西文12)若存在过点(1,0)的直线与曲线y x 和y
ax 2
15 x 4
9都相切,
则a 等于
A .
1
或-64
B .
1 或 21
4
C .-或-24
4 64
1.设过(1,0)的直线与y
3
3
x 相切于点(x 0 , x 0 ),所以切线方程为
x o
3x o 2(x X o )
2
3x 0 x 2x 0
,又(1,0)在切线上,则X 。
0或X 。
2
15
25
当X 0时,由y
0与y ax
x 9相切可得 a
4
64
3」丄
27 27 一
2 15
当X )
—时,由
y
x 与y ax X 9相切可得a
2
4 4
4
2. ( 2016 年全国II
理16) 若直线y
kx b 是曲线 y In x
y In (x 1)的切
线,
则b
所以选A .
考点:导数的几何意义•
1
,
2的切线,也是曲线
解设切点P (X。
, X03+X02—2x0),
•/y' =3+2x —2,
•••切线斜率k=3x o2+2x o —2.
•••切线方程为y-(x03+x02-2x0)=(3x02+2x0-2)(x
-x0) .
•••点A在切线上,
• 0—( x03+x02—2x0)=(3x02+2x0—2)(1—x0).即
x03—x02—x0+1=0 .
故(x0—1)2 ( x0+1 )=0.
解得x0= —1 或x0= 1 .
•当x0=—1 时,切线方程为x+y—1=0;
当x o=i时,切线方程为3 x —y—3 =0.
综上,曲线过点A(1,0)的切线方程为
3x—y—3=0 ,或x+y—仁0.
y
O x。
