《锐角三角函数》第一课时导学案
锐角三角函数导学案

25.2.1 锐角三角函数学习目标:1、理解正弦、余弦、正切、余切的概念;2、正弦、余弦、正切、余切的应用学习重点:正弦,余弦,正切、余切的概念学习难点:正弦、余弦、正切、余切的应用前置性作业:一、知识回顾1、在Rt△ABC中,∠C=90°,AC=b,BC=a,AB=c.(1)若a=3,b=4,则c= . (2)若a=3,c=4,则b= .2、小明放一个线长为120米的风筝,他的风筝线与水平地面构成30°角,他的风筝高度为多少?二、自主学习,合作探究1、概念学习如图,在Rt△ABC中,∠B的对边是,∠B的邻边是,AB称为。
2、大胆猜想,合理推证(1)在方格纸中,画一个锐角∠MAN,再在射线AM上任取两点B1 B2,并分别过B1\B2作B1C1⊥AN,作B2C2⊥AN,垂足\为C1、C2MN①测量并比较大小: ,②若改变∠MAN的大小,①中的结论还成立吗?从中你发现了什么?并将所得结果与你的同伴进行比较,(2)对于上述结论一定成立吗?能否给出证明?(3)在Rt△AB中,对于锐角∠A的每一个确定的值,其邻边与斜边、邻边与对边、对边与邻边的比值也是一个固定值吗?若是,能否给出证明。
(4)总结概念在Rt△ABC中,当锐角∠A的度数一定时,(1)把锐角∠A的对边与斜边的比叫做∠A的,记作sinA 即(2)把锐角∠A的邻边与斜边的比叫做∠A的,记作cosA 即(3)把锐角A的对边与邻边的比叫做∠A的,记作tanA 即(4)把锐角A的邻边与对边的比叫做∠A的,记住cotA 即3、知识应用(1)、如图,在Rt△ABC中,∠ACB=90°, AB=13,BC=5,则①、sinA= ; cosA= ; tanA= ; cotA=②sinB= ; cosB= ; tanB= ; cotB=ABC通过此题,你有什么发现?(2)、如图,在Rt△ABC中,∠ACB=90°,AB=10,sinA=,求BC、AC的值。
锐角三角函数导学案
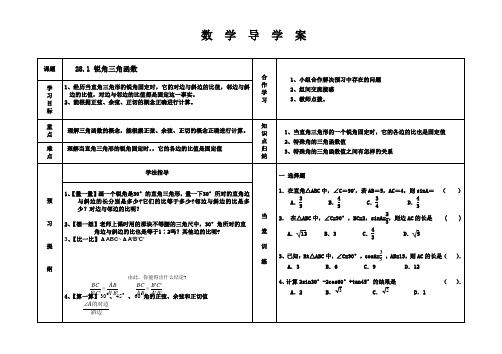
当
堂
堂
训 14、等腰三角形的腰长为 5cm,底边长为 8cm,求它的底角的正切值 练
训
练
盘 点 收 获 教 学 反 思
预
Байду номын сангаас
1、 【量一量】画一个锐角是30°的直角三角形,量一下30°所对的直角边 与斜边的长分别是多少 ?它们的比等于多少 ? 邻边与斜边的比是多 少?对边与邻边的比呢? 当 2、 【想一想】老师上课时用的那块不等腰的三角尺中,30°角所对的直 角边与斜边的比也是等于1∶2吗?其他边的比呢? 3、 【比一比】Δ ABC~Δ A’B’C’
4、 计算 2sin30°-2cos60°+tan45°的结果是 A.2 B. 3 C. 2
) .
5.已知∠A 为锐角,且 cosA≤
1 ,那么 2 A.0°<∠A ≤60°B.60°≤∠A<90 ° C.0°<∠ A≤30°D.30°≤∠A<90° 1 , 2
(
) 13、在如图所示的 Rt△ ABC 中你会求∠ A 的三角函数值吗?∠ B 呢?
6.在△ABC 中,∠A、∠B 都是锐角,且 sinA= cosB=
当
3 ,则△ABC 的形状是 ( ) 2 A.直角三角形 B.钝角三角形 C.锐角三角形 D.不能确定 7.当锐角 a>60°时,cosa 的值 ( ) . 1 1 3 A.小于 B.大于 C.大于 D.大于 1 2 2 2 二、填空题 8、设α 、β 均为锐角,且 sinα -cosβ =0,则α +β =______ 2 9.若( 3 tanA-3) +│2cosB- 3 │=0,则△ABC 是 三角形 10、 已知, 等腰△ABC•的腰长为 4 3 , •底为 30•°, •则底边上的高为______, • 周长为______. 5 11.在 Rt△ ABC 中,∠C=90°,已知 tanB= ,则 cosA=________. 2 三解答题 12、求下列各式的值 ( 1) COS 2 600 + sin 2 600 ( 2)
24.1锐角的三角函数(第一课时)教案

24.1锐角的三角函数——锐角的正切(第一课时)授课对象: 中学九年级班教学安排:一课时授课教师:一、教学背景分析(一)教材分析:1.教材的地位及作用《锐角的三角函数》是沪科版九年级数学上册第24章第一节的内容。
锐角的三角函数的概念是以前面学习的相似三角形、勾股定理的知识为基础的,本章内容是三角学中最基础的内容,也是今后进一步学习三角学的必要知识准备。
2.教材处理本节教材共分三课时完成,;第一课时是正切概念的建立及其简单应用;第二课时是正弦、余弦概念的建立及其简单应用;第三课时是综合应用。
(二)学情分析:九年级的学生具备了一定的逻辑思维能力和推理能力。
通过以前的合作学习,具备了一定的合作交流的能力.二、教学目标知识与技能: 1. 理解锐角正切(tanA)、坡度、坡角的意义;2.学会根据定义求锐角的正切值.过程与方法: 1. 经历锐角的正切的探求过程,体会数形结合的思想方法.2.三角函数的学习中,初步体验探索、讨论、论证对学习数学的重要性。
情感态度价值观:1. 在活动中培养学生乐于探究、合作交流的习惯。
2. 感受数学来源于生活又应用于生活,从而激发学生学习数学的兴趣。
三、教学重、难点教学重点:锐角的正切、坡度、坡角的定义。
教学难点:理解Rt△中一个锐角的对边与其邻边比值的对应关系。
四、教学用具多媒体课件(PPT)、几何画板五、教学过程(一)创设情境、导入新课(5分钟)利用多媒体播放“人民英雄纪念碑——民族的自豪”短片,引导学生思考:如何测量出人民英雄纪念碑的高度呢?要求学生自主探究,积极思考,回答测量高度的方法,教师引导学生分析,如直接测量法和相似法的弊端,从而导入新课——锐角的正切。
(板书课题)【设计意图】通过视频的展示,让学生身临其境地感受人民英雄纪念碑的雄伟,激发学生强烈的爱国热情和民族自豪感,同时,通过对纪念碑高度的测量自然地导入今天的教学重点。
体现新课标的要求:在关注学生数学学习水平的同时,关注学生德育教育和情感态度的发展。
1.1 锐角三角函数(第1课时)导学案

榆中五中“三导六部”课堂教学模式导学案班级: 姓名: 组长:第一课时 锐角三角函数学习目标:1..经历探索直角三角形中边角关系的过程.理解正切的意义和与现实生活的联系.2.能够用tan A 表示直角三角形中两直角边的比,表示生活中物体的倾斜程度、坡度(坡比)等.3.能够根据直角三角形的边角关系,用正切进行简单的计算.教学重点:理解正切、倾斜程度、坡度的数学意义,密切数学与生活的联系.. 教学难点:理解正切的意义,并用它来表示两边的比. 一 问题情境回顾你学过的直角三角形的知识?直角三角形边边关系: ; 角角关系: ;边角关系: 。
二、合作探究活动内容1:观察梯子的倾斜程度。
倾斜的物体在生活中随处可见,那我们该如何判断物体的倾斜程度呢?大家都会用“陡峭”或“平缓”来描述.1.图1—1和图1—2中,这里摆放的两个梯子,你能辨别出那一个比较陡一些吗?你是如何判断的?2.图1—3中,这里摆放的两个梯子,你能辨别出那一个比较陡一些吗?你又是如何判断的?图1—1图1—2三、 探求新知活动内容1:在小明家的墙角处放有一架较长的梯子,墙很高,又没有足够长的尺来测量,你有什么巧妙的方法得到梯子的倾斜程度呢?如图1-4,小明想通过测量11B C 及1AC ,算出它们的比,来说明梯子的倾斜程度;而小亮则认为通过测量22B C 及2AC ,算出它们的比,也能说明梯子的倾斜程度.你同意小亮的看法吗?(1)11Rt AB C ∆和22Rt AB C ∆有什么关系? (2)222AC C B 和111AC C B 有什么关系? (3)如果改变2B 在梯子上的位置呢? 由此你得出什么结论?结论:通过活动我们可以用倾斜角的 和 之比来刻画梯子的倾斜程度。
当倾斜角确定时,其对边与邻边之比也随之确定.这一比值只与 有关,而与直角三角形的 .图1—3表1图1—4活动内容2:结合活动内容1,请同学们思考:既然直角三角形中,一个锐角一旦确定,它的对边与邻边的比也随之确定.那么这个确定的比我们能不能用一个数学符号来表示呢?数学上,我们把这个确定的比叫做一个锐角的正切.如图1—5,我们把A ∠的对边与A ∠的邻边的比,叫做A ∠的正切(tangent ),记作tan A .即tan A A A ∠=∠的对边的邻边对于正切的定义,同学们必须明确以下几点:1.tan A 中常省略角的符号“∠”.用希腊字母表示角时也可省略如:tan α、tan β等.但用三个字母表示角和用阿拉伯数字表示角时,不能省略角的符号“∠”,要写成tan BAC ∠或tan 1∠、tan 2∠等;2、tan A 没有单位,它表示一个比值;3、tan A 是一个完的整数学符号,不可分割,不表示“tan ”乘以“A ”;4、一个角的正切是在直角三角形中定义的,因此,tan A A A ∠=∠的对边的邻边只能在直角三角形中适用;请同学们思考,梯子的倾斜程度与tan A 的值有关吗?tan A 的值越大,梯子越陡四 应用与拓展活动内容1:例题1:图1—6表示甲、乙两个手扶电梯,哪个手扶电梯比较陡?C图1—5A ∠的邻边A 的对边活动内容2:认识坡角、坡度(坡比) 坡角:坡面与水平面的夹角;坡度(坡比):坡面的铅垂高度与水平宽度的比,因此坡度(坡比)就是坡角的正切. 如图1—7,有一山坡在水平方向上每前进100m 米就升高60m ,那么山坡的坡角是α,坡度(坡比)就是:603tan 1005α== 五.练习巩固活动内容:1、如图1—8,在ABC ∆中,90C ∠=,6AC =,若3tan 4A =,则AC = ; 2、如图1—9,在ABC ∆中,10AC AB ==,16BC =,则tan B = ;3、如图1—10,某人从山脚下的点A 走了200m 后到达山顶的点B .已知山顶B 到山脚下的垂直距离是55m.求山坡的坡度(结果精确到0.001m).图1—8图1—9图1—10(乙)4m(甲)5m8m图1—6图1—7。
28.1《锐角三角函数》第1课时导学案

第二十八章锐角三角函数28.1 锐角三角函数第1课时1.知道正弦的概念,并会根据已知直角三角形的边长求一个锐角的正弦值.2.经历探究“当直角三角形的锐角固定时,它的对边与斜边的比值是固定值”这一事实的过程,体会由特殊到一般的思想方法.3.重点:知道正弦函数的概念,会根据直角三角形的边长求锐角的正弦值.请你阅读教材本课时“问题”至“探究”结束,回答下列问题.1.仿照“问题”中的解答,完成本课时第一个“思考”中的问题.根据“在直角三角形中,30°角所对的直角边等于斜边的一半”,即==,AB=2BC=100 m,需要准备100 m长的水管.2.当BC=a m时,AB的长是多少?当∠A为30°时,的值是否固定?若固定,值是多少?当BC=a m时,AB的长是2a m.当∠A为30°时,的值固定,为.3.完成本课时第二个“思考”中的问题.==,结论:在直角三角形中,当一个锐角等于45°时,无论这个三角形的大小如何,其对边与斜边的比都等于.4.对于直角三角形中的任意一个锐角∠A,其对边与斜边的比是一个固定的值吗?请你结合探究中的图证明你的结论.直角三角形中的任意一个锐角∠A,其对边与斜边的比是一个固定的值.如教材中的图,∠A=∠A',∠C=∠C',所以△ABC∽△A'B'C',所以=,即=.【归纳总结】在直角三角形中,当锐角A的度数一定时,无论三角形的大小如何,∠A的对边与斜边的比都是一个固定值.【预习自测】在直角三角形ABC中,=,若直角三角形DEF中∠D=∠B,则= .请你阅读教材本课时中有关正弦的定义至“例1”的部分,回答下列问题.1.∠A的对边记作a,∠B的对边记作b,∠C的对边记作c.2.在Rt△ABC中,∠C=90°,我们把∠A的对边与斜边的比叫做∠A的正弦,记作sin A,即sin A== .【归纳总结】在表示一个锐角的正弦值时,要注意什么问题?(1)正弦是一个比值,是没有单位的数值;(2)表示∠A的正弦值时,不要带“∠”符号,而在用三个字母表示角时,则需要带上“∠”符号.【讨论】如图,在三角形ABC中,BC=1,AC=2,sin A=吗?为什么?sin A不一定等于,因为三角形ABC不一定是直角三角形.【预习自测】在Rt△ABC中,∠C=90°,sin A=,则sin B等于(A)A. B. C. D.互动探究1:在Rt△ABC中,各边的长度都扩大10倍,那么锐角A的正弦值(C)A.扩大10倍B.缩小到原来的C.没有变化D.不能确定互动探究2:三角形在方格纸中的位置如图1所示,则sin α的值是(D)A. B. C. D.[变式训练]如图2,△ABC的三个顶点都在正方形网格的格点上,则sin A的值是(B)A. B. C. D.互动探究3:在Rt△ABC中,∠C=90°,AC=4,sin B=,所以边AB的长为(D)A.3B.4C.5D.6互动探究4:在△ABC中,AB=AC=5,BC=6,求sin B的值.解:如图,过A作AD⊥BC,垂足为D.∵AB=AC,∴BD=BC=×6=3.在Rt△ABD中,根据勾股定理,得AD===4,所以sin B==.。
锐角三角函数

锐角三角函数(第一课时)导学案学习目标:(1)经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实。
(2)理解正弦概念,知道正弦的书写规则及意义.(重点)(3)能根据正弦概念正确进行计算。
一、独立自学(独立完成,把有疑难的问题记录下来)活动一:为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?——;思考1.如果使出水口的高度为50m,那么需要准备多长的水管?——;2.如果使出水口的高度为a m,那么需要准备多长的水管?———;结论:直角三角形中,30°角的对边与斜边的比值是:———————;思考2:在Rt△ABC中,∠C=90°,∠A=45°,∠A对边与斜边的比值是一个定值吗?如果是,是多少?结论:直角三角形中,45°角的对边与斜边的比值是_____;二、合作探究活动二:任意画Rt△ABC和Rt△A′B′C′,使得∠C=∠C′=90°,∠A=∠A′=a,那么BC/AB与BC/AB有什么关系.你能解释原因吗?结论:这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比_____;正弦函数概念:规定:在Rt△BC中,∠C=90,∠A的对边记作a,∠B的对边记作b,∠C 的对边记作c.在Rt△BC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA=——=————注意:1、sinA不是sin与A的乘积,而是一个整体;sinA是线段之间的一个比值;sinA没有单位。
问题:∠B的正弦怎么表示?要求一个锐角的正弦值,我们需要知道直角三角形中的哪些边?30度45度60度角的正弦各是多少?三、精讲例题(应用知识)例1.如图,在Rt△ABC中,∠C=90°,求sin A和sin B的值例2.如图,在Rt △ABC中,∠C=90°,AB=13,BC=5求sinA和sinB的值例3、如图,在△ABC中,AB=BC=5,sinB=4/5,求△ABC 的面积。
《锐角三角函数》第一课时参考教案

课题《直角三角形的边角关系》第一课锐角三角函数(一) 一、教学目标1.经历探索直角三角形中边角关系的过程,理解锐角三角函数的意义及与现实生活的联系。
2.发展学生观察、分析、合作、解决问题的能力。
3.经历对日常生活中与正切有关的实例进行观察、分析动手实验发现规律等过程,体会数形结合的思想及数学与现实世界的联系,通过利用正切知识解决生活中的实际问题,增强学生学数学用数学的信心。
二、教材分析本章旨在探索直角三角形的边角关系,理解锐角三角函数的概念,解决与直角三角形有关的实际问题,培养学生分析问题、解决问题的能力。
本章的知识广泛应用于测量、建筑、工程技术及物理学中,其中正切与生活的联系最为密切。
因此在第一节中教材首先提供了梯子倾斜程度比较的问题,从学生身边常见的例子引入,提出引发学生思考的问题。
这样做既激发了学生的好奇心与求知欲,又充分体现了数学与现实世界的紧密联系。
通过“想一想”三个小问题得出“梯子倾斜角确定对边与邻边的比也确定”,并概括出正切的概念。
最后通过“议一议”又回到了梯子的倾斜角度问题。
这样编排,知识由易到难、层层递进,符合学生的认知规律,使学生经历了数学知识的形成全过程,满足了不同学生发展的需求。
得出正切的概念后,教材又编排了相应的例题与练习,培养学生应用知识的能力,还补充了山坡坡度的例子,使知识进一步扩充与延伸。
三、教学设计(一)情境导入师:一天下午的课外活动时间,小明、小亮、小颖三位同学在操场上一起讨论这样一个数学问题:如何测量操场上的国旗杆的高度?小明说:可以在操场上立一根与地面垂直的标杆,测得标杆的长度和标杆的影子长,再测得旗杆的影子长,它们的比值相等,就可以求得旗杆的高度。
小亮说:拿一块等腰直角三角板,调节人与旗杆的距离,使三角板的一直角边与旗杆平行,视线沿着斜边的方向刚好经过旗杆的顶端,只要测得人到旗杆的距离和眼睛到地面的高度相加,就是旗杆的高度。
小颖这段时间正在自学刚发到的数学九(下),她说:站在操场上的任一位置,用测角仪测得看旗杆顶端的仰角,比如为700,再测得人与旗杆的距离,就可以求得旗杆的高度。
三角函数导学案

费县石井中学数学组◆◆导学案(九年级) 一轮复习 授课时间: 2012.04.主备人: 滕如龙 排版人:滕如龙 审核人: 吴庆国 审 批 人: 英玉平 班 级: 姓 名: 小 组: 学案编号: 27-01—— 数学组导学案 第 1 页 共 4 页 课题 锐角三角函数(一)一、复习目标1.巩固三角函数的概念,巩固用直角三角形边之比来表示某个锐角的三角函数.2. 熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.3.掌握直角三角形的边角关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形.二、重点、难点1.重点:熟记30°,45°, 60°角的三角函数值.会计算含有特殊角的三角函数的值,会由一个特殊锐角的三角函数值,求出它的对应的角度.2.难点:运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形. 三、知识回顾回顾练习一1、如图,在Rt △ABC 中,∠C=90, AB=5,AC=3,求sinA,cosA 及tanA 。
2、 在正方形网格中,△ABC 的位置如图所示, 则cos ∠ABC 的值为________。
归纳总结一:如右图: 1、正弦:把锐角A 的__________的比叫做∠A 的正弦,记作 _____ 2、余弦:把锐角A 的__________的比叫做∠A 的余弦,记作______ 3、正切:把锐角A 的__________的比叫做∠A 的正切,记作______ 4、锐角A 的_____________________都叫做∠A 的锐角三角函数综合应用一1.在直角三角形中,若各边的长度缩小10倍,那么锐角∠A 的正弦值为( )。
A 扩大10倍 B 缩小10倍 C 没有变化 D 不能确定2.已知在Rt △ABC 中,∠C=90° SinA= 35则tanB 的值为( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
28.1《锐角三角函数》第一课时——正弦
【学习目标】
1:经历当直角三角形的锐角固定时,它的对边与斜边的比值都固定(即正弦值不变)这一事实。
2:能根据正弦概念正确进行计算
【学习重点】
理解正弦(sinA)概念,知道当直角三角形的锐角固定时,它的对边与斜边的比值是固定值这一事实.
【学习难点】
当直角三角形的锐角固定时,,它的对边与斜边的比值是固定值的事实。
B 【导学过程】
一、自学提纲:A C
1、如图在△
R t ABC中,∠C=90°,∠A=30°,BC=10m,•求AB 2、如图在△
R t ABC中,∠C=90°,∠A=30°,AB=20m,•求BC A B C
二、合作交流:
问题:为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,•在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
思考1:如果使出水口的高度为50m,那么需要准备多长的水管?;如果使出水口的高度为a m,那么需要准备多长的水管?;
结论:直角三角形中,30°角的对边与斜边的比值
思考2:在△
R t ABC中,∠C=90°,∠A=45°,∠A对边与斜边的比值是一个定值吗?•如果是,是多少?B
A C
结论:直角三角形中,45°角的对边与斜边的比值
BC B ' C '
三、教师点拨:
从上面这两个问题的结论中可知,•在一个 △R t ABC 中,∠C=90°,当∠A=30°
时,∠A 的对边与斜边的比都等于 1 2
,是一个固定值;•当∠A=45°时,∠A 的
对边与斜边的比都等于 2 2
,也是一个固定值.这就引发我们产生这样一个疑问:
当∠A 取其他一定度数的锐角时,•它的对边与斜边的比是否也是一个固定值?
探究:任意画 Rt△ABC 和 Rt △A ′B′C′,使得∠C=∠C′=90°,
∠A=∠A′=a,那么 与
AB A ' B '
有什么关系.你能解释一下吗?
结论:这就是说,在直角三角形中,当锐角 A 的度数一定时,不管三角形的大
小如何,•∠A 的对边与斜边的比
正弦函数概念:
规定:在 Rt △B C 中,∠C=90,
∠A 的对边记作 a ,∠B 的对边记作 b ,∠C 的对边记作 A
斜边c
b
B
对边a
C c .
在 △R t BC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A 的正弦,
记作 sinA ,即 sinA= = a c . sinA = ∠ A 的对边 a
=
∠ A 的斜边 c
例如,当∠A=30°时,我们有 sinA=sin30°=
;
当∠A=45°时,我们有 sinA=sin45°=
.
四、学生展示:
例 1 如图,在 Rt△ABC 中,∠C=90°,求 sinA 和 sinB 的值.
B
3
B
3 5
13
A
4 C
C
A
(1)
(2)
4 5
5
4
3
3 3
a
b
随堂练习 (1):
做课本第 79 页练习.
随堂练习 (2):
1.三角形在正方形网格纸中的位置如图所示,则 sin α 的值是﹙
﹚
3
A . 4
B . 3
3 4 C . 5 D . 5
△2.如图,在直角 ABC 中,∠C =90o ,若 AB =5,AC =4,则 sinA
=(
)
3 4
3 4 A .
B .
C .
D .
A
B C
2
3. 在△ABC 中,∠C=90°,BC=2,sinA= ,则边 AC 的长是(
)
4 A . 13
B .3
C .
D . 5
4.如图,已知点 P 的坐标是(a ,b ),则 sin α 等于(
)
a
A . b
B . a
C . a 2 + b 2
D . b
a 2 +
b 2
五、课堂小结:
在直角三角形中,当锐角 A 的度数一定时,不管三角形的大小如何,∠A•
的对边与斜边的比都是
.
在 △R t ABC 中,∠C=90°,我们把锐角 A 的对边与斜边的比叫做∠A•的
,
•记作
,
六、作业设置:
课本 第 85 页 习题 28.1 复习巩固第 1 题、第 2 题.(只做与正弦函数有关
的部分)
七、自我反思:
本节课我的收获: 。
