第一次作业
第一次平构作业

第一次平构作业平构作业,听起来就很神秘又有趣呢!一、平构作业是啥。
平构呀,就是平面构成啦。
这可是咱设计专业很基础但又超级重要的一部分。
就好比盖房子要先打地基一样,平构就是我们设计大厦的地基呢。
它主要是研究在二维平面内如何把点、线、面这些基本元素组合起来,创造出各种不同的视觉效果。
比如说,怎么让几个简单的圆形和方形组合起来,看起来就特别有节奏感,或者是特别炫酷。
我一开始接触的时候,真的是一头雾水,看着那些简单的图形,心里就想:“这能玩出什么花样来呀?”但是后来慢慢深入,才发现这里面的学问可大了去了。
二、作业的要求。
老师给的要求还真不少呢。
首先得有创意,不能随随便便画几个图形就交差。
要让人一看就眼前一亮,那种感觉就像是在一堆灰扑扑的石头里发现了闪闪发光的宝石一样。
然后呢,色彩搭配也很重要。
颜色选得好,整个作品就像被注入了灵魂一样。
要是颜色不协调,就像一个人穿了一身奇装异服,看着特别别扭。
还有啊,画面的平衡感也要把握好,不能这边重那边轻的,就像一个人走路一瘸一拐的,看着就不舒服。
我为了满足这些要求,可是费了好大的劲儿呢。
三、我的创作过程。
刚开始的时候,我完全没有灵感。
坐在桌子前,对着白纸发呆,感觉时间都停止了。
我就开始翻各种资料,看看那些大师们是怎么做的。
看着看着,突然有了一点想法,就赶紧拿起笔开始画。
我先画了一些简单的点和线,然后试着把它们组合起来。
但是画着画着,就发现不太对劲了,怎么看都觉得很普通。
我有点沮丧,就把那张纸揉成一团扔到一边去了。
不过我可没有放弃哦,我又重新开始想。
这一次,我想到了我最喜欢的音乐,那种有节奏感的旋律。
我就想,能不能把这种节奏感用图形表现出来呢?于是我又拿起笔,开始画一些长短不一、粗细不同的线条,然后用点来点缀。
慢慢地,我的作品有了雏形。
我又开始考虑色彩的问题,我选择了一些比较鲜艳的颜色,因为我觉得这样可以更好地表现出那种充满活力的感觉。
我看着自己的作品,虽然还有很多不足之处,但是心里还是挺有成就感的。
中国石油大学(北京)软件工程第一次在线作业满分答案

中国石油大学(北京)软件工程第一次在线作业满分答案
第一次在线作业
单选题 (共25道题)
展开
收起
1.(
2.5分)结构化分析建立功能模型的工具是()
A、DFD
B、判定树/判定表
C、SC
D、结构化语言
我的答案:A 此题得分:2.5分
2.(2.5分)检查软件产品是否符合需求定义的过程称为()
A、确认测试
B、集成测试
C、系统测试
D、单元测试
我的答案:A 此题得分:2.5分
3.(2.5分)软件测试方法中,黑盒测试方法和白盒测试方法是常用的方法,其中黑盒测试方法主要用于测试()
A、结构合理性
B、软件外部功能
C、程序正确性
D、程序内部逻辑
我的答案:B 此题得分:2.5分
4.(2.5分)软件开发中常采用的结构化生命周期方法,由于其特征而一般称其为()
A、瀑布模型
B、对象模型
C、螺旋模型
D、层次模型
我的答案:A 此题得分:2.5分
5.(2.5分)建立原型的目的不同,实现原型的途径也有所不同,下列不正确的类型是()
A、用于验证软件需求的原型
B、垂直原型
C、用于验证设计方案的原型
D、用于演化出目标系统的原型
我的答案:B 此题得分:2.5分
6.(2.5分)面向对象的开发方法中,()将是面向对象技术领域内占主导地位的标准建模语言。
A、Booch方法。
JZX高等数值分析第一次实验作业
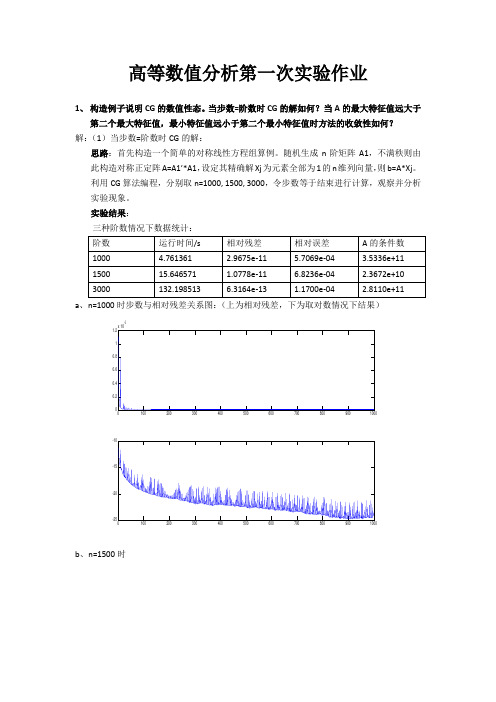
相对残差 6.1302e-16 8.7797e-09 8.0295e-09 8.5677e-09 9.1433e-09
a、 m=1 (左为相对残差,右为取对数情况)
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 1
1.5
0
-5
-10
-15
-20
-25
-30
-35
-40
1000
4.761361
2.9675e-11
5.7069e-04
3.5336e+11
1500
15.646571
1.0778e-11
6.8236e-04
2.3672e+10
3000
132.198513
6.3164e-13
1.1700e-04
2.8110e+11
a、n=1000 时步数与相对残差关系图:(上为相对残差,下为取对数情况下结果)
(2)当 A 最大特征值远大于第二个特征值,最小特征值远小于第二个最小特征值时收敛
性情况。
思路:构造题目要求的矩阵 A。首先随机生成 n 阶矩阵 B,B 不满秩,构造对角阵 A1(最
大特征值远大于第二个最大特征值,最小特征值远小于第二个最小特征值),则由此构
造出对称正定矩阵 A: b1=B’*B; A=b1’*A1*b1。同样设定精确解 Xj 为元素全部为 1 的 n
5、 构造对称不定的矩阵,验证 Lanczos 方法的近似中断,观察收敛曲线中的峰点个数和特
征值的分布关系;观察当出现峰点时,MINRES 方法的收敛性态怎样。
解:思路:类似前两题,首先构造出一个 n 阶对角阵 D,其对角线上有 m 个负值,再对随
公共关系学第一次平时作业含答案

公共关系学第⼀次平时作业含答案公共关系学第⼀次平时作业(1-3章)⼀.判断正误题(每⼩题1分,共14分)( √ )1.公共关系是⼀门综合性的应⽤科学。
( ×)2.公共关系是⼀门专业性的理论科学。
( √ )3.公共关系特指组织与公众之间的传播沟通关系。
( × )4.公众与组织之间不⼀定存在着相互影响和相互作⽤。
( × )5.公共关系传播模式是根据传播过程的反馈模式的原理设计的,但它不包含“五w ”模式的基本要素。
( × )6.艾维·李创办了世界上第⼀家宣传事务顾问所。
( √ )7.爱德华·伯尼斯出版了笫⼀本公共关系著作《公众舆论之形咸》( ×)8.有了发达的商品经济就会产⽣发达的公共关系。
( √ )9.中国公共关系事业是在改⾰开放以后才发展起呆的。
( × )10.引进西⽅的经验就可以推动中国公关事业的发展。
( √)11.公共关系90%靠⾃⼰做得对,10%靠宣传。
( √ )12.在⽐较发达的商品经济杜会⾥,公众的消费主要是由消费⼼理⽀配的。
( √ )13.产品形象是整个组织形象的基础。
(× )14.公共关系完全是为组织营造⽣存、发展环境服务的。
⼆.单项选择题(每⼩题1分,共15分)1.公共关系的英⽂是(A )。
A.public relationsB.public relationC.publication relationsD.publication relation2.公共关系可直接称为( A )。
A.公众关系B.⼈际关系C.⼈群关系D.社区关系3.组织与公众联结的⽅式是( B )。
A.⼤众传播B.传播沟通C.⼈际沟通D.舆论宣传4.现代公共关系传播的本质是组织与公众之间信息的( A )。
A.双向交流B.单向交流C.双向管理D.单向管理5.组织开展公共关系活动的基础是( C )。
A.公共关系意识B.公共关系观念C.公共关系状态D.公共关系策划6.利⽤新闻媒介揭露垄断企业“愚弄公众”的现象,形成了美国近代史上著名的(C )。
第一次 作业答案

第二章财务管理的基础知识一、计算题1.某企业年初投资100万元生产一种新产品,预计每年年末可得净收益10万元,投资年限为10年,年利率为5%。
【要求】(1)计算该投资项目年收益的现值和终值。
(2)计算年初投资额的终值。
解:(1)年收益现值P= 10×(P/A,5%,10)= 10×= (万元)年收益终值F= 10×(F/A,5%,10)=10×=(万元)(2)年初投资额终值F=100×(F/P,5%,10)=100×=(万元)2.某人准备5年后支付一笔10 000元的款项,年利率为5%。
【要求】计算此人现在应存入银行多少钱,5年的复利利息为多少元。
解:复利现值P=10000×(P/F,5%,5)=10000×=7835(元)复利利息I=F-P=10000-7835=2165(元)3.某企业2003年年初投资一个项目,预计从2006年起至2010年每年年末可获得净收益20万元,年利率为5%。
【要求】计算该投资项目年净收益的终值和现值。
解:年净收益的终值F=20×(F/A,5%,5)=20×=(万元)年收益的现值P=20×[(P/A,i,m+n)﹣(P/A,i,m) =20×[(P/A,5%,8)﹣(P/A,5%,3)=20×(﹣)=(万元)4.某企业投资一个项目,每年年初投入10万元,连续投资3年,年利率为5%。
【要求】(1)计算该项目3年后的投资总额(2)若3年的投资额于年初一次性投入,投资总额是多少?解:(1)预付年金终值F=10×(F/A,5%,3)×(1+5%)=10××=(万元)(2)预付年金现值P=10×(P/A,5%,3)×(1+5%) =10××=(万元)投资项目的年利率为8%,每季度复利一次。
七年级数学上学期第一次独立作业(含解析) 苏科版

2016-2017学年江苏省泰州市靖江市靖城中学七年级(上)第一次数学独立作业一、选择题1.﹣2的相反数是()A.﹣ B.C.2 D.±22.下列说法中,正确的是()A.1是最小的正数B.任何有理数的绝对值都不可能小于0C.任何有理数的绝对值都是正数D.最大的负数是﹣13.若b<0,则a,a﹣b,a+b,最大的是()A.a B.a﹣bC.a+b D.还要看a的符号,才能判定4.下列各组数中,互为相反数的是()A.2与B.﹣(+3)与+(﹣3)C.﹣1与﹣(﹣1)D.2与|﹣2|5.绝对值大于π而不大于6的所有正整数之和为()A.0 B.9 C.10 D.156.如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是()A.a+b<0 B.a﹣b<0 C.﹣a+b>0 D.|b|>|a|7.若a+b<0,ab<0,则下列判断正确的是()A.a,b都是正数B.a,b都是负数C.a,b异号且负数的绝对值大D.a,b异号且正数的绝对值大8.一潜水艇所在的海拔高度是﹣70米,一条海豚在潜水艇上方20米,则海豚所在的高度是海拔()A.﹣90米B.﹣70米C.﹣50米D.50米9.下列说法正确的有()①0是绝对值最小的数②绝对值等于本身的数是非正数③数轴上原点两侧的数互为相反数④两个数比较,绝对值大的反而小.A.1个B.2个C.3个D.4个10.已知:|x|=3,|y|=2,且x<y,则x+y的值为()A.﹣5 B.﹣1 C.5或1 D.﹣5或﹣1二、填空题11.绝对值等于3的数有个,它们分别是.12.三个数﹣5、﹣2、+7的和比它们的绝对值的和小.13.比较大小:﹣﹣,﹣(﹣5)﹣|﹣5|14.有一列数﹣,,﹣,,…,那么第7个数是.15.一个数从数轴上表示2的点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是.16.下面四个三角形内的数有共同的规律,请找出这个规律,确定A为.17.若a+1与5互为相反数,则a= .18.某公交车上原有20人,经过4个站点时的上下车情况如下(上车为正,下车为负):(+4,﹣8),(﹣5,+6),(﹣3,+2),(+1,﹣7),则现在车上还有人.19.若|a|=5,|b|=3,则a+b的值= ;若a+b<0,则a﹣b的值= .20.数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在这个数轴上随意划出一条长2016cm的线段AB,则它盖住的整点有个.三、解答题(共44分)21.把下列各数填入相应的数集合中﹣21,,﹣|﹣0.7|,0,2016,﹣(﹣9),12%,,﹣,自然数{ …};分数 { …}正数 { …};非负整数 { …}.22.计算(1)(﹣8)+47+8+(﹣27)(2)﹣2﹣(﹣4)﹣(+5)+(﹣8)﹣(﹣9)(3)﹣21﹣12+33+12﹣67(4)|﹣4|+|﹣5|﹣|(﹣)+(﹣0.5)|23.在数轴上表示下列各数:+6,﹣|﹣3.5|,,﹣1,0,2.5,并用“>”将它们连接起来.24.某检修小组从O地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西为负,一天中七次行驶纪录如表.(单位:km)第一次A第二次B第三次C第四次D第五次E第六次F第七次G ﹣4+7﹣9+8+6﹣5﹣2(1)画数轴表示出每次结束时的点的位置(用表格中的字母表示),并求出收工时距A地多远?(2)在第次纪录时距A地最远.(3)若每千米耗油0.3升,问共耗油多少升?25.我们知道,在数轴上,|a|表示数a表示的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a,b表示,那么A、B两点间的距离为:AB=|a﹣b|.利用此结论,回答以下问题:(1)数轴上表示2和5的两点的距离是,数轴上表示﹣2和﹣5的两点之间的距离是,数轴上表示1和﹣3的两点之间的距离是;(2)若|a+1|=2,则a= ;若|a+2|+|a﹣1|=6,则a= ;(3)当|a+2|+|a﹣1|取最小值时,此时a符合条件是;(4)当a= 时,|a+5|+|a﹣1|+|a﹣3|的值最小,最小值是.2016-2017学年江苏省泰州市靖江市靖城中学七年级(上)第一次数学独立作业参考答案与试题解析一、选择题1.﹣2的相反数是()A.﹣ B.C.2 D.±2【考点】相反数.【专题】存在型.【分析】根据相反数的定义进行解答即可.【解答】解:∵﹣2<0,∴﹣2相反数是2.故选C.【点评】本题考查的是相反数的定义,即只有符号不同的两个数叫做互为相反数.2.下列说法中,正确的是()A.1是最小的正数B.任何有理数的绝对值都不可能小于0C.任何有理数的绝对值都是正数D.最大的负数是﹣1【考点】绝对值;有理数.【分析】根据有理数、绝对值对各选项进行逐一判断即可.【解答】解:A、没有最小的正数,故本选项错误;B、0的绝对值是0,故本选项错误;C、0的绝对值是0,故本选项错误;D、最大的负数是﹣1,故本选项正确;故选D.【点评】本题考查了有理数、绝对值,熟知有理数、绝对值的性质是解答此题的关键.3.若b<0,则a,a﹣b,a+b,最大的是()A.a B.a﹣bC.a+b D.还要看a的符号,才能判定【考点】有理数大小比较.【专题】推理填空题.【分析】由于b<0,所以﹣b>0,因此即可得到a,a﹣b,a+b,最大的数.【解答】解:∵b<0,∴﹣b>0,∴a,a﹣b,a+b,最大的是a﹣b.故选B.【点评】此题主要考查了有理数的大小的比较,解决此类问题的关键是找出最大最小有理数和对减法法则的理解.4.下列各组数中,互为相反数的是()A.2与B.﹣(+3)与+(﹣3)C.﹣1与﹣(﹣1)D.2与|﹣2|【考点】绝对值;相反数.【分析】根据相反数的概念:只有符号不同的两个数叫做互为相反数进行分析即可.【解答】解:A、2与互为倒数,故此选项错误;B、﹣(+3)=﹣3与+(﹣3)=﹣3相等,故此选项错误;C、﹣1与﹣(﹣1)=1互为相反数,故此选项正确;D、2与|﹣2|相等,故此选项错误;故选:C.【点评】此题主要考查了相反数的定义,关键是正确掌握相反数定义.5.绝对值大于π而不大于6的所有正整数之和为()A.0 B.9 C.10 D.15【考点】有理数的加法;有理数大小比较.【分析】首先确定绝对值大于π而不大于6的所有正整数,然后再求和即可.【解答】解:绝对值大于π而不大于6的所有正整数是4,5,6,4+5+6=15,故选:D.【点评】此题主要考查了有理数的加法和绝对值,关键是正确确定绝对值大于π而不大于6的所有正整数.6.如图,数轴上的A、B两点分别表示有理数a、b,下列式子中不正确的是()A.a+b<0 B.a﹣b<0 C.﹣a+b>0 D.|b|>|a|【考点】数轴;绝对值.【分析】根据数轴得出a<0<b,且|a|>|b|,根据有理数的大小比较法则即可判断各个选项.【解答】解:由数轴可知:a<0<b,且|a|>|b|,A、a+b<0,正确,故本选项错误;B、a﹣b=a+(﹣b)<0,正确,故本选项错误;C、﹣a+b>0,正确,故本选项错误;D、|b|<|a|,错误,故本选项正确,故选D.【点评】本题考查了绝对值,数轴,有理数的大小比较等知识点,主要考查学生的观察能力和辨析能力.7.若a+b<0,ab<0,则下列判断正确的是()A.a,b都是正数B.a,b都是负数C.a,b异号且负数的绝对值大D.a,b异号且正数的绝对值大【考点】有理数的乘法;有理数的加法.【专题】计算题.【分析】依据有理数的加法和乘法法则,即可得到答案.【解答】解:因为ab<0,所以a,b异号,又a+b<0,所以负数的绝对值比正数的绝对值大.故选C.【点评】本题考查了有理数的加法和乘法法则.有理数的加法法则:同号两数相加,取相同的符号,并把绝对值相加;绝对值不等的异号两数加加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;一个数同0相加,仍得这个数.有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.任何数同零相乘,都得0.8.一潜水艇所在的海拔高度是﹣70米,一条海豚在潜水艇上方20米,则海豚所在的高度是海拔()A.﹣90米B.﹣70米C.﹣50米D.50米【考点】有理数的加法.【分析】根据正负数具有相反的意义,由已海豚所在的高度是海拔多少米实际就是求﹣70与20的和.【解答】解:由已知,得﹣70+20=﹣50.故选C.【点评】本题考查的是正负数的意义,关键是要明确所求为﹣70与20的和.9.下列说法正确的有()①0是绝对值最小的数②绝对值等于本身的数是非正数③数轴上原点两侧的数互为相反数④两个数比较,绝对值大的反而小.A.1个B.2个C.3个D.4个【考点】绝对值;数轴;相反数.【分析】根据绝对值具有非负性可得0是绝对值最小的数;绝对值的性质:①当a是正有理数时,a 的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零可得绝对值等于本身的数是非负数;互为相反数的两个数,它们分别在原点两旁且到原点距离相等;两个负数相比较,绝对值大的反而小进行分析即可.【解答】解:①0是绝对值最小的数,说法正确;②绝对值等于本身的数是非正数,说法错误,应是非负数;③数轴上原点两侧的数互为相反数,说法错误;④两个数比较,绝对值大的反而小,说法错误;正确的说法有1个,故选:A.【点评】此题主要考查了绝对值、相反数、有理数的比较大小,关键是掌握绝对值的性质,相反数的定义.10.已知:|x|=3,|y|=2,且x<y,则x+y的值为()A.﹣5 B.﹣1 C.5或1 D.﹣5或﹣1【考点】有理数的加法;绝对值.【分析】先求出x,y的值,再求出x+y的值即可.【解答】解:∵|x|=3,|y|=2,且x<y,∴x=﹣3,y=2或﹣2,∴x+y=﹣3+2=﹣1,x+y=﹣3+(﹣2)=﹣5.故选:D.【点评】本题主要考查了有理数的加法及绝对值,解题的关键是求出x,y的值.二、填空题11.绝对值等于3的数有 2 个,它们分别是±3 .【考点】绝对值.【分析】根据绝对值的概念可求出答案.【解答】解:绝对值等于3的数为±3,故答案为:2;±3.【点评】本题考查绝对值的概念,属于基础题型.12.三个数﹣5、﹣2、+7的和比它们的绝对值的和小14 .【考点】绝对值.【专题】计算题;实数.【分析】根据题意列出算式,计算即可得到结果.【解答】解:根据题意得:|﹣5|+|﹣2|+|+7|﹣(﹣5﹣2+7)=5+2+7﹣0=14,故答案为:14【点评】此题考查了绝对值,熟练掌握绝对值的代数意义是解本题的关键.13.比较大小:﹣>﹣,﹣(﹣5)>﹣|﹣5|【考点】有理数大小比较;正数和负数;绝对值.【专题】探究型.【分析】(1)先通分,再根据负数比较大小的法则进行比较;(2)先去括号、去绝对值符号,再根据有理数比较大小的法则进行比较.【解答】解:(1)∵﹣=﹣<0,﹣ =﹣<0,|﹣|<|﹣|,∴﹣>﹣;(2)∵﹣(﹣5)=5>0,﹣|﹣5|=﹣5<0,∴﹣(﹣5)>﹣|﹣5|.故答案为:>、>.【点评】本题考查的是有理数的大小比较,解答此类题目时要先把各数化为最简形式,再根据有理数大小比较的法则进行比较.14.有一列数﹣,,﹣,,…,那么第7个数是.【考点】规律型:数字的变化类.【专题】规律型.【分析】先看符号,奇数个为负数,偶数个为正数,再看绝对值,第一个数的分子是1,分母是12+1;第二个数的分子是2,分母是22+1;那么第7个数的分子是7,分母是72+1=50.【解答】解:第7个数的分子是7,分母是72+1=50.则第7个数为﹣.【点评】应从符号,分子,分母分别考虑与数序之间的联系.关键是找到第7个数的分子是7,分母是72+1=50.15.一个数从数轴上表示2的点开始,先向左移动3个单位长度,再向右移动6个单位长度,这个点最终所对应的数是 5 .【考点】数轴.【分析】根据题意画出数轴,进而得出符合题意的答案.【解答】解:如图所示:从2的点开始,先向左移动3个单位长度到达﹣1,再向右移动6个单位长度,到达5,这个点最终所对应的数是:5.故答案为:5.【点评】此题主要考查了数轴,正确结合数轴分析是解题关键.16.下面四个三角形内的数有共同的规律,请找出这个规律,确定A为55 .【考点】规律型:数字的变化类.【分析】观察前三个三角形可知,里面的数的规律是:10÷2=2+3;21÷3=3+4;36÷4=4+5;则有A ÷5=5+6=11,故A=11×5.【解答】解:通过分析:A=(5+6)×5=55.故答案为:55.【点评】此题考查数据的变化规律,关键是找出前三组数据的规律,利用规律,解决问题.17.若a+1与5互为相反数,则a= 4 .【考点】相反数.【分析】直接利用相反数的定义进而得出答案.【解答】解:∵a+1与5互为相反数,∴a+1=5,解得:a=4.故答案为:4.【点评】此题主要考查了相反数的定义,正确把握定义是解题关键.18.某公交车上原有20人,经过4个站点时的上下车情况如下(上车为正,下车为负):(+4,﹣8),(﹣5,+6),(﹣3,+2),(+1,﹣7),则现在车上还有10 人.【考点】正数和负数.【分析】根据有理数的加法运算,可得车上人数.【解答】解:20+4﹣8﹣5+6﹣3+2+1﹣7=10(人),故答案为:10.【点评】本题考查了正数和负数,有理数的加法运算是解题关键.19.若|a|=5,|b|=3,则a+b的值= ±8或±2 ;若a+b<0,则a﹣b的值= 8或2 .【考点】有理数的减法;绝对值;有理数的加法.【分析】根据题意,利用绝对值的代数意义确定出a与b的值,即可求出a+b,a﹣b的值.【解答】解:∵|a|=5,|b|=3,∴a=±5,b=±3,∴a=﹣5,b=﹣3时,a+b=﹣5﹣3=﹣8;a=﹣5,b=3时,a+b=﹣5+3=﹣2;a=5,b=﹣3时,a+b=5﹣3=2;a=5,b=3时,a+b=5+3=8;∵a+b<0,∴a=5,b=±3,∴a=5,b=﹣3时,a﹣b=5+3=8;a=5,b=3时,a﹣b=5﹣3=2.故答案为:±8或±2;8或2.【点评】此题考查了有理数的加法,绝对值,以及有理数的减法,熟练掌握运算法则是解本题的关键.20.数轴上表示整数的点称为整点,某数轴的单位长度为1cm,若在这个数轴上随意划出一条长2016cm的线段AB,则它盖住的整点有2016或2017 个.【考点】数轴.【分析】分类讨论:线段的两端点是整数点,线段的两端点不是整数点,根据线段的长度,可得答案【解答】解:当线段的两端点是整数点时,一条长2016cm的线段AB,则被线段AB盖住的整数有2017个,当线段的两端点不是整数点时,一条长2016cm的线段AB,则被线段AB盖住的整数有2016个,则它盖住的整点有2016或2017个;故答案为:2016或2017.【点评】本题考查的是数轴,在学习中要注意培养学生数形结合的思想,本题画出数轴解题非常直观,且不容易遗漏,体现了数形结合的思想.三、解答题(共44分)21.(8分)把下列各数填入相应的数集合中﹣21,,﹣|﹣0.7|,0,2016,﹣(﹣9),12%,,﹣,自然数{ …};分数 { …}正数 { …};非负整数 { …}.【考点】绝对值;有理数.【分析】利用有理数的分类即可写出答案.【解答】解:自然数{0,2016,﹣(﹣9)…};分数{,﹣|﹣0.7|,12%,,﹣…};正数{,2016,﹣(﹣9),12%,…};非负整数{0,2016,﹣(﹣9)…};【点评】本题考查有理数的分类,涉及绝对值,符号化简等知识,属于基础题型.22.计算(1)(﹣8)+47+8+(﹣27)(2)﹣2﹣(﹣4)﹣(+5)+(﹣8)﹣(﹣9)(3)﹣21﹣12+33+12﹣67(4)|﹣4|+|﹣5|﹣|(﹣)+(﹣0.5)|【考点】有理数的加减混合运算.【分析】根据有理数的加减混合运算,即可解答.【解答】解:(1)(﹣8)+47+8+(﹣27)=﹣8+8+47﹣27=0+20=20.(2)﹣2﹣(﹣4)﹣(+5)+(﹣8)﹣(﹣9)=﹣2+4﹣5﹣8+9=﹣2﹣5﹣8+4+9=﹣15+13=﹣2.(3)﹣21﹣12+33+12﹣67=﹣33+33+12﹣67=12﹣67=﹣55.(4)|﹣4|+|﹣5|﹣|(﹣)+(﹣0.5)|=4+5﹣|﹣1|=9﹣1=8.【点评】本题考查了有理数的加减混合运算,解决本题的关键是熟记有理数的加减法.23.在数轴上表示下列各数:+6,﹣|﹣3.5|,,﹣1,0,2.5,并用“>”将它们连接起来.【考点】有理数大小比较;数轴.【分析】把各个数在数轴上表示出来,根据数轴上的数右边的数总是大于左边的数,即可把各个数按从大到小的顺序用“>”连接起来.【解答】解:在数轴上表示为:按从大到小的顺序排列为:+6>2.5>>0>>﹣|﹣3.5|.【点评】此题考查了数轴,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.24.某检修小组从O地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西为负,一天中七次行驶纪录如表.(单位:km)第一次A第二次B第三次C第四次D第五次E第六次F第七次G ﹣4+7﹣9+8+6﹣5﹣2(1)画数轴表示出每次结束时的点的位置(用表格中的字母表示),并求出收工时距A地多远?(2)在第五次纪录时距A地最远.(3)若每千米耗油0.3升,问共耗油多少升?【考点】数轴;正数和负数.【分析】(1)把所有行驶记录相加,再根据正数和负数的意义解答;(2)分别写出各次记录时距离A地的距离,然后判断即可;(3)把所有行驶记录的绝对值相加,再乘以0.3计算即可得解【解答】解:(1)﹣4+7﹣9+8+6﹣5﹣2,=7+8+6﹣4﹣9﹣5﹣2,=21﹣20,=1千米,1﹣(﹣4)=5答:收工时检修小组在距O地东边5千米处;(2)第1次到第7次记录时距离A的分别为:0、3、6、2、8、3、1,所以,距A地最远时是第5次;(3)|﹣4|+|+7|+|﹣9|+|+8|+|+6|+|﹣5|+|﹣2|,=4+7+9+8+6+5+2,=41千米,41×0.3=31.2升.答:从出发到收工时共耗油31.2升【点评】此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示25.我们知道,在数轴上,|a|表示数a表示的点到原点的距离,这是绝对值的几何意义.进一步地,数轴上两个点A、B,分别用a,b表示,那么A、B两点间的距离为:AB=|a﹣b|.利用此结论,回答以下问题:(1)数轴上表示2和5的两点的距离是 3 ,数轴上表示﹣2和﹣5的两点之间的距离是 3 ,数轴上表示1和﹣3的两点之间的距离是 4 ;(2)若|a+1|=2,则a= ﹣3或1 ;若|a+2|+|a﹣1|=6,则a= ﹣或;(3)当|a+2|+|a﹣1|取最小值 3 时,此时a符合条件是﹣2≤a≤1 ;(4)当a= 1 时,|a+5|+|a﹣1|+|a﹣3|的值最小,最小值是8 .【考点】绝对值;数轴.【分析】利用AB=|a﹣b|,即可求出答案.【解答】解:(1)5﹣2=3,﹣2﹣(﹣5)=3,1﹣(﹣3)=4;(2)∵|a+1|=2,∴a+1=±2,∴a=﹣3或a=1,∵|a+2|+|a﹣1|=6,当a<﹣2时,∴﹣(a+2)﹣(a﹣1)=6,∴a=﹣,当﹣2≤a≤1时,∴a+2﹣(a﹣1)=6,∴3=6,此时矛盾,当a>1时,∴a+2+a﹣1=6,∴a=,综上所述,a=﹣或a=;(3)当a在数轴上表示﹣2和1之间时,此时|a+2|+|a﹣1|的最小值为3,此时﹣2≤a≤1,(4)由于当﹣5≤a≤3时,此时|a+5|+|a﹣3|最小值为8,∴若要|a+5|+|a﹣1|+|a﹣3|的值最小,只需要|a﹣1|的值最小即可,此时a=1,|a﹣1|=0,∴|a+5|+|a﹣1|+|a﹣3|最小是为8,故答案为:(1)3,3,4;(2)﹣3或1,﹣或;(3)3,﹣2≤a≤1;(4)1,8.【点评】本题考查数轴,涉及绝对值,解方程等知识,综合程度较高.欢迎您的下载,资料仅供参考!。
首次作业管理制度

首次作业管理制度一、制度目的1.1 提高作业效率作业管理制度的首要目的是提高作业效率。
通过规范作业流程、分工明确、责任到人,可以避免重复工作和资源浪费,提高生产效率,实现生产能力最大化。
1.2 保障作业质量作业管理制度的另一个重要目的是保障作业质量。
规范的作业流程和标准化的作业要求,可以有效避免因人为原因导致的作业质量问题,确保产品质量稳定可靠。
1.3 保障工作安全作业管理制度的最重要目的之一是保障工作安全。
通过明确安全生产责任、建立安全工作体系、加强安全教育培训,可以有效降低事故发生率,保障员工的安全和健康。
二、制度内容2.1 作业程序作业程序是作业管理制度的核心内容之一。
在作业程序中应明确作业流程、操作方法、质量要求、安全注意事项等内容,确保每个环节都能严格按照规定进行,保证作业的顺利进行。
2.2 作业责任作业责任是作业管理制度的关键内容之一。
应明确每个人员在作业中的职责和权利,规定各岗位的责任范围和权限,确保每个环节都有专人负责,避免责任推诿和欠缺监管。
2.3 安全保障安全保障是作业管理制度的重要内容之一。
应建立完善的安全管理体系,包括安全教育培训、危险源识别评估、安全操作规程、紧急处理预案等,全面保障员工的安全和健康。
2.4 质量控制质量控制是作业管理制度的重要内容之一。
应建立严格的质量管理体系,包括质量检测要求、质量记录保留、质量问题处理程序等,确保产品的质量稳定可靠。
2.5 过程改进过程改进是作业管理制度的重要内容之一。
应建立作业过程的改进机制,包括定期评估、监督检查、问题反馈、持续改进等,不断提高作业效率和质量水平。
三、实施步骤3.1 制定作业管理制度首先,企业应制定符合自身实际需要的作业管理制度,明确制度的目的、内容、实施步骤和责任分工等,确保制度的科学性和可行性。
3.2 培训员工其次,企业应对员工进行相关培训,包括作业程序、安全要求、质量控制等方面的培训,提高员工的操作技能和专业素养,确保作业管理制度的有效实施。
第一次拼音作业

昨天是星期一,按照一年级语文的进度,我儿子——上同学的班级正式进入第三单元:汉语拼音。
我下班接孩子的时候,上同学已经自己写完了家庭作业。
虽然我知道现在拼音讲得很快,但是一天学了这么多拼音我还是始料未及。
看着儿子的作业,我知道今天晚上任务不小。
回到家,我指导儿子练习——作业本直接改成了练习本,练好了再往一个新本上重新写一遍作业。
大概用了半个小时,作业完成。
还好吧,并没有想象中那么困难。
然后吃晚饭,稍事休息。
接下来认读学过的几个拼音,不是很熟练,但比我预期的好点——我是不是对孩子的要求太低?反正我觉得刚开始学,一天认这么多挺难的,上同学能认到这个程度已经很好了。
恰好儿子想让我给他用拼音拼写“恐龙”,于是就任由他偏离主题:用拼音拼写“恐龙”,拼写“毛笔”,拼写“大米”……最后拼写的是“恐龙之旅”,然后就研究恐龙去啦!
晚上躺在床上,儿子给我讲的是“雷利诺龙”的知识,说它们是喜欢群居的恐龙,为了躲避凶猛的霸王龙常常在夜晚活动。
它们长着大大的眼睛,能在黑暗中看清周围的环境……。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数理经济学第一次作业题
董志勇
1. You can write your answer in either English or in Chinese or in both.
2. You have to do this paper independently; giving identical answers
will be assumed cheating, which will lead to severe punishment.
3. Answer to the point; be precise and avoid unnecessary length.
1、单个垄断企业分别在两个市场上实现价格歧视,求证其曲线从下面与各曲线的水平之和相交。
2、设,为两种投入要素,共同生产一种产品,该产品的价格是,生产函数是,的价格是,的价格是,,是使得利润最大化的要素投入量,求证:和不会同时小于0。
3、生产函数是,求出要素需求曲线,对根据该生产函数进行生产而且追求利润最大化的企业进行比较静态分析,证明对该企业而言,交叉效应项的符号为负。
4、一个垄断者在两个市场上销售同一种产品,市场1的收益为,市场2的收益为,两个市场的总成本为,假设在市场1中,每销售一个单位的产品要征税t。
(a)证明t增加将会使得市场1销售得产品量降低。
(b)有关t增加对市场2中的产品的影响,最大化假设意味着什么?
(c)即使假设二阶条件总是成立,市场1中的税收的增加也可能导致总产出,请说明在什么情况下会是这样的。
(d)假设根据政府法律,市场2的产出固定在前面所述的利润最大化水平上,与不加管制的情况相比,在受到政府管制的情况下,市场1中的产出对税收增加得反应在绝对量上较小,请加以证明,并对此进行直观的经济解释。
5、垄断者在两个市场中销售其产品,收入函数分别为和。
总产出的函数。
在两个市场中,每销售一个单位的产品,征收同样的税收t。
(a)求解,和。
如果有解的话,利润最大化隐含了哪些偏导的符号?
(b)假设产出固定不变,求解,能够确定该式的符号?。
