合肥工业大学计算方法复化梯形公式实验
合肥工业大学计算方法复化梯形公式实验

《计算方法》实验报告(2) 虽然找到了原函数,但因表达式过于复杂而不便计算 (3) f(x)是由测量或计算得到的表格函数由于以上种种困难,有必要研究积分的数值计算问题。
利用插值多项式 )()(x f x P n ≈则积分dx x f ba⎰)(转化为dx x P b a n ⎰)(,显然易算。
dx x P ba n ⎰)(称为插值型求积公式。
最简单的插值型求积公式是梯形公式和Simpson 公式,。
当求积结点提供较多,可以分段使用少结点的梯形公式和Simpson 公式,并称为复化梯形公式、复化Simpson 公式。
如步长未知,可以通过误差限的控制用区间逐次分半的策略自动选取步长的方法称自适应算法。
梯形递推公式给出了区间分半前后的递推关系。
由梯形递推公式求得梯形序列,相邻序列值作线性组合得Simpson 序列, Simpson 序列作线性组合得柯特斯序列, 柯特斯序列作线性组合的龙贝格序列。
若|R 2-R 1|<,则输出R2;否则…依此类推。
如此加工数据的过程叫龙贝格算法,如下图所示:复化梯形公式)]()(2)([21110n n k k n x f x f x f h T ++=∑-=复化Simpson 公式])(4)()(2)([61021110∑∑-=+-=+++=n k k n k n k n x f x f x f x f hS梯形递推公式∑-=++=10212)(22n k k n n x f h T T 加权平均公式:n n n S T T =--1442 n n n C S S =--144222 n nn R C C =--144323 龙贝格算法大大加快了误差收敛的速度,由梯形序列O(h2) 提高到龙贝格序列的O(h8)return R2;}}实验结果:图1六、实验总结1.梯形公式的收敛速度太慢,所以我们才会选择之后的几种公式加快收敛速度。
2.通过实验可以看出,龙贝格算法大大加快了误差收敛的速度,由梯形序列O(h2) 提高到龙贝格序列的O(h8)3.在编程的过程中可以切身体验到龙贝格算法是基于前几种算法的实现才能实现的。
复化梯形公式,复化辛普森公式,复化柯特斯公式

复化梯形公式,复化辛普森公式,复化柯特斯公式
复化梯形公式、复化辛普森公式和复化柯特斯公式都是用来计算定积分的近似值的方法。
1. 复化梯形公式:将积分区间分成若干个小区间,在每个小区间上用梯形面积近似代替该小区间的曲边梯形面积,然后将这些梯形面积相加,得到积分的近似值。
2. 复化辛普森公式:将积分区间分成若干个等分小区间,在每个小区间上用矩形面积近似代替该小区间的曲边梯形面积,然后将这些矩形面积相加,得到积分的近似值。
3. 复化柯特斯公式:将积分区间分成若干个等分小区间,在每个小区间上用切线段长度近似代替该小区间的曲边梯形面积,然后将这些切线段长度相加,得到积分的近似值。
这三种方法都是通过将积分区间分成若干个小区间,然后在每个小区间上用近似方法计算该小区间的曲边梯形面积,最后将这些近似值相加得到积分的近似值。
它们的精度和误差都与分区间的大小有关。
复化梯形公式求积分

武汉工程大学计算机科学与工程学院计算方法》实验报告日期:年月日实验内容设计分析复化数值积分:将区间[a,b]n 等分,取等距节点x i a ih,iba0,1,2,..., n, hn 由定积分的区间可加性,有nf x dxxix i 1f x dx在每个小区间上利用梯形积分公式有x ii f x dx x i 1 h f x i 1 f x i 2i 1 ih n1T n f a f b 2 f x i一般记 2 i1 称做n+1 点复化梯形积分公式。
数学公式:b h n1f xdx f a f b 2 f x ia 2 i1算法描述:i1Step1:输入a,b 和正整数n;Step2:置h=(b-a)/n;Step3:F=f(a)+f(b);l=0;Step4:对j=1,2,⋯,n 循环执行5;Step5:置x=a+jh; l+=f(x);Step6:置T=h(F+2l)/2 Step7:输出T;程序源代码:#include<iostream>#include<math.h>using namespacestd;<<endl; cout<<" 请输入把 0 到 1 的范围几等分?int m1; cin>>m1;EchelonIntegral(m1); cout<<endl; char answer1;cout<<" 是否要继续求该算法? (y/n)"<<"\t"; cin>>answer1;while(answer1=='y'){cout<<"请输入把 0到 1的范围几等分? "<<"\t"; cin>>m1;EchelonIntegral(m1); //3. 直线求积分; cout<<endl;cout<<" 是否要继续求该算法? (y/n)"<<"\t"; cin>>answer1; }cout<<endl;}cout<<"用梯形积分公式求积分1/(1+pow(sin(x),2))的值测试用例实验总结复化数值积分就是为了减少数值积分的误差,可以把积分区间分成若干小区间,在每个小区间上采取低阶数值积分公式,然后把这些小区间上的数值积分结果加起来作为函数在整个区间上的近似,类似于分段差值。
复化梯形公式求积分-推荐下载
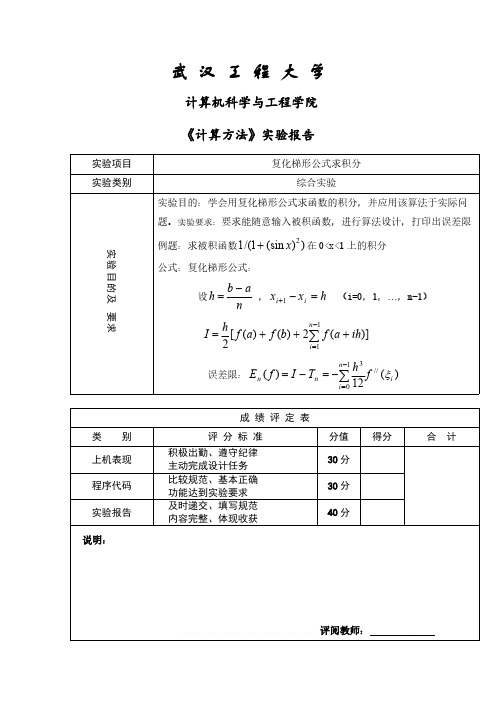
武汉工程大学计算机科学与工程学院《计算方法》实验报告实验项目复化梯形公式求积分实验类别综合实验实验目的及要求实验目的:学会用复化梯形公式求函数的积分,并应用该算法于实际问题。
实验要求:要求能随意输入被积函数,进行算法设计,打印出误差限例题:求被积函数在0<x<1上的积分))(sin1/(12x+公式:复化梯形公式:设,(i=0,1,…,n-1)nabh-=hxx ii=-+1])(2)()([211∑-=+++=niihafbfafhI误差限:)(12)(//13ininnfhTIfEξ∑-=-=-=成绩评定表类别评分标准分值得分合计上机表现积极出勤、遵守纪律主动完成设计任务30分程序代码比较规范、基本正确功能达到实验要求30分实验报告及时递交、填写规范内容完整、体现收获40分说明:评阅教师:日 期: 年 月 日实 验 内 容设计分析复化数值积分:将区间[a,b]n 等分,取等距节点n ab h n i ih a x i -==+=,,...,2,1,0,由定积分的区间可加性,有()()dxx f dx x f bani x x ii ⎰∑⎰=-=11在每一个小区间上利用梯形积分公式有()()()[]i i x x x f x f hdx x f ii +≈-⎰-112一般记()()()⎥⎦⎤⎢⎣⎡++=∑-=1122n i i n x f b f a f h T 称做n+1点复化梯形积分公式。
数学公式:()()()()⎥⎦⎤⎢⎣⎡++≈∑⎰-=1122n i i bax f b f a f h dx x f 算法描述:Step1:输入a,b 和正整数n ;Step2:置h=(b-a)/n;Step3:F=f(a)+f(b);l=0;Step4:对j=1,2,…,n 循环执行5;Step5:置x=a+jh; l+=f(x);Step6:置T=h(F+2l)/2Step7:输出T;程序源代码:#include<iostream>#include<math.h>using namespace std;double f(double x)//求函数的值;{return1/(1+pow(sin(x),2.0));}void EchelonIntegral(int n)//梯形积分{double y=0;double h=(1.0-0.0)/n;for(int i=0;i<=n;i++){double a=0.0+i*h,b=0.0+(i+1)*h;y=y+h*(f(a)+f(b))/2.0;}cout<<"对应所求的梯形求积分为"<<y<<endl;double En=0.0;double mid=(0.0+1.0)/2.0;double x=mid,p=2*sin(2*x)*sin(2*x)*(1+sin(x)*sin(x))-2*cos(2*x)*pow(1+sin(x)*sin(x),2);double f2d=p/pow(1+sin(x)*sin(x),2);for(i=0;i<n;i++){En=En+pow(h,3)/12.0*f2d;}cout<<"误差为"<<En<<endl;}/*void ParabolicIntegral(int n)//抛物线积分{double y=0;double t=(1.0-0.0)/n;for(int i=0;i<n;i++){double a=0.0+i*t,b=0.0+(i+1)*t;y=y+t*(f(a)+f(b)+4*f((a+b)/2.0))/6.0;}cout<<"对应所求的抛物线求积分为"<<y<<endl;}*/void main(){cout<<"*********************用梯形积分公式求积分1/(1+pow(sin(x),2))的值****************"<<endl;cout<<"请输入把0到1的范围几等分?"<<"\t";int m1;cin>>m1;EchelonIntegral(m1);cout<<endl;char answer1;cout<<"是否要继续求该算法?(y/n)"<<"\t";cin>>answer1;while(answer1=='y'){cout<<"请输入把0到1的范围几等分?"<<"\t";cin>>m1;EchelonIntegral(m1);//3.直线求积分;cout<<endl;cout<<"是否要继续求该算法?(y/n)"<<"\t";cin>>answer1;}cout<<endl;}计算机科学与工程学院测试用例计算机科学与工程学院实验总结复化数值积分就是为了减少数值积分的误差,可以把积分区间分成若干小区间,在每个小区间上采取低阶数值积分公式,然后把这些小区间上的数值积分结果加起来作为函数在整个区间上的近似,类似于分段差值。
合工大计算方法实验报告

《计算方法》试验报告班级:学号:姓名:实验一、牛顿下山法1 实验目的(1)熟悉非线性方程求根简单迭代法,牛顿迭代及牛顿下山法 (2)能编程实现简单迭代法,牛顿迭代及牛顿下山法 (3)认识选择迭代格式的重要性 (4) 对迭代速度建立感性的认识;分析实验结果体会初值对迭代的影响2 实验内容(1)用牛顿下山法解方程013=--x x (初值为0.6)输入:初值,误差限,迭代最大次数,下山最大次数输出:近似根各步下山因子(2)设方程f(x)=x 3- 3x –1=0 有三个实根 x *1=1.8793 , x *2=-0.34727 ,x *3=-1.53209现采用下面六种不同计算格式,求 f(x)=0的根 x *1 或x *2 x = 213xx +; x = 313-x ;x = 313+x ; x = 312-x ;x = x13+;x = x - ()1133123---x x x输入:初值,误差限,迭代最大次数输出:近似根、实际迭代次数 3 算法基本原理求非线性方程组的解是科学计算常遇到的问题,有很多实际背景.各种算法层出不穷,其中迭代是主流算法。
只有建立有效的迭代格式,迭代数列才可以收敛于所求的根。
因此设计算法之前,对于一般迭代进行收敛性的判断是至关重要的。
牛顿法也叫切线法,是迭代算法中典型方法,只要初值选取适当,在单根附近,牛顿法收敛速度很快,初值对于牛顿迭代 至关重要。
当初值选取不当可以采用牛顿下山算法进行纠正。
一般迭代:)(1k k x x φ=+ 0)()(=⇔=x f x x φ 牛顿公式:)()(1k k k k x f x f x x '-=+ 牛顿下山公式:)()(1k k k k x f x f x x '-=+λ图3.1一般迭代算法流程图 下山因子 ,,,,322121211=λ 下山条件|)(||)(|1k k x f x f <+4 算法描述一般迭代算法见流程图牛顿下山算法见流程图:5、代码:#include <iostream>#include <fstream>#include <cmath>using namespace std;class srrt{private:int n;double *a, *xr, *xi;图3.2牛顿下山算法流程图⇐⇐⇐⇐srrt (int nn){n = nn;a = new double[n+1]; //动态分配内存xr = new double[n];xi = new double[n];}void input (); //由文件读入代数方程系数void srrt_root (); //执行牛顿下山法void output (); //输出根到文件并显示~srrt (){ delete [] a, xr, xi; }};void srrt::input () //由文件读入代数方程系数{int i;char str1[20];cout <<"\n输入文件名: ";cin >>str1;ifstream fin (str1);if (!fin){ cout <<"\n不能打开这个文件" <<str1 <<endl; exit(1); } for (i=n; i>=0; i--) fin >>a[i]; //读入代数方程系数fin.close ();}void srrt::srrt_root () //执行牛顿下山法{int m,i,jt,k,is,it;double t,x,y,x1,y1,dx,dy,p,q,w,dd,dc,c;double g,u,v,pq,g1,u1,v1;m=n;while ((m>0)&&(fabs(a[m])+1.0==1.0)) m=m-1;if (m<=0){cout <<"\n程序工作失败!" <<endl;return;}for (i=0; i<=m; i++) a[i]=a[i]/a[m];for (i=0; i<=m/2; i++){w=a[i]; a[i]=a[m-i]; a[m-i]=w;k=m; is=0; w=1.0;jt=1;while (jt==1){pq=fabs(a[k]);while (pq<1.0e-12){xr[k-1]=0.0; xi[k-1]=0.0; k=k-1;if (k==1){xr[0]=-a[1]*w/a[0]; xi[0]=0.0;return;}pq=fabs(a[k]);}q=log(pq); q=q/(1.0*k); q=exp(q);p=q; w=w*p;for (i=1; i<=k; i++){ a[i]=a[i]/q; q=q*p; }x=0.0001; x1=x; y=0.2; y1=y; dx=1.0;g=1.0e+37;l40:u=a[0]; v=0.0;for (i=1; i<=k; i++){p=u*x1; q=v*y1;pq=(u+v)*(x1+y1);u=p-q+a[i]; v=pq-p-q;}g1=u*u+v*v;if (g1>=g){if (is!=0){it=1;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}else{it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{g=g1; x=x1; y=y1; is=0;if (g<=1.0e-22){if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{u1=k*a[0]; v1=0.0;for (i=2; i<=k; i++){p=u1*x; q=v1*y; pq=(u1+v1)*(x+y);u1=p-q+(k-i+1)*a[i-1];v1=pq-p-q;}p=u1*u1+v1*v1;if (p<=1.0e-20){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}else{dx=(u*u1+v*v1)/p;dy=(u1*v-v1*u)/p;t=1.0+4.0/k;it=1;while (it==1){t=t/1.67; it=0;x1=x-t*dx;y1=y-t*dy;if (k>=50){p=sqrt(x1*x1+y1*y1);q=exp(85.0/k);if (p>=q) it=1;}}if (t>=1.0e-03) goto l40;if (g>1.0e-18){it=0;if (it==0){is=1;dd=sqrt(dx*dx+dy*dy);if (dd>1.0) dd=1.0;dc=6.28/(4.5*k); c=0.0;}while(1==1){c=c+dc;dx=dd*cos(c); dy=dd*sin(c);x1=x+dx; y1=y+dy;if (c<=6.29) { it=0; break; }dd=dd/1.67;if (dd<=1.0e-07) { it=1; break; }c=0.0;}if (it==0) goto l40;}if (fabs(y)<=1.0e-06){ p=-x; y=0.0; q=0.0; }else{p=-2.0*x; q=x*x+y*y;xr[k-1]=x*w;xi[k-1]=-y*w;k=k-1;}for (i=1; i<=k; i++){a[i]=a[i]-a[i-1]*p;a[i+1]=a[i+1]-a[i-1]*q;}xr[k-1]=x*w; xi[k-1]=y*w;k=k-1;if (k==1){ xr[0]=-a[1]*w/a[0]; xi[0]=0.0; }}}}if (k==1) jt=0;else jt=1;}}void srrt::output () //输出根到文件并显示{int k;char str2[20];cout <<"\n输出文件名: ";cin >>str2;ofstream fout (str2);if (!fout){ cout <<"\n不能打开这个文件" <<str2 <<endl; exit(1); } for (k=0; k<n; k++){fout <<xr[k] <<" " <<xi[k] <<endl;cout <<xr[k] <<" +j " <<xi[k] <<endl;}fout.close ();}void main () //主函数{srrt root(6);root.input (); //由文件读入代数方程系数root.srrt_root (); //执行牛顿下山法root.output (); //输出根到文件并显示}6、输入输出输出结果如下:7、分析体会牛顿下山法作为计算方法课程中重要的知识点,在看书学习时较易大致理解其思路,但上级编写代码时却是有难度的。
复化梯形算法求解数值积分

复化梯形算法求解数值积分梯形公式是一个基本的数值积分方法,它假设被积函数在每个小区间上是线性的。
具体来说,对于一个积分区间[a,b],将其等分成n个小区间,每个小区间的宽度为h=(b-a)/n。
则积分的近似计算可以表示为:∫[a, b]f(x)dx ≈ h/2 * [f(a) + 2f(x1) + 2f(x2) + ... +2f(xn-1) + f(b)]其中,xi是每个小区间的边界点,即xi = a + i*h。
1.将积分区间[a,b]等分成n个小区间,计算小区间宽度h=(b-a)/n。
2.初始化积分值I为0。
3.通过梯形公式计算每个小区间的积分值,并将其累加到I中。
具体步骤如下:- 计算小区间边界点xi = a + i*h,i从1到n-1- 计算每个小区间的函数值f(xi)。
-将小区间首尾函数值f(a)和f(b)分别乘以h的一半(即h/2)加到I中。
- 将中间小区间的函数值f(xi)乘以h加到I中。
4.返回积分值I作为近似结果。
需要注意的是,复化梯形算法对于一些函数可能不太适用。
在积分区间内存在较大的函数值变化或函数不连续的情况下,该算法的精度可能会下降。
此时,可以考虑使用其他更复杂的数值积分方法,如复化 Simpson 算法或高斯-勒让德公式。
综上所述,复化梯形算法是一种简单有效的数值积分方法。
通过将积分区间分成多个小区间,并使用梯形公式进行近似计算,可以得到较高精度的积分结果。
然而,该方法的速度较慢,并在一些情况下可能不太适用。
因此,在实际应用中,需要根据具体问题的特点选择合适的数值积分方法。
实验6 复合梯形公式

1 实验6 复合梯形公式 (重点)编写函数,实现复合梯形公式,并求解⎰+1
0411
dx x .
算法:
第一步:输入b a ,,ε,置1←n ,a b h -← 第二步:计算)]()([**5.0b f a f h T +=
第三步:计算])*5.0(*[*5.01
∑-=+++=n j jh h a f h T S 第四步:计算T S e -=,置S T ←,n n 2←,h h *5.0← 第五步:若ε≥e 则转到第三步,否则输出T ,结束。
function u=fhtx(a,b,e)
%单独定义函数,所以这里不出现函数的参数。
end
附分组名单:
组 长
第 1组 冯怡纯 罗 佳 马枨煊 李雄伟 第 2组 葛 韵 屈乾宇 王振海 王小曼 第 3组 魏 玲 姚玉婷 蔡文博 薛 姣 第 4组 吴 萍 郭琦慧 袁 鹏 吴昌磊 第 5组 刘鸿亮 唐 朝 裴成黎 张 宏 第 6组 王晓林 李 维 邱建宇 杨 超 第 7组 陈邯蕾 宋 平 邓春燕 张玲玲 第 8组 季海燕 余 雷 林 瑶 谢腾洲。
利用复化梯形公式、复化simpson 公式计算积分

1、运用复化梯形公式、复化simpson公式计算积分
2、比较计算误差与实际误差
实验原理(算法流程图或者含注释旳源代码)
取n=2,3,…,10分别运用复化梯形公式、复化simpson公式计算积分 ,并与真值进行比较,并画出计算误差与实际误差之间旳曲线。
运用复化梯形公式旳程序代码如下:
function f=fx(x)
functionf=fx1(x)
f=x.^4;
a=0;%积分下线
b=1;%积分上线
T=[];%用来装不同n值所计算出旳成果
forn=2:10
h=(b-a)/(2*n);%步长
x=zeros(1,2*n+1);%给节点定初值
for i=1:2*n+1
x(i)=a+(i-1)*h;%给节点赋值
end
y=x.^4;%给相应节点处旳函数值赋值
实
验
结
果
分
析
及
心
得
体
会
上图是运用复化梯形公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。-0.0017是计算误差。0.0417、0.0185、0.0104、0.00670.0046、0.0034、0.0026、0.0021、0.0017是n值分别为2到10旳实际误差。
上图是运用复化simpson公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。
t=0;
for i=1:n
t=t+h/3*(y(2*i-1)+4*y(2*i)+y(2*i+1));%运用复化simpson公式求值
end
T=[T,t];%把不同n值所计算出旳成果装入T中
end
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、实验内容及要求
(1)设计复化梯形公式求积算法,编制并调试相应的函数子程序
(2)设计复化辛浦生求积算法,编制并调试相应的函数子程序
(3)用龙贝格算法计算
输入:积分区间,误差限
输出:序列Tn,Sn,Cn,Rn及积分结果(参考书本P81的表2-5)
fxk12 = fxk12 + f(x);
cout<<"the result "<<4<<" is "<<longbeige(0, 1, 0.00000001);
return0;
}
2.复化梯形公式子程序:
doubletixing(doublea,doubleb,intn)
{
doublefa = f(a);
doublefb = f(b);
doubleh = (b-a) /n;
cout<<"1"<<" "<<tixing(0, 1, 2)<<" "<<xingbusheng(0, 1, 1)<<endl;
cout<<"2"<<" "<<tixing(0, 1, 4)<<" "<<xingbusheng(0, 1, 2)<<" "<<((double(16/15))* xingbusheng(0, 1, 2)) -(double(1/15))*xingbusheng(0, 1, 1)<<endl;
double fx = f(x);
s = s + 4.0*f(x);
x = x + h / (2.0);
s = s + 2.0*f(x);
}
s = (h / 6.0)*s;
return s;*/
for(intk = 0; k <=n- 1; k++)
{
doublexk1 =a+ k*h;
x = xk1 + h / 2.0;
合肥工业大学计算方法复化梯形公式实验
《计算方法》实验报告
学号
姓名
班级
实验项目名称
实验二 数值积分
一、实验名称
实验二数值积分
二、实验目的:
(1)熟悉复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法;
(2)能编程实现复化梯形方法、复化Simpson方法、梯形递推算法、龙贝格算法;
(3)理解并掌握自适应算法和收敛加速算法的基本思想;
cout<<"3"<<" "<<tixing(0,1,8)<<" "<<xingbusheng(0,1,4)<<" "<<((double(16 / 15))* xingbusheng(0, 1, 4)) - (double(1 / 15))*xingbusheng(0, 1, 2)<<" "<<longbeige(0, 1, 0.000000001)<<endl;
复化梯形公式
ห้องสมุดไป่ตู้复化Simpson公式
梯形递推公式
加权平均公式:
龙贝格算法大大加快了误差收敛的速度,由梯形序列O(h2)提高到龙贝格序列的O(h8)
五、程序代码及实验结果
1.主程序
intmain()
{
//cout << longbeige(0, 1, 0.0000001);
cout<<"请输入你的区间和误差限度:"<<endl;
{
doubleh = (b-a) /n;
doublefa = f(a);
doublefb = f(b);
//double s = fb - fa;
doublex =a;
doublefxk12 = 0.0;
doublefxk = 0.0;
/*for (int k = 1; k <=n; k++)
{
x = x + h / (2.0);
cout<<"4"<<" "<<tixing(0, 1, 16)<<" "<<xingbusheng(0, 1, 8)<<" "<<((double(16 / 15))* xingbusheng(0, 1, 4)) - (double(1 / 15))*xingbusheng(0, 1, 2)<<" "<<longbeige(0, 1, 0.00000001)<<endl;;
doublefxk = 0.0;
for(intk = 1; k <=n- 1; k++)
{
doublexk =a+ k*h;
fxk = f(xk) + fxk;
}
doubleres = (h / 2.0)*(fa + 2.0*fxk + fb);
returnres;
}
3.复化辛浦生公式子程序:
doublexingbusheng(doublea,doubleb,intn)
(1)找不到用初等函数表示的原函数
(2)虽然找到了原函数,但因表达式过于复杂而不便计算
(3)f(x)是由测量或计算得到的表格函数
由于以上种种困难,有必要研究积分的数值计算问题。
利用插值多项式 则积分 转化为 ,显然易算。 称为插值型求积公式。最简单的插值型求积公式是梯形公式和Simpson公式,。当求积结点提供较多,可以分段使用少结点的梯形公式和Simpson公式,并称为复化梯形公式、复化Simpson公式。如步长未知,可以通过误差限的控制用区间逐次分半的策略自动选取步长的方法称自适应算法。梯形递推公式给出了区间分半前后的递推关系。由梯形递推公式求得梯形序列,相邻序列值作线性组合得Simpson序列, Simpson序列作线性组合得柯特斯序列, 柯特斯序列作线性组合的龙贝格序列。若|R2-R1|<,则输出R2;否则…依此类推。如此加工数据的过程叫龙贝格算法,如下图所示:
doublex, y, z;
cin>>x>>y>>z;
cout<<"根据龙贝格算法求出的精确值为:"<<longbeige(x, y, z)<<endl;
cout<<"K"<<" "<<"T"<<" "<<"S"<<" "<<"C"<<" "<<"R"<<endl;
cout<<"0"<<" "<<tixing(0, 1, 1)<<endl;
取n=2,4,8,16,精确解为0.9460831
四、实验原理及算法描述
在许多实际问题中,常常需要计算定积分 的值。根据微积分学基本定理,若被积函数f(x)在区间[a,b]上连续,只要能找到f(x)的一个原函数F(x),便可利用牛顿-莱布尼兹公式 求得积分值。
但是在实际使用中,往往遇到如下困难,而不能使用牛顿-莱布尼兹公式。
