《结构力学》第四章 静定拱
合集下载
《结构力学》第四章静定拱
受力特点概述
静定拱在荷载作用下，拱身主要承受 压力作用，这使得拱具有较好的受压 性能。
拱身受压力作用
由于拱的曲线形状和荷载作用位置的 不同，拱身内力分布通常不均匀，需 要进行详细的内力分析。
内力分布不均匀
静定拱在荷载作用下，其变形主要以 压缩变形为主，弯曲变形相对较小。
变形以压缩为主
影响因素分析
面内失稳
1
拱在面内发生屈曲，导致承载力急剧下降。
面外失稳
2
拱在面外方向发生侧倾或扭转，失去原有形状。
局部失稳
3
拱的局部区域发生失稳，如拱脚的局部压曲等。
提高稳定性的措施
合理选择拱的轴线形式 使拱在受力时能够均匀分布荷载，避 免应力集中。
加强拱的横向联系
通过设置横撑、横系梁等构件，增强 拱的横向稳定性。
贰
静定拱的受力特点
受力分析基本假设
拱身是理想弹性体 在分析中，假设拱身材料符合胡克定律， 即应力与应变成正比关系。 荷载作用在拱的节点上 为简化计算，通常将荷载（如均布荷载、 集中力等）作用在拱的节点上进行分析。 忽略拱身自重影响 在分析中，通常忽略拱身自重对受力的影 响，或将其简化为等效荷载进行处理。
增加拱的刚度
采用高强度材料、增加截面尺寸等措 施，提高拱的整体刚度。
考虑施工方法和顺序
合理的施工方法和顺序可以有效减少 拱在施工过程中的变形和应力，有利 于提高稳定性。
陆
静定拱的工程应用
桥梁工程中的应用
拱桥
静定拱是拱桥的主要结构形式，能够承受较大的竖向荷载和水平推 力，具有良好的经济性和美观性。
习题一
某静定拱的跨度为L，矢高为f，承受均布 荷载q作用，试求其拱脚处的水平推力H和 竖向反力V。
李廉锟《结构力学》笔记和课后习题(含考研真题)详解-第4章 静定拱【圣才出品】
第4章 静定拱4.1 复习笔记【知识框架】【重点难点归纳】一、拱的基本概念及特点 ★★表4-1-1 拱的基本概念及特点表4-1-2 有拉杆和无拉杆三铰拱的区别与联系二、三铰拱的计算 ★★★★★1．支座反力的计算（见表4-1-3）表4-1-3 支座反力的计算2．内力的计算（见表4-1-4）表4-1-4 三铰拱的内力计算三、三铰拱的合理拱轴线（见表4-1-5） ★★★表4-1-5 三铰拱的合理拱轴线4.2 课后习题详解复习思考题1．拱的受力情况和内力计算与梁和刚架有何异同？答：（1）拱与梁的受力情况和内力计算的区别①约束反力方面，拱在竖向荷载作用下会产生水平反力（推力），而梁在竖向荷载作用下不会产生水平反力（推力）；②内力分布方面，由于水平推力的存在，拱的弯矩常比跨度、荷载相同的梁的弯矩小得多，使得拱截面上的应力分布较为均匀；③内力分析方法方面，若只有竖向荷载时，梁只需进行简单的整体分析即可求解，而拱由于水平力的存在，需要整体分析与局部分析相结合。
（2）拱与刚架的受力情况和内力计算的异同①内力分析方法方面，拱与刚架的受力情况和内力计算的特点和所应用方法基本一致，例如三铰刚架也属于拱式结构；②拱的轴线是曲线，刚架杆的轴线是直线，在应用平衡条件计算内力时，拱仍然取投2．在非竖向荷载作用下怎样计算三铰拱的反力和内力？能否使用式（4-1）和（4-2）？答：（1）对于三铰拱承受非竖向荷载的情况，可将非竖向荷载分解为水平荷载和竖向荷载。
（2）仍然可以应用式（4-1）和（4-2），将水平反力加上非竖向荷载水平方向上的分量一起代入公式中进行求解。
(4-1)o AV AV o BV BV o c H F F F F M F f ⎫⎪=⎪⎪=⎬⎪⎪=⎪⎭cos sin (4-2)sin cos o H o S S H o N S H M M F y F F F F F F ϕϕϕϕ⎫=-⎪⎪=-⎬⎪=+⎪⎭3．什么是合理拱轴线？试绘出图4-2-1各荷载作用下三铰拱的合理拱轴线形状。
第四章-静定拱
§4-1 基本概念 2.常见形式
铰 静 拱 三 拱—— 定 拱两 拱 铰 静 结 无 拱 超 定 构 铰
三铰拱
两铰拱
无铰拱
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-1 基本概念 3. 几何特性：
拱 顶 拱轴线 (拱轴 )拱高 起拱线来自拱趾 、 ) ( 跨度
内力不仅与三铰拱位置有关， 内力不仅与三铰拱位置有关，且与拱轴线形 状有关。
谢
谢 ！
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线
3.方法： 方法： 先作出压力线， ⑴ 先作出压力线，然后以压力线代 替拱轴。 替拱轴。 ° M 利用弯矩方程： ⑵ 利用弯矩方程： = M − Hy ° M∗ 令 M = M − Hy = 0 ⇒ y = H 即为合理拱轴线的纵坐标。 y即为合理拱轴线的纵坐标。
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线（Optimal centre line of arch） 三铰拱的合理拱轴线（ arch）
1.定义： 定义： 在已知荷载作用下， 在已知荷载作用下，能选择三铰拱的 轴线， 轴线，使得拱的所有横截面上的弯矩 为零。该拱的轴线就称为三铰拱的合 为零。该拱的轴线就称为三铰拱的合 理拱轴线。 理拱轴线。 条件： 2.条件： 拱轴线与压力线重合时， 拱轴线与压力线重合时，满足横截面 上的弯矩M Q=0 而仅有轴力N 上的弯矩M＝0、Q=0，而仅有轴力N。
l 9
dy 2 tgϕ = = (6 − x) dx 9
截面1 截面1：x1 = 1.56m
y1 = 1.75m tgϕ1 = 1 ϕ1 = 450
铰 静 拱 三 拱—— 定 拱两 拱 铰 静 结 无 拱 超 定 构 铰
三铰拱
两铰拱
无铰拱
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-1 基本概念 3. 几何特性：
拱 顶 拱轴线 (拱轴 )拱高 起拱线来自拱趾 、 ) ( 跨度
内力不仅与三铰拱位置有关， 内力不仅与三铰拱位置有关，且与拱轴线形 状有关。
谢
谢 ！
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线
3.方法： 方法： 先作出压力线， ⑴ 先作出压力线，然后以压力线代 替拱轴。 替拱轴。 ° M 利用弯矩方程： ⑵ 利用弯矩方程： = M − Hy ° M∗ 令 M = M − Hy = 0 ⇒ y = H 即为合理拱轴线的纵坐标。 y即为合理拱轴线的纵坐标。
第四章 静定拱式结构（Arch） 静定拱式结构（Arch）
§4-4 三铰拱的合理拱轴线（Optimal centre line of arch） 三铰拱的合理拱轴线（ arch）
1.定义： 定义： 在已知荷载作用下， 在已知荷载作用下，能选择三铰拱的 轴线， 轴线，使得拱的所有横截面上的弯矩 为零。该拱的轴线就称为三铰拱的合 为零。该拱的轴线就称为三铰拱的合 理拱轴线。 理拱轴线。 条件： 2.条件： 拱轴线与压力线重合时， 拱轴线与压力线重合时，满足横截面 上的弯矩M Q=0 而仅有轴力N 上的弯矩M＝0、Q=0，而仅有轴力N。
l 9
dy 2 tgϕ = = (6 − x) dx 9
截面1 截面1：x1 = 1.56m
y1 = 1.75m tgϕ1 = 1 ϕ1 = 450
《结构力学》第四章 静定结构的位移计算 (3)
A M k M P ds
B EI
2
R 1
cos
( FP R
sin
)
Rd
0
EI
d
FPR3
2EI
FPk 1
A
B Bx 2 By 2
B kP
B
A M k M P ds B EI
2
(1)
(FPR sin
)
Rd
0
EI
R
O
FP R2 （
）
EI
（1）梁与刚架
三、结构的外力虚功
作用在结构上的外力可能是单个的集中力、力 偶、均布力，也可能是一个复杂的力系，为了 书写方便，通常将外力系的总虚功记为：
W = Fk × km
其中，Fk为作功的力或力系，称为广义力; km为广义力作功的位移，称为广义位移。 下面讨论几种常见广义力的虚功。
1) 集中力的虚功
Pk
k
M
4EIk
GAl 2
kP
若截面为矩形，则：A bh, I bh3 /12,k 6 l 1, 2
h / l 1 , 10
h/l 1 , 15
则：
Q kP
( h)2
Q
M kP
l
kP 25% kMP
对于粗短杆来说，剪 切变形产生的位移不可忽
Q
kP 1%
1
m
ds
第i根杆件静力状态上的力在位移状态的位移上所 作的虚功：
Vi
s FNk
mds
s FQk mds
s Mk
1
m
ds
整个杆件结构各个截面上的内力在位移状态的位 移上的所作的总虚功：
N
N
N
B EI
2
R 1
cos
( FP R
sin
)
Rd
0
EI
d
FPR3
2EI
FPk 1
A
B Bx 2 By 2
B kP
B
A M k M P ds B EI
2
(1)
(FPR sin
)
Rd
0
EI
R
O
FP R2 （
）
EI
（1）梁与刚架
三、结构的外力虚功
作用在结构上的外力可能是单个的集中力、力 偶、均布力，也可能是一个复杂的力系，为了 书写方便，通常将外力系的总虚功记为：
W = Fk × km
其中，Fk为作功的力或力系，称为广义力; km为广义力作功的位移，称为广义位移。 下面讨论几种常见广义力的虚功。
1) 集中力的虚功
Pk
k
M
4EIk
GAl 2
kP
若截面为矩形，则：A bh, I bh3 /12,k 6 l 1, 2
h / l 1 , 10
h/l 1 , 15
则：
Q kP
( h)2
Q
M kP
l
kP 25% kMP
对于粗短杆来说，剪 切变形产生的位移不可忽
Q
kP 1%
1
m
ds
第i根杆件静力状态上的力在位移状态的位移上所 作的虚功：
Vi
s FNk
mds
s FQk mds
s Mk
1
m
ds
整个杆件结构各个截面上的内力在位移状态的位 移上的所作的总虚功：
N
N
N
结构力学-静定拱
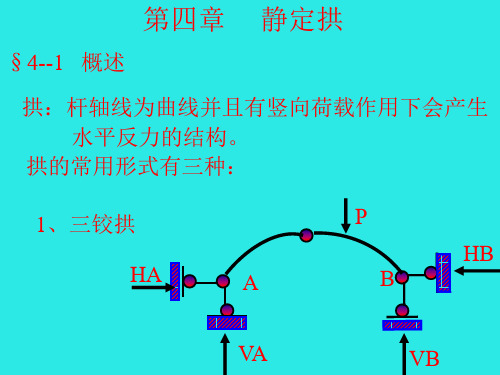
H=M’C/f 2 内力计算：
截面Ｋ的弯矩： M=[Vax－P1(x－a1)]－Hy
即 M=M’－Hy
A
P1
P2
B
ＫC
剪力：
Ｑ=VA cos --P1 cos--H sin V’A
V’B
＝Ｑ’ cos --H sin
轴力：
HA
P1 Ｋ
A
P2
B
HB
N=(VA--P1) sin+
Hcos
第四章 静定拱
§4--1 概述
拱：杆轴线为曲线并且有竖向荷载作用下会产生 水平反力的结构。
拱的常用形式有三种：
1、三铰拱
HA
A
P
HB B
VA
VB
2 两铰拱
3 无铰拱
拱的各部分名称如右图：拱 趾
起拱线
A
拱轴线
拱
拱高f
趾
B
跨度l
§4--2 三铰拱的数解法
1 支座反力计算
如右图： 由MB=0
a1
b1
VA
VB
=Q’sin +Hsin
综上所述，三铰平拱的内力计算公
式可写为：
M=M’--Hy
Q=Q’ cos --H sin
N=Q’ sin --H cos
§4--3 三铰拱的合理拱轴线
当拱上所有截面的弯矩都为零而只有轴力时，这
时的拱轴线为合理拱轴线。其方程为： y=M’/H
q
例４－２
y
a2
b2
P1
P2
MA=0
HA
A
HB B
HA=HB=H
l1
MC=0
VA
l2 VB
VAl1－P1(l1－a1)－Hf=0 l
结构力学4静定拱
x 、 y，截面切线的倾斜
角为 θ 。且左半拱的为
FHA
正值，右半拱的 θ 为负
值。
考虑截面左侧部份平衡,由 FH
K f
A
x
B
x
l/ 2
FVA
F2
F1 K
?
l/ 2
MK
FN K y
F SK
FHB F
VB
由∑MK=0可得
FVA
M K ? ?FVA ?x ? F1?x ? b1?? F2 ?x ? b2 ??? FH ?y F1 F2
a2 a3
F3
B
F0 VB
退出
返回
00:42
§4-2 三铰拱的数值解
结构力学
三铰拱任意截面K上的内力MK、FSK和FNK的计 算公式：
MK
?
M
0 K
?
FH y
FSK ? FS0K cos? ? FH sin?
FNK ? FS0K sin? ? FH cos?
拱的弯矩要比同跨度同荷载的简支梁的弯矩小 很多，当跨度比较大时采用拱比用梁要更为经济合 理。
FND ? FS0D sin?D ? FH cos?0
退出
返回
00:42
§4-2 三铰拱的数值解
结构力学
考虑整体平衡
y
F
F
C
由∑X=0，得 FHA ? FHB ? FH
K
由∑MA=0
FHA
F1a1 ? F2a2 ? F3a3 ? FVBl ? 0
得
FVB
?
1 l
?F1a1
?
F2a2 ?
F3a3 ?
由∑MB=0，得
A
x
结构力学第4章静定拱(f)
FH
FH
由边界条件
x 0, y 0 : x 0, y 0 :
A qc
B0
合理拱轴线的方程为
y qc (cosh x 1)
FH
§4-3 三铰拱的合理拱轴线
例4-3 试求三铰拱在垂直于拱轴线的均布荷载作用下的合理 拱轴线。
解：由图a，荷载为非竖向荷载。
思路：假定拱处于无弯矩状态，根据平衡 条件推求合理拱轴线方程。
Fi ai l
Fx 0 FAH FBH FH
相应简支梁
取左半拱为隔离体
MC 0
FH
FAV l1 F1(l1 a1) f
可 得
FAV FBV
FA0V FB0V
FH
M
0 C
f
三铰拱的反力只与 荷载及三个铰的位置有 关，与拱轴线形状无关；
推力FH 与拱高 f 成反比。
§4-2 三铰拱的计算
§4-2 三铰拱的计算
2、内力的计算
压力为正
任一截面的轴力等于该截面一 侧所有外力在该截面法线方向 上的投影代数和。
FN FAV sin FH cos F1 sin (FAV F1) sin FH cos FS0 sin FH cos
相应简支梁
§4-2 三铰拱的计算
2、内力的计算
区别拱与梁的主要标志：推力的存在与否。
§4-1 概述
拉杆拱： 拱两支座间的拉杆代替支座承受水平推力
拉杆做成折线形可获得较大空间
高跨比：f/l
平拱： 两拱趾在同一水平线上 斜拱： 两拱趾不在同一水平线上
§4-2 三铰拱的计算
1、支座反力的计算
由拱的整体平衡
M B 0 FAV
Fibi l
M A 0 FBV
第四章结构力学静定拱
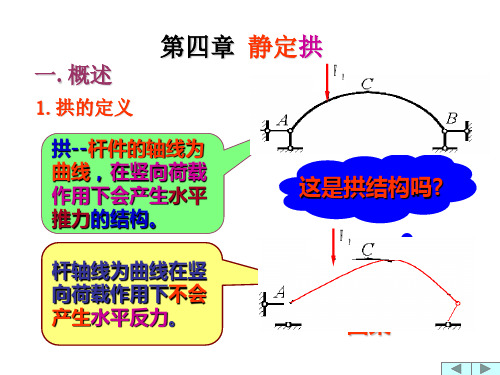
15kN
A
K左
A
K右
12.5kN
12.5kN
FºSK左＝12.5kN
FºSK右＝－2.5kN
( F H 1 0 k N ,F S 0 K 左 1 2 . 5 k N ,F S 0 K 右 2 . 5 k N )
( s i n 0 .4 4 7 ,c o s 0 .8 9 4 )
FSK左FS0K左cosFHsin12.50.894100.447
r FP1 90。 D D
C
FQD A
FP2 B
FRA
FRB
M D FRD rD
FQD FRD sin D FND FRD cos D
r D ——截面D形心到FRD作用线之距离。
D ——FRD作用线与截面D轴线切线的夹角。
由此看出，确定截面内力的问题归结为确定 截面一边所有外力的合力之大小、方向及作用线 的问题。
tgy'4l2f
(l2x)a b
F
V
0 A
FP1
D
F
0 SD
代梁
a2+b2 a
b
2) FºSD是代梁截面D的剪力，设为正方向。 故FºSD可能大于零、等于零或小于零。
下面用上述公式求FSK、FNK。
xK＝4m y'41 624(1624)1 2 FºSK左＝12.5kN
5
1 2
FºSK右＝－2.5kN
FP2 E FP1
D
FRA A
o
C FP1 FP2
FRA
FRB
FP3
FP3 F
B
FRB
在上图所示力多边形中，射线1－2代表FRA与 FP1合力的大小和方向；射线2－3代表FRA与FP1、 FP2合力的大小和方向。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
B
YB0
YB=YB0
YA=YA0
XA=XB =H
无力Y关与A .拱荷轴载线与形跨M状度c0 一定时，水平推 力与矢Y高A0 成反比.
H
1 f
[YA
l 2
P1
(
l 2
a1)]
M
0 c
[YA0
l 2
P1(Βιβλιοθήκη l 2a1 )]H= MC0 / f
二、三铰拱的数解法 y P1 K C
----内力计算 P2
拉杆
超静定拱
拉杆拱
超静定拱
两铰拱
无铰拱 斜拱
高差h
拱 (arch)
一、概述
4.拱的有关名称 顶铰
拱肋 拱趾铰
拱肋 矢高 拱趾铰
跨度
二、三铰拱的数解法 ----支反力计算
P1
C
P2
三铰拱的竖向反 力与其等代梁的
A
f
B XB 反H力相等;水平反
XA
l/2 l/2
YA
l
YB
等代梁请A 问P:1有水平C荷载,或P2 YA铰 不 论0 是 还Ca不1平是再拱正a顶2确,右部的边b,1或吗的?结b2
第四章 静定拱
拱 (arch)
一、概述
杆轴线为曲线 在竖向荷载作 用下不产生水
平反力。
1.拱的定义 这是拱结构吗?
曲梁
拱--杆轴线为曲
线，在竖向荷载 作用下会产生水
拱
平推力的结构。
拱 (arch) 2.拱的受力特点
一、概述 拱
曲梁
P
拱比梁中的弯矩小
拱 (arch)
一、概述
3.拱的分类
静定拱
三铰拱
下轴向a1受压。 b1
NK Q 0Ksin H cos
YA0
a2
b2 YB0
三、三铰拱的合理拱轴线
(reasonable axis of arch)
M M0H y0
y M0 H
只限于三铰平拱受 竖向荷载作用
使拱在给定荷载下只 产生轴力的拱轴线，被 称为与该荷载对应的合 理拱轴
在竖向荷载作用下，三 铰拱的合理拱轴线的纵 坐标与相应简支梁弯矩 图的竖标成正比。
载及A 三三个x铰铰拱y的的位内f 置力有不关但，与B而荷 XB X A
XA且与拱轴l/线2 的形状l/有2x 关。
YA
QK M K P1
NK
P1
M
0 K
YA 由于推力的l 存在，拱Y的B
YA0
QK0
弯矩比相应简支梁的弯矩要
小。 P1
A
KC
P2
B
三铰拱在竖向荷载作用
MK
M
0 K
Hy
QK Q 0Kcos H sin
试求图示对称三铰拱在均布荷载作用下 的合理拱轴线
MC0=ql2/8 H=ql2/8f M0=qlx/2-qx2 /2 =qx(l-x)/2 y=4fx(l-x)/l2
抛物线