【强烈推荐】四年级最典型的30道应用题:定义+数量关系+例题详解
四年级数学下册解答应用题训练30篇经典题型带答案解析
四年级数学下册解答应用题训练30篇经典题型带答案解析一、人教四年级下册数学应用题1.小红、小丽和小芳去商店买文具,小红花了11.36元,比小丽多花了2.75元,小丽比小芳少花了1.97元,小芳花了多少元?2.六年级同学分组参加课外兴趣小组,每人只能参加一个小组。
科技类每5人一组,艺术类每3人一组,共有37名学生报名,正好分成9个组。
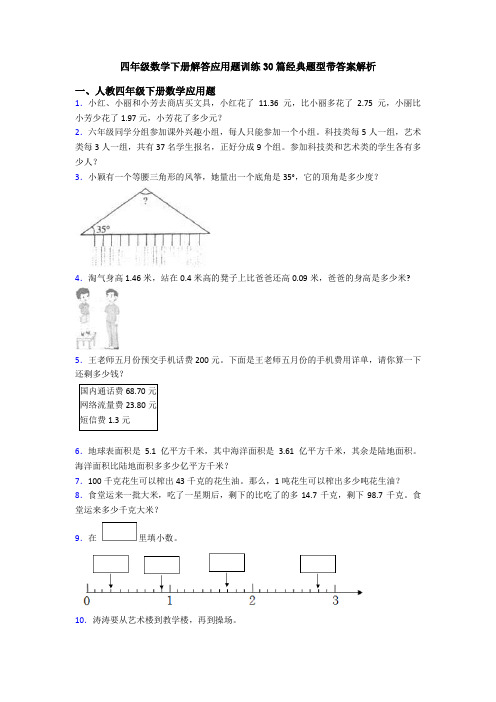
参加科技类和艺术类的学生各有多少人?3.小颖有一个等腰三角形的风筝,她量出一个底角是35°,它的顶角是多少度?4.淘气身高1.46米,站在0.4米高的凳子上比爸爸还高0.09米,爸爸的身高是多少米?5.王老师五月份预交手机话费200元。
下面是王老师五月份的手机费用详单,请你算一下还剩多少钱?国内通话费68.70元网络流量费23.80元短信费1.3元6.地球表面积是5.1亿平方千米,其中海洋面积是3.61亿平方千米,其余是陆地面积。
海洋面积比陆地面积多多少亿平方千米?7.100千克花生可以榨出43千克的花生油。
那么,1吨花生可以榨出多少吨花生油?8.食堂运来一批大米,吃了一星期后,剩下的比吃了的多14.7千克,剩下98.7千克。
食堂运来多少千克大米?9.在里填小数。
10.涛涛要从艺术楼到教学楼,再到操场。
(1)请你画出涛涛从艺术楼去教学楼,再到操场最近的路。
(2)从艺术楼去教学楼,再到操场最近的距离是186米。
如果涛涛平均每分走62米,从艺术楼沿最近的路先到教学楼再到操场要多少分?11.爸爸带着小军去超市购物,爸爸带的钱数的小数点向左移动一位就是小军带的钱数,两人一共带了148.5元钱。
请你算一算,爸爸和小军各带了多少元钱?12.学校要购买48个足球。
甲、乙两家体育用品商店一种足球的原价都是每个33元,这两家商店的优惠方式如下:甲店:每个足球优惠8元。
乙店:买10个足球免费赠送2个,不足10个不赠送。
请你帮忙算一算,到哪家商店买更便宜?便宜多少钱?13.(1)四位老师带上六名同学,怎样购票合算?需要多少钱?(2)六名老师带上3名同学,怎样购票合算?需要多少钱?14.一个成人10天大约需要多少克食盐?合多少千克?再估一估,一年大约需要多少千克食盐?15.红红家有一口可以装满3升水的锅,中午妈妈给锅中注入了5满碗水熬粥,正好注入了半锅水。
:必考30道典型应用题:定义+数量关系+例题详解!

小学数学老师:必考30道典型应用题:定义+数量关系+例题详解!
应用题作为小学数学的一道“坎”,很多孩子都在应用题这个地方丢分。
想要孩子应用题少丢分甚至不丢分,首先需要让孩子弄懂的就是小学数学试卷中常考的应用题题型有哪些?
了解常考题型之后,再根据这些题型做一些针对训练。
不过小学数学应用题总共有30类,而这30类应用题都有相应的典型应用题,家长们让孩子吃透这些应用题,孩子的数学应用题就能够大幅度提升。
小学数学对孩子来讲最难的估计就是应用题了,想要对应用题进行突破就要花费一些时间找出问题所在,然后复习,做题训练,查漏补缺,很快就能将数学成绩提升上来。
特别是六年级的孩子,面临着小升初,如果连小学的应用题都没有掌握到位,到了初中学习数学会更加的困难。
如果家中的小孩数学应用题丢分严重,各位家长们就可以打印这份小学数学老师整理的必考30道典型应用题:定义+数量关系+例题详解!孩子轻松吃透应用题难题。
小学数学孩子一看就懂的三十类图解应用题

十九、“牛吃草”问题【含义】“牛吃草”问题是大科学家牛顿提出的问题,也叫“牛顿问题”。
这类问题的特点在于要考虑草边吃边长这个因素。
【数量关系】草总量=原有草量+草每天生长量×天数【解题思路和方法】解这类题的关键是求出草每天的生长量。
例1: 一块草地,10头牛20天可以把草吃完,15头牛10天可以把草吃完。
问多少头牛5天可以把草吃完?解草是均匀生长的,所以,草总量=原有草量+草每天生长量×天数。
求“多少头牛5天可以把草吃完”,就是说5 天的草总量要 5 天吃完的话,得有多少头牛?设每头牛每天吃草量为1,按以下步骤解答:20天内草生长量原有草量10头牛20天把草吃完………10天1×15×10=原有草量+10天内生长量5天1×?×5=原有草量+5天内生长量1头牛1天吃的草原有草量………10天内草生长量1头牛1天吃的草?头牛5天把草吃完20天1×10×20=原有草量+20天内生长量15头牛10天把草吃完………1头牛1天吃的草原有草量5天内草生长量(20-10)天内草的生长量为1×10×20-1×15×10=50 草每天的生长量为50÷(20-10)=5原有草量=10天内总草量-10内生长量=1×15×10-5×10=1005 天内草总量=原有草量+5天内生长量=100+5×5=125(1)求草每天的生长量因为,一方面20天的草总量就是10头牛20天所吃的草,即(1×10×20);另一方面,20天的草总量又等于原有草量加上20天的生长量,所以1×10×20=原有草量+20天生长量同理1×15×10=原有草量+10天生长量由此可知(20-10)天草的生长量为1×10×20-1×15×10=50因此,草每天的生长量为50÷(20-10)=5(2)求原有草量原有草量=10天总草量-10生长量=1×15×10-5×10=100(3)求5 天草总量5 天草总量=原有草量+5天生长量=100+5×5=125(4)求多少头牛 5 天吃完草因为每头牛每天吃草量为1,所以每头牛5天吃草量为5。
四年级数学下册解答应用题训练30篇真题带答案解析
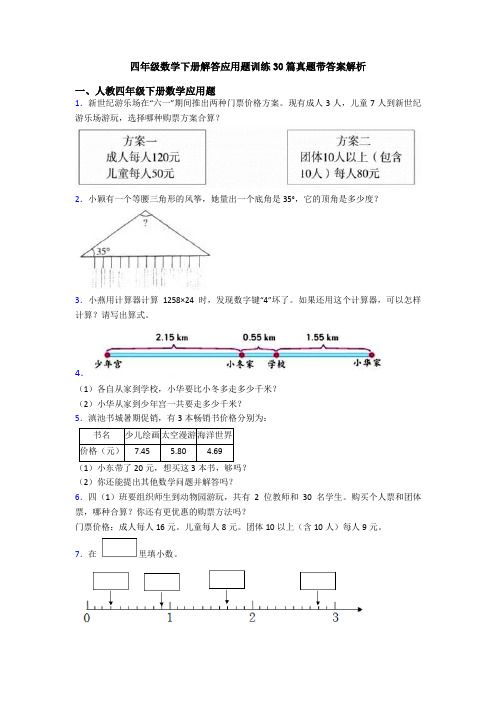
四年级数学下册解答应用题训练30篇真题带答案解析一、人教四年级下册数学应用题1.新世纪游乐场在“六一”期间推出两种门票价格方案。
现有成人3人,儿童7人到新世纪游乐场游玩,选择哪种购票方案合算?2.小颖有一个等腰三角形的风筝,她量出一个底角是35°,它的顶角是多少度?3.小燕用计算器计算1258×24时,发现数字键“4”坏了。
如果还用这个计算器,可以怎样计算?请写出算式。
4.(1)各自从家到学校,小华要比小冬多走多少千米?(2)小华从家到少年宫一共要走多少千米?5.滇池书城暑期促销,有3本畅销书价格分别为:书名少儿绘画太空漫游海洋世界价格(元)7.45 5.80 4.69(2)你还能提出其他数学问题并解答吗?6.四(1)班要组织师生到动物园游玩,共有2位教师和30名学生。
购买个人票和团体票,哪种合算?你还有更优惠的购票方法吗?门票价格:成人每人16元。
儿童每人8元。
团体10以上(含10人)每人9元。
7.在里填小数。
8.一种牛奶有三种售法:一箱(24瓶)70元,一组(3瓶)10元,1瓶4元。
四(1)班开展联欢会要买56瓶这样的牛奶,怎样买最省钱?最少要多少钱?9.涛涛要从艺术楼到教学楼,再到操场。
(1)请你画出涛涛从艺术楼去教学楼,再到操场最近的路。
(2)从艺术楼去教学楼,再到操场最近的距离是186米。
如果涛涛平均每分走62米,从艺术楼沿最近的路先到教学楼再到操场要多少分?10.探索园。
(1)上面是同一种盒装面巾纸的价钱。
一家宾馆要买45盒这种面巾纸,怎样买最省钱?列式解答。
(2)810÷45=(810÷9)÷(45÷9)=90÷5=18你能用这种方法计算下面两道题吗?试一试!①2800÷56=②360÷24=11.学校要购买48个足球。
甲、乙两家体育用品商店一种足球的原价都是每个33元,这两家商店的优惠方式如下:甲店:每个足球优惠8元。
数学四年级下册典型的30道应用题:定义+数量关系+例题详解

归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量;1份数量×所占份数=所求几份的数量;另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1. 买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解:买1支铅笔多少钱?0.6÷5=0.12(元)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例2. 3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6天耕地多少公顷?解:1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6天耕地300公顷。
例3. 5辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解:1辆汽车1次能运多少吨钢材?100÷5÷4=5(吨)7辆汽车1次能运多少吨钢材?5×7=35(吨)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式105÷(100÷5÷4×7)=3(次)答:需要运3次。
归总问题【含义】解题时,常常先找出“总数量”,然后再根据其它条件算出所求的问题,叫归总问题。
所谓“总数量”是指货物的总价、几小时(几天)的总工作量、几公亩地上的总产量、几小时行的总路程等。
【数量关系】1份数量×份数=总量;总量÷1份数量=份数;总量÷另一份数=另一每份数量【解题思路和方法】先求出总数量,再根据题意得出所求的数量。
四年级数学下册解答应用题训练30篇(经典版)带答案解析

四年级数学下册解答应用题训练30篇(经典版)带答案解析一、人教四年级下册数学应用题1.学校组织120名师生去春游,请你设计一种最省钱的租车方案,租金是多少元?2.王叔叔周日骑车旅行,上午骑行38.5千米,比下午多骑行2.65千米,王叔叔周日一共骑行了多少千米?3.在□里填上适当的分数或小数。
4.小强身高1.35米,他站在0.5米高的凳子上时,比爸爸高0.05米。
求爸爸的身高是多少米。
5.滇池书城暑期促销,有3本畅销书价格分别为:书名少儿绘画太空漫游海洋世界价格(元)7.45 5.80 4.69(1)小东带了20元,想买这3本书,够吗?(2)你还能提出其他数学问题并解答吗?6.100千克花生可以榨出43千克的花生油。
那么,1吨花生可以榨出多少吨花生油?7.一辆新能源汽车行100km耗电13千瓦时。
8.爸爸带着小军去超市购物,爸爸带的钱数的小数点向左移动一位就是小军带的钱数,两人一共带了148.5元钱。
请你算一算,爸爸和小军各带了多少元钱?9.五一放假期间,某游乐园推出两种优惠方案。
(1)东东一家去游乐园游玩,选哪种方案合算?(2)四(2)班有40名学生,在2名老师的带领下组织去游乐园。
请你选择合适的方案并解答。
10.某购物网上某品牌乒乓球,A、B两店的价格如下图。
李老师要买30个乒乓球,该去哪家店买?11.一根小棒长12厘米,把它剪成3段(每段都取整厘米数),首尾相连搭成三角形,可以怎样剪?请写出来。
12.三个数分别是a、b、c,a与b的和是39.08,b与c的和是21.68,a、b、c三个数的和是58.58。
三个数各是多少?13.直角三角形的一个锐角是另一个锐角的2倍。
请问这两个锐角各是多少度?14.小芳储蓄罐里有78.42元,昨天用11.9元买了一支钢笔,今天妈妈又给她2.75元。
现在储蓄罐里有多少钱?15.已知∠1 、∠2 、∠3 是一个三角形的三个内角,∠1 的度数是∠2与∠3的度数和。
∠1是多少度?这个三角形是什么三角形?16.在一个三角形中,当其中两个内角的和等于第三个角时,按角分类,这是一个()三角形,为什么?请用你喜欢的方式说明。
小学数学30种典型应用题分类讲解附带例题和解题过程

小学数学30种典型应用题讲解应用题可分为一般应用题与典型应用题。
没有特定的解答规律的两步以上运算的应用题,叫做一般应用题。
题目中有特殊的数量关系,可以用特定的步骤和方法来解答的应用题,叫做典型应用题. 以下主要研究30类典型应用题:1、归一问题2、归总问题3、和差问题4、和倍问题5、差倍问题6、倍比问题7、相遇问题8、追及问题9、植树问题10、年龄问题11、行船问题12、列车问题13、时钟问题14、盈亏问题15、工程问题16、正反比例问题17、按比例分配18、百分数问题19、“牛吃草”问题20、鸡兔同笼问题21、方阵问题22、商品利润问题23、存款利率问题24、溶液浓度问题25 、构图布数问题26、幻方问题27、抽屉原则问题28、公约公倍问题29、最值问题30、列方程问题1 归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1 买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解(1)买1支铅笔多少钱? 0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式 0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例2 3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6 天耕地多少公顷?解(1)1台拖拉机1天耕地多少公顷? 90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷? 10×5×6=300(公顷)列成综合算式 90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6 天耕地300公顷。
四年级数学解答应用题训练30篇带答案解析

四年级数学解答应用题训练30篇带答案解析一、人教四年级下册数学应用题1.已知∠1 、∠2 、∠3 是一个三角形的三个内角,∠1 的度数是∠2与∠3的度数和。
∠1是多少度?这个三角形是什么三角形?2.学校食堂运来大米和面粉各80袋,大米每袋75千克,面粉每袋25千克,大米和面粉共多少千克?3.王叔叔周日骑车旅行,上午骑行38.5千米,比下午多骑行2.65千米,王叔叔周日一共骑行了多少千米?4.1000千克芒果能制作芒果干147千克,1千克芒果能制作芒果干多少克?5.小东在家探究用不同的思路计算两个长方形(如下图)拼组后的面积总和。
(1)小东想先分别求出两个长方形的面积,再求面积总和,应该列式为________。
(2)小东想通过找寻拼成后大长方形的数据来计算长方形的面积,应该列式为________。
(3)小东进一步探究,发现了这两个算式之间的关系,就是我们这学期所学的一种运算定律。
你知道是什么运算定律吗?请写出这种运算定律的名称,并用含有字母的算式把它表示出来。
6.100千克花生可以榨出43千克的花生油。
那么,1吨花生可以榨出多少吨花生油?7.一辆新能源汽车行100km耗电13千瓦时。
8.食堂运来一批大米,吃了一星期后,剩下的比吃了的多14.7千克,剩下98.7千克。
食堂运来多少千克大米?9.服装店购进某种衬衫24件,进货价是90元/件,按照每件115元卖出后,一共可以赚多少元钱?10.在里填小数。
11.一副三角板1.35元,比一支圆珠笔便宜0.1元,小红买一副三角板和一支圆珠笔共付了5元,应找回多少元?12.遗爱湖公园有大小两种游船,每条大船能坐8人,每条小船能坐6人。
实验小学136名师生去划船。
租了大船和小船共18条,正好全部坐满。
他们租了多少条大船?13.学校要购买48个足球。
甲、乙两家体育用品商店一种足球的原价都是每个33元,这两家商店的优惠方式如下:甲店:每个足球优惠8元。
乙店:买10个足球免费赠送2个,不足10个不赠送。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
归一问题【含义】在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
这类应用题叫做归一问题。
【数量关系】总量÷份数=1份数量;1份数量×所占份数=所求几份的数量;另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例1. 买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解:买1支铅笔多少钱?0.6÷5=0.12(元)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例2. 3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6天耕地多少公顷?解:1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6天耕地300公顷。
例3. 5辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解:1辆汽车1次能运多少吨钢材?100÷5÷4=5(吨)7辆汽车1次能运多少吨钢材?5×7=35(吨)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式105÷(100÷5÷4×7)=3(次)答:需要运3次。
归总问题【含义】解题时,常常先找出“总数量”,然后再根据其它条件算出所求的问题,叫归总问题。
所谓“总数量”是指货物的总价、几小时(几天)的总工作量、几公亩地上的总产量、几小时行的总路程等。
【数量关系】1份数量×份数=总量;总量÷1份数量=份数;总量÷另一份数=另一每份数量【解题思路和方法】先求出总数量,再根据题意得出所求的数量。
例1. 服装厂原来做一套衣服用布3.2米,改进裁剪方法后,每套衣服用布2.8米。
原来做791套衣服的布,现在可以做多少套?解:这批布总共有多少米?3.2×791=2531.2(米)现在可以做多少套?2531.2÷2.8=904(套)列成综合算式3.2×791÷2.8=904(套)答:现在可以做904套。
例2. 小华每天读24页书,12天读完了《红岩》一书。
小明每天读36页书,几天可以读完《红岩》?解:《红岩》这本书总共多少页?24×12=288(页)小明几天可以读完《红岩》?288÷36=8(天)列成综合算式24×12÷36=8(天)答:小明8天可以读完《红岩》。
例3. 食堂运来一批蔬菜,原计划每天吃50kg,30天慢慢消费完这批蔬菜。
后来根据大家的意见,每天比原计划多吃10kg,这批蔬菜可以吃多少天?解:这批蔬菜共有多少千克?50×30=1500(千克)这批蔬菜可以吃几天?1500÷(50+10)=25(天)列成综合算式50×30÷(50+10)=25(天)答:这批蔬菜可以吃25天。
和差问题【含义】已知两个数量的和与差,求这两个数量各是多少,这类应用题叫和差问题。
【数量关系】大数=(和+差)÷2;小数=(和-差)÷2【解题思路和方法】简单的题目可以直接套用公式;复杂的题目变通后再用公式。
例1. 甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解:甲班人数:(98+6)÷2=52(人)乙班人数:(98-6)÷2=46(人)答:甲班有52人,乙班有46人。
例2. 长方形的长和宽之和为18厘米,长比宽多2厘米,求长方形的面积。
解:长=(18+2)÷2=10(厘米)宽=(18-2)÷2=8(厘米)长方形的面积10×8=80(平方厘米)答:长方形的面积为80平方厘米。
例3. 有甲乙丙三袋化肥,甲乙两袋共重32千克,乙丙两袋共重30千克,甲丙两袋共重22千克,求三袋化肥各重多少千克。
解:甲乙两袋、乙丙两袋都含有乙,从中可以看出甲比丙多(32-30)=2千克,且甲是大数,丙是小数。
由此可知:甲袋化肥重量:(22+2)÷2=12(千克)丙袋化肥重量:(22-2)÷2=10(千克)乙袋化肥重量:32-12=20(千克)答:甲袋化肥重12千克,乙袋化肥重20千克,丙袋化肥重10千克。
例4. 甲乙两车原来共装苹果97筐,从甲车取下14筐放到乙车上,结果甲车比乙车还多3筐,两车原来各装苹果多少筐?解:从甲车取下14筐放到乙车上,结果甲车比乙车还多3筐,说明甲车是大数,乙车是小数,甲与乙的差是(14×2+3),甲与乙的和是97,因此:甲车筐数:(97+14×2+3)÷2=64(筐)乙车筐数:97-64=33(筐)答:甲车原来装苹果64筐,乙车原来装苹果33筐。
和倍问题【含义】已知两个数的和及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做和倍问题。
【数量关系】总和÷(几倍+1)=较小的数;总和-较小的数=较大的数;较小的数×几倍=较大的数【解题思路和方法】简单的题目直接利用公式,复杂的题目变通后利用公式。
例1. 果园里有杏树和桃树共248棵,桃树的棵数是杏树的3倍,求杏树、桃树各多少棵?解:杏树有多少棵?248÷(3+1)=62(棵)桃树有多少棵?62×3=186(棵)答:杏树有62棵,桃树有186棵。
例2. 东西两个仓库共存粮480吨,东库存粮数是西库存粮数的1.4倍,求两库各存粮多少吨?解:西库存粮数:480÷(1.4+1)=200(吨)东库存粮数:480-200=280(吨)答:东库存粮280吨,西库存粮200吨。
例3. 甲站原有车52辆,乙站原有车32辆,若每天从甲站开往乙站28辆,从乙站开往甲站24辆,几天后乙站车辆数是甲站的2倍?解:每天从甲站开往乙站28辆,从乙站开往甲站24辆,相当于每天从甲站开往乙站(28-24)辆。
把几天后甲站车辆数当作1倍量,则乙站车辆数就是2倍量,两站的车辆总数(52+32)就相当于(2+1)倍,那么几天后甲站车辆数减为:(52+32)÷(2+1)=28(辆)所求天数为:(52-28)÷(28-24)=6(天)答:6天以后乙站车辆数是甲站的2倍。
例4. 甲乙丙三数之和是170,乙比甲的2倍少4,丙比甲的3倍多6,求三数各是多少?解:乙丙两数都与甲数有直接关系,因此把甲数作为1倍量。
因为乙比甲的2倍少4,所以乙数加上4就变成甲数的2倍;又因为丙比甲的3倍多6,所以丙数减去6就变为甲数的3倍;这时(170+4-6)就相当于(1+2+3)倍。
那么,甲数=(170+4-6)÷(1+2+3)=28乙数=28×2-4=52丙数=28×3+6=90答:甲数是28,乙数是52,丙数是90。
差倍问题【含义】已知两个数的差及大数是小数的几倍(或小数是大数的几分之几),要求这两个数各是多少,这类应用题叫做差倍问题。
【数量关系】两个数的差÷(几倍-1)=较小的数;较小的数×几倍=较大的数【解题思路和方法】简单的题目直接利用公式,复杂的题目变通后利用公式。
例1. 果园里桃树的棵数是杏树的3倍,而且桃树比杏树多124棵。
求杏树、桃树各多少棵?解:杏树有多少棵?124÷(3-1)=62(棵)桃树有多少棵?62×3=186(棵)答:果园里杏树是62棵,桃树是186棵。
例2. 爸爸比儿子大27岁,今年爸爸的年龄是儿子年龄的4倍,求父子二人今年各是多少岁?解:儿子年龄:27÷(4-1)=9(岁)爸爸年龄:9×4=36(岁)答:父子二人今年的年龄分别是36岁和9岁。
例3. 商场改革经营管理办法后,本月盈利比上月盈利的2倍还多12万元,又知本月盈利比上月盈利多30万元,求这两个月盈利各是多少万元?解:如果把上月盈利作为1倍量,则(30-12)万元就相当于上月盈利的(2-1)倍,上月盈利:(30-12)÷(2-1)=18(万元)本月盈利:18+30=48(万元)答:上月盈利是18万元,本月盈利是48万元。
例4. 粮库有94吨小麦和138吨玉米,如果每天运出小麦和玉米各是9吨,问几天后剩下的玉米是小麦的3倍?解:由于每天运出的小麦和玉米的数量相等,所以剩下的数量差等于原来的数量差(138-94)。
把几天后剩下的小麦看作1倍量,则几天后剩下的玉米就是3倍量,那么(138-94)就相当于(3-1)倍,因此,剩下的小麦数量:(138-94)÷(3-1)=22(吨)运出的小麦数量:94-22=72(吨)运粮的天数:72÷9=8(天)答:8天以后剩下的玉米是小麦的3倍。
倍比问题【含义】有两个已知的同类量,其中一个量是另一个量的若干倍,解题时先求出这个倍数,再用倍比的方法算出要求的数,这类应用题叫做倍比问题。
【数量关系】总量÷1个数量=倍数;另1个数量×倍数=另1总量【解题思路和方法】先求出倍数,再用倍比关系求出要求的数。
例1. 100千克油菜籽可以榨油40千克,现在有油菜籽3700千克,可以榨油多少?解:3700kg是100kg的多少倍?3700÷100=37(倍)可以榨油多少千克?40×37=1480(千克)列成综合算式40×(3700÷100)=1480(千克)答:可以榨油1480千克。
例2. 今年植树节这天,某小学300名师生共植树400棵,照这样计算,全县48000名师生共植树多少棵?解:48000名是300名的几倍?48000÷300=160(倍)共植树多少棵?400×160=64000(棵)列成综合算式400×(48000÷300)=64000(棵)答:全县48000名师生共植树64000棵。
例3. 凤翔县今年苹果大丰收,田家庄一户人家4亩果园收入11111元,照这样计算,全乡800亩果园共收入多少元?全县16000亩果园共收入多少元?解:800亩是4亩的几倍?800÷4=200(倍)800亩收入多少元?11111×200=2222200(元)16000亩是800亩的几倍?16000÷800=20(倍)16000亩收入?2222200×20=44444000(元)答:全乡800亩果园共收入2222200元,全县16000亩果园共收入44444000元。
