(完整版)二次根式培优专题讲座
(完整版)培优专题：二次根式
二次根式培优一、 知识的拓广延伸 1、挖掘二次根式中的隐含条件一般地，我们把形如 ,a(a 0)的式子叫做二次根式，其中a 0-a 0。
根据二次根式的定义，我们知道：被开方数 a 的取值范围是a 0，由此我们判断下列式子有 意义的条件：____ ____ ____ 1/ x 1(1 八 x 1 \1 x ; (2)、 -- 2；2V x(3) <1—T J—2； (4) —-; (5) V3—r(x竺x 1Vx 2(1) 、根据二次根式的这个性质进行化简： ① 数轴上表示数a 的点在原点的左边，化简2a⑤ 若为a,b,c 三角形的三边，贝U ■(a b c)2 "a b c ^ ------------⑥ 计算：J (4研&妬5)2 _____________________ (2) 、根据二次根式的定义和性质求字母的值或取值范围教科书中给出：一般地，根据算术平方根的意义可知：'a a(a 0)，在此我们可将其拓展为:2、也2的化简 a(a 0) a(a 0)②化简求值:1其中a= 5③已知,3,化简2m4m 2 m 1 .m 2 6m 912am J 2m m2 1,求m的取值范围①若②若J(2 x)2J(6 2x)2 4 x，则x的取值范围是 ______________________________③若 a J2b 14 J7 b ,求J a2 2ab b2的值；④已知:y= ,2x 5 .5 2x 3,求2xy的值。
.二次根式,a的双重非负性质：①被开方数a是非负数，即a 0②二次根式,a是非负数，即...a 0 例1.要伸x 1有意义，则x应满足( ).J2x 11 11 1A. 1< x< 3 B . x< 3 且X M丄C .丄v x v 3 D . - vx< 32 2 2 2例2 (1)化简打—1 J—x = ____________ .(2)若.E .C=(x+ y)2,贝U x —y 的值为()(A) —1 . (B)1 . (C)2 . (D)3 .例3(1)若a、b为实数，且满足丨a — 2 | +一b2=0,则b —a的值为()A. 2B. 0C. —2D.以上都不是⑵已知x, y是实数，且(x y 1)2与2x y 4互为相反数，求实数y x的倒数三，如何把根号外的式子移入根号内我们在化简某些二次根式时，有时会用到将根号外的式子移入根号内的知识，这样式子的化简更为简单。
《二次根式课件》公开课课件
二次根式的历史与文化背景
01
二次根式的起源
二次根式最初起源于古希腊数学家毕达哥拉斯学派，他们研究了直角三
角形的边长关系，发现了直角三角形的勾股定理。
02 03
二次根式的发展历程
随着数学的发展，二次根式在各个历史时期都得到了广泛的应用和研究 。特别是在文艺复兴时期，数学家们开始系统地研究二次根式的性质和 运算方法。
二次根式的性质
总结词
二次根式具有非负性、算术平方根的单调性、算术平方根的取值范围等性质。
详细描述
二次根式的被开方数是非负数，因此二次根式本身也是非负数。此外，算术平 方根具有单调性，即随着被开方数的增大，其平方根也单调增大。最后，算术 平方根的取值范围是非负实数。
二次根式的化简
总结词
化简二次根式的方法包括因式分解、配方法、直接开平方法 和分母有理化等。
二次根式在代数式变形中的应用
总结词
简化表达式
详细描述
二次根式在代数式变形中有着重要的应用，它可以简化复杂的代数表达式。通过利用二 次根式的性质和运算法则，可以将复杂的代数表达式化简为更简单的形式，方便后续的
运算和分析。
二次根式在代数式变形中的应用
总结词：因式分解
详细描述：在代数式变形中，二次根式还可以用于因式分解 。通过提取公因式和利用二次根式的性质，可以将多项式进 行因式分解，从而更好地理解和分析代数式的结构。
详细描述
化简二次根式是数学中常见的代数运算之一。通过因式分解 或配方法，将二次根式化为最简形式。如果被开方数是多项 式，则可以使用直接开平方法或分母有理化进行化简。化简 后的二次根式更易于计算和运用。02 二次 Nhomakorabea式的运算
二次根式的加减法
(完整版)《二次根式》培优试题及答案
《二次根式》提高测试〔一〕判断题：〔每题1分，共5分〕1．ab 2)2(-＝－2ab ．…………………〔〕【提示】2)2(-＝|－2|＝2．【答案】×．2．3－2的倒数是3＋2．〔 〕【提示】231-＝4323-+＝－〔3＋2〕．【答案】×．3．2)1(-x ＝2)1(-x ．…〔〕【提示】2)1(-x ＝|x －1|，2)1(-x ＝x －1〔x ≥1〕．两式相等，必须x ≥1．但等式左边x 可取任何数．【答案】×． 4．ab 、31b a 3、bax 2-是同类二次根式．…〔 〕【提示】31b a 3、ba x 2-化成最简二次根式后再判断．【答案】√． 5．x 8，31，29x +都不是最简二次根式．〔 〕29x +是最简二次根式．【答案】×．〔二〕填空题：〔每题2分，共20分〕6．当x __________时，式子31-x 有意义．【提示】x 何时有意义？x ≥0．分式何时有意义？分母不等于零．【答案】x ≥0且x ≠9． 7．化简－81527102÷31225a ＝_．【答案】－2aa ．【点评】注意除法法那么和积的算术平方根性质的运用． 8．a －12-a 的有理化因式是____________．【提示】〔a －12-a 〕〔________〕＝a 2－22)1(-a ．a ＋12-a ．【答案】a ＋12-a ． 9．当1＜x ＜4时，|x －4|＋122+-x x ＝________________．【提示】x 2－2x ＋1＝〔 〕2，x －1．当1＜x ＜4时，x －4，x －1是正数还是负数？ x －4是负数，x －1是正数．【答案】3．10．方程2〔x －1〕＝x ＋1的解是____________．【提示】把方程整理成ax ＝b 的形式后，a 、b 分别是多少？12-，12+．【答案】x ＝3＋22．11．a 、b 、c 为正数，d 为负数，化简2222d c ab d c ab +-＝______．【提示】22d c ＝|cd |＝－cd ．【答案】ab ＋cd ．【点评】∵ ab ＝2)(ab 〔ab ＞0〕，∴ ab －c 2d 2＝〔cd ab +〕〔cd ab -〕．12．比拟大小：－721_________－341．【提示】27＝28，43＝48．【答案】＜．【点评】先比拟28，48的大小，再比拟281，481的大小，最后比拟－281与－481的大小．13．化简：(7－52)2000·(－7－52)2001＝______________． 【提示】(－7－52)2001＝(－7－52)2000·〔_________〕[－7－52．] 〔7－52〕·〔－7－52〕＝？[1．]【答案】－7－52． 【点评】注意在化简过程中运用幂的运算法那么和平方差公式． 14．假设1+x ＋3-y ＝0，那么(x －1)2＋(y ＋3)2＝____________．【答案】40． 【点评】1+x ≥0，3-y ≥0．当1+x ＋3-y ＝0时，x ＋1＝0，y －3＝0．15．x ，y 分别为8－11的整数局部和小数局部，那么2xy －y 2＝____________．【提示】∵ 3＜11＜4，∴_______＜8－11＜__________．[4，5]．由于8－11介于4与5之间，那么其整数局部x ＝？小数局部y ＝？[x ＝4，y ＝4－11]【答案】5．【点评】求二次根式的整数局部和小数局部时，先要对无理数进行估算．在明确了二次根式的取值范围后，其整数局部和小数局部就不难确定了． 〔三〕选择题：〔每题3分，共15分〕16．233x x +＝－x 3+x ，那么………………〔 〕〔A 〕x ≤0 〔B 〕x ≤－3 〔C 〕x ≥－3 〔D 〕－3≤x ≤0【答案】D ． 【点评】此题考查积的算术平方根性质成立的条件，〔A 〕、〔C 〕不正确是因为只考虑了其中一个算术平方根的意义．17．假设x ＜y ＜0，那么222y xy x +-＋222y xy x ++＝………………………〔 〕〔A 〕2x 〔B 〕2y 〔C 〕－2x 〔D 〕－2y 【提示】∵ x ＜y ＜0，∴ x －y ＜0，x ＋y ＜0．∴222y xy x +-＝2)(y x -＝|x －y |＝y －x ．222y xy x ++＝2)(y x +＝|x ＋y |＝－x －y ．【答案】C ． 【点评】此题考查二次根式的性质2a ＝|a |．18．假设0＜x ＜1，那么4)1(2+-x x －4)1(2-+xx 等于………………………〔〕〔A 〕x 2 〔B 〕－x 2〔C 〕－2x 〔D 〕2x【提示】(x －x 1)2＋4＝(x ＋x 1)2，(x ＋x 1)2－4＝(x －x 1)2．又∵ 0＜x ＜1，∴ x ＋x 1＞0，x －x1＜0．【答案】D ．【点评】此题考查完全平方公式和二次根式的性质．〔A 〕不正确是因为用性质时没有注意当0＜x ＜1时，x －x1＜0．19．化简aa 3-(a ＜0)得………………………………………………………………〔 〕〔A 〕a - 〔B 〕－a 〔C 〕－a - 〔D 〕a【提示】3a -＝2a a ⋅-＝a -·2a ＝|a |a -＝－a a -．【答案】C ． 20．当a ＜0，b ＜0时，－a ＋2ab －b 可变形为………………………………………〔 〕〔A 〕2)(b a + 〔 B 〕－2)(b a -〔C 〕2)(b a -+-〔D 〕2)(b a ---【提示】∵ a ＜0，b ＜0，∴ －a ＞0，－b ＞0．并且－a ＝2)(a -，－b ＝2)(b -，ab ＝))((b a --．【答案】C ．【点评】此题考查逆向运用公式2)(a ＝a 〔a ≥0〕和完全平方公式．注意〔A 〕、〔B 〕不正确是因为a ＜0，b ＜0时，a 、b 都没有意义．〔四〕在实数范围内因式分解：〔每题3分，共6分〕21．9x 2－5y 2；【提示】用平方差公式分解，并注意到5y 2＝2)5(y ．【答案】〔3x ＋5y 〕〔3x －5y 〕． 22．4x 4－4x 2＋1．【提示】先用完全平方公式，再用平方差公式分解．【答案】(2x ＋1)2(2x －1)2．〔五〕计算题：〔每题6分，共24分〕23．〔235+-〕〔235--〕； 【提示】将35-看成一个整体，先用平方差公式，再用完全平方公式．【解】原式＝(35-)2－2)2(＝5－215＋3－2＝6－215．24．1145-－7114-－732+；【提示】先分别分母有理化，再合并同类二次根式．【解】原式＝1116)114(5-+－711)711(4-+－79)73(2--＝4＋11－11－7－3＋7＝1．25．〔a 2m n －m ab mn ＋m n n m 〕÷a 2b 2mn； 【提示】先将除法转化为乘法，再用乘法分配律展开，最后合并同类二次根式． 【解】原式＝〔a 2m n－mab mn ＋mn n m 〕·221b a nm＝21b n m m n ⋅－mab 1n m m n ⋅＋22b ma n n m n m ⋅ ＝21b －ab 1＋221b a ＝2221ba ab a +-． 26．〔a ＋ba abb +-〕÷〔b ab a +＋a ab b -－ab b a +〕〔a ≠b 〕． 【提示】此题应先将两个括号内的分式分别通分，然后分解因式并约分． 【解】原式＝b a ab b ab a +-++÷))(())(()()(b a b a ab b a b a b a b b b a a a -+-+-+--＝b a b a ++÷))((2222b a b a ab b a b ab b ab a a -++----＝ba b a ++·)())((b a ab b a b a ab +-+-＝－b a +．【点评】此题如果先分母有理化，那么计算较烦琐． 〔六〕求值：〔每题7分，共14分〕27．x ＝2323-+，y ＝2323+-，求32234232y x y x y x xy x ++-的值． 【提示】先将条件化简，再将分式化简最后将条件代入求值． 【解】∵ x ＝2323-+＝2)23(+＝5＋26，y ＝2323+-＝2)23(-＝5－26．∴x ＋y ＝10，x －y ＝46，xy ＝52－(26)2＝1．32234232y x y x y x xy x ++-＝22)())((y x y x y x y x x +-+＝)(y x xy y x +-＝10164⨯＝652． 【点评】此题将x 、y 化简后，根据解题的需要，先分别求出“x ＋y 〞、“x －y 〞、“xy 〞．从而使求值的过程更简捷． 28．当x ＝1－2时，求2222ax x a x x+-+＋222222ax x x a x x +-+-＋221ax +的值．【提示】注意：x 2＋a 2＝222)(a x +，∴ x 2＋a 2－x22a x +＝22a x +〔22a x +－x 〕，x 2－x22a x +＝－x 〔22a x +－x 〕．【解】原式＝)(2222x a x a x x-++－)(22222x a x x a x x -++-＋221ax +＝)()()2(22222222222x a x a x x x a x x a x x a x x -++-+++-+-＝)()(22222222222222x a x a x x x a x x a x a x x x -++-+++++-=)()(222222222x a x a x x a x x a x -+++-+＝)()(22222222x a x a x x x a x a x -++-++＝x1．当x ＝1－2时，原式＝211-＝－1－2．【点评】此题如果将前两个“分式〞分拆成两个“分式〞之差，那么化简会更简便．即原式＝)(2222x a x a x x-++－)(22222x a x x a x x -++-＋221ax +＝)11(2222a x x a x +--+－)11(22x x a x --+＋221a x +＝x1． 七、解答题：〔每题8分，共16分〕29．计算〔25＋1〕〔211+＋321+＋431+＋…＋100991+〕．【提示】先将每个局部分母有理化后，再计算． 【解】原式＝〔25＋1〕〔1212--＋2323--＋3434--＋…＋9910099100--〕＝〔25＋1〕[〔12-〕＋〔23-〕＋〔34-〕＋…＋〔99100-〕] ＝〔25＋1〕〔1100-〕 ＝9〔25＋1〕．【点评】此题第二个括号内有99个不同分母，不可能通分．这里采用的是先分母有理化，将分母化为整数，从而使每一项转化成两数之差，然后逐项相消．这种方法也叫做裂项相消法． 30．假设x ，y 为实数，且y ＝x 41-＋14-x ＋21．求xy y x ++2－xyy x +-2的值．【提示】要使y 有意义，必须满足什么条件？].014041[⎩⎨⎧≥-≥-x x 你能求出x ，y 的值吗？].2141[⎪⎪⎩⎪⎪⎨⎧==y x 【解】要使y 有意义，必须⎩⎨⎧≥-≥-014041[x x ，即⎪⎪⎩⎪⎪⎨⎧≥≤.4141x x ∴ x ＝41．当x ＝41时，y ＝21．又∵x y y x ++2－xyy x +-2＝2)(x y y x +－2)(xy y x -＝|xy y x +|－|xy y x -|∵ x ＝41，y ＝21，∴ y x ＜x y ．∴ 原式＝x y y x+－y x xy+＝2yx 当x ＝41，y ＝21时，原式＝22141＝2．【点评】解此题的关键是利用二次根式的意义求出x 的值，进而求出y 的值．。
(完整版)二次根式培优
二次根式专题一 二次根式(0)a a ≥非负性的综合应用1。
已知实数,a b 满足120a b -+-=，则a b +=_______。
2。
若3245423y x x =-+-+，求(5)x y 的值。
3。
已知220xy y x +--=，求x 与y 的值。
专题二 利用二次根式的性质将代数式化简4。
把()1a b a b---化成最简二次根式正确的结果是（ ） A 。
a b - B.b a - C.b a --D 。
a b --5.已知实数a 在数轴上的位置如图所示，则22(3)(5)a a -+-化简后为（ ）A 。
2B 。
-8 C.82a - D.22a --6.化简:222(2)(1)(2)x x x +--+-.7.已知2()1a <，化简：22(1)a a -。
二次根式的乘除运算专题一 二次根式的分母有理化1. 阅读下列运算过程：2323333⨯==⨯2525555⨯==⨯. 数学上将这种把分母的根号去掉的过程称作“分母有理化”，那么化简6的结果是（ ） A ．2 B ．6 C 66 2.化简65+，甲、乙两位同学的解法如下：6565(65)(65)-=++-=6—5；乙：5-6565-656565-6561=++=+=+））（（.下列说法正确的是( )A ．甲、乙的解法都正确B ．甲正确，乙不正确C ．甲、乙的解法都不正确D ．乙正确、甲不正确 3.观察下列各式，通过分母有理化,把不是最简二次根式的化成最简二次根式:121+=1(21)2121(21)(21)⨯--=-+-=2—1， 132+=1(32)3232(32)(32)⨯--=-+-=3—2， 同理可得：143+=4-3,… .从计算结果中找出规律，并利用这一规律计算（121++132++143++…+120132012+）（20131+）的值．专题二 二次根式乘除中的规律与方法4. 计算：（1)(21)(21)+-=______；(2）(32)(32)+-=______； （3）(23)(23)+-=______；(4)552)=______；根据以上规律,请写出用n （n 为正整数）表示上述规律的式子：___________。
115 二次根式 (培优讲义)-2022年初升高数学无忧衔接(解析版)
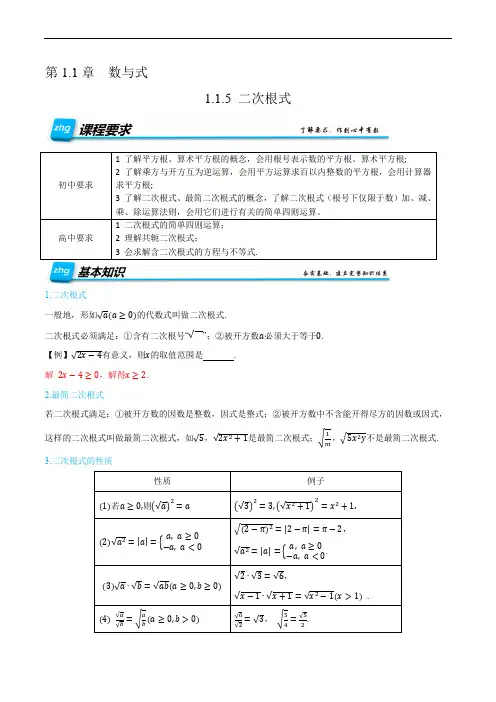
第1.1章数与式1.1.5 二次根式初中要求1 了解平方根、算术平方根的概念，会用根号表示数的平方根、算术平方根;2 了解乘方与开方互为逆运算，会用平方运算求百以内整数的平方根，会用计算器求平方根;3 了解二次根式、最简二次根式的概念，了解二次根式（根号下仅限于数）加、减、乘、除运算法则，会用它们进行有关的简单四则运算。
高中要求1 二次根式的简单四则运算；2 理解共轭二次根式；3 会求解含二次根式的方程与不等式.1.二次根式一般地，形如√a(a≥0)的代数式叫做二次根式.二次根式必须满足：①含有二次根号“√”；②被开方数a必须大于等于0.【例】√2x−4有意义，则x的取值范围是.解2x−4≥0，解得x≥2.2.最简二次根式若二次根式满足：①被开方数的因数是整数，因式是整式；②被开方数中不含能开得尽方的因数或因式，这样的二次根式叫做最简二次根式，如√5，√2x2+1是最简二次根式；√1m，√5x2y不是最简二次根式.3.二次根式的性质性质例子(1)若a≥0,则(√a)2=a(√3)2=3,(√x2+1)2=x2+1.(2)√a2=|a|={a,a≥0−a,a<0√(2−π)2=|2−π|=π−2，√a2=|a|={a,a≥0−a,a<0.(3)√a∙√b=√ab(a≥0,b≥0)√2∙√3=√6，√x−1∙√x+1=√x2−1(x>1).(4)√a√b =√ab(a≥0,b>0)√6√2=√3，√54=√52.【题型一】二次根式的运算【典题1】化简(1)√12+√13−√34−√5∙√35(2)−√3x3+√2m2x+x2∙√12x(x>0,m<0)解析(1)√12+√13−√34−√5∙√35=2√3+√33−√32−√3=5√36；(2)−√3x3+√2m2x+x2∙√12x=−√3x∙√x2+√2x∙ √m2+√x4∙12x=−x∙√3x−m√2x+2x√3x=x∙√3x−m√2x.点拨1.化简二次根式，先把二次根式化为最简二次根式，再合并同类二次根式；2.在化简过程中，要灵活运用二次根式的运算公式.有时根据需要，可把根号外的数或式放进根号里，如a∙√b a =√a2∙ba=√ab是否正确呢？【典题2】化简(1)√x2+1x2−2 (0<x<1)(2)√9−4√5解析(1)√x2+1x2−2=√x2−2∙x∙1x+(1x)2=√(x−1x)2=|x−1x|，∵0<x<1，∴x−1x >0，∴|x−1x|=x−1x即√x2+1x2−2=x−1x.(2)√9−4√5=√5−4√5+4=√(√5)2−2⋅2⋅√5+22=√(√5−2)2=√5−2.点拨1.观察根号内式子结构，确定是否能凑成一个数或式子的平方；2.遇到形如√A±√B(A,B是常数)的双重根式，注意对A的“拆解”，再试图配方成一个数的平方.变式练习1.已知a<0，b<0，c<0，化简下列根式：(1)√a b = (2)√ab 3= (3)√ab 3c=答案 (1)−√a∙bb(2) −b √ab (3) b √a∙c c解析 (1)√a b =√−a √−b=√−a∙(−b )−b=−√a∙bb； (2)√ab 3=√ab ∙√b 2=−b √ab ； (3)√ab 2c=√acb 2c 2=√a∙c∙√b 2√c 2=(−b )√a∙c −c=b √a∙c c.2. 若√(5−x)(x −3)2=(x −3)√5−x ，则x 的取值范围是________. 答案 3≤x ≤5解析 依题意得{5−x ≥0x −3≥0，解得3≤x ≤5.3.化简(1)(√3−x)2+√(x −4)2 ； (21+√2√2+√3√3+√4√4+√5√5+√6；(3)√7+4√3+√7−4√3．答案 (1)7−2x (2) √6−1 (3) 4 解析 (1) ∵3−x ≥0，∴x ≤3，x −4<0∴(√3−x)2+√(x −4)2=3−x +4−x =7−2x . (2) 1+√2+√2+√3√3+√4+1√4+√5√5+√6=√2−1+√3−√2+√4−√3+√5√4+√6−√5=√6−1；(3)√7+4√3√7−4√3=√(2+√3)2√(2−√3)2=2+√3+2−√3=4. 4.先观察下列等式，再回答问题 ①√1+112+122=1+11−11+1=112；②√1+122+132=1+12−12+1=116；③√1+132+142=1+13−13+1=1112.(1)根据上面三个等式，请猜想√1+142+152的结果(直接写出结论)(2)根据上面各等式反映的规律，试写出含n(n 为正整数)表示一般规律的等式，并加以验证； (3)根据上述的规律，解答问题：设m=√1+112+122+√1+122+132+√1+132+142+⋯+√1+120122+120132，求不超过m的最大整数[m].答案(1)1120 (2)1+1n(n+1)(3)2012解析(1)观察可得，√1+142+152=1120；(2) √1+1n2+1(n+1)2=11n(n+1)，√1+1n2+1(n+1)2=√n2(n+1)2+(n+1)2+n2n2(n+1)2=√[n(n+1)+1]2n2(n+1)2=n(n+1)+1n(n+1)=1+1n(n+1)；(3)m=√1+112+122+√1+122+132+√1+132+142+⋯+√1+120122+120132=112+116+1112+⋯+112012×2013=1×2012+(12+16+112+⋯+12012×2013)=2012+⋯+(1−12+12−13+13−14+⋯+12012−12013)=2012+(1−12013)，∴不超过m的最大整数[m]是2012.【题型二】比较大小【典题1】试比较下列各组数的大小：√3−√2和3；(2)√12−√11和√11−√10.解析(1)∵√3−√2=√3+√2，而(√3+√2)2=5+2√6，若要比较√3−√2和3⇔比较5+2√6和9⇔即2√6和4，显然2√6>4，故√3−√2>3.(2)方法1共轭根式法∵√12−√11=√12−√111=√12−√11)(√12+√11)√12+√11=√12+√11，√11−√10=√11−√101=√11−√10)(√11+√10)√11+√10=√11+√10，又√12+√11>√11+√10，∴√12−√11<√11−√10．方法2 分析法比较√12−√11和√11−√10只需比较√12+√10和2√11，只需比较(√12+√10)2=22+2√120和(2√11)2=44，只需比较2√120和22，易得2√120>22，故√12−√11<√11−√10.点拨1.√m−√n与√m+√n为共轭根式，其积为不含根号的数或式子，其和或平方和形式都有“特色”.若x=3+√2，y=3−√2，则xy=1，x+y=6，x2+y2=22；2.比较两数或式子大小常见的方法是作差法；本题中根据根式的特点，有共轭根式法和分析法.其中分析法，思考形式是“若要证明XXX，只需要证明YYY”.变式练习1.试比较下列各数大小(1)√2+√6与√3+√5(2) √23−√21与√21−√19答案(1) √2+√6<√3+√5(2)√23−√21<√21−√19解析(1) (√2+√6)2=8+4√3，(√3+√5)2=8+2√15,∵4√3<2√15，∴(√2+√6)2<(√3+√5)2，∴√2+√6<√3+√5.(2) √23−√21=√23+√21√21−√19=√21+√19，∵√23+√21>√21+√19，∴√23+√21<√21+√19，∴√23−√21<√21−√19.2.比较大小√b√a√a+√b(a>0,b>0)答案√b +√a≥√a+√b解析√b +√a(√a+√b)=(√b −√a)+(√a−√b)=√ab(√a−√b)+√ba(√b−√a)=(√a−√b)(√ab−√ba)当a≥b时，√a−√b≥0，√ab −√ba≥0,∴(√a−√b)(√ab−√ba)≥0，即√b +√a≥√a+√b；当a<b时，√a−√b<0，√ab −√ba<0,∴(√a−√b)(√ab−√ba)>0，即√b +√a>√a+√b；综上所得√b√a≥√a+√b.【题型三】含根号的方程与不等式【典题1】 解方程√x 2+5x +1−2x +1=0. 解析 移项得√x 2+5x +1=2x −1， 两边平方得x 2+5x +1=4x 2−4x +1， 解得x 1=0，x 2=3，把x 1=0，x 2=3代入原方程检验得x 1=0是方程的增根，x 2=3是原方程的根， 故原方程的根是x =3.点拨 含根式的方程，两边平方容易产生增根，故注意检验.【典题2】解不等式√x 2−1≥x −2.解析 原不等式等价于{x −2≥0x 2−1≥(x −2)2或{x −2<0x 2−1≥0，解得x ≥1或x ≤−1.点拨 含根式的不等式√f(x)≥g(x)等价于{g (x )≥0f (x )≥g 2(x)或{g (x )<0f (x )≥0.变式练习1.解方程√2x +14=x +3. 答案 1解析 方程两边平方得2x +14=x 2+6x +9，解得x 1=1，x 2=−5，把x 1=1，x 2=−5代入原方程检验得x 2=−5是方程的增根，x 1=1是原方程的根， 故原方程的根是x =1. 2.解不等式√x 2−1<x −2. 答案 无解解析 不等式等价于{x −2>0x 2−1≥0x 2−1<(x −2)2，化简得{x ≥2x ≥1或x ≤−1x <54，该不等式无解.3.解方程√x +2+√x −1=3. 答案 2解析 方程等价于√x +2=3−√x −1，两边平方得x +2=9−6√x −1+x −1，化简得√x −1=1，解得x =2， 代回方程检验可得x =2是方程的根，故方程的根式x =2.。
二次根式培优专题
二次根式培优专题一、选择题1．下列各式中，不是二次根式的是（ ）A ．45 B ．3π- C ．14 D ．122、现有边长AB ＝10，BC ＝5的矩形纸片ABCD ，对角线BD 。
在AB 上取一点G ，以DG 为折痕，使DA 落在DB 上，则AG 的长是：（ ） A 、555+ B 、5510+ C 、555- D 、5510-3．下列说法正确的是（ ）A ．若a a -=2，则a<0 B ．0,2>=a a a 则若 C ．4284b a b a = D ．5的平方根是54．下列式子一定是二次根式的是（ ） A ．2--x B ．x C ．22+x D ．22-x5．下列各式中，一定能成立的是（ ）A ．22)5.2()5.2(=- B ．22)(a a = C ．1-x 122=+-x x D ．3392+⋅-=-x x x6．下列说法错误的是 ( ） A ．962+-a a 是最简二次根式 B.4是二次根式C ．22b a +是一个非负数 D.162+x 的最小值是47．若13-m 有意义，则m 能取的最小整数值是（ ） A ．m=0 B ．m=1 C ．m=2 D ．m=38．二次根式132(3)mm ++的值是（ ） A ．23 B ．32 C ．22 D ．09．化简2||(0)x x y x y --<<的结果是（ ） A ．x y 2- B ．y C ．y x -2 D ．y -10.已知2218102x xx x ++=，则x 等于（ ） A ．4 B ．±2 C ．2 D ．±4 11．若32+=a ，32-=b ，则a 与b 的关系是（ ） A ．互为相反数；B ．互为倒数；C ．互为负倒数；D ．以上均不对。
12．已知：a=，b=，则a 与b 的关系是（ ） A ．ab=1 B ．a+b=0 C ．a ﹣b=0 D ．a 2=b 213．若1≤x ＜2，则的值为（ ） A ．2x ﹣4 B ．﹣2 C ．4﹣2xD ．214．已知，ab ＞0，化简二次根式a 的正确结果是（ ） A ． B ． C ．﹣ D ．﹣15．把中根号外面的因式移到根号内的结果是（ ） A ．B ．C ．D ．16．化简二次根式22aa a+-的结果是﹙ ﹚A ．2--a B ．2---a C ．2-a D ．2--a 17．若x<0，则xx x 2-的结果是（ ） A ．0 B ．—2 C ．0或—2 D ．218．已知a<02a 2a │可化简为（ ） A ．－a B ．a C ．－3a D ．3a19．若11x x ---2()x y =+，则x －y 的值为（ ） A ．－1 B ．1 C ．2 D ．320．已知：1080n 是整数，则满足条件的最小正整数n 为（） A ．2 B ．3 C ．30 D ．120．二、填空1．实数在数轴上的位置如图1所示，化简————。
二次根式培优专题讲座
2 .代数式2x3 . 4x 13的最小值是（ ）（A ）0 （ B ） 3 （ C ） 3.5 （ D ）13 .若m 适合关系式.3x 5y 2 m 2x 3y m 、x 199 y . 199 x y ，求 m 的值.6.已知：y E 贡〒扌，求弟；22的值.5. 化简：23 610 4 3 2 26. 化简：\ 13 2 5 2 7 2 35二、二次根式的化简技巧 （一）构造完全平方第16章二次根式培优专题1.化简所得的结果为（拓展）计算 一、二次根式的非负性 1.若|2004 a Ja 2005 a ,则 a 20042= ______________________ :111I “ 22 32 I 1 32 4212003212200424 .已知x 、y 为实数，且y x 9 . 9 y 4，求x y 的值.3.化简:.23 6 6 4 23 <25 .已知y ■ x 88 x 18，求代数式一x —y — V x <'y 2xy x 、y y . x 的值.4.化简：2 T 2 3 .2 .2 32.化简；612 -24 .（二）分母有理化 1•计算J”5、3 3.57.55.74.化简:L L 的值.49.4747\ 49,35 .5 .. 73 2 5,7°5.化简:3 .3、62=2「6 .2.分母有理化: 2 6 2 .35 .6.化简:.10 . 14 .15 .21 '3.计算：：2 31 I 37.化简:、6 4 3 3 2 18 . 12 2 .6（三）因式分解（约分） V2 V5 v 32、30 6 2 4.3 ° 1 .化简:8.化简:2.化简: ,6显,6 .3 2 13.化简: 6 43 3 2；6 、3 .32三、二次根式的应用 （一）无理数的分割 1.设a ,为3535的小数部分，b 为6 3 3. 6 3 3的小数部分，则——的值为（）b a（A ） 6 2 1 （B ） -（C ） — 1（D ） 2、3 —4282 .设，5 1的整数部分为x，小数部分为y，试求x2 3丄xy y2的值.45 1 23 .设.19 8 3的整数部分为a ,小数部分为b，试求a b -的值b 为___________ .4 .若x . 2^1 x 『2x—1 .2 成立，贝U( )1 1 3(A) x - (B) - x 1 (C) x 1 (D) x -2 2 25. 已知3 1.732 , . 30 5.477，求2.7 的值.(二)最值问题1. 设a、b、c均为不小于3的实数，贝a 2 .. b 1 |2 . c 1 |的最小值是_______ .2 .代数式vx2 4 v(12 x)29的最小值是______________ .3 .若x，y为正实数，且x y 4那么x2 1 y2 4的最小值是4.实数a，b满足a2 2a 12. 设x 2 2 2 ，y(A) x y (B) x y (C)3 .已知-15 x2、19 x2.36 12a a210 |b 3| |b 2|，则a b的最大值为________________ .(三)性质的应用1 .设m、x、y均为正整数，且6. 已知x，y都为正整数，且x . y 1998，求x y的值.7. 是否存在正整数x、y(x y)，使其满足x ... y 1476 ?若存在, 请求出x、y的值；若不存在，请说明理由.(四)因式分解I'm 28 x y，则x y m2 2 2 ，则( )x y (D) 不能确定2 ，贝U 15 x219 x2的值(1) x44 (2) 4x252(3) 16x49(五)有二次根式的代数式化简1. 已知2“)yy(6Jx 5“)，求一x——的值.2x 5 xy 3y2.已知扳 仮j y 4j y 仮2五，求空_华E —到的值。
二次根式ppt课件
通过案例讲解二次根式在实际问 题中的应用
分析数学模型和实际问题之间的 关系
课程安排
4. 课堂练习和总结（10分钟）
提供课堂练习，检验学生对所 学内容的掌握情况
总结本节课的重点和难点，进 行回顾和总结
PART 02
二次根式的基本概念
二次根式的定义
总结词：非负数
详细描述：二次根式是指根号内含有未知数的数学表达式，它必须满足被开方数为非负数，否则没有 意义。
要点二
培养学生的数学思维和解决问题 的能力，例如
让学生自己设计一个与二次根式相关的问题并解决它等。
PART 06
总结与回顾
主要知识点回顾
二次根式的定义
二次根式是一种可以用来解决各 种实际问题的数学工具，它表示 一个非负数通过开方得到的平方
根。
二次根式的性质
二次根式具有非负性、有界性、正 值性等性质，这些性质在解决实际 问题时具有重要的应用价值。
PART 04
二次根式的应用
代数领域的应用
01
02
03
根式与方程的解
通过二次根式，我们可以 求解一元二次方程的解， 确定其实数根和虚数根。
根式的化简
在代数运算中，对根式进 行化简可以简化表达式， 提高运算效率。
根式与不等式
利用根式可以求解一元二 次不等式，通过确定不等 式的解集，解决实际问题 。
- \sqrt{3}$等。
解决与二次根式相关的实际问题，例如 ：计算圆的面积或周长等。
掌握和运用二次根式的运算法则和公式 ，例如：$(a+b)\sqrt{a} = a\sqrt{a}
+ b\sqrt{a}$等。
综合练习题
要点一
通过综合题目，考察学生对二次 根式的全面理解和运用，例如
九年级数学培优教程整理篇(全)
第1讲 二次根式的性质和运算考点·方法·破译1．了解二次根式、最简二次根式、同类二次根式的定义，能准确进行辨析； 2．掌握二次根式有关性质，并能熟练运用性质进行化简；3．会根据二次根式的性质挖掘题中隐含条件，求参数的值（或取值范围）.经典·考题·赏板【例１】 （荆州）下列根式中属最简二次根式的是（ ）A.【解法指导】判断式子是否为最简二次根式的条件有两点：①被开方式中不能含分母；②被开方式中不能有可开尽方的数或式子. B 中含分母，C 、D 含开方数4、9，故选A.【变式题组】1．⑴（中山）下列根式中不是最简二次根式的是（ ）A.A ．①,②B ．③,④C ．①,③D ．①,④【例２】(黔东南)方程480x -=，当y ＞0时，m 的取值范围是（ ）A ．0＜m ＜1B ．m ≥2C ．m ＜2D ．m ≤2【解法指导】本题属于两个非负数的代数和问题，隐含两个代数式均为0的结论.由题意得4x －8＝0，x －y －m ＝0.化为y ＝2－m ，则2－m ＞0，故选C.【变式题组】2．（宁波）若实数x 、y 2(0y =，则xy 的值是__________.3．2()x y =+，则x －y 的值为（ ）A ．－ 1B ．1C ．2D ．34．有意义的x 的取值范围是（ ） A ．x ＞3B ．x ≥3C ．x ＞4D ．x ≥3且x ≠45.（怀化）22(4)0a c --=，则a －b －c ＝________.【例３是同类二次根式的是（ ）A BCD 【解法指导】判断几个二次根式是否为同类二次根式应先把它们都化为最简二次根式，再看被开方数是否一样. A = B 不能化简；=D ==.故本题应选D.【变式题组】6a＝________．7．在下列各组根式中，是同类二次根式的是（）ABCD8．已知最简二次根式ba＝_______，b＝______.【例４】下列计算正确的是（）A=B4=C=D．(11+=【解法指导】正确运用二次根式的性质①2(0)a a=≥；②(0)0(0)(0)a aa aa a⎧⎪===⎨⎪-⎩＞＜；③0,0)a b=≥≥；0,0)b a=≥＞进行化简计算，并能运用乘法公式进行计算.A、B中的项不能合并.D. 2(111+-=-=-.故本题应选C.【变式题组】9. （聊城）下列计算正确的是（）A．=B=C3=D3=-10．计算：200720074)(4⋅=_____________11．22-=_____________12．(济宁)已知a）A．a B．－a C．－1 D．013．已知a＞b＞0，a＋b＝的值为（）A．2B．2 CD．12【例５】已知xy＞0，化简二次根式的正确结果为（）ABC．D．【解法指导】先要判断出y＜0，再根据xy＞0知x＜0.故原式=.选D.【变式题组】14．已知a 、b 、c 为△AB C 三边的长，则化简a b c --_______.15===中找出规律，并利用这一规律计算：1)2006++⋅=_________.16．已知，则0＜x ＜1=_________.【例６】（辽宁）⑴先化简吗，再求值：11()ba b b a a b ++++，其中a =b =⑵已知x =，y =值为________. 【解法指导】对于⑴，先化简代数式再代入求值；对于⑵，根据已知数的特征求xy 、x ＋y 的值，再代入求值.【解】⑴原式＝22()()()()ab a a b b a b a b ab a b ab a b ab +++++==++，当12a =，12b =时，ab ＝1，a ＋b⑵由题意得：xy ＝1，x ＋y ＝10, 10199=-. 【变式题组】17．（威海）先化简，再求值：(a ＋b )2＋(a －b)(2a ＋b)－3a 2，其中2a =--2b =.18．（黄石）已知a 是4的小数部分，那么代数式22224()()442a a a a a a a a a+-+⋅-+++的值为________.【例７】已知实数x 、y 满足(2008x y =，则3x 2－2y 2＋3x －3y －2007的值为（ ）A ．－2008B ．2008C ．－1D ．1【解法指导】对条件等式作类似于因式分解的变形，找出a 、b 的关系，再代入求值.解:∵(2008x y =，∴(x =y =(y =x =，由以上两式可得x ＝y .∴(2008x =, 解得x 2＝2008，所以3x 2－2y 2＋3x －3y －2007＝3x 2－2x 2＋3x －3x －2007＝x 2－2007＝1，故选D.【变式题组】19．若a ＞0，b ＞0=的值.演练巩固·反馈提高01．若4m =，则估计m 的值所在的范围是（ ）A ．1＜m ＜2B ．2＜m ＜3C ．3＜m ＜4D ．4＜m ＜502．n 的最大值为（ ）A ．12B ．11C ．8D ．303．（黄石）下列根式中，不是．．最简二次根式的是（ ）A.04．（贺州）下列根式中，不是最简二次根式的是（ ）A.05．下列二次根式中，是最简二次根式的是（ ）A.06．（常德）设a ＝20， b ＝(－3)2, c =11()2d -=, 则a 、b 、c 、d 、按由小到大的顺序排列正确的是（ ）A ．c ＜a ＜d ＜bB ．b ＜d ＜a ＜cC ．a ＜c ＜d ＜bD ．b ＜c ＜a ＜d07．（十堰）下列运算正确的是（ ）A =B =C ．21)31=-D 53=-08．如果把式子(1a -根号外的因式移入根号内，化简的结果为（ ）A ．B C ．D ．09．2x -化简的结果为2x －3，则x 的取值范围是（ ）A ．x ≤1B ．x ≥2C ．1≤x ≤2D ．x ＞010．（怀化）函数y =中自变量的取值范围是________.11．（湘西）对于任意不相等的两个数a ，b ，定义一种运算a ※b ＝32=-那么12※4＝________.12．（荆州）先化简，再求值：22321121a a a a a a-+÷-+-，其中a =13．（广州）先化简，再求值：((6)a a a a -+--，其中12a =. 培优升级·奥赛检测01．（凉山州）已知一个正数的平方根是3x －2和5x ＋6，则这个数是________.02．已知a 、b 是正整数，且满足是整数，则这样的有序数对（a ，b ）共有________对.03．（全国竞赛）设12a =，则5432322a a a a a a a+---+=-________. 04．（全国竞赛）设x =a 是x 的小数部分,b 是x 的小数部,则a 3＋b 3＋3ab ＝________.05．（重庆竞赛）已知2y =，则x 2＋y 2＝________.06．（全国竞赛）已知1a =，a =2a =，那么a 、b 、c 的大小关系是（ ）A ．a ＜b ＜cB ．b ＜a ＜cC ．c ＜b ＜aD ．c ＜a ＜b07．（武汉联赛）已知y =（x ，y 均为实数），则y 的最大值与最小值的差为（ ）A 3B ．3C 3D08．（全国竞赛）已知非零实数a 、b 满足24242a b a -++=，则a ＋b 等于（ ） A ．－1B ．0C ．1D ．209．（全国竞赛） ）A ．5-B ．1C ．5D ．110．已知0(0,0)x y x y -=>>的值为（ ）A ．13 B ．12C ．23 D ．3411．已知152a b c +-=-，求a ＋b ＋c 的值.12．已知9+9a 和b ，求ab －3a ＋4b ＋8的值.第2讲 二次根式的化简与求值考点·方法·破译1．会灵活运用二次根式的运算性质化简求值.2．会进行二次根式的有理化计算，会整体代入求值及变形求值. 3．会化简复合二次根式，会在根式范围内分解因式.经典·考题·赏板【例１】2=的值等于__________ 【解法指导】通过平方或运用分式性质，把已知条件和待求式的被开方数都用1x x+表示或化简变形. 解：两边平方得，124x x ++=，12x x+= ，两边同乘以x 得，212x x += ，∵2315x x x ++=，29111x x x ++=，∴原式【变式题组】1．若14aa +=（0＜a ＜1）=________2=- ） A ．1a a -B ．1a a-C ．1a a+D ．不能确定【例２】（全国初中数学联赛）满足等式＝2003的正整数对（x ,y ）的个数是（ ） A ．1 B ．2 C ．3 D ．4【解法指导】对条件等式作类似于因式分解的变形，将问题转化为求不定方程的正整数解.0=，∴0=0>0=，则xy ＝2003，且2003是质数，∴正整数对（x ,y ）的个数有2对，应选B . 【变式题组】3．若a ＞0，b ＞0=的值.【例３】1)a =<<，求代数式22632x x x x x x +-+÷-. 【解法指导】视x －2，x 2-4x=a 的代数式表示x －2，x 2-4x ，注意0＜a ＜1的制约.解：平方得，12x a a =++，∴12x a a -=+，2221442x x a a-+=++， 222142x x a a-=+-，∴化简原式＝(3)(2)(2)3x x x x x x +---+ ＝2211()1()211()a a a a a a a a aa a++-+-=++--【变式题组】 4．（武汉）已知32x x +=+，求代数式35(2)242x x xx -÷----的值.5．（五羊杯竞赛）已知1m =+1n =-且22(714)(367)8m m a n n -+--=，则a 的值等于（ ） A．－5B ．5C ．－9D ．9【例４】（全国竞赛）如图，点A 、C 都在函数(0)y x x=>的图像上，点B 、D 都在x 轴上，且使得△OAB、△BCD 都是等边三角形，则点D 的坐标为________.【解法指导】解：如图，分别过点A 、C 作x 轴的垂线，垂足分别为E 、F .设OE=a，BF=b ，则a ，CF，所以，点A 、C的坐标为（a）、（2a＋b ），所以2(2)a b =+=a b ⎧=⎪⎨=-⎪⎩因此，点D 的坐标为（,0）【变式题组】6．（邵阳）阅读下列材料，然后回答问题.在进行二次根式化简时，我们有时会碰上如1323235+，，一样的式子，其实我们还可以将其进一步化简：335333535=⨯⨯=； （一） 36333232=⨯⨯=； （二） ()()()131313132132-=-+-⨯=+； （三） 以上这种化简的步骤叫做分母有理化，132+还可以用以下方法化简：()()()13131313131313131322-=+-+=+-=+-=+； （四）（1）请你用不同的方法化简352+；①参照（三）试得：352+=_____________________________；（要有简化过程）②参照（四）试得：352+=_____________________________；（要有简化过程）（22n ++++【例５】（五羊杯竞赛）设a 、b 、c 、d 为正实数，a＜b ，c ＜d ，bc ＞ad ，.【解法指导】虽然不能用面积公式求三角形面积(为什么?)a 、c 为直角边的直角三角形的斜边，从构造图形入手，将复杂的根式计算转化为几何问题加以解决.解：如图，作长方形ABCD ，使AB ＝b －a ，AD ＝c ，延长DA 至E ，使DE ＝d ，延长DC 至F ，使DF ＝b ，连结EF 、FB 、EB ，则BF＝，EF＝，BE ，从而知△BEF 就是题设的三角形，而S △BEF ＝S长方形ABCD ＋S △BCF ＋S △ABE －S △DEF ＝(b －a )c ＋12(d －c )(b －a )－12bd ＝12(bc －ad )【变式题组】7．(北京竞赛)已知a 、b 均为正数，且a ＋b ＝2，求U演练巩固·反馈提高01．已知x =，y =值为__________ 02．设1a =，则32312612a a a +--＝（ ）A ． 24B ．25C ．10D ．1203．（天津）计算2001200019991)1)1)2001--+=__________04．（北京竞赛）若有理数x 、y 、z 1()2x y z =++，则2()x yz -=__________05．（北京竞赛）正数m 、n 满足430m n +--==__________06．（河南竞赛）若1x =，则32(2(15x x x -+++-的值是（ ）A ．2B ．4C ．6D ．807．已知实数a 满足2000a a -=，那么22000a -的值是（ ） A ．1999B ．2000C ．2001D ．200208．设a =b =c =a 、b 、c 之间的大小关系是（ ） A ．a ＜b ＜cB ．c ＜b ＜aC ．c ＜a ＜bD ．a ＜c ＜b09．已知1x =培优升级·奥赛检测01．（信利杯竞赛）已知1x =+2111242x x x +-=+--__________025==__________03．（江苏竞赛）已知(2002x y =，则2234x xy y --6658x y --+=__________04．7x =，则x ＝__________05．(T 1杯联赛) 已知x =，y =，那么22y x x y +=__________06．（武汉选拔赛）如果a b +=a b -=，3333b c b c +=-，那么333a b c -的值为（ ）A ．B ．2001C ．1D ．007．（绍兴竞赛）当12x +=时，代数式32003(420052001)x x --的值是（ ）A ．0B ．－1C ．1D ．20032-08．（全国联赛）设a 、b 、c 为有理数，且等式a +=成立，则29991001a b c ++的值是（ ） A ．1999B ．2000C ．2001D ．不能确定09．计算：（1（2（34947+++（410．已知实数a 、b 满足条件1b a b a -=<，化简代数式11()(1)a b a b---，将结果表示成不含b 的形式.11．已知21(0)a x a a +=>12．（奥林匹克竞赛）已知自然数x、y、z0=，求x＋y＋z的值.第3讲一元二次方程的解法考点·方法·破译1．掌握一元二次方程根的定义并能应用根的定义解题；2．掌握一元二次方程的四种解法，并能灵活应用各种解法解方程；3．会应用一元二次方程解实际应用题。
完整版二次根式培优专题讲座
2 .代数式2x3 . 4x 13的最小值是（ ）（A ）0 （ B ） 3 （ C ） 3.5 （ D ）13 .若m 适合关系式.3x 5y 2 m 2x 3y m 、x 199 y . 199 x y ，求 m 的值.6.已知：yE 贡〒扌，求弟；2 2的值.第16章二次根式培优专题1.化简所得的结果为（拓展）计算 一、二次根式的非负性 1.若|2004 a Ja 2005 a ,则 a 20042= ______________________ :111I “ 22 32 I 1 32 4212003212200426.化简：\ 13 2 5 2 7 2 35二、二次根式的化简技巧2.化简；612 -24 .4 .已知x 、y 为实数，且y x 9 . 9 y 4，求x . y 的值.3.化简:.23 6 6 4 23 <25 .已知y ■ x 88 x 18，求代数式一x —y — J x <y2xy x 、y y . x的值.4.化简：2 T 2 3 .2 .2 35.化简：23 610 4 3 2 2（二）分母有理化1 11 •计算：3 V3 5（3 3』517.5 5.7149.47 47\ 49的值.4.化简:,3 5 .5 ..73 2 5 、75.化简:3 .3 .62 「2「62.分母有理化:2 62 .3 56.化简:V2暑.10 . 14 .15 .217.化简:、6 4 3 3 218 . 12 2 .6（三）因式分解（约分）1 .化简:V2 V5 A/32、30 6 2 4.3&化简：—5 " 3V35 3/5 3/7 72.化简:,6显,6 .3 2 1三、二次根式的应用（一）无理数的分割1.设a,为3 5 3 5的小数部分，b为 6 3 3 . 6 3 3的3.化简:6 43 3 2；6 、3 .3 2小数部分，则- 1—的值为（）b a(A) 6 2 11 (B) - (C) —14 2(D) 2•3^2 .设，5 1的整数部分为x，小数部分为y，试求x2 3丄xy y2的值.45 1 23 .设.19 8 3的整数部分为a ,小数部分为b，试求a b -的值b(二)最值问题1. 设a、b、c均为不小于3的实数，贝a 2 .. b 1 |2 . c 1 |的最小值是_______ .2 .代数式点2 4 J(12 x)29的最小值是______________ .3 .若x，y为正实数，且x y 4那么x2 1 y2 4的最小值是4. 实数a，b满足a2 2a 1 .36 12a a210 |b 3| |b 2|，则a b的最大值为________________ .(三)性质的应用1 .设m、x、y均为正整数，且2. 设x 2 2 2 ，y(A) x y (B) x y (C)3 .已知-15 x219 x27. 是否存在正整数x、y(x y)，使其满足、、x ... y 1476 ?若存在, 请求出x、y的值；若不存在，请说明理由.(四)因式分解(1) x44 (2) 4x252(3) 16x49为___________ .4 .若，x . 2x 1 x . 2x 1 2成立，则( )1 1 3(A) x - (B) - x 1 (C) x 1 (D) x -2 2 25.已知3 1.732 , . 30 5.477，求2.7 的值.6.已知x，y都为正整数，且x . y 1998，求x y的值.I'm 28 x y，则x y m2 2 2 ，则( )x y (D) 不能确定2 ，贝U 15 x219 x2的值(五)有二次根式的代数式化简1.已知2“)Jy(6』x 5“)，求一x——的值.2x xy 3y4.比较、.2012 . 20石与.2013 2012 的大小.5. 比较t 1- -与；3的大小.V2 V3 V56.比较- 2012 1与2012 1的大小.V2013 1 V2013 1（六）比较数的大小1.设a>b>c>d>0且，: ab cd, y ac bd, z3 -57.比较'、8 ，5与的大小.8 .比较门一2与‘一3的大小. va 3 va 4"匸订，求2；:y 3y的值2.比较与..5 ；3的大小.3 .已知：: 8 ■-7 y8 7，求:： y 2 ：y的值.<8 J7 v x V y3.比较m . n 与m 2013 ■. n 2013 的大小.4 .已知a1,求12 ,3 2a a2a 1.a22a 12a的值.a------------------- 22 b a的值.5 .已知为实数■- ad 、、bc .则x、y、z的大小关系.。
二次根式培优专题讲座
第16章二次根式培优专题一、二次根式的非负性1 •若|2004a Ja 2005 a,则a 2004J _______________________2 •代数式2x3 ・4x 13的最小值是( )(A) 0 ( B) 3 ( C) 3.5 ( D) 13 •若m适合尖系式.3x 5y 2 m 2x 3y m 、x 199 y . 199 x y ‘ 求m 的值.4 •已知x、y为实数，且yx9 . 9y4，求xy的值.8x18,求代数式一x—y— 2xy ________ 的Vx v y x、y y . x 值.6.E贡〒扌，求弟；2已知：y 2的值.二、二次根式的化简技巧（一）构造完全平方1（拓展）计 算111 I u 22 32 I 1 32 425.化简:23 610 43226.化简：\ 132 52 72351 •化简所得的结果为2•化简；612-24 .3 •化简:.23 66 4 23 <24•化简:2T 23 .2 .2 320042（二）分母有理 "化 1 -计算J”5、3 3.57.5 5.72 •分母有理化：厂厂:3•计算：：$31 13（三）因式分解（约分）2 •化简:,6显 ,6 .3 2 13 •化简:6 4332;6 、3 .321 •化简:V2 V5 v 32 > 30 6 2 4.3L L 的值. 49.47 47\ 494 •化简:,35 .5 .. 7 3 2 5,7 05.化简：3 .3、6 2=2 r6 .6 •化简：.10 . 14 .15 .21 17.化简:、6 4332 18 .12 2 .68 •化简:三、二次根式的应用(一)无理数的分割1•设a,为3 5 3 5的小数部分，b为633 ・633的小数部分，则一一的值为( )b a(A) 621 (B) - (C) —1 (D) 2、3 —4 2 82•设亠F勺整数部分为x，小数部分为y，试求x23± xy护的值.45 1 23 •设・19 8 3的整数部分为a ,小数部分为b，试求a b ■的值b为__________ ・(-)最值问题1. 设a、b、c均为不小于3的实数，贝a2 ..b1 |2・c1|的最小值是______ •2 .代数式vx2 4v(12x)29的最小值是______________ .3 •若x，y为正实数，且xy4那么x21 y24的最小值是4•实数a，b满足a2 2a 1m 28 x y，贝U x y m222、则()19 x2的值2，贝U 15 x22. 设x 2 2 2 ，y(A) xy (B) xy (C)3 •已知-15 x2、19 x24 •若x.21 x『2x—1 .2成立，贝U（1 1 3(A) x - (B)・ x 1 (C) x 1 (D) x・2 2 25. 已知3 1.732 , . 30 5.477，求2.7 的值..36 12a a2 10 |b 3| |b 2|，则a b的最大值为_______________ .（三）性质的应用1 •设m、x、y均为正整数，且6.已知x，y都为正整数，且x・y 1998,求xy的值.7・是否存在正整数x、y（x y），使其满足x ... y 1476 ?若存在，请求出x、y的值；若不存在，请说明理由.（四）因式分解（五）有二次根式的代数式化简已知 —-的值.(1) x 44 (2) 4x 2 52 (3) 16X 491.求一奖2u)yy (6Jx 5t£)2x 5 xy 3y。
初中数学精品培优课件 星课堂 第5讲二次根式(43张)
有意义，则x-2≥0,即x≥2.
所以4x+1≥9,即y≥9.
1.(星课堂·茂名中考)若代数式 x 1
x2
有意义，则x的取值
范围是(
) (B)x≥1 (D)x≥1且x≠2
x 1 有意义,必须同时满足 x2
(A)x>1且x≠2 (C)x≠2 【解析】选D.要使代数式
x-1≥0,x-2≠0两个条件,解得x≥1且x≠2.
=(
)
【解析】选D.根据公式 a 2 =|a|可知： a 12 1 ＝ |a-1|-1，由于a＜1，所以a－1＜0，因此|a-1|-1＝ (1－a)－1＝－a.
6.(星课堂·日照中考)已知x,y为实数，且满足 1 x
y 1 1 y 0 ，那么x星课堂-y星课堂=_____.
外面.
【例2】(星课堂·黄石中考)已知x＜1，则x 2 2x 1 结果是( (A)x－1 【思路点拨】 ) (B)x＋1 (C)－x－1
化简的
(D)1－x
【自主解答】选D.∵当x＜1时, x－1＜0,
∴原式 x 12 x 1 1－x.
4.(星课堂·凉山中考)已知 y 2x 5 5 2x 3 值为( (A)-15 (C) 15
b b
)
【解析】选B. a 与 b 不能合并.
9.(星课堂·孝感中考)下列计算正确的是( (A) 8－ 2＝ 2 (B) 2 3＝ 5
)
(C) 2 3 6
(D) 8 2 4
【解析】选A.根据二次根式的性质得： 8－ 2＝ 2 2－ 2＝ 2 ；
2 与 3 不是同类二次根式； 2 3 6 6; 8 2 4 2.
所以x≥5.
【中考冲刺】初三数学培优专题 01 二次根式的化简与求值(含答案)(难)
二次根式的化简与求值阅读与思考二次根式的化简与求值问题常涉及最简根式、同类根式，分母有理化等概念，常用到分解、分拆、换元等技巧.有条件的二次根式的化简与求值问题是代数变形的重点，也是难点，这类问题包含了整式、分式、二次根式等众多知识，又联系着分解变形、整体代换、一般化等重要的思想方法，解题的基本思路是：1、直接代入直接将已知条件代入待化简求值的式子. 2、变形代入适当地变条件、适当地变结论，同时变条件与结论，再代入求值.数学思想：数学中充满了矛盾，如正与负，加与减，乘与除，数与形，有理数与无理数，常量与变量、有理式与无理式，相等与不等，正面与反面、有限与无限，分解与合并，特殊与一般，存在与不存在等，数学就是在矛盾中产生，又在矛盾中发展.=x , y , n 都是正整数）例题与求解【例1】 当x =时，代数式32003(420052001)x x --的值是（ ） A 、0 B 、－1 C 、1 D 、20032-（绍兴市竞赛试题）【例2】 化简（1(ba b ab b -÷-- （黄冈市中考试题）（2（五城市联赛试题）（3（北京市竞赛试题）（4（陕西省竞赛试题）解题思路：若一开始把分母有理化，则计算必定繁难，仔细观察每题中分子与分母的数字特点，通过分解、分析等方法寻找它们的联系，问题便迎刃而解.思想精髓：因式分解是针对多项式而言的，在整式，分母中应用非常广泛，但是因式分解的思想也广泛应用于解二次根式的问题中，恰当地作类似于因式分解的变形，可降低一些二次根式问题的难度.【例3】比6大的最小整数是多少？（西安交大少年班入学试题）解题思路：直接展开，计算较繁，可引入有理化因式辅助解题，即设x y==想一想：设x=求432326218237515x x x xx x x--++-++的值. （“祖冲之杯”邀请赛试题）的根式为复合二次根式，常用配方，引入参数等方法来化简复合二次根式.【例4】 设实数x ，y 满足(1x y =，求x ＋y 的值.（“宗泸杯”竞赛试题）解题思路：从化简条件等式入手，而化简的基本方法是有理化.【例5】 （1的最小值.（2的最小值.（“希望杯”邀请赛试题）解题思路：对于（1）为a ，b 的直角三角形的斜边长，从构造几何图形入手，对于（2），设y =A （x ，0），B (4，5)，C (2，3)相当于求AB ＋AC 的最小值，以下可用对称分析法解决.方法精髓：解决根式问题的基本思路是有理化，有理化的主要途径是乘方、配方、换元和乘有理化因式.【例6】 设2)m a =≤≤，求1098747m m m m m +++++-的值.解题思路：配方法是化简复合二次根式的常用方法，配方后再考虑用换元法求对应式子的值.能力训练A级1.化简：7()3“希望杯”邀请赛试题）2.若x y x y+=-=，则xy＝_____(北京市竞赛试题)3.+（“希望杯”邀请赛试题）4. 若满足0＜x＜y=x，y）是_______（上海市竞赛试题）5.2x－3，则x的取值范围是（）A. x≤1B. x≥2C. 1≤x≤2D. x＞06）A．1B C. D. 5（全国初中数学联赛试题）7．a，b，c为有理数，且等式a+=成立，则2a＋999b＋1001c的值是（）A．1999 B. 2000 C. 2001D. 不能确定（全国初中数学联赛试题）8、有下列三个命题甲：若α，β是不相等的无理数，则αβαβ+-是无理数；乙：若α，β是不相等的无理数，则αβαβ-+是无理数；丙：若α，β其中正确命题的个数是（）A. 0个B. 1个C. 2个D. 3个（全国初中数学联赛试题）9、化简：（1（2（3（4（天津市竞赛试题）（5（“希望杯”邀请赛试题）10、设52x=，求代数式(1)(2)(3)(4)x x x x++++的值.（“希望杯”邀请赛试题）117x=，求x的值.12、设x x ==（n 为自然数），当n 为何值，代数式221912319x xy y ++的 值为1985？B 级1. 已知3312________________x y x xy y ==++=则. (四川省竞赛试题)2. 已知实数x ，y 满足(2008x y =，则2232332007x y x y -+--＝＿＿＿＿（全国初中数学联赛试题）3. 已知42______1x x x ==++2x 那么. （重庆市竞赛试题）4. a =那么23331a a a ++＝＿＿＿＿＿. （全国初中数学联赛试题）5. a ，b 为有理数，且满足等式14a +=++则a ＋b ＝（ ）A . 2B . 4C . 6D . 8(全国初中数学联赛试题)6． 已知1,2a b c ===，那么a ，b ，c 的大小关系是（ ）.Aa b c << B . b ＜a ＜c C . c ＜b ＜c D . c ＜a ＜b(全国初中数学联赛试题)7.=） A . 1a a -B .1a a - C . 1a a+ D . 不能确定 8. 若[a ]表示实数a 的整数部分，则等于（ ）A . 1B . 2C . 3D . 4（陕西省竞赛试题）9． 把(1)a - ）A .B C. D . （武汉市调考题）10、化简：（1 （“希望杯”邀请赛试题）（210099++（新加坡中学生竞赛试题）（3（山东省竞赛试题）（4 （太原市竞赛试题）11、设01,x << 1≤<.（“五羊杯”竞赛试题）12的最大值.13、已知a , b , c为有理数，证明：222a b c a b c ++++为整数.二次根式的化简与求值例1 A 提示：由条件得4x 2－4x －2 001＝0． 例2 (1)原式＝()aba b a b++()1ba b b a b⎡⎤⎢⎥-⎢⎥+-⎣⎦·a b b -＝2ab (2)原式＝()()()()257357257357+-++++＝26－5．(3)原式＝()()()()633326332+-+++＝316332+++＝62-；（4）原式＝()()()5332233323325231-+-+-++＝332-．例3 x ＋y ＝26，xy ＝1，于是x 2＋y 2＝(x ＋y )2－2xy ＝22，x 3＋y 3＝(x ＋y )(x 2－xy ＋y 2)＝426，x 6＋y 6＝(x 3＋y 3)2－2x 3y 3＝10582．∵0＜65-＜1，从而0＜()665-＜1，故10 581＜()665+＜10582． 例4 x ＋21x +＝211y y ++＝21y +－y …①；同理，y ＋21y +＝211x x ++＝21x +－x …②．由①＋②得2x ＝－2y ，x ＋y ＝0． 例5 (1)构造如图所示图形，PA ＝24x +，PB ＝()2129x -+．作A 关于l 的对称点A '，连A 'B 交l 于P ，则A 'B ＝22125+＝13为所求代数式的最小值． (2)设y ＝()2245x -+＋()2223x -+，设A (x ，0)，B (4，5)，C (2，3)．作C 关于x 轴对称点C 1，连结BC 1交x 轴于A 点．A 即为所求，过B 作BD ⊥CC 1于D 点，∴AC ＋AB ＝C 1B ＝2228+＝217． 例 6 m ＝()2212111a a -+-•+＋()2212111a a ---•+＝()211a -+＋()211a --．∵1≤a ≤2，∴0≤1a -≤1，∴－1≤1a -－1≤0，∴m ＝2．设S ＝m 10＋m 9＋m 8＋…＋m －47＝210＋29＋28＋…＋2－47 ①，2S ＝211＋210＋29＋…＋22－94 ②，由②－①，得S ＝211－2－94＋47＝1 999．A 级 1．1 2．52- 3．0 提示：令1997＝a ，1999＝b ，2001＝c ． 4． (17，833)，(68，612)，( 153，420) 5．B 6．C 7．B 8．A 9．(1)()2x y + (2)原式＝32625++-＝()()22325+-＝325++．(3)116- (4)532--(5)32+ 10．48提示：由已知得x 2 ＋5x ＝2，原式＝(x 2＋ 5x ＋4)(x 2＋5x ＋6)． 11．由题设知x ＞0，(27913x x ++＋27513x x -+)(27913x x ++－27513x x -+)＝14x ．∴27913x x ++－27513x x -+＝2，∴227913x x ++＝7x ＋2，∴21x 2－8x－48＝0．其正根为x ＝127． 12．n ＝2 提示：xy ＝1，x ＋y ＝4n ＋2． B 级 1． 64 2．1 提示：仿例4，由条件得x ＝y ，∴(x －22008x -)2＝2 008，∴x 2－2008－x 22008x -＝0，∴22008x -(22008x -－x )＝0，解得x 2＝2 008．∴原式＝x 2－2 007＝1． 3．9554．1 提示：∵(32－1)a ＝2－1，即1a＝32－1． 5．B 提示：由条件得a ＋b 3＝3＋3，∴a ＝3，b ＝1，∴a ＋b ＝4． 6．B 提示：a －b ＝6－1－2＞322+－1－2＝0．同理c －a ＞0 7．B 8．B 9．D 提示：注意隐含条件a －1＜0． 10．(1)1 998 999. 5 提示：设k ＝2 000，原式＝212k k --． (2)910 提示：考虑一般情形()111n n n n +++＝1n －11n + (3)原式＝()()8215253532+-++-＝()()253253532+-++-＝53+．(4)2－53- 11．构造如图所示边长为1的正方形ANMD ，BCMN ．设MP ＝x ，则CP ＝21x +，AP ＝()211x +-，AC ＝5，AM ＝2，∴AC ≤PC ＋PA ＜AM ＋MC ，，则5≤21x +＋()211x +-＜1＋2 12．设y ＝2841x x -+－2413x x -+＝()2245x -+－()2223x -+，设A (4，5)，B (2，3)，C (x ，0)，易求AB 的解析式为y ＝x ＋1，易证当C 在直线AB 上时，y 有最大值，即当y ＝0，x ＝－1，∴C (－1，0)，∴y ＝22． 13．33a bb c ++＝()()()()3333a bb cb c b c +-+-＝()222333ab bc bac b c -+--为有理数，则b 2 －ac ＝0．又a 2＋b 2＋c 2＝(a ＋b ＋c )2－2(ab ＋bc ＋ac )＝(a ＋b ＋c )2－2(ab ＋bc ＋b 2)＝()2c b a ++－2b （a ＋b ＋c ）＝（a ＋b＋c ）（a －b ＋c ），∴原式＝a －b ＋c 为整数．。
培优专题——二次根式2222
培优专题——二次根式1.把1a a-的根号外的因式移到根号内等于 。
2. 若最简二次根式23412a +与22613a -是同类二次根式，则______a =。
3. 能使等式22x x x x =--成立的x 的取值范围是（ ） A. 2x ≠ B. 0x ≥ C. 2x D. 2x ≥4. 对于所有实数,a b ，下列等式总能成立的是（ ） A.()2a b a b +=+ B. 22a b a b +=+ C. ()22222a b a b +=+ D. ()2a b a b +=+ 5．代数式x x 224129++-+()的最小值是_____________． 6.已知2310x x -+=，求2212x x+-的值。
7. 已知,a b 为实数，且()1110a b b +---=，求20052006a b -的值。
8. 化简：()()351.0,0a b a b ≥≥ ()2.x y x y-+ ()3213.a a a ---9. 计算及化简： ⑴. 2211a a a a ⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭ ⑵. 2a b a b ab a b a b -+----⑶.x y y x y x x y x y y x y x x y -+-+- ()53236.32b ab a b b a ⎛⎫⋅-÷ ⎪⎝⎭10. 已知：3232,3232x y +-==-+，求32432232x xy x y x y x y -++的值。
11. 已知：1110a a+=+，求221a a +的值。
12. 已知：,x y 为实数，且113y x x -+-+，化简：23816y y y ---+。
13. 已知()11039322++=+-+-y x x x y x ，求的值。
（一）构造完全平方1．化简22111(1)n n +++，所得的结果为_____________． （拓展）计算2222222220041200311413113121121111++++++++++++2．设a 为5353--+的小数部分，b 为336336--+的小数部分，则a b 12-的值为 （A ）126+- （B ）41 （C ）12-π （D ）832π-- 3．设5151+-的整数部分为x ，小数部分为y ，试求2212x xy y ++的值． 4.设1983-的整数部分为a ，小数部分为b ，试求1a b b ++的值5.已知732.13=，477.530=，求7.2的值．直升考试真题的结果为化简二次根式若aa b b a a b a 2)(,.1---< 2.“双钩函数”其表达式为：)0,0,(>>+=b a b a xb ax y 为常数，且其中，求最值如下例子： ()多少？取得最小值？最小值是为何值时，当）对于函数（取得最小值？为何值时，当）若函数表达式为（。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第16章二次根式培优专题
一、二次根式的非负性
1
．若2004a a -=，则22004a -=_____________． 2．代数式13432---x x 的最小值是（ ） （A ）0 （B ）3 （C ）3.5 （D ）1 3．若m 适合关系式
=，求m 的值．
4．已知x 、y 为实数，且499+---=y x y ，求y x +的值．
5．已知1888+-+-=x x y ，求代数式x
y y x xy
y x y x ---+2的值．
6．已知：211881+-+-=x x y ，求22-+-++x
y
y x x
y y x 的值．
二、二次根式的化简技巧 （一）构造完全平方
1
_____________． （拓展）计算
222222222004
1200311413113121121111++++++++++++
Λ．
2．化简241286+++．
3．化简：2
32
46623+--．
4
5
6
（二）分母有理化
1．计算：49
4747491
7557153351331++++++++ΛΛ的值．
2．分母有理化：5
326
2++．
3．计算：3
212
32+++
-．
（三）因式分解（约分） 1．化简：253
2306243
+--+．
2
3
4．化简：(
)(
)
7
52
37
553++++．
5．化简：
．
6
．
7
．
8
三、二次根式的应用 （一）无理数的分割
1．设a ，为5353--+的小数部分，b 为336336--+的
小数部分，则
a
b 1
2-的值为（ ） （A ）126+- （B ）41 （C ）12
-π
（D ）832π--
2
的整数部分为x ，小数部分为y ，试求2212x xy y ++的值．
3
的整数部分为a ，小数部分为b ，试求1
a b b
++的值
（二）最值问题
1．设a 、b 、c 均为不小于3的实数，则|12|12--+++-c b a 的最小值是_______．
2．代数式x x 224129++-+()的最小值是_____________． 3．若y x ，为正实数，且4=+y x
那么的最小值是_____________．
4．实数b a ，
10|3||2|b b =-+--，则
22a b +的最大值为_____________．
（三）性质的应用
1．设m 、x 、y 均为正整数，且y x m -=-28，则m y x ++ =_________．
2．设Λ+++=222x ，Λ222=y ，则（ ） （A ） y x > （B ） y x < （C ） y x = （D ） 不能确定 3．已
知
2=-，
则的值
为 ．
4
=成立，则（ ） （A ）12x ≥
（B ）112x ≤≤（C ）1x >（D ）3
2
x = 5．已知732.13=，477.530=，求7.2的值．
6．已知y x ，都为正整数，且1998=+y x ，求y x +的值．
7．是否存在正整数)(y x y x <、，使其满足1476=+y x ？若存在，请求出x 、y 的值；若不存在，请说明理由．
（四）因式分解
（1）44-x （2）2254-x （3）9164-x
（五）有二次根式的代数式化简
1．已知)56()2(y x y y x x +=+
的值．
2
=
的值。
3．已知：7
878+-=x ，7
878-+=
y ，求：
y
x xy
y x +++2的值．
4．已知3
21
+=a ，求a a a a a a a -+---+-2221
2121的值．
5．已知：a ，b 为实数，且2
222
2+-+-=
a a a
b ．求
(
)
2
22a b a b ---+-的值．
（六）比较数的大小
1．设a ＞b ＞c ＞d ＞0
且，
x y z ===则x 、y 、z 的大小关系．
2
的大小．
3
4
5
6
7
3
2
的大小．
8
的大小．。