五年级奥数速算与巧算肖翠君整理
五年级奥数(教案)第1讲:速算与巧算(二)

=2×3×3
=18
练习2:[8分]
计算:
[1]16÷3.2÷2.5
[2]12.5×36.8÷3.68
[3][7.5×5.1×8.4]÷[1.7×4.2×2.5]
[4]9.3×3.2÷3.23×6.46÷1.6÷3.1
分析:
[1][2]两个题目主要是利用除法的性质来解题。[3][4]两个题目跟例题的类型也是一样的,先变成有倍数关系的两个数相除,然后再把结果相乘,最后得出结果。
是不是也需要花相当长的时间呢?那么对于这种类型的题目有没有更简便
的方法呢?思考一下。
生:老师我发现,被除数里数字与除数里的数字存在着倍数关系。
师:谁和谁存在倍数关系?
生:4.8与2.4,7.5与2.5,8.1与2.7。
师:是的,正好存在三对倍数关系的数。从这里出发,我们可以怎么去思考呢?
生:我们可以分别相除,然后再把结果相乘,这样和原来的结果是一样的。
一、复习导入[3分]
师:同学们,上节课我们学了什么?
生:速算与巧算。
师:是的,主要学了哪些速算的方法呢?
生:特殊的数字相乘能够凑整。
师:是的,特殊的数字,比如说25和4相乘等于100,125和8相乘等于1000。
这些特殊的数字,其实在小数里也是适用的。所以当看到特殊数字的时候,
我们可以直接将它们凑在一起,使计算变得简便,如果没有这样的两个数,
师:这个就是解题的关键。现在会做了吗?
生:最后我们可以利用乘法分配律的逆运算来解答,[7.2+2.8]×11.11=10×
11.11=111.1。
师:这是第一小题,接下来看第二小题,不仅有乘法,加法,还有减法,对吗?
(完整版)小学五年级奥数速算与技巧、包含与排除.doc

小学五年级奥数题——速算与巧算在日常生活和解答数学问题时,经常要进行计算,在数学课里我们学习了一些简便计算的方法 ,但如果善于观察、勤于思考 ,计算中还能找到更多的巧妙的计算方法 ,不仅使你能算得好、算得快 ,还可以让你变得聪明和机敏 .例 1:计算: 9.996+ 29.98+ 169.9+ 3999.5算式中的加法看来无法用数学课中学过的简算方法计算,但是 ,这几个数每个数只要增加一点 ,就成为某个整十、整百或整千数,把这几个数“凑整”以后,就容易计算了.当然要记住 ,“凑整”时增加了多少要减回去.9.996+ 29.98+ 169.9+ 3999.5=10+ 30+ 170+ 4000-( 0.004+ 0.02+ 0.1+ 0.5)=4210- 0.624=4209.376例 2:计算: 1+ 0.99- 0.98- 0.97+ 0.96+ 0.95- 0.94-0.93 ++ 0.04+ 0.03- 0.02- 0.01 式子的数是从 1 开始 ,依次减少0.01, 直到最后一个数是0.01, 因此 ,式中共有100 个数而式子中的运算都是两个数相加接着减两个数,再加两个数 ,再减两个数这样的顺序排列的 .由于数的排列、运算的排列都很有规律,按照规律可以考虑每 4 个数为一组添上括号 ,每组数的运算结果是否也有一定的规律?可以看到把每组数中第 1 个数减第 3 个数 ,第 2 个数减第 4 个数 ,各得 0.02, 合起来是 0.04,那么 ,每组数(即每个括号)运算的结果都是0.04,整个算式 100 个数正好分成 25 组 ,它的结果就是25 个 0.04 的和 .1+ 0.99- 0.98- 0.97+ 0.96+ 0.95 - 0.94- 0.93 ++ 0.04+0.03 -0.02 -0.01 =( 1+ 0.99- 0.98- 0.97)+( 0.96+ 0.95 -0.94- 0.93 )++( 0.04+ 0.03- 0.02- 0.01 )=0.04× 25=1如果能够灵活地运用数的交换的规律,也可以按下面的方法分组添上括号计算:1+ 0.99- 0.98- 0.97+ 0.96+ 0.95 - 0.94- 0.93 ++ 0.04+0.03 -0.02 -0.01 =1+( 0.99- 0.98- 0.97+ 0.96)+(0.95 -0.94- 0.93 + 0.92)++( 0.03- 0.02- 0.01 )=1例 3:计算: 0.1+ 0.2+ 0.3++ 0.8 +0.9+0.10 + 0.11+ 0.12++ 0.19+ 0.20这个算式的数的排列像一个等差数列,但仔细观察 ,它实际上由两个等差数列组成,0.1+0.2+ 0.3++ 0.8+ 0.9 是第一个等差数列,后面每一个数都比前一个数多0.1,而 0.10+ 0.11+0.12++ 0.19+ 0.20 是第二个等差数列,后面每一个数都比前一个数多0.01, 所以 ,应分为两段按等差数列求和的方法来计算.0.1+ 0.2+ 0.3++ 0.8+0.9+ 0.10+ 0.11 + 0.12++0.19+ 0.20=( 0.1+ 0.9)×9÷ 2+( 0.10+0.20 )× 11÷2=4.5+ 1.65=6.15例 4:计算: 9.9× 9.9+ 1.99算式中的 9.9× 9.9 两个因数中一个因数扩大10 倍 ,另一个因数缩小10 倍 ,积不变 ,即这个乘法可变为99× 0.99; 1.99 可以分成0.99+ 1 的和 ,这样变化以后 ,计算比较简便.9.9× 9.9+ 1.99=99× 0.99+ 0.99+ 1=( 99+ 1)× 0.99 +1=100例 5:计算: 2.437× 36.54+ 243.7× 0.6346虽然算式中的两个乘法计算没有相同的因数,但前一个乘法的 2.437 和后一个乘法的243.7 两个数的数字相同,只是小数点的位置不同,如果把其中一个乘法的两个因数的小数点.按相反方向移动同样多位,使这两个数变成相同的,就可以运用乘法分配律进行简算了2.437× 36.54+ 243.7× 0.6346=2.437× 36.54+ 2.437× 63.46=2.437×( 36.54+ 63.46)=243.7* 例 6:计算: 1.1×1.2 ×1.3× 1.4×1.5算式中的几个数虽然是一个等差数列,但算式不是求和,不能用等差数列求和的方法来计算这个算式的结果.平时注意积累计算经验的同学也许会注意到7、 11 和 13 这三个数连乘的积是1001,而一个三位数乘1001,只要把这个三位数连续写两遍就是它们的积,例如 578× 1001=578578,这一题参照这个方法计算,能巧妙地算出正确的得数.1.1× 1.2× 1.3× 1.4× 1.5=1.1× 1.3× 0.7× 2× 1.2× 1.5=1.001× 3.6=3.6036计算下列各题并写出简算过程:1. 5.467+ 3.814+ 7.533+ 4.1862. 6.25× 1.25× 6.43. 3.997+ 19.96+ 1.9998 + 199.74. 0.1+ 0.3++ 0.9+ 0.11+ 0.13+ 0.15++ 0.97+ 0.995. 199.9× 19.98- 199.8× 19.976. 23.75× 3.987+ 6.013× 92.07+ 6.832× 39.87*7 . 20042005 × 20052004 - 20042004 ×20052005 *8 .(1+ 0.12+ 0.23)×( 0.12+ 0.23+ 0.34)-( 1+ 0.12+ 0.23+ 0.34)×( 0.12+ 0.23 )计算下列各题并写出简算过程:1. 6.734- 1.536+ 3.266- 4.4642. 0.8÷ 0.1253. 89.1+ 90.3+ 88.6+ 92.1+ 88.9+ 90.84. 4.83× 0.59+ 0.41× 1.59- 0.324× 5.95. 37.5× 21.5× 0.112+ 35.5× 12.5× 0.112包含与排除1、某班有40 名学生 ,其中有 15 人参加数学小组,18 人参加航模小组,有 10 人两个小组都参加. 那么有多少人两个小组都不参加?两个小组共有(15+18) -10=23 (人) ,都不参加的有40-23=17(人)答:有 17 人两个小组都不参加 .--2、某班45 个学生参加期末考试,成绩公布后 ,数学得满分的有 10 人 ,数学及语文成绩均得满分的有 3 人 ,这两科都没有得满分的有29 人.那么语文成绩得满分的有多少人?45-29-10+3=9 (人)答:语文成绩得满分的有9 人 .3、 50 名同学面向老师站成一行.老师先让大家从左至右按1,2,3,,49,50 依次报数;再让报数是 4 的倍数的同学向后转,接着又让报数是 6 的倍数的同学向后转 .问:现在面向老师的同学还有多少名 ?4 的倍数有 50/4 商 12 个 ,6 的倍数有 50/6 商 8个,既是 4又是 6的倍数有 50/12 商 4 个.4 的倍数向后转人数 =12,6 的倍数向后转共8 人 ,其中 4 人向后 ,4 人从后转回 .面向老师的人数 =50-12=38(人)答:现在面向老师的同学还有38 名.4、在游艺会上 ,有 100 名同学抽到了标签分别为 1 至 100 的奖券 .按奖券标签号发放奖品的规则如下:( 1)标签号为 2 的倍数 ,奖 2 支铅笔;( 2)标签号为 3 的倍数 ,奖 3 支铅笔;( 3 )标签号既是 2 的倍数 ,又是 3 的倍数可重复领奖;( 4)其他标签号均奖 1 支铅笔 .那么游艺会为该项活动准备的奖品铅笔共有多少支?2 的倍数有100/2 商 50 个 ,3 的倍数有100/3 商 33 个 ,2 和 3 人倍数有100/6 商 16 个 .领 2 支的共准备( 50— 16)*2=68, 领 3 支的共准备( 33— 16)*3=51, 重复领的共准备16*( 2+3)=80,其余准备100-( 50+33-16 ) *1=33共需要 68+51+80+33=232(支)答:游艺会为该项活动准备的奖品铅笔共有232 支.5、有一根长为180 厘米的绳子 ,从一端开始每隔后将标有记号的地方剪断.问绳子共被剪成了多少段3 厘米作一记号?,每隔 4 厘米也作一记号,然3 厘米的记号:180/3=60, 最后到头了不划,60-1=59 个4 厘米记号: 180/4=45,45-1=44 个 ,重复的记号:180/12=15,15-1=14 个 ,所以绳子中间实际有记号 59+44-14=89 个 .剪 89 次 ,变成 89+1=90 段答:绳子共被剪成了 90 段 .6、东河小学画展上展出了许多幅画,其中有 16 幅画不是六年级的 ,有 15 幅画不是五年级的 . 现知道五、六年级共有25 幅画 ,那么其他年级的画共有多少幅?1,2,3,4,5 年级共有 16,1,2,3,4,6 年级共有 15,5,6 年级共有 25所以总共有( 16+15+25) /2=28 (幅) ,1,2,3,4 年级共有28-25=3 (幅)答:其他年级的画共有 3 幅.---7、有若干卡片 ,每张卡片上写着一个数 ,它是 3 的倍数或 4 的倍数 ,其中标有 3 的倍数的卡片占 2/3, 标有 4 的倍数的卡片占 3/4, 标有 12 的倍数的卡片有15 张 .那么 ,这些卡片一共有多少张?12 的倍数有2/3+3/4-1=5/12,15/(5/12)=36(张)答:这些卡片一共有36 张.----8、在从 1 至 1000 的自然数中 ,既不能被 5 除尽 ,又不能被7 除尽的数有多少个?5 的倍数有1000/5 商 200 个 ,7 的倍数有 1000/7 商 142 个,既是 5 又是 7 的倍数有1000/35商 28 个 .5 和 7 的倍数共有 200+142-28=314 个 .1000-314=686答:既不能被 5 除尽 ,又不能被 7 除尽的数有686 个.---9、五年级三班学生参加课外兴趣小组,每人至少参加一项 .其中有 25 人参加自然兴趣小组 ,35 人参加美术兴趣小组 ,27 人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12 人, 参加自然同时又参加美术兴趣小组的有8 人 ,参加自然同时又参加语文兴趣小组的有9 人,语文、美术、自然 3 科兴趣小组都参加的有 4 人 .求这个班的学生人数 .25+35+27-( 8+12+9) +4=62(人)答:这个班的学生人数是62 人.-- --10、如图 8-1,已知甲、乙、丙 3 个圆的面积均为 30,甲与乙、乙与丙、甲与丙重合部分的面积分别为 6,8,5,而 3 个圆覆盖的总面积为 73.求阴影部分的面积 .甲、乙、丙三者重合部分面积=73+( 6+8+5) -3*30=2阴影部分面积=73-( 6+8+5) +2*2=58答:阴影部分的面积是58.11、四年级一班有 46 名学生参加 3 项课外活动 .其中有 24 人参加了数学小组 ,20 人参加了语文小组 ,参加文艺小组的人数是既参加数学小组又参加文艺小组人数的 3.5 倍 ,又是 3 项活动都参加人数的 7 倍 ,既参加文艺小组也参加语文小组的人数相当于 3 项都参加的人数的 2 倍 , 既参加数学小组又参加语文小组的有10 人 .求参加文艺小组的人数 .设参加文艺小组的人数是X,24+20+X-( X/305+2/7*X+10 ) +X/7=46, 解得 X=21答:参加文艺小组的人数是21 人.________________________________________-12、图书室有 100 本书 ,借阅图书者需要在图书上签名.已知在 100 本书中有甲、乙、丙签名的分别有 33,44 和 55 本 ,其中同时有甲、乙签名的图书为29 本 ,同时有甲、丙签名的图书有25 本,同时有乙、丙签名的图书有36 本 .问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过 ?三个人一共看过的书的本数是:甲 +乙 +丙(-甲乙 +甲丙 +乙丙)+甲乙丙 =33+44+55(- 29+25+36)+甲乙丙 =42+甲乙丙 ,当甲乙丙最大时 ,三人看过的书最多,因为甲、丙共同看过的书只有25 本,比甲乙和乙丙共同看到的都少,所以甲乙丙最多共同看过25 本.三人总共看过最多有42+25=67(本) ,都没看过的书最少有100-67=33 (本)答:这批图书中最少有33 本没有被甲、乙、丙中的任何一人借阅过.________________________________________13、如图 8-2,5 条同样长的线段拼成了一个五角星.如果每条线段上恰有1994 个点被染成红色,那么在这个五角星上红色点最少有多少个?五条线上右发有 5*1994=9970 个红点 ,如果所有交叉点上都放一个红点,则红点最少 ,这五条线有 10 个交叉点 ,所以最少有9970-10=9960 个红点答:在这个五角星上红色点最少有9960 个 .14、甲、乙、丙同时给100 盆花浇水 .已知甲浇了 78 盆 ,乙浇了 68 盆 ,丙浇了 58 盆 ,那么 3 人都浇过的花最少有多少盆?甲和乙必有 78+68-100=46 盆共同浇过 ,丙有 100-58=42 没浇过 ,所以 3 人都浇过的最少有46-42=4(盆)答: 3 人都浇过的花最少有 4 盆 .15、甲、乙、丙都在读同一本故事书 ,书中有100 个故事 .每个人都从某一个故事开始,按顺序往后读 .已知甲读了 75 个故事 ,乙读了 60 个故事 ,丙读了 52 个故事 .那么甲、乙、丙 3 人共同读过的故事最少有多少个?乙和丙共同读过的故事至少有60+52-100=12(个) ,甲无论从哪里开始都必定要读这12 个故事.答:甲、乙、丙 3 人共同读过的故事最少有12 个.15、甲、乙、丙都在读同一本故事书 ,书中有100 个故事 .每个人都从某一个故事开始,按顺序往后读 .已知甲读了 75 个故事 ,乙读了 60 个故事 ,丙读了 52 个故事 .那么甲、乙、丙 3 人共同读过的故事最少有多少个?乙和丙共同读过的故事至少有60+52-100=12(个) ,甲无论从哪里开始都必定要读这12 个故事.答:甲、乙、丙 3 人共同读过的故事最少有12 个.________________________________________-8、在从 1 至 1000 的自然数中 ,既不能被 5 除尽 ,又不能被 7 除尽的数有多少个 ?5 的倍数有 1000/5 商 200 个 ,7 的倍数有1000/7 商 142 个,既是 5 又是 7 的倍数有 1000/35 商 28 个 .5 和 7 的倍数共有 200+142-28=314 个 .1000-314=686答:既不能被 5 除尽 ,又不能被7 除尽的数有686 个 .题中的除尽应该是整除吧.11、四年级一班有46 名学生参加 3 项课外活动 .其中有 24 人参加了数学小组,20 人参加了语文小组 ,参加文艺小组的人数是既参加数学小组又参加文艺小组人数的 3.5 倍 ,又是 3 项活动都参加人数的7 倍 ,既参加文艺小组也参加语文小组的人数相当于 3 项都参加的人数的 2 倍 , 既参加数学小组又参加语文小组的有10 人 .求参加文艺小组的人数.设参加文艺小组的人数是X,24+20+X-( X/305+2/7*X+10 ) +X/7=46, 解得 X=21答:参加文艺小组的人数是21 人.。
五年级《速算与巧算》奥数教案

板书:
原式= + + +
=2
练习2:(5分)
计算: + + + -
分析:
将算式中的分数先化成最简分数,然后会发现化简后每个分数都是 。
板书:
原式= + + + -
=1
三、小结:(5分)
整数的加法交换律、结合律对分数的加减计算同样适用。
第二课时(50分)
师:那么我们可不可以将式子写成这种形式。
板书:
原式=(1- )+( - )+( - )+……+( - )
=1- + - + - +……+ -
=1-
=
师:从式子中我们发现中间的分数都是一加一减刚好抵消的。将数列中的每一
项分解,然后重新组合,使之能消去一些项,最终达到求和的目的,我们
把这种解题方法叫做裂项相消法。
生: ,老师,我知道了,给式子加上一个 ,再在最后减去一个 ,
+ = , + = , + = ,最后式子变成1+2+3+4+5+ + - 。
师:恩恩,同学的反应能力很快,那么请你将过程板书到黑板上。
板书:
原式=1+2+3+4+5+ + + + +( + )-
=15+ + + +( + )-
=15+ + +( + )-
练习1:(5分)
计算: - + +
分析:
五年级奥数——巧算与速算(含解析)
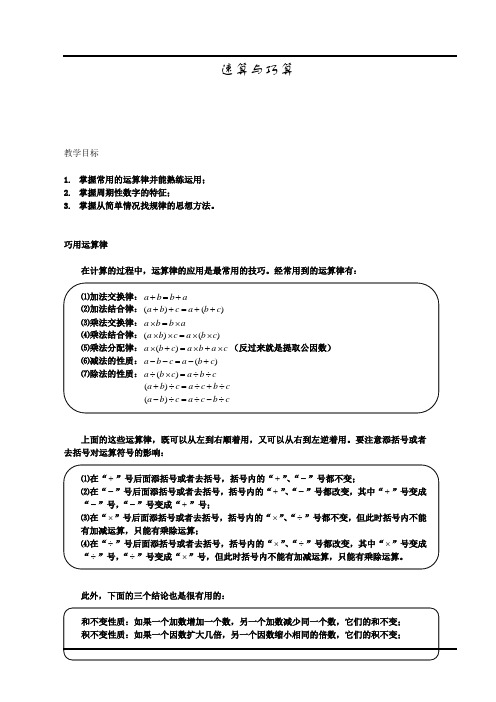
速算与巧算教学目标1.掌握常用的运算律并能熟练运用;2.掌握周期性数字的特征;3.掌握从简单情况找规律的思想方法。
巧用运算律在计算的过程中,运算律的应用是最常用的技巧。
经常用到的运算律有:⑴加法交换律:a b b a+=+⑵加法结合律:()()++=++a b c a b c⑶乘法交换律:a b b a⨯=⨯⑷乘法结合律:()()⨯⨯=⨯⨯a b c a b c⑸乘法分配律:()⨯+=⨯+⨯(反过来就是提取公因数)a b c a b a c⑹减法的性质:()--=-+a b c a b c⑺除法的性质:()÷⨯=÷÷a b c a b c+÷=÷+÷a b c a c b c()-÷=÷-÷()a b c a c b c上面的这些运算律,既可以从左到右顺着用,又可以从右到左逆着用。
要注意添括号或者去括号对运算符号的影响:⑴在“+”号后面添括号或者去括号,括号内的“+”、“-”号都不变;⑵在“-”号后面添括号或者去括号,括号内的“+”、“-”号都改变,其中“+”号变成“-”号,“-”号变成“+”号;⑶在“⨯”号后面添括号或者去括号,括号内的“⨯”、“÷”号都不变,但此时括号内不能有加减运算,只能有乘除运算;⑷在“÷”号后面添括号或者去括号,括号内的“⨯”、“÷”号都改变,其中“⨯”号变成“÷”号,“÷”号变成“⨯”号,但此时括号内不能有加减运算,只能有乘除运算。
此外,下面的三个结论也是很有用的:商不变性质:如果除数和被除数同时扩大或缩小相同的倍数,它们的商不变。
【例1】(“走进美妙的数学花园”初赛)计算:11353715⨯-⨯【分析】根据“一个因数扩大若干倍,另一个因数缩小相同的倍数,积不变”的道理,进行适当变换,再提取公因数,进而凑整求和。
原式11353735=⨯-⨯⨯=⨯-⨯11351115=-⨯(113111)5=10【例2】(武汉明心奥数挑战赛)计算:1234567981⨯【分析】原式123456799912345679(101)9(12345679012345679)9=⨯⨯=⨯-⨯=-⨯=⨯=1111111119999999999[巩固] 计算:123456789876543219⨯[分析] 原式12345678987654321(101)=⨯-=-12345678987654321012345678987654321=111111110888888889【例3】(“走进美妙的数学花园”决赛)计算:⨯+⨯+÷-⨯+2237.522.312.523040.7 2.51【分析】原式2233 2.522.35 2.523 2.50.7 2.50.4 2.5=⨯⨯+⨯⨯+⨯-⨯+⨯=⨯⨯+⨯+-+2.5(223322.35230.70.4)2.5(669111.5230.70.4)=⨯++-+=⨯2.5803.2=⨯÷803.2104=÷80324=2008[巩固] 计算:199.919.98199.819.97⨯-⨯[分析] (法1)原式199.919.9819.98199.7=⨯-⨯=⨯-19.98(199.9199.7)=⨯19.980.2(法2)也可以用凑整法来解决。
五年级奥数倒推法KKKK(肖翠君)
例4 篮子里有一些梨.小刚取走总数的一半 多一个.小明取走余下的一半多1个.小军取 走了小明取走后剩下一半多一个.这时篮子 里还剩梨1个.问:篮子里原有梨多少个? 分析 依题意,画图进行分析.
解:列综合算式: {[(1+1)×2+1]×2+1}×2 =22(个) 答:篮子里原有梨22个.
例5 甲乙两个油桶各装了15千克油. 售货员卖了14千克.后来,售货员从 剩下较多油的甲桶倒一部分给乙桶 使乙桶油增加一倍;然后从乙桶倒 一部分给甲桶,使甲桶油也增加一 倍,这时甲桶油恰好是乙桶油的3倍. 问:售货员从两个桶里各卖了多少 千克油?
2、甲、乙两桶油各有若干千克,如果要从甲桶中倒出和
乙桶同样多的油放入乙桶,再从乙桶中倒和甲桶剩下的 同样多的油放入甲桶。这时两桶油恰好都是36千克。问 两桶油原来各有多少千克?
分析:此题可以从最后的两桶油都是36千克往前推:第二次倒入: 乙桶倒出和甲桶同样多的油放入甲桶得到甲桶是36千克,则36千克 是甲桶原有油的2倍;所以没倒入之前甲桶有油36÷2=18千克,则 乙桶此时是36+18=54千克,即第一次倒入之后甲桶是18千克,乙桶 是54千克;而乙桶的54千克,是第一次倒入时,从甲桶倒入了和它 原来同样多的油得到的,所以乙桶原来有油:54÷2=27千克,则甲 原来有油18+27=45千克. 36÷2=18(千克)36-18=18(千克)乙36+18=54(千克); 第一次甲桶倒入乙桶的油为:54÷2=27(千克), 所以原来乙桶有油:27千克 甲桶有油:18+27=45(千克),
甲乙丙各有棋子若干个.甲先给乙、丙一些棋子,使乙、 丙每人的棋子数各增加一倍.然后乙也把自己的一些 棋子给甲、丙使每人的棋子数各增加一倍;最后丙也 按甲和乙的棋子数分别给甲、乙一些棋子,此时三人 都各有16个棋子.开始时三人各有多少个棋子? 甲 乙 丙
(完整版)奥数知识点速算与巧算

(完整版)奥数知识点速算与巧算速算与巧算引导:1、计算(凑十法)1+2+3+4+5+6+7+8+9+102、计算(凑整法)1+3+5+7+9+11+13+15+17+192+4+6+8+10+12+14+16+18+202+13+25+44+18+37+56+753、计算(用已知求未知)1+2+3+4+5+6+7+8+9+10+11+12+13+14+155+6+7+8+9+104、计算(改变运算顺序)10-9+8-7+6-5+4-3+2-15、计算(带着“+”、“-”号搬家)1-2+3-4+5-6+7-8+9-10+11一、凑十法:利用个位数相加之和都等于10的技术题1、计算1+2+3+4+5+6+7+8+9+10这种逐步相加的方法,好处是可以得到每一步的结果,但缺点是麻烦、容易出错;而且一步出错,以后步步都错。
若是利用凑十法,就能克服这种缺点。
二、凑整法:同学们还知道,有些数相加之和是整十、整百的数,如:巧用这些结果,可以使那些较大的数相加又快又准。
像10、20、30、40、50、60、70、80、90、100等等这些整十、整百的数就是凑整的目标。
题2、计算1+3+5+7+9+11+13+15+17+19解:这是求1到19共10个单数之和,用凑整法做:题3、计算2+4+6+8+10+12+14+16+18+20解:这是求2到20共10个双数之和,用凑整法做:题4、计算2+13+25+44+18+37+56+75解:用凑整法:三、用已知求未知利用已经获得较简单的知识来解决面临的更复杂的难题这是人们认识事物的一般过程,凑十法、凑整法的实质就是这个道理,可见把这种认识规律用于计算方面,可使计算更快更准。
题5、计算:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19 +20 解:由例2和例3,已经知道从1开始的前10个单数之和及从2开始的前10个双数之和,巧用这些结果计算这道题就容易了。
五年级奥数- 巧算与速算
速算与巧算一、考点、热点回顾:1、掌握小学数学中常用的速算方法,并根据数字特点选择恰当方法计算。
二、典型例题:例1计算72.19+6.48+27.81-1.38-5.48-0.62。
解:观察发现,有些加数可以凑整;有的加数和减数尾数相同,可以抵消。
于是:72.19+6.48+27.81-1.38-5.48-0.62=(72.19+27.81)+(6.48-5.48)-(1.38+0.62)=100+1-2=99例2用简便方法计算 1.25×67.875+125×6.7875+1250×0.053375。
解:观察发现:相加的三个乘积中分别有1.25、125、250,因此想到利用积不变的性质,使三个积有相同的因数。
于是:1.25×67.875+125×6.7875+1250×0.053375=1.25×67.875+1.25×678.75+1.25×53.375=1.25×(67.875+678.75+53.375)=1.25×800=1000例3计算1999+199.9+19.99+1.999。
解法一:观察发现,构成这四个加数的数字和排列顺序完全相同,因此可以把它们都看作1999与某个数的积,于是:1999+199.9+19.99+1.999=1999×(1+0.1+0.01+0.001)=1999×1.111=(2000-1)×1.111=2222-1.111=2220.889解法二:观察发现这四个加数分别接近2000、200、20、2,于是1999+199.9+19.99+1.999=2000+200+20+2-1.111=2220.889例4计算(1+0.33+0.44)×(0.33+0.44+0.55)-(1+0.33+0.44+0.55)×(0.33+0.44)。
五年级奥数-组合图形的面积(一)肖翠君KK
• 图中三个正方形的边长分别是1厘米、2厘米和3厘米,求图 中阴影部分的面积。
用最上面的一条长斜线与小正方形的边大 正方形的边三个正方形的边构成直角梯形 再减去另外两条斜边与正方形边构成的两 个直角三角形就是阴影面积的大小 直角梯形面积(3+1)×(1+2+3)÷2=12 左边三角形面积1×(1+2)÷2=1.5 右边三角形面积3×3÷2=4.5 阴影面积12-1.5-4.5=6
练习:如下图)已知大正方形的边长是12厘米, 求中间最小正方形的面积。
我们先求出最大正方形的面积,即:12×12=144(平 方厘米).再分析最外两层:,在图中添两条辅助线 (虚线),不难看出三角形1、2、3、4、5、6、7、8 的面积是相等的.进而推断,由三角形2、4、6、8组 成的较小正方形的面积是大正方形面积的一半,即: 144÷2=72(平方厘米).以此类推,每个较小正方形 面积都是与之最近的较大正方形面积的一半,于是, 用144÷2÷2=36(平方厘米),便求出了题中最小的 正方形的面积是36平方厘米.
例 、 图中ABCD是长方形,三角形EFD的面积比三角形 ABF的面积大6平方厘米,求ED的长。 因为三角形EFD的面积比三角形 ABF的面积大6平方厘米,所以, 三角形BCE的面积比长方形ABCD 的面积大6平方厘米。三角形BCE 的面积是6×4+6=30平方厘米, EC的长则是30×2÷6=10厘米。 因此,ED的长是10-4=6厘米。
• 如图,平行四边形BCEF中,BC=8厘米, • 直角三角形中,AC=10厘米,阴影部分面积比 • 三角形ADH的面积大8平方厘米。 • 求AH长多少厘米?
SΔABC=10×8÷2=40, 根据题意: S阴影=8+SΔADH, ∴S平行四边形=8+SΔABC(上式两边都 加上S梯形BCHD), ∴S平行四边形=48, ∴高CH=48÷8=6, ∴AH=AC-CH=4㎝.
