材料力学教案第5章 弯曲应力
材料力学弯曲应力原创教案

弯曲应力我们开始弯曲这一章,我们讲了拉压、扭转、剪切,现在我们要讲弯曲。
弯曲的情况要比拉压和扭转更加复杂一些,它所涉及的问题更多一些,它和工程实际联系的更加紧密一些。
因此,这一章和下一章都是特别重要的章节。
在这一章中,我们首先要讨论弯曲正应力,横截面上有弯矩,那它就有了正应力,同时还要考虑弯曲切应力的问题,横截面上有剪力,说明它有切应力存在。
了解了正应力和切应力的情况,我们要讨论梁的强度和破坏,这个思路和前面几章是一样的。
特别的,要强调薄壁杆件中弯曲切应力的处理,最后呢,我们要讲组合变形的应用。
不仅仅是弯曲,而是弯曲和拉压,弯曲和扭转组合在一起的时候,如何来处理它的应力问题。
因此,这章的内容是比较多的。
工程实际例子我们来看看弯曲在工程中的应用。
这是一个厂房,这是一个大梁,这个吊车可以在这个大梁上运动。
对于这样一个问题,我们可以把它简化成一个简支梁,这个吊车的移动呢可以处理成一个移动荷载。
那么对于这个移动荷载而言,它所导致的应力如何计算?行车移动时,它的应力如何变化?这就是本章的内容之一。
我们再看看这个图片,这是我们拍摄的汽车的下部分,大家注意一些这个部分,这是就是汽车的板簧,它的模型就是这个样子,可以看成好几个钢板的组合,那么,为什么要设计成这个样子呢?它有什么优点呢?这也是本章要解决的问题。
这是一个运动员,撑杆跳,对吧。
大家常常见到,利用这个杆的助力,人可以跳的更高。
我们可以处理成这样一个模型。
她在跳高的过程中,杆就发生了弯曲。
那么,这个时候,跳杆横截面上的应力和杆曲率半径有什么关系?这个杆在什么情况下才满足强度要求?大家看看这个场面,对于这个场面,我们截面几何性质那章提到过,都是薄壁杆件,那么薄壁杆件有弯曲正应力和弯曲切应力,专门有一小节来讲解它的弯曲切应力,看看这些切应力有什么特点?如何避免薄壁杆件的强度失效?这也是本章的问题这个大家都熟悉,著名的比萨斜塔。
对于这个结构,初步计算,我们可以简化成这样一个均质圆筒,那么它有哪些变形效应?它的危险截面、危险点在哪儿?如何计算其应力?这也是本章可以解决的问题。
材料力学弯曲应力原创教案

材料力学弯曲应力原创教案弯曲应力我们开始弯曲这一章,我们讲了拉压、扭转、剪切,现在我们要讲弯曲。
弯曲的情况要比拉压和扭转更加复杂一些,它所涉及的问题更多一些,它和工程实际联系的更加紧密一些。
因此,这一章和下一章都是特别重要的章节。
在这一章中,我们首先要讨论弯曲正应力,横截面上有弯矩,那它就有了正应力,同时还要考虑弯曲切应力的问题,横截面上有剪力,说明它有切应力存在。
了解了正应力和切应力的情况,我们要讨论梁的强度和破坏,这个思路和前面几章是一样的。
特别的,要强调薄壁杆件中弯曲切应力的处理,最后呢,我们要讲组合变形的应用。
不仅仅是弯曲,而是弯曲和拉压,弯曲和扭转组合在一起的时候,如何来处理它的应力问题。
因此,这章的内容是比较多的。
工程实际例子我们来看看弯曲在工程中的应用。
这是一个厂房,这是一个大梁,这个吊车可以在这个大梁上运动。
对于这样一个问题,我们可以把它简化成一个简支梁,这个吊车的移动呢可以处理成一个移动荷载。
那么对于这个移动荷载而言,它所导致的应力如何计算?行车移动时,它的应力如何变化?这就是本章的内容之一。
我们再看看这个图片,这是我们拍摄的汽车的下部分,大家注意一些这个部分,这是就是汽车的板簧,它的模型就是这个样子,可以看成好几个钢板的组合,那么,为什么要设计成这个样子呢?它有什么优点呢?这也是本章要解决的问题。
这是一个运动员,撑杆跳,对吧。
大家常常见到,利用这个杆的助力,人可以跳的更高。
我们可以处理成这样一个模型。
她在跳高的过程中,杆就发生了弯曲。
那么,这个时候,跳杆横截面上的应力和杆曲率半径有什么关系?这个杆在什么情况下才满足强度要求?大家看看这个场面,对于这个场面,我们截面几何性质那章提到过,都是薄壁杆件,那么薄壁杆件有弯曲正应力和弯曲切应力,专门有一小节来讲解它的弯曲切应力,看看这些切应力有什么特点?如何避免薄壁杆件的强度失效?这也是本章的问题这个大家都熟悉,著名的比萨斜塔。
对于这个结构,初步计算,我们可以简化成这样一个均质圆筒,那么它有哪些变形效应?它的危险截面、危险点在哪儿?如何计算其应力?这也是本章可以解决的问题。
《材料力学》 第五章 弯曲内力与弯曲应力

第五章 弯曲内力与应力 §5—1 工程实例、基本概念一、实例工厂厂房的天车大梁,火车的轮轴,楼房的横梁,阳台的挑梁等。
二、弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线。
变形特点——杆轴线由直线变为一条平面的曲线。
三、梁的概念:主要产生弯曲变形的杆。
四、平面弯曲的概念:受力特点——作用于杆件上的外力都垂直于杆的轴线,且都在梁的纵向对称平面内(通过或平行形心主轴且过弯曲中心)。
变形特点——杆的轴线在梁的纵向对称面内由直线变为一条平面曲线。
五、弯曲的分类:1、按杆的形状分——直杆的弯曲;曲杆的弯曲。
2、按杆的长短分——细长杆的弯曲;短粗杆的弯曲。
3、按杆的横截面有无对称轴分——有对称轴的弯曲;无对称轴的弯曲。
4、按杆的变形分——平面弯曲;斜弯曲;弹性弯曲;塑性弯曲。
5、按杆的横截面上的应力分——纯弯曲;横力弯曲。
六、梁、荷载及支座的简化(一)、简化的原则:便于计算,且符合实际要求。
(二)、梁的简化:以梁的轴线代替梁本身。
(三)、荷载的简化:1、集中力——荷载作用的范围与整个杆的长度相比非常小时。
2、分布力——荷载作用的范围与整个杆的长度相比不很小时。
3、集中力偶(分布力偶)——作用于杆的纵向对称面内的力偶。
(四)、支座的简化:1、固定端——有三个约束反力。
2、固定铰支座——有二个约束反力。
3、可动铰支座——有一个约束反力。
(五)、梁的三种基本形式:1、悬臂梁:2、简支梁:3、外伸梁:(L 称为梁的跨长) (六)、静定梁与超静定梁静定梁:由静力学方程可求出支反力,如上述三种基本形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全部支反力。
§5—2 弯曲内力与内力图一、内力的确定(截面法):[举例]已知:如图,F ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l F Y l FaF m F X AYBY A AX)(F, 0 , 00 , 0-=∴==∴==∴=∑∑∑ F AX =0 以后可省略不求 ②求内力xF M m l a l F F F Y AY C AY s ⋅=∴=-==∴=∑∑ , 0)( , 0∴ 弯曲构件内力:剪力和弯矩1. 弯矩:M ;构件受弯时,横截面上存在垂直于截面的内力偶矩。
材料力学第五章弯曲应力

37
dM * Sz b d x 0 Iz dM 由微分关系 Fs dx * FsS z I zb
dM S d x I zb
* z
dFs
由切应力互等定理,得
FsS I zb
* z
计算Sz*
38
由切应力互等定理,得
FsS I zb
* z
31
1 矩形截面梁 切应力分布假设 (1) 各点切应力方向平行 于剪力Fs; (2) 切应力沿宽度均匀分布。
用平衡条件导出切应力公式 取研究对象
32
用平衡条件 定理
右截面上的FN2
A1
FN 2 d A
A1为右截面 pn1的 面积。 右截面正应力为:
例 3 ( 书例5.3)
已知:T形截面铸 铁梁,[t]= 30 MPa,[c]=160 MPa。Iz=763cm4, 且 |y1|=52mm。 求:校核梁的强度。
解:(1) 求弯矩图
支反力 RA 2.5 kN, RB 10.5 kN
作出弯矩图
27
(1) 求弯矩图 支反力
RA 2.5 kN, RB 10.5 kN
材 料 力 学
第五章
弯 曲 应 力
2013年5月20日
1
§5. 1 纯弯曲
横力弯曲
梁的横截面上同时有弯 矩和剪力的弯曲。
纯弯曲
梁的横截面上只有弯矩 时的弯曲。 横截面上只有正应 力而无切应力。
纯弯曲的变形特征
2
纯弯曲的变形特征
3
纯弯曲的变形特征
材料力学教案第5章弯曲应力
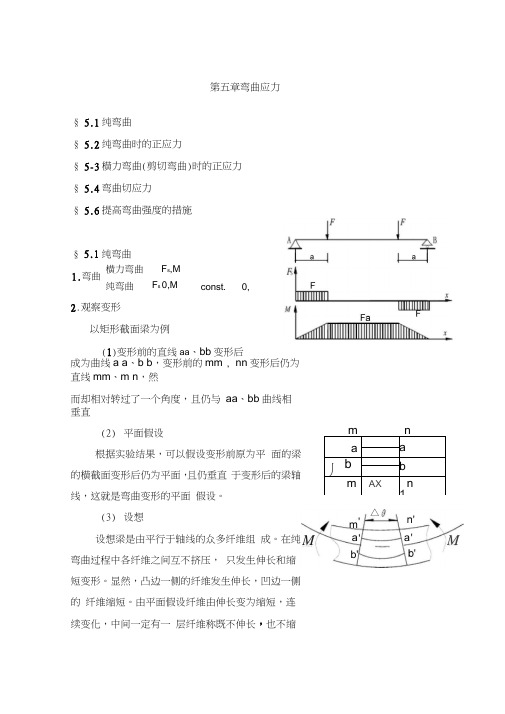
§ 5.1纯弯曲§ 5.2纯弯曲时的正应力§ 5-3横力弯曲(剪切弯曲)时的正应力 § 5.4弯曲切应力 § 5.6提高弯曲强度的措施成为曲线a a 、b b ,变形前的mm , nn 变形后仍为直线mm 、m n ,然而却相对转过了一个角度,且仍与 aa 、bb 曲线相垂直(2) 平面假设根据实验结果,可以假设变形前原为平 面的梁的横截面变形后仍为平面,且仍垂直 于变形后的梁轴线,这就是弯曲变形的平面 假设。
(3) 设想设想梁是由平行于轴线的众多纤维组 成。
在纯弯曲过程中各纤维之间互不挤压, 只发生伸长和缩短变形。
显然,凸边一侧的纤维发生伸长,凹边一侧的 纤维缩短。
由平面假设纤维由伸长变为缩短,连续变化,中间一定有一 层纤维称既不伸长,也不缩第五章弯曲应力§ 5.1纯弯曲 1.弯曲 横力弯曲 纯弯曲 F s ,M F s 0,M const.0,2.观察变形 以矩形截面梁为例 (1)变形前的直线aa 、bb 变形后1aa丿bbm AXn 1mn△m Maa M b'短,这一层纤维为中性层。
(4)中性轴中性层与横截面的交线称为中性轴,由于整体变形的对称性,中性轴由与纵向对称面垂直。
P139 note:可以证明,中性轴为形心主轴。
§ 5.2纯弯曲时的正应力1.正应力分布规律:r①变形几何关系Y②物理关系•③静力关系(1)变形几何关系取dx微段来研究,竖直对称轴为为z轴,距中性层为y的任一纤维b by d d yd(2)物理关系因为纵向纤维之间无正应和,每一纤维都是单向拉伸或者单向压缩,当应力小于比例极限时,由胡克定律(b)此式表明:任意纵向纤维的正应力与它到中性层的距离成正比。
在横截面上,任意点的正应力与该点到中性轴的距离成正比。
亦即沿截面高度,正应力按直线规律变化。
(3)静力关系横截面上的微内力。
dA 组成垂直于横截面的空间平行力学。
材料力学第5章弯曲应力

M
M
中性轴
z
m
n
y
o
o
dA
z
mn
y
dx
Mzy
Iz
max
Mz Wz
M
MZ:横截面上的弯矩
y:到中性轴的距离
IZ:截面对中性轴的惯性矩
M
中性轴
§5-2 惯性矩的计算
一、静矩 P319
y
Sz ydA
A
z dA
zc
c y
S y zdA
yc
A
o
z
分别为平面图形对z 轴和 y 轴的静矩。
ySc Az ydA
F M
F
a
B
F
Fa
5.3 梁弯曲时的正应力
若梁在某段内各横截
面上的弯矩为常量, F
F
a
a
剪力为零, 则该段梁 A 的弯曲就称为纯弯曲。
B
Fs
在 AC 和 DB 段 内 横 截 面上既有弯矩又有剪 M 力, 这种情况称为横 力弯曲或剪切弯曲。
F F
Fa
平面假设
变形前原为平面的梁的横截面变形后仍保持为 平面, 并绕垂直于纵对称面的某一轴旋转, 且仍 然垂直于变形后的梁轴线。这就是弯曲变形的 平面假设。
C y'
a
x'
xc
b
注意!C点必须为截面形心。
六、组合截面的惯性矩
Iy Iyi
Iz Izi
例2:求对倒T字型形心 轴yC和zC的惯性矩。
解:1. 取参考轴yOz 2. 求形心
2cm y(yc)
1 c1
6 cm
yc
Ai yi A
y
c 1
材料力学《第五章》弯曲应力

1
2
c
O1
d
O2
a
1 1 2
b
2
M
d
O2
c
O1
a
1
b
2
O z y
由变形的连续形可知:
从伸长到缩短的过程中,必存在一 层纵向纤维既不伸长也不缩短,保 持原来的长度。 中性层:由既不伸长也不缩短的纵 M 向纤维组成。 中性轴:中性层与梁横截面的交线。 中性轴垂直于梁横截面的纵向对称轴。 a
1
1
2
c
O1
d
O2
a
1 1 2
b
2
M
d
O2
c
O1
b
2
3. 在伸长区,梁宽度减小, 在缩短区,梁宽度增加。 与轴向拉、压时变形相似。
上海交通大学
O z y
二、假设 1. 梁弯曲平面假设 梁弯曲变形后,横截面仍保持为平 面,并仍与已变弯后的梁轴线垂直, 只是绕该截面内某轴转过一个微小 M 角度。 2. 单向受力假设 设想梁由许多层纵向纤维组成,弯 曲时各纵向纤维处于单向受拉或单 向受压状态。 由实验现象和假设可推知: 弯曲变形时: 靠近梁顶面的纵向纤维受压、缩短; 靠近梁底面的纵向纤维受拉、伸长。
O1Biblioteka 1dqr2
O2
M
a
1
y
b
2
中性层下方,y 为正值, s 也为正值,表示为拉应力; 中性层上方,y 为负值, s 也为负值,表示为压应力。 y =0 (中性轴上),s = 0 ; y |max (上、下表层), s max 。
由(b)式可得s 的分布规律,但因r 的数值未知,中性轴的位置未确定, y 无从算起,所以仍不能计算正应力,用静力学关系解决。
材料力学第五章 弯曲应力

F F d F 0 N 2 N 1 S
将FN2、FN1和dFS′的表达式带入上式,可得
* M M d M * S S b d x 0 z z
I z I z
简化后可得
dM S z* dx I z b
dM F S ,代入上式得 由公式(4-2), dx
* 式中 S z
A1
y1dA ,是横截面距中性轴为 y 的横线 pq 以下的面积对中性轴的静矩。同理,
可以求得左侧面 rn 上的内力系的合力 FN 1 为
M * FN 1 S z Iz
在顶面rp上,与顶面相切的内力系的合力是
d F b d x S
根据水平方向的静平衡方程
F 0 ,可得
综上所述,对于各横截面剪力相同的梁和剪力不相同的
细长梁(l>5h),在纯弯曲情况下推导的弯曲正应力公式 (5-2)仍然适用。
例5-1
图5-10(a)所示悬臂梁,受集中力F与集中力
偶Me作用,其中F=5kN,Me=7.5kN· m,试求梁上B点左邻 面1-1上的最大弯曲正应力、该截面K点处正应力及全梁的 最大弯曲正应力。
第五章 弯曲应力
5.1 弯曲正应力 5.2 弯曲切应力简介 5.3 弯曲强度条件及其应用 5.4 提高梁弯曲强度的主要措施
5.1 弯曲正应力
上一章研究表明,一般情况下,梁横截面上同时存在
剪力FS和弯矩M。由于只有切向微内力τ dA才可能构成剪力, 也只有法向微内力σdA才可能构成弯矩,如图5-1(a)所示。 因此,在梁的横截面上将同时存在正应力σ和切应力τ(见图 5-1(b))。梁弯曲时横截面上的正应力与切应力分别称为 弯曲正应力与弯曲切应力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 弯曲应力§5.1 纯弯曲§5.2 纯弯曲时的正应力§5-3 横力弯曲(剪切弯曲)时的正应力 §5.4 弯曲切应力 §5.6 提高弯曲强度的措施§5.1 纯弯曲 1.⎩⎨⎧===----στ,0,,0,const M F MF S S 纯弯曲横力弯曲弯曲2.观察变形 以矩形截面梁为例(1)变形前的直线aa 、bb 变形后成为曲线a a ''、b b '',变形前的mm ,nn 变形后仍为直线m m ''、n m '',然而却相对转过了一个角度,且仍与a a ''、b b ''曲线相垂直。
(2)平面假设根据实验结果,可以假设变形前原为平面的梁的横截面变形后仍为平面,且仍垂直于变形后的梁轴线,这就是弯曲变形的平面假设。
(3)设想设想梁是由平行于轴线的众多纤维组成。
在纯弯曲过程中各纤维之间互不挤压,只发生伸长和缩短变形。
显然,凸边一侧的纤维发生伸长,凹边一侧的纤维缩短。
由平面假设纤维由伸长变为缩短,连续变化,中间一定有一层纤维称既不伸长,也不缩短,这一层纤维为中性层。
(4)中性轴中性层与横截面的交线称为中性轴,由于整体变形的对称性,中性轴由与纵向对称面垂直。
P139note :可以证明,中性轴为形心主轴。
§5.2 纯弯曲时的正应力1.正应力分布规律:①变形几何关系 ②物理关系 ③静力关系 (1)变形几何关系取d x 微段来研究,竖直对称轴为y 轴,中性轴为z 轴,距中性层为y 的任一纤维b b ''的线应变。
()ρθρθρθρεyy =-+=d d d (a )(2)物理关系因为纵向纤维之间无正应和,每一纤维都是单向拉伸或者单向压缩,当应力小于比例极限时,由胡克定律ε=σEρ=σy E(b )此式表明:任意纵向纤维的正应力与它到中性层的距离成正比。
在横截面上,任意点的正应力与该点到中性轴的距离成正比。
亦即沿截面高度,正应力按直线规律变化。
(3)静力关系横截面上的微内力σd A组成垂直于横截面的空间平行力学。
这一力e系可能简化为三个内力分量:⎪⎪⎭⎪⎪⎬⎫===⎰⎰⎰N A iz Aiy AA y M A z M AF d d d σσσ 横截面上的内力与截面左侧的外力必须平衡。
在纯弯曲情况下,截面左侧的外力只有对z 轴的力偶矩M e 。
由于内外力必须满足平衡方程,故:①⎰===∑N Ax A F F 00d σ(c )式(b )代入式(c )⎰⎰==AAA y EA 0d d ρσ∵ 0≠ρ=ρEconst E∴⎰==AZ S A y 0d结论:Z 轴(中性轴)通过形心。
② ⎰===∑Aiy y A z M M 00d σ (d )式(b )代入式(d )⎰⎰==AAA yz EA z 0d d ρσ ⎰==AI A yz 0yzd结论:y 轴为对称轴,上式自然满足③ ⎰====∑Aiz e z A y M M M M d σ0(e ) 式(b )代入式(e )⎰⎰==AAA y EA y M d d 2ρσ (f )∵⎰=AZ I A y d 2∴式(f )可写成ZEI M=ρ1(g )d式中ρ1为梁轴线变形后的曲率,EI Z 称为梁的抗弯刚度。
2.纯弯曲时梁的正应力计算公式 由式(g )和式(b )中消去ρ1得zy I M =σ讨论:(1)导出公式时用了矩形截面,但未涉及任何矩形的几何特性,因此,公式具有普遍性。
(2)只要梁有一纵向对称面,且载荷作用于对称面内,公式都适用。
(3)横截上任一点处的应力是拉应力还是压应力可直接判定,不需用y 坐标的正负来判定。
§5-3 横力弯曲(剪切弯曲)时的正应力1.纯弯曲正应力公式推广应用于横力弯曲ZI yM ⋅=σ 讨论:公式的适用条件 (1)平面弯曲(2)纯弯曲或l/h ≥5的横力弯曲(σ,τ) (3)应力小于比例极限。
2.最大正应力ZI y M maxmax max =σ 引入记号:maxy IW Z Z =ZW M max max =σW ——抗弯截面系数(m 3) 讨论:(1)等直梁而言σmax 发生在最大弯矩断面,距中性轴最远处y max 。
(2)对于变截面梁不应只注意最大弯矩M max 截面,而应综合考虑弯矩和抗弯截面系数W Z 两个因素。
3.强度条件][maxmaxσσ≤=ZW M (1)对抗拉抗压强度相同的材料,只要[]σσ≤max即可(2)对抗拉抗压强度不等的材料(如铸铁)则应同时满足:[][]⎭⎬⎫≤≤c c t t σσσσmax max4.强度计算 (1)强度校核(2)设计截面尺寸:[]σmaxM W Z ≥(3)确定许用载荷:[]Z W M σ≤maxExample1 空气泵操作杆,右端受力F 1=8.5kN ,1-1、2-2截面相同,均为h/b =3的矩形,若[σ]=50MPa ,试选用1-1、2-2截面尺寸。
Solution ①求F 2072.05.838.0020=⨯-=∑F M1162.F =kN②求截面弯矩M 1=8.5×(0.72-0.08)=5.44kN·mM 2=16.1×(0.38-0.08)=4.38kN·m故:4451.M M max ==kN·m③设计截面[]561008815010445⨯=⨯=σ≥..M W max Z mm 3621223max bh h bh y I W Z Z === ∵52100881233⨯≥==.b W bh z mm 37413100881233..b =⨯⨯≥mm∴h =125mm§5.4 弯曲切应力⎩⎨⎧--τσS F M 横力弯曲切应力的分布规律与梁的横截面形状有关,因此以梁的横截面形状不同分别加以讨论。
1.矩形截面梁(1)切应力的分布规律⎩⎨⎧沿截面宽度均匀分布切应力平行的方向与剪力切应力假设ττS F 当h >b 时,按上述假设得到的解答与精确解相比有足够的准确度。
(2)切应力沿截面高度的变化规律①从梁中取出d x 段,而微段上无载荷作用。
②截面上的σ和τ的分布如图 ③研究微块的平衡()()*1**12*ZA ZA A Z S IM M Ay I M M AI y M M A F d d d d d d +=+=+==⎰⎰⎰N σ (a )式中:⎰=*1*A z A y S d 为离中性轴为y 的横线以下面积对中性轴之静矩。
Z zA Z A ZA I MS A y I MA I My A F **1*1*1====⎰⎰⎰N d d d σ(b )考虑到微块顶面上相切的内力系的合力x b F S d d τ'='(c )00'12=--=∑N N S x F F F F d (d )式(a )、(b )、(c )代入式(d )()0**='--+x b S IM S I M M ZzZd d τ (e )bI S x M Z Z*d d ='τ (d ) ∵S F xM=d d ∴bI S F Z *ZS =τ'(f )由切应力互等定理,横截面上pq 线处切应力为b I S F Z ZS *=τ(g )这就是矩形截面梁弯曲切应力计算公式。
④讨论:a . 横力弯曲下梁的纵向纤维层之间存在切应力b. 矩形截面如图 1y b A d d =⎰⎰⎪⎪⎭⎫ ⎝⎛-===2/2211*1*42h yA Zy h b y by A y S d d or∴说明切应力τ沿截面高度按抛物线规律变化。
c. 当2h y ±=时,τ=0当y =0时,ZS I h F 82max ==ττd. 考虑到123bh I Z =bh F bh F S S⨯==5.123max τ 2.工字形截面梁(1)计算表明:截面上剪力F S 的95~97%由腹板承担,故只考虑腹板上的切应力分布规律,而腹板是一个狭长矩形,矩形截面切应力两个假设均适用(τ方向与F S 一致,设宽度均布),采用矩形截面方法可得: 0*b I S F Z ZS =τ式中:()⎪⎪⎭⎫ ⎝⎛-+-=2200202*428y h b h h b S Z ()⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+-=22002020428y h b h h b b I F Z S τ 以y=0,20hy ±=代入上式得()⎥⎦⎤⎢⎣⎡--=8820020max h b b bh b I F Z S τ ⎪⎪⎭⎫ ⎝⎛-=882020minbh bh b I F Z Sτ⎪⎪⎭⎫ ⎝⎛-=22242y h I F Sτ∵b 0<<b ∴τmax ≈τmin 于是近似认为hb F S0max =τ (2)翼缘中切应力分布比较复杂,且数量很小,无实际意义,不予讨论。
(3)工字梁翼缘的全部面都距中性轴较远,每一点的正应力都很大,所以工字梁的最大特点是,用翼缘承担大部分弯矩,腹板承担大部分剪力。
3.圆形及圆环形截面梁(1)bI S F Z ZS y *=τ*Z S ——阴影面积对中性轴的静矩b ——为弦AB 的长度 在中性轴上 ππ3422*maxR R SZ ⋅= b =2R44R I Z π=AF R F S S34342max==πτ (2)圆环形截面AFs ⋅=2max τ 4.弯曲切应力的强度校核 (1)强度条件[]ττ≤=b I S F Z Zs max*max max最大切应力发生于中性轴处,故*m ax Z S ——中性轴以上或以下截面面积对中性轴之静矩(2)细长梁而言,强度控制因素,通常是弯曲正应力,一般只按正应力强度条件进行强度计算,不需要对弯曲切应力进行强度校核。
(3)只在下述情况下,才进行弯曲切应力强度校核:①梁的跨度较短。
②在梁的支座附近作用较大的载荷,以致梁的弯矩较小,而剪力颇大。
③铆接或焊接的工字梁,如腹板较薄而截面高度颇大,以致厚度与高度的比值小于型钢的相应比值,这时对腹板进行切应力校核。
④经焊接,铆接或胶而成的梁,对焊缝、铆钉或胶合面一般进行剪切计算。
§5.6 提高弯曲强度的措施弯曲正应力为控制梁的主要因素。
由梁的强度条件:[]σσ≤=ZWMmaxmax合理安排梁的受力情况,降低M max。
采用合理截面形状,提高W Z1.合理安排梁的受力情况,降低M max(1)合理布置梁的支座(2)合理布置载荷①载荷置于合理位置②将集中力分为较小的集中力③将集中力分为分布力2.梁的合理截面,提高W Z 由强度条件()()[]σσ==x W x M x 得 []Z W M σ≤max可见W Z 越大,梁承受的弯矩就越大。
