中科大信号与系统2014期中考试答案
2014年期中试卷

南京信息工程大学2013-2014学年第二学期《信号与系统》期中考试试卷题目部分,(卷面共有23题,100分,各大题标有题量和总分)一、单项选择题(每空2分×8个空,共16分)1. ()sin 6t t t dt πδ∞-∞⎛⎫+-= ⎪⎝⎭⎰A.3π; B.132π+; C. 162π+ ; D.6π 2. 请选择下列信号中的线性系统( )A. ()()5y t x t =+;B. ()()()()cos y t x t u t =;C. ()()2y t tx t =;D. ()()2y t t x t =;3. 下列叙述正确的是( )。
A 、各种数字信号都是离散信号;B 、数字信号的幅度只取0和1;C 、各种离散信号都是数字信号 ;D 、将数字信号滤波可得模拟信号; 4. ()()210060Sa t Sa t +的最低抽样率为( )A.120π; B.60π; C.100π;D.200π;5. ()t e t δ-的积分为( ) A. ()t e u t -;B. -()t e u t -;C. -()t e u t -+()t e t δ-;D. ()u t ;6. 10j t e 的周期为( ) A .10π; B.5π; C.8π; D.4π; 7. 如图1所示,电路中()s e t 、()s i t 表示激励源,()u t 、()i t 表示电路的响应,图中a的网络函数为( ),图中b 的网络函数为( )。
()s e t 1ΩC ()s i t 1Ω图1A. 211s s s +++B.211s s s +++ C. 2211s ss s ++++D. 221s s s s+++二、填空题(每空2分×10个空,共20分)1. 波形()()1cos f t K t ω=+⎡⎤⎣⎦(K 为常数)的直流分量 。
2. ()()cos f t u t t =的微分为 。
(完整word版)信号与系统考试试题及答案,推荐文档

长沙理工大学拟题纸课程编号 1拟题教研室(或老师)签名 教研室主任签名 符号说明:)sgn(t 为符号函数,)(t δ为单位冲击信号,)(k δ为单位脉冲序列,)(t ε为单位阶跃信号,)(k ε为单位阶跃序列。
一、填空(共30分,每小题3分)1. 已知)()4()(2t t t f ε+=,求_______)("=t f 。
)('4)(2)("t t t f δε+2. 已知}4,2,4,3{)(},1,2,2,1{)(=-=k h k f ,求______)()(=*k h k f 。
}4,6,8,3,4,10,3{)()(-=*k h k f3. 信号通过系统不失真的条件为系统函数_______)(=ωj H 。
0)(t j Kej H ωω-=4. 若)(t f 最高角频率为m ω,则对)4(t f 取样的最大间隔是______。
m T ωπωπ4max max ==5. 信号t t t f ππ30cos 220cos 4)(+=的平均功率为______。
101122222=+++==∑∞-∞=n n F P6. 已知一系统的输入输出关系为)3()(t f t y =,试判断该系统是否为线性时不变系统______。
故系统为线性时变系统。
7. 已知信号的拉式变换为)1)(1(1)(2-+=s s s F ,求该信号的傅立叶变换)(ωj F =______。
故傅立叶变换)(ωj F 不存在。
8. 已知一离散时间系统的系统函数2121)(---+=z z z H ,判断该系统是否稳定______。
故系统不稳定。
9. =+-+⎰∞∞-dt t t t )1()2(2δ______。
310. 已知一信号频谱可写为)(,)()(3ωωωωA e A j F j -=是一实偶函数,试问)(t f 有何种对称性______。
关于t=3的偶对称的实信号。
二、计算题(共50分,每小题10分)1. 已知连续时间系统的单位冲激响应)(t h 与激励信号)(t f 的波形如图A-1所示,试由时域求解该系 统的零状态响应)(t y ,画出)(t y 的波形。
信号与系统期中考试参考答案_326004751

《信号与系统》期中考试试题2011年11月 A 卷一、填空(25分)1、(3分)已知2()(e )()t f t t u t -=+,则()f t ''=(2e )()()()t u t t t δδ-'+-+。
解:2()(2e )()(e )()(2e )()()t t t f t t u t t t t u t t δδ---'=-++=-+()(2e )()(2e )()()(2e )()()()t t t f t u t t t t u t t t δδδδ---''''=++-+=+-+2、(3分)若()f t 的最高截止频率为m ω,则对(/2)(4)f t f t 抽样的最大时间间隔为2/(9)m πω。
解:{}{}{}11(/2)(4)(/2)*(2)(2)*(/4)24f t f t f t f t F F ωωππ==FF F , (2)F ω的截止频率为0.5m ω,(/4)F ω的截止频率为4m ω,根据卷积性质知(/2)(4)f t f t 的最高截止频率为4.5m ω,因此最低抽样频率为9s m ωω=,最大时间间隔2/(9)m m T πω=。
3、(3分)已知实信号()f t 的频谱可写成(2/2)()()e j F A ωπωω-+=,其中()A ω为实奇函数,试问该信号波形满足何种对称性(2)(2)f t f t -+=-+。
解:由题意知2()j ()j F e A ωωω=,而[][]*j ()j ()A A ωω=-,即*j 2j2()()F e F e ωωωω⎡⎤=-⎣⎦,从而(2)(2)f t f t -+=-+,即()f t 关于2t =反对称。
4、(3分)由Parseval 定理计算2sin d t t t π+∞-∞⎛⎫= ⎪⎝⎭⎰2π。
解:{}[]sin()()()()t Sa t u u t ππππωπωπ⎧⎫==+--⎨⎬⎩⎭F F ,因此2sin d t t t π+∞-∞⎛⎫= ⎪⎝⎭⎰21d 2πππωππ2-=⎰。
信号与系统2014试卷A答案

浙江农林大学天目学院 2013 - 2014 学年第 二 学期考试卷(A 卷)答案 课程名称: 信号与系统 课程类别: 必修 考试方式: 闭卷 适用专业: 电子信息工程注意事项:1、本试卷满分100分。
2、考试时间 120分钟。
一、 单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的选项填在题后的括号内。
每小题2分,共20分)D 、A 、D 、A 、C 、A 、C 、A 、B 、C二、简答题(10分)系统微分方程的算子形式为)()()(H ),()()(p D p N p t e p H t r ==其中为转移算子,设其特征方程无重根,且N(p)的幂次低于D(p)幂次,归纳该线性系统的时域分析法。
系(部): 专业班级: 姓名: 学号: 装 订 线 内 不 要 答 题三、计算题(70分)1、(15分)求以下两个信号的卷积。
⎩⎨⎧<<=值其余t t t x 0101)( ⎩⎨⎧<<=值其余t t tt h 020)(答:03t 3t 2t -5.03t 21-t 25.0210.5t 1t 000t 22=≥++=<≤=<≤=<≤=<时,卷积当)(时,卷积当)(时,卷积当时,卷积当;时,卷积当t2、有一幅度为1,脉冲宽度为2ms 的周期矩形脉冲,其周期为8ms ,如图所示,求频谱并画出频谱图。
(10分)解:Fn 为实数,可直接画成一个频谱图。
3、(共15分)已知)()(ωj F t f ⇔,求下列信号的傅里叶变换。
(1)f(1-t) (2))2(t tf (3)dtt df t)( (1) ωωj e j F t f --⇔-)()1( (2)ωωd j dF j t tf )2/(2)2(⇔(3) ωωωωd j dF j F dt t df t )()()(--⇔4、(10分)一线性系统的频响曲线如下图所示,求信号t t t e 2cos 2cos 22)(++=作用下的零状态响应.解:(1).o m om om E E E 02,02,2.2.1.∠=∠==(2).00)2(,21)1(,02)0(∠=-∠=∠=j H jj H H π(3).)2cos(24)(π-+=t t r5、(10分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad j F j F t f ωωωω设有函数()(),dt t df t s =求⎪⎭⎫⎝⎛2ωs 的傅里叶逆变换。
信号与系统期中考试答案,DOC

一、(15%)已知连续时间信号x t ()和离散时间信号x n []的波形图如下图所示。
画出下列各信号的波形图,并加以标注。
1.()()11xt x t =-,2.()()221x t x t =-,3.3()()x x t ττ=-第三个自变量不为t !! 4.{}1[][][]e x n x n Even x n ==,5.2[][][1]x n x n n δ=-答案二、(25%)简要回答下列问题。
1. 推导离散时间信号[]0j n xn e ω=成为周期信号的条件(3%);若是周期信号,给出基波周期的求法(3%)。
答案:若为周期信号,则00()j nj n N e e n ωω+=∀,。
推出01j N e ω=,再推出02,,0N k k z k ωπ=∈≠。
得出02k Nωπ=为有理分数。
2.指出离散时间信号[]j n x n e ω=频率取值的主值范围(2%),指出它的最低频率和最高频率(2%)。
答案2πωπωπ-≤<≤<或0。
min max 02,21),k k z k k z ωπωππ=∈=+∈或。
而或(。
3. 断下列两个系统是否具有记忆性。
①()()()()222y t x t x t =-,(1%)②[][][]0.51y n x n x n =--。
(1%)答案①无记忆性②有记忆性4.简述连续时间和离散时间线性时不变(LTI )系统的因果性、稳定性与单位冲激响应(Unitimpulseresponse )的关系(4%)。
答案因果性与()()()[][][]h t h t u t h n h n u n ==或互为充要条件。
稳定性与|()||[]|n h t dt h n +∞+∞=-∞-∞<+∞<+∞∑⎰或互为充要条件。
5. 很广泛一类因果系统可用常系数微分方程:()()00k k NM k k k k k k d y t d x t a b dt dt ===∑∑表征,画出该类系统的增量线性系统结构(2%),用该结构说明全响应的构成方法及每一部分的物理含义(4%),在什么条件下该类系统为LTI 系统(3%)? 答案()()()x i y t y t y t =+,()()*()x y t x t h t =是仅由输入信号引起响应:零状态响应,()i y t 是仅由初始状态引起的响应:零输入响应。
信号与系统期中考试试卷

中国计量学院2013 ~ 2014 学年第 二 学期《 信号与系统 》课程期中考试试卷开课: 信息 ,考试时间: 2014 年 5 月 日 时 考试形式:闭卷□、开卷□√,只允许带 教材和计算器 入场 考生姓名: 学号: 班级: 所选专业:一、(共20分)1、(4分)计算函数值dt ttt t f 2sin )(2)(⎰∞+∞-=δ 2、(4分)判断由方程10)(2)(+=t x t y 描述的系统是否为线性时不变系统。
3、(4分)连续时间系统⎰+-=22)(1)(T t T t d x Tt y ττ是否为因果系统?4、(4分)一周期矩形脉冲的周期为100us,脉冲宽度为20us, 脉冲高度为2,求该信号的谱线间隔f 和有效频带宽度B f 。
5、(4分)某系统的系统函数()1/(1)=+H j j ωω,此系统是否满足无失真传输条件?说明理由。
二、(共24分)1、(8分)1()f t 和2()ft 的波形如下图所示,试写出1()f t 和2()f t 的表达式,并画出卷积12()()()g t f t f t =*的波形。
tt2、(8分)求∑∞-∞=-=n n t t f )2()(δ周期信号的傅里叶变换。
3、(8分)某系统频率响应特性为ωωj j H +=11)(, 当输入())3sin()2sin()sin(t t t t x ++=时,求系统的稳态输出()t y 。
三.(12分)(1).单个矩形脉冲f 1(t)的波形如图,试写出单个矩形脉冲f 1(t)的频谱函数 F 1(j ω)的表达式,并画出其幅度频谱图。
(2)试写出f 2(t)的频谱函数F 2(j ω)的表达式。
tt四、(10分) 某线性非时变系统的频率响应为)(ωj H1,2||7()0,H jw ωω≤≤⎧=⎨⎩其它,对于输入信号为图1所示的周期方波信号f(t)(周期T=2π,脉冲宽度)πτ=,求系统的响应y(t)。
五、(16分)下图(a )是某音频信号m(t)的频谱,图(b )所示系统用于给音频信号加密(扰频),输出y(t)是输入m(t)经加密后的信号。
中国科学技术大学信号与系统习题
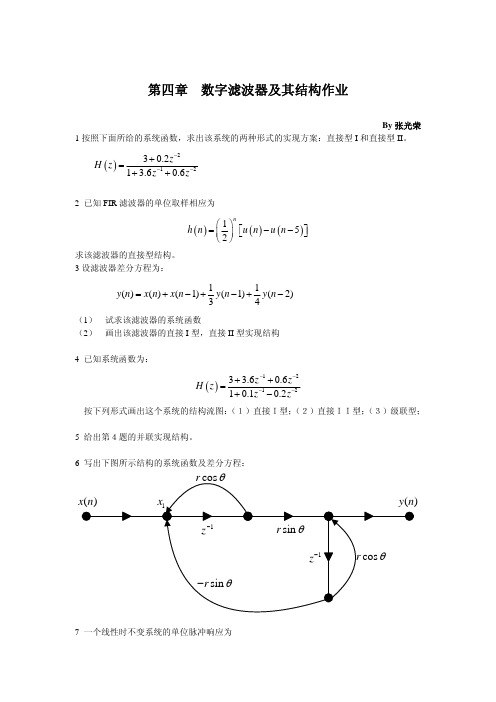
第四章 数字滤波器及其结构作业
By 张光荣
1按照下面所给的系统函数,求出该系统的两种形式的实现方案:直接型I 和直接型II 。
()2
1230.21 3.60.6z H z z z
−−−+=++
2 已知FIR 滤波器的单位取样相应为
()()()152n h n u n u n ⎛⎞=−−⎡⎤⎜⎟⎣⎦⎝⎠
求该滤波器的直接型结构。
3设滤波器差分方程为:
11()()(1)(1)(2)34
y n x n x n y n y n =+−+−+− (1) 试求该滤波器的系统函数
(2) 画出该滤波器的直接I 型,直接II 型实现结构
4 已知系统函数为:
()12
12
3 3.60.610.10.2z z H z z z −−−−++=+− 按下列形式画出这个系统的结构流图:(1)直接I型;(2)直接II型;(3)级联型;
5 给出第4题的并联实现结构。
6 写出下图所示结构的系统函数及差分方程:
7 一个线性时不变系统的单位脉冲响应为
07()0n
a n h n ⎧≤≤=⎨⎩其他(1) 画出该系统的直接型FIR 结构图。
(2) 证明该系统的系统函数为
88
11()1a z H z az
−−−=− 并由该系统函数画出由FIR 系统和IIR 系统级联而成的结构图。
(3) 比较(1)和(2)两种系统实现方法,哪一种需要较多的延迟器?哪一种实现需要较多
的运算次数?。
信号与系统期末A卷答案及评分标准-12自动化

)补考( )重修( )
S 域的右半平面映射到 Z 域的单位圆内。 ( × ) 离散信号的频谱一定是连续的。 ( × ) 当系统是线性时不变时,其零状态响应是输入和冲激响应的卷积。 ( √ ) 卷积只适用于线性系统。 ( √ ) 当信号在������ < 0时,������(������) = 0,则该信号为因果信号。 ( √ )
时频变换
������(������) = ∫ ������(������)������
−∞
−�����������������
������������ ; ������(������) = ∫ ������(������)������
0−
解: ������(s) =
2 ������ −4������ ⟷ ������(������) = 2������ −3(������−4) ������(������ − 4) ������ + 3
∞
时延 频谱搬移 微分特性 卷积微积分特 性
������(������ ± ������0 ) ⟷ ������(������)������ ±������������������0 ; ������(������ ± ������0 ) ⟷ ������(������)������ ±������������0 ; ������(������ − ������) ⟷ ������ −������ ������(������) ������(������)������ ±������������0 ������ ⟷ ������(������ ∓ ������0 ); ������(������)������ ±������0 ������ ⟷ ������(������ ∓ ������0 ); 1 ������(������)������������������(������������ ������) ⟷ [������(������ + ������������ ) + ������(������ − ������������ )] 2 (������) (������) ������ ������ ⟷ (������������) ������(������); ������ (������) (������) ⟷ ������ ������ ������(������) ������ ′ (������) = ������1′ (������) ∗ ������2 (������) = ������1 (������) ∗ ������2′ (������) ������ (−1) (������) = ������ 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1)是线性系统;
所以为线性。
考虑到对输入有限制,部分的a*x(t)可能无对应的输出,所以此题按此思路答非线性也判为对。
2)不是线性系统
对应的输出并不等于是
或者分情况讨论,b为0是为线性系统,b不为0是为非线性系统
3)是线性,时不变,非因果系统
线性:计算对应的输出发现等于
时不变性:计算对应的输出等于
因果性:与未来的时刻有关故为非因果系统;或者分情况讨论:当t<0时,若h==0,则为因果,否则,非因果。
4)线性,时不变,可逆系统
线性与时不变型:写出输入为的输出与原系统对比可得输出,或者考虑到零输入对应零输出需要要求,对此分情况讨论也给分。
时不变性同理。
可逆。
或者将y(t)写成,在进行后面的判断。
二
经分析,当或者时,y(t)=0;
当时,
当时,
当时,
(0,3)
在各个端点都是连续的,所以连续。
对1的结果求导即可
当时,
当时,
当时,
方法二:
由卷积性质先计算,,然后积分计算y(t),计算量比较少
三
四
1)
特征方程
解得
那么齐次方程为
代入求解可得
零输入响应为
2)考虑两个LTI 系统级联
第一个LTI 系统的单位冲激响应为
第二个LTI 系统的单位冲激响应满足
同样解齐次方程得
那么当 时
3)
4)
5)不稳定
因为
五
770171.cos 3cos 41()4
周期为2,1==
,其余为04X ()[()()(7)(7)]
2
j t j t j t j t t t
e e e e X X ππππππωπ
πωδωπδωπδωπδωπ--±±=+++==-+++-++
2.cost+cos2t
非周期
X ()=[(1)(1)(2)(2)]
πωπδωδωδωπδωπ-+++-++ 12122213.非周期
,sin (){0,1所以,x(t)=cos 0.5
1=-sin((0.5))t 0.5
()()
别的形式的答案:X(j )=-)sgn()],或:
2
有一般的卷积方法:,01(){sgn()0.5,0
co j j j j t
j X j t t t t X j e
X j e j j X j e j e t j ωωωωπωππωωωπ
ππωωπωωπωπωωωππωω----<=<---=--+->==--<2122s ()[()()]
1()*2[sgn()sgn()]
2j t j X j X j X X e ω
πωωπδωπδωπωπ
πωπωπ-=++-==-
--+
六
(t)Xc(nT)(t nT)
(jw)Xc(nT)e (1)(e )Xd(n)e (nT)e (2)
由(1)(2)式可得(e )(j /)1(jw)(j(w ))12(e
)(j())(j(n jwnT n j j n j n n n j s n j s n s s s Xp Xp Xd Xc Xd Xp T Xp Xc nw T n Xd Xc f Xc T T T δπ+∞=-∞+∞-=-∞+∞+∞Ω-Ω-Ω=-∞=-∞Ω+∞=-∞+∞Ω=-∞
=-==
==Ω=
-Ω=-=Ω-∑∑∑∑∑∑2))s n n f π+∞=-∞∑。
