电子-声子相互作用
固体物理学中的电子声子光子相互作用与电子声子光子材料
固体物理学中的电子声子光子相互作用与电子声子光子材料在固体物理学的研究领域中，电子、声子和光子是极为重要的三个基本粒子。
它们之间的相互作用在材料的特性以及电子、声子和光子的行为中扮演着重要的角色。
本文将探讨固体物理学中电子、声子和光子相互作用的相关原理，并介绍电子声子光子材料的研究进展。
1. 电子声子相互作用在固体中，电子声子相互作用是一个重要的能量转移过程。
当声子与电子相互作用时，声子的能量和动量可以传递给电子，导致电子发生能级的改变。
这种相互作用对于材料的热导率和电导率等性质具有重要影响。
研究表明，电子和声子之间的相互作用可以通过库仑相互作用和矩阵元素的耦合来描述。
库仑相互作用是由电子间的静电相互作用引起的，而矩阵元素的耦合描述的是电子和声子之间的共振转移过程。
2. 电子光子相互作用电子光子相互作用是指电子与光子之间的相互作用过程。
在固体物理学中，这种相互作用被广泛应用于半导体器件和光电子学中。
在半导体器件中，通过改变电子能带结构和光子的能量，可以调控材料的光电性能。
当光子与半导体中的电子相互作用时，可以激发电子从价带跃迁到导带，形成光电子激发态。
这种相互作用在光电二极管、太阳能电池等器件中得到广泛应用。
3. 声子光子相互作用声子光子相互作用是指声子与光子之间的相互作用过程。
在固体物理学中，这种相互作用在光学材料和声子晶体等研究领域中具有重要意义。
当光子与声子相互作用时，光子的能量和动量可以转移到声子上，导致声子的能级和动量发生改变。
这种相互作用可以通过光谱分析等技术来研究材料的光学性质和声学性质。
4. 电子声子光子材料的研究进展近年来，固体物理学中电子声子光子材料的研究受到了广泛关注。
这些材料具有特殊的电子、声子和光子相互作用特性，对于光电子器件、能量转换和信息存储等领域具有重要应用潜力。
例如，石墨烯材料是一种电子声子光子材料，其具有优异的导电性能和光学性质。
石墨烯中的电子和声子相互作用可以通过光学谱和声学谱等实验手段来研究。
二维半导体电声子相互作用
二维半导体中的电声子相互作用（Electron-Phonon Interaction）是指在二维材料中，电子与晶格振动（即声子）之间的相互耦合作用。
这种作用对材料的电子性质有着显著影响，特别是在载流子的有效质量、迁移率、超导性以及光学性质等方面。
具体来说，在二维半导体中，当电子在能带内移动时，其运动会导致晶格原子微小振动（声子激发），反过来，这些晶格振动又会改变电子的能量和动量状态。
这种动态过程通过以下几种效应体现：
1. 散射效应：电子通过与声子交换能量和动量，会发生散射，影响电子的平均自由程和迁移率。
2. 超导电性：在低温下，强的电声子相互作用可以导致BCS （Bardeen-Cooper-Schrieffer）机制下的超导现象，即电子配对形成库珀对。
3. 激子束缚：在某些情况下，电声子相互作用还可以引起电子和空穴的结合，形成激子。
4. 电子有效质量修正：由于电子与晶格相互作用，实际的电子质量会比裸电子质量大，这是因为电子需要克服晶格产生的势垒才能在能带内移动。
5. 热载流子效应：在高载流子密度或高温下，电声子相互作用将影响载流子的能量弛豫过程。
因此，深入理解二维半导体中的电声子相互作用对于优化器件性能、开发新型电子和光电子器件至关重要。
在理论研究上，通常使用量子力学的方法，如格林函数方法、第一性原理计算等来模拟和计算电声子相互作用的影响。
高温超导材料中电子-声子相互作用机制的探究
高温超导材料中电子－声子相互作用机制的探究高温超导材料是一类具有重要应用前景的材料，在低温条件下表现出极低的电阻和完全抗磁性。
然而，要理解高温超导的基本机制，我们需要深入了解其中的电子-声子相互作用。
电子-声子相互作用是高温超导材料中一个至关重要的机制。
它指的是电子和晶格振动之间的相互作用。
在传统的低温超导材料中，超导机制主要是通过库伦相互作用来实现的，即超导电子形成库伦对。
但是在高温超导材料中，束缚电子-声子相互作用是实现超导的关键。
高温超导材料中电子-声子相互作用的机制有多种可能性。
最常见和被广泛接受的理论是BCS理论的修正版本。
BCS理论揭示了低温超导材料中电子-声子相互作用导致库伦配对的形成。
对于高温超导材料，研究者认为其超导机制可能涉及到电子-声子相互作用的其他机制，如电子-声子相互作用的强耦合效应或者是电子自旋相互作用。
这些机制被认为是高温超导机制的重要组成部分。
一种解释高温超导材料中电子-声子相互作用的机制的方法是使用声子谱的研究。
声子谱可以提供关于材料中声子能量和态密度的信息。
实验观察到的声子谱特征对于理解材料的超导性质至关重要。
例如，一些实验证据表明声子谱的峰值出现在超导转变温度附近并且与材料的超导性质密切相关。
这表明声子在高温超导材料中发挥着关键作用。
另外一种研究高温超导材料中电子-声子相互作用机制的方法是使用拉曼光谱技术。
拉曼光谱技术可以提供关于材料中声子的信息，包括声子频率和衰减率。
通过分析拉曼光谱数据，可以确定声子-声子散射、声子-电子散射或者声子自能的性质。
这些信息对于理解声子在材料中的角色以及电子-声子相互作用的本质具有重要意义。
此外，一些理论模拟方法也被用于研究高温超导材料中电子-声子相互作用的机制。
通过计算模拟，可以预测材料的电子能谱和声子能谱，从而揭示电子-声子相互作用的动力学行为。
这些模拟方法可以提供关于高温超导机制的定量理解，帮助我们深入理解高温超导材料中电子-声子相互作用的本质。
超导体中的声子热耦合nature
一、超导体的基本原理超导体是指在一定条件下电阻突然消失而导电性达到最大值的物质。
超导体的基本原理是由于其电子成对运动和库仑排斥力的屏蔽，使得电子对的结合能足够大，超越了材料晶格的振动能量而形成了超导态。
二、声子热耦合声子是晶格振动的量子，它是介质中能量最低的激发态。
在超导体中，声子热耦合指的是电子与声子之间的相互作用。
声子热耦合对超导体的超导性质有着重要影响，它不仅可以影响超导临界温度，还可以影响超导态的对称性和电子的配对机制。
三、超导体中的声子热耦合机制超导体中声子热耦合的机制是一个复杂的问题，主要包括以下几个方面：1. 电子-声子相互作用：超导体中的电子通过与晶格的振动相互作用，引起了声子的产生和吸收。
这种相互作用使得电子在晶体中的传导变得更加复杂，大大影响了超导电性的性质。
2. 能带结构和电子输运：超导体的能带结构对声子热耦合有重要影响。
它通过晶格振动的分布和密度，调节了声子热耦合的强度。
3. 声子场的量子统计效应：声子是玻色子，其统计行为对超导体的声子热耦合也有着很大的影响。
声子场的量子统计效应会导致声子的配对和集体激发现象，从而影响超导电性的行为。
四、超导体中的声子热耦合与超导态的对称性声子热耦合不仅对超导体的临界温度有着重要影响，还可以影响超导态的对称性。
在高温超导体中，声子热耦合常常导致超导态的对称性发生变化，从而影响电子对的配对机制和超导性质。
五、超导体中的声子热耦合实验研究近年来，通过高分辨率的声子谱实验和声子能谱的测量，科学家们对超导体中声子热耦合进行了深入的研究。
这些研究不仅揭示了声子热耦合对超导性质的重要影响，还为超导体的理论模型提供了重要的实验验证。
六、超导体中的声子热耦合的应用前景超导体中的声子热耦合机制的深入研究，不仅有助于理解超导体的超导机制，还可以为新型超导体材料的设计和合成提供重要参考。
通过对声子热耦合的深入理解，科学家们可以设计出更高临界温度的超导体材料，为超导应用技术提供更广阔的发展空间。
高二物理竞赛课件极化子和电子-声子相互作用
半导体中, 若声子云半径大于晶格常数, 称
为“大极化子“；而小极化子局域在单胞内.
rpe,h
2mer,.hl .LO
12
,
其中 mer,.lh.为刚性点阵中电子或空穴的有效
质量.
●有效质量 me,h mrp.l . 1 e,h 6 其中
e ,h
e2 8 0LO
2mer,.lh.LO
极化子和电子-声子相互作用
极化子和电子-声子相互作用 1.电子对晶格的极化 ●在至少是部分离子键的半导体中,电子吸
引正离子,排斥负离子. 空穴情况正好相反. ●极化结果使晶格产生畸变—等同于纵模
光学声子的叠加(纵模声子会引起体积的 压缩和膨胀,而横模声子不会产生这样效 果).这样,自由载流子将与”声子云”相伴随. 2. 极化子 ●带电载流子与声子云的整体称为极化子. ●极化子中声子云半径 rpe ,h
1
2
1
b
1
s
为夫勒利希耦合系数,描述带电载流子与
LO声子的耦合. b 和 s 分别为LO 的高 频和低频介电常数.
对于非离子键晶体,根据
s
b 1
f L2o
f
0,s
b ,
因此, e,h 0.
一般半导体, e,h 1. 总之,实际离子键晶体中，电子或空穴的 有效质量 me ,h 相对刚性点阵中 mer,.lh.变大, 这种现象称为质量重整化.
,h
3. 电子-声子相互作用
电子-声子散射：
E
i eBiblioteka Eefphonon ,
kei
kef
k phonon G .
分类：
①夫勒利希作用
载流子与伴随着光学声子电场的作用. ②形变势散射 ●因为能隙的宽度以及能带结构取决于晶 格参数和基元中原子分布,所以, 形变调制 了能带结构. E a a, 若 a a 1, E : 5 10eV .
半导体材料中的电子与声子相互作用研究
半导体材料中的电子与声子相互作用研究半导体材料一直是电子学和能源转换领域的关键材料之一。
在半导体材料中，电子与声子（晶格中的振动）之间存在着相互作用，这种相互作用对于半导体的物理性质和应用有着重要的影响。
因此，研究半导体材料中电子与声子的相互作用是当前材料科学与物理学研究的热点之一。
1. 引言半导体材料的电子与声子相互作用被广泛研究，旨在深入了解其物理特性、改进半导体器件的性能以及开发新的应用。
通过研究电子与声子的相互作用，可以揭示材料的能带结构、载流子输运特性和热导率等重要性质。
2. 电子与声子的相互作用机制在半导体材料中，电子与声子之间存在着复杂的相互作用机制。
一方面，电子通过散射与晶格中的声子发生相互作用，这种作用包括弹性散射和非弹性散射。
另一方面，声子对电子输运和能带结构有着重要的影响，如声子散射可以引起电子能带结构的畸变，并影响载流子的散射。
3. 电子与声子的相互作用对半导体性能的影响电子与声子的相互作用在半导体材料的物理性质和器件性能中发挥着重要作用。
一方面，通过调控电子与声子的相互作用，可以改变半导体材料的能带结构和电子输运行为，从而实现控制半导体器件特性的目的。
另一方面，电子与声子的相互作用还会导致半导体材料的热导率的变化，这对于半导体材料在热管理和热电转换领域的应用有着重要的意义。
4. 电子与声子相互作用的研究方法研究电子与声子相互作用的方法主要包括实验方法和理论方法。
实验方法主要通过光学谱学、拉曼散射等技术来探测电子与声子的相互作用机制。
理论方法则通过计算模拟等手段来解释实验结果，并深入分析电子与声子的相互作用机制和物理过程。
5. 应用前景与展望半导体材料中电子与声子相互作用的研究不仅可以帮助我们深入理解半导体材料的物理性质，还可以为新型半导体材料的设计和开发提供指导。
例如，通过调控电子与声子的相互作用，可以实现半导体材料的热电转换和热管理的优化，进一步提高能源转换效率。
此外，电子与声子的相互作用还可以用于设计新型的光电器件和磁电器件，推动新一代半导体技术的发展。
超导论文
姓名李娟
学号201001020135
年级 2010
专业物理学
系（院）理学院
指导教师蒋华
引言
1957年，巴丁（J.Bardeen）、库珀（L.V.Cooper）和施里弗（J.R.Schrieffer）共同创立了BCS理论，这一理论从微观上解释了超导电性，1957年诺贝尔物理学奖。
BCS理论指出，超导现象产生涉及三个因素；1、电子-声子之间的相互作用2、能隙 3、动量空间的凝聚。
一、电子-声子之间的相互作用
磁通量子化的实验明确揭示超导电性来自两个电子，说明两个电子之间存在相互吸引作用，同时同位素效应指出尽管晶格结构在超导相变前后未发生变化，但在决定传导电子行为的改变上，晶格点阵必定还起了重要作用。
那么电子之间是如何相互吸引的？电子与晶格点阵之间又有什么关系？
1950年弗列里希（Frohlich）指出：电子-声子相互作用能把两个电子耦合在一起，这种耦合就好像两个电子之间有相互作用一样，为了明确其物理图像，Frohlich给出了如下一个物理模型：整齐排列的晶格点阵，当电子1通过晶格时，
-。
电子-声子相互作用
q cLq
cL
1 3
m M
1/
2
vF
其中vF kF / m为费米速度。
这就是著名的玻母-司台夫(Bohm-Staver)声速公式
4、电子与光频声子的相互作用
离子晶体中的光频支纵振动会产生极化电场
它将对离子晶体中的传导电子产生强烈的耦合作用。 耦合作用比LA声子对传导电子的作用强得多。
因此，主要是LO声子与传导电子的相互作用对离子晶体中的载流子特性产生影响。
电子-声子互作用的高阶微扰过程由上述基本过程组成
（a）先发射后吸收q声子，物理实质是电子带着晶格畸变运动，对电子自能产 生修正。 （b）为电子系统对声子扰动场的屏蔽，将改变离子间的互作用势，从而对声子 频率产生修正。 （c）两个电子通过声子的间接互作用，在一定条件下将成为电子之间的有效吸 引势，它是产生超导电性的主要机制。
j ,l
能带电子与晶格振动的相互作用势为
Hep
Hei
H
0 ei
V (rj l ul ) V (rj l)
j ,l
ul • V (ri l) h(rj )
j ,l
j
其中电子与声子互作用的单体势为：h(r) ul • V (r l)
l
若选布洛赫函数
k (r) uk (r)eik•r ,
H
为自由电子近似的哈密顿量
e
H
为电子之间的库仑互
ee
作用。
根据海森伯方程：
•
i Pq
[Pq , H ]和对易式[Pq ,Qq' ]
i qq'
可导出运动方程
••
Qq q2Qq M q q 如果能确定q与Qq之间的关系，则声子频率的修正就可以求出。
电子声子相互作用
利用机器学习算法对电子声子相互作用进行预测和优化，提高计算 效率和准确性。
开发并行计算框架
利用高性能计算资源，开发并行计算框架，加速大规模电子声子相 互作用模拟。
新材料中电子声子相互作用的深入研究
研究新型二维材料
针对新型二维材料，研究其电子 声子相互作用特性，探索其独特
的物理性质和潜在应用。
电子声子相互作用还可能导致热载流子的产生和能量耗散，影响器件的散热性能和 稳定性。
在光电器件中的应用
在光电器件中，电子声子相互作用会 影响光吸收、光发射和光电导等过程。
在光发射过程中，电子与声子的相互 作用会影响光的发射波长和强度，从 而影响发光器件的颜色和亮度。
在光吸收过程中，电子与声子的相互作 用会影响光吸收谱的形状和强度，从而 影响器件的光响应范围和灵敏度。
在磁电器件中的应用
01
在磁电器件中，电子声子相互作用会影响磁电阻、磁致伸缩等 磁电效应。
02
电子与声子的相互作用会影响磁性材料的磁矩和磁化强度，从
而影响磁电器件的磁响应和灵敏度。
电子声子相互作用还可能影响磁性材料的热稳定性，从而影响
03
器件的长期稳定性和可靠性。
在热电器件中的应用
1
在热电器件中，电子声子相互作用会影响热电转 换效率。
非晶体材料中的电子声子相互作用也是其物 理性质的重要影响因素。与晶体材料不同， 非晶体材料的电子和声子运动耦合较弱，但 仍然对材料的热导率和电导率产生影响。
研究非晶体材料中的电子声子相互作 用有助于深入了解其物理性质，为非 晶体材料的应用提供理论支持。
在纳米材料中的应用
纳米材料中的电子声子相互作用对其物理性质的影响更加显著。由于纳米材料的尺寸效应，电子和声子的运动状态会发生改 变，导致其热导率和电导率等物理性质发生显著变化。
固体物理学中的电子声子光子自旋相互作用与电子声子光子自旋材料
固体物理学中的电子声子光子自旋相互作用与电子声子光子自旋材料随着科学技术的不断发展，固体物理学作为物理学的一个重要分支，研究了电子、声子、光子和自旋等在物质中的相互作用与性质。
在固体物理学领域中，电子声子光子相互作用和电子声子光子自旋材料是研究的热点之一。
本文将主要探讨电子声子光子自旋相互作用以及相关的材料。
一、电子声子光子自旋相互作用电子声子光子自旋相互作用是指电子、声子、光子和自旋之间的相互作用。
在固体物理学中，电子声子相互作用是研究的重点之一。
电子声子相互作用的研究不仅可以揭示物质的电导特性，还可以解释超导、磁电效应等现象。
声子是晶格振动的量子态，与电子之间的相互作用可以影响材料的电子结构和输运性质。
例如，在超导材料中，声子能够引起电子的吸引作用，从而产生电子对的库伦相互作用，导致电阻为零的超导现象。
光子也是固体物理中的重要相互作用载体。
光子和电子之间的相互作用可以导致材料的光电特性，如吸收、发射、散射等。
此外，光子与电子的相互作用还被应用于光电子器件和光通信领域。
在固体物理学领域中，自旋是电子最基本的性质之一。
自旋与电子的运动状态密切相关，可以调节电子的磁性、电子自旋共振等性质。
电子自旋与光、声子相互作用也被广泛研究，开辟了自旋电子学和自旋光子学领域。
以上是固体物理学中电子声子光子自旋相互作用的简要介绍，下面将探讨与电子声子光子自旋相互作用相关的材料。
二、电子声子光子自旋材料电子声子光子自旋材料是指具有特殊电子、声子、光子和自旋相互作用的材料。
这些材料通常具有独特的电学、磁学、光学性质，对于实现新型电子器件和光子器件具有重要意义。
在电子声子光子自旋材料中，压电材料是其中的重要一类。
压电材料通过电场的作用可以产生应变，从而引起声子的激发和运动。
压电材料广泛应用于声波传感器、表面声波器件等领域。
磁性材料也是电子声子光子自旋材料的重要代表之一。
磁性材料中的电子自旋与磁矩的相互作用可以引发磁性行为。
固体物理学中的电子自旋声子相互作用与电子自旋声子材料
固体物理学中的电子自旋声子相互作用与电子自旋声子材料在固体物理学中，电子自旋声子相互作用是一个重要的研究领域。
它指的是电子自旋与晶格的声子之间的相互作用，对于理解固体的性质和开发新材料具有重要的意义。
一、电子自旋声子相互作用的概念和机制电子自旋声子相互作用是指电子自旋与晶格的声子之间的耦合效应。
电子自旋是电子的一个固有性质，它可以看作电子固有的自旋磁矩。
而声子则是固体中的一种集体激发，代表了晶格振动的量子。
电子自旋声子相互作用可以通过下面的机制进行解释：当晶格发生振动时，电子自旋的自旋磁矩也会受到振动的影响，从而发生相互作用。
这种相互作用可以导致电子自旋的重分布，进而影响固体的电子结构和磁性等性质。
二、电子自旋声子相互作用的研究方法和技术为了研究电子自旋声子相互作用，科学家们采用了一系列的实验技术和理论模型。
其中一种常用的实验技术是中子散射，通过观察散射中中子的能量和动量变化，可以得到电子自旋声子相互作用的信息。
另外，X射线散射和拉曼散射等技术也可以用于研究电子自旋声子相互作用。
在理论上，研究者们利用密度泛函理论（DFT）和量子场论等方法建立了多种模型来描述电子自旋声子相互作用。
这些模型可以通过计算来预测材料的性质和行为，从而为实验提供指导。
三、电子自旋声子材料的研究与应用由于电子自旋声子相互作用的重要性，科学家们对这方面的研究非常活跃。
他们希望通过深入理解电子自旋声子相互作用，开发新的材料，改善现有材料的性能。
一种重要的应用是在磁性材料的研究中。
通过调控电子自旋声子相互作用，可以实现磁性材料的控制和调控。
这对于磁存储器件和磁传感器等领域具有重要意义。
另外，电子自旋声子相互作用还可以用于开发新的拓扑材料。
拓扑材料是一种具有特殊电子结构和导电性质的材料，具有巨大的应用潜力。
通过电子自旋声子相互作用的调控，可以实现拓扑材料的设计和制备。
此外，电子自旋声子材料的研究还涉及到能源存储和转换等领域。
例如，研究者们希望通过电子自旋声子相互作用来提高材料的热导率和热电效应，从而提高能量转换的效率。
固体理论-5 电子声子相互作用
固体理论——电子声子相互作用主讲翦知渐固体理论-电子声子相互作用-物理图像第五章电子声子相互作用1电子与晶格的基本相互作用形式§1 物理图像§2 电子与声频支声子的相互作用子与声频支声子的相作用§3 声子的自能修正§4 电子与光频支声子的相互作用§5 有效电子-声子相互作用而电子-声子相互作用的形变势可写为其中为（相对）形变量为形变势常数由实验确定∆(r )为（相对）形变量，c 1为形变势常数，由实验确定单位体积形变后膨胀为所以体积的相对变化为根据声子声学模的长波方法，有所以对于长波声子体积相对变化为所以，对于长波LA 声子，体积相对变化为其中，只有纵波对体积变化有贡献：e q ·q而对横波指标σ的求和为0故电子-声子互作用的二次量子化形式可表示为单体势对态向量的均量的平均：代表湮灭一个k 电子和一个q 声子，产生一个k+q 电子代表湮灭一个k 电子，产生一个q 声子和一个k -电子q当k在费米球外，k -q在费米球内时，也可代表如下过程箭头向上代表电子，箭头向下代表空穴这几个过程是电子-声子相互作用的一级微扰过程，可用于解释晶体的输运特性电子-声子互作用的高阶微扰过程由上述基本过程组成二级微扰的物理过程：（）先发射然后吸收a ）先发射，然后吸收q 声子——物理实质是电子带着晶格畸变运动，对电子自能产生修正空穴对然后再复合放出声子（b ）产生电子-空穴对，然后再复合放出声子——代表电子系统对声子扰动场的屏蔽，它会改变离子间的互作用势，从而对声子频率产生修正（c ）两个电子通过声子的间接互作用，在一定条件下将成为电子之间的有效吸引势，它是产生超导电性的主要机制§2 电子与声频支声子的相互作用形变势模型是电子与声子互作用的连续模型，更严格的推导应当从晶格模型出发。
对于简单晶格只有声频支振动晶格模型：设l 格点离子与j 电子(r j ) 之间的相互作用势能为V ( r j -l )，所以无晶格振动时，电子-离子相互作用为设晶格振动位移为u l ( t )，此时电子-离子互作用为0,()ei j l i ij l iH V l =−≡=∑∑r l l R a 故电子-声子相互作用为：其中定义了电-声互作用的单体势若采用布洛赫函数作为电子体系二次量子化态向量的基函数（非平面波），则态+k 向量为其中C k ，C k 是能带电子的产生湮灭算符，满足对易关系：则电声互作用可表示为进一步，可利用其中是偏振方向的单位矢量则电声互作用的二次量子化形式可化为其中N为元胞数，M为原子质量，s为格波的偏振指标现在考虑布洛赫函数的积分其中作了代换r → r + l(r+ l) = u k ( r)+l)=(并且利用了布洛赫函数的性质：uk作离子势的傅里叶展开可得因此有为简单起见，用平面波代替布洛赫函数，取得到晶格模型中电子-声子互作用的哈密顿其中利用了i|e⋅k>=k rK n 为倒格矢所以可得到波矢条件波矢条件实际上就是动量守恒条件，但与通常的动量守恒有区别，其中存在选取K n 的不确定性？当采用简约区方案时怎样选取K n ？当采用简约区方案时，K n 的选取应保证散射后的电子态k '也在第一布里渊区内，k '= k + q + K n ——k +q 因为k + q 可能超出BZ1 选取Kn 的讨论k +q (1)k q 位于BZ 内取K n = 0，则有k '= k + q此时总波矢守恒，称为正常散射或简称N 过程长波近似下，有LA 与TA 声子：e qs 平行或垂直于q而只有LA 声子对N 过程有贡献，因为因子e qs · q 的存在使得横波声子的贡献为0此时其中对于金属，可采用集体坐标表示电子离子作用势采用库仑势电子离子互作用势采用库仑势利用声子简正坐标和电子集体坐标此式可用于计算电声作用可得对声子频率的修正k +q BZ 边界(2)k + q 超出BZk + q 一般在邻近布里渊区内，K 0，使得k '= k +此时需要取n ≠使得q + K n 回到BZ 内，因此总波矢守恒条件相差一个倒格矢因e q T · K n ≠ 0，此时TA （横波）声子也有贡献由于从k到k'为大角度散射，显然散射前后电子速度发生了大角度偏转故称度偏转，故称Kn≠ 0的过程为倒逆过程或U过程注意到，采用BZ并未改变物理实质从下图可以看出速度)k+q)从下图可以看出，速度v (k') 与v (k + q) 是相同的U过程主要在高温较大时存在，对金属的高温特性有重要影响程要在高q较大时存在对属的高特性有要影响2 电子-声子互作用过程的守恒定律(1) 准动量守恒：ħk'= ħk + q + K()(q n)若忽略晶格周期性，则相当于晶格常数a →0，因此倒格矢b 这是由于晶格结构的周期性和不连续性形成的→∞，BZ趋于无穷大——自然k + q 不会超出BZ，所以此时动量严格守恒：Kn = 0(2) 能量守恒：对于实过程（可观测的）能量是守恒的电声系统从初态| i > 跃迁到终态|f >,其几率为（含时微扰论）其中什么样的过程是可观测的？只有能够确定电子的初终态能量变化ΔE|εkεk|时，这跃迁才是可能的，即所谓实过程按照测E=|'–时，这一跃迁才是可能的，即所谓实过程——不准关系应要求t ħ/ΔE ，而此时跃迁几率可以写成δ函数t最大为弛豫时间τ（相继两次散射的平均间隔时间），所以当τ ħ/∆E 时才是实过程。
晶体中声子与电子相互作用研究
晶体中声子与电子相互作用研究晶体是由原子或分子通过一定的有序排列形成的固体物质。
在晶体结构中，声子（即晶格振动）和电子是两种重要的基本激发模式。
晶体中的声子与电子相互作用不仅是固体物理学中的一个重要课题，也对我们理解和应用晶体材料具有重要意义。
声子是晶体中原子或分子振动的量子化表现，其具有能量和动量，并且能够传递这些量子化的能量和动量。
声子在固体中传递能量和动量的过程是通过晶格的振动传递来完成的。
在晶体结构中，原子通过键相互连接，形成稳定的晶格结构。
晶体中原子的振动引发了晶格的振动，形成声子。
声子的性质和数量与晶体的结构和化学成分密切相关，因此通过研究声子可以了解晶体的物理特性。
例如，研究声子能谱可以获得晶体的热传导性质，从而为热管理和材料设计提供依据。
与声子相比，电子在晶体中具有不同的行为和性质。
电子是带电粒子，具有电荷和自旋，其行为受到晶格结构以及外加电场等因素的影响。
在化学键的连接作用下，晶体中的电子呈现出不同的性质，如导电性、绝缘性和半导体性等。
通过研究晶体中电子的行为和相互作用，我们可以深入了解晶体材料的电学特性，并为电子器件的设计和应用提供重要参考。
晶体中的声子和电子之间的相互作用由声子-电子散射过程完成。
在这个过程中，声子与电子发生相互作用，并且能量和动量得到交换。
由于声子携带能量和动量的特性，声子-电子散射过程在电子输运、热传导以及其他物理现象中起到重要的作用。
声子-电子相互作用的研究对于理解和应用晶体材料具有重要意义。
例如，高温超导材料的研究表明，超导性的出现与晶格振动（声子）和电子相互作用密切相关。
通过调控声子-电子相互作用，我们可以改变材料的电学和热学特性，从而实现对材料性能的调控。
此外，声子-电子相互作用还在功能材料研究中发挥着重要作用。
例如，铁电材料中声子-电子相互作用的影响可以引起电-声效应，实现电声转换，从而为声音传输和声学设备提供新的可能性。
另外，光催化材料中声子-电子相互作用的研究可以提高能量转化效率，实现光催化反应的高效进行。
固体物理学中的电子声子光子自旋磁子相互作用与电子声子光子自旋磁子材料
固体物理学中的电子声子光子自旋磁子相互作用与电子声子光子自旋磁子材料固体物理学中的电子、声子、光子、自旋与磁子相互作用固体物理学研究了固态材料中的物理性质和现象，其中电子、声子、光子、自旋和磁子是关键的研究对象。
这些粒子或波动的相互作用在固态材料的性能和行为中起着重要作用。
本文将探讨固体物理学中的电子、声子、光子、自旋和磁子的相互作用，以及相关材料的特性。
一、电子电子是带负电荷的基本粒子，是化学元素中原子的组成部分。
在固体物理学中，电子在固态材料中的行为对于材料的电子输运、能带结构和电子态密度等性质具有重要影响。
电子的运动状态可以通过色散关系和态密度等参数来描述。
电子在固体中可以发生散射，与其他粒子相互作用。
散射机制包括晶格散射、杂质散射、界面散射等。
这些散射过程会影响电子的能量、动量和自旋状态。
利用电子的散射行为，可以研究材料的输运性质和电子态密度分布。
除了散射，电子在固体中还会与声子、光子、自旋和磁子发生相互作用。
这些相互作用对于固体的电子输运、光学性质和磁性行为等方面起到重要作用。
二、声子声子是固体中的晶格振动模式，是晶体中原子相对平衡位置的偏移。
声子激发可以通过固体中原子的相对位移来传播。
声子与固体材料中的其他粒子相互作用，包括与电子、光子、自旋、磁子的相互作用。
声子与电子之间的相互作用被称为电声耦合。
电声耦合会影响声子的色散关系和声子的寿命。
在一些材料中，电声耦合可以导致声子的局域化和激发出声子能隙。
这些声子能隙对于材料的热学和电输运性质具有重要影响。
声子还可以与光子相互作用，这种相互作用称为声光耦合。
声光耦合可以通过声子在材料中的散射和吸收来描述。
声光耦合对固体中的光学性质和声子的输运行为具有重要影响。
三、光子光子是光的量子，具有电磁波粒二象性。
光子在固体物理学中的研究涉及材料的光学性质和光与其他粒子的相互作用。
光子与电子、声子、自旋、磁子的相互作用对固体材料的光学和电子性质产生重要影响。
电子与声子的输运和相互作用
电子与声子的输运和相互作用在现代科学技术的发展中，电子与声子的输运和相互作用是一个重要的研究领域。
电子和声子是凝聚态物质中两种不可或缺的基本粒子，它们之间的输运和相互作用关系着物质的性质和功能。
本文将从电子与声子的本质、输运机制和相互作用等方面，探讨它们在凝聚态物质中的重要性和应用前景。
首先，我们先来看一下电子和声子的本质。
电子是原子、分子和固体中负电带电粒子，具有质量和电荷。
而声子是物质中的晶格振动，类似于固体中的“声波粒子”。
与电子相比，声子没有电荷，只具有动量和能量。
电子和声子的输运机制是凝聚态物质中的重要现象。
在固体中，电子的输运主要是靠电子的能量和动量传递来实现。
当一个电子在固体中受到外部电场的作用时，它会通过与晶格中的离子相互作用，从而引起晶格的畸变。
这种畸变会以声子的形式传播，从而传递了电子的能量和动量。
声子的传播可以看作是晶格的振动，一旦声子到了晶体的边界，它会通过散射的方式与外界进行作用，从而实现电子的输运。
电子和声子之间还存在着相互作用。
电子和声子之间的相互作用主要表现在电子的散射过程中。
当电子和声子碰撞时，会发生能量和动量的交换。
这种相互作用在输运过程中起到了重要的调控作用。
例如，在一些高温超导体中，电子和声子之间的相互作用导致了电子对的形成，从而使得超导性的产生和传输。
此外，电子和声子的输运和相互作用也在热电材料和光电材料等应用领域发挥着重要作用。
在热电材料中，通过控制电子和声子的输运机制，可以实现高效的热电转换，将热能转化为电能，从而提高材料的能量利用效率。
而在光电材料中，电子和声子的相互作用也决定了材料对光的吸收和发射特性，从而影响了光电转换效率和光电器件的性能。
综上所述，电子与声子的输运和相互作用是凝聚态物质中的重要现象。
它们之间的相互作用关系着物质的性质和功能，对于研究凝聚态物质的基本特性以及应用前景具有重要意义。
未来，我们可以通过深入研究电子与声子之间的输运和相互作用，开发新的功能材料和器件，推动科学技术的创新和发展。
电子与声子耦合在材料性能中的作用
电子与声子耦合在材料性能中的作用在材料科学领域中，电子与声子的相互作用被广泛研究，因为它在材料性能调控和应用中发挥着重要的作用。
电子和声子是材料中两种重要的激发类型，其耦合可以通过影响材料的导电性、热导性以及光学性能等方面来实现。
首先，电子与声子的耦合对于材料的导电性能具有重要作用。
在一些材料中，电子与声子的耦合会导致电子的散射，从而影响电子的输运特性。
这种耦合可以通过引入强烈的电声相互作用来实现。
例如，在超导体材料中，由于电子与声子耦合增强，电子在材料中的流动遇到较少的散射，从而导致材料的超导性能增强。
另外，在磁性材料中，电子与声子的耦合可以引起磁声相互作用，从而影响材料的磁性。
这些例子表明，电子与声子的耦合在导电性能的调控中扮演着重要的角色。
其次，电子与声子的耦合对材料的热导性能也有显著影响。
热导性是材料的重要性能参数，直接关系到材料的热管理和能源转换效率。
电子与声子的耦合可以影响材料内部热传导的方式。
在一些材料中，电子与声子的强烈耦合会导致热传导的减弱，从而提高材料的热绝缘性能。
这种现象被广泛应用于热电材料的设计和制备中。
热声效应是其中的典型例子，基于电子与声子耦合的热声效应可以将热能转化为声能，为声波发生装置的设计提供新思路。
此外，电子与声子的耦合也在光学性能调控中起到重要的作用。
在某些材料中，电子与声子的耦合会导致光的散射和吸收特性发生变化，从而调控材料的光学性能。
这种耦合可以通过调控材料的电子结构和声子谱来实现。
例如，一些光学材料的性能可以通过光伏效应来改善，这种效应依赖于电子与声子之间的能量转化。
此外，电子与声子的耦合还广泛应用于光学存储和信息处理领域，以实现光子器件的高效率和高性能。
综上所述，电子与声子的耦合在材料科学中起到了重要的作用。
从导电性、热导性到光学性能，电子与声子之间的相互作用对材料的性能调控起到了关键作用。
深入理解和掌握电子与声子的耦合机制，将有助于开发新型材料和优化已有材料的性能，进一步推动材料科学的发展。
纳米材料中的多体效应研究
纳米材料中的多体效应研究近年来，随着纳米科技的发展，纳米材料已经逐渐成为了研究和应用的热点。
在纳米材料的研究中，多体效应开始逐渐受到人们的关注，其对纳米材料的物理性质和应用有着不可忽视的影响。
本文将围绕多体效应在纳米材料中的研究展开讨论。
一、多体效应的概念多体效应（many-body effect）是指当多个粒子相互作用时产生的量子力学效应。
在纳米材料中，多个纳米粒子的相互作用对材料的性质有着显著的影响。
多体效应主要分为两种：电子-电子相互作用和电子-声子相互作用。
二、电子-电子相互作用在纳米材料中的研究电子-电子相互作用是指在纳米材料中，电子之间的相互作用引起的多体效应。
这种效应主要包括电荷、自旋和相位等几个方面。
在纳米材料中，电子-电子相互作用对材料的电学、热学和光学性质都有着显著的影响。
1. 电荷多体效应电荷多体效应是指当电子之间发生相互作用时，电子的能量被重新调配，从而导致材料的电学性质发生变化。
在纳米材料中，因为电子之间的距离比较接近，所以电荷多体效应比较显著。
在一些高温超导材料和强关联体系中，电荷多体效应在纳米尺度下被广泛研究。
2. 自旋多体效应自旋多体效应是指当电子之间发生相互作用时，电子的自旋影响了材料的物理性质。
相关研究表明，在一些自旋玻璃和量子自旋体系中，自旋多体效应在纳米尺度下有着显著的影响。
3. 相位多体效应相位多体效应是指当电子之间发生相互作用时，电子的相位差影响了材料的电学、光学和热学性质。
在一些复杂的电子系统中，相位多体效应对材料的物理性质有着重要的影响。
三、电子-声子相互作用在纳米材料中的研究电子-声子相互作用是指在纳米材料中，电子与声子之间发生相互作用引起的多体效应。
这种效应主要包括声子传输、压电效应和声子谱等几个方面。
在纳米材料中，由于声子的量子效应比较显著，所以电子-声子相互作用对材料性质有着深刻的影响。
1. 声子传输多体效应声子传输多体效应是指当声子在纳米材料中传输时，由于与电子的相互作用而导致的材料传输性质的改变。
银的阻尼因子
银的阻尼因子
在物理学中，阻尼是指减缓或抑制振动或运动的现象。对于银（Ag）这样的金属，其阻 尼因子主要与其电导率和电子-声子相互作用有关。
1. 电导率：银是一种良好的导电金属，具有高电导率。高电导率意味着银中的自由电子可 以在外加电场的作用下迅速移动，这对于电流的传输非常有利。然而，高电导率也会导致银 中的自由电子在振动或运动过程中遭受较少的阻尼，因为电子可以更快地回到平衡位置。
银的阻尼因子
2. 电子-声子相互作用：金属中的振动是由晶格中的原子或离子的振动引起的。在银中， 自由电子与晶格振动之间存在相互作用，即电子-声子相互作用。这种相互作用会导致电子在 振动或运动过程中受到阻尼，因为电子与晶格振动之间的相互作用会转移能量，使电子的振 动逐渐减弱。
综上所述，银的阻尼因子主要受到其高电导率和电子-声子相互作用的影响。高电导率使 得银中的自由电子在振动或运动过程中受到较少的阻尼，而电子-声子相互作用则会导致电子 的振动逐渐减弱。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
设晶体的体积V=N=1，那么
W (r ) 1/ 2 (u u ) NM {u (r ) u (r )} 2 L
e (a e
q q q
iq r
iq r aq e )
LO声子的极化电场可写为
iq r E (r ) 4F eq (aq eiqr aq e ) q
电子-声子互作用过程的守恒定律
动量：k ' (k q K n ) 总动量相差K n , 这是由晶格结构的周期 性和不连续性造成的
* 散射前后能量守恒 电声子作用的实（可观察的）过程和虚（不观察的）过程
对于实过程：电声子散射两次平均时间间隔：
, E
E | k k q |
生修正。
（b）为电子系统对声子扰动场的屏蔽，将改变离子间的互作用势，从而对声子 频率产生修正。
（c）两个电子通过声子的间接互作用，在一定条件下将成为电子之间的有效吸
引势，它是产生超导电性的主要机制。
2、电子与声频支声子的相互作用
形变势模型是电子与声子互作用的连续模型
更严格的推导应当从晶格模型出发；对于简单晶格只有声频支振动。
L 1 1 利用LST关系得：F 8 0
若设电场的势
iqr (r ) (q eiqr q e ) q
1/ 2
iqr iqr ) 与前面方程对照可知： 则由 E(r ) (r ) i q(q e q e q
iq r (eq q)( aq eiqr aq e ) 2 Vq
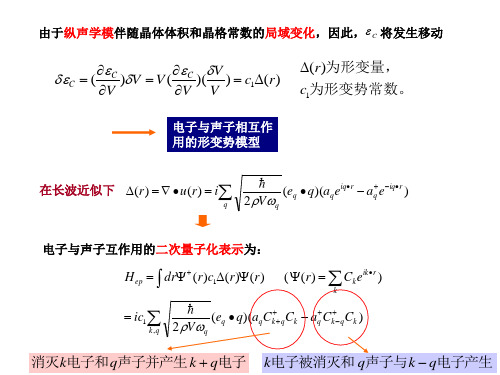
电子与声子互作用的二次量子化表示为：
H ep dr (r )c1(r ) (r ) ic1
k ,q
( (r ) Ck eikr )
k
(eq q)(aq Ck q Ck aq Ck q Ck ) 2 Vq
Ck ,
N V (e q) 其中Dq i 2M q q q
* 对于金属，采用集体坐标表示。设金属为单价，电子与离子间互作用取库仑势
H ep M qQq q ,
q
2 N 4e 其中M q i 2 (eq q) M q
（1）k q在第一布里渊区
取Kn 0, 这时k ' k q, 总波矢守恒，称为正常 散射过程或简称 N过程
在长波近似下，有 eqs 平行或垂直于波矢 q的解， 分别代表LA与T A声子。显然，只有 LA声子的贡献：
H ep Dq (aq a )C
q k ,q k q
*当离子不动时，电子与离子的互作用为：
0 H ei V (rj l ) j ,l
l Rl li ai
i
*实际上离子在不断地振动，互作用为：
H ei V (rj l ul )
j ,l
能带电子与晶格振动的相互作用势为
0 H ep H ei H ei V (rj l ul ) V (rj l ) j ,l
消灭k电子和q声子并产生 k q电子
k电子被消灭和 q声子与k q电子产生
当k在费米球外而 k q在费米球内时
代表电子
代表空穴
以上是Hep的一级微扰过程，它用于解释晶体的输运特性。
电子-声子互作用的高阶微扰过程由上述基本过程组成
（a）先发射后吸收q声子，物理实质是电子带着晶格畸变运动，对电子自能产
1/ 2
由晶体的周期性边界条件得：
r r l
* k'
k ' | V (r l ) | k
对离子势作傅里叶展开
dru
(r )uk (r )ei ( k k ')r V (r ) ei ( k k ')l
V (r ) Vp eipr
p
N 1 H ep i (eqs p ) 2 M k ,k ' q , s p N qs V p k ' | e ipr | k (aqs a qs )C k 'C k
3、声子的自能修正
电子系统对声子扰动场的屏蔽，将改变离子
间的互作用势，从而对声子频率产生修正。 考虑单价金属，设N个离子组成的简单晶 格浸没在均匀电子气体中 与电子集体振荡相似，未微扰的LA声子频 率在长波范围内为
4Ne 2 M
2 q
这里取单体积，N=-1， 为正点阵元胞体
积。LA声子的哈密顿：
ul V (ri l ) h(rj )
j ,l j
其中电子与声子Байду номын сангаас作用 的单体势为： h(r ) ul V (r l )
l
若选布洛赫函数
k (r) uk (r)eikr ,
uk (r l ) uk (r)
作为电子系统二次量子化态向量的基函数，则
1、互作用过程
能带论只计及晶格周期场对电子的作用（即原子或离子位置固定的情形） 考虑晶格振动时，原子（离子）偏离平衡位置，引起势能的改变。能带
电子将受到晶格位移所产生附加势场的作用，这就是电子和晶格振动的 相互作用。 电子与声子相互作用。
在能带极值附近，电子的能量：
导带
C
2k 2 k C 2m 其中 C为带边能量，可理解为 能带电子的势能 , 为晶格周期势对电子的 作用。
最后得到LA声子的色散关系
q cL q
1 m cL vF 3 M 其中vF k F / m为费米速度。
这就是著名的玻母-司台夫(Bohm-Staver)声速公式
1/ 2
4、电子与光频声子的相互作用
离子晶体中的光频支纵振动会产生极化电场
它将对离子晶体中的传导电子产生强烈的耦合作用。 耦合作用比LA声子对传导电子的作用强得多。 因此，主要是LO声子与传导电子的相互作用对离子晶体中的载流子特性产生影响。 在长波近似下，LO声子的位移场可写为：
u (r ) u (r ) 2 NM L
1 NM
q q
e Q e
q q q iq r
iq r
e (a e
q
iq r aq e )
这里M为折合质量，这里还忽略了L对q的依赖关系。
光频支纵振动位移所产生的电场
E (r )
4 12 W (r ) 1 4 22
k ,k '
ul k ' | V (r l ) | k Ck'Ck
l k ,k '
(aqs a )Ck'Ck eiql {eqs k ' | V (r l ) | k } qs l k , k ' q , s 2 NM qs 其中，N为元胞数，M为原子质量， s代表格波的偏振指标。
q i
4F (eq q)aq 2 q
根据海森伯方程：
i P q [ Pq , H ]和对易式 [ Pq , Qq ' ] qq ' i
可导出运动方程
Qq 2 q Qq M q q 如果能确定q与Qq之间的关系，则声子频 率的修正就可以求出。
晶格振动必然产生离子密度的起伏，可用离子密度的傅里叶分量
1/ 2
e
l
i ( k q k ') l
为简单起见，用平面波代替布洛赫函数，取 uk (r ) ( N) 得到晶格模型中电子与声子互作用的哈密顿
1/ 2
N Vq K {eqs (q K n )}(aqs a H ep i ) C qs k q K n Ck n k q , s 2 Mqs
i
傅里叶展开
i iq r i (r ) q e q i 其中离子密度的傅里叶 分量为 q i(
N 1/ 2 ) (eq q)Qq M
（2）
i q与q 的关系
i 由于离子运动比电子运动慢得多，因此，离子运动产生的 q 当作“静态试
探电荷”，可用线性响应理论处理：
价带
由于纵声学模伴随晶体体积和晶格常数的局域变化，因此， C 将发生移动
V C ( C )V V ( C )( ) c1(r ) V V V
电子与声子相互作 用的形变势模型 在长波近似下 (r ) u (r ) i
q
(r )为形变量， c1为形变势常数。
（2）k q超出第一布里渊区
取K n 0, 所取k q K n回到第一布里渊区，这 时eqT K n 0, 这时LA与T A声子都对互作用有贡献 。
k’
k
由于从k到k’为大角度散射，显然散射前后电子速度发生了大角度偏转，
故常称 K n 0 的过程为U过程或倒逆过程
U过程主要在高温大q时存在，对金属的高温特性有重要影响
i 表示。 q
这个起伏的效果相当于对电子气体加上一外扰动场，引起电子气体的响应运动。
i （ 1） 离子密度起伏 q
晶格振动位移将产生极化
P(r ) Neu(r ),
由极化可得到离子密度
其中u(r ) ( NM )1/ 2 eqQq eiqr
q
1 N 1/ 2 (r ) P(r ) i( ) (eq q)Qq eiqr e M q
E (r ) E (q )e iqr
q
D(q) (q) E (q)
于是得到
q
1 (q) i q (q)
这样可得运动方程的右边为
2 4Ne 2 (eq q) 1 (q) 2 1 (q) M q q Q Qq q q 2 M q (q) ( q)