12级《高等数学》(上)(理工类)期末统考的通知
辽宁省大连市2022-2023学年高一上册12月期末考试数学试卷(含解析)

辽宁省大连市2022-2023学年高一上册12月期末考试数学试卷(含解析)第Ⅰ卷(选择题)一、单项选择题(本大题共8小题,每题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{}1,2,3,4A =,集合()(){}130B x x x =+-<,则A B = ()A.{}1,0,1,2,3- B.{}1,2,3 C.{}1,2 D.{}2【答案】C2.已知向量()1,2a =r ,(),4b x =- ,且//a b r r,则实数x =()A.2B.1C.1- D.2-【答案】D3.若1x ,2x ,…,10x 的方差为2,则131x +,231x +,…,1031x +的方差是()A.18B.7C.6D.2【答案】A4.中国共产党第二十次全国代表大会于2022年10月16日在北京开幕.党的二十大报告鼓舞人心,内涵丰富.某学校党支部评选了5份优秀学习报告心得体会(其中教师2份,学生3份),现从中随机抽选2份参展,则参展的优秀学习报告心得体会中,学生、教师各一份的概率是()A.120 B.35C.310D.910【答案】B5.下列函数中,其图像如图所示的函数为()A.13y x-= B.23y x=C.13y x = D.23y x -=【答案】A6.“北溪”管道泄漏事件的爆发,使得欧洲能源供应危机成为举世瞩目的国际公共事件.随着管道泄漏,大量天然气泄漏使得超过8万吨类似甲烷的气体扩散到海洋和大气中,将对全球气候产生灾难性影响.假设海水中某种环境污染物含量P (单位:mg L )与时间t (单位:天)间的关系为:0ektP P -=⋅,其中0P 表示初始含量,k 为正常数.令2121P P t t μ-=-为[]12,t t 之间海水稀释效率,其中1P ,2P 分别表示当时间为1t 和2t 时的污染物含量.某研究团队连续20天不间断监测海水中该种环境污染物含量,按照5天一期进行记录,共分为四期,即(]0,5,(]5,10,(]10,15,(]15,20分别记为Ⅰ期,Ⅱ期,Ⅲ期,Ⅳ期,则下列哪个时期的稀释效率最高().A.Ⅰ期B.Ⅲ期C.Ⅲ期D.Ⅳ期【答案】A7.已知0x >,0y >,且满足20x y xy +-=,则92x y+的最大值为()A.9 B.6 C.4D.1【答案】D8.已知定义域为D 的函数()f x ,若1x D ∀∈,都2x D ∃∈,满足()122x f x a +=,则称函数()f x 具有性质()P a .若函数()f x 具有性质()1P ,则“()f x 存在零点”是“2D ∈”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B二、多项选择题(本大题共4小题,每题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.)9.十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国数学家哈利奥特首次使用“<”和“>”符号,不等号的引入对不等式的发展影响深远.若a ,b ,R c ∈,则下列命题正确的是()A.若0ab ≠且a b <,则11a b> B.若a b >,01c <<,则a bc c <C.若1a b >>,1c >,则log log a b c c<D.若1a b <<-,0c >,则c ca b b a ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭【答案】BCD10.同时掷红、蓝两枚质地均匀的骰子,事件A 表示“两枚骰子的点数之和为5”,事件B 表示“红色骰子的点数是偶数”,事件C 表示“两枚骰子的点数相同”,事件D 表示“至少一枚骰子的点数是奇数”,则()A.A 与C 互斥B.B 与D 对立C.A 与D 相互独立D.B 与C 相互独立【答案】AD11.已知点P 为ABC 所在平面内一点,且230PA PB PC ++=,若E 为AC 的中点,F 为BC 的中点,则下列结论正确的是()A.向量PA 与PC可能平行B.点P 在线段EF 上C.:2:1PE PF =D.::1:2:3PAB PAC PBC S S S =△△△【答案】BC12.已知函数()()21350f x x x x =+->,()22e2xf x x =+-,()3ln 24f x x x =+-的零点分别为1x ,2x ,3x ,则下列结论正确的是()A.123x x x <<B.232x x +=C.()310f x <D.()()3223f x f x =【答案】BC第Ⅱ卷(非选择题)三、填空题(本大题功4小题,每小题5分,共20分.)13.2log 522log 4+=______.【答案】714.已知向量a ,b满足()1,2a =- ,(),1b x =r ,3a b += ,则实数x =______.【答案】115.在考察某中学的学生身高时,采用分层抽样的方法抽取男生24人,女生16人,得到了男生的平均身高是170cm ,女生的平均身高是165cm ,则估计该校全体学生的平均身高是______cm .【答案】16816.函数()()()224f x xxax b =-++满足:x ∀∈R ,都有()()20222024f x f x -=-,则函数()f x 的最大值为______.【答案】16四、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.如图所示,在ABC 中,D 为BC 边上一点,且2BD DC =.过D 点的直线EF 与直线AB 相交于E 点,与直线AC 相交于F 点(E ,F 两点不重合).(1)用AB,AC 表示AD;(2)若AE AB λ=,AF AC μ=,求12λμ+的值.【答案】(1)1233AD AB AC=+(2)3.【解析】【小问1详解】在ABD △中,由AD AB BD =+,又2BD DC =,所以23BD BC =,所以23AD AB BD AB BC=+=+ ()23AC ABAB =+- 2233AB ACAB =-+ 1233AB AC =+【小问2详解】因为1233AD AB AC =+ ,又AE AB λ= ,AF ACμ=所以1AB AE λ= ,1AC AF μ=,所以3231A E D A A F μλ=+,又,,D E F 三点共线,且A 在线外,所以有:12133λμ+=,即123λμ+=.18.已知集合{}13A x x =-≤≤,集合{}22,R B x m x m m =-≤≤+∈.(1)若{}03A B x x ⋂=≤≤,求实数m 的值;(2)若:p x A ∈,R :q x B ∈ð,且p 是q 的充分条件,求实数m 的取值范围.【答案】(1)2m =(2){5m m >或}3m <-.【解析】【小问1详解】因为{}03A B x x ⋂=≤≤,所以2023m m -=⎧⎨+≥⎩,所以21m m =⎧⎨≥⎩,所以2m =;【小问2详解】{R 2B x x m =<-ð或}2x m >+,:p x A ∈,R :q x B ∈ð,且p 是q 的充分条件由已知可得R A B ⊆ð,所以23m ->或21m +<-,所以5m >或3m <-,故实数m 的取值范围为{5m m >或}3m <-.19.近年来,“直播带货”受到越来越多人的喜爱,目前已经成为推动消费的一种流行的营销形式.某直播平台800个直播商家,对其进行调查统计,发现所售商品多为小吃、衣帽、生鲜、玩具、饰品类等,各类直播商家所占比例如图1所示.(1)该直播平台为了更好地服务买卖双方,打算随机抽取40个直播商家进行问询交流.如果按照分层抽样的方式抽取,则应抽取小吃类、玩具类商家各多少家?(2)在问询了解直播商家的利润状况时,工作人员对抽取的40个商家的平均日利润进行了统计(单位:元),所得频率分布直方图如图2所示.请根据频率分布直方图计算下面的问题;(ⅰ)估计该直播平台商家平均日利润的中位数与平均数(结果保留一位小数,求平均数时同一组中的数据用该组区间的中点値作代表);(ⅱ)若将平均日利润超过420元的商家成为“优秀商家”,估计该直播平台“优秀商家”的个数.【答案】(1)小吃类16家,玩具类4家;(2)(i )中位数为342.9,平均数为352.5;(2)128.【解析】【小问1详解】()40125%15%10%5%5%16⨯-----=,4010%4⨯=,所以应抽取小吃类16家,玩具类4家.【小问2详解】(i )根据题意可得()0.00130.0030.0050.007501a ⨯++++⨯=,解得0.002a =,设中位数为x ,因为()0.0010.003500.2+⨯=,()0.0010.0030.007500.55++⨯=,所以()3000.0070.20.5x -⨯+=,解得342.9x ≈,平均数为()2250.0012750.0033250.0073750.0054250.0024750.0015250.00150352.5⨯+⨯+⨯+⨯+⨯+⨯+⨯⨯=,所以该直播平台商家平均日利润的中位数为342.9,平均数为352.5.(ii )4504200.0020.0010.0015080012850-⎛⎫⨯++⨯⨯=⎪⎝⎭,所以估计该直播平台“优秀商家”的个数为128.20.第56届世界乒乓球团体锦标赛于2022年在中国成都举办,国球运动又一次掀起热潮.现有甲乙两人进行乒乓球比赛,比赛采用7局4胜制,每局11分制,每赢一球得1分,选手只要得到至少11分,并且领先对方至少2分(包括2分),即赢得该局比赛.在一局比赛中,每人只发2个球就要交换发球权,如果双方比分为10:10后,每人发一个球就要交换发球权.(1)已知在本场比赛中,前三局甲赢两局,乙赢一局,在后续比赛中,每局比赛甲获胜的概率为35,乙获胜的概率为25,且每局比赛的结果相互独立,求甲乙两人只需要再进行两局比赛就能结束本场比赛的概率;(2)已知某局比赛中双方比分为8:8,且接下来两球由甲发球,若甲发球时甲得分的概率为23,乙发球时乙得分的概率为12,各球的结果相互独立,求该局比赛甲得11分获胜的概率.【答案】(1)925;(2)49.【解析】【小问1详解】设“甲乙两人只需要再进行两局比赛就能结束本场比赛”为事件A ,若两局比赛就能结束,则只能甲连胜两局,所以()3395525P A =⨯=;【小问2详解】设“该局比赛甲得11分获胜”为事件B ,甲得11分获胜有两类情况:甲连得3分,则甲11:8获胜;甲得3分,乙得1分,则甲11:9获胜,此时有三种情况,每球得分方分别为乙甲甲甲,甲乙甲甲,甲甲乙甲,所以()22112112111221143323322332233229P B =⨯⨯+⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=.21.已知函数()14xb f x a =++的定义域为R ,其图像关于点11,22⎛⎫⎪⎝⎭对称.(1)求实数a ,b 的值;(2)求122022202320232023f f f ⎛⎫⎛⎫⎛⎫+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值;(3)若函数()412log 22xg x f x x+⎛⎫=++ ⎪-⎝⎭,判断函数()g x 的单调性(不必写出证明过程),并解关于t 的不等式()()2121g t g t -++>.【答案】(1)2,2a b ==-(2)1011(3)103t -<<【解析】【小问1详解】有条件可知函数()f x 经过点11,22⎛⎫ ⎪⎝⎭,()()112210122f f f ⎧⎛⎫= ⎪⎪⎪⎝⎭∴⎨⎪+=⨯⎪⎩,即12112411114b a b b aa ⎧+=⎪⎪+⎨⎪+++=⎪++⎩,解得:2,2a b ==-,()2414242xx xf x -=+=++;【小问2详解】由于120222************1,1,,1202320232023202320232023+=+=+= ,1202222021101110121,1,,1202320232023202320232023f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫∴+=+=+= ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,1220221011202320232023f f f ⎛⎫⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;【小问3详解】由于42log 2x y x +=-是奇函数,根据函数平移规则,()()12h x g x =-也是奇函数,并且由于()f x 是增函数,42log 2xy x+=-也是增函数,()h x ∴也是增函数,定义域为()2,2-不等式()()2121g t g t -++>等价于()()11212022g t g t --++->,即()()2120h t h t -++>,()()()2122h t h t h t ->-+=--,由于()h x 是增函数,2122212222t t t t ->--⎧⎪∴-<-<⎨⎪-<+<⎩,解得103t -<<;综上,(1)2,2a b ==-;(2)1220221011202320232023f f f ⎛⎫⎛⎫⎛⎫+++=⎪ ⎪⎝⎭⎝⎭⎝⎭;(3)103t -<<.22.已知函数()f x 的图像与函数()31xg x =-的图像关于直线y x =对称,函数()()9log 1h x x a =-+.(1)若4a =,求()()()F x f x h x =⋅在[]0,4x ∈上的最大值;(2)设()()(){}max ,2H x f x h x =,[]0,4x ∈,求()H x 的最小值,其中{},max ,,a a ba b b a b ≥⎧=⎨<⎩.【答案】(1)()F x 在[]0,4x ∈上的最大值为12(2)()H x 的最小值()()()3min 33log 1,0log 1,082log 3,8a a a H x a a a ⎧-≤⎪⎪⎛⎫=+<<⎨ ⎪⎝⎭⎪⎪-≥⎩【解析】【小问1详解】解:因为函数()f x 的图像与函数()31xg x =-的图像关于直线y x =对称,即()f x 与()g x 互为反函数,所以()()3log 1f x x =+当4a =,有()()9log 41h x x =-+,则()()()()()3939log 1log 41log 1log 5F x x x x x =+⋅-+=+⋅-()()331log 1log 52x x =+⋅-,又[]0,4x ∈时,[][]11,5,51,5x x +∈-∈,所以()()33log 10,log 50x x +≥-≥,所以()()()()()()()()2233223333log 1log 511111log 1log 5log 15log 29222882x x F x x x x x x ⎛⎫++-⎡⎤=+⋅-≤=+-=--+≤ ⎪⎣⎦⎝⎭,当且仅当()()33log 1log 52x x x ⎧+=-⎨=⎩,即2x =时等号同时成立,所以()F x 在[]0,4x ∈上的最大值为12;【小问2详解】解:()()()9322log 1log 1h x x a x a =-+=-+,()()2f x h x <等价于11x x a +<-+,即x x a <-,因为[]0,4x ∈,当0a ≤时,x a x a x -=-≥恒成立,所以()()2f x h x ≤,则()()3log 1H x x a =-+,所以()H x 在[]0,4x ∈上单调递增,所以()()()min 30log 1H x H a ==-;当04a <<时,[)[],0,,,4a x x a x a x a x a ⎧-∈⎪-=⎨-∈⎪⎩,此时当0,2a x ⎡⎤∈⎢⎥⎣⎦时,()()2f x h x <,当,42a x ⎛⎤∈ ⎥⎝⎦时,()()2f x h x >,所以()()()33log 1,0,2log 1,42a a x x H x a x x ⎧⎡⎤-+∈⎪⎢⎥⎪⎣⎦=⎨⎛⎤⎪+∈ ⎥⎪⎝⎦⎩,()H x 在0,2a x ⎡⎤∈⎢⎥⎣⎦上单调递减,在,42a x ⎛⎤∈ ⎥⎝⎦上单调递增,所以()min 3log 122a a H x H ⎛⎫⎛⎫==+ ⎪ ⎪⎝⎭⎝⎭;当4a ≥时,x a a x -=-,当48a ≤<时,()H x 与上一种情况相同,所以()min 3log 122a a H x H ⎛⎫⎛⎫==+ ⎪ ⎪⎝⎭⎝⎭;当8a ≥时,x a a x x -=-≥恒成立,所以()()2f x h x <,则()()3log 1H x a x =-+,所以()H x 在[]0,4x ∈上单调递减,所以()()()min 34log 3H x H a ==-;综上,()H x 的最小值()()()3min 33log 1,0log 1,082log 3,8a a a H x a a a ⎧-≤⎪⎪⎛⎫=+<<⎨ ⎪⎝⎭⎪⎪-≥⎩.。
浙江省杭州市2023_2024学年高二数学上学期12月阶段联考试题含解析

考生须知:1.本卷共4页满分150分,考试时间120分钟;2.答题前,在答题卷指定区域填写班级、学号和姓名;考场号、座位号写在指定位置;3.所有答案必须写在答题纸上,写在试卷上无效;4.考试结束后,只需上交答题纸.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的,1.准线方程为2y =的抛物线的标准方程是()A.24x y = B.24x y =-C.28x y= D.28x y=-2.直线210x ay +-=和直线()3110a x ay ---=垂直,则a =()A.1B.12C.1或12D.1或12-3.已知在等比数列{}n a 中,4816a a ⋅=,则6a 的值是()A.4B.-4C.±4D.164.如图,在三棱台111ABC A B C -中,且112AB A B =,设1,,AB a AC b AA c ===,点D 在棱11B C 上,满足112B D DC = ,若AD xa yb zc =++,则()A.11,,163x y z === B.111,,632x y z ===C.11,,136x y z === D.111,,362x y z ===5.已知等差数列{}n a 的前n 项和为n S ,且202220230,0S S ><,则下列说法错误的是()A.10120a < B.10110a >C.数列{}n a 是递减数列D.{}n S 中1010S 最大6.已知圆221:20(0)C x ax y a -+=>,直线:0l x =,圆1C 上恰有3个点到直线l 的距离等于1,则圆1C 与圆222:(1)(1C x y -+=的位置关系是()A.内切B.相交C.外切D.相离7.已知圆22:(4)1C x y +-=上有一动点P ,双曲线22:197x y M -=的左焦点为F ,且双曲线的右支上有一动点Q ,则PQ QF +的最小值为()A.1- B.5- C.7D.58.阅读材料:空间直角坐标系O xyz -中,过点()000,,P x y z 且一个法向量为(),,n a b c =的平面α的方程为()()()0000a x x b y y c z z -+-+-=,阅读上面材料,解决下面问题:已知平面α的方程为21x y z -+=,点()3,1,1Q -,则点Q 到平面α距离为()A.6B.2C.102D.34二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知()()2,2,2,1,2,1a b =-=-,则下列说法正确的是()A.()1,4,1a b +=-B.a∥bC.a b⊥D.3cos ,23a ab -=10.已知直线()():2220l mx m y m m R ++--=∈,圆22:(1)(2)25C x y -+-=,点P 为圆C 上的任意一点,下列说法正确的是()A.直线l 恒过定点()1,1B.直线l 与圆C 恒有两个公共点C.直线l 被圆C 截得最短弦长为D.当1m =-时,点P 到直线l 距离最大值是252+11.已知数列{}{},n n a b 满足()*123111,23n n n a a a a b n N S n++++=∈ 是{}n a 的前n 项和,下列说法正确的是()A.若2n a n n =+,则232n n nb +=B.若n b n =,则{}n a 为等差数列C.若1n b n =+,则{}n a 为等差数列D.若2nn b =,则()122nn S n =-⋅+12.已知抛物线2:4C y x =的焦点为F ,准线l 与x 轴交于点M ,过M 的直线l 与抛物线C 相交于()()1122,,,A x y B x y 两点,点D 是点A 关于x 轴的对称点,则下列说法正确的是()A.124y y =- B.4AF BF +的最小值为10C.,,B F D 三点共线D.0MB MD ⋅>三、填空题:本题共4小题,每题5分,共20分.13.在空间直角坐标系O xyz -中,已知点()()3,1,4,2,1,5M N -,则MN =__________.14.过点()0,0作圆22:430C x y y +-+=的两条切线,切点为A B 、,则劣弧长 AB =__________.15.如图,已知正方形0000A B C D 的边长为2,分别取边00000000,,,D A A B B C C D 的中点1111,,,A B C D ,并连接形成正方形1111A B C D ,继续取边11111111,,,D A A B B C C D 的中点2222,,,A B C D ,并连接形成正方形2222A B C D ,继续取边22222222,,,D A A B B C C D 的中点3333,,,A B C D ,并连接形成正方形3333,A B C D ,依此类推;记011A A B 的面积为1122,a A A B 的面积为2,a ,依此类推,()*1n n n A A B n N -∈ 的面积为n a ,若12310231024n a a a a +++=,则n =__________.16.设12F F 、是椭圆2222:1(0)x y C a b a b+=>>的左、右焦点,点,P Q 为椭圆C 上的两点,且满足21260,2PF Q PF QF ∠==,则椭圆C 的离心率为__________.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本题满分10分)如图,在长方体1111ABCD A B C D -中,12,3,4AB AD AA ===,点,E F 分别为棱1,AB DD的中点,(1)求证:1C F ⊥平面BCF ;(2)求直线1C F 与平面1DEC 所成角的正弦值.18.(本题满分12分)已知数列{}n a 满足11a =,点()*111,n n n N a a +⎛⎫∈⎪⎝⎭在直线210x y -+=上.(1)求证:数列11n a ⎧⎫+⎨⎬⎩⎭是等比数列,并求出{}n a 的通项公式;(2)求满足11635n a ≤≤的n 的取值构成的集合.19.(本题满分12分)已知动点P 与两个定点()()1,0,4,0A B 的距离的比是2.(1)求动点P 的轨迹C 的方程;(2)直线l 过点()2,1,且被曲线C 截得的弦长为3,求直线l 的方程.20.(本题满分12分)已知等差数列{}n a 前n 项和为n S ,满足343,10a S ==.数列{}n b 满足12b =,*112,n n n nb a n N b a ++=∈.(1)求数列{}{},n n a b 的通项公式;(2)设数列{}nc 满足()*1(1)32,n n n n n c n N a b +-+=∈,求数列{}n c 的前n 项和n T .21.(本题满分12分)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,底面ABCD 为正方形,2,,AB PA E F ==分别为,PB PD 的中点.(1)求平面CEF 与底面ABCD 所成角的余弦值;(2)求平面CEF 与四棱锥P ABCD -表面的交线围成的图形的周长.22.(本题满分12分)已知双曲线C 的中心为坐标原点,上顶点为()0,2,离心率为2.(1)求双曲线C 的渐近线方程;(2)记双曲线C 的上、下顶点为12,,A A P 为直线1y =上一点,直线1PA 与双曲线C 交于另一点M ,直线2PA 与双曲线C 交于另一点N ,求证:直线MN 过定点,并求出定点坐标.2023学年第一学期金华卓越联盟12月阶段联考高二年级数学参考答案命题人:东阳二中吕夏雯陆琳琳;审题人:汤溪中学张拥军一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.D 【解析】242pp =⇒=,又抛物线开口向下,所以抛物线的方程为28,D x y =-正确.2.C 【解析】()()311201a a a a -⋅+⋅-=⇒=或1,C 2a =正确.3.C 【解析】2486616,4,C a a a a ⋅==∴=±正确.4.A 【解析】1111111111111212,,3333AD AA A D A D A B AC AD AA A B AC =+=+∴=++又111111111,,,2263A B a AC b AA c AD a b c ===∴=++ ,A 正确.5.D 【解析】()()120222022101110121011101220221011002a a S a a a a +==+>⇒+>()1202320231012101220232023002a a S a a +==<⇒<,则10110a >所以数列{}n a 单调递减,{}n S 中1011S 最大.D 正确.6.B 【解析】圆上3个点到直线的距离是1,则圆心到直线的距离应是1,12aa a -∴=-,则2a =,圆1C 的圆心为()2,0,半径是2,圆2C 的圆心为(,半径是1,则12C C =,所以两圆的位置关系是相交.B 正确.7.D 【解析】圆心()0,4C ,取双曲线的左焦点()224,0,1,6F PQ QC QF QF ≥-=+ ,则()22216555PQ QF QC QF QC QF CF +≥-++=++≥+=PQ QF ∴+的最小值为5+,D 正确.8.A 【解析】平面α的法向量()1,1,2n =-,在平面α上任取一点()1,0,1A -,则()4,1,0QA =- ,556A 66QA n d n ⋅== 正确.二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项是符合题目要求的.全部选对的得5分,部分选对的得2分,有选错的得0分.9.ACD 【解析】()1,4,1a b +=- ,选项A 正确,a b λ≠ ,选项B 错误;()()2122210a b -⋅+⋅+⋅-=∴⊥选项C 正确;()12324,2,4cos ,23236a b a a b -=--∴->=⋅,选项D 正确,正确答案是A.C.D 10.ABD 【解析】直线():2220l m x y y +-+-=,所以恒过定点()1,1.选项A 正确;因为定点()1,1在圆C 内,所以直线l 与圆C 恒有两个公共点.选项B 正确;l 被圆C 截得的最短弦长2516-=C 错误;当1m =-时,:0l x y -=,点P 到直线l 的距离的最大值是25522+=+,选项D 正确.正确答案是A.B.D11.ABD 【解析】当2n a n n =+,则11n a n n =+,所以()221322n n n n n b +++==,选项A 正确;已知12311123n a a a a n n++++= ,当1n =时,11a =,当2n ≥时,12311111231n a a a n n -++++=-- ,则(11,1n n a a n n n=∴==时也成立),所以{}n a 为等差数列,选项B 正确;已知123111123n a a a a n n++++=+ ,当1n =时,12a =,当2n ≥时,1231111231n a a a a n n -++++=- ,则(11,1n n a a n n n=∴==时不成立),所以{}n a 不是等差数列,选项C 不正确;已知123111223n n a a a a n++++= ,当1n =时,12a =,当2n ≥时,112311112231n n a a a a n --++++=- ,则1112,2(1n n n n a a n n n--=∴=⋅=时不成立),所以12,1;2,2n n n a n n -=⎧=⎨⋅≥⎩当1n =时,12S =,1n =时,12112,222322n n a S n -==+⋅+⋅++⋅ ()2122222122n nn S n n -=⋅+⋅++-⋅+⋅ ()()22314122022222212212n n n nnn S n n n ----=++++-⋅=+-⋅=-⋅-- 所以()122,1nn S n n =-⋅+=时也成立,选项D 正确.正确答案是A.B.D 12.CD【解析】设直线:1l x my =-,联立方程组224,4401y x y my x my ⎧=-+=⎨=-⎩,则121244y y m y y +=⎧⎨=⎩,选项A 不正确;221212144y y x x =⋅=,所以()121244114559AF BF x x x x +=+++=++≥=当且仅当2142x x ==时等号成立,所以4AF BF +的最小值为9,选项B 不正确;()11,D x y -,设:l x ny t =+,联立方程组224,440y x y ny t x ny t ⎧=--=⎨=+⎩,则121244y y my y t -+=⎧⎨-=-⎩,所以1t =,即直线BD 过点F ,选项C 正确;对于D 选项,()()22111,,1,MB x y MD x y =+=+-,22121212114214440MB MD x x x x y y m m ∴⋅=+++-=+-++=+>,选项D 正确.正确答案是C.D三、填空题:本题共4小题,每题5分,共20分.【解析】()1,2,1,MN MN =-∴==.14.23π【解析】圆C :22(2)1x y +-=,2,63COB COA ACB ππ∠∠∠∴==∴=,故劣弧长23AB π=.15.10【解析】由题意可知三角形的面积构成首项为12,公比为12的等比数列,12311122110231,1012102412nnn a a a a n ⎛⎫⎛⎫- ⎪ ⎪ ⎪⎝⎭⎝⎭∴+++==-=∴=-.16.9【解析】如图,过1F 作12F M QF = ,连接2MF ,因为122PF QF = ,所以12260F PF PF Q ∠∠==,设2QF t =,则11222,,22,2PF t MF t PF a t MF a t ===-=-,在2PMF 中,222222||||PM PF PM PF MF +-=,即22222294846644t a at t at t a at t +-+-+=-+,化简得1210859,,99a t PF a PF a ===,所以1006480221299c t a ==,所以离心率219c a =.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.【解析】(1)方法一:因为F 是1DD 的中点,所以111112,D F D C FD DC D FC ==== 和FDC 是等腰直角三角形,所以1145D FC CFD ∠∠==,1C F CF ∴⊥,因为BC ⊥平面111,CDD C C F ⊂平面11CDD C ,所以1BC C F ⊥,,BC CF ⊂平面11BCF C F ∴⊥平面BCF方法二:以D 为原点,DA 所在直线为x 轴,DC 所在直线为y 轴,1DD 所在直线为z 轴建立空间直角坐标系,()()()()()()()110,3,0,2,3,0,0,0,2,0,2,4,2,0,0,0,2,2,0,2,2,C B F C CB CF C F ==-=--所以111440,0,C F CF C F CB C F ⋅=-=⋅=∴⊥平面BCF ;(2)()()13,1,0,0,2,4DE DC == ,设平面1DEC 的法向量为(),,n x y z =,则130240DE n x y DC n y z ⎧⋅=+=⎪⎨⋅=+=⎪⎩ ,所以取()2,6,3n =- ,又()10,2,2C F =--,11132sin cos ,14||C F n C F n C F n θ⋅∴==== .直线1C F 与平面1DEC所成角的正弦值为14.18.【解析】(1)由已知得111212121,21111n n n n nn a a a a a a ++++=+∴==++,且11120a +=≠,所以数列11n a ⎧⎫+⎨⎬⎩⎭是等比数列,112n n a ∴+=,则1;21n n a =-(2)因为11635n a ≤≤,所以111,52163,626463215n n n ≤≤≤-≤∴≤≤-,得2log 66n ≤≤,又因为*n N ∈,所以n 的取值构成的集合是{}3,4,5,6.19.【解析】(1)设点(),P x y=,化简得2210210x y x +-+=,所以动点P 的轨迹C 的方程为22(5)4x y -+=;(2)由(1)可知点P 的轨迹C 是以()5,0为圆心,2为半径的圆,可计算得圆心()5,0到直线l的距离1d ==,①当直线l 的斜率不存在时,圆心到直线l 的距离是3,不符合条件,②当直线l 的斜率存在时,设直线l 的方程为()12y k x -=-,即210kx y k --+=,所以1d ==,化简得229611k k k ++=+,解得0k =或34k =-,所以直线l 的方程是1y =或34100x y +-=.20.【解析】(1)设数列{}n a 的公差为1123,4610a d d a d +=⎧∴⎨+=⎩,解得11,1,n a d a n ==∴=.()11211,2n n n n b n b n b b n n ++++=∴= ,且121b =,所以n b n ⎧⎫⎨⎩⎭是等比数列,2,2n nn n b b n n∴=∴=⋅(也可用累乘法求{}n b 的通项公式)(2)()()()()1111(1)3211(1)(1)(1)12212212n n n nn n n n n n n c n n n n n n ++++⎛⎫-+--==-+=- ⎪ ⎪+⋅⋅+⋅⋅+⋅⎝⎭,()1111(1)212n n n T n ++∴=---+⋅21.【解析】(1)以A 为原点,以AB 所在直线为x 轴,AD 所在直线为y 轴,AP 所在直线为z 轴建立空间直角坐标系,平面ABCD 的法向量为()0,0,1m =,()()()()()2,2,0,1,0,1,0,1,1,1,2,1,1,1,0C E F CE EF =--=- ,设平面CEF 的法向量为(),,n x y z = ,所以200CE n x y z EF n x y ⎧⋅=--+=⎪⎨⋅=-+=⎪⎩ ,所以取()1,1,3n = ,所以cos ,||||11m n m n m n ⋅〈〉=== ,所以平面CEF 与底面ABCD所成角的余弦值为11;(2)由对称性可知平面CEF 与棱PA 交于一点,设交点()()40,0,,1,0,1,1330,3Q t QE t QE n t t =-⋅=+-=∴= ,103QE QF ∴==又CE CF ==,所以围成的图形的周长为210263+22.【解析】(1)设双曲线方程为22221(0,0)y x a b a b-=>>,由上顶点坐标可知2a =,则由52c e a ==可得225,1c b c a ==-,双曲线的渐近线方程为2y x =±.(2)由(1)可得()()120,2,0,2A A -,设()()1122,,,M x y N x y ,设直线MN 的方程为y kx m =+,与2214y x -=联立可得()2224240k x kmx m -++-=,且()22Δ1640k m =-+>,则212122224,44km m x x x x k k --+==--,()2212122248,44k m m y y y y k k -+-∴+==--设()1213,1,,A P A P P t k k t t ∴=-=,2111233,4A P A P MA MA MA k k k k k ∴=-=-⋅= ,得2212MA NA k k ⋅=-2221221222441641612,124y y k m m k x x m ++---+-∴⋅=-=--,化简得22(2)3,4m m +=-。
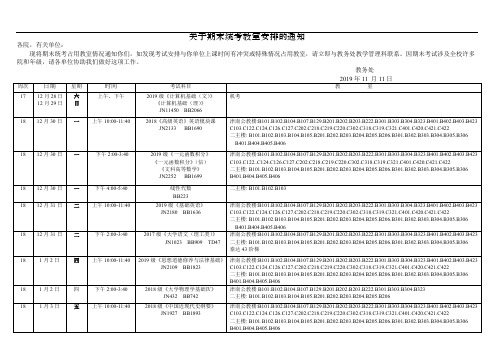
关于期末统考教室安排的通知
18
12月31日
二
下午2:00-3:40
2017级《大学语文(理工类)》
JN1023 BB909 TD47
津南公教楼:B101.B102.B104.B107.B129.B201.B202.B203.B222.B301.B303.B304.B323.B401.B402.B403.B423
B401.B40430日
一
下午4:00-5:40
线性代数
BB223
二主楼: B101.B102.B103
18
12月31日
二
上午10:00-11:40
2019级《基础英语》
JN2180 BB1636
津南公教楼:B101.B102.B104.B107.B129.B201.B202.B203.B222.B301.B303.B304.B323.B401.B402.B403.B423
C103.C122..C124.C126.C127.C202.C218.C219.C220.C302.C318.C319.C321.C401.C420.C421.C422
二主楼: B101.B102.B103.B104.B105.B201.B202.B203.B204.B205.B206.B301.B302.B303.B304.B305.B306
二主楼: B101.B102.B103.B104.B105.B201.B202.B203.B204.B205.B206.B301.B302.B303.B304.B305.B306
泰达43阶梯
18
1月2日
四
上午10:00-11:40
2019级《思想道德修养与法律基础》
JN2109 BB1823
(整理)高等数学大纲(物理类)

《高等数学》教学大纲课程名称:高等数学适用层次、专业:理科、工科各专业学时:320学时学分:20学分课程类型:通识教育平台课课程性质:必修课一、课程的教学目标与任务高等数学是理、工、管等相关专业的第一基础课,特别是对物理类各专业,更是显得尤为重要,它是为培养我国社会主义现代化建设所需要的高质量专门人才服务的。
课程的学习情况事关学生后继课程的学习,事关学生学习目标的确定以及学生未来的走向。
在这一课程学习结束后,学生才能进入各相关课程的学习阶段。
高等数学是四年大学学习开始必须学好的基础理论课程。
课程的基础性、理论性强,与相关课程的学习联系紧密,是全国硕士研究生入学考试统考科目,关系到学生综合能力的培养,课程的学习情况直接关系到学校的整体教学水平。
本课程的教学目标:1.熟悉和掌握高等数学研究问题的基本方法,弄清具体与抽象,特殊与一般,有限与无限等辩证关系,学习科学的思想方法,以利于辩证唯物主义世界观的培养与形成;2.掌握高等数学的基本知识,基本理论与基本技能,提高抽象思维,逻辑推理与运算能力,为后继课程和进一步获得数学知识奠定必要的数学基础;3.培养学生的综合运用知识分析和解决问题的能力,使学生充分认识到高等数学在自然科学与社会科学中的广泛应用。
二、课程讲授内容及基本要求(一)函数与极限(总学时:16学时;理论学时:16;实验学时:0)1.具体内容:函数;极限;连续函数。
2. 基本要求:(1)理解映射、函数、复合函数的概念;理解极限的概念(对极限的ε-N,ε-δ定义可在学习过程中逐步加深理解,对于给出ε求N或δ不作过高要求。
);理解函数在一点连续的概念。
掌握基本初等函数的性质及其图形,掌握极限的四则运算准则;会用两个重要极限求极限;会建立简单实际问题中的函数关系式;(2)了解函数的奇偶性、单调性、周期性和有界性;了解反函数的概念;了解两个极限存在准则(夹逼准则和单调有界准则);了解无穷小、无穷大以及无穷小阶的概念,会用等价无穷小求极限;了解间断点的概念,并会判别间断点的类型;了解初等函数的连续性和闭区间上连续函数的性质(介值定理和最大、最小值定理)。
邵阳学院2012上期末考试安排表(更新)

1A208 蒋胜晖
71-140 1B102 赵伟科 271-309 1B301
1B604 杨甲山 1C203 谢文平 1C204 袁琳
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4) 2日9:00-11:00 大学英语(4)
51-104 1C604 张亚平 1B104 胡建明 1C101 黄大川 1C602 唐爱英 1A309 刘中文 1C304 刘让强 1A102 陈日升 1A401 刘期努 1A409 袁晓军 1B402 李丹 1C102 袁爱国 1A609 谢云辉 1B201 罗跃平 1C504 1A402 李中 黄娜
高数上册期末试卷(含答案)

一、填空题(每小题2分,共20分)1. 0,2.21,3. t −,4. 4,5. )41 0(]41 0[,或,,6. (0, 2), 6. C x x ++arctan 3)1(分给缺C ,8. 0,9. 34−,10. 23.二、试解下列各题(每小题6分,共24分)1. xx x x x x 4sin 3553lim 22++=∞→原式 2分 444sin 3553lim20⋅⋅++=→xx x x x 4分 5124153=⋅⋅=6分 2. )1(sin )]1sin(sin ['⋅−='xx y 2分)1(1cos )]1sin(sin ['⋅−=xx x 3分x x x 1cos )1sin(sin 12=4分dx x x x dx y dy 1cos )1sin(sin 12='= 6分3. x x x d )111(22+−=⎰原式 1分 dx x dx x dx x ⎰⎰⎰+−++=21)1111(21 3分 .111ln 21C xx x +−−+= 6分 dx xx⎰+=422cos 2cos 1 4.π原式 2分⎰+=42)1(sec 21πdx x 3分40)(tan 21πx x += 5分 821π+= 6分三、试解下列各题(每小题7分,共28分)42021lim 1.x e x x x −→−−=原式 2分30422lim 2x xe x x x −→+−= 4分 22012422lim 22x e x e x x x −−→−+−= 5分x e x xe x x x 24812lim 2230−−→+−= 6分21−= 7分)(02/1 4422x x x e x ++−=−或用泰勒公式3分, 答案2分2. )(x df x ⎰=原式 1分dx x f x xf ⎰−=)()( 3分C xxx x x +−'=ln )ln ( 5分 C xx+−=ln 21 7分 分给求出注:2 ln 1)ln ()( xxx x x f −='= 1 2 1 0 1 3.==−====−t x t x dt dx t x 时,,时,且,则,令 1分 dt t f ⎰−=11 )(原式 2分dt tdt e t ⎰⎰+++=−1 0 01 11 114分 1001)1ln()]1ln([t e t t +++−=− 6分)1ln(e += 7分⎪⎩⎪⎨⎧<+≥=−−1 111 1)1(1x e x x x f x ,,或 2分 dx xdx e x ⎰⎰−+=2 1 10 1111+原式 4分下面同上}2 1 2{ }1 1 1{ 4.21−=−=,,,,,两平面的法向量为n n 1分所求直线的方向向量2111−−=kj s 2分}3 4 1{,,= 4分334112−=+=−z y x 对称式方程为6分 ⎪⎩⎪⎨⎧+=+−=+= 3341 2t z t y t x 参数方程为 7分四、应用题(每小题7,共21分)分 其体积为 则圆柱体的底面半径,设内接圆柱体的高为3 20)4()2( 1.2222R h h R h V hR r h <<−=−=π分4 )43(22h R V −='πR h V 3320=='得:唯一驻点 令 5分 023<−=''h V π又,圆柱体体积最大时故当,332R h = 7分dx x x dx x x V ⎰⎰−+−=2422422)cos (sin )sin (cos 2.πππππ3分dx x dx x ⎰⎰−=2442cos 2cos πππππ4分2442sin 22sin 2πππππxx−=5分π= 7分)1(3d 3.12 C x x y y +=''='⎰1分232632−==−x y y x 得又由 2分 得 代入)1(32)2,0(='∴−y 3分 '=+y x 332 4分23232d )323(C x x x x y ++=+=∴⎰5分.2322)2,0(31−+=∴−=−x x y C ,代入得再将 7分。
2024届广东省衡水金卷高三上学期12月联考数学试题及答案
2024届高三年级12月份大联考数学试题本试卷共4页,22题。
全卷满分150分。
考试用时120分钟。
注意事项:1.答题前,先将自己的姓名、准考证号填写在答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接写在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{A x y ==,{}29B x x =>,则()R A B = ð( )A.[3,2]-- B.(,3)(2,)-∞--+∞ C.[2,3]- D.(,2)(3,)-∞-+∞ 2.已知复数i 4i 1z =-,则z 在复平面内对应的点的坐标为( )A.41,1717⎛⎫ ⎪⎝⎭B.4,17⎛ ⎝C.41,1717⎛⎫- ⎪⎝⎭D.41,1717⎛⎫-- ⎪⎝⎭3.已知(1,3)a = ,(2,5)b = ,则向量a 在向量b 上的投影向量为()A.51,2⎛⎫ ⎪⎝⎭ B.3485,2929⎛⎫ ⎪⎝⎭ C.24,33⎛⎫ ⎪⎝⎭ D.2,15⎛⎫ ⎪⎝⎭4.已知函数()f x 是定义在R 上的奇函数,当0x >时,()1f x ax =+,若(2)5f -=,则不等式1()2f x >的解集为()A.11,0,26⎛⎫⎛⎫-∞- ⎪ ⎪⎝⎭⎝⎭B.11,00,26⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭C.11,,26⎛⎫⎛⎫-∞-+∞ ⎪ ⎪⎝⎭⎝⎭D.11,0,26⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭5.过抛物线,22(0)y px p =>的焦点F 作直线交抛物线于(1A x ,(2,B x -两点,则p =( )A.1B.2C.3D.46.复印纸按照幅面的基本面积,把幅面规格分为A 系列、B 系列、C 系列,其中A 系列的幅面规格为:0A ,1A ,2A ,3A ,…,8A ,所有规格的纸张的长度(以x 表示)和幅宽(以y 表示)的比例关系都为::1x y =;将0A 纸张沿长度方向对开成两等分,便成为1A 规格;将1A 纸张沿长度方向对开成两等分,便成为2A 规格;…,如此对开至8A 规格.现有0A ,1A ,2A ,3A ,…,8A 纸各一张,已知0A 纸的幅面面积为21m ,则0A ,1A ,2A ,3A ,…,8A 这9张纸的面积之和是()A.2511m 256 B.2511m 512 C.2255m 128 D.2255m 2567.已知()0.0,P x y 是l :60x y +-=上一点,过点P 作圆O :2216x y +=的两条切线,切点分别为A ,B ,则当直线AB 与l 平行时,直线AB 的方程为()A.4x y += B.8x y +=C.3316x y += D.338x y +=8.函数2()2ln f x x x x=-+,若21()0f m f n ⎛⎫+= ⎪⎝⎭,则213m n +的最小值为( )A. B.4 C. D.1二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.一组互不相等的样本数据1x ,2x ,…,21n x -,其平均数为x ,方差为2s ,极差为m ,中位数为n ,去掉最大值后,余下数据的平均数为x ',方差为2s ',极差为m ',中位数为n ',则下列选项一定正确的有()A.n n '= B.x x '> C.22s s '< D.m m '=10.函数()sin()f x A x ωϕ=+(0A >,0ω>,π2ϕ<)的部分图象如图所示,将函数()f x 的图象上所有点的横坐标变为原来的3倍,纵坐标变为原来的2倍,然后向左平移3π4个单位长度,得到函数()g x 的图象,则( )A.1A =B.()g x 的解析式为2π2sin 33y x ⎛⎫=+ ⎪⎝⎭C.7π,02⎛⎫ ⎪⎝⎭是()g x 图象的一个对称中心D.()g x 的单调递减区间是11π5π3π,3π44k k ⎡⎤--⎢⎥⎣⎦,k ∈Z 11.若[lg ]M ,(lg )M 分别为lg M 的整数和小数部分,则下列不等式一定成立的有()A.0.0013log 2.999e < B.[lg ](lg )M M ≥C.42log 3log π1>- D.23log 3log 5>12.棱长为6的正四面体ABCD 的四个顶点均在球O 的表面上,若点M 为球面上的任意一点,则()OA OB OB OA OM ⋅-+⋅ 的取值可以为( )A.2-B.3C.5D.三、填空题:本题共4小题,每小题5分,共20分.13.已知函数2()tan (0)1a f x x a a ϕ⎛⎫=+> ⎪+⎝⎭的最小正周期为2π,则a =________.14.圆锥侧面展开图为圆心角为直角,半径为2的扇形,则圆锥的体积为________.15.在7()ax y z -+的展开式中,记m n k x y z 项的系数为(,,)f m n k ,若70(3,2,2)9f =,则a 的值为________.16.已知双曲线C :22221(0,0)x y a b a b -=>>的左、右焦点分别为1F ,2F ,倾斜角为π3的直线2PF 与双曲线C 在第一象限交于点P ,若1221PF F F PF ∠≥∠,则双曲线C 的离心率的取值范围为________.四、解答题:本题共6小题,共70分.解答应写出必要的文字说明,证明过程或演算步骤.17.(本小题满分10分)已知数列{}n a 为等差数列,数列{}n b 为等比数列,212b b -=,326b b -=.(1)求数列{}n b 的通项公式;(2)设数列{}n a 的前n 项和为n S ,若63S b =,124S b =,求n S .18.(本小题满分12分)已知在ABC △中,内角A ,B ,C 所对的边分别为a ,b ,c ,且22cos 2cos cos c B b B C a -=+.(1)求B ;(2)若AB ,3a =,求ABC △的周长.19.(本小题满分12分)身高体重指数(BMI )这个概念,是由19世纪中期的比利时通才凯特勒最先提出,它的计算公式如下:身高体重指数(BMI )=体重(kg )÷身高(m )的平方.成人的BMI 数值低于18.5,则体重过轻,在[18.5,24)则正常;在[24,28)为过重,在[28,32)为肥胖,不低于32为非常肥胖,且专家指出最理想的体重指数是22.某科研小组设计了一套方案;并在两类人群中进行对比实验,其中科学饮食组采用科学饮食方案,对照组采用随意饮食方案.半年后,分别在两组中各随机选取100人,BMI 都分布在[]16,36内,按BMI 分成5组进行统计:[16,20),[20,24),[24,28),[28,32),[32,36).统计后分别制成如下的频率分布直方图.科学饮食组对照组(1)求a ,b ,并估计科学饮食组的80%分位数(结果精确到小数点后两位);(2)现采用分层抽样的方法从对照组选取的100人中抽取25人,再从这25人中随机抽取2人,记其中“肥胖”(不含非常肥胖)的人数为X ,求X 的分布列与数学期望.20.(本小题满分12分)如图,AE ⊥平面ABCD ,CF ⊥平面ABCD ,AD AB ⊥,//AD BC ,3AB AD ==,6AE BC ==.(1)求证://DE 平面BCF ;(2)试求CF 为何值时,直线CE 与平面BEF .21.(本小题满分12分)函数2()ln f x x x=+在4x =处的切线方程为()y h x =.(1)求()h x ;(2)已知113a <<,过(,)ab 可作()f x 的三条切线,证明:()()h a b f a <<.22.(本小题满分12分)已知椭圆C :22182x y +=,O 为坐标原点,若椭圆C '与椭圆C 的离心率相同,焦点都在同一坐标轴上,椭圆C '的长轴长与椭圆C 的长轴长之比为1:(1)求椭圆C '的方程;(2)已知点P 在椭圆C 上,点A ,B 在椭圆C '上,若OP OA OB =+ ,则四边形OAPB 的面积是否为定值?若是,求出定值;若不是,请说明理由.。
(完整版)《高等数学》课程教学大纲
《高等数学》课程教学大纲授课专业:通信工程专业学时:136学时学分:8学分开课学期:第1、第2学期适用对象:通信工程专业学生一、课程性质与任务本课程是理、工类专业的专业基础课,通过本课程的学习,要使学生掌握微积分学的基本概念、基本理论和基本运算技能,为学习后继课程和进一步获得数学知识奠定必要的数学基础。
要通过各个教学环节逐步培养学生的抽象思维能力、逻辑推理能力、空间想象能力和自学能力,还要特别注意培养学生的熟练运算能力和综合运用所学知识去分析解决问题的能力。
二、课程教学的基本要求通过本课程的学习,学生基本了解微积分学的基础理论;充分理解微积分学的背景思想及数学思想。
掌握微积分学的基本方法、手段、技巧,并具备一定的分析论证能力和较强的运算能力。
能较熟练地应用微积分学的思想方法解决应用问题。
三、课程教学内容高等数学(上)第一章函数、极限与连续(10学时)第二章导数和微分(12学时)第三章微分中值定理与导数的应用(12学时)第四章函数的积分(16学时)第五章定积分的应用(8学时)第六章无穷级数(10学时)高等数学(下)第七章向量与空间解析几何(6学时)第八章多元函数微分学(14学时)第九章多元函数微分学的应用(10学时)第十章多元函数积分学(I)(16学时)第十一章多元函数积分学(II)(10学时)第十二章常微分方程(12学时)四、教学重点、难点重点:极限的概念与性质;函数连续性的概念与性质;闭区间上连续函数的性质;微分中值定理与应用;用导数研究函数的性质;不定积分、定积分的计算;微积分学基本定理;正项级数敛散性的判定;幂级数的收敛定理;二元函数全微分的概念及性质;计算多元复合函数的偏导数与微分;隐函数定理及应用;重积分、曲线积分与曲面积分的计算;曲线积分与路径的无关性。
难点:极限的概念与理论;微分中值定理的应用;一元函数的泰勒定理;二元函数的极限;计算多元复合函数的偏导数与微分;对坐标的曲面积分的概念及计算;高斯公式;斯托克斯公式。
期末考试安排
2
河南理工大学2014~2015学年第一学期期末考试安排表
人 数 主考 教师 各 班 所 在 考 场 备注 1班 2306 3607 3212 3212 2班 3班 4班 5班 6班 7班 8班
考试课程
考试时间
地球科学 地质单12 38 煤及煤层气地质学 水污染控制工程(上) 环境12 55
1月21日下午 1月23日上午 1月21日下午
符勇 潘结南 李成杰
人 数 主考 教师 宋党育 齐永安 符勇 潘结南 各 班 所 在 考 场 备注 1班 2406 2406 2班 2406 2406 3班 2407 2407 4班 2407 2407 5班 2409 2409 6班 7班 8班
考试课程
考试时间
地球科学 勘查12 150 煤及煤层气地质学
1月21日下午 1月23日上午
各学院、处、室及学生班级: 本学期期末考试定于2015年1月20日开始,1月24日结束。现将期末考试安排、考试要求、考试课程及相关事宜印发给你们,请认真组织实施。 一、考试安排: 考试时间:上午:8:30~10:30 下午:15:00~17:00 考试地点:本次期末考试课程安排在1号教学楼、2号教学楼、3号教学楼、理化楼、电气楼、经管楼和计算机楼进行。 二、考场要求: ①考生必须携带考试卡,依照监考老师摆放考试卡的指定位置就座,严格按《河南理工大学学生考场规则》参加考试。 ②主考教师提前15分钟将考场报告单和试卷一并带到考场,交予监考教师。 ③监考教师应认真履行监考职责,严格按《河南理工大学监考守则》进行监考,提前15分钟到达考场接收试卷,用考试卡随机安排考生座位。考 试结束后认真填写考场报告单,考场报告单一式两份,一份交主考教师,一份交教务处教务科。 三、考试组织: ①本安排表中所有课程均为期末统考课程,试卷印制由主考教师所在学院负责统一安排。公共课程考试由开课学院统一组织教师于开考前15分钟 将试卷和考场报告单送到考场。专业课程考试由主考教师于开考前15分钟将试卷和考场报告单送到考场。 ②本安排表中未列出但需在最后一周考试的课程,由任课教师按日常课程考试程序组织考试。 ③各学院应严格按照《河南理工大学课程考试条例》和《河南理工大学课程考试试卷保密管理暂行规定(修订)》组织实施本次考试。 四、评卷: 2013、2014级的《高等数学》、《大学英语》、《大学物理》、《大学计算机基础》的评卷工作由开课学院统一安排教师在指定地点采取流水作 业的方式进行,其余课程的评卷工作由各学院安排教师在教研室进行。 五、任课教师请于考试后4天内在网上提交成绩并打印成绩单,成绩单一式两份,经任课教师签名后,一份交学院教学科研办公室,一份交教务处 教务科。同时将教学档案归档。 六、注意事项: 本学期所有课程的试卷均按教务处主页上“下载园地”中的试卷模板印刷,期末考试的考试类型都应是闭卷,且应注明。
海南大学《高等数学》2023-2024学年第一学期期末试卷
海南大学《高等数学》2023-2024学年第一学期期末试卷函授站 姓名 学号 成绩一、选择题(每小题2分,共20分)1、下列函数中,( )是偶函数。
A. x x x f sin )(3=B. 1)(3+=x x fC. x x a a x f --=)(D. x x x f sin )(2= 2、下列各对函数中,( )中的两个函数相等.A . 2)1ln(xx x y -=与x x g )1ln(-= B . 2ln x y =与x g ln 2= C . x y 2sin 1-=与x g cos = D . )1(-=x x y 与)1(-=x x y3、=++-∞→)33)(1(16lim 2n n n n ( ) A.1 B.2C.6D.∞4、下列等式中成立的是( )22sin lim .=∞→x x a x 112)12sin(lim .0=++→x x b x1)sin(sin lim .0=→x x c x 1sin lim .1=→x x d x5、下列变量中,为无穷小量的是( )A .()11n nn +-→∞() B x →+0) C .2log 0x x +→() D .2222x x x +→-() 6、下列变量中,是无穷小量的为( ) A. )0(1ln +→x xB. )1(ln →x xC. )0(e 1→-x x D. )2(422→--x x x 7、当=k ( )时,⎩⎨⎧<+≥+=0203)(2x k x x x x f 在0=x 处连续。
A. 0 B. 3C. 2D. 18、极限=∆-∆+→∆xx x x x 000sin )sin(lim ( )A. 1B. cos x 0C. sin x 0D.不存在9、下列等式成立的是( ) A. B.C. D.10、下列凑微分正确的是( )。
A .)1(ln x d xdx = B.)(sin )11(2x d dx x=- C. )1()(2x d dx x -=- D. )(x d dx x =二、填空题(每小题3分,共15分)1、设6)(+=x x f ,则)1)((+x f f =2、已知3)(,8ln )(-=+=x x g x x f ,则=)]([x g f _______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华南理工大学广州学院
关于12级《高等数学》(上册•理工类)期末统考的通知
通知要点
一、
考试的性质、目的与时间; 二、
考试的重点内容与要求; 三、
考试的形式、试卷结构与题型示例。
一、 考试的性质、目的与时间
本校《高等数学》(上册)期末统考是检查本课程教学状况、评定学生学习成绩的常规考试。
它是根据教育部颁发的高等数学“教学基本要求”及本校制定的教学大纲命题的。
目的是测定学生对本课程的基本概念、基本理论和基本运算技能掌握的程度,以及运用所学的知识分析问题和解决问题的能力,促进本课程教学质量的提高。
考试时间定于2013年1月11日上午9:00-11:00。
二、考试的重点内容与要求
考试的范围是教材的第一、二、三、四、五、六章(第七章列入第二学期讲授,本次不考)。
以下分三个部分明确考试的重点与要求:
1. 函数、极限与连续
理解函数的概念、会求函数的定义域和函数值。
了解函数的几种特性。
了解分段函数、复合函数和初等函数的概念。
掌握16个函数及一些常见函数的图形(16个函数是
1
y C y x y y x
μ====、、、e a ln log ;x x a y y y x y x ====、、、 sin cos tan cot ;
y x y x y x y x ====、、、arcsin arccos arctan arccot y x y x y x y x ====、、、)。
理解数列与函数极限的概念(含N ε-定义,但对给出ε找N 不作要求)。
理解左、右极限的概念、以及极限存在与左右极限之间的关系。
理解无穷小与无穷大的概念及两者的关系,理解无穷小的性质。
掌握极限的四则运算法则。
了解复合函数的极限运算法则。
会用两个重要极限求极限。
了解无穷小的阶的概念,会用等价无穷小求极限。
理解函数在点0x 处连续与间断的概念。
了解初等函数的连续性。
理解闭区间上连续函数的性质(最值定理、零点定理)。
2. 导数与微分、微分中值定理与导数的应用
理解可导与导数的概念及导数的表达式。
理解左导数与右导数的概念。
掌握导数的几何意义(含曲线的切线方程与法线方程)。
掌握函数可导性与连续性的关系。
记16个函数的求导公式及函数的和、差、积、商的求导法则。
掌握复合函数的求导法则。
会求高阶导数、会求隐函数及由参数方程所确定的函数的一阶导数。
了解可微与微分的概念。
掌握基本初等函数的微分公式与微分运算法则。
了解一阶微分形式的不变性。
会求函数的一阶微分。
熟悉罗尔定理、拉格朗日中值定理得内容(对两个定理的分析证明不作要求)。
会用洛必达
法则求未定式的极限。
掌握用导数判定函数的单调性及曲线的凹凸性的方法。
会求曲线的拐点。
会用函数的单调性证明简单的不等式。
理解函数的极值与最值的概念,掌握求函数的极值和最值的方法,会解有关最值的应用题。
3. 不定积分、定积分及其应用
理解原函数与不定积分的概念,掌握不定积分的性质,记11个基本积分公式(11个公式的
左端是:d ,k x ⎰d ,x x μ⎰1d ,x
x ⎰21d ,1x x +⎰,x cos d ,x x ⎰sin d ,x x ⎰21d ,cos x x ⎰
21d ,sin x x ⎰e d ,x x ⎰
d x a x ⎰)。
掌握四种积分法(直接积分法、第一类换元法、第二类换元法及分部积分法)。
理解定积分的定义、几何意义及定积分的性质(含“两点补充规定”)。
会用积分上限函数
及其导数的定理求函数的导数。
会用牛顿—莱布尼茨公式。
熟练掌握定积分的换元法与分部积分法。
会求无穷限的反常积分。
掌握定积分应用的元素法,会求平面图形的面积(直角坐标情形)及旋转体的体积。
考生应按上述指定的重点内容与课本的相关例题及教师布置的习题结合起来,运用相关内
容的基本概念、基本理论和基本方法指导做题;反之又应从做题的过程中熟练掌握所指定的重点内容。
考生还应注意各部分知识间的联系,提高综合分析问题和解决问题的能力。
三、考试的形式、试卷结构与题型示例
1.
考试形式为闭卷、笔试。
满分100分,考试时间为120分钟。
2.
试卷内容比例:函数、极限与连续约20%,一元函数微分学约40%,一元函数积分学约40%. 3.
试卷题型比例:填空题15%,单项选择题15%,计算题49%,解答题21%. 4.
题型示例
一、填空题(本大题共5小题,每小题3分,共15分。
把答案写在横线上)
1.函数1y x
=
+的定义域是 。
2.0sin 5lim 2x x x →= 。
3.设()f x 可导,[]ln ()y f x =,则dy = 。
4.不定积分
⎰= 。
5.反常积分
60
x e dx +∞-⎰= 。
二、单项选择题(本大题共5小题,每小题3分,共15分)
1.设2,01(),,12
x x f x x x ⎧<≤=⎨<<⎩在点1x =处必定 ( ) A .连续但不可导 B .连续且可导
C .不连续但可导
D .不连续,故不可导
2.曲线y 在点4x =处的切线方程是 ( ) A .114y x =- B .112
y x =+ C .114y x =+ D .124
y x =+ 3.下列函数在区间[1,1]-上满足罗尔定理条件的是 ( )
A .21
x B .3x C .x D .21
1x +
4.设()f x 为连续函数,则下列等式中正确的是
( ) A .()()f x dx f x '=⎰ B .()()d
f x dx f x C dx =+⎰
C .()()d f x dx f x =⎰
D .()()d f x dx f x dx =⎰
5.已知()0232a
x x dx -=⎰,则a =
(
) A .1- B .0 C .1
2 D .1
三、计算题(本大题共7小题,每小题7分,共49分)
1.求极限 ()01
1lim x x x e x x e →---。
2.设函数1sin 2 ,0
(), ,0 x x f x a
bx x +≤⎧=⎨+>⎩在点 0x =处可导,求,a b 的值。
3.设参数方程()
1sin cos x t t y t t =-⎧⎪⎨=⎪⎩确定y 是x 的函数,求dy
dx 。
4.设方程2290y xy -+=确定隐函数()y y x =,求d d y
x 。
5.计算定积分
1ln e x xdx ⎰。
6.求不定积分
2arcsin x 。
7.求不定积分
3。
四、解答题(本大题共3小题,每小题7分,共21分) 1.求函数()()23213
f x x x =--的极值。
2.证明不等式:当
0x >
时,1ln(x x ++>
3.如图,在区间[]0,1上给出函数2y x =,问a 为何值时,图中阴影部分的面积1A 与2A 之和最小?
一. 1. 1[,0)(0,)3-+∞ 2. 52 3.()()
f x dx f x ' 4.()322133x C -+ 5.16. 二. 1.A 2.C 3.D 4.D 5.A 三. 1.12 2.1,2a b == 3.cos sin 1sin cos dy t t t dx t t t -=-- 4.y y y x
'=- 5. ()2114e +. 6.()31arcsin 3x C +
7.3221(1)3
x C - 四.1. 极大值()213f =,极小值()20f = 2. 利用函数的单调性可证明之 3. 12
a =。
