4年级奥数几何计数问题例题
四年级 奥数 讲义 246学子 教案库 0410_几何计数

1.小明把他现有的巧克力棒摆成了如图所示的形状,其中每一条小短边代表一个巧克力棒,那么:1)一共有______个巧克力棒;(30)2)这些巧克力棒共构成了________个三角形;(27)3)嘴馋的小明吃掉一个巧克力棒后(图中两端带有箭头的小边),剩下的图形中还有_____个三角形;(22)2.数一数右图中各有多少个三角形:(1)_____个;(2)______个;(38;32)3.如图,是一个5×7的网格,且每一个小格都是边长为1的正方形:1)一共能数出______条线段;(288)2)从中可以数出______个矩形;(420)3)从中可以数出_______个正方形;(85)4)所有矩形(包括长方形和正方形)的面积之和为_______;(2940)5)包含有“※”的矩形共有____个,这其中有____个正方形;(120;20)4.如图所示,共有_____个三角形,其中包含“★”的三角形共有______(20;12)5.数一数右图中有多少个矩形:(1)_______;(2)________;(192;40)6.木板上钉着有16个钉子,形成4行4列的正方形钉阵。
那么用橡皮筋一共能套出_______个正方形,______个三角形;(20;516)7.如图,在一个中国象棋盘中:1)某一个○車出现的走法最多有_____种可能;(1530)2)某一个○马出现的走法最多有_____种可能;(504)(1)(2)(1)(2)1. 数一数右图中共有_______个矩形;(17)2. 如图,一共有_____个三角形;包含有阴影部分的三角形共有________(48;38)3. 图中一共有_____个正方形,一共有______个三角形;(22;76)4. 观察给出的图形,每条线段都是水平或者竖直的,且边界上各个边的长度分别是1厘米、2厘米、3厘米、4厘米,那么: 1)矩形的个数为_______;(100) 2)正方形的个数为_______;(12) 3)所有矩形的面积和为________;(2500)5. 图中10个钉组成的正三角形点阵中,用橡皮筋可套出_________个三角形;(105)6. 右图是一个4×8的矩形网格,每一个小格都是一个正方形,那么:1)包含有“★”的矩形共有______个;(120)2)既包含“★”又包含“※”的矩形有____个;(30)3)只包含“★”或“※”中的某一个符号的矩形有_______个;(132)※★。
(完整版)四年级奥数第一讲_图形的计数问题

第一讲图形的计数问题一、知识点:几何图形计数问题常常没有不言而喻的次序,并且要数的对象往常是重叠交织的,要正确计数就需要一些智慧了.实质上,图形计数问题,往常采纳一种简单原始的计数方法-一列举法.详细而言,它是指把所要计数的对象一一列举出来,以保证列举时无一重复、.无一遗漏,而后计算其总和.正确地解答较复杂的图形个数问题,有助于培育同学们思想的有序性和优秀的学习习惯.二、典例解析:例( 1)数出右图中总合有多少个角解析:在∠ AOB内有三条角分线 OC1、OC2、OC3,∠ AOB被这三条角分线分红 4 个基本角,那么∠ AOB内总合有多少个角呢?第一有这 4 个基本角,其次是包括有 2 个基本角构成的角有 3 个(即∠ AOC2、∠ C1OC3、∠ C2OB),而后是包括有 3 个基本角构成的角有 2 个(即∠ AOC3、∠C1OB),最后是包括有 4 个基本角构成的角有 1 个(即∠ AOB),因此∠ AOB内总合有角:4+3+2+1=10(个)解:4+3+ 2+ 1=10(个)答:图中总合有10 个角。
方法 2:用公式计算:边数×(边数—1)÷ 25 ×( 5-1 )÷ 2=10练一练:数一数右图中总合有多少个角?例( 2 )数一数共有多少条线段?共有多少个三角形?解析:①要数多少条线段:先看线段 AB、AD、AE、AF、AC纵向线段,再看 BC、MN、 GH 这 3 条横向线段:(4×3÷2)×5+(5×4÷2)×3=60(条)②要数有多少个三角形,先看在△ ABC中,被 GH和 MN分红了三层,每一层的三角形同样多,因此只需算出一层三角形个数就能够了。
(5 ×4÷2)×3=30(个)答:在△ ABC中共有线段60 条,共有三角形30 个。
练一练:图中共有多少个三角形?例( 3)数一数图中长方形的个数解析:长边线段有:6× 5÷ 2=15宽边线段有: 4 ×3÷2=6共有长方形: 15×6 = 90(个)答:共有长方形90 个。
四年级上册数学试题-奥数计数模块几何计数问题 全国通用(图片版无答案)

1、数一数图中共有个正方形.
2、下图有()个正方形.
3、数一数,下图中共有个正方形.
4、下图有()条线段.
6、数一数图中共有个三角形.
7、数一数,填一填.
()条线段()个角8、图中共有个三角形.
9、数一数,图中有条线段.
10、下图中一共有个三角形.
11、观察下图,数一数图中共有条线段.
12、数一数,图中共有()个长方形.
13、下图中有多少个正方形?()
14、数一数,下图中看不见的小正方体有个.
15、下图共有个三角形.
16、图中共有个正方形.
17、下图是由一些边长相同的小正方形构成,那么,此图中的正方形共有个.
18、数一数下图中,有多少条线段?有多少个三角形?
19、数一数,图中共有()个三角形.
20、下图有个三角形.。
小学奥数 四年级奥数春季班 几何计数
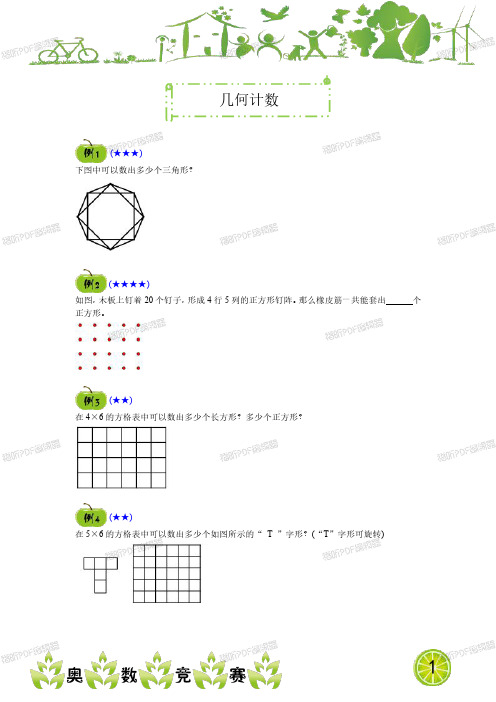
几何计数
下图中可以数出多少个三角形?
如图,木板上钉着20个钉子,形成4行5列的正方形钉阵。
那么橡皮筋一共能套出个正方形。
在4×6的方格表中可以数出多少个长方形?多少个正方形?
在5×6的方格表中可以数出多少个如图所示的“T”字形?(“T”字形可旋转) (★★★)
(★★★★)
(★★)
(★★)
下图中包含★的长方形共有多少个?
在下图中只包含一个★的长方形有多少个?
如图,用9枚钉子钉成水平和竖直间隔都为1的正方阵。
用一根橡皮筋将3枚不共线的钉子连接起来就形成一个三角形。
其中面积为1的三角形有多少个?
本讲总结
枚举法——按照大小和位置
对应法——找到对应关系
容斥原理——不重不漏
和面积相关——熟悉公式
利用图形对称性
重点例题:例4,例6,例7
(★★★)
(★★★★)
(★★★★★)。
小学四年级奥数竞赛班讲义 第41讲:几何计数
1
【例5】(★★★★) 在下图中只包含一个★的长方形有多少个?
★ ★
【例6】(★★★★) 如图,用9枚钉子钉成水平和竖直间隔都为1的正方阵。用一根橡 皮筋将3枚不共线的钉子连接起来就形成一个三角形。其中面积为 1的三角形有多少个?
【例7】(★★★★★) 图中一共有多少个三角形?
本讲总结 枚举法——按照大小和位置 对应法——找到对应关系 容斥原理——不重不漏 和面积相关——熟悉公式 利用图形对称性 重点例题:例4,例5,例6
几何计数
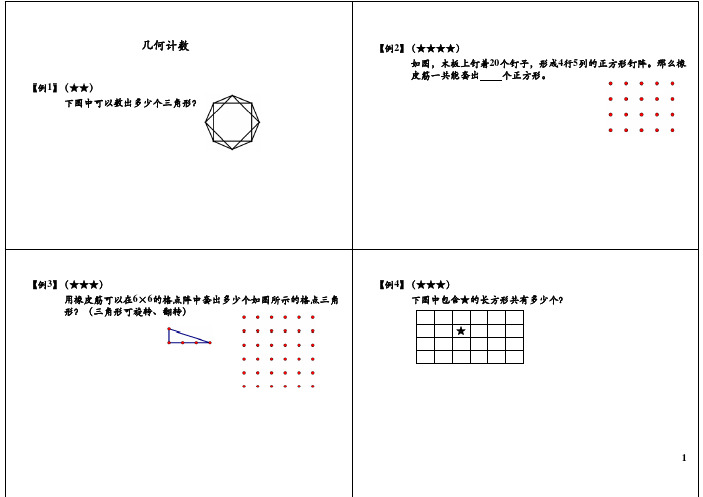
【例1】(★★) 下图中可以数出多少个三角形?
【例2】(★★★★) 如图,木板上钉着20个钉子,形成4行5列的正方形钉阵。那么橡 皮筋一共能套出 个正方形。
【例3】(★★★) 用橡皮筋可以在6×6的格点阵中套出多少个如图所示的格点三角 形?(三角形可旋转、翻转)
【例4】(★★★) 下图中包含★的长方形共有多少个?
2
奥数几何计数题库及答案

奥数几何计数题库及答案1. 题目一:一个圆的半径为5厘米,求圆内接正六边形的边长。
答案:圆内接正六边形的边长等于圆的半径。
因此,边长为5厘米。
2. 题目二:一个正方体的棱长为10厘米,求其外接球的半径。
答案:正方体的体对角线等于外接球的直径。
体对角线的长度为\(\sqrt{3} \times 10\) 厘米,所以外接球的半径为\(\frac{\sqrt{3} \times 10}{2}\) 厘米。
3. 题目三:一个圆柱的底面半径为3厘米,高为10厘米,求其侧面积。
答案:圆柱的侧面积等于底面周长乘以高,公式为 \(2\pi r\times h\)。
代入数值得 \(2\pi \times 3 \times 10 = 60\pi\) 平方厘米。
4. 题目四:一个正四面体的棱长为a厘米,求其表面积。
答案:正四面体的表面积由四个等边三角形组成,每个三角形的面积为 \(\frac{\sqrt{3}}{4}a^2\)。
因此,总表面积为 \(4 \times \frac{\sqrt{3}}{4}a^2 = \sqrt{3}a^2\) 平方厘米。
5. 题目五:一个长方体的长、宽、高分别为a、b、c厘米,求其对角线的长度。
答案:长方体的对角线长度可以通过勾股定理求得,公式为\(\sqrt{a^2 + b^2 + c^2}\) 厘米。
6. 题目六:一个圆锥的底面半径为r厘米,高为h厘米,求其体积。
答案:圆锥的体积公式为 \(\frac{1}{3}\pi r^2 h\) 立方厘米。
7. 题目七:一个球的直径为d厘米,求其表面积。
答案:球的表面积公式为 \(4\pi r^2\),其中r为半径,即\(\frac{d}{2}\) 厘米。
代入得 \(4\pi\left(\frac{d}{2}\right)^2 = \pi d^2\) 平方厘米。
8. 题目八:一个圆环的内圆半径为r1厘米,外圆半径为r2厘米,求其面积。
答案:圆环的面积等于外圆面积减去内圆面积,公式为 \(\pir2^2 - \pi r1^2\) 平方厘米。
小学奥数:几何计数(一).专项练习及答案解析
1.掌握计数常用方法;2.熟记一些计数公式及其推导方法;3.根据不同题目灵活运用计数方法进行计数.本讲主要介绍了计数的常用方法枚举法、标数法、树形图法、插板法、对应法等,并渗透分类计数和用容斥原理的计数思想.一、几何计数在几何图形中,有许多有趣的计数问题,如计算线段的条数,满足某种条件的三角形的个数,若干个图分平面所成的区域数等等.这类问题看起来似乎没有什么规律可循,但是通过认真分析,还是可以找到一些处理方法的.常用的方法有枚举法、加法原理和乘法原理法以及递推法等.n条直线最多将平面分成21223(2)2n n n++++=++……个部分;n个圆最多分平面的部分数为n(n-1)+2;n个三角形将平面最多分成3n(n-1)+2部分;n个四边形将平面最多分成4n(n-1)+2部分……在其它计数问题中,也经常用到枚举法、加法原理和乘法原理法以及递推法等.解题时需要仔细审题、综合所学知识点逐步求解.排列问题不仅与参加排列的事物有关,而且与各事物所在的先后顺序有关;组合问题与各事物所在的先后顺序无关,只与这两个组合中的元素有关.二、几何计数分类数线段:如果一条线段上有n+1个点(包括两个端点)(或含有n个“基本线段”),那么这n+1个点把这条线段一共分成的线段总数为n+(n-1)+…+2+1条数角:数角与数线段相似,线段图形中的点类似于角图形中的边.数三角形:可用数线段的方法数如右图所示的三角形(对应法),因为DE上有15条线段,每条线段的两端点与点A相连,可构成一个三角形,共有15个三角形,同样一边在BC 上的三角形也有15个,所以图中共有30个三角形.数长方形、平行四边形和正方形:一般的,对于任意长方形(平行四边形),若其横边上共有n条线段,纵边上共有m条线段,则图中共有长方形(平行四边形)mn个.模块一、简单的几何计数【例 1】七个同样的圆如右图放置,它有_______条对称轴.教学目标例题精讲知识要点7-8-1几何计数(一)【考点】简单的几何计数【难度】1星【题型】填空【关键词】迎春杯,六年级,初赛,试题【解析】如图:6条.【答案】6条【例 2】下面的表情图片中:,没有对称轴的个数为()(A) 3 (B) 4 (C) 5 (D) 6【考点】简单的几何计数【难度】2星【题型】选择【关键词】华杯赛,初赛,第1题【解析】通过观察可知,第1,2,5这三张图片是有对称轴的,其他的5张图片都没有对称轴,所以没有对称轴的个数为5,正确答案是C。
小学奥数几何图形计数习题【三篇】
小学奥数几何图形计数习题【三篇】
导读:本文小学奥数几何图形计数习题【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【第一篇】图1-69中有多少个等腰直角三角形?
解图1-69中有
5×5+4×4=41
个点.在每点标一个数,它等于以这点为直角顶点的等腰直角三角形的个数.因此,共有等腰直角三角形
4×8+5×16+6×4+10×4+8×4+11×4+16×1
=268(个)
【第二篇】(1)图1-70(a)中有多少个三角形?
(2)图1-70(b)中又有多少个三角形?
解(1)图1-70(a)中有6 条直线.一般来说,每3 条直线能围成一个三角形,但是这3
条直线如果相交于同一点,那么,它们就不能围成三角形了.【第三篇】问8条直线最多能把平面分成多少部分?。
小学奥数:几何计数一.专项练习及答案解析
7-8-1几何计数(一)教课目的掌握数常用方法;熟一些数公式及其推方法;依据不一样目灵巧运用数方法行数.本主要介了数的常用方法枚法、数法、形法、插板法、法等,并渗透分数和用容斥原理的数思想.知识重点一、几何计数在几何形中,有多风趣的数,如算段的条数,足某种条件的三角形的个数,若干个分平面所成的地区数等等.看起来仿佛没有什么律可循,可是通真分析,是能够找到一些理方法的.常用的方法有枚法、加法原理和乘法原理法以及推法等.n条直最多将平面分红223⋯⋯n(n2n2)个部分;n个2最多分平面的部分数n(n-1)+2;n个三角形将平面最多分红3n(n-1)+2部分;n个四形将平面最多分红4n(n-1)+2部分⋯⋯在其余数中,也常用到枚法、加法原理和乘法原理法以及推法等.解需要仔、合所学知点逐渐求解.摆列不与参加摆列的事物相关,并且与各事物所在的先后序相关;合与各事物所在的先后序没关,只与两个合中的元素相关.二、几何计数分类数段:假如一条段上有n+1个点(包含两个端点)(或含有n个“基本段”),那么n+1个点把条段一共分红的段数n+(n-1)+⋯+2+1条数角:数角与数段相像,段形中的点似于角形中的.数三角形:可用数段的方法数如右所示的三角形(法),因DE上有15条段,每条段的两头点与点A相,可构成一个三角形,共有15个三角形,同一在BC上的三角形也有15个,所以中共有30个三角形.数方形、平行四形和正方形:一般的,于随意方形(平行四形),若其横上共有n 条段,上共有条段,中共有方形(平行四形)个.m mn例题精讲模块一、简单的几何计数【例1】七个同的如右搁置,它有_______条称.7-8-1.几何计数(一).题库题库版page1of10【考点】简单的几何计数【难度】1星【题型】填空【重点词】迎春杯,六年级,初赛,试题【分析】如图:6条.【答案】6条【例2】下边的表情图片中:,没有对称轴的个数为()(A)3(B)4(C)5(D)6【考点】简单的几何计数【难度】2星【题型】选择【重点词】华杯赛,初赛,第1题【分析】经过观察可知,第1,2,5这三张图片是有对称轴的,其余的5张图片都没有对称轴,所以没有对称轴的个数为5,正确答案是C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1.用3根等长的火柴可以摆成一个等边三角形.如图19-1,用这样的等边三角形拼合成一个更大的等边三角形.如果这个大等边三角形昀每边由20根火柴组成,那么一共要用多少根火柴?[分析与解]把大的等边三角形分为20“层”分别计算火柴的根数:最上一“层”只用了3根火柴;从上向下数第二层用了3×2=6根火柴;从上向下数第三层用了3×3=9根火柴;……从上向下数第20层用了3×20=60根火柴.所以,总共要用火柴3×(1+2+3+…+20)=630根.【巩固提高】1.如下图,一个三角形分成36个小三角形.把每个小三角形涂上红色或蓝色,两个有公共边的小三角形要涂上不同的颜色,已知涂成红色的三角形比涂成蓝色的三角形多,那么多_____个.2.右图是由小立方体码放起来的,其中有一些小方体看不见.图中共有_____个小立方体.3.数一数,下图是由_____个小立方体堆成的.要注意那些看不见的.例2.如图19-2,用长短相同的火柴棍摆成3×1996的方格网,其中每个小方格的边都由一根火柴棍组成,那么一共需用多少根火柴棍?[分析与解]横放需1996×4根,竖放需1997×3根,共需1996×4+1997×3=13975根.【巩固与提高】1.如图下图是一个4×328的长方形,每个小正方形的边长为1厘米,请你计算这个图形中所有线段的长度之和是多少?例3.图19-3是一个跳棋棋盘,请你计算出棋盘上共有多少个棋孔?[分析与解]把棋盘分割成一个平行四边形和四个小三角形,如下图.平行四边形中棋孔数为9×9=81,每个小三角形中有10个棋孔,所以棋孔共有81+10×4=121个.或直接数出有121个.例4.如图19-4,在桌面上,用6个边长为l的正三角形可以拼成一个边长为1的正六边形.如果在桌面上要拼出一个边长为6的正六边形,那么,需要边长为1的正三角形多少个?[分析与解]如图AB=6,组成△AOB需要边长为1的正三角形共:1+3+5+7+9+11=36个,而拼成边长为6的正六边形需要6个△AOB,因此总共需要边长为1的正三角形36×6=216个.【巩固提高】如图一个正六边形,每条边上均与分布着998个点(不包括两个端点),分别连接不相邻的两条边上相互对应的两点,这样就把这个六边形分割成多个等边三角形,请问可以分割出多少个等边三角形?例5.如图19-5,其中的每条线段都是水平的或竖直的,边界上各条线段的长度依次为5厘米、7厘米、9厘米、2厘米和4厘米、6厘米、5厘米、1厘米.求图中长方形的个数,以及所有长方形面积的和.[分析与解]确定好长方形的长和宽,长方形就唯一确定,而图中只需确定好横向线段,竖向线段,即可.于是横向线段有(1+2+3+4)=10种选法,竖向线段也有(1+2+3+4)=10种选法,则共有10×10=100个长方形.这些长方形的面积和为:(5+7+9+2+12+16+11+21+18+23)×(4+6+5+1+10+11+6+15+12+16)=124×86=10664(平方厘米).例6.如图19-6,18个边长相等的正方形组成了一个3×6的方格表,其中包含“*”的长方形及正方形共有多少个?[分析与解]我们把所求的长、正方形按占有的行数分为三类,每类的长、正方形的个数相等.其中只占有下面一行的有如下12种情况:于是共有12×3=36个正、长方形包含“*”.【巩固提高】1.下图中长方形(包括正方形)总个数是_____.2.如图19-10,AB,CD,EF,MN互相平行,则图中梯形个数与三角形个数的差是多少?[分析与解]图中共有三角形(1+2+3+4)×4=40个,梯形(1+2+3+4)×(1+2+4)=60个,梯形比三角形多60-40=20个.例7.图19-7是由若干个相同的小正方形组成的.那么,其中共有各种大小的正方形多少个?[分析与解]每个4×4正方形中有:边长为1的正方形4×4个;边长为2的正方形3×3个;边长为3的正方形2×2个,边长为4的正方形1×1个.总共有4×4+3×3+2×2+1×1=30个正方形.现在5个4×4的正方形,它们重叠部分是4个2×2的正方形.因此,图中正方形的个数是30×5-5×4=130.例8.图19-8中共有多少个三角形?[分析与解]边长为1的正三角形,有16个.边长为2的正三角形,尖向上的有3个,尖向下的也有3个.因此共有16+3+3=22个.例9.图19-9是由18个大小相同的小正三角形拼成的四边形,其中某些相邻的小正三角形可以拼成较大的正三角形.那么,图中包含“*”的各种大小的正三角形一共有多少个?[分析与解]设小正三角形的边长为1,分三类计算计数包含*的三角形中,边长为1的正三角形有1个;边长为2的正三角形有4个,边长为3的正三角形有1个;因此,图中包含“*”的所有大、小正三角形一共有1+4+1=6个.【巩固提高】1.图形中有_____个三角形.2.下图中共有_____个正方形.例10.在图19-1l中,共有多少个不同的三角形?[分析与解]下图中共有35个三角形,两个叠加成题中图形时,又多出5+5×2=15个三角形,共计35×2+15=85个三角形.【巩固提高】在下图中有多少条线段,有多少个三角形?例11.如图19-12,一块木板上有13枚钉子.用橡皮筋套住其中的几枚钉子,可以构成三角形、正方形、梯形等等,如图19-13.那么,一共可以构成多少个不同的正方形?[分析与解]按正方形的面积分类,设最小的正方形面积为1,面积为1的正方形有5个,如图a所示;面积为2的正方形有4个,如图b所示;面积为4的正方形有1个,如图c所示;还有1个面积比4大的正方形,如图d所示;于是,一共可以构成5+4+1+1=11个不同的正方形.【巩固提高】1.如下图,方格纸上放了20枚棋子,以棋子为顶点的正方形共有_____个.3.如图19-14,用9枚钉子钉成水平和竖直间隔都为1厘米的正方阵.用一根橡皮筋将3枚不共线的钉子连结起来就形成一个三角形.在这样得到的三角形中,面积等于1平方厘米的三角形共有多少个?[分析与解]我们分三种情况来找面积为1平方厘米的三角形,这些三角形的底与高分别为1厘米或2厘米,利用正方形的对称性:(1)等腰直角三角形,如下图a所示有△AOC,△COE,△EOG,△GOA,△BOH,△DFB,△FHD,△HBF,共计8个,其中以AC,CF,FG,GA为底的各一个,以BF,DH为底的各两个.(2)直角三角形,如图b所示有△ACH,△CHD,△ACD,△DHA,△BEF,△BCE,△CEF,△CFB,△DEG,△DGH,△EGH,△EHD,△GAB,△GBF,△FAB,△FGA,共计16个,其中以AD、CH、BE、CF、DG、EH、FA、GB为斜边的各两个.(3)钝角三角形,如图c所示有△ABE,△AHE,△ADE,△AFE,△CBG,△CFG,△CDG,△CHG共计8个,其中以AE、CG为边的各四个.于是,综上所述,共有面积为1平方厘米的三角形32个.例12.如图19-15,木板上钉着12枚钉子,排成三行四列的长方阵.那么用橡皮筋共可套出多少个不同的三角形?[分析与解]我们先任意选取三个点,那么第1个点有12个位置可以选择,第2个点有11个位置可以选择,第3个点有10个位置可以选择,但是每6种选法对应的都是同一个图形,如下图,ABC,ACB,BAC,BCA,CAB,CBA 均是同一个图形.所以有12×11×10÷6=220种选法,但是如果这3点在同一条直线上就无法构成三角形,其中每行有4种情况,共3×4;每列有1种情况,共1×4;2个边长为2的正方形的4条对角线,共4种情况.所以,可以套出220-3×4-1×4-4=200个不同的三角形.【巩固提高】1.下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的3个点为顶点,可以构成三角形.在这些三角形中,与阴影三角形有同样大小面积的有多少个?例13.如图19-16,正方形ACEG的边界上有A,B,C,D,E,F,G这7个点,其中B,D,F分别在边AC,CE,EG上.以这7个点中的4个点为顶点组成的不同四边形的个数等于多少?[分析与解]如果暂时不考虑点之间的排列位置关系,从7个点中任取4个点,则第一个点有7个位置可选,第二个点有6个位置可选,第三个点有5个位置可选,第四个点有4个位置可选,而不考虑先后,那么有4×3×2×1=24种选法的实质是一样的,所有可能的组合数目应该是(7×6×5×4)÷24=35.我们只要从中减去不能构成四边形的情形.对图19-16而言,任取4个点而又不构成四边形的情形只能发生在所取的4个点中有3个来自正方形ACEG的一条边,而另一个则任意选取的时候,例如选定A、B、C3点,第4个点无论如何选取都不能构成四边形.正方形的4条边中有3条都存在这样的情况.而每次这种情况发生时,第4个顶点的选取有4种可能.所取的顶点只有4个,因此不可能出现同时选择了2条有3点共线的边的情况.那么需要排除的情况有4×3=12种.所以,满足题意的四边形个数有35-12=23个.【巩固提高】如下图,在三角形AFJ的边界上有A,B,C,……J,K,L共12个点,以这12个点中的3个点位顶点的三角形共有多少个?。
